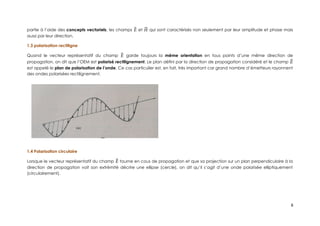
Le document présente un cours sur la physique des ondes électromagnétiques, couvrant des concepts fondamentaux tels que les équations de Maxwell, la propagation des ondes et les caractéristiques des antennes. Les chapitres incluent des notions de base en physique, les opérateurs mathématiques utilisés dans ce domaine, et des détails sur la propagation en espace libre diélectrique. L'objectif principal est d'acquérir des connaissances fondamentales sur les interactions des champs électriques et magnétiques dans divers milieux.

1. Institut National des Postes, des Technologies de l’Information et de la Communication
Département MTIC
Laboratoire des Transmissions
PHYSIQUE APPLIQUEE
Formateur : MOULOUNGUI Cyr Aime
Tel : 062 97 02 97
Inspecteur des Télécommunications
1

2. Objectifs du cours
 Acquérir les connaissances de bases de la physique dans le domaine des ondes électromagnétiques.
 Acquérir les connaissances de bases d’établissement des équations de bilan de liaison Hertziennes.
Programme du cours
Chapitre 1 : Notions fondamentales
1. Coordonnées cartésiennes
2. Operateur gradient
3. Operateur divergence
4. Operateur Rotationnelle
5. Operateur Laplacien
Chapitre 2 : Propagation des ondes électromagnétiques en espace libre diélectrique.
1. Phénomène de propagation
2. Milieu de propagation
3. Les équations de Maxwell
4. Equation de propagation des Ondes électromagnétique en espace libre diélectrique.
5. Propriété des ondes électromagnétiques
6. Puissance transportée par une onde électromagnétique
Chapitre 3 : Les antennes
1. Caractéristiques des antennes
2. Diagramme de rayonnement
2

3. 3. Puissance isotrope rayonnée équivalente
Chapitre 4 : Propagation des ondes Hertzienne
1. Caractéristiques électriques de l’atmosphère
2. Absorption et diffusion par l’eau et les gaz.
3. Influence de l’ionosphère
4. La diffraction par le sol.
5. Bilan de liaison Hertzienne
3

4. Chapitre 1 : Notions fondamentales
1- COORDONNEES CARTESIENNES
4
Dans un repère orthonormé direct (o, ux, uy, uz) un point de
l’espace est représenté par ses coordonnées cartésiennes (x, y,
z). Le vecteur position du point M s’écrit
⃗
OM=x⃗
ux + y ⃗
uy + z ⃗
uz
Lorsque les coordonnées x, y ou z du point M subissent une
variation élémentaire dx, dy ou dz, le point M se déplace
respectivement de dx ⃗
ux , dy ⃗
uy ou dz ⃗
uz
Ainsi le volume dV est un parallélépipède rectangle d’arrête dx,
dy et dz alors
dV = dx dy dz

5. 2- OPERATEUR GRADIENT
Le gradient est un vecteur obtenu à partir d’un champ de scalaires. Dans un système de coordonnées donne, chaque
composante du gradient correspond à une dérivation par rapport à la coordonnée d’espace correspondante.
3- OPERATEUR DIVERGENCE
La divergence est un scalaire obtenu à partir d’un champ de vecteur. Chaque terme correspond à une dérivation de l’une des
composantes du vecteur par rapport à la coordonnée d’espace correspondante.
4- OPERATEUR ROTATIONNEL
Le rotationnel est un vecteur obtenu à partir d’un champ de vecteurs. Chaque composante du rotationnel correspond à des
dérivations par rapport aux autres coordonnées d’espaces.
Dans l’espace, si le champ de vecteur est uniforme son rotationnelle reste nul. Qualitativement, on peut dire qu’un champ de
vecteurs a rotationnelle non nul tourne ou tends à faire tourner les objets à l’action de ce champ.
5
Un fort gradient signifie de fortes variations de valeurs du
champ sur de courtes distances.
Physiquement, si la divergence d’un champ de vecteurs est non nulle
en un point, alors il existe une source de champ en ce point.

6. 5- OPERATEUR LAPLACIEN
Le Laplacien est un opérateur de dérivation spatiale qui peut s’appliquer à un champ scalaire ou à un champ de vecteurs
L’expression du Laplacien d’un champ scalaire est
L’expression du Laplacien d’un champ de vecteur est
Chapitre 2 : PROPAGATION DES ONDES ELECTROMAGNETIQUES
1- PHENOMENE DE PROPAGATION
Considérons un émetteur E ; son élément rayonnant est constitué par une antenne qui envoie dans l’espace une onde
électromagnétique (OEM). Cette OEM, qui est composée d’un champ électrique E et d’un champ magnétique H, gagne de
proche en proche tout le milieu ambiant.
6

7. Intéressons-nous à la propagation suivant une direction P. L’espace étant rapporté à un repère (O x y z). (Oz) est de même
direction et de même sens que (OP) ; par conséquent, les axes (Ox) et (Oy) sont perpendiculaires à la direction de propagation.
Une onde émise à l’instant t0 est en M à l’instant t et en M
'
à l’instant t
'
. C’est ce phénomène qui constitue la propagation de
l’OEM considérée selon l’expérience de HERTZ en 1880.
1.1 Surface d’onde
Le lieu des points de l’espace atteints à un instant t par une OEM émise à un instant antérieur t0 est constitué par une surface dite
surface d’onde. Comme il y a le même intervalle de temps Δt=t−t0 entre l’instant d’émission t0 et l’instant t où l’un quelconque
des ponts de cette surface a été atteint, une telle surface est, par définition, une surface équiphasse.
Dans le cas particulier où le milieu de propagation est homogène et isotrope, la vitesse de propagation est la même dans toutes
les directions. Il en résulte que les surfaces d’ondes sont des sphères contrées sur l’émetteur, de rayond=v(t−t0), v étant la vitesse
de propagation des OEM dans le milieu considéré.
Dans ce cas également, l’affaiblissement subi par l’OEM est identique quelle que soit la direction de considérée. On pourrait donc
penser que ces surfaces d’ondes sphériques sont aussi des surfaces équiamplitudes. Il faudrait, pour cela que l’émetteur considéré
soit omnidirectionnel, c’est – à-dire qu’il rayonne de façon identique dans toutes les directions de l’espace. Or nous savons qu’un
tel émetteur (source isotrope) n’est qu’une vue de l’esprit et qu’en pratique, les émetteurs utilisés sont, aux mieux omnidirectionnels
dans un certain plan.
1.2 Caractère vectoriel du rayonnement
Les champs ⃗
E et ⃗
H sont caractérisés par leur amplitude et leur phase.
Nous venons de parler de l’amplitude et de la phase de l’onde, au sujet des champs ⃗
E et ⃗
H qui le constituent. Il ne faut pas oublier
la troisième caractéristique de ces champs qui est leur direction. C’est en cela que réside le caractère vectoriel du rayonnement
électromagnétique et c’est ce qui différencie fondamentalement l’étude des OEM de celle des lignes (raisonnement à partir des
concepts scalaires, la tension et le courant qui sont caractérisés par leur amplitude et leur phase). Nous raisonnerons dans cette
7

8. partie à l’aide des concepts vectoriels, les champs ⃗
E et ⃗
H qui sont caractérisés non seulement par leur amplitude et phase mais
aussi par leur direction.
1.3 polarisation rectiligne
Quand le vecteur représentatif du champ ⃗
E garde toujours la même orientation en tous points d’une même direction de
propagation, on dit que l’OEM est polarisé rectilignement. Le plan défini par la direction de propagation considéré et le champ ⃗
E
est appelé le plan de polarisation de l’onde. Ce cas particulier est, en fait, très important car grand nombre d’émetteurs rayonnent
des ondes polarisées rectilignement.
1.4 Polarisation circulaire
Lorsque le vecteur représentatif du champ ⃗
E tourne en cous de propagation et que sa projection sur un plan perpendiculaire à la
direction de propagation voit son extrémité décrire une ellipse (cercle), on dit qu’il s’agit d’une onde polarisée elliptiquement
(circulairement).
8

9. Une onde est dite elliptique lorsque les composantes du champ électrique, Ex et Ey tout en restant sinusoïdales et de même
fréquence, ne sont pas en phase.
Un cas particulier de déphasage
π
2
donne les équations :
Ex=E1.cos(ωt−kz)
Ey=E2.cos(ωt−kz+
π
2 )
(Ex)²
(E1)²
+
(Ey)²
(E2)²
=1;Equation d’une ellipse
La polarisation est dite circulaire si de plus, les amplitudes sont égales E1 = E2
(Ex)²+(Ey)²=E1²Equation d’un cercle.
Le sens de la polarisation est donné par le signe du déphasage :
9

10. +π
2
Ellipse tourne à gauche (polarisation circulaire gauche)
−π
2
Ellipse tourne à droite (Polarisation circulaire droite)
C’est un cas de polarisation que l’on rencontre assez fréquemment pour les télécommunications spatiales ou pour le radar, en
ondes métriques et inférieures.
1.5 L’onde plane
Dans le cas où la distance d est très grande devant la longueur d’onde, on peut confondre localement la surface d’onde
sphérique avec son plan tangent et considérer que l’on a à faire à une surface d’onde plane (plan d’onde) perpendiculaire à Oz
et parallèle à xoy. D’où le nom souvent employé d’onde planes.
Si enfin nous nous intéressons à une OEM polarisée rectilignement, ⃗
E et ⃗
H ont la même direction en tous les points du plan d’onde.
Nous pouvons dire qu’à un instant donné le champ électrique ⃗
E et le champ magnétique ⃗
H ont les mêmes valeurs en tous les
points du plan d’onde. Cela implique que ⃗
E et ⃗
H ne dépendent ni de x, ni de y ; ils sont uniquement fonction de z et de t, il en
résulte que :
∂⃗
E
∂ x
=0;
∂⃗
E
∂ y
=0;
∂⃗
H
∂ x
=0;
∂⃗
H
∂ y
=0.
2- MILIEUX DE PROPAGATION
Un milieu de propagation est caractérisé par :
 Sa constante diélectrique ou permittivité électrique ε (F/m)
 Sa perméabilité magnétique μ (H/m)
 Sa conductivité σ (Ω
−1
/m)
3- LES EQUATIONS DE MAXWELL
10

11. Il s’agit d’un groupe d’équations faisant intervenir les six composantesEx,Ey,Ez et H x, H y,H z des champs électriques et
magnétiques, la constante diélectrique ε, la perméabilité magnétique μ et la conductivité électrique σ du milieu considéré.
MAXWELL les a établies en 1860 en généralisant, aux régimes variables au cours du temps, les résultats précédemment obtenus,
dans le cas des régimes indépendants du temps par FARADAY, AMPERE et GAUSS.
3.1 Notion de champ électrique généré par une charge (Maxwell-Gauss)
Une charge électrique génère un champ électrique autour d’elle.
Le flux électrique sortant d’une surface est proportionnel à la charge électrique qui s’y trouve.
div⃗
E=
τ
ε
; ou ⃗
∇.⃗
E ¿
∂Ex
∂x
+
∂ Ey
∂ y
+
∂Ez
∂z
=
τ
ε
(τ, densité volumique de charges électriques)
3.2 Notion de champ magnétique généré par un aimant (Maxwell-Flux)
Il est impossible de séparer les pôles Nord et Sud d’un aimant
Le flux magnétique à travers une surface vaut toujours zéro (0). Les lignes de champ d’un aimant reviennent toujours sur elle-
même. Ce qui sort d’une surface revient également.
div⃗
H=0 ; ou ⃗
∇.⃗
H=
∂ Hx
∂ x
+
∂ H y
∂ y
+
∂ H z
∂z
=0
3.3 Induction électrique (Maxwell-Faraday)
Si on fait varier le flux magnétique dans un circuit cela provoque un courant électrique dans ce circuit.
C’est le fonctionnement des alternateurs, des dynamos qui consiste à faire bouger un aimant près d’un circuit pour générer un
courant dans le circuit.
11

12. −μ
∂H x
∂t
=
∂ Ez
∂ y
−
∂Ey
∂z
−μ
∂H y
∂t
=
∂ Ex
∂ z
−
∂ Ez
∂x
−μ
∂H z
∂t
=
∂Ey
∂ x
−
∂Ex
∂ y
3.4 Induction magnétique (Maxwell-Ampère)
Un courant provoque un champ magnétique.
Un fil parcouru par un courant génère un champ magnétique autour de lui perpendiculaire au courant dont le sens est déterminé
par la règle de la main droite.
C’est grâce à ce phénomène que l’on fabrique des électroaimants
σ Ex+ε
∂Ex
∂t
=
∂H z
∂ y
−
∂H y
∂ z
σ Ey+ε
∂ Ey
∂t
=
∂ Hx
∂ z
−
∂ Hz
∂ x
σ Ez+ε
∂ Ez
∂t
=
∂ H y
∂ x
−
∂ Hx
∂ y
4- OPERATEUR NABLA
12
r ⃗
ot ⃗
E ou⃗
∇∧⃗
E=−μ
∂⃗
H
∂t
r ⃗
ot ⃗
H ou ⃗
∇∧⃗
H=σ ⃗
E+ε
∂⃗
E
∂t

13. L’opérateur Nabla est un vecteur dont les composantes sont les dérivées partielles par rapport à la coordonnée concernée.
Important : Grace a l’opérateur Nabla on peut trouver simplement de composition de divers operateurs par exemple le laplacien
d’un champ scalaire. =
13
Lorsqu’on applique
l’opérateur Nabla a un
champ de scalaires par
lequel il est multiplié, on
retrouve l’opérateur
gradient
Lorsqu’on applique l’opérateur Nabla
a un champ de vecteur, la
multiplication peut être un produit
scalaire, on retrouve l’opérateur
divergence
Lorsqu’on applique l’opérateur Nabla
a un champ de vecteur, la
multiplication peut être un produit
vectoriel, on retrouve l’opérateur
rotationnelle

14. Ou le laplacien d’un champ vectoriel.
5- EQUATIONS DE PROPAGATION DES OEM EN ESPACE LIBRE DIELECTRIQUE
4.1 Diélectrique parfait (vide)
Dans ce cas σ=0 etτ=0, propriétés dont nous tenons compte pour établir l’équation de propagation du champ⃗
E.
On sait que ∆ ⃗
E ¿ gr ⃗
ad(¿⃗
E)−¿ r ⃗
ot r ⃗
ot(⃗
E)
On a r ⃗
ot r ⃗
ot ¿ donc r ⃗
ot r ⃗
ot ¿ car σ=0
or r ⃗
ot r ⃗
ot ⃗
E=gr ⃗
ad (¿⃗
E)−∆⃗
E
Comme¿⃗
E=0 car τ=0 il nous reste donc : ∆ ⃗
E−ε μ
∂
2
⃗
E
∂t
2
=0
En partant de l’autre relation, nous établirons de même l’équation de propagation du champ ⃗
H:
∆⃗
H −ε μ
∂2
⃗
H
∂t2
=0
14

15. L’étude de cette équation de propagation montre que :
1
√ε μ
est la vitesse de propagation de l’OEM.
- Dans un milieu diélectrique pur : v=
1
√ε μ
ε est la constante diélectrique absolue et μ la perméabilité magnétique absolue du milieu considéré.
- Dans le vide ou dans l’air :
ε=ε0=
1
36π .10
9
(F/m) ; μ=μ0=4π 10−7
(H /m)
c=
1
√ε0 μ0
=3.108
m/s
Comme ε=εr ε0 et μ=μr μ0 (εr et μr étant la constante diélectrique relative et la perméabilité magnétique relative du milieu
considéré).
v=
1
√ε0 μ0
1
√εr μr
=
c
√εr μr
Dans la plupart des cas : μr=1; donc v=
c
√εr
n=√εr est appelé indice de réfraction du milieu.
Pour un diélectrique parfait, la solution de l’équation de propagation est, en régime sinusoïdal :
⃗
E=⃗
E0 e
iω(t−
z
v )
15

16. Pour une propagation se faisant selon l’axe des z, on peut également l’écrire :
⃗
E=⃗
E0 ei(ωt−kz)
en introduisant le paramètre de propagation k=
ω
v
=
2π
λ
6- PROPRIETES DES OEM SE PROPAGEANT EN ESPACE LIBRE DIELECTRIQUE
Soit une onde plane, à polarisation rectiligne, se propageant vers les z positifs. A un instant donné, Eet H ont les mêmes valeurs en
tout point du plan d’onde, c’est – à –dire ∀ x et y.
Donc
∂⃗
E
∂ x
=0 ;
∂⃗
H
∂ y
=0
Par conséquent l’équation devient :
∂
2
⃗
E
∂z
2
−
1
v
2
∂
2
⃗
E
∂t
2
=0
La propagation se faisant vers les z positifs, une telle relation admet, en régime sinusoïdal, une solution de la forme :
⃗
E=⃗
E0 cosω(t−
z
v ) dans laquelle ⃗
E0 est un vecteur constant ∀( x, y ,z ,t)
6.1 ⃗
E et ⃗
H sont perpendiculaires à la direction de propagation
Comme
∂Ex
∂x
=
∂Ey
∂ y
=0 la relation
∂Ex
∂x
+
∂ Ey
∂ y
+
∂Ez
∂z
=0 devient
∂Ez
∂ z
=0
Alors :
ω
v
Eoz sinω(t−
z
v )=0 et Eoz =0
16

17. On remarque que l’OEM n’a aucune composante selon la direction de propagation. On dit que c’est une onde transversale
électromagnétique dont les composantes sont :
Ex=Eox cosω(t−
z
v )
Ey=Eoy cosω(t−
z
v )
6.2 ⃗
E et ⃗
H sont perpendiculaires entre eux
Les axes (0x) et (0y) étant dans le plan d’onde, nous avons toujours le droit de choisir (0x) de telle sorte que E0 soit porté par cet
axe. Le champ électrique ⃗
E est alors, en tout point, parallèle à (0x) puisque l’onde est polarisée rectilignement. Nous avons alors :
⃗
E=E0 cosω(t−
z
v )⃗
x
Ce champ électrique est accompagné d’un champ magnétique.
⃗
H=
E0
μv
cosω(t−
z
v )⃗
y
Par conséquent ⃗
E et ⃗
H sont perpendiculaires entre eux. Pour une OEM se déplaçant en espace libre diélectrique, cette propriété
est tout à fait générale ; on l’exprime par la relation : ⃗
E .⃗
H=0
6.3 Relation d’amplitude et de phase entre ⃗
E et ⃗
H
17

18. En posant H0=
E0
μv
, nous avons :
⃗
E=E0 cosω(t−
z
v )⃗
x
⃗
H=H 0cos ω(t−
z
v )⃗
y
⃗
E et ⃗
H sont donc en phases dans le temps et le rapport de leurs amplitudes est :
E0
H0
=μ v=μ
1
√εμ
=
√μ
ε
(Ω)
Cette quantité est appelée l’impédance d’onde du milieu diélectrique considérée.
Dans le cas du vide ou de l’air :
√μ
ε
=
√μ0
ε0
=120π=376,6Ω
7- PUISSANCE TRANSPORTEE PAR UNE OEM PLANE
7.1 L’énergie électromagnétique
En régime indépendant du temps, nous savons que la densité d’énergie électromagnétique renfermée dans un élément de
volume diélectriquedV , soumis à un champ électrique ⃗
E , se compose :
 D’une énergie électrique : (ε E
2
2 )dV en joule/m3
18

19.  D’une énergie magnétique : (μ H
2
2 )dV en joule/m3
 L’énergie totale est donc :
ε E
2
+μ H
2
2
dV en joule/m3
NB : En régime variable au cours du temps, l’expression qui vient d’être écrite reste valable, à condition de considérer qu’elle
représente l’Energie instantanée contenue à l’intérieur du volume dV. Elle se calcule en tenant compte des valeurs de ⃗
E et ⃗
H
a l’instant considéré qui sont donnée par :
⃗
E=E0 cosω(t−
z
v )
⃗
H=H 0cos ω(t−
z
v )
Comme nous avons montré que √ε E0=√μ H0 , les deux formes d’énergie sont égales. Donc l’énergie électromagnétique
contenue dans le volume diélectrique dV à un instant t est donnée par :
dW =
ε E2
+μ H2
2
dV=ε E2
dV =μ H2
dV
7.2 La densité de puissance instantanée
a) Une OEM se propageant selon la direction oz et constituée :
 d’un champ ⃗
E (Ex ,0,0) avec Ex=E0 cosω(t−
z
v )
19

20.  d’un champ ⃗
H (0, Hy ,0) avec H y=H 0cos ω(t−
z
v )
Soit un élément de volumedV , de section unité u et de hauteur dz:
dW =ε E
2
udz=√ε E√μH uv dt=Ex H y udt
La puissance instantanée par unité de surface ou densité de puissance transportée par cette onde est :
p=
1
u
dW
dt
=Ex H y
b) Traitons maintenant le cas général d’une onde dont la direction de propagation ne coïncide pas avec l’axe des z. Elle est
constituée d’un champ ⃗
E(Ex , Ey , Ez) et d’un champ⃗
H (Hx , H y , H z).
L’énergie électromagnétique instantanée contenue dans un volume V est :
W =
1
2
∫
0
v
|ε (E)2
+μ(H)2
|dV
La puissance instantanée est :
dW
dt
=∫
0
v
(εE
∂ E
∂t
+μH
∂ H
∂t )dV
Compte tenu des équations de MAXWELL :
ε ⃗
E
∂⃗
E
∂t
+μ⃗
H
∂⃗
H
∂t
=⃗
Er ⃗
ot ⃗
H −⃗
H r ⃗
ot ⃗
E=−¿(⃗
E∧⃗
H )
20

21. Donc :
dW
dt
=−∫
v
¿(⃗
E∧⃗
H )dV=−∫
S
(⃗
E∧⃗
H ).⃗
ndS
(⃗
E∧⃗
H ).⃗
ndS a les dimensions d’une puissance (W ),
dW
dt
représente donc la puissance instantanée sortant du volume V, limité par
la surface S, par unité de temps.
Le vecteur ⃗
P=⃗
E∧⃗
H appelé vecteur de POYNTING, est la densité de puissance instantanée(w/m
2
).
Remarque : Le trièdre formé par ⃗
E , ⃗
H et ⃗
P est de sens direct. ⃗
E et ⃗
H étant perpendiculaires à la direction de propagation, ⃗
P est
dirigé selon cette direction de propagation.
21

22. Bibliographie : Transmission dans les lignes et dans l’espace Lignes, Dunod Université 1998
22