Ce document aborde les concepts fondamentaux de l'électromagnétisme et de la transmission des ondes, comprenant les champs électromagnétiques, les lois de Maxwell, et l'analyse des ondes dans divers milieux. Il est structuré en chapitres couvrant les champs, les matériaux, et les applications associées, tout en identifiant clairement les vecteurs et phaseurs dans les formules. L'auteur exprime également sa gratitude envers un contributeur pour la qualité des figures présentées.





















 ∆y + [Fz ](x,y+∆y) ∆z − [Fy ](x,z+∆z)∆y − [Fz ](x,y) ∆z (1.27)
abcda
F · dl = [Fz ](x,y) ∆z + [Fx ](y,z+∆z) ∆x − [Fz ](x+∆x,y) ∆z − [Fx ](y,z) ∆x (1.28)
adef a
F · dl = [Fx ](y,z) ∆x + [Fy ](x+∆x,z)∆y − [Fx ](y+∆y,z) ∆x − [Fy ](x,z) ∆y (1.29)
af gba
D’autre part, on a respectivement avec la partie droite :
G · dS = [Gx ](x,y,z) ∆y∆z (1.30)
S[abcd]
G · dS = [Gy ](x,y,z) ∆z∆x (1.31)
S[adef ]
G · dS = [Gz ](x,y,z) ∆x∆y (1.32)
S[af gb]
En r´unissant les ´quations qui vont ensemble (par exemple (1.27) avec (1.30) et ainsi de
e e
suite), on trouve que :
∆[Fz ](x,y) ∆[Fy ](x,z)
− = [Gx ](x,y,z) (1.33)
∆y ∆z
∆[Fx ](y,z) ∆[Fz ](x,y)
− = [Gy ](x,y,z) (1.34)
∆z ∆x
∆[Fy ](x,z) ∆[Fx ](y,z)
− = [Gz ](x,y,z) (1.35)
∆x ∆y
Avec des parcours infinit´simaux, il est facile de voir que les trois expressions ci-dessus
e
correspondent ` :
a
∇×F = G (1.36)](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-22-320.jpg)
 ∆y∆z (1.38)
[adcb]
F · dS = [Fx ](x+∆x) ∆y∆z (1.39)
[hef g]
F · dS = −[Fy ](y) ∆z∆x (1.40)
[af ed]
F · dS = [Fy ](y+∆y) ∆z∆x (1.41)
[hgbc]
F · dS = −[Fz ](z) ∆x∆y (1.42)
[abgf ]
F · dS = [Fz ](z+∆z) ∆x∆y . (1.43)
[hcde]
Le cˆt´ droit de (1.37) donne simplement g∆x∆y∆z d’o` :
oe u
∆Fx ∆Fy ∆Fz
+ + = g. (1.44)
∆x ∆y ∆z
Avec un volume infinit´simal, le terme de gauche de l’´quation ci-dessus est la divergence
e e
de F donc :
∇·F = g (1.45)
Cette derni`re expression est ce qui ressort du th´or`me de Green. En effet, en com-
e e e
parant (1.25) et (1.37), on s’aper¸oit tr`s vite que (1.45) d´coule naturellement.
c e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-23-320.jpg)




 = [E 1 ](0,0,1) + [E 2 ](0,0,1)
12πǫo (2ax + az ) 4πǫo (−ax + az )
= √ − √
4πǫo (5) 5 4πǫo (2) 2
= (0.5367ax + 0.2683ay ) − (−0.3536ax + 0.3536ay )
= 0.8902ax − 0.0852az
= 0.8943(0.9954ax − 0.0953az ) V/m
On remarque que le champ ´lectrique pointe en s’´loignant de la charge posi-
e e
tive. Les lignes de champ ´lectrique partent toujours de la charge positive vers
e
la charge n´gative selon la convention utilis´e.
e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-28-320.jpg)
 = [dE](0,0,z)
dQk
= a
2 k
4πǫo Rk
o` :
u
Q
dQ = ρl (rdφ) = rdφ .
2πr
Par des consid´rations de sym´trie, on remarque que chaque segment infi-
e e
◦
nit´simal et son oppos´ de 180 sur l’anneau, donneront un champ ´lectrique
e e e
dont la seule composante non-nulle sera Ez . Or cette composante s’obtient
comme suit :
2π Q 2π
2πr
rdφ Q 1
[E](0,0,z) = 2
cos αk az = 2
cos αk dφ az
0 4πǫo Rk 0 4πǫo Rk 2π
2π
Qz 1
= 2 + z 2 )3/2 2π
dφ az
4πǫo (r 0
Qz
= a .
2 + z 2 )3/2 z
4πǫo (r](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-29-320.jpg)
 = [dE](0,0,z)
0
∞
ρs 2πrdr z
= az
0 4πǫo (r 2 + z 2 )3/2
ρs z ∞ r
= dr az
2ǫo 0 (r 2 + z 2 )3/2
∞
√ −1
r 2 +z 2 0
ρs z
= az .
2ǫo |z|
Finalement, on observe que le champ ´lectrique a une amplitude ind´pendante
e e
de z car il vaut ρs /2ǫo partout. De plus, il est toujours orient´ selon la normale
e
a
` la feuille de part et d’autre de l’axe z.
2.3 Champ d’induction magn´tique statique
e
La loi d’Amp`re concerne les forces produites par des courants I1 et I2 circulant dans
e
des fils comme sur la figure 2.7 ; ce sont les forces magn´tiques. Un peu comme pour
e
l’´lectricit´, les observations des exp´riences d’Amp`re confirment que :
e e e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-30-320.jpg)


 =
4π R2
µI dz sin α
= aφ
4πR2
µIr dz
= aφ
4π(z 2 + r 2 )3/2](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-33-320.jpg)
 = [dB](r,φ,0)
−∞
∞
µIr z
= √ aφ
4π r 2 z2 + r2
−∞
µI
= aφ .
2πr
Le calcul du champ d’induction fait dans l’exemple pr´c´dent assume un courant
e e
“filiforme” i.e. un courant qui se d´place le long d’un fil infiniment mince. Il existe deux
e
autres types de distributions de courant moins localis´es :
e
• Le courant de surface qui circule sur une ´paisseur infime a la surface d’un corps
e `
– souvent conducteur – est comparable ` l’eau de pluie qui tombe en bordure d’un
a
toit lors d’une averse. On lui associe une densit´ de courant de surface J s exprim´e
e e
en A/m.
• Le courant de volume passant au travers une section se compare a la pluie qui
`
passe par une ouverture. La densit´ de courant volumique, ou simplement densit´
e e
2
de courant, J est en A/m .
On remarque que les densit´s de courant sont des quantit´s vectorielles qui pointent
e e
dans la direction du mouvement des charges (positives) produisant le courant. L’int´gration
e
le long d’un parcours perpendiculaire ` la direction de J s donne le courant total I ; de
a
mˆme que l’int´gration sur une surface perpendiculaire ` J . Si le parcours ou la surface
e e a
n’est pas perpendiculaire en tout point, il faudra en tenir compte par le biais du cosinus
du changement d’angle. Par exemple, le courant I pour les cas de la figure 2.11 vaut
Js w et Jπa2 si les densit´s de courant sont uniformes sur la largeur et sur la section
e
respectivement.
J
Js
a
w
Figure 2.11 – Densit´s de courant de surface et de volume.
e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-34-320.jpg)
 = −2 dB1 cos α ax
µJso dx y
= −2 ax
2π x 2 + y2 x2 + y2
µJso y dx
= − ax .
π(x2 + y 2)](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-35-320.jpg)
 = [dB](0,y>0,0)
0
µJso y ∞ dx
= − 2
a
2 x
π 0 x +y
∞
µJso y 1 x
= − arctan ax
π y y 0
µJso
= − ax .
2
De mani`re g´n´rale, autant dans le demi-espace y > 0 que y < 0, on ´crit :
e e e e
µ
B = J s × an
2
o` an est la normale ` la feuille de courant du cˆt´ du demi-espace consid´r´.
u a oe ee
2.4 Conducteur et conductivit´
e
Les mat´riaux sont constitu´s d’atomes, chacun ayant un noyau de protons (charges po-
e e
sitives) et neutrons autour duquel gravite les ´lectrons (charges n´gatives). Un ion est un
e e
atome dont le nombre de charges positives diff`re de celui des charges n´gatives.
e e
Certains ´lectrons se situent dans des bandes d’´nergie telles qu’ils peuvent se d´placer
e e e
d’un atome ` l’autre. Ce sont des ´lectrons libres par opposition a la majorit´ qui eux,
a e ` e
sont intimement li´s au noyau. La capacit´ d’un ´lectron libre de se d´placer d’un atome
e e e e
a
` l’autre – sa mobilit´ – d´pend du type de mat´riau. Lorsqu’un grand nombre d’´lectrons
e e e e
mobiles est impliqu´, le mat´riau est conducteur. Par contre, il existe des mat´riaux o`
e e e u
vraiment tr`s peu d’´lectrons sont disponibles pour participer ` la conduction. Ce sont
e e a
des isolants aussi appel´s di´lectriques. Entre les deux extrˆmes se trouvent les semi-
e e e
conducteurs o` , avec un niveau d’´nergie minimal, des ´lectrons li´s peuvent devenir
u e e e
libres en passant par dessus une bande d’´nergie interdite. Cette derni`re est, pour les
e e
semi-conducteurs, plus ´troite que celle pour les di´lectriques, ce qui explique la possibilit´
e e e
plus ´lev´e qu’un ´lectron devienne libre. Sur la figure 2.13, on observe les bandes d’´nergie
e e e e
selon le type de mat´riau. On y observe que la bande ` ´nergie minimale des conducteurs
e ae
n’est pas compl`tement remplie contrairement aux autres.
e
Sans entrer dans les d´tails, la vitesse de mobilit´ des ´lectrons libres v e est propor-
e e e
tionnelle ` une constante µe pr`s, au champ ´lectrique appliqu´ :
a e e e
v e = −µe E . (2.11)
Le courant ´lectrique r´sultant du mouvement des ´lectrons sera d’autant plus grand que
e e e
la vitesse de ces ´lectrons est ´lev´e car :
e e e
∆Q = Ne q(∆S)(vd ∆t) (2.12)
|∆Q|
I = = Ne |q|ve ∆S (2.13)
∆t](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-36-320.jpg)
![2.5 Di´lectrique et champ de d´placement
e e 2-27
E
Bande permise
disponible
Bande
interdite
Bande
permise
Conducteur Semi−conducteur Isolant
Figure 2.13 – Diagramme des bandes d’´nergie pour diff´rent type de mat´riau.
e e e
Mat´riau
e σ [ S/m] Mat´riau
e σ [ S/m]
argent 6.1 × 107 eau de mer 4
cuivre 5.8 × 107 germanium 2.2
or 4.1 × 107 silicium 1.6 × 10−3
aluminium 3.5 × 107 eau fraˆ ıche 10−3
tungst`ne
e 1.8 × 107 terre s`che
e 10−5
fer 4.8 × 106 bakelite 10−9
mercure 1.0 × 106 verre 10−10 − 10−14
Table 2.1 – Conductivit´ de certains mat´riaux.
e e
o` Ne est le nombre d’´lectrons libres par m`tre cube ; q, la charge de l’´lectron et ∆S, la
u e e e
section consid´r´e. Ainsi la quantit´ Ne |q|ve permet une relation directe entre la densit´
ee e e
de courant de conduction, not´e J c et le champ ´lectrique E. C’est la conductivit´ σ
e e e
exprim´e en Siemens/m`tre ou mhos/m`tre :
e e e
Jc = σ E . (2.14)
Le tableau 2.1 contient diff´rentes valeurs de conductivit´ selon les mat´riaux.
e e e
2.5 Di´lectrique et champ de d´placement
e e
Il a ´t´ dit que le champ ´lectrique produit par une charge d´pend du milieu via la
ee e e
permittivit´ ǫ. Si le milieu est le vide, alors la permittivit´ est ǫo mais, dans un di´lectrique,
e e e
il existe des atomes constitu´s de charges positives et n´gatives li´es ensemble. Sous l’effet
e e e
du champ ´lectrique, ces atomes deviennent polaris´s i.e. le nuage d’´lectrons de l’atome
e e e
a tendance a ˆtre d´centr´ cr´ant ainsi un dipˆle ´lectrique comme sur la figure 2.14.
` e e e e o e
L’intensit´ du dipˆle est d´finie par le moment dipolaire ´lectrique p donn´ par :
e o e e e
p = Qd (2.15)](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-37-320.jpg)







 = −4az V /m.
√
a+ a2 +z 2 √ a
3. [E](0,0,z) = 2πz ln z
− a2 +z 2
az .
−(ρo a/ǫo )az z < −a
4. [E](0,0,z) = (ρ z/ǫ )a −a < z < a
o o z
(ρo a/ǫo )az z>a .
5. dF 1 = − µ8o√2π2 dxdyax , dF 2 = − µ8o√2π2 dxdyay .
I1 I I1 I
6. a) µo Jso (ay + az ) W b/m2 ; b) −µo Jso az W b/m2 .
(µo Jo a)ay z < −a
7. [B](0,0,z) = −(µo Jo z)ay −a < z < a
−(µo Jo a)ay z>a.
2
8. [B](0,0,z) = − µ2I (a2 +z 2 )3/2 az W b/m2 .
o a
9. a) D = 10−6 az C/m2 , E ≈ 36000πaz V /m ;
b) D = 10−6 az C/m2 , E ≈ 9000πaz V /m.
Q
4πǫ r2 r < a
o
Q Q
10. D = 4πr2 ar partout ; E = a<r<b
16πǫo r2
Q
4πǫo r 2
r>b
11. a) H = 0.1 ax A/m, B = 4π × 10−8 ax W b/m2 ;
b) H = 0.1 ax A/m, B = 4π × 10−6 ax W b/m2 .](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-45-320.jpg)


![3-38 Les lois de Maxwell
S
B
C
dS
Figure 3.1 – Illustration de la loi de Faraday.
Sous forme math´matique, la loi de Faraday s’´crit :
e e
d
E · dl = − B · dS (3.1)
C dt S
f em
o` S est la surface d´limit´e par le contour ferm´ C tel que cela apparaˆ a la figure 3.1
u e e e ıt `
En mots, toute variation du flux magn´tique, provoque une force ´lectromotrice ; le
e e
flux magn´tique [Ψ]s , exprim´ en Webers, ´tant d´fini comme suit :
e e e e
[Ψ]s = B · dS . (3.2)
S
Les points int´ressants ou ` consid´rer suivent :
e a e
• On doit observer la r`gle de la main droite pour choisir le sens d’int´gration du
e e
parcours et le sens de la normale ` la surface.
a
• Toute surface S d´limit´e par C convient pour faire le calcul du flux magn´tique1 ;
e e e
le r´sultat n’en sera pas affect´. On a alors avantage a r´fl´chir sur le choix de la
e e ` e e
surface car certaines pourront faciliter le travail.
• Le signe n´gatif vient de la loi de Lenz qui dit que la f em est telle que le courant
e
produit tend ` s’opposer au changement du flux magn´tique qui l’a engendr´. Un flux
a e e
entrant et augmentant dans le temps induit une f em qui produit un flux sortant ;
un flux entrant et diminuant dans le temps induit une f em qui produit un flux
entrant.
• Si le parcours C est constitu´ de plusieurs tours de fil – N tours – alors la surface S
e
prend l’allure d’une h´lico¨ comme sur la figure 3.2 (N = 2), le flux est coup´ N
e ıde e
fois par la surface et la f em s’en trouve multipli´e par N comparativement a celle
e `
produite par un seul tour :
dΨ
f em = −N (3.3)
↑ dt .
1
En effet, pour avoir une int´grale de surface d´pendant uniquement des limites, il suffit que la diver-
e e
gence de l’int´grande soit nulle. On verra plus tard que ∇ · B = 0.
e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-48-320.jpg)


![3.3 Loi d’Amp`re
e 3-41
puis,
d
f em = − (aBo (b + vo t))
dt
= −aBo vo .
◮ Exprimez le courant Iboucle et dites si une force ext´rieure est n´cessaire pour
e e
maintenir la vitesse du rail mobile constante.
f em −aBo vo
Iboucle = = .
R R
Le courant Iboucle circule dans le sens horaire, passant de gauche a droite (ax )
`
dans le rail mobile. Une force magn´tique agit sur le rail. Selon (2.9), cette
e
force est orient´e vers le bas (−ay ), s’opposant donc au mouvement du rail tel
e
que pr´vu par la loi de Lens. Une force ext´rieure doit ˆtre appliqu´e :
e e e e
aBo vo a2 Bo vo
2
F ext = −F m = aBo ay = ay .
R R
3.3 Loi d’Amp`re
e
La seconde ´quation de Maxwell est un peu plus compliqu´e. Elle provient principale-
e e
ment des observations de Oersted ` propos des champs magn´tiques produits par les
a e
courants. La contribution math´matique de Maxwell lui a permis d’affirmer que des
e
champs ´lectriques variant donnent naissance ` des champs magn´tiques. Ce dernier a
e a e
d’ailleurs pr´dit longtemps avant que le ph´nom`ne soit observ´, la propagation des ondes
e e e e
´lectromagn´tiques. La loi d’Amp`re sous la forme int´grale, s’´crit ainsi :
e e e e e
d
H · dl = [I]s + D · dS (3.4)
C dt S
o` S est une surface d´limit´e par le contour ferm´ C.
u e e e
Cette ´quation ressemble ` celle de Faraday sauf qu’il y a deux termes a droite de
e a `
l’´galit´. Cette diff´rence provient du fait qu’il existe un courant ´lectrique mais pas de
e e e e
courant magn´tique. On peut pousser plus loin et se demander pourquoi. La r´ponse : les
e e
charges magn´tiques isol´es n’existent pas et ne se d´placent pas non plus, par cons´quent.
e e e e
Pour ajouter ` la ressemblance, on utilise l’analogie jusqu’` dire que C H · dl est la force
a a
magn´tomotrice f mm.
e
Le terme [I]s repr´sente le courant dˆ au mouvement des charges ´lectriques passant
e u e
au travers la surface S. Ce courant peut ˆtre de conduction dans un conducteur ou de
e
convection par un nuage de charges dans l’espace. Il ne peut ˆtre li´ aux ph´nom`nes
e e e e
de polarisation ou de magn´tisation dans le mat´riau car l’effet de ces ph´nom`nes est
e e e e
consid´r´ implicitement dans les d´finitions de D ou H respectivement.
ee e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-51-320.jpg)
![3-42 Les lois de Maxwell
Le second terme de droite d( S D · dS)/dt repr´sente aussi un courant – on peut s’en
e
convaincre en regardant les unit´s – mais diff´rent de celui auquel on est habitu´. Il s’agit
e e e
du courant de d´placement r´sultant de la variation du flux ´lectrique Ψe au travers une
e e e
surface S :
[Ψe ]s = D · dS . (3.5)
S
Le flux ´lectrique se d´finit de mani`re analogue au flux magn´tique rencontr´ dans
e e e e e
l’´quation de Faraday. En cons´quence, les courants de conduction, de convection et de
e e
d´placement sont tous responsables de produire un champ magn´tique.
e e
Si on suppose un courant de conduction, [Ic ]s , il peut provenir autant d’un courant
filiforme, de surface, de volume ou d’une combinaison de ceux-ci. Formul´ de par sa
e
densit´, le courant de conduction vaut :
e
[Ic ]s = J c · dS . (3.6)
S
De plus, sachant que le champ de d´placement et la densit´ de courant de conduction sont
e e
intimement li´s au champ ´lectrique via la permittivit´ et la conductivit´ selon (2.19) et
e e e e
(2.14) respectivement, l’´quation d’Amp`re devient :
e e
d
H · dl = σE · dS + ǫE · dS . (3.7)
C S dt S
Il faut cependant suivre quelques r`gles pour d´terminer la valeur de la force magn´to-
e e e
motrice f mm avec cette derni`re ´quation :
e e
• le courant [Ic ]s ne peut ˆtre qu’un courant de conduction de volume ;
e
• les int´grales de surface sont ´valu´es en accordance avec la r`gle de la main droite
e e e e
expos´e auparavant ; la normale ` la surface est orient´e selon le sens choisi du
e a e
parcours C ;
• les surfaces S de chaque membre de droite doivent ˆtre absolument identiques2 ;
e
cependant toute surface quelconque d´limit´e par le parcours ferm´ C convient .
e e e
Exemple 3.3
Soient les champs
√
H(t) = ±Ho δ(t ∓ µǫz)ay
√ pour z ≷ 0
E(t) = µ Ho δ(t ∓ µǫz)ax
ǫ
o` δ(·) repr´sente la fonction impulsion.
u e
Comme on verra plus tard, il s’agit des champs d’une onde ´lectromagn´tique
e e
plane et uniforme. On peut d’abord remarquer qu’une telle onde se d´place
e
2
On rappelle que la divergence de l’int´grande doit ˆtre nulle pour avoir le choix de la surface. Dans
e e
ce cas ci, on a plutˆt ∇ · (J + dD/dt) = 0.
o](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-52-320.jpg)
![3.3 Loi d’Amp`re
e 3-43
dans la direction z+ si z > 0 et z− si z < 0. Pour bien le voir, il faut tracer
l’amplitude d’un des champs au temps t = 0 puis ` un temps to > 0 pour
a
diff´rentes valeurs de z.
e
◮ Exprimez le courant produit par le mouvement des charges ` l’int´rieur de la
a e
section rectangulaire limit´e par les points (0, 0, 0.2), (0, 1, 0.2), (0, 1, −0.2) et
e
(0, 0, −0.2).
Pour commencer, on isole la composante du courant de conduction :
d
[Ic ]s = J · dS = H · dl − D · dS
S C dt S
Les termes de droite peuvent ˆtre ´valu´s s´par´ment :
e e e e e
1 0.2
√ √
H · dl = [Ho δ(t − µǫz)]x=0 ay ·(dyay ) + [Ho δ(t − µǫz)]x=0 ay ·(−dzaz )
C 0 z=0.2 0 y=1
0
0 1
√ √
+ [−Ho δ(t + µǫz)]x=0 ay ·(−dzaz ) + [−Ho δ(t + µǫz)]x=0 ay ·(−dyay )
−0.2 y=1 0 z=−0.2
0
0 0.2
√ √
+ [−Ho δ(t + µǫz)]x=0 ay ·(dzaz ) + [Ho δ(t − µǫz)]x=0 ay ·(dzaz )
−0.2 y=0 0 y=0
0 0
√ √
= Ho δ(t − 0.2 µǫ) + 0 + 0 + Ho δ(t − 0.2 µǫ) + 0 + 0
√
= 2Ho δ(t − 0.2 µǫ)
et, sachant que dS = dydz(−ax ) :
0 1
√ √
D · dS = [ µǫHo δ(t + µǫz)]x=0 ax · (−dydzax )
S −0.2 0
0.2 1
√ √
+ [ µǫHo δ(t − µǫz)]x=0 ax · (−dydzax )
0 0
0 0.2
√ √ √
= − µǫHo δ(t + µǫz)dz + δ(t − µǫz)dz
−0.2 0
√ √
√ u(t + µǫz) 0 u(t − µǫz) 0.2
= − µǫHo √ + √
µǫ z=−0.2
− µǫ z=0
√ √
= Ho (u(t − 0.2 µǫ) − u(t) − u(t) + u(t − 0.2 µǫ))
et ainsi :
d √
D · dS = −2Ho δ(t) + 2Ho δ(t − 0.2 µǫ) .
dt S
Finalement, le courant de conduction passant au travers la surface vaut :
[Ic ]s = 2Ho δ(t) .](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-53-320.jpg)
![3-44 Les lois de Maxwell
Il est int´ressant d’interpr´ter ces derniers r´sultats. On s’aper¸oit selon l’ex-
e e e c
pression de [Ic ]s , que le courant de conduction est responsable de l’´mission de
e
l’onde ´lectromagn´tique en produisant une impulsion au temps t = 0. C’est
e e
en quelque sorte, une source s(t) plac´e dans la plan z = 0 variant temporel-
e
lement qui produit l’onde. Cette impulsion se propage dans le milieu avec une
vitesse finie car elle est per¸ue en un instant t = to plus tard sous la forme
c
d’un champ ´lectrique et d’un champ magn´tique pour tout point des plans
e e
z = ±zo lesquels se situent ` ´gale distance du plan z = 0. La relation entre
ae
le d´lai to et la position zo d´pend de la vitesse de propagation de l’onde. On
e e
v´rifie facilement que pour cet exemple, la vitesse de propagation, not´e plus
e e
tard vp , vaut :
zo zo 1
vp = = √ = √ .
to µǫzo µǫ
Si le milieu est le vide, on prends ǫ = ǫo et µ = µo. Avec les valeurs de ces
constantes, on trouve alors que vp = c ≈ 3 × 108 m/s la vitesse de la lumi`re e
dans le vide !
On remarque aussi que la forme temporelle de l’amplitude des champs observ´s
e
a
` une certaine distance reproduit celle de la source nonobstant le d´lai de
e
propagation. En fixant le temps et en observant cette fois suivant l’axe z, la
forme spatiale de l’amplitude des champs observ´s ressemblerait a la forme
e `
temporelle de la source invers´e i.e. s(−t).
e
Finalement, on note que l’amplitude des champs ne d´croˆ pas en fonction de
e ıt
la distance z car la source a une dimension infinie (ce qui n’existe pas dans la
r´alit´). Cette onde est dite uniforme.
e e
3.4 ´
Equation de continuit´
e
L’´quation de continuit´ est une ´quation suppl´mentaire aux ´quations de Maxwell qui
e e e e e
fait le pont entre les charges et le courant. On l’appelle aussi la loi de conservation des
charges. On ne peut d´montrer l’´quation de continuit´ qu’en assumant que physiquement,
e e e
les charges ´lectriques ne peuvent disparaˆ
e ıtre. Si la charge nette a l’int´rieur d’un volume
` e
varie, c’est que des charges ont quitt´ ou sont entr´es dans le volume. Le signe des charges
e e
et le principe de superposition des charges sont consid´r´s dans l’´quation de continuit´.
ee e e
On pr´sente la loi de conservation des charges avant les deux derni`res ´quations de
e e e
Maxwell, parce qu’elle intervient dans la d´monstration de l’une des deux.
e
Selon cette loi, le courant produit par le mouvement des charges au travers une surface
ferm´e S doit correspondre au taux de d´croissance de la charge dans le volume V d´limit´
e e e e
par la surface ferm´e S – cette charge est not´e [Q]V :
e e
d
J · dS = − ρ dv . (3.8)
S dt V
[Q]V](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-54-320.jpg)
![´
3.5 Equations de Gauss 3-45
Une charge positive qui quitte le volume cr´e un courant positif de conduction ou de
e
convection – le terme [I]s a ´t´ employ´ pr´c´demment pour d´signer ce type de courant.
ee e e e e
En mˆme temps, la charge contenue dans le volume a diminu´ d’o` le signe n´gatif.
e e u e
J
Q(t)
dS
Figure 3.5 – Principe de la conservation des charges.
On note que [Q]V peut ˆtre une charge ponctuelle, provenir d’une densit´ lin´ique,
e e e
surfacique, volumique de charges ou encore une combinaison de tous ces modes. La figure
3.5 sch´matise le concept physique.
e
3.5 ´
Equations de Gauss
Les ´quations de Gauss se d´rivent directement des ´quations de Faraday et d’Amp`re en
e e e e
prenant une surface ferm´e. Si les deux premi`res font appels ` des int´grales de ligne des
e e a e
champs ´lectrique et magn´tique sur des parcours ferm´s, les deux derni`res ´quations de
e e e e e
Maxwell sont des int´grales de surfaces ferm´es.
e e
On sait qu’une int´grale sur une surface ferm´e donne le bilan du flux ´manant du
e e e
volume d´limit´ par la surface. Elle indique donc la pr´sence d’une source si positive, ou
e e e
d’un absorbant si n´gative. Dans le cas pr´sent, l’int´grale est reli´e aux charges qui sont
e e e e
sources de flux ´lectrique ou de flux magn´tique.
e e
dS2
S1 C1 S2
C2
dS1
Figure 3.6 – Deux parcours d’int´gration de sens oppos´s d´limitant une surface ferm´e.
e e e e
Pour la d´monstration, on consid`re deux parcours C1 et C2 identiques mais se par-
e e
courant dans des sens oppos´s comme sur la figure 3.6. Ils d´limitent chacun des surfaces
e e
diff´rentes S1 et S2 . Les deux surfaces mises ensemble forment donc une surface “pa-
e
tato¨
ıdale” ferm´e.
e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-55-320.jpg)

![´
3.5 Equations de Gauss 3-47
3.5.2 Charges ´lectriques
e
Comme il a ´t´ fait avec l’´quation de Faraday, on reprend les deux contours ferm´s C1
ee e e
et C2 identiques mais parcourus dans le sens oppos´. La surface ferm´e S de la figure 3.6
e e
est obtenue en prenant les deux surfaces quelconques S1 et S2 d´limit´es par les deux
e e
contours. On obtient :
H · dl + H · dl = 0
C1 C2
d
0 = J · dS + D · dS
S=S1 +S2 dt S=S1 +S2
d’o`
u
d
D · dS = − J · dS . (3.11)
dt S S
Ainsi, le courant de d´placement ´manant d’une surface ferm´e est ´gal au courant dˆ
e e e e u
aux charges quittant le volume d´limit´ par la surface ferm´e. Or, la loi de conservation
e e e
des charges indique justement comment le courant I(t) est li´ ` la variation de la charge
ea
´lectrique par unit´ de temps :
e e
d [Q]V
J · dS = I(t) = − (3.12)
S ↑ dt
Partant de (3.11) et de (3.12), on d´duit imm´diatement la derni`re ´quation de Maxwell :
e e e e
D · dS = [Q]V . (3.13)
S
La charge [Q]V exclut les ph´nom`nes de polarisation qui sont pris en compte implicite-
e e
ment dans la d´finition de D.
e
Formul´e en terme de densit´ volumique, on obtient :
e e
D · dS = ρ dv . (3.14)
S V
La seconde loi de Gauss sur le champ ´lectrique indique simplement que le bilan du flux de
e
d´placement ´manant d’une surface ferm´e est ´gal ` la charge contenue dans le volume
e e e e a
d´limit´ par la surface.
e e
Cette loi de Gauss permet d’expliquer la continuit´ du courant au travers un conden-
e
sateur pour un signal variant dans le temps. Avec une surface ferm´e autour d’une seule
e
plaque d’un condensateur, on fait le lien entre le courant de d´placement et le courant de
e
conduction. Selon (3.11) appliqu´e ` la surface ferm´e S de la figure 3.7, on a :
e a e
d
D · dS = i(t) (3.15)
dt S
o` i(t) repr´sente le courant fourni par la source et entrant dans le condensateur. En
u e
supposant que le champ D = ǫE est normal et uniforme entre les deux plaques de surface](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-57-320.jpg)

![´
3.5 Equations de Gauss 3-49
trouver les courants de conduction et de d´placement passant par une surface
e
S d´limit´e par C. Les deux mani`res sont bonnes mais on choisira ici la
e e e
seconde :
d
f mm = [Ic ]s + D · dS .
dt S
On prend comme surface l’h´misph`re sup´rieure pour faciliter le traitement
e e e
qui suit.
• D’abord, le courant dˆ au mouvement des charges se limite a celui de
u `
conduction :
[Ic ]s = I
puisqu’il passe au travers S.
• La d´termination du courant de d´placement n´cessite la connaissance
e e e
du flux ´lectrique. Partant de la loi de Gauss, on utilise les d´ductions
e e
suivantes :
– avec deux h´misph`res – inf´rieure et sup´rieure qui forment ainsi
e e e e
une surface ferm´e – le flux ´lectrique est ´gal ` Q selon la loi de
e e e a
5
Gauss ;
– les deux h´misph`res sont identiques ; donc le flux traversant chacune
e e
d’elles vaut la moiti´ i.e. :
e
Q
D · dS = .
S 2
– la d´riv´e par rapport au temps du flux traversant la surface S com-
e e
bin´e ` la loi de conservation des charges donne donc :
e a
d 1 dQ 1
D · dS = = − I
dt S 2 dt 2
La f mm est ensuite d´duite en substituant les ´quations des courants :
e e
1 I
f mm = I − I = .
2 2
On aurait trouv´ un r´sultat identique en prenant l’h´misph`re inf´rieure.
e e e e e
Dans ce cas, il n’y a pas de courant de conduction qui passe au travers de
la surface et le courant, par le champ de d´placement, change de signe pour
e
respecter la r`gle de la main droite.
e
5
Il est int´ressant de noter que l’expression du champ E produite par une sph`re charg´e s’obtient
e e e
Q
facilement : sph`re ǫEr dS = 4πr2 ǫEr = Q donc E = 4πǫr2 ar
e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-59-320.jpg)








![3-58 Les lois de Maxwell
πz πz πz
H v = H1 cos(πx) cos( )ax + H2 sin(πx) sin( )ay + H3 cos(πx) sin( )az .
2d 2d d
L’espace est divis´ est trois r´gions tel que sur la figure 3.14 :
e e
• un conducteur parfait pour z < 0 ;
• le vide lorsque 0 < z < d ;
• un di´lectrique parfait ayant µ = µo , σ = 0 et ǫ = 4ǫo pour z > d.
e
◮ D´terminez ρs et J s sur la surface du conducteur en z = 0 et indiquez les
e
termes des champs – les Ei et les Hi – qui doivent ˆtre nuls a cause des
e `
conditions dures.
Des ´quations (3.46) ` (3.49), on d´duit respectivement :
e a e
0 = az × [E]z=0
πz πz
= [E1 sin(πx) sin( )]z=0 (ay ) + [E2 cos(πx) cos( )]z=0 (−ax )
2d 2d
0 car sin(0)=0 E2 cos(πx) car cos(0)=1
donc forc´ment :
e
E2 = 0 .
D’autre part, avec la seconde ´quation aux limites, on a :
e
[J s ]z=0 = az × [H]z=0
πz πz
= [H1 cos(πx) cos( )]z=0 (ay ) + [H2 sin(πx) sin( )]z=0 (−ax )
2d 2d
H1 cos(πx) 0
puis, de la troisi`me :
e
πz
0 = az · µo [H]z=0 = µo [H3 cos(πx) sin( )]z=0
d
0
de laquelle on ne peut rien conclure. De la derni`re, on retire :
e
[ρs ]z=0 = az · ǫo [E]z=0
πz
= ǫo [E3 sin(πx) cos( )]z=0 = ǫo E3 sin(πx) .
d
E3 sin(πx)
◮ Exprimez les champs dans le di´lectrique E d et H d , a l’interface avec le vide.
e `
On reprend les conditions aux limites (3.42) ` (3.45) avec z = d, ρs = 0 et
a
Js = 0 :
[Edx ]z=d+ = [Evx ]z=d− = E1 sin(πx) car sin(π/2) = 1
Edy z=d+ = Evy z=d− = 0 car E2 = 0](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-68-320.jpg)
![3.7 Conditions aux limites 3-59
[Hdx ]z=d+ = [Hvx ]z=d− = 0 car cos(π/2) = 0
Hdy z=d+ = Hvy z=d− = H2 sin(πx) car sin(π/2) = 1
µo [Hdz ]z=d+ = µo [Hvz ]z=d− = 0 car sin(π) = 0
4ǫo [Edz ]z=d+ = ǫo [Evz ]z=d− = −ǫo E3 sin(πx) car cos(π) = −1 .
Exprim´es sous une forme plus succincte, on aboutit aux ´quations :
e e
E3
[E d ]z=d+ = E1 sin(πx)ax − sin(πx)az
4
[H d ]z=d+ = H2 sin(πx)ay .
◮ Si on remplace le di´lectrique par un autre conducteur parfait, donnez les
e
modifications ` apporter aux composantes Ei et Hi des champs.
a
On doit maintenant appliquer les conditions aux limites dures a z = d. On
`
obtient alors :
πz
0 = (−az ) × [E]z=d− = [E1 sin(πx) sin( )]z=d (−ay )
2d
E1 sin(πx)
car E2 est d´j` ´gal ` z´ro. Cette expression implique maintenant que :
eae a e
E1 = 0
Ensuite :
[J s ]z=d = (−az ) × [H]z=d−
πz πz
= [H1 cos(πx) cos( )]z=d− (−ay ) + [H2 sin(πx) sin( )]z=d− (ax )
2d 2d
0 H2 sin(πx)
0 = (−az ) · µo [H] z=d−
πz
= [H3 cos(πx) sin( )]z=d−
d
0
[ρs ]z=d = (−az ) · ǫo [E]z=d−
πz
= −ǫo E3 sin(πx) cos( ) .
d z=d−
ǫo E3 sin(πx)
Aucune information suppl´mentaire ne peut ˆtre extraite des trois derni`res
e e e
´galit´s en ce qui concerne les composantes des champs. On connaˆ cependant
e e ıt
les expressions du courant de surface et de la densit´ surfacique de charges sur
e
ce deuxi`me conducteur.
e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-69-320.jpg)

![3.7 Conditions aux limites 3-61
dans le plan xy, pour t = 0 et t = 1 s.
Question 5
Une source tension connect´e ` un condensateur ` plaques parall`les g´n`re un champ
e a a e e e
´lectrique uniforme (on n´glige les effets de bords) entre les plaques :
e e
E = 180 sin(2π × 106 t) sin(4π × 106 t) az V /m .
La surface de chacune des plaques est de 0.1 m2 tandis que l’espacement entre les deux
plaques, constitu´ d’air, n’est que de 2 mm. En supposant que le champ ´lectrique est nul
e e
a
` l’ext´rieur de la r´gion directement entre les deux plaques, calculez la valeur efficace du
e e
courant fourni par la source.
Note#1 : la valeur efficace d’un signal harmonique – sinus ou cosinus – correspond ` la a
√
valeur crˆte divis´e par 2.
e e
Note#2 : la valeur crˆte d’une somme de signaux harmoniques ` diff´rentes fr´quences
e a e e
se calcule comme la norme d’un vecteur puisque les fonctions harmoniques forment une
base orthogonale.
Question 6
Divers types de charges sont plac´es, en coordonn´es cart´siennes, comme suit : une
e e e
charge ponctuelle de 1 µC ` (1, 1, −1.5) ; une charge lin´ique uniforme ayant une densit´ de
a e e
2 µC/m le long d’une ligne droite partant de (−1, −1, −1) jusqu’` (3, 3, 3) ; et une charge
a
surfacique r´partie uniform´ment sur la surface planaire en x = 0 entre les droites z = −1
e e
et z = 1 avec une densit´ de −1 µC/m2 . D´terminez le flux ´lectrique [Ψe ]S ´manant de la
e e e e
surface ferm´e cubique S limit´e par les plans x = ±2, y = ±2 et z = ±2.
e e
Question 7
Pour chacune des distributions de charges suivantes, d´terminez le flux de d´placement
e e
´manant de la surface ferm´e indiqu´e :
e e e
a) ρ(x, y, z) = ρo (x + y + z)2 pour 0 < x < 1, 0 < y < 1 et 0 < z < 1 ;
b) ρ(r, φ, z) = ρo cos2 (φ) pour 0 < r < 1, 0 < φ < π/2 et 0 < z < 1.
Question 8
Soit E = Eo cos(6π × 108 t − 2πz) ax V /m. D´terminez le taux d’augmentation tem-
e
porelle des composantes du champ d’induction Bx , By et Bz au temps t = 10−8 s et a la
`
position (1, 1, 0.25) m.
Question 9
8 2
Soient J = 0 et H = Ho e−(3×10 t−z) ay A/m. D´terminez le taux d’augmentation
e
temporelle des composantes du champ de d´placement Dx , Dy et Dz au temps t = 10−8 s
e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-71-320.jpg)
 ` t = 0 si l’autre mat´riau est un conducteur parfait et :
a e
[H](0,0,0+ ) = Ho (3ax − 4ay ) cos(ωt) ;](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-72-320.jpg)
 si l’autre mat´riau est un mat´riau magn´tique ayant µ = 20µo et :
e e e
[H](0,0,0− ) = Ho (10ax + az ) ;
c) le rapport [B](0,0,0− ) /[B](0,0,0+ ) avec les mˆmes conditions qu’en b).
e
Question 15
Deux plaques infinies parfaitement conductrices sont localis´s ` x = 0 et x = 0.1 m.
e a
Les champs ´lectromagn´tiques dans l’espace entre les deux plaques sont d´crits par :
e e e
E = Eo sin(10πx) cos(3π × 109 t) az V /m
Eo
H = cos(10πx) sin(3π × 109 t) ay A/m .
120π
a) D´montrez que E satisfait les conditions aux limites ;
e
b) d´duisez la densit´ de courant de surface sur les deux plaques.
e e
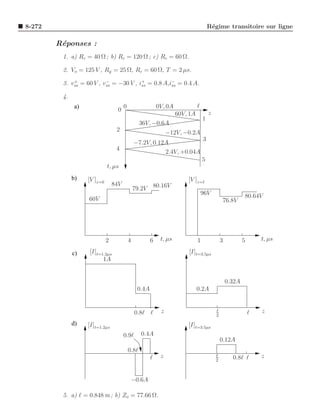
R´ponses :
e
√
2
1. f em = − 2
ωBo cos(ωt + π/4) V .
1 1
2. f em = Bo bvo xo +vo t
− xo +a+vo t
V
1
3. a) f em = Bo ab ω sin(ωt) V ; b) [Ψ]s = − 2 Bo (ab2 ), f em = 0
c) [Ψ]s = −Bo (ab2 ) sin(φ) cos(φ), f em = Bo (ab2 ) ω cos2 (ωt) − ω sin2 (ωt) V .
4. [Id (t = 0)]s = 0.1ǫo Eo A, [Id (t = 1)]s = −0.1e−1 ǫo Eo A.
5. I = 1.118 mArms .
6. S
D · dS = 3.3923 µC.
5
7. a) D · dS = 2 ρo ; b) D · dS = π ρo .
8
∂Bx ∂By ∂Bz
8. ∂t
= 0, ∂t
= 2πEo , ∂t
= 0.
∂Dx ∂Dy ∂Dz
9. ∂t
= −0.7358 Ho, ∂t
= 0, ∂t
= 0.
10. −0.08 Jo (C/m3 )/s.
Eo
11. B = 3×108
(0.6ax − 0.8az ) cos (3π × 108 t + 0.2π(4x + 3z)) W b/m2 .
12. β 2 − α2 = ω 2 µo ǫo .
√ √
13. a) 1.5 ; b) 3/ 5 ; c) 2/ 5.
14. a) [J s (t = 0)](0,0,0) = Ho (4ax + 3ay ) ;
b) [H](0,0,0+ ) = 10Ho(ax + 2az ) ; c) 8.989 .
15. a) [Ez ]x=0 = 0 et [Ez ]x=0.1 = 0 donc les composantes tangentielles sont bien nulles ;
Eo
b) [J s ]x=0 = −[J s ]x=0.1 = 120π sin(3π × 109 t) az .](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-73-320.jpg)


![4-66 Statique et Quasi-statique
4.2 Applications directes aux champs statiques
d
Les quatre ´quations de Maxwell se r´sument ainsi lorsque
e e dt
=0:
E · dl = 0 (4.1)
C
H · dl = [Ic ]s = J · dS (4.2)
C S
D · dS = ρ dv (4.3)
S V
B · dS = 0 (4.4)
S
tandis que celle de continuit´ devient :
e
J · dS = 0 . (4.5)
S
On voit imm´diatement le d´couplage des champs ´lectrique et magn´tique. L’´quation
e e e e e
(4.1) indique que le champ ´lectrique est maintenant conservatif : l’int´grale de ligne est
e e
une fonction des points de d´part et d’arriv´e mais est ind´pendante du parcours suivi.
e e e
Avec (4.2), on remarque que le champ magn´tique statique est cr´´ uniquement par le
e ee
d´placement de charges libres. Pas de courant de d´placement car il n’y a aucune variation
e e
de la charge dans le temps, propri´t´ aussi indiqu´e par (4.5). Le courant de convection
ee e
ou de conduction [I]s existe au travers une boucle ferm´e. e
L’utilisation la plus simple et la plus directe des ´quations de Maxwell statiques consiste
e
a e
` d´river l’expression des champs statiques. Dans certaines conditions o` il est possible
u
de se servir des sym´tries, les int´grales se simplifient. Il suffit de bien choisir la surface
e e
ou le parcours d’int´gration, analyser la g´om´trie et faire ressortir des produits scalaires
e e e
nuls (angle droit entre les deux vecteurs) ou maximum (angle nul). Souvent le travail de
calcul se r´alise rapidement si le travail de r´flexion a ´t´ bien men´.
e e ee e
Rien de mieux que quelques exemples pour se fixer les id´es. On s’apercevra que les
e
´quations les plus employ´es dans ce genre d’op´ration sont celles ayant un membre de
e e e
droite non-nul ; les autres m`nent ` la solution triviale ou servent simplement a confirmer
e a `
l’absence de certaines composantes des champs provoqu´e par la sym´trie.
e e
Exemple 4.1
Un fil infini de rayon a est charg´ uniform´ment avec une densit´ volumique
e e e
3
ρo C/m comme sur la figure 4.1.
◮ Exprimez le champ ´lectrique dans le vide ` une distance r du centre du fil.
e a
Il y a lieu de se servir de la sym´trie de fil pour choisir une surface ferm´e
e e
car on parle de charge ´lectrique. La meilleure est une surface constitu´e d’un
e e
partielles du deuxi`me ordre obtenue par combinaison des deux premi`res ´quations de Maxwell. C’est le
e e e
protocole suivi dans le prochain chapitre.](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-76-320.jpg)


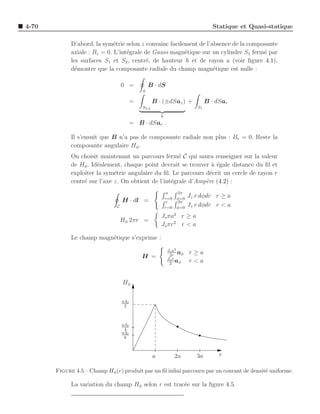





![4-76 Statique et Quasi-statique
équipotentielles z
+Q
+d
2
E
−d
2
−Q
´
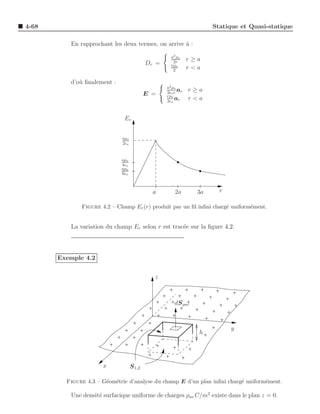
Figure 4.8 – Equipotentielles et lignes de champ ´lectrique d’un dipˆle ´lectrique.
e o e
la figure 4.8. Le dipˆle ´lectrique ´tant constitu´ d’une charge +Q et d’une charge −Q,
o e e e
la charge nette est nulle.
On se rend compte qu’en consid´rant le plan milieu et normal au segment reliant les
e
deux charges :
• le champ ´lectrique est perpendiculaire en tout point du plan ;
e
• le plan correspond ` une ´quipotentielle.
a e
Ainsi, en pla¸ant un plan conducteur parfait exactement a la position de ce plan, la
c `
cartographie du champ ´lectrique et de la fonction de potentielle ne serait nullement
e
affect´e. Si maintenant, on retire la charge −Q par exemple, le champ ´lectrique devient
e e
nul automatiquement du cˆt´ de la charge n´gative mais demeure inchang´ de l’autre cˆt´
oe e e oe
du plan conducteur.
équipotentielle z
+Q
+Q
d d
[E]S
- -- - - - - - -- - - - - - - - - ⇔
conducteur parfait ρs d
−Q
image
Figure 4.9 – Th´orie des images sur une charge ´lectrique +Q.
e e
En cons´quence, mettre un plan conducteur parfait ` cˆt´ d’une charge ´lectrique
e a oe e
correspond ` simuler une charge de signe oppos´ ` une distance ´quivalente sous le plan
a ea e
conducteur. C’est l’image de la charge ´lectrique statique comme le r´sume la figure 4.9. En
e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-86-320.jpg)
![4.4 Th´orie des images
e 4-77
fait, la charge image est cr´´e par une distribution non-uniforme de la densit´ surfacique
ee e
de charges ρs ` la surface du conducteur. Cette densit´ de charges est de mˆme signe que
a e e
la charge image et sa valeur d´pend de l’intensit´ du champ de d´placement D a cette
e e e `
position.
En pr´sence de plusieurs charges ´lectriques, le plan conducteur parfait simulera autant
e e
de charges de l’autre cˆt´ avec une mˆme configuration, de mˆmes grandeurs mais de signes
oe e e
oppos´s. On comprend facilement qu’une densit´ lin´aire ρl , surfacique ρs ou volumique
e e e
ρ de charges peut ˆtre imag´e de la mˆme mani`re, toujours avec le signe oppos´.
e e e e e
Exemple 4.6
Une charge lin´aire infinie ayant une densit´ ρl est plac´e parall`lement a une
e e e e `
distance d d’un plan conducteur. Pour se fixer les id´es, la charge lin´aire est
e e
a (x = 0, z = d) et le conducteur est ` z = 0.
` a
◮ Trouvez l’expression de la densit´ surfacique de charges ` la surface du conduc-
e a
teur.
On sait que ρs = −[D⊥ ]S = −ǫ[E⊥ ]S par l’application de la condition aux
limites du champ ´lectrique sur la surface S. Or, selon ce qui a ´t´ trouv´
e ee e
a l’exemple 4.1, le champ ´lectrique produit par une charge lin´aire infinie
` e e
4
vaut :
ρl
E+ = ar
2πǫr
avec r 2 = d2 + y 2.
La charge image produit un champ ´lectrique de mˆme magnitude E− = E+ .
e e
Remarquons que l’image de la charge annule la composante tangentielle du
champ ´lectrique sur le conducteur afin que soit respect´ les condition aux
e e
limites. Le champ total est la somme vectorielle des deux champs soit, dans le
plan z = 0 :
[E⊥ ]S = [E + + E − ]z=0 = 2E+ cos θ .
L’angle θ repr´sente l’angle d’inclinaison entre le champ ´lectrique et la nor-
e e
male an = az du plan conducteur. Son cosinus s’exprime ais´ment en fonction
e
de d et y puisque cos θ = √d .
2 2
d +y
On obtient finalement
ρl d
[E⊥ ]S =
πǫ(d2 + y 2 )
donc
ρl d
ρs = − .
π(d2 + y 2 )
4
Il suffit de comprendre que la densit´ lin´aire ´quivaut ` ρl = ρ(πa2 ) i.e. le produit de la densit´
e e e a e
volumique par la surface du fil.](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-87-320.jpg)


 − [V ](0,0,0) [V ](0,0,0) − [V ](−a,0,0)
≈ − (4.24)
a a a
1
≈ 2 ([V ](−a,0,0) + [V ](a,0,0) − 2[V ](0,0,0) ) . (4.25)
a
On proc`de de mani`re similaire par la d´riv´e seconde en y :
e e e e
∂2 V 1
≈ ([V ](0,−a,0) + [V ](0,a,0) − 2[V ](0,0,0) ) , (4.26)
∂y 2 (0,0,0) a2
on r´organise puis on substitue (4.25) et (4.26) dans (4.19) sans la variable z, pour obtenir :
e
1
[V ](0,0,0) ≈ ([V ](−a,0,0) + [V ](a,0,0) + [V ](0,−a,0) + [V ](0,a,0) ) . (4.27)
4
Cette ´quation indique qu’une approximation valable du potentiel en un point donn´ est
e e
celle d´termin´e en prenant la moyenne des potentiels des noeuds voisins ´quidistants.
e e e
Cette formule provient des s´ries de Taylor tronqu´es, ce qui permet de connaˆ rapide-
e e ıtre
2
ment l’ordre de grandeur de l’erreur : ici de a .
La suite de la m´thode consiste ` appliquer l’´quation des diff´rences finies (4.27) aux
e a e e
noeuds dans le domaine de d´finition, en tenant compte des conditions impos´es par le
e e
potentiel des conducteurs agissant comme fronti`res. Il faut maintenant solutionner ce
e
syst`me qui comporte souvent beaucoup d’inconnues (le potentiel a chaque noeud). Selon
e `
les contraintes, on pourra utiliser :
• la solution matricielle :
On g´n`re la matrice des multiples ´quations – une ´quation pour chaque noeud
e e e e
du domaine de d´finition – des diff´rences finies qui est ensuite invers´e. L’inversion
e e e
d’une matrice aussi grande est grandement acc´l´r´e si l’on consid`re la propri´t´
ee e e ee
“sparse” de la matrice.
• la solution par relaxation :
On d´bute en supposant que tous les potentiels sont nuls sauf ceux impos´s sur les
e e
conducteurs, et on r´sout successivement les ´quations en utilisant la derni`re valeur
e e e
obtenue des quatre potentiels n´cessaires ` chacun des noeuds. La solution corrig´e
e a e
apr`s une it´ration sert comme nouvelle solution de d´part a la prochaine it´ration.
e e e ` e
On r´p`te tant que la correction ` appliquer ` un seul des noeuds d´passe un seuil
e e a a e
fix´ au d´part.
e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-90-320.jpg)

 + [V ](a,0,0) ) (ǫr1 [V ](0,−a,0) + ǫr2 [V ](0,a,0) )
[V ](0,0,0) ≈ + (4.29)
4 2(ǫr1 + ǫr2 )
Exemple 4.8
La figure 4.13 montre un domaine de d´finition de 4 par 4 unit´s contenant
e e
deux di´lectriques : celui du haut est l’air et celui du bas a une constante
e
di´lectrique ǫr1 = 9. Le potentiel aux limites de ce domaine vaut 0 V alors
e
`
qu’un seul noeud du domaine a un potentiel fixe de 1 V . A cause de la sym´trie,
e
seulement 5 valeurs du potentiel sont inconnues soient Va , Vb , Vc , Vd et Ve .
◮ D´terminez ces 5 valeurs du potentiel en assumant un seul di´lectrique de
e e
constante ǫr = 9.](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-92-320.jpg)

![4-84 Statique et Quasi-statique
on obtient Va = 0.1317 V, Vb = 0.2195 V, Vc = 0.3073 V, Vd = 0.6146 V et
Ve = 0.3268 V.
Note : les matrices ` inverser sont de grandes dimensions dans les probl`mes pratiques
a e
2 2 2 2
rencontr´s (N M × N M avec N et M repr´sentant le nombre d’unit´s en largeur et en
e e e
hauteur du domaine de d´finition). Par contre, elles contiennent une quantit´ importante
e e
d’´l´ments nuls, faisant d’elles des matrices ´parses (“sparse matrix”). Les math´maticiens
ee e e
se sont amus´s ` trouver un algorithme optimal d’inversion de ce type de matrices, algo-
e a
rithme que l’on retrouve dans MatlabTM .
4.6 De l’´lectromagn´tisme aux circuits
e e
La th´orie des circuits, bien connue et largement employ´e en ing´nierie, n’est applicable
e e e
que dans le cas statique et quasi-statique comme beaucoup semble l’oublier. Elle suppose :
• des d´lais de propagation nuls entre deux points d’un mˆme noeud ;
e e
• des ´l´ments tr`s petits par rapport ` la longueur d’onde de sorte qu’ils r´agissent
ee e a e
au premier ordre de la fr´quence.
e
L’effet de propagation est couvert dans les chapitres ult´rieurs sur les lignes de transmis-
e
sion entre deux points. L’effet des ´l´ments suit dans cette section.
ee
Mais avant, il est int´ressant de voir comment les lois fondamentales des circuits
e
´lectriques d´rivent des ´quations de Maxwell.
e e e
• L’´quation de Faraday statique (4.1) est l’extension de la loi des mailles car en
e
statique et quasi-statique, on a :
0 = − E · dl
C
b c a
= − E 1 · dl1 − E 2 · dl2 − ... − E K · dlK
a b z
= V1 + V2 + ... + VK .
• De la mˆme mani`re, l’´quation de continuit´ statique (4.5) est l’extension de la loi
e e e e
des noeuds :
0 = J · dS
S
= J 1 · dS 1 + J 2 · dS 2 + ... + J K · dS K
S1 S2 SK
= [Ic ]S1 + [Ic ]S2 + ... + [Ic ]SK
o` l’ensemble des K surfaces Si forment une surface ferm´e S.
u e
On comprend maintenant qu’aux fr´quences plus ´lev´es, les deux lois fondamentales
e e e
de Kirchoff ne tiennent plus ; il faut alors revenir au source soit l’´lectromagn´tisme.
e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-94-320.jpg)

![4-86 Statique et Quasi-statique
Le voltage Vab fait apparaˆ des charges +Q et −Q sur chacune des plaques,
ıtre
soit des densit´s surfaciques de charges ρsa = Q/A et ρsb = −Q/A respective-
e
ment. Le champ ´lectrique peut ˆtre d´duit de plusieurs mani`res :
e e e e
• par l’application des conditions aux limites sur une plaque conductrice
pour trouver E et D⊥ ;
• par l’int´grale de Gauss statique sur une surface ferm´e constitu´e d’un
e e e
boite rectangulaire plac´e de part et d’autre d’une plaque conductrice
e
comme ` l’exemple 4.2 ;
a
• par l’int´grale sur un surface infinie comme ` l’exemple 4.2 et superposi-
e a
tion des champs avec deux plaques.
On comprend que, selon la configuration id´ale, le champ ´lectrique est uni-
e e
forme dans le di´lectrique. On trouve alors :
e
ρsa
E = (−az ) .
ǫ
La diff´rence de potentiel entre les deux plaques peut maintenant ˆtre d´termi-
e e e
n´e comme suit (dl = −dzaz ) :
e
b
Vab = − E · dl
a
a
ρsa
= dz
b ǫ
ρsa
= d.
ǫ
La capacitance vaut donc :
Qa ρsa A
C = =
Vab ρsa d/ǫ
ǫA
= .
d
4.6.2 Conductance
La conductance G est l’inverse de la r´sistance R d´finie ` partir de la loi d’Ohm R = V /I
e e a
en Ohms (Ω). Dans la structure qui servait ` la capacit´, on remplace le di´lectrique par
a e e
un mat´riau dont la conductivit´ est finie mais non-nulle. Un courant de conduction [Ic ]S
e e
(ou plus simplement I) traverse un mat´riau lorsqu’une tension Vab est appliqu´e aux
e e
bornes a et b. Or les deux quantit´s sont reli´es au champ ´lectrique via :
e e e
I = J · dS = σE · dS (4.32)
S S
b
Vab = E · dl (4.33)
a](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-96-320.jpg)




![4.6 De l’´lectromagn´tisme aux circuits
e e 4-91
On remarque que le champ d’induction dans le mat´riau est uniforme. Le flux
e
magn´tique qui traverse une boucle est facile ` calculer ; il vaut :
e a
µ NI πa2
Ψ1boucle = .
h
Il faut bien voir que l’analyse a ´t´ faite en ne prenant qu’une partie de lon-
ee
gueur h du sol´no¨
e ıde. L’obtention de l’inductance par unit´ de longueur qui
e
est not´e L d´coule de (4.37) en divisant ensuite par h. Donc :
e e
µ N I πa2
L 1 h
L = = N
h h I
µ N 2 πa2
= .
h2
4.6.3.2 Inductance interne
L’inductance telle que d´finie ` l’´quation (4.35), exige que tout le flux soit li´ par le
e a e e
courant complet. C’est le cas usuel en pratique, car on suppose que le courant dans un bon
conducteur est confin´ ` la surface – courant de surface J s – o` il contribue enti`rement
ea u e
au flux. Parfois, le flux entier ne peut ˆtre li´ ` tout le courant : une partie seulement
e e a
du courant est li´e ` une partie du flux. Il convient alors de travailler sur des ´l´ments
e a ee
diff´rentiels du flux pond´r´s au prorata de la fraction du courant qui contribue au flux,
e ee
puis d’int´grer sur la surface par laquelle passe le flux entier. On parle alors d’inductance
e
interne et d’inductance externe. Pour l’inductance interne, le flux int´gr´ est li´ a une
e e e `
partie du courant, et non ` tout le courant :
a
Ψ
Lint = ε dS
S [I]dS
o` ε repr´sente la partie du flux li´e du courant li´e au courant passant par dS. L’induc-
u e e e
tance totale de l’arrangement est la somme des inductances interne et externe ; on int`gre
e
alors tout le flux.
B
Figure 4.18 – Surface d´limit´e par deux boucles de fil conducteur.
e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-101-320.jpg)










![4-102 Statique et Quasi-statique
Io
qu’il a une amplitude de w
:
Io
H = − ay pour 0 < x < d (4.53)
w
0<y<w
et − ℓ < z < 0 .
Il est nul partout ailleurs.
Le flux magn´tique li´ au courant est simplement le flux traversant une section trans-
e e
versale aux plaques soit Ψ = µHy (ℓd). On peut d´duire imm´diatement l’expression de
e e
l’inductance qui sera utile plus tard dans la d´monstration :
e
Ψ µℓd
L = = . (4.54)
Io w
Si le courant est sinuso¨ ¯
ıdal, on utilise la notion de phaseur donc I = Io et :
¯ Io
Hy0 = − . (4.55)
w
L’indice 0 est rajout´ pour indiquer qu’il s’agit d’une composante du champ proportion-
e
nelle ` la puissance z´ro de la fr´quence.
a e e
Comme le champ magn´tique varie dans le temps, il doit exister un champ ´lectrique
e e
suivant les ´quations de Maxwell. L’expansion de l’´quation de Faraday sous forme diff´-
e e e
rentielle avec des phaseurs donne (aucune variation suivant x et y) :
¯
∂ Ex Io
¯
= −jωµ Hy0 = jωµ (4.56)
∂z w
qui a comme solution g´n´rale :
e e
¯ Io ¯
Ex1 = jωµ z + C .
w
¯
La constante C est d´termin´e par l’application de la condition aux limites du champ
e e
e a ¯
´lectrique tangentiel ` z = 0. Il faut que [Ex ]z=0 = 0 car il ne peut y avoir de composante
¯
tangentielle du champ ´lectrique sur un conducteur. Ainsi, avec C = 0, on obtient :
e
¯ Io
Ex1 = jωµ z . (4.57)
w
Avant de poursuivre, il est bon d’ouvrir une parenth`se pour montrer que l’une des
e
deux expressions des champs (4.55) et (4.57) – lesquelles correspondent aux expressions
dans le cas quasi-statique o` la composante du premier ordre en fr´quence est largement
u e
celle pr´dominante – ´tablit la r´action de l’inductance obtenue dans la th´orie des circuits.
e e e e
En effet, ` l’entr´e de la structure, l’expression du champ ´lectrique en basse fr´quence
a e e e
(indice bf ) se limite ` celle du premier ordre soit :
a
¯ ¯ µℓ
[Exbf ]z=−ℓ ≈ [Ex1 ]z=−ℓ = −jω Io
w](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-112-320.jpg)
![4.8 Analyse de comportement en quasi-statique 4-103
et la tension d´velopp´e aux bornes de la source courant vaut :
e e
d
¯
Vbf = ¯ ¯
[Ex ]z=−ℓ dx = d [Ex ]z=−ℓ
0
µℓd
= jω Io
w
L
soit, fin de parenth`se :
e
¯
Vbf = jωLIo ! (4.58)
Jusqu’ici, on a v´rifi´ l’´quation de Faraday, mais a-t-on satisfait celle d’Amp`re. La
e e e e
r´ponse est non ; il faut donc poursuivre le d´veloppement pour les composantes d’ordres
e e
sup´rieurs en fr´quence qui m`ne ` une s´rie convergeant vers la solution ´lectromagn´tique.
e e e a e e e
Il y a cependant quelques d´tails ` pr´ciser au pr´alable :
e a e e
• Les conditions aux limites s’appliquent pour d´duire la valeur de la constante r´sul-
e e
tant de l’int´grale ind´finie.
e e
• Pour le champ ´lectrique, aucune composante tangentielle ` chaque puissance en
e a
fr´quence ne doit exister en z = 0.
e
• Pour le champ magn´tique, on force un courant fixe ` l’entr´e dont la densit´ vaut
e a e e
Io
Jso = w . On convient que la densit´ de courant peut varier suivant z et qu’il est
e
probable que la densit´ ` z = 0 soit tout-`-fait diff´rente de celle a z = −ℓ. On
e a a e `
applique donc la contrainte ` l’entr´e z = −ℓ. Or la composante statique Hy0 satis-
a e
fait pleinement et ` elle seule, la condition aux limites impos´e sur la composante
a e
tangentielle [Hy ]z=−ℓ = Jso ; les autres composantes d’ordres sup´rieurs du champ
e
magn´tique tangentiel doivent par cons´quent ˆtre nulle ` z = −ℓ.
e e e a
En y substituant (4.57) dans l’´quation d’Amp`re avec phaseurs, il d´coule :
e e e
¯
∂ Hy Io
¯
= −jωǫ Ex = ω 2 µǫ z .
∂z w
La solution g´n´rale est :
e e
¯ 1 Io ¯
Hy2 = ω 2 µǫ z 2 + C
2 w
¯
dans laquelle la constante C est d´termin´e par le fait que les composantes d’ordres
e e
sup´rieurs de Hy sont nulles ` z = −ℓ. Ainsi, on obtient :
e a
¯ 1 Io
Hy2 = ω 2 µǫ (z 2 − ℓ2 ) . (4.59)
2 w
En recommen¸ant de la mˆme mani`re depuis le d´but avec l’´quation de Faraday et
c e e e e
¯
la composante Hy2 , on trouve la composante du troisi`me ordre en fr´quence du champ
e e
e ¯
´lectrique Ex3 , puis celle du quatri`me ordre en fr´quence du champ magn´tique Hy4 ,
e e e ¯
e e e ¯
puis celle du cinqui`me ordre en fr´quence du champ ´lectrique Ex5 et ainsi de suite. Par](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-113-320.jpg)
![4-104 Statique et Quasi-statique
¯ ¯
exemple, de (4.55) dans laquelle on remplace Hy0 par Hy2 et on applique la conditions
aux limites, on d´duit :
e
¯ 1 Io z 3
Ex3 = j ω 3µ2 ǫ ( − ℓ2 z) .
2 w 3
Finalement, ` l’entr´e z = −ℓ :
a e
¯ 1 Io
[Ex3 ]z=−ℓ = −j ω 3 µ2 ǫℓ3 (4.60)
3 w
¯ 2 5 3 2 5 Io
[Ex5 ]z=−ℓ = −j ω µ ǫ ℓ (4.61)
15 w
.
.
.
Il faut bien comprendre que le champ ´lectrique ` l’int´rieur du mat´riau sans perte
e a e e
est la somme de toutes les composantes aux diff´rents ordres en fr´quence. Cette somme
e e
infinie converge vers une valeur bien connue :
¯ ¯ ¯ ¯
[Ex ]z=−ℓ = [Ex1 ]z=−ℓ + [Ex3 ]z=−ℓ + [Ex5 ]z=−ℓ . . . (4.62)
µ Io √ 1 √ 2 √
= −j ω µǫℓ + (ω µǫℓ)3 + (ω µǫℓ)5 . . . (4.63)
ǫ w 3 15
√
tan(ω µǫℓ)
ou
¯ µ Io √
[Ex ]z=−ℓ = −j tan(ω µǫℓ) . (4.64)
ǫ w
Cette derni`re ´quation (4.64) reste valide quelle que soit la fr´quence. Cependant, on
e e e
prouve facilement que le cas quasi-statique est respect´ si on pose la condition suivante a
e `
√
savoir ω µǫℓ ≪ 1 soit :
1
f ≪ √ . (4.65)
2π µǫℓ
On observe avec grand int´rˆt que la fr´quence pour laquelle le comportement de l’induc-
ee e
tance suit celui indiqu´ dans la th´orie des circuits d´pend des dimensions de la structure.
e e e
`
A partir d’une certaine fr´quence, le cas quasi-statique n’est plus applicable et il faut
e
passer ` la th´orie des micro-ondes. On pourrait riposter en disant qu’une solution est de
a e
diminuer la taille des structures ce qui permet de pousser plus loin la fr´quence limite.
e
Malheureusement, on ne peut sans cesse miniaturiser les structures sans qu’interviennent
des probl`mes d’ordre :
e
• m´canique – la construction rel`vera du d´fi,
e e e
• thermique – il faut dissiper la puissance via la surface,
• physique mˆme – transistors dont la base n’aurait que quelques atomes d’´paisseur !
e e
C’est l` que les choses se compliquent et que se jouera l’avenir.
a
Une autre observation int´ressante (en particulier lorsqu’on traitera des lignes de trans-
e
mission en r´gime sinuso¨ permanent) peut ˆtre tir´e de cette analyse. Avec (4.64) dans
e ıdal e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-114-320.jpg)

![4-106 Statique et Quasi-statique
e ` ¯ e e ¯
L’´tape suivante consiste a entrer Ex0 de (4.67) dans la loi d’Amp`re pour d´duire Hy .
Donc, on obtient :
¯
∂ Hx Vo
¯
= −jωǫ Ex0 = jωǫ
∂z d
ce qui donne :
¯ Vo ¯
Hy1 = jωǫ z + C .
d
¯
Comme il n’y a pas de courant surfacique sur les plaques ` z = 0, il faut que [Hy ]z=0 = 0
a
¯
On trouve alors C = 0 d’o` :
u
¯ Vo
Hy1 = jωǫ z . (4.68)
d
¯
Il faut maintenant prendre Hy1 dans l’´quation de Faraday pour fermer la boucle, v´rifier
e e
la condition aux limites du champ ´lectrique tangentiel ` z = −ℓ. On reprend tout a
e a `
e e ¯
partir de l’´quation d’Amp`re avec Ex2 et ainsi de suite, d’o` :
u
¯ 1 Vo
Ex2 = ω 2 µǫ (z 2 − ℓ2 ) (4.69)
2 d
¯ 1 Vo
Hy3 = −j ω 3 µǫ2 (z 3 − 3ℓ2 z) (4.70)
6 d
En continuant le d´veloppement, on trouve que le champ magn´tique a l’entr´e z = −ℓ
e e ` e
est une s´rie infinie de puissance en fr´quence qui converge vers :
e e
¯ ¯ ¯ ¯
[Hy ]z=−ℓ = [Hy1 ]z=−ℓ + [Hy3 ]z=−ℓ + [Hy5 ]z=−ℓ . . . (4.71)
ǫ Vo √ 1 √ 2 √
= −j ω µǫℓ + (ω µǫℓ)3 + (ω µǫℓ)5 . . . . (4.72)
µ d 3 15
√
tan(ω µǫℓ)
o`
u
¯ ǫ Vo √
[Hy ]z=−ℓ = j tan(ω µǫℓ) . (4.73)
µ d
a e e ¯ a ¯
Comme le courant ` l’entr´e, not´ I, correspond ` w [Hy ]z=−ℓ , on peut obtenir une
¯ ¯
relation Vin /Iin et d´duire l’expression de l’imp´dance vue ` l’entr´e (voir l’´quation (4.66)
e e a e e
pour les d´finitions de Zo et de β) :
e
¯ 1 1
Zin =
w j ǫ 1 tan(ω √µǫℓ)
µ d
= −jZo cot(βℓ) . (4.74)
Le comportement est bien celui d’un condensateur ` basse fr´quence, i.e. lorsque
a e
√
ω µǫℓ ≪ 1 ; car, suivant cette condition, on a :
¯ 1 1
Zinbf = (4.75)
w j ǫ 1 ω √µǫℓ
µ d
1
= (4.76)
ǫℓw
jω
d
C
1
= ! (4.77)
jωC](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-116-320.jpg)




![4.8 Analyse de comportement en quasi-statique 4-111
Un galvanom`tre est constitu´ d’une armature ferromagn´tique µra = 500 dont la
e e e
section carr´ vaut c × c = 1 cm × 1 cm, de longueur moyenne ℓa = 8 cm et dont l’entrefer a
e
une forme cylindrique. Dans cet entrefer est plac´ une bobine ferromagn´tique µrb = 103
e e
de rayon rb = 0.5 cm comportant 40 tour de fils formant un cadre. La bobine et son
cadre peuvent pivoter librement. Un aimant dans l’armature produit un potentiel scalaire
magn´tique NI = 200 A · tours.
e
La forme de l’entrefer et de la bobine fait en sorte que le flux dans les petits entrefers
qui s´parant l’armature de la bobine de = 0.5 mm, est radial avec une densit´ uniforme.
e e
On consid`re que la r´luctance de la bobine correspond ` celle d’une bloc de longueur
e e a
´gale a ℓb = 2rb = 1 cm avec une section identique ` celle de l’armature.
e ` a
a) Calculez la densit´ de flux dans les petits entrefers ;
e
b) Si un ressort ayant une constante de rappel de couple k = 2 × 10−7N · m/◦ est reli´ e
au cadre, calculez sur quel angle θ le cadre pivote avec un courant de 2 mA dans le
fil du cadre.
R´ponses :
e
ρo r 2
3a
r<a
1. D = Dr (r)ar avec Dr (r) = ρo a2
3r
r>a .
Ir
18πa2
r < 3a
I
2πr
3a < r < 4a
2. H = Hφ (r)aφ avec Hφ (r) = I 25a2 −r 2
2πr 9a2
4a < r < 5a
0 r > 5a .
0 r<a
1
3. E = Er (r)ar avec Er (r) = r2
V/m a < r < b
−6
r2
V/m r > b .
4. a) Vab = 0 ; b) Vab = −7 V .
ln(r/b) Vo
5. a) V = Vo ln(a/b) ; b) E = a.
r ln(b/a) r
6. V1 = (V2 + 28)/4, V2 = (V1 + V3 )/4, V3 = (V2 + 28)/4 ;
par sym´trie V1 = V3 = 8 V , V2 = 4 V ;
e
7. V1 = 0.8 V et V2 = 0.4 V.
8. a) V1 = 41 V , V2 = 40.5 V , V3 = 38 V , V4 = 71 V , V5 = 80 V ;
83 3
b) [E]2 = − 2d ay + 2d ax V /m ; c) [ρs ]p = −38ǫo /d C/m2 .](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-121-320.jpg)
![4-112 Statique et Quasi-statique
4πǫ
9. a) d = 1.99 cm ; b) C = 1/a−1/b donc a = 2 cm ;
c) prendre b → ∞, r = a = 9 cm.
ǫr2 d1
10. a) E 1 = Ez1 az et ǫ1 Ez1 = ǫ2 Ez2 , [V ]z=d1 = ǫr2 d1 +ǫr1 d2
Vo ;
b) C/A = ǫ2 d11 ǫ21 d2 = ǫr2 dǫr1 ǫr1d2 .
ǫ
+ǫ
ǫo
1 +ǫ
r2
2
11. B = µ 2πr , L = µ N c ln(1 + b/a).
NI
2π
12. a) ΨGF AB = 226 × 10−6 W b ;
b) ΨBD = Ψentref er = ΨEG = 33.36 × 10−6 W b, Bentref er = 0.1112 W b/m2 .
2
Q dr Q2
13. a) dWe = − 8πǫo a2 ; b) Pe = 32π 2 ǫo a4
= 0.2235 N/m2.
14. a) ℜentref er = 5.066 × 106 H −1 , Ψentref er = Ψ = 17.41 × 10−6 W b,
donc Bentref er = 0.2217 W b/m2 ;
b) T = F rb = 2 × B(Nc I)c rb = kθ[◦ ], θ = 8.9◦ .](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-122-320.jpg)







![5-120 Onde plane uniforme
du temps. Donc e−αz d´croˆ lorsque z augmente ce qui fait dire que l’onde s’att´nue en
e ıt e
se propageant. La seconde onde se d´place dans la direction z− et, comme pour l’onde
e
αz
positive, e d´croˆ car z diminue en fonction du temps. Dans les deux cas, α est respon-
e ıt
sable de la baisse de l’amplitude de l’onde d’o` son appellation, constante d’att´nuation.
u e
Les unit´s de α sont les N´pers par m`tre qu’on note Np/m. L’att´nuation par unit´ de
e e e e e
α
longueur vaut L1 = e soit, en d´cibels :
e
L1 [dB] = 20 log(eα ) = 8.686 α . (5.25)
|ej(ωt−βz) | t=0
T
t= 4 T t≈T
t= 2
z
λ
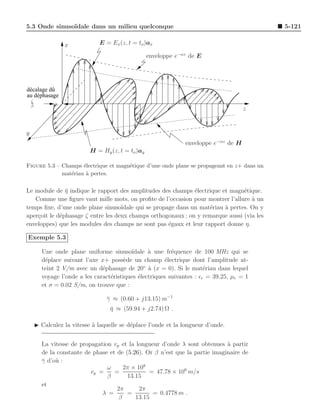
Figure 5.2 – Longueur d’onde λ et p´riode T d’une onde sinuso¨
e ıdale.
Quant ` la constante β, elle intervient dans la phase de l’onde qui varie avec le d´place-
a e
ment. C’est la constante de phase. Elle est directement reli´e a la longueur d’onde λ de la
e `
fa¸on suivante. La longueur d’onde λ correspond ` la distance sur laquelle la phase change
c a
de 2π radians en fixant le temps. La p´riode est l’´quivalent dans le domaine du temps
e e
de la longueur d’onde comme le montre la figure 5.2. Ainsi, on a βλ = 2π ou encore :
2π ω
β = = . (5.26)
λ vp
La derni`re ´galit´ de (5.26) est obtenue en multipliant le num´rateur et le d´nominateur
e e e e e
par f – la fr´quence du signal sinuso¨
e ıdal – et en sachant que λ = vp /f o` vp est la vitesse
u
de phase ´quivalente ` la vitesse de propagation de l’onde plane.
e a
Le d´veloppement de (5.19) pour le champ magn´tique donne cette fois :
e e
+ −
¯
Hy = H + e−αz e−jβz+jξh + H − eαz ejβz+jξh (5.27)
E + −αz −jβz+jξ+−jζ E − αz jβz+jξ−−jζ
= e e − e e . (5.28)
η η
L’argument de l’imp´dance caract´ristique η tel que d´fini en (5.21) correspond au retard
e e ¯ e
angulaire du phaseur du champ magn´tique sur celui du champ ´lectrique. On peut v´rifier
e e e
que ce retard ζ varie entre les bornes suivantes selon la nature du mat´riau :
e
0 ≤ arg{¯} = ζ < 45◦ .
η (5.29)](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-130-320.jpg)
![5-122 Onde plane uniforme
◮ Exprimez le champ magn´tique H(x, t) (la direction du vecteur n’est pas de-
e
mand´e).
e
Cette fois, on a besoin des deux param`tres de propagation. Il ne faut pas
e
oublier que l’onde se propage en x+ seulement et non en z+ ou z−. Il suffit
donc de prendre l’expression de l’onde positive et remplacer z par x.
On n’oublie pas le terme d’att´nuation e−αx car le milieu est a pertes. Avec
e `
η = (60.0∠0.0457) Ω
¯
¯ x=0 = (2.0∠π/9)aE V/m
[E]
on trouve alors :
2 −αx
H(x, t) = e cos(2π × 108 t − β x + π/9 − arg{¯})
η
η
= 0.0333 e−0.6x cos(2π × 108 t − 13.15 x +0.3491 − 0.0457) A/m .
+0.3034
5.4 Puissance et vecteur de Poynting
¯ ¯
La d´termination des constantes complexes E + ou E − se fait en appliquant des condi-
e
tions aux limites ou encore en connaissant la puissance d´livr´e par la source. On peut
e e
comprendre facilement que la puissance transport´e par l’onde est reli´e a l’amplitude
e e `
du champ ´lectrique, laquelle est li´e ` celle du champ magn´tique via le module de
e e a e
l’imp´dance intrins`que. Reste ` savoir dans quelle mesure l’amplitude des champs ´lectro-
e e a e
magn´tiques influence la puissance de l’onde.
e
Depuis 1884, on sait, par l’entremise du physicien anglais John H. Poynting que le
vecteur E × H joue un rˆle important dans la quantit´ d’´nergie transport´e par une
o e e e
onde ´lectromagn´tique, d’o` le nom de vecteur de Poynting not´ P :
e e u e
P = E ×H . (5.30)
En regardant les unit´s r´sultantes de ce produit, des V /m · A/m = W/m2 , on se convainc
e e
facilement qu’il s’agit d’une densit´ de puissance. On pourrait aussi pr´senter la chose
e e
d’un angle plus physique en d´montrant que le travail n´cessaire pour produire l’onde et,
e e
de l`, la puissance instantan´e P(t) fournie par la source, ´quivaut a l’int´grale du vecteur
a e e ` e
de Poynting P sur une surface ferm´e entourant compl`tement la source :
e e
P(t) = P · dS . (5.31)
S
Un vecteur poss`de aussi une direction. Celle du vecteur de Poynting aP pointe dans
e
la direction de propagation de l’onde tout simplement.
L’onde ´lectromagn´tique est donc le moyen de propagation de la puissance fournie
e e
par une source rayonnante. Elle :](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-132-320.jpg)
![5.4 Puissance et vecteur de Poynting 5-123
• renferme la puissance – de densit´ correspondant au module du vecteur de Poynting ;
e
• et la transporte – elle se d´place dans la direction du vecteur de Poynting.
e
Dans un volume d´limit´ par une surface ferm´e, outre les sources, diff´rentes composantes
e e e e
sont susceptibles de modifier le bilan de puissance, i.e. la diff´rence de puissance entre ce
e
qui entre et ce qui sort du volume. Pour ce faire, on utilise le th´or`me de la divergence :
e e
P · dS = (∇ · P ) dv (5.32)
S V
combin´e a une identit´ vectorielle :
e ` e
∇ · (E × H) = H · ∇ × E − E · ∇ × H (5.33)
puis aux ´quations de Faraday et d’Amp`re. Le tout d´bouche sur :
e e e
∂H ∂E
∇ · P = −µH · − σE · E − ǫE ·
∂t ∂t
∂ 1 ∂ 1
= − σE(t)2 − ( 2 ǫE(t)2 ) − ( µH(t)2 ) (5.34)
∂t ∂t 2
pd we wm
puis finalement, sur le th´or`me de Poynting :
e e
∂ ∂
P · dS = − pd dv − we dv − wm dv (5.35)
S V ∂t V ∂t V
o` pd , we et wm sont respectivement la densit´ de puissance dissip´e, la densit´ d’´nergie
u e e e e
´lectrique emmagasin´e et la densit´ d’´nergie magn´tique emmagasin´e.
e e e e e e
x
[P z ]z0 (∆x∆y)
[P z ]z0 +∆z (∆x∆y)
z
∆z
y
∆V
Figure 5.4 – Bilan de puissance d’une onde plane dans un volume.
Si on ignore le signe n´gatif, les trois termes de droite du th´or`me de Poynting s’in-
e e e
terpr`tent ainsi :
e
• σE 2 ∆V est la puissance dissip´e dans le volume ` cause du courant de conduction
e a
pr´sent dans le volume ∆V , c’est l’effet joule qui produit un ´chauffement.
e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-133-320.jpg)
![5-124 Onde plane uniforme
[P z ]t=0 [P z ]z=z0 < Pz >
z t
λ T
2 2
[E x ]z=z0
Figure 5.5 – Variation de la densit´ de puissance dans le temps et suivant la direction de
e
propagation.
• 1 ǫE 2 ∆V et 1 µH 2 ∆V repr´sentent les ´nergies ´lectrique et magn´tique qui sont
2 2
e e e e
contenues dans le volume. Un condensateur charg´ emmagasine de l’´nergie ´lectrique,
e e e
r´ciproquement pour une inductance avec l’´nergie magn´tique. Ainsi, une variation
e e e
e.g. une diminution sur un laps de temps de chacune de ces ´nergies disponibles,
e
signifie qu’une certaine quantit´ de puissance a quitt´ le volume.
e e
On peut voir le bilan des puissances entrant et sortant d’un volume produit par une
onde ´lectromagn´tique uniforme plane sur la figure 5.4 tandis que la figure 5.5 montre
e e
comment varie la densit´ de puissance d’une onde plane dans un mat´riau a pertes.
e e `
Il est possible de d´terminer la puissance instantan´e d’une onde ´lectromagn´tique
e e e e
passant au travers une surface quelconque. Il suffit alors d’int´grer le vecteur de Poynting
e
sur la surface en question et non pas sur une surface ferm´e :
e
[P(t)]S = P · dS . (5.36)
S
Si la surface est plac´e parall`lement ` la direction de l’onde, aucune puissance ne traverse
e e a
la surface. Par contre, un ´l´ment de surface bien transversal a la direction verra un
ee `
maximum de puissance passer au travers. De l`, l’importance du produit scalaire. Pour
a
faire une comparaison, le Soleil d’hiver ` Qu´bec2 , atteint une ´l´vation maximale par
a e ee
rapport au sol de moins de 90−46.8−23.5 ≈ 20 au 21 d´cembre. L’angle de 90−20 = 70◦
◦
e
entre la rayonnement solaire aP et la normale au sol fait que chaque unit´ de surface au
e
sol re¸oit 34% de la puissance maximale. En ´t´, l’´l´vation maximale tourne autour de
c e e ee
90 − 46.8 + 23.5 ≈ 67 ce qui procure 92% (le cosinus de 90 − 67 = 23◦ ) de la puissance
◦
maximale par unit´ de surface au sol ! Bien sˆ r, il y a aussi la dur´e d’´clairement et la
e u e e
r´flexion des rayons au sol qui interviennent.
e
En circuit, on s’int´resse bien plus ` la puissance moyenne qu’` sa valeur instantan´e.
e a a e
Il en va de mˆme pour l’onde ´lectromagn´tique. Pour all´ger la nomenclature, on utilise
e e e e
indiff´remment le terme de puissance (tout court) pour d´signer la puissance moyenne par
e e
opposition ` la puissance instantan´e. De plus, dans le r´gime sinuso¨
a e e ıdal permanent avec
2
Qu´bec se trouve ` une latitude de 46.8◦ ; l’obliquit´ de l’´cliptique est de 23.5◦.
e a e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-134-320.jpg)
![5.4 Puissance et vecteur de Poynting 5-125
des phaseurs, on peut obtenir rapidement la densit´ de puissance (sous-entendre moyenne)
e
via le vecteur de Poynting moyen < P > d´fini comme suit :
e
1 1 ¯
<P > = P dt = EH cos(arg{¯}) aP = Re P
η (5.37)
T T 2
o` T est la p´riode du signal, et
u e
¯ 1¯ ¯∗
P = E×H (5.38)
2
est le vecteur de Poynting complexe. Avec cette densit´ de puissance, la puissance moyenne
e
passant par une surface S est d´duite maintenant par l’´quivalent de (5.36) a savoir :
e e `
[< P >]S = < P > ·dS . (5.39)
S
Exemple 5.4
La Terre est ` 150 millions de kilom`tres du Soleil. La densit´ de puissance
a e e
optimale fournie par le Soleil sur la Terre tourne autour de 1360 W/m2 sur
tout le spectre.
◮ D´terminez la puissance moyenne ´mise par le Soleil.
e e
On peut assumer que le Soleil est une source isotrope (qui ´met uniform´ment
e e
dans toute les directions). De plus, le vide interstellaire est un di´lectrique
e
sans pertes (σ = 0) et l’effet des plan`tes Mercure et V´nus est n´gligeable.
e e e
Ainsi, selon (5.31), la puissance du Soleil serait de :
< PSoleil > = (1360)dS = 4π(150 × 109 )2 (1360) = 3.84 × 1026 W .
sph`re
e
◮ Estimez le niveau maximal du champ ´lectrique au sol si on suppose que toute
e
la densit´ de puissance est ramen´e ` une seule composante spectrale.
e e a
Puisque le mat´riau (l’air) est assum´ sans perte, les champs ´lectrique et
e e e
magn´tique sont en phase. Le vecteur de Poynting complexe de (5.38) s’´crit
e e
simplement comme :
¯
1 ¯ E∗ 1 E 2 ∠0◦
¯
P = E ∗ as−t = as−t
2 η ¯ 2 ηo
o` as−t est un vecteur unitaire Soleil-Terre.
u
Ainsi, avec l’aide de (5.37) :
1 E 2 cos(0)
1360 = =⇒ E = (377)(2)(1360) = 1012 V/m !
2 ηo](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-135-320.jpg)
![5-126 Onde plane uniforme
Exemple 5.5
Soit une onde ´lectromagn´tique qui se propage dans l’eau de mer (ǫr = 80,
e e
µr = 1 et σ = 4 S/m) dans la direction z−. Le champ ´lectrique s’exprime
e
ainsi :
[E(t)]z=0 = 1.0 cos(2π × 105 t) ax V/m
a
` z = 0.
◮ D´terminez la densit´ de puissance instantan´e et la densit´ de puissance
e e e e
moyenne de l’onde en tout point.
On doit commencer par trouver les expressions g´n´rales de E(z, t) et H(z, t).
e e
ıtre ¯ ¯a e `
Il faut connaˆ γ ainsi que η ` la fr´quence de 105 Hz dans le milieu. A partir
des ´quations (5.16) et (5.20), les valeurs obtenues sont :
e
γ ≈ (1.257 + j1.257) m−1
¯
η ≈ 0.314 + j0.314 = (0.444∠ π/4) Ω.
¯
Donc :
E = 1.0e1.257z cos(2π × 105 t + 1.257z) ax V/m
1.0
H = −e1.257z cos(2π × 105 t + 1.257z − π/4) ay A/m .
0.444
2.25
Le signe n´gatif devant l’expression de H vient du fait que le produit vectoriel
e
E × H doit pointer dans la direction z− qui est la direction de propagation
de l’onde. Autre remarque : l’exponentielle affectant le module tend vers “0”
au fur et ` mesure que z diminue et devient n´gatif. Ceci, parce que le milieu
a e
est ` pertes.
a
Le vecteur de Poynting instantan´ est donn´ par :
e e
P = 2.25e2.514z cos(2π × 105 t + 1.257z)
× cos(2π × 105 t + 1.257z − π/4) (−az ) W/m2
Pz = −1.125e2.514z cos(π/4) + cos(4π × 105 t + 2.514z − π/4) W/m2
Le signe n´gatif devant l’expression de Pz signifie que la puissance s’´coule
e e
dans la direction z−. Finalement, la puissance par unit´ de surface normale a
e `
l’axe z est :
< Pz > = −1.125e2.514z cos(π/4) = −0.8e2.514z W/m2 .
◮ D´duisez la puissance incidente sur une surface rectangulaire de 2 m × 1 m
e
plac´e comme sur la figure 5.6.
e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-136-320.jpg)
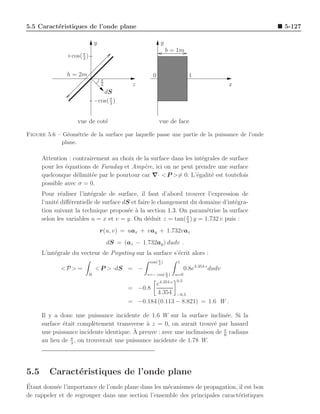















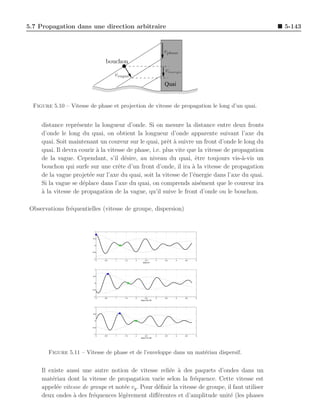
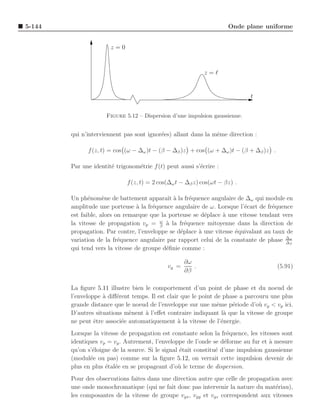



![5-148 Onde plane uniforme
Exemple 5.12
L’expression du phaseur du champ ´lectrique d’une onde plane se propageant
e
en z+ dans un mat´riau sans perte, est la suivante :
e
¯
[E]z=0 = Eo ∠0 ay .
◮ Donnez l’expression compl`te du champ ´lectrique pour avoir une polarisation
e e
RCP.
La composante Ex est nulle ` t = 0, z = 0 puisque Ey est maximale selon la
a
donn´e du probl`me. En effet :
e e
Ey (z, t) = Eo cos(ωt − βz) .
Pour tourner dans le sens horaire, Ex doit donc d´croˆ pour atteindre un
e ıtre
minimum lorsque Ey devient nulle ` son tour soit ` 90◦ comme argument. Il
a a
ne faut pas oublier que le produit vectoriel ax × ay = az doit pointer hors de
soi. La composante Ex suit donc la fonction d’un sinus n´gatif. Ainsi :
e
Ex (z, t) = −Eo sin(ωt − βz) .
En cons´quence, le vecteur du champ ´lectrique s’´crit :
e e e
π
E(z, t) = Eo cos(ωt − βz + )ax + cos(ωt − βz)ay .
2
Dans une polarisation elliptique (REP ou LEP), la plus g´n´rale de toute, la diff´rence
e e e
se situe ` l’un des deux niveaux suivants pour une onde qui se d´place suivant l’axe z± :
a e
• amplitudes diff´rentes des composantes transverses du vecteur du champ ´lectrique
e e
i.e. Ex = Ey ;
• d´phasage quelconque δξ = ξy − ξx ∈ ] − π, π].
e
Toutes combinaisons d’amplitudes et de d´phasages fournissent une polarisation elliptique.
e
Ceci procure de nombreux cas de figure que toutes les autres polarisations deviennent des
cas particuliers.
La figure 5.16 illustre quelques cas et montre la grande diversit´ d’allures du lieu du
e
phaseur du champ ´lectrique. Sur la figure 5.17, on remarque les deux param`tres de
e e
l’ellipse :
• l’angle d’inclinaison ψe :
1
ψe = arctan(tan(2αe ) cos(δξ )) (5.100)
2](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-158-320.jpg)
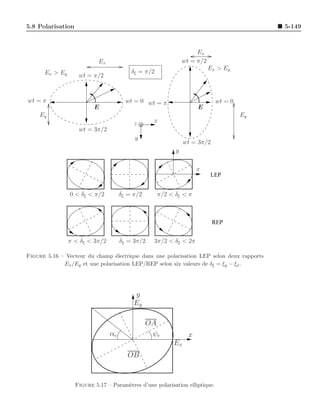
![5-150 Onde plane uniforme
• ainsi que le rapport axial6 AR (de l’anglais “Axial Ratio”) :
OA
AR = (1 ≤ AR ≤ ∞)
OB
|Ey sin(ψe ) sin(δξ )|
= . (5.101)
|Ex sin(ψe ) − Ey cos(ψe ) cos(δξ )|
toujours avec tan(αe ) = Ey /Ex ;
Exemple 5.13
Soient deux ondes ` la mˆme fr´quence polaris´es lin´airement et voyageant
a e e e e
dans le mˆme milieu sans perte, dans la mˆme direction z+ :
e e
¯
E 1 (z) = E1 e−jβz ax
¯
E 2 (z) = E2 e−jβz ejξ ay .
On consid`re que E1 , E2 sont constants.
e
◮ D´duisez quelles sont les polarisations obtenues dans les cas ci-dessous :
e
• ξ = 0, E1 = 4 mV/m, E2 = 3 mV/m ;
• ξ = π/2, E1 = E2 = 3 mV/m ;
• ξ = π/2, E1 = 4 mV/m, E2 = 3 mV/m ;
• ξ = 7π/4, E1 = E2 = 3 mV/m.
Dans le premier cas, les deux ondes sont en phase. Donc, quelle que soit la
relation d’amplitude, la polarisation est lin´aire mais oblique car aucune des
e
deux composantes n’est nulle. L’inclinaison vaut arctan(3/4) = 36.87◦ .
Les composantes ´tant en retard l’une de l’autre de ±90◦ et les amplitudes
e
e e `
´tant ´gales, la polarisation est circulaire. A t = 0, z = 0, le phaseur est plac´e
◦
a
` 0 car [Ey ]t=z=0 = 0. Cependant ` t = ǫ, [Ex ]t,z=0 a diminu´, tout comme
a e
[Ey ]t,z=0 . Il faut donc tourner dans le sens anti-horaire en regardant vers l’axe
z+, ce qui indique une polarisation LCP.
Par rapport au cas pr´c´dent, seules les amplitudes changent. La polarisation
e e
devient elliptique pour cette raison mais demeure a gauche d’o` LEP. On
` u
peut rajouter que le rapport axial s’´value directement grˆce aux amplitudes
e a
de chacune des ondes et vaut 4/3 avec un angle d’inclinaison de 0◦ .
Le dernier cas montre des amplitudes ´gales mais un d´phasage diff´rent de
e e e
◦
±90 . La polarisation reste encore elliptique. Les calculs des param`tres tels
e
6
Le rapport axial doit toujours ˆtre plus grand ou ´gal ` l’unit´ ; si l’expression (5.101) donne un
e e a e
r´sultat inf´rieur ` l’unit´, prendre l’inverse (·)−1 .
e e a e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-160-320.jpg)
![5.8 Polarisation 5-151
l’inclinaison et le rapport axial commencent avec celui de αe lequel vaut 45◦ .
On trouve alors :
1
ψe = arctan(∞) = 45◦ ou π/4
2
|3 sin(π/4) sin(7π/4)|
AR = = 2.4142 .
|3 sin(π/4) − 3 cos(π/4) cos(7π/4)|
Un petit laps de temps plus tard, [Ex ]t,z=0 diminue contrairement a [Ey ]t,z=0 .
`
Le vecteur tourne dans le sens horaire ce qui indique une polarisation REP.](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-161-320.jpg)






![5-158 Onde plane uniforme
6. γ = (0.00083 + j0.00476) m−1, η = (163.53∠9.9◦)Ω.
¯ ¯
7. a) 20 m ; b) 10 m ; c) 62.83 m ; d) E/H = 70.62 Ω, ∠E − ∠H = 0.1476π rad.
8. a) γ = (0.0349 + j0.0565) m−1 ; b) η = (59.4∠31.7◦) Ω ;
¯ ¯
−3
c) σ = 10 S/m, ǫ = 18ǫo , µ = µo .
9. E(z, t) = − 2.686 e−0.016z cos(2π × 105 t − 0.0246z + 0.1834π) ay V /m.
10. a) ǫr = 9 ; b) ǫr = 4 ; c) ǫr = 2.25 ; d) ǫr = 16.
11. a) 5 m ; b) d105 = 0.5 m, d104 = 0.1581 m.
12. le mat´riau se comporte comme un di´lectrique imparfait ;
e e
a) γ = (1.0883 × 10 + j0.036276) m−1, η = (217.66 + j0.653) Ω ;
¯ −4
¯
8
b) vp = 1.732 × 10 m/s, λ = 173.21 m ; c) δp = 9.189 km.
13. le mat´riau se comporte comme un bon conducteur ;
e
a) γ = 0.4π(1 + j) m−1 , η = 0.1π(1 + j) Ω ;
¯ ¯
b) vp = 5 × 105 m/s, λ = 5 m ; c) δp = 0.796 m.
14. η = 12π 2 ejπ/6 Ω, a) [P(z = 0, t = 0)]s = 3.0771 W ;
¯
b) [< P(z = 0) >]s = 1.5385 W ; c) [< P(z = 1) >]s = 0.2082 W .
15. η = (3.531∠26.57◦) Ω,
¯
a) < P >= 0.005064e−2z az W/m2 donc [< Pz >](3,2,1) = 0.685 mW/m2 ;
b) [∆ < P >]box = 0.005064(1 − e−2 ) = 0.00438 W .
1
16. a) aβ = 5 (3ax + 4az ) ; b) λ = 20 m
c) λx = 33.333 m, λy = ∞, λz = 25 m ;
d) vpx = 3.333 × 108 m/s, vpy = ∞, vpz = 2.5 × 108 m/s.
17. a) aβ = 0.8ax − 0.6ay ; b) oui car aE · aβ = 0 ;
c) f = 1.5 GHz, circulaire gauche ;
¯
d) H = (−j7.96ax − j10.6ay + 13.3az )e−jπ(8x−6y) µ A/m.
18. a) f = 225 MHz ; b) f = 225 MHz.
19. a) β = (0.8πax + 0.6πay + πaz ) rad/m ; b) vpi = 3.25 × 108 m/s.
√ √
20. a) vp1.4 = 2.2136 kωo , vp1.6 = 2.0656 kωo ;
√
b) vg1.5 = 1.4142 kωo .
21. a) circulaire droite, Emax = Eo ; b) lin´aire en x, Emax = 2Eo
e
◦
c) elliptique droite ψe = 31.7 , Emax = 1.618Eo , AR = 2.62 ;
d) circulaire gauche, Emax = Eo .](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-168-320.jpg)

![6-160 R´flexion et transmission
e
millieu #1 millieu #2
onde ¯+
E1
incidente ¯+
E2
onde
transmise
onde ¯−
réfléchie E1
z
z=0
Figure 6.1 – Onde ` incidence normale sur un plan de s´paration de deux milieux.
a e
• 1 et 2 indiquent les milieux dans lesquels se trouve l’onde. Le mat´riau #1 contient
e
l’onde incidente et l’onde r´fl´chie ; il remplie le volume z < 0, alors que le mat´riau
e e e
#2, contenant l’onde transmise occupe le volume z > 0.
L’onde incidente se propage dans le premier milieu (z < 0) suivant la direction z+
normale ` la surface de s´paration z = 0 ; l’onde r´fl´chie part dans la direction oppos´e
a e e e e
z−, tandis que l’onde transmise continue son chemin dans le second milieu (z > 0) en
direction z+. La polarisation n’intervient pas car le champ ´lectrique, comme le champ
e
magn´tique d’ailleurs, ne poss`de qu’une composante parall`le ` la surface de s´paration.
e e e a e
Les expressions des champs dans chacun des milieux deviennent :
¯ ¯ γ ¯ ¯
E1x (z) = Ei e−¯1 z + Er eγ1 z (6.1)
¯ ¯ γ
E2x (z) = Et e−¯2 z (6.2)
¯ ¯ γ ¯ ¯
H1y (z) = Hi e−¯1 z + Hr eγ1 z (6.3)
1 ¯ −¯1 z ¯ ¯
= Ei e γ − Er eγ1 z (6.4)
η1
¯
¯ ¯ γ
H2y (z) = Ht e−¯2 z (6.5)
1 ¯ −¯2 z
= Et e γ (6.6)
η2
¯
u ¯ ¯ ¯ ¯
o` Ei , Er , Hi et Hr sont les composantes des champs incidents et r´fl´chis qui sont tous
e e
dans le milieu #1 ; E¯t et Ht sont les champs transmis dans le milieu #2.
¯
Les conditions aux limites des composantes tangentielles doivent ˆtre satisfaites en
e
z=0:
¯ ¯
[E1x ]z=0− = [E2x ]z=0+ (6.7)
¯ ¯
[H1y ]z=0− = [H2y ]z=0+ . (6.8)
En les appliquant avec les paires d’´quations (6.1) ` (6.6), il s’ensuit que :
e a
¯ ¯ ¯
Ei + Er = Et (6.9)
1 ¯ ¯ 1 ¯
Ei − Er = Et . (6.10)
η1
¯ η2
¯](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-170-320.jpg)

![6-162 R´flexion et transmission
e
du champ magn´tique transmise vaut le double de celle incidente. Il n’en est rien.
e
En fait, un courant de surface Js = 2[Hi ]z=0− apparaˆ sur le conducteur mais ni
ıt
le champ ´lectrique, ni le champ magn´tique est transmis. L’onde est r´fl´chie en
e e e e
◦
totalit´ et le phaseur du champ ´lectrique r´fl´chi pivote de 180 au niveau de la
e e e e
surface de s´paration, alors que le phaseur du champ magn´tique reste en phase.
e e
Ceci respecte une des caract´ristiques de l’onde plane a savoir le produit vectoriel
e `
des deux champs indique la direction de propagation ; or, cette derni`re change de
e
sens lorsqu’il y a r´flexion.
e
Exemple 6.1
Une onde plane ` 150 kHz se propage dans l’air z < 0 et arrive a incidence
a `
normale sur le sol z > 0 dont la surface se situe en z = 0. Les param`tres
e
−4
´lectriques du sol valent ǫr = 5, µr = 1 et σ = 10 S/m.
e
◮ Donnez les expressions compl`tes des champs ´lectromagn´tiques de l’onde
e e e
r´fl´chie et transmise si le vecteur-phaseur du champ ´lectrique incident a
e e e `
−
z = 0 s’´crit :
e
¯
[E i ]z=0− = Eo ∠0 ax .
On a besoin absolument des param`tres de propagation dans les deux milieux
e
a
` la fr´quence de 150 kHz. On trouve :
e
η1 = 377Ω
¯ γ1 = j3.14 × 10−3 m−1
¯
.
η2 = (104.56∠0.59)Ω γ2 = (6.28 + j9.43) × 10−3 m−1
¯ ¯
Ainsi, de (6.11) et (6.14) :
¯ 104.56∠0.59 − 377∠0
Γ =
104.56∠0.59 + 377∠0
= 0.633∠2.82
τE = 0.447∠0.464 .
¯
Il est maintenant possible d’exprimer les champs :
¯ ¯ ¯
[Er ]z=0− = Γ[Ei ]z=0− = 0.633 Eo∠2.82
E r = 0.633 Eo cos(3π × 105 t + 3.14 × 10−3 z + 2.82) ax V /m
¯
[E − ]z=0−
¯
[Hr ]z=0− = − r = −(2.65 × 10−3 )(0.633 Eo∠2.82)
η1
¯
H r = 1.68 × 10−3 Eo cos(3π × 105 t + 3.14 × 10−3 z + 2.82) (−ay ) A/m](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-172-320.jpg)
![6.3 Lois de r´flexion et de r´fraction
e e 6-163
et
¯ ¯ ¯
[Et ]z=0+ = τE [Ei ]z=0− = 0.447 Eo∠0.464
−3
E t = 0.447 Eo e−6.28×10 z cos(3π × 105 t − 9.43 × 10−3 z + 0.464) ax V /m
¯
[Et+ ]z=0+
¯
[Ht ]z=0+ = = (9.56 × 10−3∠ − 0.59)(0.447 Eo∠0.464)
η2
¯
−3
H t = 4.28 × 10−3 Eo e−6.28×10 z
cos(3π × 105 t − 9.43 × 10−3 z − 0.126) ay A/m .
On v´rifie ais´ment que les conditions aux limites sont satisfaites car en z = 0
e e
et t = 0 (quoique vraies ∀t) :
Eo + 0.633 Eo cos(2.82) = 0.447 Eo cos(0.464)
et d’autre part :
Eo
− 1.68 × 10−3 Eo cos(2.82) = 4.28 × 10−3 Eo cos(−0.126) .
377
6.3 Lois de r´flexion et de r´fraction
e e
La r´flexion ` incidence oblique sur une interface plane s´parant deux mat´riaux diff´rents,
e a e e e
requiert l’application des quatre conditions aux limites en plus de l’application de la loi1
de Snell-Descartes.
Au d´part, cette section pr´suppose que les deux mat´riaux de part et d’autre du plan
e e e
de s´paration ont une conductivit´ nulle – donc sans perte.
e e
Soit une onde plane incidente dont le vecteur de propagation β fait un angle θi avec
la normale du plan de s´paration an .
e
La satisfaction des conditions aux limites en z = 0 oblige :
• qu’une partie de l’onde soit r´fl´chie avec un angle θr et que l’autre partie soit
e e
transmise avec un angle θt comme il apparaˆ sur la figure 6.2.
ıt
• qu’` un temps fixe, les creux se situent aux mˆmes endroits de part et d’autre de la
a e
surface de s´paration ; il en est de mˆme pour les crˆtes. Les longueurs d’onde ap-
e e e
parentes de part et d’autre, le long de la surface, sont donc identiques. La fr´quence
e
´tant forc´ment la mˆme, les vitesses de phase de part et d’autre sont aussi iden-
e e e
tiques (voir figure 6.3).
1
La loi de la r´fraction a plutˆt ´t´ d´couverte par le physicien arabe Ibn Sahl vers 984. En 1621,
e o ee e
Snell, un scientifique flamand d´riva math´matiquement la loi mais ne publia pas sa d´couverte. Descartes
e e e
d´montra ind´pendamment la loi par des arguments de conservation du moment dans son trait´ de 1637
e e e
“Discours de la m´thode” sans donner cr´dit ` Snell. Rejetant la solution de Descartes, Fermat arrivera
e e a
a
` la mˆme solution en se basant sur le parcours le plus rapide. Cette loi de r´fraction prend donc le nom
e e
de Descartes pour les fran¸ais, alors qu’ailleurs elle est nomm´e loi de Snell.
c e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-173-320.jpg)












![6-176 R´flexion et transmission
e
6.5 Incidence sur un conducteur parfait
L’analyse de l’incidence sur un conducteur parfait forme l’autre cas extrˆme – le premier
e
cas extrˆme ´tant l’incidence sur le di´lectrique parfait vue pr´c´demment. On peut s’y
e e e e e
prendre de plusieurs fa¸ons. Mais utiliser les ressources mises en place jusqu’` pr´sent
c a e
facilite la chose.
Aucune onde ne se propage dans un conducteur parfait. Les composantes tangentielles
du champ ´lectrique sur la surface du conducteur s’´liminent, ce qui implique :
e e
¯ ¯
[E i ]z=0− + [E r ]z=0− = 0 (6.55)
¯ ¯
E i e−jβ1x sin θ1 + E r e−jβ1 x sin θ1 = 0 (6.56)
¯
E i = −E ¯ r . (6.57)
¯ ¯
En polarisation parall`le, on obtient de plus E⊥i = E⊥r inversant aussi E r par rapport a
e `
la convention tout en conservant un mˆme module. Donc :
e
¯ ¯
Ei = −Er . (6.58)
Ceci signifie que le coefficient de r´flexion vaut −1 qu’importe l’angle d’incidence et la
e
polarisation :
Γcond = −1 . (6.59)
En contre-partie, un courant de surface et des charges sont induits sur la surface de
s´paration pour satisfaire les conditions aux limites des composantes perpendiculaires de
e
E et parall`les de H.
e
Dans le demi-espace occup´ par le mat´riau #1 (pas le conducteur), un diagramme
e e
` certains endroits, le champ double d’amplitude par rapport
d’onde stationnaire s’´tablit. A
e
a
` Ei , ` d’autres endroits, il est compl`tement annul´. Ce diagramme ne varie pas dans
a e e
le temps, d’o` le terme stationnaire. Effectivement, en essayant avec une polarisation
u
perpendiculaire (on obtient le mˆme r´sultat avec une polarisation parall`le), le champ
e e e
total dans ce mat´riau s’exprime comme :
e
¯ ¯
E1 = Ei + Er¯ (6.60)
¯ ¯
= Ei e−jβ1(x sin θ1 +z cos θ1 ) ay + Er e−jβ1(x sin θ1 −z cos θ1 ) ay (6.61)
¯ ¯
E1 = Ei e−jβ1x sin θ1 e−jβ1 z cos θ1 − ejβ1 z cos θ1 (6.62)
−2j sin(β1 z cos θ1 )
E1 = 2 Ei |sin(β1 cos θ1 z)| . (6.63)
Le diagramme stationnaire ne d´pend que de z, la distance au plan de s´paration. Il se
e e
r´p`te ` tous les multiples de λ1z /2 i.e. λ1 /(2 cos θ1 ).
e e a
Si on d´pla¸ait la surface du conducteur ` z = ±kλ1z /2 (k entier), le diagramme
e c a
resterait identique dans tout le reste de l’espace du mat´riau #1 ! Cette propri´t´ sera
e ee
longuement revue dans le chapitre sur le r´gime sinuso¨
e ıdal permanent dans les lignes de
transmission.](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-186-320.jpg)


























![7.8 D´termination des param`tres de ligne
e e 7-203
à plaques parallèles coaxiale conducteur bifilaire
externe
ǫr ǫr
ǫr d a a a
b 2d
w conducteur
interne
fil au dessus d’un bifilaire blindée rubanée (‘‘stripline’’)
plan de masse
b
ǫr ǫr
a a a 2d
h ǫr
w
2d
Figure 7.9 – Section de lignes de transmission usuelles.
infinit´simal dz. De l`, on d´termine la charge en fonction de la diff´rence de
e a e e
potentiel ; le flux magn´tique, en fonction du courant.
e
Les conditions aux limites doivent ˆtre respect´es sur les plaques conductrices.
e e
Elles le sont car, ` x = 0 et x = d, le champ ´lectrique est bien perpendi-
a e
culaire et le champ magn´tique, tangentiel. Les deux conditions aux limites
e
applicables d´montrent qu’une densit´ surfacique de charges et une densit´ de
e e e
courant de surface existent ` la surface des plaques :
a
[ρs ]x=0 = ax · ǫEx ax = ǫEx
[ρs ]x=d = −ax · ǫEx ax = −ǫEx
[J s ]x=0 = ax × Hy ay = Hy az
[J s ]x=d = −ax × Hy ay = −Hy az .
Il est clair que les densit´s de charges et de courant demeurent des fonctions
e
de z et t parce qu’elles d´coulent de Ex et Hy . Ainsi, la propagation de l’onde
e
est support´e par les charges et les courants sur les plaques qui se d´placent
e e
aussi selon la relation spatio-temporelle du type (z − t/vp ).
Il devient facile de d´terminer la charge de ρs ou le flux de J s .
e
• La charge contenue est d´termin´e ` partir de (7.27) et de la densit´
e e a e
surfacique ρs sur la surface du segment d’une plaque dont la dimension
vaut w dz :
ǫw dz
Q = ǫEx w dz = V
d
ρs](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-213-320.jpg)



![7.8 D´termination des param`tres de ligne
e e 7-207
∆S2 1 ,4 = ∆y∆z(−ax )
2
0V
V2,4 V3,4 Vab Vab
Q C
[∇V ]2 1 ,4
2
y (j)
∆y
x (i)
∆z
z
∆x
Figure 7.12 – R´alisation de l’int´grale de Gauss num´rique ` l’aide de quelques ´chantillons
e e e a e
pr´lev´s aux noeuds d’un maillage.
e e
– de longueur ∆z plac´ ´galement de part et d’autre du plan contenant la section
ee
d’analyse – un demi cylindre ∆z/2 de chaque cˆt´ ;
oe
– ` base rectangulaire avec un maillage cart´sien (un cylindre a base rectangulaire
a e `
est un parall´l´pip`de rectangle) ;
ee e
– qui passe ` mi-chemin entre des points d’´chantillonnage du potentiel ;
a e
– entourant compl`tement un des conducteurs avec une base suivant le plus long
e
parcours ferm´ C possible pour am´liorer la pr´cision de l’int´grale num´rique.
e e e e e
La figure 7.11 illustre les six surfaces formant ensemble un parall´l´pip`de rectangle
ee e
ferm´e autour du conducteur central. On remarque que les surfaces S av et S ar ont
e
des normales suivant l’axe z. Aucun flux ´lectrique ne les traverse ; on aura pas a
e `
int´grer sur ces 2 surfaces. Les quatre autres surfaces seront d´compos´es en petites
e e e
lani`res de largeur ∆x ou ∆y selon qu’il s’agisse d’une surface horizontale ou ver-
e
ticale. Chaque lani`re est consid´r´e comme un ´l´ment de surface pour l’int´grale,
e ee ee e
au travers laquelle passe une flux ´lectrique uniforme.
e
On rappelle que le gradient d’une fonction scalaire donne la pente dans chacune
des directions. Dans le cas num´rique pr´sent, on approxime le gradient par une
e e
variation finie du potentiel selon chacun des axes x et y :
Vi+1,j −Vij Vi,j+1 −Vij
∆V ∆V
[∇V ]i+ 1 ,j+ 1 ≈ ax + ay . (7.59)
2 2 ∆x ∆y
Il s’adonne qu’avec un parall´l´pip`de rectangle les ´l´ments num´riques de surface
ee e ee e
d’int´gration ∆S sont d´finies soit par ±∆y ∆zax , soit par ±∆x ∆zay ; le signe
e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-217-320.jpg)
![7-208 Ligne de transmission
d´pend de l’orientation de la surface ∆S consid´r´e. On s’int´resse donc a une seule
e ee e `
des deux composantes du gradient ` la fois, ` cause du produit scalaire avec l’´l´ment
a a ee
num´rique de surface correspondante. L’int´grale devient une somme de produits
e e
sur l’ensemble des ´l´ments num´riques de surface qui constituent le cylindre :
ee e
Q = D · dS
S
= D · dydzax + D · (−dydzax ) + D · dxdzay + D · (−dydzay ) (7.60)
Sd Sg Sh Sb
≈ ǫ(−[∇x V ]d+ 1 ,j )∆y∆z + ǫ(−[∇x V ]g− 1 ,j )(−∆y∆z)
2 2
j j
+ ǫ(−[∇y V ]i,h+ 1 )∆x∆z + ǫ(−[∇y V ]i,b− 1 )(−∆x∆z) (7.61)
2 2
i i
Vd,j −Vd+1,j Vg,j −Vg−1,j
≈ ǫ( )∆y∆z + ǫ( )∆y∆z
j
∆x j
∆x
Vi,h −Vi,h+1 Vi,b −Vi,b−1
+ ǫ( )∆x∆z + ǫ( )∆x∆z (7.62)
i
∆y i
∆y
≈ ∆z ǫ(Vd,j −Vd+1,j ) + ǫ(Vg,j −Vg−1,j ) + ǫ(Vi,h −Vi,h+1 ) + ǫ(Vi,b −Vi,b−1 ) (7.63)
i,j
Le passage de (7.62) ` (7.63) implique que tous les ∆Si,j soient ´gaux donc ∆x =
a e
∆y. Cette derni`re condition, quoique non-essentielle d´coule de la m´thode des
e e e
diff´rences finies montr´e ` la section 4.5. On indique sur la figure 7.12 la base du
e e a
cylindre par la ligne pointill´e, un ´l´ment de surface et l’estimation du gradient du
e ee
potentiel en un point ` partir des ´chantillons voisins.
a e
• Faire les rapports Q/Vab puis C/∆z
On obtient ainsi la capacitance d’un bout de fil de longueur ∆z par le rapport Q/Vab .
La capacitance par unit´ de longueur C requiert la division par ∆z qui annule le
e
terme ∆z au num´rateur de l’expression de Q.
e
Exemple 7.5
Soit une ligne de transmission assum´e sans perte dont la section est faite d’un
e
conducteur interne mince de 2 mm de largeur ` l’int´rieur d’un conducteur
a e
externe carr´ de 6 mm de cˆt´. Le mat´riau est un di´lectrique de constante
e oe e e
ǫr = 10 non-magn´tique (µ = µo ). On applique la m´thode des diff´rences
e e e
finies en d´composant la section d’analyse en mailles carr´es de 1 mm comme
e e
sur la figure 7.13. Si une tension de 1.000 V est appliqu´e sur le conducteur
e
interne par rapport ` celui externe fix´e ` 0 V, la matrice des potentiels en
a e a](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-218-320.jpg)


![7.9 Mode quasi-TEM 7-211
substrat diélectrique
7400 plan de masse
ligne imprimée
Figure 7.14 – Exemple d’un circuit imprim´ avec lignes micro-rubans.
e
air
ǫr2 = 1
w
substrat
d ǫr1
plan de masse
Figure 7.15 – Section d’une ligne micro-ruban avec lignes de champ ´lectrique.
e
Un exemple de ce type est la ligne de transmission micro-ruban que l’on rencontre
fr´quemment sur des circuits imprim´s de syst`mes micro-ondes ou num´riques/informa-
e e e e
tiques. Cette ligne consiste g´n´ralement en une plaquette de di´lectrique (ou substrat)
e e e
a
` haute permittivit´, sur laquelle sont imprim´es d’un cˆt´ des bandes de cuivre, et de
e e oe
l’autre cˆt´ une couche pleine de cuivre appel´e “plan de masse”. Les figures 7.14 et 7.15
oe e
reproduisent un exemple de lignes micro-ruban d’un circuit informatique et une coupe de
l’une d’elles. Dans ce genre de ligne, les champs ´lectromagn´tiques sont distribu´s dans
e e e
le substrat, mais aussi dans l’air au-dessus du substrat du cˆt´ des bandes. Avec un calcul
oe
exact en ´lectromagn´tisme – sans passer par les notions de statique ou quasi-statique,
e e
on verrait qu’une partie de la puissance disponible contenue dans les champs pr´sentse
dans l’air est rayonn´e i.e. ´mise ` la mani`re d’une antenne. On peut toutefois traiter
e e a e
la ligne comme si le mode TEM continuait d’exister ; la supposition produit des r´sultats
e
approximatifs qui sont d’autant plus proches de la r´alit´ avec un substrat a constante
e e `
16
di´lectrique ´lev´e .
e e e
7.9.1 Constante di´lectrique effective
e
La difficult´ d’une ligne en mode quasi-TEM, est de d´terminer la constante ´lectrique
e e e
effective ǫref f , car une partie des champs se retrouve dans le substrat de constante ǫr1
et l’autre partie dans un autre di´lectrique ǫr2 (pour la ligne micro-ruban, le second
e
di´lectrique est l’air, d’o` ǫr2 = 1), tel que reproduit sur la figure 7.15. La valeur de la
e u
constante ´lectrique effective se situe quelque part entre ces deux valeurs extrˆmes ]ǫr1 ,ǫr2 [
e e
16
Plus la permittivit´ du substrat est ´lev´e, plus les champs se confinent dans le di´lectrique, ce qui
e e e e
diminue les pertes par rayonnement.](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-221-320.jpg)



























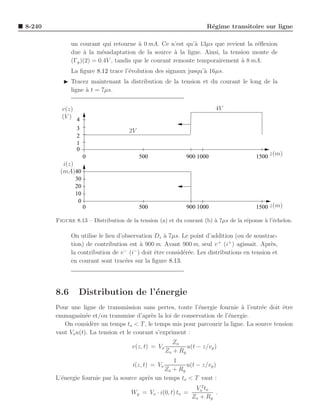


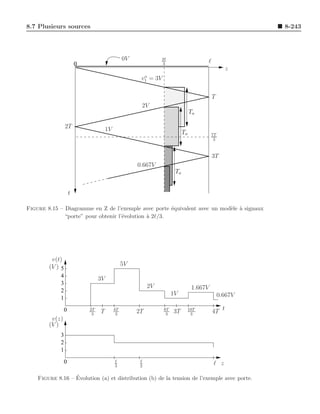















![8.10 Imp´dance r´active
e e 8-259
• Γ(t = ti = T = 1 µs, z = ℓ) = 1
• Γ(t → ∞) = −1.
Par contre, le coefficient de r´flexion de la charge au niveau de la source Γ(t =
e
ti , z = 0) vaut 1 ` t = ti = 2T = 2 µs !
a
[V ]z=0 [V ]z=ℓ
V0
V0
2
−1
V0 e
0 L 0 L
2T 2T + Z0 t T T+ Z0 t
[I]z=0 [I]z=ℓ
V0
Z0
V0 −1
Z0 (1 −e )
V0
2Z0
0 0
2T 2T + L
Z0
t T T+ L
Z0
t
´
Figure 8.33 – Evolution de la tension et du courant ` la source et ` la charge avec charge
a a
inductive.
Le trac´ de l’´volution de la tension quelque part sur la ligne se divise en trois
e e
parties menant au r´sultat de la figure 8.33 :
e
• pour 0 < t < to = zo /vp , aucun signal n’est visible car v o = v + n’est pas
encore arriv´ ;
e
• pour to < t < ti = 2T − to , il n’y a que
Zo
v+ = Vo = 5 u(t − z/vp ) V
Zo + Rg
• pour t ≥ ti , le signal de retour v − (t) se superpose :
– ` t = ti , on a [v − ]t=ti = 5 V ;
a
– alors qu’` t → ∞, [v − ]t→∞ = −5 V
a
– entre les deux,
v − (t) = 10e−(t−2T +z/vp )/τ u(t − 2T + z/vp ) − 5 V
pour permettre de raccorder les deux points par une exponentielle.
Il reste ` d´terminer la constante de temps τ . Il faut revenir au principe phy-
a e
sique de l’analyse descriptive pour bien comprendre. L’inductance ne “voit”
que la ligne de transmission au moment de sa r´action. Les autres r´sistances
e e
au loin (ici, celle de la source) affecterait la r´ponse via la r´flexion de v − .
e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-269-320.jpg)

![8.10 Imp´dance r´active
e e 8-261
Quoique d’apparence plus compliqu´e que l’exemple pr´c´dent, la difficult´ est
e e e e
du mˆme ordre de grandeur. Le diagramme en Z ´quivalent apparaˆ sur la
e e ıt
figure 8.35.
L’´volution de la tension ou du courant ` z = 0 se divise en deux parties :
e a
• pour 0 < t < ti = 2T1 :
Zo1
[v + ]z=0 = 10 = 5 u(t) V
Zo1 + Rg
1
[i+ ]z=0 = 10 = 100 u(t) mA
Zo1 + Rg
• pour t ≥ 2T1 , le signal de retour v − (t) se superpose tel que :
– ` t = ti , le condensateur se comporte comme un court-circuit et
a
150−50
[v − ]t=ti = 5 150+50 = 2.5 V, [i− ]t=ti = 100(−0.5) = −50 mA ;
– ` t → ∞, le condensateur est compl`tement charg´ et agit comme
a e e
− −
un circuit ouvert : [v ]t→∞ = 5(1) = 5 V, [i ]t→∞ = 100(−1) =
−100 mA.
– entre les deux,
v − (t) = 5 − 2.5e−(t−2T1 )/τ u(t − 2T1 ) V ,
i− (t) = −100 + 50e−(t−2T1 )/τ u(t − 2T1 ) mA .
La constante de temps est d´termin´e en inspectant le sch´ma. Le condensa-
e e e
teur ne “voit” que l’entr´e des deux lignes de transmission. On remplace les
e
lignes par leur imp´dance caract´ristique respective pour d´montrer que ces
e e e
imp´dances r´sistives sont connect´es en s´rie d’o` :
e e e e u
τ = (Zo1 + Zo2 )C = (50 + 150)(100 × 10−12 ) = 20 ns .
On obtient finalement des courbes d’´volution de la figure 8.36.
e
8.10.2 Conditions initiales non-nulles
Lorsque les conditions initiales aux bornes de l’´l´ment r´actif sont non-nulles, on doit
ee e
r´´crire les ´quations selon les conditions aux limites. Impossible d’y aller par inspection
ee e
car le comportement au temps t = ti est ind´termin´. Par exemple, au front montant
e e
de l’´chelon de tension, la capacit´ ne r´agit pas comme un court-circuit ayant d´j` une
e e e ea
certaine charge accumul´e (donc une tension ` ses bornes).
e a
L’application des conditions aux limites se fait dans le domaine de Laplace sans oublier
la fameuse condition initiale. Le coefficient de r´flexion Γ(s) – et celui de transmission
e
τ (s) si n´cessaire – est d´duit en trouvant le rapport V − (s)/V + (s). On peut donc ex-
e e
primer v (t) et le superposer ` v + (t). On continue le mˆme proc´d´ pour les r´flexions
−
a e e e e
++ −−
suppl´mentaires v (t), v (t), etc.
e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-271-320.jpg)
![8-262 R´gime transitoire sur ligne
e
[V ]z=0 , V
10
9.08
5
0 20 40 t, ns
(a)
[I]z=0 , mA
100
50 18.4
0 20 40 t, ns
(b)
´
Figure 8.36 – Evolution de la tension et du courant ` la source avec charge discontinuit´
a e
capacitive.
Exemple 8.12
Soit la ligne termin´e dans une inductance de l’exemple 8.10. Au temps t = T − ,
e
le courant traversant l’inductance s’´levait ` 50 mA.
e a
◮ R´´crivez l’expression de v(z, t) sur la ligne.
ee
Pour satisfaire la condition au niveau de la charge inductive pour t > T :
Vo d Vo v − (z = ℓ, t)
+ v − (z = ℓ, t) = L −
2 dt 2Zo Zo
soit parce que la d´riv´e d’une constante est nulle :
e e
L d v − (z = ℓ, t) Vo
+ v − (z = ℓ, t) = − .
Zo dt 2
La solution g´n´rale de l’´quation diff´rentielle est la suivante :
e e e e
Vo
v − (z = ℓ, t) = Ae−(t−T )/(L/Zo ) u(t − T ) − u(t − T ) .
2
On reconnaˆ la constante de temps L/Zo , car l’inductance se charge via Zo .
ıt
Elle fait aussi apparaˆ une constante A qui est d´termin´e par la condition
ıtre e e
initiale ` l’inductance :
a
Vo v − (z = ℓ, t)
− = Iinit = 50 mA .
2Zo Zo t=T −](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-272-320.jpg)



![8-266 R´gime transitoire sur ligne
e
Exercices
Question 1
Z0 = 60Ω
Rg = 40Ω T = 1µs
Rc
vg (t) = 100u(t)V
z=0 z=ℓ
Soit le syst`me montr´ sur la figure ci-dessus. Pour chacun des cas demand´s, d´termi-
e e e e
nez la valeur de Rc :
a) v(0.5ℓ, 1.7 µs) = 48 V ;
b) v(0.6ℓ, 2.8 µs) = 76 V ;
c) i(0.3ℓ, 4.4 µs) = 1 A.
Question 2
t=0
Z0 = 100Ω [V ]z=0 [V ]z=ℓ
Rg T = ℓ/vp 100V 90V
Rc 75V
V0
0 2 4 t, µs 0 2 4 t, µs
z=0 z=ℓ
Soit le syst`me montr´ sur la figure ci-dessus o` l’interrupteur est ouvert depuis suf-
e e u
fisamment longtemps pour que le syst`me ait atteint un r´gime permanent. A t = 0,
e e `
l’interrupteur se ferme et les ´volutions de la tension pendant les 5µs suivantes sont ob-
e
serv´es aux positions z = 0 et z = ℓ. D´duisez les valeurs de Vo , Rg , Rc et T .
e e
Question 3
Une ligne de transmission d’une imp´dance caract´ristique de 75 Ω, se termine dans
e e
e ` l’autre extr´mit´, on retrouve une source tension continue Vo
une charge r´sistive Rc . A e e
en s´rie avec son imp´dance r´elle interne Rg . Lorsque le r´gime permanent est atteint,
e e e e
on note une tension de 30 V et un courant de 1.2 A sur la ligne. D´terminez la tension et
e
le courant de l’onde positive et de l’onde n´gative en ´tat permanent.
e e](https://image.slidesharecdn.com/emgrenier-121202025718-phpapp01/85/Electromagnetique-grenier-276-320.jpg)