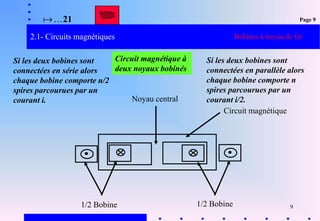
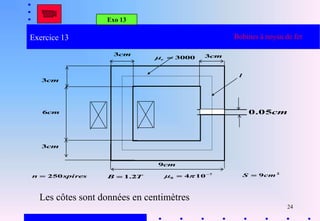
Ce document traite des bobines à noyau de fer, notamment leurs analogies électriques et magnétiques, ainsi que des caractéristiques des circuits magnétiques. Il aborde des concepts tels que l'inductance, les pertes lors de l'utilisation et les applications pratiques dans l'électrotechnique et l'électronique. Les sections incluent des explications sur les circuits monophasés, triphasés et des exercices pratiques pour comprendre les principes associés.

1. 1
1- Analogies électrique/magnétique
2- Bobines monophasées
2.1- Circuits magnétiques
2.2- Allure du courant absorbé
3- Bobines triphasées
2.3- Schéma équivalent
COURS 03
Chapitre - 3 Bobines à noyau de fer

2. 2
Éléments de la bobine à noyau de fer
en approximation linéaire
Bobines à noyau de fer


f

n
i
v
f


  

 Flux crée par la bobine ou flux principal

 Flux traversant le circuit magnétique
f

Flux de fuite
dt
d
n
ri
v




3. 3
Éléments de la bobine à noyau de fer
en approximation linéaire
Bobines à noyau de fer


f

n
i
v
Inductance de fuite:
i
n
l
f
f


Enroulement de n spires, circuit magnétique de réluctance 
Résistance de l ’enroulement:
s
l
r 

Conducteur de longueur l, de section s, matériau de résistivité 
Inductance propre:
i
n
n
L 





2
Enroulement de n spires, circuit magnétique de réluctance 

4. 4
1-Relation entre les grandeurs magnétiques
et électriques
Bobines à noyau de fer
Relations entre le flux (ou induction) et la tension
Relations entre le flux et le courant
)
(
)
(
)
( t
t
t
ni 
 


t
L
V
t
i 
 
sin
*
2
)
( 

L
n2


t
S
n
V
t
B 

sin
*
2
)
( 
S
n
V
B

2
max 
D ’où


dt
d
n
t
V
t
v 
 cos
*
2
)
( S
t
B
t
n
V
t )
(
sin
*
2
)
( 
 


et
Expression de Bmax
Page 9

5. 5
1- Analogies électrique/magnétique Bobines à noyau de fer
Circuit électrique:
i
e
R
Circuit magnétique:
Expression: Ri
e 
Force électromotrice : e (V)
Résistance électrique : )
(
R
Courant électrique : )
(A
i
Expression: 
 

Force magnétomotrice : )
(At

Réluctance magnétique: )
*
( 1

 Wb
At
Flux magnétique : )
(Wb

 


f

n
i

6. 6
1- Analogies électrique/magnétique
circuit électrique circuit magnétique
e
D d p ou tension (V)
ni


force magnétomotrice
(A t
t)
i courant (A)  flux (W b)
S
l
R
s
1
 résistance ()
s conductivité S
l

1

 réluctance
(
1
.

W b
A t )
 perméabilité
E
j s

densité de courant
(
2
.

m
A )
H
B 

induction magnétique
(T)
E
champ électrique
(
1
.

m
V )
H
champ magnétique
(
1
.

m
A )


 dl
E
i
R
e loi d'Ohm 


 dl
H

 théorème d'Ampère

 dS
j
i conservation du courant 
 dS
B
 conservation du flux
 


f

n
i
i
e
R
Bobines à noyau de fer
19

 Page 8

7. 7
2.1- Circuits magnétiques Bobines à noyau de fer
Un circuit magnétique est la partie ferromagnétique guidant le
flux magnétique d ’un système électrique:
Exemples: le noyau d ’un transformateur ou le corps d ’un
moteur


Page 8

8. 8
2.1- Circuits magnétiques
Bobine
Circuit magnétique
Culasse
Circuit magnétique à
un noyau bobiné
 Noyau central
Le flux traverse les culasses
et revient par les noyaux
latéraux
Bobines à noyau de fer
20

 Page 8

9. 9
2.1- Circuits magnétiques
1/2 Bobine
1/2 Bobine
Circuit magnétique
Noyau central
Circuit magnétique à
deux noyaux bobinés
Si les deux bobines sont
connectées en série alors
chaque bobine comporte n/2
spires parcourues par un
courant i.
Si les deux bobines sont
connectées en parallèle alors
chaque bobine comporte n
spires parcourues par un
courant i/2.
Bobines à noyau de fer
21

 Page 9

10. 10
2.2- Allure du courant absorbé
dt
d
n
ri
v



dt
d
ns
dt
d
n
v
B



dt
dB
ns
v
 t
V
v 
cos
2

t
V
ns
dt
dB

cos
2
1
 t
V
ns
B 

sin
2
1

Pour obtenir l ’allure du courant absorbé i, on passe
de v à B
Bobines à noyau de fer
Page 9

11. 11
2.2- Allure du courant absorbé
Pour obtenir l ’allure du courant absorbé i, on passe de v à B et de B à H au
moyen du cycle d ’hystérésis ou un tableau de B(H)
De H on en déduit i
n
Hl
i 

ns
V
B
2
max 
L ’induction magnétique est sinusoïdale de valeur maximale
La puissance active consommée par le circuit magnétique est appelée
pertes fer.
max
2
*
50
*
* B
f
M
q
p
Hz
kg
k
w
w
f 








Bobines à noyau de fer
Page 9

12. 12
2.2- Allure du courant absorbé
Influence de la saturation sur le courant
B(t)
H(t)
B(H)
Bobines à noyau de fer
Page 9

13. 13
2.3- Schéma équivalent d ’ une bobine à noyau de fer
f


  

 Flux crée par la
bobine

 Flux traversant le
circuit magnétique
f
 Flux de fuite


f

n
i
v

dt
d
n
ri
v 

Bobines à noyau de fer
22

 Page 9

14. 14
2.3- Schéma équivalent d ’ une bobine à noyau de fer
Le circuit magnétique est représenté par une réactance 
X
Les pertes fer sont représentés par une résistance 
R
Bobines à noyau de fer
Page 10

dt
d
n
ri
v 

f



 
 i
L
n *


 
i
l
n f
f
*





*
L
X  
*
f
f
l
x 

15. 15
2.3- Schéma équivalent d ’ une bobine à noyau de fer


f

n
i
v
Bobines à noyau de fer
Le circuit magnétique est représenté par une réactance 
X
Les pertes fer sont représentés par une résistance 
R
La contribution de l ’inductance de fuite est: f
l
Les pertes joules sont représentés par une résistance r
Prise en compte des imperfections de la bobine
Prise en compte du circuit magnétique
Page 10

16. 16
2.3- Schéma équivalent à une bobine à noyau de fer Bobines à noyau de fer
Pertes fer:

R
V
pf
2
'

Pertes joules:
2
ri
pj 
Puissance magnétique stockée:

X
V
Qfer
2
'

23


r

X
I
v

f
l

R 
X

R
I
i
'
v
Page 10

17. 17
Pertes fer
La puissance active consommée par le circuit magnétique est
appelée pertes fer et s'exprime en fonction du facteur de
qualité des tôles magnétiques q , de la masse des tôles M ,
de la fréquence d'utilisation f et de l'induction magnétique
maximale max
B dans le circuit magnétique :
Bobines à noyau de fer
Page 9
2
max
1
50
















T
Hz
kg
kg
W
W
f
B
f
M
q
P

18. 18
Pertes par courants de Foucault

19. 19
Pertes par hystérésis Bobines à noyau de fer

20. 20
Aspects Pratiques Technologie Bobines à noyau de fer
L ’apparence d ’une bobine à noyau de fer est différente suivant l ’utilisation .
La disposition pratique consiste à utiliser soit un circuit magnétique cuirassé, soit
torique.
En basse fréquence, le circuit magnétique est feuilleté pour limiter les pertes par
courants de Foucault.
Pour les utilisations à des fréquences plus élevées, on a recours à la ferrite dont la
résistance électrique est importante

21. 21
Aspects Pratiques Application Bobines à noyau de fer
En Électrotechnique, on rencontre les bobines à noyau de fer dans
les électroaimants ( relais, contacteurs, levage ), les bobines
d ’usage courant, les plateaux magnétiques de machines - outil ou
les paliers magnétiques.
En Électronique, on les trouvent dans les inductances de filtrage, les
selfs HF ajustables ou non. Dans ces cas, les noyaux en ferrite sont de
mise.

22. 22
3- Bobines triphasées
Exo 13
1

2
 3

0
3
2
1 

 


Les trois enroulements sont montés sur un même circuit magnétique.
Bobines à noyau de fer
Circuit magnétique à
trois noyaux bobinés
24

 Page 10

23. 23
Exercice 13
Un système électromagnétique est destiné à placer une induction
magnétique de 1.2 T dans un entrefer. Le circuit magnétique de
section carrée est de 3*3 cm2
Calculez la réluctance du circuit magnétique ?
Calculez la valeur du courant i qui doit circuler dans la bobine?
Calculez l ’inductance de la bobine ?
Exo 13

24. 24
Exercice 13
Exo 13
Bobines à noyau de fer
cm
05
.
0
cm
3 cm
3
cm
3
cm
3
cm
6
cm
9
3000

r

l
spires
n 250
 T
B 2
.
1

7
0 10
4 
 
 2
9cm
S 
Les côtes sont données en centimètres

25. 25
Exo 13
Bobines à noyau de fer
Réluctance du circuit magnétique
S
e
S
l
air
fer
*
* 0









)
10
*
9
)(
10
*
4
(
10
*
05
.
0
)
10
*
9
)(
10
*
4
(
3000
3
.
0
4
7
2
4
7 









1
5
5
4
.
10
*
305
.
5
10
*
42
.
4
10
*
842
.
8 







 Wb
At
air
fer
Inductance de la bobine H
n
L 1178
.
0
10
*
305
.
5
250
5
2
2




Exercice 13

26. 26
Exo 13
Bobines à noyau de fer
Flux magnétique dans le noyau
Wb
S
B 3
4
10
*
08
.
1
10
*
9
*
2
.
1
* 





On a: 


ni
Alors: A
n
i 29
.
2
250
10
*
08
.
1
*
10
*
305
.
5 3
5






Exercice 13

27. 27
Exercice 14
Un système électromagnétique est destiné à placer une induction
magnétique de 1.4 T dans un entrefer. Le circuit magnétique de
section carrée est fait d’un matériau ferromagnétique dont la loi
d’aimantation est la suivante
B (T) 0 0.50 0.80 1.00 1.20 1.40 1.60 1.80
H(A/m) 0 220 490 760 1300 2450 4700 11500
Exo 14
Calculez la valeur du courant i qui doit circuler dans la bobine?
Page 10

28. 28
Exercice 14
8
.
0
25
l
spires
n 1200
 T
B 4
.
1
 7
0 10
4 
 

25
*
25

S
25
25
25
80
130
Les côtes sont données en millimètres
Page 10

29. 29
Exercice 14
Flux magnétique dans le noyau et dans l ’entrefer S
B *


Champs magnétique d ’excitation dans l ’entrefer
0

B
He 
Champs magnétique d ’excitation dans le fer H Voir courbe de B(H)
Force magnétomotrice dans l ’entrefer (f.m.m)e = He*e
Force magnétomotrice dans le fer (f.m.m)fer = H*l
Page 10

30. 30
Exercice 14
)
(wb
 )
( 2
m
S )
(T
B )
/
( m
A
H )
(m
l )
(AT
f.m.m
entrefer 6
10
*
25
*
25
*
4
.
1
 6
10
*
25
*
25

4
.
1 6
0
10
*
11
.
1


B 3
10
*
8
.
0

891
fer 6
10
*
25
*
25
*
4
.
1
 6
10
*
25
*
25

4
.
1 2450(tableau) 3
10
*
4
*
)
25
80
(

 1029
(f.m.m)total= 891+1029 = 1920AT = n*i=1200*i
A
i 6
.
1
1200
1920


Page 10

31. 31