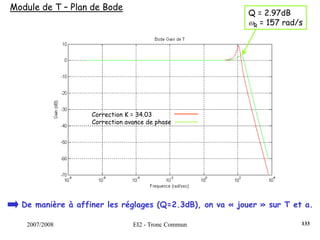
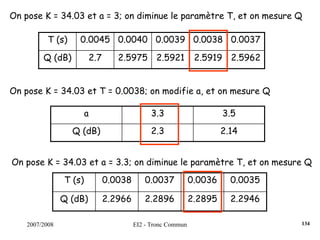
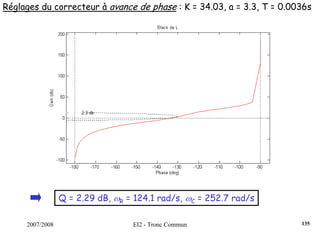
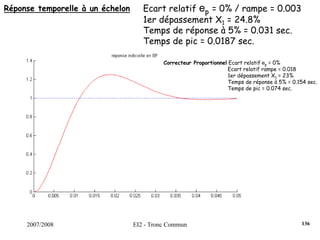
Le document traite des systèmes asservis et de la commande automatique, couvrant des sujets tels que la modélisation des systèmes dynamiques, les types de régulateurs et les critères de performance. Il aborde les concepts de stabilité, précision et rapidité, tout en détaillant des méthodes de synthèse de régulateurs et des exemples pratiques. Le cours est structuré en chapitres qui explorent les systèmes linéaires continus et leurs applications industrielles.
















![→ Le régime permanent a la même forme que l'excitation.
• Tout système (2) a une réponse en sortie composée d'un régime transitoire et d'un régime
permanent.
• Le régime transitoire tend vers 0 si les racines de l'équation caractéristique sont à partie
réelle négative. Dans le cas contraire, le système est instable
La résolution d'équation par cette voie peut être assez vite difficile et fastidieuse. Une façon
de simplifier les calculs est d'utiliser la transformée de Laplace. En fait, la transformée de
Laplace fournit un outil puissant de résolution dans un espace "fréquentiel" de problèmes
posés dans l'espace "temporel" sous forme d'équations différentielles linéaires et à
coefficients constants : elle permet en fait de transformer les équations différentielles en
une simple équation algébrique.
B. TRANSFORMEE DE LAPLACE
1. Définition
Soit f(t) une fonction du temps, définie pour tout t ≥ 0. Soit s une variable complexe. On
appelle Transformée de Laplace de la fonction f(t) la fonction de la variable complexe notée
F(s) telle que :
F s f t e f t dts t
( ) [ ( )] ( )= = ⋅− ⋅
∞
∫L
0
⋅ (9)
L'existence de F(s) suppose bien sûr que l'intégrale converge. Cette transformation est
bijective ; f(t) est dite transformée inverse de F(s) :
f t F s( ) [ ( )]= L-1
(10)
Exemple 1. Calculer la transformée de Laplace de f(t) =1 avec f(0)=0. On obtient alors :
F s e dt
s
e
s
s t s t
( ) [ ]= = − ⋅− ⋅
∞
− ⋅ ∞
∫0
0
1 1
=
⋅
Exemple 2. Calculer la transformée de Laplace de f(t) = t avec f(0)=0.
F s e t dts t
( ) = ⋅− ⋅
∞
∫0
On pose :
u t u
v e v
s
es t s t
= =
= = −− ⋅ − ⋅
'
'
1
1
⋅
On obtient alors :
Cours de Commande 9](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-17-320.jpg)
![F s u v dt u v u v dt
s
e t
s
e d
s s
e
s
s t s t
s t
( ) ' [ ] '
[ ]
[ ]
= ⋅ ⋅ = ⋅ − ⋅ ⋅
= − ⋅ ⋅ + ⋅ ⋅
= ⋅ − ⋅ =
t
∞
∞
∞
− ⋅ ∞ − ⋅
∞
− ⋅ ∞
∫ ∫
∫
0
0
0
0
0
0 2
1 1
1 1 1
2. Propriétés
• La Transformation de Laplace est une transformation linéaire :
L[ ( ) ( )] ( ) ( )f t f t F s F s1 2 1 2+ = +
L[ ( )] ( )a f t a F s⋅ = ⋅
• La Transformée de Laplace de la dérivée d'une fonction f(t) est égale à :
L[ ] ( ) ( )
df
dt
s F s f= ⋅ − 0
• La Transformée de Laplace de la dérivée seconde d'une fonction f(t) est égale à :
L[ ] ( ) ( ) ( )
d f
dt
s F s s f
df
dt
2
2
2
0 0= ⋅ − ⋅ −
• La Transformée de Laplace de l'intégrale d'une fonction f(t) est égale à :
L[ ( ) ] ( ) ( ) ( )f t dt G s
s
F s
s
g⋅ = = ⋅ + ⋅∫
1 1
0 , avec
dg t
dt
f t
( )
( )=
• Théorème du retard. Soit une fonction f(t) nulle pour t<0 et admettant une transformée
de Laplace F(s). Alors, si on retarde cette fonction d'un temps T, on obtient :
L[ ( )] ( )f t T e F ss T
− = ⋅− ⋅
L− − ⋅
+ = ⋅1
[ ( )] ( )F s a e f ta t
• Théorème de la valeur initiale. lim ( ) lim ( )
t s
f t s F s
→ →∞+
= ⋅
0
• Théorème de la valeur finale. lim ( ) lim ( )
t s
f t s F s
→∞ →
= ⋅
0
Ce dernier théorème est utilisé de manière fréquente dans la suite de ce cours pour
déterminer la valeur de la sortie du système en régime permanent (une fois le régime
transitoire terminé).
Cours de Commande 10](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-18-320.jpg)

![tous les types de situations rencontrés, ni tous les types de signaux d'entrée, on a pris
l'habitude de se référer à certains signaux. Ces derniers correspondent à des situations
rencontrées lors de l'évolution d'un système d'un état à l'autre et concernent donc l'analyse
transitoire du système. Par opposition, l'analyse harmonique permet l'étude de la réponse
du système à une entrée sinusoïdale en fonction de la fréquence.
a) Entrées pour analyse transitoire
• L'impulsion de Dirac (u(t)=δ(t)). La réponse est dite impulsionnelle. L’impulsion de
Dirac est la limite lorsque ∆t tend vers 0 d'un créneau rectangulaire de hauteur de 1/∆t et
de durée ∆t. Sa transformée de Laplace est égale à 1.
• L'échelon unité (u(t)=0, t<0, u(t)=1, t≥0). La réponse est dite réponse indicielle ou
réponse à un échelon de position.
• La fonction rampe (u(t)=0, t<0 ; u(t)=a.t, t≥0). La réponse est dite réponse à une rampe
ou réponse à un échelon de vitesse.
Lors de l'analyse transitoire, on caractérise la rapidité (temps de réponse), la nature plus ou
moins oscillante du système (dépassement ou non), et la précision.
b) Entrée pour analyse harmonique
Si on applique un signal sinusoïdal à un système linéaire, on sait que la réponse est
sinusoïdale (voir précédemment). On montre également qu'une fois le régime transitoire
établi, la sortie est sinusoïdale, de même pulsation que l'entrée, mais d'amplitude et de phase
différente. La fonction de transfert s'écrit alors (avec s = jω, ω étant la pulsation du signal
d’entrée)
01
01
)()(
)()(
)(
ajaja
bjbjb
jF nn
mm
+⋅++⋅
+⋅++⋅
=⋅
ωω
ωω
ω (16)
La représentation pour l'analyse harmonique peut se faire des trois manières différentes mais
équivalentes :
• Plan de Bode. Il représente le gain FdB=20 log[|F(jω)|] et φ=Arg[F(jω)] en fonction
de ω dans un plan semi-logarithmique. (Ci-dessous, représentation d’un système du
premier ordre de gain statique 10 et de constante de temps 0.01 sec.).
Cours de Commande 13](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-21-320.jpg)
![• Plan de Black. Il s'agit d’une représentation équivalente à celle de Bode, mais tracée
dans un seul plan, φ=Arg[F(jω)] étant placé en abscisse et FdB=20 log[|F(jω)|] en
ordonnée, chaque point du plan correspondant à une pulsation. Le lieu est donc
gradué en ω croissantes. (Ci-dessous, représentation d’un système du premier ordre
de gain statique 10 et de constante de temps 0.01 sec.).
• Plan de Nyquist. Il s'agit de la représentation graphique paramètrée par ω de l'affixe
de F(jω) . Le lieu est gradué en ω croissantes. (Ci-dessous, représentation d’un
système du premier ordre de gain statique 10 et de constante de temps 0.01 sec.).
Cours de Commande 14](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-22-320.jpg)


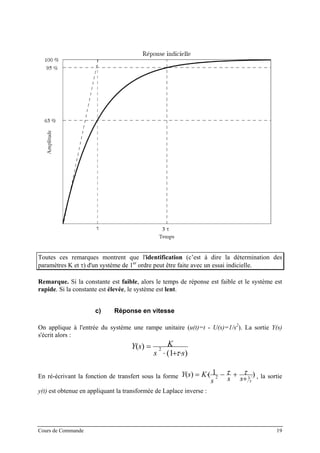
 Représentations de Bode et de Black
Le gain est exprimé en dB :
))(log(20 ωjFFdB ⋅=
La représentation dans le plan de Bode se fait sur 2 tracés (gain et phase) en fonction de ω.
Dans le plan de Black, on trace le lieu dans le plan [FdB,φ], ce qui impose de le graduer en ω
et de l'orienter.
Exemple. Analyse harmonique d'un système du 1er
ordre (avec K = 10 et τ = 0.01 sec)
Cours de Commande 21](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-29-320.jpg)
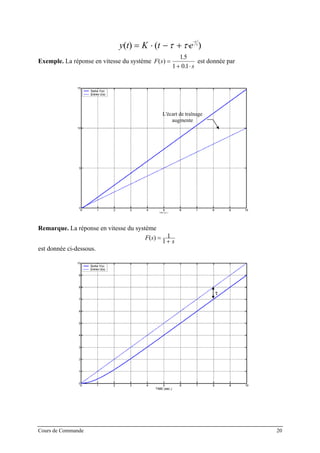
![ω = ∞
ω = 0
ωc
Pour ω ω τ= =c
1 , alors on a Arg[ ( )]F jω = − °45 .
4. Conclusions
Le comportement dynamique d'un système est entièrement décrit par sa constante de temps τ.
La fréquence de coupure d'un système est définie par :
fc =
⋅ ⋅
1
2 π τ
• Un système du 1er
ordre est un filtre passe-bas.
• Un système rapide est un système ayant une large bande passante (faible constante de
temps).
• Une système lent a une bande passante étroite.
B. UN 1ER
ORDRE PARTICULIER : L'INTEGRATEUR
1. Définition
L'intégrateur est régi par l'équation différentielle :
)(
)(
tuK
dt
tdy
⋅=⋅τ
La fonction de transfert est alors déduite en utilisant la Transformée de Laplace :
Cours de Commande 23](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-31-320.jpg)

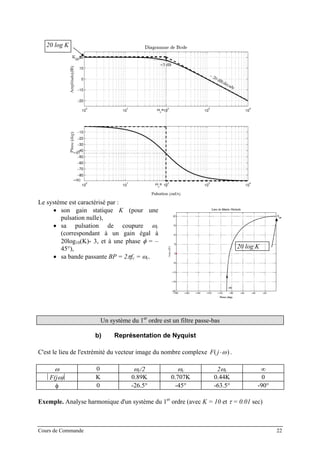
]([lim 00 τ
2. Réponse en vitesse
On note et(t) = yc(t) – Ay(t) (Transformée de Laplace = Et(s)) avec la consigne égale à une
rampe unitaire, i.e.
2
1)()(
s
sYtty cc =→=
Aussi, on obtient :
)
'1
'1(1)( 2 s
AK
s
sEt
⋅+
−⋅=
τ
On applique le théorème de la valeur finale :
∞=
⋅+
−=⋅= →→∞→
)
'1
'1(1lim)(lim)(lim 00 s
AK
s
sEste s
t
s
t
t τ
Cours de Commande 26](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-34-320.jpg)

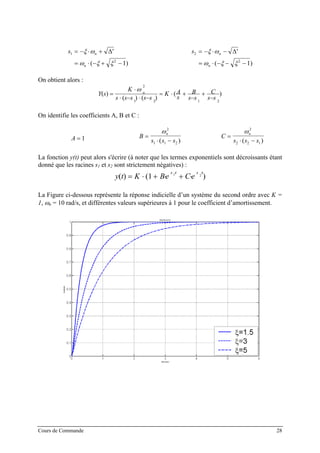

![c) Calcul des dépassements successifs
Donc, en notant yk la valeur du k-ième maxima (ou minima), on obtient :
s K
e k
s K
e
k
s K
e
k k
k
k
n
n
k
k
k
k
n
n
= ⋅ −
−
⋅ ⋅ − ⋅
⋅
⋅ −
+
⇒ = ⋅ −
−
⋅ ⋅ +
⇒ = ⋅ −
−
⋅ ⋅ ⋅ − ⋅ ⋅
⋅ ⋅
⋅
⋅ −
− ⋅
⋅
−
− ⋅
⋅
−
( cos(
[ cos( )]
[ (cos( ) cos( ) sin( ) sin( ))]
1
1
1
1
1
1
1
1
1
2
2
2
1
2
1
2
2
2
2
ξ ω
π
ω ξ
ξ
π
ξ
ξ
π
ξ
ξ
ω ξ
π
ω ξ
φ
ξ
π φ
ξ
π φ π φ
)yk
yk
yk
⇒ = ⋅ − − ⋅
−
⋅⋅ −
− ⋅
⋅
−
s K
e
k
k
k
[ ( ) cos( )]1 1
1
2 1
1
2
2
ξ
π
ξ
ξ
φyk
Or, comme cos( )φ = −1 2
ξ , on obtient alors :
])1(1[
2
1
12
ξ
πξ
−
⋅⋅−
−⋅
⋅−−⋅=⇒
k
k
k
eKy
On peut ainsi prédéterminer le niveau de
chacun des dépassements. Le 1er
dépassement
a lieu pour k = 1 :
]1[
2
1
1
ξ
πξ
−
⋅−
+⋅= eKy
Le dépassement relatif est noté X1 et s’écrit :
2
1
1
ξ
πξ
−
⋅−
= eX
d) Coefficient d'amortissement ξ
D'après l'expression des dépassements, on a :
Cours de Commande 32](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-40-320.jpg)

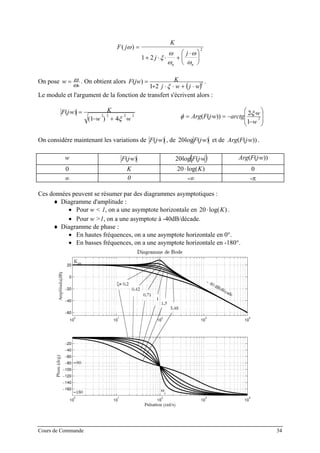
![Les 2 asymptotes du diagramme d'amplitude se coupent en ( log( ), )20⋅ K nω . La Figure ci-
avant décrit, dans le plan de Bode, le lieu de transfert d’un système du second ordre avec un
gain statique K = 10, une pulsation propre ωn = 100 rad/s, et différentes valeurs du coefficient
d’amortissement.
1. Etude du gain
On souhaite maintenant savoir la valeur de w pour laquelle on obtient un module maximum.
On calcule la dérivée du module par rapport à w :
2
32222
23
]4)1[(
)21(44)(
ww
ww
dw
wjFd
⋅⋅+−
⋅−⋅⋅−⋅
−=
⋅
ξ
ξ
On a donc un module maximum pour w annulant :
0)21(44
23
=⋅−⋅−⋅ ξww
Une des solutions est w = 0. En posant que , on a alors0>w
2
21 ξ⋅−=w . La condition
d'existence de cette solution est queξ < 0 707. .
a) Pulsation de résonance
On dit alors qu'il y a résonance si ξ < 0.707, la pulsation de résonance étant égale à :
ω ω ξr n= ⋅ − ⋅1 2 2
La pulsation de résonance ωr est inférieure à la pulsation propre non amortie ωn . Ces deux
pulsations deviennent plus proches quand le coefficient d'amortissement diminue, pour être
égales quand ξ = 0 : le système est alors un oscillateur libre.
b) Facteur de surtension (ou de résonance)
Ce facteur permet de quantifier la valeur du "pic" de gain à la fréquence de résonance. On
suppose donc que le coefficient d'amortissement ξ est inférieur à 0.707. La valeur maximum
du gain est atteinte pour la fréquence de résonance, i.e.
2
21 ξ⋅−=w . Donc, on a :
2
12
)(
ξξ −⋅⋅
=⋅ KwjF MAX
On appelle facteur de surtension (ou de résonance) le rapport Q défini par :
)12log(20
12
1)( 2
2
ξξ
ξξ
−⋅⋅⋅−=⇒
−⋅⋅
=
⋅
= dBMAX Q
K
ujF
Q
Cours de Commande 35](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-43-320.jpg)

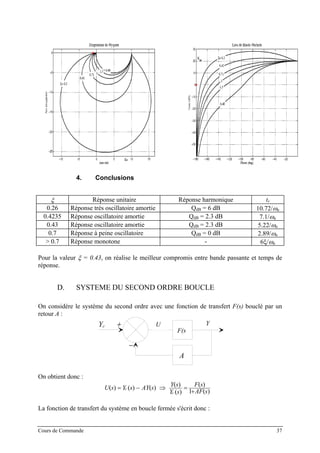

![Cours de Commande 39
V. SYSTEMES DE DEGRE QUELCONQUE – SYSTEMES A RETARD
A. FONCTION DE TRANSFERT ET FORME CANONIQUE
Soit un système linéaire ayant la fonction de transfert H(s) défini par
D(s)
N(s)
H(s)=
avec d°(N) = n et d°(D) = m. La forme canonique de ce système s’écrit
F(s)
s
KH(s) c
=
avec K le gain statique, F(0) = 1 et c un entier appelé « classe du système » tel que
c > 0 : c = nombre de pôles à l’origine (nombre d’intégrateurs)
c < 0 : c = nombre de zéros à l’origine (nombre de dérivateurs)
La fonction de transfert de F(s) est défini par
s) ...s)
s) ...τs)τ
T(T(
((
F(s)
21
21
11
11
++
++
=
où TB
iB et τB
jB peuvent être à parties réelles positives ou négatives.
Si Re[TB
iB] > 0 pour tout i, alors H(s) est stable,
S’il existe des TB
iB (ou des τB
jB ) complexes, ils apparaissent par paires conjuguées. Dans
ce cas, on les rassemble dans un terme du second ordre de la forme : )ω
s
ω
sξ(
ii
i 2
2
21 ++ .
L’entier ξB
iB peut être positif, négatif, ou nul. Si ξB
iB > 0 pour tout i, alors H(s) est stable
Pour résumer, la fonction de transfert peut être écrite sous la forme d’un produit de polynôme
d’ordre 0, 1 ou 2 tel que
∏=
=
N
i
i(s)FF(s)
1
avec
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
++
+∈
i
ii
γ
i
βα )
ω
s
iω
s
i(
,)isT(,s,iK(s)iF 2
2
21
1
ξ
et αB
ιB, βB
ιB, γB
ιB entiers relatifs
B. REPONSE HARMONIQUE, LIEUX DE TRANSFERTS
Comme il a été mentionné précédemment, l’analyse harmonique d’un système se fait en
mettant sur l’entrée du système un signal sinusoïdal. En notant u(t) l’entrée du système, on a
t)(ωUu(t) sin1=
Pour la classe de systèmes considérée, une entrée sinusoïdale implique une sortie sinusoïdale,
à savoir](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-47-320.jpg)
![Cours de Commande 40
)ωtsin(Yy(t) 1 Φ+=
avec
[ ] ])(jωArg[F)F(jωArgΦ)(jωF)F(jω
U
Y N
i
i
N
i
i ∑==∏==
== 111
1
Les gains étant exprimés habituellement en dB, on obtient
[ ] [ ] ∑==∑=
==
N
i
i
N
i
i )](jωArg[F)F(jωArgΦ)(jωFLogdBF
11
1020
Pour résumer
Le gain en dB du système soumis à une entrée sinusoïdale est égal à la somme des gains en
dB des systèmes élémentaires composants ce système.
La phase du système soumis à une entrée sinusoïdale est égale à la somme des phases des
systèmes élémentaires composants ce système.
1. Représentation dans le plan de Bode
• USous-système proportionnelU F(s) = K > 0
[ ] [ ] °=== 01020 KArgΦKLogdBF
Les courbes d’amplitude et de phase sont :
ω
dB FdB
20logK
0
1 100.1
Φ°
ω0
1 100.1
• USous-systèmeU F(s) = sP
α
P
°×== 90][1020 αΦωLogαdBF
La courbe d’amplitude est une droite de pente 20α dB par décade (ou 6α dB/octave).
La courbe de phase est une horizontale à °×90α
EXEMPLE. Pour α > 0, les courbes d’amplitude et de phase sont :](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-48-320.jpg)
![Cours de Commande 41
ω
dB FdB
20α
0
1 100.1
-20α
Φ°
ω0
1 100.1
90α
• USous-systèmeU F(s) = (1+ sT)P
β
P :
[ ]TωAβΦ]Tω[LogβdBF tan11010
22
=+=
Les courbes d’amplitude et de phase se déduisent de celles du premier degré : pour le gain,
pente de [sign(β)20dB] par décade à partir de la pulsation de coupure … (voir Chapitre III).
EXEMPLE. Si β > 0 et T > 0, les courbes d’amplitude et de phase sont
0.1 1 10
0
45β
90β
0
10β
20β
ωT
ωT
dB FdB
Φ°
3β
6β
7β
0.1
1
10
β
REMARQUE . Si T < 0, alors
β
Tjω1+ =
β
Tjω1− : le gain est donc inchangé ; on obtient donc
la même courbe d’amplitude. Par contre, on a T]jωArg[1+ =− T]jωArg[1− : ceci implique
alors une symétrie de la courbe de phase par rapport à l’axe des ω.](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-49-320.jpg)
![Cours de Commande 42
• USous-systèmeU
γ
)
ω
s
ω
s(sF 2
2
21)( ++= ξ
Les courbes se déduisent de celles du second degré :
La courbe de gain en dB en fonction de log(ω) a 2 asymptotes (ω est porté en
échelle logarithmique): une asymptote horizontale FB
dBB = 0 quand ω → 0 et une
asymptote oblique de pente 40γ dB par décade (ou 12γ dB/octave) quand ω
→ ∞ . On démontre que ces 2 asymptotes se coupent au point [ω = ωB
nB ; FB
dBB =
0].
La courbe Φ( ω) a 2 asymptotes horizontales : Φ = 0 quand ω → 0 et Φ =
γ x180° quand ω → ∞
UExempleU. Tracer dans le plan de Bode, en utilisant les approximations asymptotiques et
pseudo- asymptotiques, les courbes d’amplitude et de phase de la fonction de transfert :
s)s)(s(
F(s)
5121
10
++
=
UAMPLITUDEU. On trace les amplitudes des 4 termes élémentaires en utilisant les approximations
asymptotiques pour les 2 constantes de Temps .
5s1
1
+ 5s1
1
+
5s1
1
+
0.01 0.1 1 10
-60
-40
-20
0
20
40
60
0.2
34
18
0.5
dB FdB
ω
K=10
1/s
1/1+5s
1/1+2s
La somme des 4 termes élémentaires présente donc une pente de -20dB/décade (-6dB/octave)
entre 0 et 0.2 rd/s, de –40dB/décade (-12dB/octave) entre 0.2 rd/s et 0.5 rd/s, et de –60
dB/décade (-18dB/octave) entre 0.5 rd/s et ∞.](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-50-320.jpg)
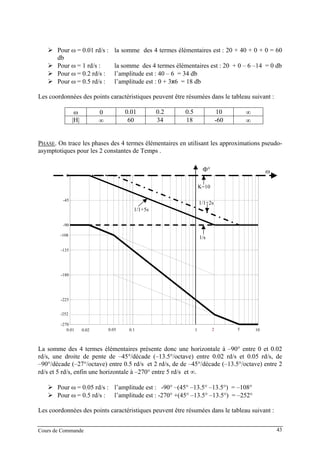
![Cours de Commande 44
ω 0 0.02 0.05 2 5 ∞
Arg[H] −90° −90° −108° −252° −270° −270°
2. Représentation dans le plan complexe : lieu de Nyquist
La construction point par point est longue et fastidieuse. On utilise donc, en pratique, les
tracés dans le plan de Bode.
⇒ Variations de F(ω) et Φ(ω)
⇒ Lieu de Nyquist
EXEMPLE.
s)s)(s(
F(s)
5121
10
++
= . Des tracés (pseudo) asymptotiques précédents, on déduit le
tableau des variations suivant :
ω 0 ∞
|F| ∞ 0
Arg[F] -90° - -270°
Quand ω varie de 0 à ∞, on se rapproche de l’origine en tournant dans le sens inverse
trigonométrique de –90° à –270°. Le lieu de Nyquist a donc l’allure suivante :
Re
Im
ω=∞
ω=0
3. Représentation dans le plan de Black
La représentation dans Black est basée sur les mêmes outils que la représentation dans le plan
de Bode. Il s’agit donc d’un outil parfaitement adapté à la représentation fréquentielle de
systèmes d’ordre quelconque (en particulier pour la synthèse des correcteurs - voir chapitres
suivants).](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-52-320.jpg)
![Cours de Commande 45
4. Caractéristiques de la réponse fréquentielle
Pour les systèmes de degré quelconque les définitions (Chapitre 2) de pulsation de coupure,
ωB
cB , bande passante, pulsation de résonance, ωB
RB , et coefficient de surtension, Q , restent
valables.
C. SYSTEME A DEPHASAGE MINIMAL (OU NON MINIMAL)
1. Problème
Soit un système linéaire de fonction de transfert F(s) inconnue dont on ne connaît que la
courbe de module )F(jω . Le problème est de déterminer
[ ])F(jωArgΦ(ω) =
REPONSE. Il existe une infinité de systèmes SB
0B, SB
1B, SB
2B, ,… de fonction de transfert FB
0B(s), FB
1B(s),
FB
2B(s),… qui possèdent la même courbe de module )F(jω . Ces systèmes ne différent que par
la présence de facteurs
τ
τ
s1
s-1
(s)D1
+
= τ > 0 ou (et)
2
2
2 2
2
21
21
nn
i
nn
i
ω
s
ω
s
ω
s
ω
s
(s)D
++
+−
=
ξ
ξ
ζ > 0 et ωB
nB > 0
En effet :
1
ωj1
ωj-1
ω)(jD
τ
τ
1 =
+
= et )(ωAω)](jArg[D τtan21 −=
1
21
21
2
2
2
2
2 =
+
−
=
nn
nn
ω
ωj
ω
ω
-
ω
ωj
ω
ω
-
ω)(jD
ξ
ξ
et =ω)](jArg[D2
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥−−
≤−
n2
n
2
n
n2
n
2
n
ωω;2
ω/ω-1
ω/ως2
Atan2
ωω;
ω/ω-1
ω/ως2
Atan2
π
Il existe alors un seul système SB
0B, de fonction de transfert FB
0B(s), sans termes déphaseurs tel
que :
)F(jω)(jωF =0 ⇒ ∫
−
=
∞+
∞−
du
ωu
ω)F(jF(ju)-LnLnω(ωΦ
π 220
2)
2. Définition
Un système est à déphasage minimal s’il ne possède pas de zéro à partie réelle positive. Il est
à déphasage non minimal s’il possède un (ou plusieurs) zéro à partie réelle positive.
3. Réponse indicielle d’un système à déphasage non minimal
La réponse indicielle, y(t), d’un système à non minimum de phase possédant un seul zéro à
partie réelle positive (cas le plus fréquent) « démarre dans le mauvais sens ».](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-53-320.jpg)
![Cours de Commande 46
0
t
y
t
y
Système SB
0B à minimum de phase Système SB
1B à non minimum de phase
UPreuveU. Le système SB
0B admet pour fonction de transfert
1
10
++
++=
...sa
...sbK(s)F n
n
m
m
avec K > 0 (non
restrictif), et
aB
nB > 0 → le système SB
0 Best supposé stable
bB
mB > 0 → le système SB
0 Best à minimum de phase
Le système SB
1B admet comme fonction de transfert
τ
τ
s
-s(s)F(s)F
+
=
1
101
Pour le système SB
0B, la première dérivée non nulle est positive
dt
dy(0)
> 0 ; ou si
dt
dy(0)
= 0 alors 2
2
dt
y(0)d
> 0 …
En effet, d’après les théorèmes de la dérivée et de la valeur initiale sur la transformée de
Laplace
n
m
n
n
m
mm-n
sm-n
m-n
a
b
K)]
s
1
1...sa
1...sb
Ks(s[lim
dt
y(0)d
=⋅
++
++
=
∞→
> 0
Pour le système SB
1B,B Bla première dérivée non nulle est négative
τ
τ
τ
τ -
a
b
K)]
s
1
s1
s-1
1...sa
1...sb
Ks(s[lim
dt
y(0)d
n
m
n
n
m
mm-n
sm-n
m-n
⋅=⋅
+
⋅
++
++
=
∞→
< 0
4. Exemple
Tracer dans le plan de Bode, en utilisant les approximations asymptotiques et pseudo-
asymptotiques, les courbes d’amplitude et de phase des deux fonctions de transfert
s).s)((
s.(s)F
1011
5010
++
+= et
s).(s
s)s)(.(
(s)F
101)1(
1501
21
++
−+
=
FB
0B(s) est à minimum de phase et FB
1B(s) est à non minimum de phase (un terme déphaseur du
premier ordre)
s
s(s)F(s)F
+
−=
1
101](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-54-320.jpg)
![Cours de Commande 47
GAINS. Les courbes d’amplitude des deux fonctions de transfert sont évidemment
identiques. On trace les amplitudes des 3 constantes de Temps en utilisant les approximations
asymptotiques. La somme des 3 termes élémentaires présente donc une horizontale à 0 dB
entre 0 et 1 rd/s, une droite de pente de –20dB/décade (-6dB/octave) entre 1 rd/s et 2 rd/s,
une horizontale à –6 dB entre 2 et 10 rd/s, et une droite de pente de -20dB/décade (-
6dB/octave) entre 10 rd/s et ∞.
PHASES. Les On trace les phases des 3 constantes de Temps en utilisant les approximations
pseudo-asymptotiques. Arg[FB
0B(s)] présente donc une horizontale à 0° entre 0 et 0.1 rd/s, une
droite de pente –45° /décade (–13.5°/octave) entre 0.1 rd/s et 0.2 rd/s, une horizontale à –
13.5° entre 0.2 et 1 rd/s, une droite de pente de –90°/décade (–27°/octave) entre 1 rd/s et 10
rd/s, une horizontale à –58.5° entre 10 et 20 rd/s, une droite de pente –45°/décade (–
13.5°/octave) entre 20 rd/s et 100 rd/s, enfin une horizontale à –90° entre 100 rd/s et ∞. On
trace la phase du terme déphaseur en utilisant les approximations pseudo-asymptotiques.
Arg[FB
1B(s)] présente donc une horizontale à 0° entre 0 et 0.1 rd/s, une droite de pente –135°
/décade (–40.5°/octave) entre 0.1 rd/s et 0.2 rd/s, de –90° /décade (–27°/octave) entre 0.2 et 1
rd/s, de –135° /décade (–40.5°/octave)entre 1 rd/s et 10 rd/s, une horizontale à –238.5° entre
10 et 20 rd/s, une droite de pente –45°/décade (–13.5°/octave) entre 20 rd/s et 100 rd/s, enfin
une horizontale à –270° entre 100 rd/s et ∞.
La phase FB
0B(s) de varie entre 0 et –90° et celle de FB
1B(s) entre 0 et –270°. Le déphasage de
FB
0B(s) de varie donc entre 0 et 90° et celui de FB
1B(s) entre 0 et 270°. Ceci justifie l’appellation
de système à non minimum de phase pour FB
0B(s).
Les courbes d’amplitude et de phase exactes (tracées avec la boîte à outils « commande » de
Matlab) sont données par la figure page suivante. On constate un écart faible avec les
constructions (pseudo) asymptotiques.
Remarque. Les réponses indicielles yB
0B(t) et yB
1B(t) de FB
0B(s) et FB
1B(s) (tracées avec la boîte à
outils « commande » de Matlab) sont les suivantes
0 1 2 3 4 5 6 s
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
y0
y1
t
y1
(t)
y0
(t)](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-55-320.jpg)
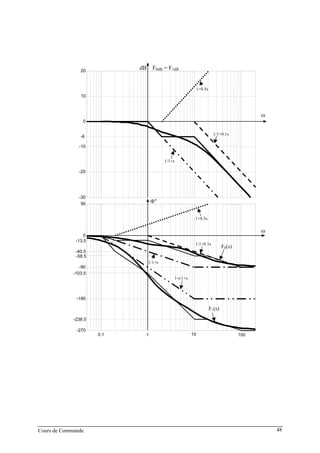
![D. SYSTEME DU SECOND ORDRE EQUIVALENT A UN
SYSTEME D’ORDRE QUELCONQUE
De nombreux systèmes asservis ou régulés présentent une surtension en régime harmonique,
tout comme les systèmes du second ordre.
DEFINITION. Le système du second ordre équivalent à un système d’ordre quelconque,de
fonction de transfert F(s) est le système du second ordre présentant la même surtension Q, la
même pulsation de résonance ωR et le même gain statique |F(0)|.
Notons F2(s) la fonction de transfert du système du second ordre équivalent
2
2
21
2
nn ω
s
ω
s
K(s)F
++
=
ξ
La différence principale entre les lieux de transfert du système réel et du système équivalent
apparaît principalement en hautes fréquences, c’est à dire pour les pulsations supérieures à la
pulsation de coupure.
ω
ωR ωn
Q
dB F
|F|
|F 2|
Généralement, les réponses temporelles sont relativement voisines l’une de l’autre. Par
exemple, pour les deux réponses indicielles y(t) et y2(t) (réponses du système réel et du
système équivalent), les dépassements X1 et X12 et les instants mis pour atteindre les
dépassements tp et tp2 seront proches. En conséquence, on utilise pour les systèmes de degré
quelconque la relation X1 = X1(Q) calculée pour les systèmes du second degré :
Q (valeur naturelle) →
2
111
2
/Q--
=ξ → )
-
π
(-X 2
1
1
exp
ξ
ξ=
2 2
1
1
[ln( )]
2 ln( )
π X
Q
π X
+
= ⇔ )]1-Q-(Qexp[-πX 2
1 =
Cours de Commande 49](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-57-320.jpg)
 τsin1=
On retrouve donc ici un régime permanent sinusoïdal :
( )Φ+= tYy(t) ωsin1
avec 1
jω-
e
U
Y
1
1
==
τ et ττ ω
jω-
eArg −=⎥⎦
⎤
⎢⎣
⎡=Φ
Par convention on choisit comme diagramme fonctionnel du retard pur
yu τs-e
EXEMPLE. Soit l’asservissement ci dessous dont on désire étudier la stabilité en boucle
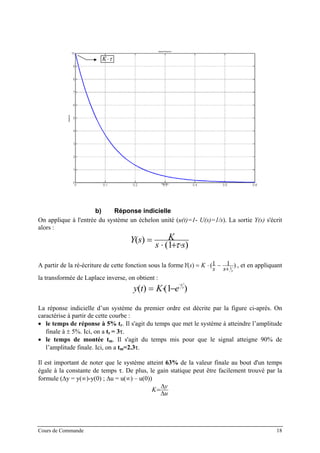
fermée.](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-58-320.jpg)


![)(
)()(1
1)( sd
sFsC
se
+
−=
Par définition, on a
La sensibilité S(s) :
)()(1
1)(
sFsC
sS
+
= ,
Le transfert de boucle : L(s) = C(s)F(s) ,
La différence de retour : [1 + L(s)] .
b) Sensibilité aux erreurs de modèles
L’objectif est de quantifier l’influence des erreurs de modèles sur la sortie y. On suppose que
w=0. La fonction de transfert en asservissement est
)()(1
)()()(
)(
sFsC
sRsFsC
sH
Y
Y c
c
+
==
Supposons que la consigne yc soit sinusoïdale, de pulsation ω. La fonction de transfert
précédente s’écrit
)()(1
)()()(
)(
ωω
ωωωω
jFjC
jRjFjC
jH c
+
=
La variation ∆F(jω) sur F(jω) entraîne une variation ∆H(jω). A partir de l’approximation du
premier ordre de ∆H(jω)
F
CF
CRF
dF
dHH c
∆
+
=∆≅∆ 2)1(
,
on obtient
F
F
CFH
H ∆⋅
+
=∆
1
1
La variation relative du lieu de transfert du processus se transmet sur la variation relative du
lieu de transfert en asservissement par l’intermédiaire, à nouveau, de la sensibilité S(s).
c) Sensibilité complémentaire
L’objectif est de minimiser la sensibilité S(s) grâce à un réglage judicieux de C(s). Cette
minimisation revient, d’une façon équivalente, à avoir (1-S) proche de 1. Ainsi, la sensibilité
complémentaire est définie par
L
L
CF
CFsSsT
+
=
+
=−=
11
)(1)(
La fonction de transfert en asservissement s’écrit alors
)()()( sRsTsH c=
B. REDUCTION DES SCHEMAS BLOCS
La représentation des éléments d'un système par leur fonction de transfert permet de les
combiner pour réduire les schémas fonctionnels. Une liste non exhaustive des simplifications
induites par ces réductions est donnée ci-après :
Cours de Commande 54](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-62-320.jpg)

![• un argument )
cos
sin
tan(
ϕ
ϕψ
+
=
A
A .
Démonstration On calcule T(jw) en posant )sin(cos)( ϕϕω ⋅+⋅= jAjL .
FTBF
A j
A j
A j A j A
A A
A
A j A j j A A
A A
A
A j
A A
A
=
⋅ + ⋅
+ ⋅ + ⋅
=
⋅ + ⋅ ⋅ + ⋅ − ⋅ ⋅
+ ⋅ + ⋅
= ⋅
+ ⋅ − ⋅ ⋅ ⋅ + ⋅ + ⋅ ⋅ ⋅ + ⋅
+ ⋅ + ⋅
= ⋅
+ + ⋅
+ ⋅ +
=
(cos sin )
(cos sin )
(cos sin ) ( cos sin )
( cos ) sin
cos cos sin cos sin sin cos sin
( cos ) sin
cos sin
cos
ϕ ϕ
ϕ ϕ
ϕ ϕ ϕ ϕ
ϕ ϕ
ϕ ϕ ϕ ϕ ϕ ϕ ϕ
ϕ ϕ
ϕ ϕ
ϕ
1
1
1
1
1 2
2 2 2
2 2
2 2 2
2
ϕ
1 2 2
+ ⋅ +
⋅ + + ⋅
A A
A j
cos
[( cos ) sin ]
ϕ
ϕ ϕ
T(jω)
On en déduit alors le module
A
A A
A
A
A A
A A
A
A A
=
+ ⋅ +
⋅ + +
=
+ ⋅ +
⋅ + ⋅ +
=
+ ⋅ +
1 2
1 2
1 2
1 2
2
2 2
2
2
2
cos
( cos ) sin
cos
cos
cos
ϕ
ϕ ϕ
ϕ
ϕ
ϕ
FTBF|T(jω)|
ainsi que l’argument
ψ
ϕ
ϕ
=
+
arctg
A
[
sin
cos
]
CONCLUSION Pour tout ω, à un point du lieu de transfert de boucle L(jω) de coordonnées
[ A( ), ( )ω ϕ ω ] correspond un point du lieu de transfert de la sensibilité complémentaire T(jω)
de coordonnées [ B( ), ( )ω ψ ω ].
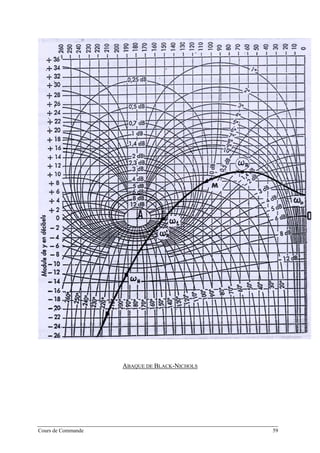
Pour réaliser cette transformation, on utilise l'abaque de Black-Nichols, sur lequel
apparaissent des contours en gain et des contours en phase. Cet abaque réalise la
transformation :
X
X
X
( )
( )
( )
ω
ω
ω
→
+1
2. Détermination graphique du lieu de transfert de la sensibilité
complémentaire
Cours de Commande 57](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-65-320.jpg)





![22
)(21
)(
)(21
)(
nnnn
ss
KsU
ss
KsY
ωω
ξ
ωω
ξ +⋅+
=⋅
+⋅+
=
en supposant que l'entrée est une impulsion de Dirac. Si le coefficient d'amortissement est
supérieur ou égal à 1, alors la réponse ne présente pas d'oscillations. Sinon, la réponse est
oscillante.
C. CRITERES DE STABILITE D'UN SYSTEME BOUCLE
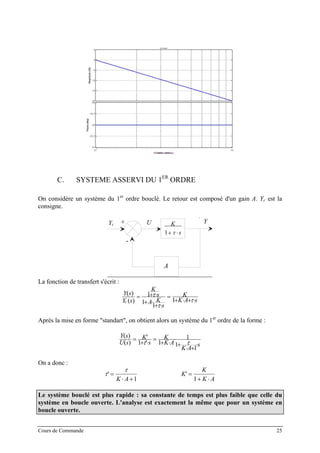
On considère le système bouclé suivant :
Rc(s)
yc
L(s)
+
e
d
+ yyr +
-
Ce système est décrit par les fonctions de transfert suivantes
Transfert de boucle : L(s),
Fonction de transfert en asservissement : TR
L
LR
Y
Y cc
c
=
+
=
1
Fonction de transfert en régulation : S
LD
Y =
+
=
1
1
On rappelle que S(s) est la sensibilité, T(s) la sensibilité complémentaire, [1+L(s)] la
différence de retour et Rc(s) le précompensateur. Si on suppose que Rc(s) est une fonction de
transfert stable (on rappelle que le précompensateur est réglé par l’utilisateur, qui peut
(doit ?) le rendre donc stable), la fonction de transfert en asservissement est stable si la
fonction de transfert T(s) est stable. T(s) (et donc le système en boucle fermée) est stable si
les pôles de T(s) sont à partie réelle négative. Or, ces pôles sont les racines de l'équation
suivante :
0)(1 =+ sL (EQUATION CARACTERISTIQUE DU SYSTEME EN BOUCLE FERMEE)
Donc, étant donné la forme de la fonction de transfert de régulation, la condition de stabilité
de cette dernière est la même que la stabilité de la fonction de transfert en asservissement.
L’analyse de la stabilité du système en boucle fermée (que ce soit en asservissement ou en
régulation) revient donc à étudier les racines de l’équation 1 + L(s) = 0.
Dans le but d’analyser la stabilité du système en boucle fermée, il est nécessaire de
déterminer de façon "simple" les racines de cette équation. Pour cela, deux types d'approches
sont possibles :
• Méthodes ALGEBRIQUES,
• Méthodes GRAPHIQUES.
Cours de Commande 64](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-72-320.jpg)


![ω étant une pulsation, la variable est donc considérée positive. A(ω) admet comme racine ω1
= 1.9 rad/s (= 4 11/ . ), et B(ω) ω2 = 0 rad/s et ω3 = 10 rad/s.
Re
Im
ω2
ω1
ω3
Les racines des parties réelles et imaginaires étant distinctes et régulièrement alternées, on
peut alors conclure que le système en boucle fermée est stable.
EXEMPLE 2. Soit un système dont le transfert de boucle est donné par :
)1.01()1(
)(
sss
KsL
⋅+⋅+⋅
=
On étudie alors la structure intrinsèque de l'équation caractéristique :
1 1
1 1 01
1 1 01
1 1 01
11 01
1 1 01
2 3
+ ⋅ = +
⋅ + ⋅ + ⋅
=
+ ⋅ + ⋅ + ⋅
⋅ + ⋅ + ⋅
=
+ + ⋅ + ⋅
⋅ + ⋅ + ⋅
R s F s
K
s s s
K s s s
s s s
K s s s
s s s
( ) ( )
( ) ( . )
( ) ( .
( ) ( . )
. .
( ) ( . )
)
1+L(s)
Les racines de l'équation caractéristique sont donc déterminées en résolvant l'équation :
01 11 03 2
. .⋅ + ⋅ + + =s s s K
En remplaçant la variable complexe s par la variable jω, et en séparant explicitement la partie
réelle et la partie imaginaire de l'équation caractéristique, on a :
( . ) ( . )K j− ⋅ + ⋅ − ⋅ =11 01 03
ω ω ω
⇒ = − ⋅ = − ⋅A K B( ) . , ( ) .ω ω ω ω11 012 3
ω
ω étant une pulsation, la variable est donc considérée positive. A(ω) admet comme racine
ω1 11= K / . rad/s, et B(ω) ω2 = 0 rad/s et ω3 = 10 rad/s.
Le système est stable en boucle fermée si :
] [
] [
ω ω ω
ω ω
1 2 3
2 311
0 11
0 11
0 11
∈
⇒ ∈
⇒ < <
⇒ < <
⇒
10
< <
,
/ . ,
/ .
K
K
K
K
Cours de Commande 67](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-75-320.jpg)

![La fonction F(s) évaluée sur le contour (C ) est 1+L(s). L’objectif est donc clair : il
s’agit d’évaluer le nombre de zéros de 1+L(s) situé dans le demi-plan complexe droit,
ce qui indiquera la nature stable ou instable du système bouclé.
Afin d’illustrer la démarche, on suppose que le système étudié admet un transfert de boucle
L(s) de gain statique K et que
0))L(j(lim =
∞→
ω
ω
La variable s évoluant sur le demi-complexe droit, et étant donné que s ≡ jω, la construction
de (G) s’effectue de la manière suivante
M décrit [OA], i.e. s = jω avec ω ∈ [0,∞[. M’, l’image de M par 1+L(jω), décrit un
contour pour ω croissant.
M décrit [BO], i.e. s = -jω avec ω ∈ [0,∞[. On a 1+L(-jω)= 1+conj(L(jω)). L(jω) étant
un fraction rationnelle, M’ décrit alors le symétrique du lieu précédent.
M décrit le demi-cercle de rayon infini. Pour un système physique, le degré du
numérateur de L(s) est inférieur ou égal au degré du dénominateur : dans la figure ci-
dessous, on suppose qu’il est strictement inférieur ⇒ |L(jω)| → 0 pour ω → ∞ ⇒
|1+L(jω)| → 1. Donc, M’ est infiniment proche du point 1 sur l’axe réel. Le contour
(G) est donc fermé.
En appliquant le théorème de Cauchy, on peut déterminer le nombre Z de zéros de 1+L(s) à
partie réelle positive (Z devant être nul pour que le système soit stable) si on connaît :
M
A
R
Im
OO
B
Re
(C)
ω=0
Re(1+L)
Im(1+L)
0 1
ω>0
ω<0
(G)
ω=+∞
1+L(s)
ω=-∞
1+K
le nombre P de pôles de 1+L(s) dans le demi plan droit,
le nombre N de tours que fait l'image de (C) par 1+L(s) autour de l'origine, compté
dans le sens trigonométrique.
Etant donné un système dont le transfert de boucle est L(s), P le nombre de pôles instables de
1+L(s) et N le nombre de tours de (G) autour de 0. Le système asservi est stable si et
seulement si :
Z = P-N = 0
Cours de Commande 69](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-77-320.jpg)

![Si des pôles sont sur l’axe imaginaire, on ne peut plus utiliser le contour de Nyquist
précédent. En effet, sont-ils à l’intérieur ou à l’extérieur ? Aussi, on utilise le contour de
Nyquist modifié.
Dans ce cas, on fait éviter au contour de
Nyquist les pôles par des demi-cercles dont le
rayon r tend vers 0.
Cas d'un intégrateur s = 0
On pose avec ρ → 0.θ
ρ j
es =
Cas d'un oscillateur pur s=±jω0
On pose avec ρ → 0.θ
ρω j
ejs =±= 0
Le diagramme de Nyquist présente alors
autant de branches infinies qu'il y a de pôles
sur l'axe imaginaire.
00
A
ρρ →→ 00
0+
0-
ρρ →→ 00
ρρ →→ 00
R→∞
(C)
Supposons que )()( sl
s
ksL c
= avec k le gain statique de L(s), l(0)=1, c la classe de L(s). La
portion de contour (G) (résultat de la transformation de (C ) par L(s)) correspondante au pôle
multiple situé à l’origine est un cercle de centre O et de rayon k/ρc
(vu que
cc s
ksl
s
ksL =→=→ )0()0( )), ce qui implique qu’il s’agit d’un cercle de centre O et de rayon
infini. Il s’agit maintenant de définir le sens de parcours de ce cercle : on a Arg[k/sc
] = -c
Arg[jω]. On obtient donc le tableau de variation suivant
M 0-
→ 0+
Arg[s] -π/2 → π/2
Arg[L(s)] cπ/2 → -cπ/2
Lorsque M parcourt le demi-cercle de rayon ρ, de 0-
à 0+
(dans le sens trigonométrique), son
image par L(s) parcourt c demi-cercles (dans le sens inverse trigonométrique) de rayon infini.
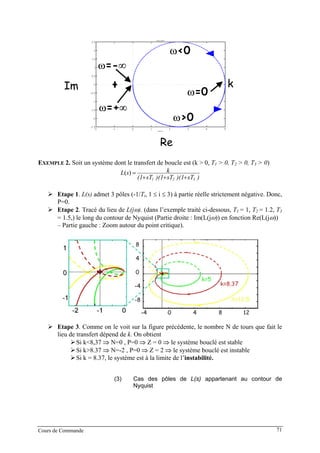
EXEMPLE 3. Soit un système dont le transfert de boucle est (k > 0, T1 > 0, T2 > 0, T2 > T1)
)sT)(1sTs(1
ksL
21 ++
=)(
Etape 1. L(s) admet 3 pôles (-1/Ti, 1 ≤ i ≤ 2 et 0) et sont donc tous à l’extérieur du
contour de Nyquist modifié. Donc, P=0.
Cours de Commande 72](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-80-320.jpg)
![Etape 2. On trace le lieu de transfert de L(jω), tout d’abord pour ω ∈ ]0 ∞ [. Il est aisé
de vérifier que
Pour ω → 0+
, | L(jω)| → ∞ ; Re[L(jω)] → -k(T1+T2) ; Arg[L(jω)] = -π/2 rad.
Pour ω → ∞, | L(jω)| → 0 ; Arg[L(jω)] = -3π/2 rad.
De plus, on peut montrer que le point d’intersection entre l’axe des réels et le
lieu de transfert est d’abscisse –k(T1+T2)/ T1T2.
On obtient le tracé pour ω ∈ ]-∞ 0[ par symétrie par rapport à l’axe des
abscisses. Une fois obtenu les deux branches qui correspondent aux pulsations
non nulles (rouges sur la figure ci-dessus), il convient de fermer le contour en
étudiant le comportement du lieu de transfert au voisinage de 0.
Pour s → 0, le transfert de boucle est L(s) = K/s. Donc, si s → 0,alors |L| → ∞.
D’un point de vue phase, on obtient Arg[L(s)] = -Arg[s]. Donc, on a
M 0-
→ 0+
Arg[s] -π/2 → π/2
Arg[L(s)] π/2 → -π/2
Ce tableau conduit donc au tracé en pointillés de la figure ci-dessus. Le
« passage » de 0-
à 0+
se fait dans le sens inverse de s (variation en sens
opposée, voir tableau). Le rayon de ce cercle est infini.
Etape 3. Comme on le voit sur la figure précédente, le nombre N de tours que fait le
lieu de transfert autour du point critique (symbolisé par les deux disques noirs), le
système sera stable ou instable. Cette propriété dépend évidemment de k. On obtient
Si k(T1+T2)/T1T2 < 1 (cas où le point critique est représenté par le disque noir
de gauche), (G) n’entoure pas le point critique ⇒ N=0, P=0 ⇒ Z=0 ⇒ le
système bouclé est stable.
Si k(T1+T2)/T1T2 < 1 (cas où le point critique est représenté par le disque noir
de droite), (G) entoure 2 fois le point critique dans le sens trigonométrique
inverse ⇒ N=-2, P=0 ⇒ Z=2 ⇒ le système bouclé est instable.
Cours de Commande 73](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-81-320.jpg)

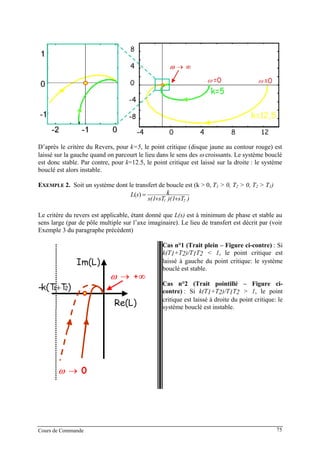
![(1) Critère du revers dans le plan de Bode
Dans le plan de Bode, le point critique admet pour coordonnées (( log( ); )20 1 180⋅ − ° = (0 dB;-
180°). Le critère consiste donc à déterminer la valeur du gain du transfert de boucle quand
son argument est égal à -180°.
• Si le gain du transfert de boucle d’un système satisfaisant les hypothèses H1-H2 est
inférieur à 0 dB (gain naturel < 1) pour φ π= − , alors le système en boucle fermée est
stable.
• Si le gain du transfert de boucle d’un système satisfaisant les hypothèses H1-H2est
supérieur à 0 dB (gain naturel > 1) pour φ π= − , alors le système en boucle fermée est
stable.
EXEMPLE
(2) Critère du revers dans le plan de Black-Nichols
Dans le plan de Black, le point critique est (0 dB;-180°).
Si le lieu de transfert de boucle d'un système satisfaisant les hypothèses H1-H2 laisse, en
parcourant dans le sens des ω croissants, le point critique [-180° ; 0 dB] à droite, le système
est stable en boucle fermée. Il est instable dans le cas contraire.
EXEMPLE
Cours de Commande 76](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-84-320.jpg)
![3. Influence du gain statique sur la stabilité
L'influence du gain statique est très importante quant à la stabilité du système. En effet,
comme il a été vu précédemment, il est possible, avec un gain statique mal adapté, de faire
passer le lieu de transfert de boucle au dessus du point critique, et donc de rendre instable le
système en boucle fermée (malgré un amélioration de certaines performances comme la
rapidité).
CONCLUSION. Il existe donc une valeur appelée Gain Critique qui place le système en boucle
fermée à la limite de l'instabilité : le lieu de transfert de boucle passe alors par le point
critique. Le gain critique définit la stabilité absolue.
D. DEGRE DE STABILITE D'UN SYSTEME BOUCLE
Apprécier le degré de stabilité, c'est quantifier l'éloignement du lieu de transfert du point
critique. Il est important de prendre en compte qu'on ne peut se contenter de se placer trop
près du point critique : il faut prévoir des MARGES.
• Si le lieu de transfert de boucle est trop proche du point critique, on peut montrer qu'il
existe une résonance importante. En effet, on a alors un coefficient d'amortissement ξ
faible, donc un système faiblement amorti et donc un temps de réponse important.
• Les variations du gain statique k (en pratique, cela peut être dû aux composants
électroniques) peuvent rendre le système instable en faisant passer le lieu de transfert de
l'autre côté du point critique.
• Il ne faut oublier l'influence des retards : ils peuvent avoir un effet déstabilisateur en
déplaçant le lieu de transfert de boucle vers les phases négatives.
• Les processus physiques sont souvent en milieu bruité et non linéaires : le modèle
mathématique souffre donc souvent d'imprécisions.
Il faut donc préserver le système de ces problèmes : la stabilité doit être ROBUSTE face à
eux. Des valeurs "limites" permettent d'assurer une stabilité relativement robuste.
• MARGE DE GAIN mG. La marge de gain,
notée mG, est la variation de gain qui
fait passer le lieu de transfert de boucle
par le point critique. Cette marge est
égale à la distance en gain entre le lieu
de transfert de boucle et le point
critique, pour Arg[L] = -180°.
• MARGE DE PHASE mφ. La marge de
phase, notée mφ, est la phase que l’on
doit ajouter pour que le lieu de transfert
de boucle passe exactement par le point
critique. Cette marge est à la distance
en phase entre le lieu de transfert de
boucle et le point critique, pour 0=dB
L
dB.
Cours de Commande 77](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-85-320.jpg)
![• MARGE DE GAIN-PHASE mGφ. La marge de
module, notée mGφ, est la plus petite
distance entre le point critique et le lieu de
transfert de boucle.
Les marges habituellement exigées sont
10dB < mg < 15dB
45° < mφ < 50°
.25 < mgφ < .5
PRECISION STATIQUE DES SYSTEMES ASSERVIS
E. INTRODUCTION
L‘objectif de l’asservissement d’un système est de faire suivre à la sortie y(t) une loi fixée par
la consigne (on suppose dans la suite que yc(t) = yr(t)). Le but est d'avoir une erreur e(t)=yc(t)-
y(t) tendant vers 0. La performance du système asservi en terme de précision statique est
évaluée par le calcul de l’erreur de poursuite en régime établi
)(lim)(lim 0
sEste st
⋅= →∞→
L'erreur permanente est égale à l'écart en régime permanent, ou erreur statique. Le système
étudié est (avec L(s) le transfert de boucle et D(s) l’entrée de perturbation) :
Y (s)E(s)
L(s) +
−
Yc(s)
+
D(s)
On a
[ ])()(
)(1
limlimlim 00
sDsY
sL
sE(s)se(t) c
sst
−⋅
+
=⋅= →→∞→
F. SYSTEME SANS PERTURBATION ET ENTREE VARIABLE
On suppose que D(s) = 0. On obtient alors
Cours de Commande 78](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-86-320.jpg)
![[ ])(
)(1
limlimlim 00
sY
sL
sE(s)se(t) c
sst
⋅
+
=⋅= →→∞→
L'erreur est liée à la forme de yc(t) et au transfert de boucle.
• INFLUENCE DE yc(t) (rappel) Si yc(t) est un échelon, alors l'erreur est appelée écart en
position ou relatif (et est noté ep(t)). Si yc(t) est une rampe, alors l'erreur est appelée
écart en vitesse ou de traînage) (et est noté et(t)).
• INFLUENCE DE L(S). La forme de la réponse va dépendre du nombre d'intégrateurs que
contient L(s). Donc, on a :
)(
)(
)(
sMs
sNK
sL r
⋅
⋅
=
avec r, nombre entier appelé classe du système. A noter que :
+++=+++=== 2
21
2
21 1)(;1)(;1)0(;1)0( sbsbsMsasasNMN
1. Système de classe 0
Le système est tel que
)(
)(
)(
sM
sNK
sL
⋅
= .
On obtient
[ ])(limlimlim 00
sY
NKM
MsE(s)se(t) c
sst
⋅
⋅+
⋅=⋅= →→∞→
• L’ENTREE EST UN ECHELON D’AMPLITUDE YC. L’écart statique est obtenu en appliquant le
théorème de la valeur finale, avec Yc(s) = YC/s.
[ ] 1
limlimlim 00 K
YC
s
YC
NKM
MsE(s)se(t))(e sst
p
+
=⋅
⋅+
⋅=⋅==∞ →→∞→
• L’ENTREE EST UNE RAMPE DE PENTE YC. L’écart de traînage est obtenu en appliquant le
théorème de la valeur finale, avec Yc(s) = YC/s.
∞=⎥⎦
⎤
⎢⎣
⎡
⋅
⋅+
⋅=⋅==∞ →→∞→ 200
limlimlim
s
YC
NKM
MsE(s)se(t))(e sst
t
2. Système de classe 1
Le système est tel que
)(
)(
)(
sMs
sNK
sL
⋅
⋅
= .
On obtient
[ ])(limlimlim
2
00
sY
NKMs
Ms
E(s)se(t) c
sst
⋅
⋅+⋅
⋅
=⋅= →→∞→
• L’ENTREE EST UN ECHELON D’AMPLITUDE YC.
[ ] 0limlimlim
2
00
=⋅
⋅+⋅
⋅
=⋅==∞ →→∞→ s
YC
NKMs
Ms
E(s)se(t))(e sst
p
Cours de Commande 79](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-87-320.jpg)
![• L’ENTREE EST UNE RAMPE DE PENTE YC.
K
YC
s
YC
NKMs
Ms
E(s)se(t)e sst
t =⎥⎦
⎤
⎢⎣
⎡
⋅
⋅+⋅
⋅
=⋅==∞ →→∞→ 2
2
00
limlimlim)(
3. Système de classe 2
Le système est tel que
)(
)(
)( 2 sMs
sNK
sL
⋅
⋅
= .
On obtient
[ ])(limlimlim 2
3
00
sY
NKMs
Ms
E(s)se(t) c
sst
⋅
⋅+⋅
⋅
=⋅= →→∞→
• L’ENTREE EST UN ECHELON D’AMPLITUDE YC.
[ ] 0limlimlim 2
3
00
=⋅
⋅+⋅
⋅
=⋅==∞ →→∞→ s
YC
NKMs
Ms
E(s)se(t))(e sst
p
• L’ENTREE EST UNE RAMPE DE PENTE YC.
0limlimlim)( 22
3
00
=⎥⎦
⎤
⎢⎣
⎡
⋅
⋅+⋅
⋅
=⋅==∞ →→∞→ s
YC
NKMs
Ms
E(s)se(t)e sst
t
PRECISION CLASSE 0 CLASSE 1 CLASSE 2
)(ep ∞ 1+K
YC 0 0
)(et ∞ ∞
K
YC 0
REMARQUES
• Les calculs précédents montrent clairement qu’il est intéressant d’avoir au moins un
intégrateur dans la boucle de régulation, de façon à pouvoir au moins annuler l’écart de
position.
• Il faut néanmoins limiter l’emploi de ces intégrateurs car ils peuvent rendre le système
instable, vu qu’ils introduisent un déphasage de -90° (voir partie précédente).
• Une des possibilités de rendre le système « relativement » précis est d’augmenter le gain :
en le rendant ainsi très grand, les écarts non nuls dans le tableau ci-dessus tendront vers 0.
Là aussi, comme pour les intégrateurs, il faut faire attention à ne pas rendre le système
instable.
G. SYSTEME AVEC PERTURBATIONS SEULES
On suppose que yc(t) = 0. On obtient alors
[ ])(
)(1
limlimlim 00
sD
sL
sE(s)se(t) sst
−⋅
+
=⋅= →→∞→
L'erreur est liée à la forme de d(t) et au transfert de boucle.
Cours de Commande 80](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-88-320.jpg)

![sera systématiquement nulle (même si le nombre de dépassements est important …). On
définit donc un critère de performance (avec T égal à ∞ ou 2 tr).
∫=
T
f[e(t)]dtI
0
Ce critère dépend évidemment des paramètres du système asservi. Le but est maintenant de
régler judicieusement ces paramètres de façon à minimiser la valeur de I, ce réglage
dépendant du choix de la fonction f.
I. CRITERES DE PERFORMANCE
1. Critère IAE (Integral of Absolute Error)
Le critère choisi est
∫=
T
dte(t)I
0
Par ce critère, tous les éléments de la réponse transitoire sont pris en compte. Plus la réponse
est nerveuse et oscillatoire, plus l’intégrale est importante. On favorise ici les systèmes à
amortissement moyen (réponse peu oscillante), et on pénalise les systèmes trop énergétiques.
Pour un système du second ordre, le critère I est minimum pour un coefficient
d’amortissement égal à 0.7.
2. Critère ISE (Integral of Square Error)
Le critère, encore appelé de l’erreur quadratique ou de Hall-Satorius, est
∫=
T
]dtt[eI
0
2)(
Du fait que les écarts soient élevés au carré et inférieurs à 1, on minimise l’influence des
dépassements de faible amplitude. En fait, on cherche surtout à minimiser l’aire du premier
dépassement, ce qui impose un temps de montée plus faible, et donc un amortissement plus
faible également. Pour un système du second ordre, le critère I est minimum pour un
coefficient d’amortissement égal à 0.43.
3. Critère ITAE (Time Multiplied by Absolute Error)
Le critère choisi est
∫ ⋅=
T
dte(t)tI
0
L’introduction de la variable temps va favoriser les systèmes à réponse oscillante. Pour un
système du second ordre, le critère I est minimum pour un coefficient d’amortissement égal à
0.7.
Cours de Commande 82](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-90-320.jpg)
![4. Critère ITSE (Time Multiplied by Square Error)
Le critère choisi est
∫ ⋅=
T
dt[e(t)]tI
0
2
Ce critère insiste plutôt sur l’erreur en fin de régime transitoire (effet de la variable du temps)
sans trop pénaliser le début du régime transitoire. Pour un système du second ordre, le critère
I est minimum pour un coefficient d’amortissement égal à 0.58.
Cours de Commande 83](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-91-320.jpg)




![Ta
1
aT
1
T
1
0
20 loga
10 loga
ω
db |C|
Ta
1
10T
1
90°
-90°
Arg[C]°
ω
ΦM
T
1
10aT
1
aT
10
DIAGRAMME DE BODE DU CORRECTEUR A AVANCE DE PHASE
Cours de Commande 89](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-97-320.jpg)
![Les expressions algébriques du gain et de la phase de C(jω) sont
22
222
1
1
ωT
ωTa
)jωC(
+
+
= )Tω(A)aTω(A)]jωArg[C( tantan −=
L’avance de phase maximale ΦM a lieu pour ω = ωM
( ) 0
11 22222 ωT
T
ωTa
aT
dω
)]jωArg[C(d
=
+
−
+
= ⇒
aT
ωM
1=
Cette avance de phase maximum est
1
1sin
2
1tan1tantan
+
−==−==
a
aA
a
a-A
a
AaA)]jωArg[C(Φ MM
⇒
1a
1a
AsinΦM
+
−
= ou
M
M
sinΦ1
sinΦ1
a
−
+
=
On constate qu’avec
aT
1 voisin de ωR ou au moins
T
1ω
aT
1 R<< , on a une action
stabilisante efficace, d’autant plus importante que a est grand.
Q
-180°
-90° 0°
dB
ω = ∞
L1(jω)
ω = 0
Φ°
L(jω)
ωR
T
1ω
aT
1 R<<ACTION DU CORRECTEUR A AVANCE DE PHASE AVEC SUR LE LIEU DE TRANSFERT
DE BOUCLE DU SYSTEME
Cours de Commande 90](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-98-320.jpg)
![Il est très important d’effectuer un réglage satisfaisant des paramètres, sous peine d’avoir une
correction inefficace pour Rω
aT
1 > ou déstabilisante pour Rω
T
1< .
Q
-180°
-90° 0°
A dB
ω = ∞
L1(jω)
ω = 0
Φ°
L(jω)
ωR
CORRECTEUR A AVANCE DE PHASE MAL REGLE
(correction inefficace)
Q
-180°
-90° 0°
A dB
ω = ∞
L1(jω)
ω = 0
Φ°
L(jω)
ωR
CORRECTEUR A AVANCE DE PHASE MAL REGLE
(action déstabilisante)
Rω
aT
1 >
R
ω
T
1<
En pratique, le coefficient a est souvent limité à 10 car, pour de fortes valeurs de a, on voit
apparaître deux contre-indications (cela revient à avoir une action dérivée très forte)
- elles augmentent fortement l’incidence des bruits de capteurs sur la commande (dans
le rapport a).
- elles conduisent à de fortes sollicitations des actionneurs pour des variations brusques
de la consigne ou de la perturbation
EXEMPLE.
C(s)
yc
u
d
y
−
+
F(s)
+
+e
1
0
1
0
Considérons une variation en échelon de d (ou de yc) qui induit une variation brusque, sur
l’écart e, d’amplitude e0. Pour le régulateur proportionnel, de gain K, la variation e0 sur e
induit une variation instantanée u0 sur u de valeur : u0 = K e0. Pour un correcteur à avance de
phase, de même gain K, cette variation brusque est : u0 = aK e0. En effet, d’après le théorème
de la valeur initiale, on a
0
0
s
0 eaK]
s
e
Ts1
aTs1
s[Klimu =
+
+
=
∞→
Cours de Commande 91](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-99-320.jpg)
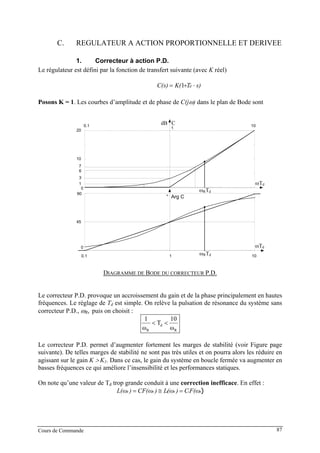
![D. REGULATEUR A ACTION PROPORTIONNELLE -
INTEGRALE
1. Correcteur à action P.I.
Le régulateur est défini par la fonction de transfert suivante (avec K réel)
i
i
i sT
sTK)
sT
K(C(s) +=+= 111
Posons K = 1. Les courbes d’amplitude et de phase de C(jω) dans le plan de Bode sont
0
-90
-45
0
iT
1
iT10
1
iT
100
ω
ω
db |C|
Arg[C]
DIAGRAMME DE BODE DU CORRECTEUR P.D.
Le correcteur P.D. provoque un accroissement du gain et de la phase en basses fréquences.
On choisit généralement, pour que l’effet déstabilisant de ces modifications de gain et de
phase soit faible, avec ωR la pulsation de résonance du système sans correcteur
R
i
R ω
10T
ω
1 <<
Cours de Commande 92](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-100-320.jpg)
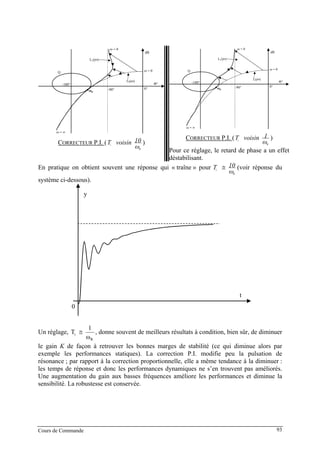
![2. Correcteur à retard de phase
Ce correcteur est en fait un correcteur P.I. « approché » sans toutefois introduire d’intégration
(avec b > 1)
bTs
TsKC(s)
+
+=
1
1
Posons K = b. Les courbes d’amplitude et de phase de C(jω) dans le plan de Bode sont les
symétriques, par rapport à l’axe des ω, de celles du correcteur à avance de phase
aT
10
bT
1
0
20 logb
-90°
-45°
0
10 logb
dB |C|
Arg[C]°
ω
ωaT
10
DIAGRAMME DE BODE DU CORRECTEUR A RETARD DE PHASE
Le retard de phase maximum ΦM introduit par le correcteur à retard de phase a lieu pour ω =
ωM te que
bT
1
ωM = . Le retard de phase maximum introduit par le correcteur pour cette
pulsation est :
1b
1b
AsinΦM
+
−
= ou
M
M
sinΦ1
sinΦ1
b
−
+
=
Ce n’est pas l’effet du retard de phase qui est utilisé ici, mais plutôt la différence de gain entre
les basses et les hautes fréquences, et donc la capacité que le correcteur a à introduire du gain
en basses fréquences, ce qui augmentera alors le gain statique du système en boucle fermée, et
Cours de Commande 94](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-102-320.jpg)
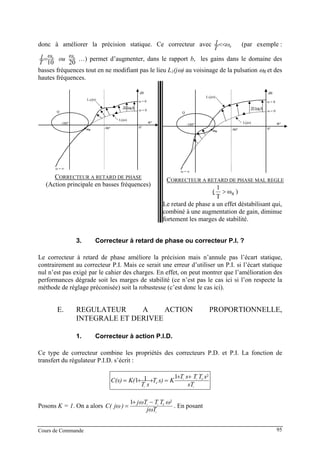
![di
n
n TT
ec ωav
ω
ω
w 1== et
d
i
T
T
2
1=ξ ,
on obtient
wj
wwj
C(jw)
ξ
ξ
2
21 2−+
=
On en déduit une deuxième forme canonique de la fonction de transfert du P.I.D. :
n
n
ω
s
ω
s
ω
s
s)C(
n
ξ
ξ
2
21 2
2
++
= avec
T
Tet
TT
ω
d
i
di
n
2
11 == ξ
Les formules inverses sont
ω
Tet
ω
T
n
d
n
i
ξ
ξ
2
12
== . Etudions maintenant les
variations de la phase de C(jw) :
wj
wj)w(
jw)C(
ξ
ξ
2
21 2 +−
= ⇒ )(w
-w
w
AArg[C(jw)] 190
1
2
tan 2 ≤°−=
ξ
⇒ )(w
-w
w
AArg[C(jw)] 190
1
2
tan 2 ≤°+=
ξ
La courbe de phase de C(jw) est donc celle du second degré, changée de signe et décalée de
90°
Arg[C]°
+90°
-90°
w
1010.1
ζ
ζ’
Etudions maintenant les variations du gain de C(jw) :
2
2
2
2
2222
22222
42
12
4
1
4
41
ξξ
ξ
ξξ
ξ w
ww
w)w(
jw)C( +
−
+=
+−
=
Cours de Commande 96](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-104-320.jpg)
![Bode de C(jw)
pulsation réduite : w
0
5
10
15
20
25
30
35
40
10
-1
10
0
10
1
-90
-45
0
45
90
A
B
C
D
E
F
A
B
C
D E
F
Phase (deg)
Gain (dB)
L’effet du correcteur P.I.D pour R
di
ω
TT
1ωn <= est :
Q
-180°
-90° 0°
dB
ω = ∞
L1(jω)
ω = 0
Φ°
ωn
ω = 0
ωR
L’’(jω)
L’(jω)
L(jω)
L’’(jω)
L(jω)
L’(jω)
EFFET D’UN REGULATEUR P.I.D. ζ < ζ ‘< ζ’’
On constate une augmentation des performances due à l’intégration (basses fréquences) et une
action stabilisante (haute fréquence) importante due à l’avance de phase pour ω > ωn. On note
que le point ω = ωn est un point invariant car |C(jων)| = 1 et arg[C(jων)] = 0. En d’autres
Cours de Commande 98](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-106-320.jpg)

![K F(s)
isT
1
sTd
d
e yyC u
_ _
+
+
++
+
Régulateur P.I.D.
Processus
mesure
consigne commande
La commande s’écrit
-y)y
sTTsT
sT)(sT
sT
K(y]-y)-sT)(y
sT
K[(u C
dii
i
d
i
dC
i
21
11111
++
+++=+=
Le diagramme ci-dessus est donc équivalent à
F(s)
2
dii
i
sTTsT1
sT1
++
+
d
yyC u
_
+
++
Processus
mesure
consigne commande
)dsT
isT
1
K(1 ++
K(s)RC(s)
yr
2. Correcteur à avance – retard de phase
Ce type de correcteur combine les avantages des correcteurs à avance et retard de phase et sa
fonction de transfert s’écrit (avec a > 1 et b > 1)
bT's
T's
sT
aTsKC(s)
+
+×
+
+=
1
1
1
1
La méthode de réglage est la suivante
On commence par régler les coefficients a et T du terme à avance de phase, avec a le
plus grand possible mais respectant les exigences d’amplitude des bruits (transmis sur
les capteurs) et de sollicitation des actionneurs (en pratique a<10). On choisit
aT
1
voisin de ωR.
On règle ensuite les coefficients b et T du terme à retard de phase afin d’obtenir les
performances désirées (par exemple la précision statique), d’où la valeur de b. On
choisit
10
ω
T'
1 R
< .
Cours de Commande 100](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-108-320.jpg)



![u
-
+ yC(s) F1(s) F2(s)
+
R(s)
+ -
P
+ u’’e’eyr
La perturbation est mesurée via l’élément R(s). On peut alors écrire
)(
1
)1(
)(
1
)(
21
1
21
21
21
sP
FCF
F
RFF
sY
FCF
FCFsY r
+
−
+
+
=
Si R = 1/F1, alors la sortie est indépendante de la perturbation. On constate que la stabilité
n’est pas affectée par cette chaîne de tendance car elle n’intervient pas au dénominateur des
deux fractions de l’expression précédente.
3. Chaîne d’anticipation
Une chaîne d’anticipation permet d’injecter en un point de la chaîne directe un signal fonction
de la grandeur de consigne.
-
yC(s) F1(s) F2(s)
+ u’’
+ e
+
R(s)
yr
On obtient alors
[ ] rrr Y
FCF
FCFRF
YRY)Y(YCFFY
21
212
12
1+
+
=⇒+−=
Si F2R=1, alors Y = Yr. Dans tous les cas, on constate que la stabilité n’est pas affectée par la
chaîne d’anticipation.
B. METHODES INDUSTRIELLES DE SYNTHESE D’UN PID
Le problème de synthèse d’un correcteur n’est plus alors qu’un problème de réglage des
actions proportionnelle, intégrale et dérivée. Comme les méthodes doivent être utilisées en
milieu industrielle, elles se doivent d’être simples et rapides à mettre en œuvre, tout en étant
le plus précises et efficaces possible. Il existe deux types de méthodes : empiriques et
analytiques.
Cours de Commande 104](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-112-320.jpg)


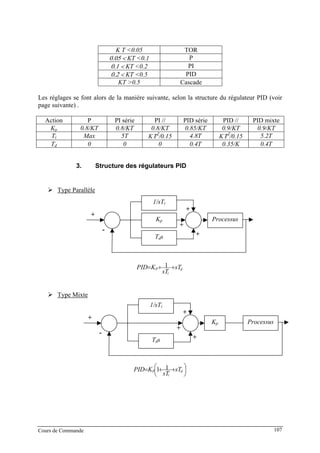
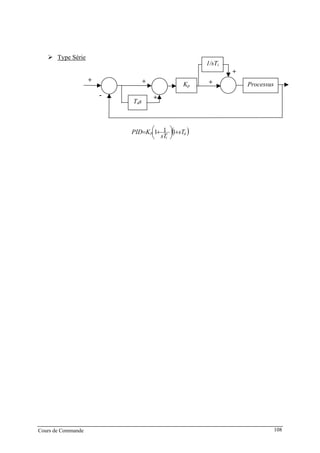



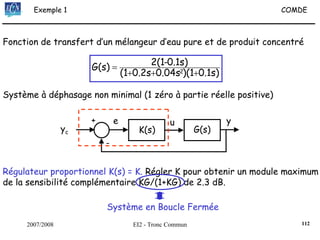
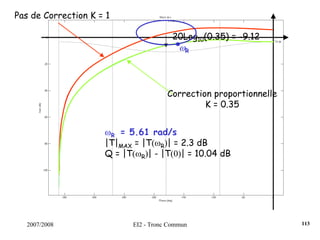
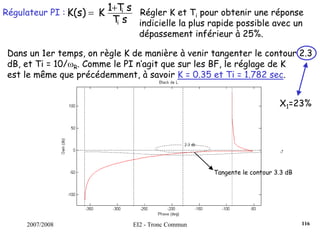
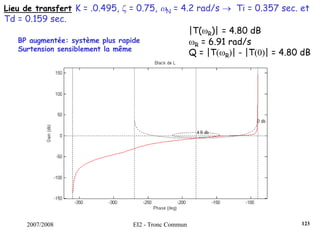
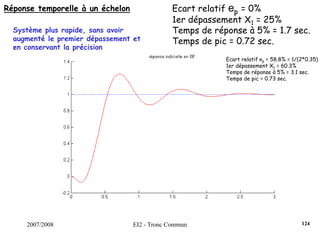
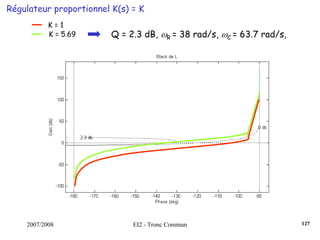
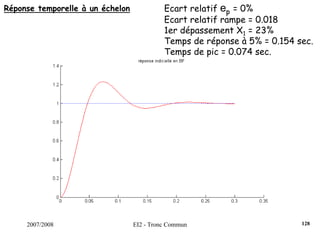
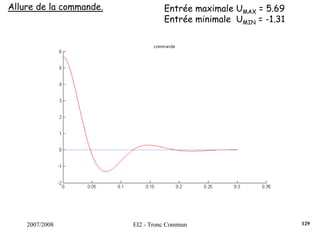
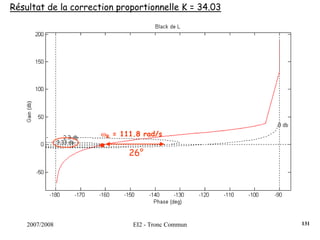
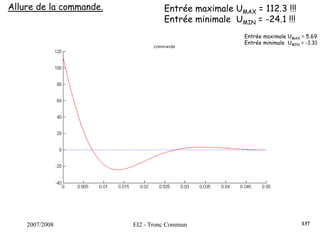
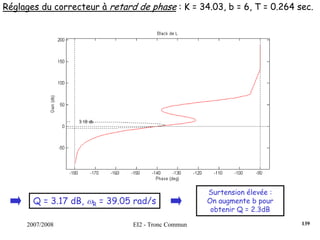
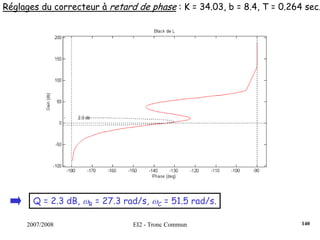
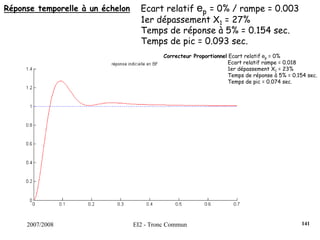
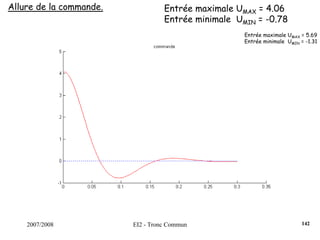
![2007/2008 EI2 - Tronc Commun
Régulateur PID : Régler K, Ti et Td pour obtenir une réponse indicielle la
plus rapide possible avec un dépassement infé-
-rieur à 25%.s)T
sT
1(1KK(s) d
i
++=
Dans un 1er temps, on règle K de manière à venir tangenter le contour 2.3
dB, K = 0.35. Ensuite, on choisit ωN < ωR = 5.61 rad/s. On fixe ωN = 4.2
rad/s. La dérivée se fait par l’intermédiaire d’un filtre, avec τ = 0.001s
(τ <<< 1/ωN). On pose ζ = [0.5;0.75;1].
Surtension Q minimum pour ζ = 0.75.
On choisit donc ce cofficient ζ et on augmente le gain K de manière à
obtenir un premier dépassement de 25%, ce qui induira un système le
plus rapide possible.
122](https://image.slidesharecdn.com/35039799-cours-commande-2009-2010-150714220714-lva1-app6892/85/35039799-cours-commande-2009-2010-130-320.jpg)