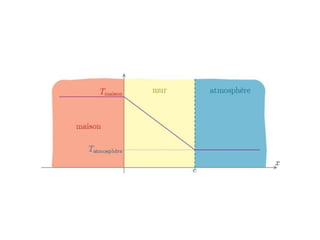
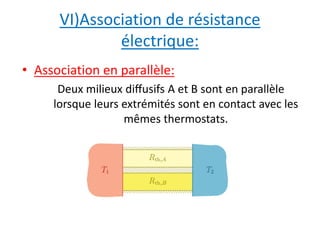
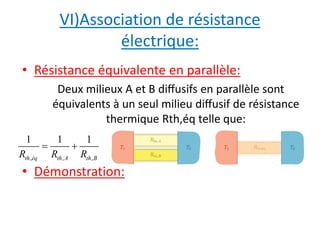
Le document explore la notion de résistance thermique dans le contexte de la diffusion thermique, en utilisant l'exemple d'un mur simple pour expliquer le profil de température et le flux thermique. Il définit la résistance thermique comme un paramètre indépendant des différences de température et illustre son application à des géométries variées ainsi que les analogies avec des systèmes électriques. En conclusion, la résistance thermique est essentielle pour simplifier les calculs et améliorer la compréhension des transferts thermiques sans sources internes.

1. Diffusion thermique
Notion de résistance thermique

2. I)Présentation sur un exemple:
• Circonstance:
Nous pourrons parler de résistance thermique dans
un phénomène de diffusion :
en régime permanent stationnaire
sans terme de source
Reste maintenant à savoir ce qu’est cette résistance
thermique.

3. I)Présentation sur un exemple:
• Exemple du mur simple:
But:
Déterminer du profil de température au sein
d’un mur simple de maison
Hypothèses:
pas de transferts conducto-convectifs.
Problème à symétrie plane.
Pas de sources internes dans le mur.

5. I)Présentation sur un exemple:
Equation de diffusion vérifiée par la température :
T r t
( ; )
c T q
 
0 v
t

    

2
T
x
2 0





6. I)Présentation sur un exemple:
Condition aux limites:
 0;  maison T x  t T  ;  atmosphère T x  e t T

7. I)Présentation sur un exemple:
Expression de la température dans le mur :
  atmosphère maison
maison
T T
T x x T
e

 

8. I)Présentation sur un exemple:
Expression du flux allant de la maison vers
l’atmosphère :
S

 T T
 maison atmosphère maison atmosphère
   
e

9. I)Présentation sur un exemple:
• Généralisation:
Autrement dit en généralisant un peu avec des
milieux 1 et 2, on obtient :
    1 2 1 2 1 2 1 2 quelquechose T T T T autrechose         
C’est cette « autre chose » qui est la résistance
thermique.

10. II)Définition:
• Un milieu diffusant dont les limites sont aux
températures T1 et T2 a une résistance
thermique Rth:
 
 1 2
1 2
th
T T
R




11. II)Définition:
Remarques:
•Rth est indépendant de T1- T2 et de φ(1-2)
Ils dépendent uniquement de la conductivité thermique et
de grandeurs géométriques.
•Pour se souvenir des conventions, c’est facile : les chiffres
représentant les milieux sont dans le même ordre dans T1-
T2 et de φ(1-2)

12. III)Résistance thermique d’un milieu
unidimensionnel:
La résistance thermique d’un milieu diffusif
unidimensionnel de longueur l, de section S et
de conductivité λ s’écrit :
th
l
R
 S


13. III)Notion de résistance thermique et
géométrie:
 
 1 2
1 2
th
T T
R



La relation
est vraie quelque soit la géométrie.
1

Géométrie plane:
 
th
th
Géométrie cylindrique (en conduction radiale):
S
G
R L
2 .
 
2
1
ln
th
l
G
R
R


14. V)Analogie électrique:
• Nous pouvons faire une analogie entre les
aspects électriques et les aspects thermiques
conformément à ce tableau.

15. V)Analogie électrique:
• De cette manière il est assez facile de se
souvenir de la définition de la résistance
termique
U = Ri 1→2 T1 − T2 = Rth Φ1→2
• Il est possible de transposer un problème de
diffusion en un problème électrique dès lors
que :
• ➜ le régime est permanent stationnaire ;
• ➜ il n’y a pas de terme de source.

16. VI)Association de résistance
électrique:
• Association en parallèle:
Deux milieux diffusifs A et B sont en parallèle
lorsque leurs extrémités sont en contact avec les
mêmes thermostats.

17. VI)Association de résistance
électrique:
• Résistance équivalente en parallèle:
Deux milieux A et B diffusifs en parallèle sont
équivalents à un seul milieu diffusif de résistance
thermique Rth,éq telle que:
1 1 1
 
R R R
th , éq th , A th ,
B • Démonstration:

18. VI)Association de résistance
électrique:
• Association en série:
Deux milieux diffusifs A et B sont en série
lorsqu’ils sont mis bout à bout :

19. VI)Association de résistance
électrique:
• Résistance équivalente en série:
Deux milieux A et B diffusifs en série sont
équivalents à un seul milieu diffusif de résistance
thermique Rth,éq telle que:
th,éq th,A th,B R  R  R
• Démonstration:

20. Conclusion:
• La notion de résistance thermique est
fondamentale car:
– Elle permet une simplification calculatoire dans le
calcul des flux en RP et sans sources internes.
– Une compréhension plus physique des transferts
thermiques.