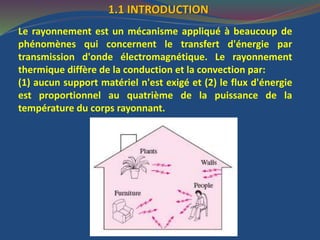
Le document traite du rayonnement thermique, en expliquant ses mécanismes, propriétés et mesures, ainsi que son comportement au sein du spectre électromagnétique. Il aborde des concepts clés comme l'émittance, la réflectivité, et l'irradiation, tout en présentant les caractéristiques des surfaces idéales et réelles. Des principes tels que la loi de Kirchhoff et l'approximation du corps gris sont également discutés en lien avec les échanges radiatifs entre surfaces.

2. 1.1 INTRODUCTION
Le rayonnement est un mécanisme appliqué à beaucoup de
phénomènes qui concernent le transfert d'énergie par
transmission d'onde électromagnétique. Le rayonnement
thermique diffère de la conduction et la convection par:
(1) aucun support matériel n'est exigé et (2) le flux d'énergie
est proportionnel au quatrième de la puissance de la
température du corps rayonnant.

3. 1.2 Le Spectre électromagnétique

4. Les parties du spectre électromagnétique sont illustrées dans
fig. 1. Le rayonnement thermique est défini comme une partie
du spectre située entre les longueurs d'onde 10-7 m et. 10-4 m.
Cet intervalle contient le spectre visible très étroit, entre
3.9.10-7 m à 7.8.10-7 m.
L’unité utilisé pour mesurer la longueur d'onde est le
micromètre : 1 μm = 10-6m. Dans cette unité, le rayonnement
thermique occupe l’intervalle entre 0.1 μm à 100 μm, et la
partie visible du spectre est de 0.39 à 0.78 μm. Une autre unité
courante de longueur d'onde est l'angström : 1A° = 10-10m.
La vitesse de propagation de toutes les ondes
électromagnétiques dans un vide est : c = λv = 3.10-8 m/s
Où λ est la longueur d'onde et le v est la fréquence du
rayonnement.

5. 2. PROPRIÉTÉS ET DÉFINITIONS
Le mot spectral est employé pour indiquer la dépendance
de la longueur d'onde pour n'importe quelle quantité de
rayonnement. La valeur de la quantité à une longueur
d'onde indiquée s'appelle une valeur monochromatique.
2.1 Absorptivité, réflectivité, et transmissivité
Chaque fois que l'énergie radiante
est incidente sur n'importe quelle
surface, une partie peut être
absorbée, une partie peut être
reflétée, et une partie peut être
transmise par le corps récepteur.
Définissons :

6. Il est clair que : α+ρ+τ=1
La plupart des solides, ceux qui ne sont pas être visiblement
transparent ou semi transparent, ne transmettent pas le
rayonnement, et on a : α+ρ =1
α :la fraction du rayonnement d'incident absorbé
=Absorptivité.
ρ : la fraction du rayonnement d'incident qui est réfléchie =
Réflectivité.
τ : la fraction du rayonnement d'incident transmis =
Transmissivité.

7. 3. Grandeurs Radiatives
3.1 Puissance émissive totale (Emittance) :
Le concept l’émittance est introduit pour quantifier le flux
d’énergie émis d’un corps par unité de surface. La puissance
émissive spectrale, Eλ est défini comme le taux de transfert
d'énergie radiante émise à la longueur d'onde λ dans toutes les
directions par unité de surface.
L’émittance totale, E (W/m2), est le flux radiatif émis par unité
de surface dans toutes les directions et à toutes les longueurs
d'onde possibles.

8. 3.2 Irradiation (L’éclairement)
L’éclairement est le flux reçu par unité de surface
réceptrice, en provenance de toutes les directions.
L’irradiation spectrale est taux de d'énergie radiante reçue
à la longueur d'onde λ dans toutes les directions par unité
de surface.
L’irradiation totale, G(W/m2), est le flux radiatif reçu par
unité de surface provenant de toutes les directions et à
toutes les longueurs d'onde possibles.

9. 3.3 Radiosité
Elle représente flux radiatif total, quittant une surface. Ainsi la
radiosité est la somme des flux radiatif émis et réfléchie d'une
surface. Comme l’émittance totale, la radiosité totale J est une
intégration à travers toutes les directions et toutes les longueurs
d’ondes.

10. 3.4 Surfaces spéculaires et surfaces diffuses
La réflexion de l'énergie thermique radiante par une surface
peut être décrite à l'aide de deux modèles idéaux. Le
réflecteur parfait (miroir) est montré dans fig. 2 (a) ; dans ce
cas-ci l'angle d'incidence, Φi est égal l'angle effectuée par le
rayon reflété, Φr. Une surface diffuse est montrée dans fig. 2
(b) ; dans ce cas-ci le rayonnement est réfléchi vers toutes les
directions.

11. 3.5 Intensité du rayonnement
Angle solide
C’est le rapport entre la surface
différentielle, dA2, sur une sphère de
rayon r par le rayon de cette sphère au
carré. C’est la région qui contient tous
les rayons issus d’un point situé au
centre d’une surface dA2, intercepté par
une surface dA2

12. Nous définirons l'intensité de rayonnement, I, comme l'énergie
radiante par unité de temps par unité d’angle solide par unité de
surface de l'émetteur projeté à la normale à la ligne de la vue du
récepteur. Pour la géométrie représentée dans fig. 3, l'énergie
rayonnée de l'élément dA1 interceptée par l'élément dA2 est :

13.     12
2
cos sin
dq
I d d
dA
En substituant ces deux équations et en intégrant suivant une
surface hémisphérique on obtient :
 12 1(cos )dq I dA d
Ce qui est la relation générale entre tout la puissance émissive
d'une surface (dans ce cas-ci, l'élément dA1) et intensité de
rayonnement. Si la surface d’émission est parfaitement diffuse,
I = constante, nous obtenons :
12
2
dq
E I
dA
 

14. 4. Rayonnement du Corps Noir
La surface idéale dans l'étude du rayonnement thermique
est le corps noir, qui est défini par α= 1. Ainsi le corps noir
absorbe tout le rayonnement thermique incident,
indépendamment des caractéristiques spectrales ou
directionnelles. Un tel corps peut être approché par un petit
trou aboutissant dans une cavité.

15. 4.1 Emittance d’un corps noir
L’émittance totale (hémisphérique) d'un corps noir est donné
par l'équation de Stefan-Boltzmann : Eb = σT4
Où σ est la constante de Stefan-Boltzmann,
σ= 5.6697 .10-8 W/m2.K4.
4.2 Distribution spectrale du corps noir
Généralement une surface émet différentes quantités
d'énergie à différentes longueurs d'onde. L’émittance totale
d’un corps noir peut être exprimé comme :
4
0
b bE E d T  

 
Ebλ est L’émittance monochromatique.

16. La première expression précise pour Ebλ a été déterminée par
Max Planck :
C1 et C2 sont des constantes.
Les courbes de Ebλ en fonction de λ pour différentes
températures sont illustrées dans la figure

17. 5. Surfaces Réelles et le Corps Gris
5.1 L’émissivité
Une surface réelle a émittance totale E inferieure à celle d’un
corps noir. Le rapport entre l’émittance d'un corps et celui d'un
corps noir à la même température est l'émissivité totale ε :
ε=E/Eb
L'émissivité (hémisphérique) monochromatique, ελ sera utile
pour traiter les surfaces réelles qui montrent une
dépendance spectrale de l’émissivité.
ελ=Eλ/Ebλ

18. 5.2 La loi de Kirchhoff
Considérons un petit corps en équilibre thermique avec une
cavité noire, le bilan des flux échangé par le corps doit être
nul. Par conséquent, le rayonnement émis par le corps doit
être égal au rayonnement qu’il a absorbé:
 4 4
S SA T A T
Donc nous obtenons: α (T) =ε (T).
Cette équation est connue comme loi de Kirchhoff, et pour des
valeurs monochromatiques, on peut montrer que la loi de
Kirchhoff est : αλ (T) =ε λ (T).

19. 5.3 L'approximation du corps gris
L’émittance monochromatique d'une surface réelle n'est pas
une fraction constante de celle d'une surface noire Une
idéalisation très utile est celle du corps gris, défini comme
suit : ε λ = constante
Donc l’émittance totale d’un corps gris devient :
4
0 0
bE E d E d T     
 
   

20. 6. Echanges radiatifs : Surfaces Noires
Dans cette section, et dans ce qui suit, nous limiterons notre
discussion aux surfaces diffuses, de plus, nous considérerons
seulement les propriétés totales hémisphériques. La notation
suivante sera employée dans ce chapitre :
Qi = flux net d'énergie émis par la surface i.
Qij = flux d'énergie quittant la surface i et intercepté par la
surface j.
Q'ij = flux d'énergie émis par la surface i et absorbé par la
surface j.
= flux net d'énergie échangé entre la surface i et la surface j.&ijQ

21. Considérons la configuration la plus simple, celle de deux plan
infinis, noirs et parallèles, maintenus aux températures, le T1 et
le T2 , L'échange net de l'énergie entre les surfaces 1 et 2 est :
= Q’12 −Q’21 =α2A1 Eb1− α1A2 Eb2= A1 Eb1− A2 Eb2 (α2 =α1=1) par
unité de surface:
&12Q
/A=Eb1− Eb2=σ(T1
4− T2
4)&12Q

22. 6.1 Facteur de forme
Le facteur de forme (également appelé
un facteur d'aspect) prend compte des
caractéristiques géométriques de
l'échange radiatif entre deux surfaces.
Le facteur de forme Fij est défini comme
fraction du rayonnement quittant la
surface i qui est arrêtée par la surface j.
Pour les surfaces arbitrairement
orientées : Ai et Aj.
Fij =Qij /Ai Ji
Qij est le flux radiatif quittant Ai et intercepté par la surface
Aj; Ji est la radiosité de la surface Ai, qui représente le flux
radiatif quittant Ai dans tous les sens. On suppose que les
surfaces sont isothermes, diffuses, et de radiosité uniforme.

23. 6.2 Propriétés du facteur forme
Il y a quatre propriétés importantes du facteur de forme utiles
dans les calcul des échanges radiatifs entre les surfaces.
6.2.1 Subdivision de la surface réceptrice
Pour obtenir toute l’énergie rayonnée de A1 à A2.,
il faut faire la somme de toutes les fractions de
l'énergie rayonnées de A1 à chacune partie de A2.
A2=∑ΔA2i 1 2 1 2iA A A AF F   
6.2.2. Subdivision d’une surface émettrice
1 2 1 21
1
1
iA A i A AF A F
A
    A1=∑ΔA1i

24. 6.2.3. Propriété des cavités
La troisième propriété importante est que la somme des
facteurs de forme pour n'importe quelle surface fermé égal à
l’unité. Pour une surface émettrice A1 complètement entouré
par n surfaces réceptrices Ai (qui comprennent également A1) :


 1
1
1i
n
A A
i
F
6.2.4. Théorème de Réciprocité
1 2 2 11 2A A A AA F A F 

25. Abaques de calcul du facteur de forme pour quelques géométries

29. 6.3. Echanges radiatifs dans une Cavité Noire
Pour une Cavité se composant de n surfaces noires, le flux net de l'énergie échangé
entre n'importe quels deux des surfaces est :
ijQ& = Q’ij −Q’ji =FijAi Ebi− FjiAj Ebj
En appliquant le théorème de réciprocité on a :
ijQ&
ijQ &= FijAi (Ebi− Ebj) =
Le flux de chaleur net émis par une surface i :
1
 
n
i ij
i
Q Q
Et d’après la propriété des cavités on obtient:
1
( )

  
n
i i bi ij bj
i
Q A E F E
Où la sommation comprend le terme j = i. Le système des équations
avec qi propose une analogie avec un réseau électrique.

30. Pour n = 3 l'analogie est illustrée dans Fig.11, où les points nodaux sont maintenus
aux potentiels représentant leurs émittance de corps noir. Les résistances entre les
nœuds sont des résistances spatiales, Rij =1/AiFij.

31. 7. Échanges Radiatifs : Surfaces Grises
Pour cavité constituées de surfaces opaque et grises. Le rayonnement peut quitter
une surface par émission propre ou par réflexion de l'irradiation qui provient
d'autres surfaces de cavité (fig. 12). Nous commençons l’analyse du problème en
effectuant les bilans énergétiques au niveau des surfaces pour obtenir les relation
des flux net quittant une surface, et en représentant les résultats sous forme de
réseau électrique.
7.1 Relations d’échanges radiatifs : Représentation en réseau
Le terme Qi, qui est le flux radiatif net quittant la surface i, égale à la différence entre
la radiosité et l'irradiation extérieure, et peut être exprimée comme :
Qi = Ai (Ji−Gi)
Ji=εiEbi+ρiGi

32. Éliminant le Gi entre ces équations nous trouvons : le flux radiatif net quittant la
surface Ai : bi i
i
i i i
(E -J )
Q =
(1- )/ A 
Cette équation constitue la base pour l'analogue électrique des surfaces grises. Le
numérateur, Ebi−Ji, peut être considéré comme une un potentiel, alors que le
dénominateur, (1−εi) εiAi peut être considéré comme résistance de surface.
7.2 Résistance radiative spatiale
Considérer maintenant l'échange radiatif entre deux
surfaces de la cavité (fig. 12). En suivant le même analyse
que celui du corps noir, notons que le terme Qij a été définie
comme le flux net quittant surface i et intercepté par la
surface j. par conséquent, l'échange radiatifs net entre les
deux surfaces peut être exprimé en termes de radiosités
extérieurs, comme suit :
' ' =ij ij ji ij i i ji j jQ Q Q F A J F A J  &
Donc on obtient :
-1
( )/( )ij i j ij jQ J J F A &
Le terme Qij constitue élément de réseau électrique analogue, pour lequel (Ji −Jj) est
le potentiel et (AiFij)-1 est une résistance radiative spatiale.

33. 7.3 Bilan énergétique au nœud Ji.
Nous voyons que le flux radiatif net de à la surface Ai, qi, égal la somme des flux
radiatif net à partir de Ai vers toutes les autres surfaces Qij, voir fig13.
Le réseau correspond à un bilan énergétique sur le nœud représentant la radiosité
(potentiel). Du réseau nous pouvons voir que le flux net à partir de la surface A1, q1,
à la forme :
Q1= Q12 + Q12+… =( J1− J2)/ (F12A1 )-1+ ( J1− J3)/ (F13A1 )-1+…

34. 7.4 La cavité composée de Deux Surface
L'exemple le plus simple d'une cavité est celui deux surfaces qui échangent le
rayonnement seulement l’une avec l’autre.
Nous pouvons employer l’analogie électrique pour résoudre le problème.
Donc le flux radiatif net entre les deux surfaces peut être exprimé comme suit :

35. 7.5 Ecrans protecteurs
Une application importante est l'utilisation des écrans pour réduire le flux de chaleur
par rayonnement. Un cas spécifique est l'utilisation de plaque d’aluminium dans des
murs de construction. Considérer deux plans gris infinis de fig. 13 pour lesquels :

36. Si un écran protecteur mince, le corps 3, est mis entre les deux murs, le flux de par
unité de surface à l’équilibré est :
q13/A= q32/A=q/A, ou:
Si ε1=ε2 et ε3,1=ε3,2 nous obtenons:
4 4 4
2 1 3( )/2T T T 