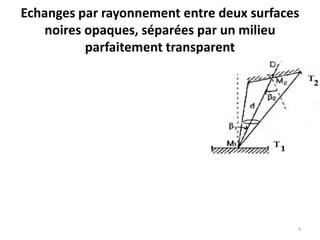
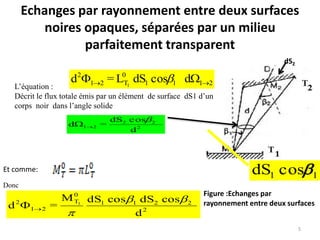
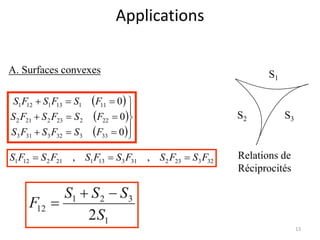
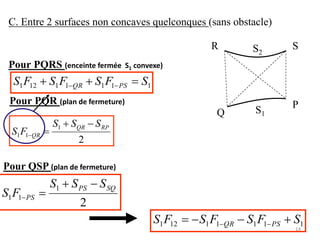
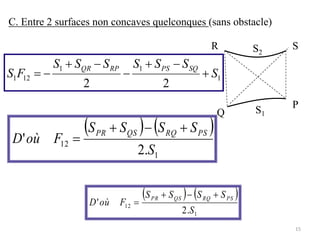
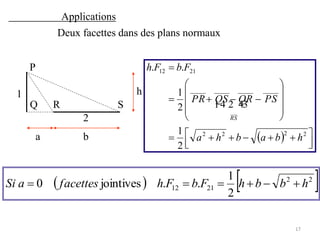
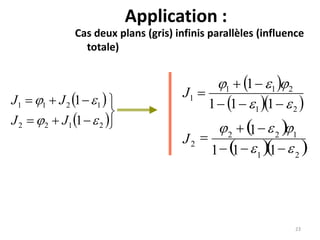
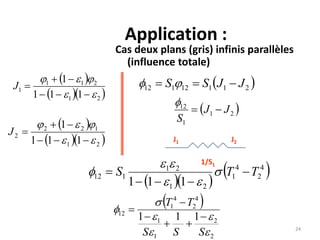
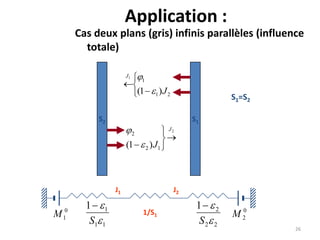
Le document traite du calcul des échanges de chaleur par rayonnement, en se concentrant sur différents cas, tels que les surfaces noires et grises, ainsi que les facteurs de forme associés. Il présente des méthodes théoriques et des équations pour déterminer le flux échangé entre différentes surfaces, en tenant compte des propriétés géométriques et thermiques. Les applications et cas pratiques sont également abordés, notamment pour des configurations de surfaces infinies et concaves.