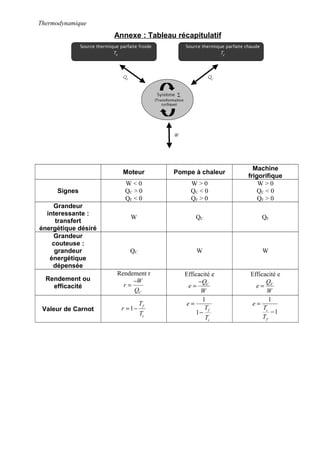
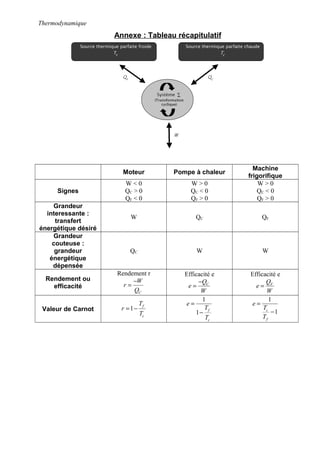
Le chapitre porte sur le fonctionnement des machines thermiques, notamment les moteurs, les machines frigorifiques et les pompes à chaleur. Il présente les principes de la thermodynamique, le calcul du rendement et l'efficacité de ces machines, tout en comprenant un cycle Carnot et des applications pratiques. Les erreurs courantes et les distinctions importantes liées aux conventions algébriques des échanges énergétiques sont également mises en avant.

1. Thermodynamique
TD T5 : Machines thermiques
But du chapitre
• Etudier le fonctionnement d’un moteur, d’une machine frigorifique, d’une pompe à chaleur
ou d’un climatiseur.
Plan prévisionnel du chapitre
TD T5 : Machines thermiques
Savoirs et savoir-faire
Ce qu’il faut savoir :
• L'écriture particulière des principes de la thermodynamique sur un cycle.
• La définition du rendement ou de l’efficacité d'une machine thermique.
• Les signes des transferts thermiques et des travaux échangés par l'agent thermique dans un
moteur, un réfrigérateur et une pompe à chaleur dithermes.
• L'existence d'une performance maximale (rendement ou efficacité de Carnot) imposée par le
deuxième principe pour toute machine thermique ditherme.
Ce qu’il faut savoir faire :
• Représenter le schéma de principe d'une machine thermique, en y indiquant les travaux et
les transferts thermiques algébriques mis en jeu.
• Identifier un cycle moteur ou récepteur d'après le sens de parcours du cycle sur un graphique
• Calculer le rendement ou l’efficacité d'une machine thermique.
• Retrouver l'expression du rendement ou de l'efficacité de Carnot.
Erreurs à éviter/ conseils :
• II est essentiel de bien distinguer les conventions algébriques choisies pour décrire les
échanges énergétiques du sens réel de ces échanges. Pour l'étude d'une seule machine, on
définit généralement les échanges énergétiques par rapport à l'agent thermique (ils sont donc
positifs lorsque l'énergie est effectivement reçue par celui-ci). En présence de plusieurs
machines en interaction, on fixe les conventions au début de l'étude et on s'y tient jusqu'à la
fin.
• La performance d'une machine thermique (rendement ou efficacité) est définie positive :
attention de bien respecter cette contrainte.
Applications du cours
Application 1 : Calculer le rendement d’un moteur thermique
Application 2 : Calculer l’efficacité d’une pompe à chaleur
Une pompe à chaleur fonctionne de manière réversible avec les deux sources suivantes :
• un réservoir d'eau, pseudo-source chaude (de température variable), considéré comme une
phase condensée idéale de capacité thermique C et initialement à la température Tco = 288 K;
• l'atmosphère, une source froide à la température TF = 288 K.
La pompe à chaleur sert à chauffer l'eau dont la température finale vaut Tcf = 320 K.
Déterminer l'efficacité e de cette pompe à chaleur.
Un gaz parfait décrit le cycle moteur ABCDA ci-dessous,
composé de deux transformations adiabatiques réversibles et de
deux transformations isobares. Exprimer son rendement en
fonction de γ, VA et VD.

2. Thermodynamique
Application 3 : Cycle de Carnot
Un fluide (gaz parfait) décrit un cycle réversible constitué par :
• AB : détente isotherme à T2 ;
• BC : adiabatique de T2 à Tl > T2 ;
• CD : compression isotherme à Tl ;
• DA : adiabatique de Tl à T2.
a) Représenter un tel cycle en coordonnées de Clapeyron (P. V) ou en diagramme entropique (T,
S). S'agit-il d'un cycle type moteur thermique ou type pompe à chaleur ? Comparer les aires des
deux représentations du cycle.
b) Définir l'efficacité e d'un tel système. La calculer par méthode graphique. Dépend-elle de la
nature du fluide ?
Exercices
Exercice 1 : Climatiseur
Exercice 2 : Cycle de Stirling d’un moteur ditherme et irreversibilité

3. Thermodynamique
Exercice 3 : Etude d’un moteur à explosion
Description du moteur à explosion

4. Thermodynamique
Modélisation du moteur à explosion

5. Thermodynamique
Quelques questions
On cherche à déterminer le rendement du moteur à explosion. On note a = Vmax/Vmin, le taux de
compression ou rapport volumique.
1°) Exprimer les transferts thermiques QC et QF durant les étapes isochores CD et EB en fonction
des températures Tc et TD d’une part et TE et TB d’autre part.
2°) Exprimer le rendement du moteur sur l’ensemble du cycle en fonction de Tc, TD,TE et TB puis
en fonction de a et γ.
3°) Calculer le rendement pour a = 3 puis a = 9.
4°) Expliquer pourquoi les rendements effectivement observés sont en réalité de 10 à 20 % plus
faibles.
5°) Quelle est l’influence du taux de compression sur le rendement ? Quel phénomène limite
l’augmentation du taux de compression ?

6. Thermodynamique
Annexe : Tableau récapitulatif
Moteur Pompe à chaleur
Machine
frigorifique
Signes
W < 0
QC > 0
QF < 0
W > 0
QC < 0
QF > 0
W > 0
QC < 0
QF > 0
Grandeur
interessante :
transfert
énergétique désiré
W QC QF
Grandeur
couteuse :
grandeur
énergétique
dépensée
QC W W
Rendement ou
efficacité
Rendement r
C
W
r
Q
−
=
Efficacité e
CQ
e
W
−
=
Efficacité e
FQ
e
W
=
Valeur de Carnot 1
f
c
T
r
T
= −
1
1 f
c
e
T
T
=
−
1
1c
f
e
T
T
=
−

7. Thermodynamique
Annexe : Tableau récapitulatif
Moteur Pompe à chaleur
Machine
frigorifique
Signes
W < 0
QC > 0
QF < 0
W > 0
QC < 0
QF > 0
W > 0
QC < 0
QF > 0
Grandeur
interessante :
transfert
énergétique désiré
W QC QF
Grandeur
couteuse :
grandeur
énergétique
dépensée
QC W W
Rendement ou
efficacité
Rendement r
C
W
r
Q
−
=
Efficacité e
CQ
e
W
−
=
Efficacité e
FQ
e
W
=
Valeur de Carnot 1
f
c
T
r
T
= −
1
1 f
c
e
T
T
=
−
1
1c
f
e
T
T
=
−