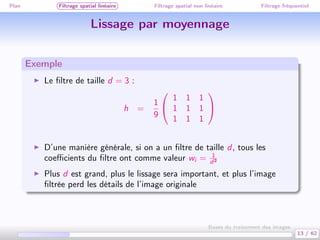
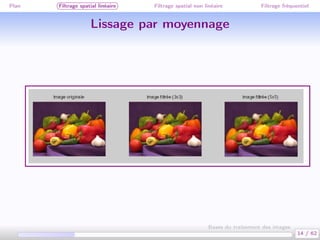
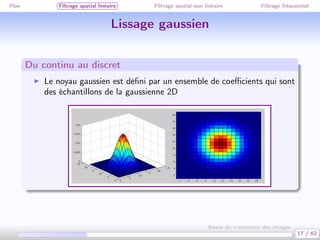
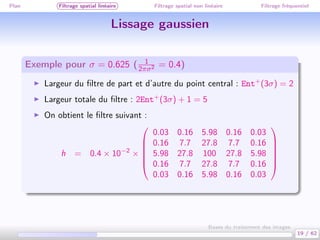
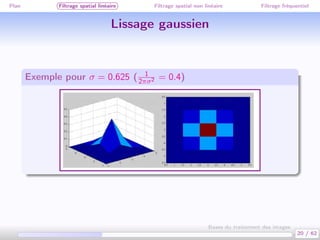
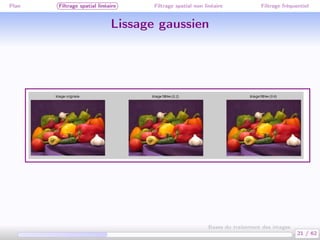
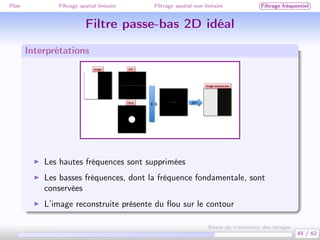
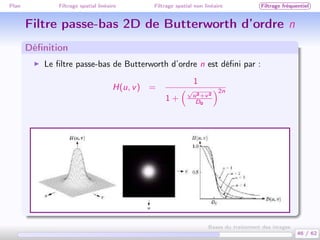
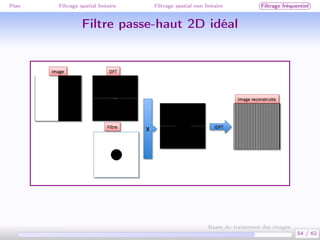
Ce document traite des bases du traitement des images, en se concentrant sur différentes méthodes de filtrage, y compris le filtrage spatial linéaire et non linéaire, ainsi que le filtrage fréquentiel. Il aborde des concepts clés tels que la réduction du bruit, la convolution, et différents types de filtres comme le filtre médian et le lissage gaussien. Les applications et exemples illustrent comment ces techniques peuvent être utilisées pour améliorer la qualité des images.