Cet article étudie le temps d'atteinte pour les processus de Bessel en relation avec l'activation neuronale et propose un algorithme appelé 'Walking on Moving Spheres' (WOMS) pour simuler le premier temps d'arrêt d'un processus de Bessel. Les résultats incluent des formules explicites pour le temps d'atteinte et une méthode numérique améliorée pour le calcul du temps d'arrêt. L'élaboration d'une procédure efficace pour simuler ce processus est également discutée, en s'appuyant sur le lien entre les processus de Bessel et les mouvements browniens.

1. Lecture d’article pour le cours Mod`eles
al´eatoires pour les neurosciences
Hitting time for Bessel Processes Walk on moving
spheres algorithm (WOMS) [2]
Victor Bontemps
Avril 2019
1 Pr´esentation de l’article
En neurosciences, le temps d’activation d’un neurone est g´en´eralement mod´elis´e
comme le temps d’atteinte d’un processus stochastique associ´e au poten-
tiel de la membrane. Lorsqu’on ´etudi´e le circuit ´electrique ´equivalent as-
soci´e `a un neurone, le processus d’Ornstein-Uhlenbeck apparaˆıt de mani`ere
naturelle. Dans le mod`ele de Feller, les processus de Bessel g´en´eralis´es
apparaissent comme une alternative plus r´ealiste au processus d’Ornstein-
Uhlenbeck. Lorsqu’on consid`ere ces mod`eles, l’intervalle d’interspike est in-
terpr´et´e comme le premier temps de passage du potentiel de membrane d’un
seuil fix´e et il est ´etroitement li´e au premier temps d’atteinte d’une courbe
pour certains processus de Bessel.
Dans cet article, les auteurs ´etudient le temps d’atteinte de bornes pour
les processus de Bessel. Les r´esultats majeurs et l’algorithme principal sont
obtenus dans le cas des processus de Bessel.
1

2. 2 Etude des r´esulats
2.1 Premi`eres d´efinitions
Avant tout, nous allons ´etudier les carr´es de Bessel qui constituent le lien
central entre le processus de Bessel et le mouvement brownien.
Consid´erons un mouvement brownien mutidimensionnel (de dimension n) :
Bt = (B1
t , B2
t , B3
t , ..., Bn
t )
On consid`ere sa norme euclidienne au carr´e : Yt = n
k=1(Bk
t )2
. Avec la
formule d’Itˆo, on a : dYt = 2 n
k=1 Bk
t dBk
t + ndt
Si on note Wt =
n
1
t
0 Bk
s dBk
s
√
Ys
On remarque que < Wt >= n
1
t
0
( Bk
s√
Ys
)2
ds =
t
0
n
1 (Bk
s )2
Ys
ds = t
Par la caract´erisation de Levy, on conclut que Wt est un mouvement brown-
ien, on peut r´e´ecrire l’´equation v´erifi´ee par Yt:
dYt = 2
√
YtdWt + ndt
On peut d´esormais d´eterminer l’´equation v´erifi´ee par la norme de Bt : Zt =
(Yt). On utilise encore un fois Itˆo, on trouve :
dZt = n−1
2
1
Zt
dt + dWt
Comme nous allons le voir juste apr`es cette ´equation caract´erise un processus
de Bessel de dimension n.
Plus g´en´eralement, on d´efinit les processus de Bessel comme des solutions
de syst`emes d’´equations stochastiques.
Le processus de Bessel de dimension δ issu de y est la solution du
syst`eme d’´equation diff´erentiel stochastique suivant :
(1)
Zδ,y
t = Zδ,y
0 + δ−1
2
t
0
1
Zδ,y
s
+ Bt
Zδ,y
0 = y, y ≥ 0
δ est la dimension et ν = δ
2
− 1 est nomm´e l’index
La densit´e est donn´ee par les deux formules suivantes:
(2.1) py(t, x) = x
t
(x
y
)ν
e−x2+y2
2t Iv(xy
t
) pour t≥ 0, y ≥ 0, x ≥ 0
2

3. (2.2) p0(t, x) = 1
2ν
1
tν+1
1
Γ(ν+1)
xδ−1
e−x2
2t pour t≥ 0, x ≥ 0
O`u nous avons utilis´e la fonction de Bessel et la fonction Gamma :
Iv(z) = ∞
0 (z
2
)ν+2n 1
n!Γ(ν+n+1)
et Γ(z) =
∞
0
tz−1
e−t
dt
Remarque :
• Iv(x) est solution de x2
I”
v (x) + xIv(x) + (x2
− v2
)Iv(x) = 0
Figure 1: Repr´esentation graphiques de fonctions de Bessel
3

4. 2.2 M´ethode des images pour les processus de Bessel
Dans cette section, les auteurs ´etudient le premier temps d’atteinte d’une
courbe par le processus de Bessel issu de l’origine. Pour la courbe ψ(t) , on
introduit le temps d’arrˆet qui correpsond au premier instant ou le processus
d´epasse la courbe : τψ = inf{t > 0; Zδ,0
0 ≥ ψ(t)}
L’id´ee fondamentale est la suivante, soit F mesure σ-finie satisfaisant
toutes les conditions d’int´egrablit´e permettant d’´ecrire les ´egalit´es suivantes.
Alors pour a ≥ 0, on consid`ere la fonction u et la fonction ψ ainsi :
u(t, x) = p0(t, x) − 1
a
∞
0
py(t, x)F(dy)
ψ(t) = inf{x; u(t, x) < 0}
Ainsi pour tout t > 0, par d´efinition de l’infimum on a :
u(t, x) est solution du syst`eme:
(3)



∂u
∂t
= 1
2
∂2u
∂x∂x
− δ−1
2
∂
u(t,x)
x
∂x
u(t, ψ(t)) = 0
u(0, .) = δ0
Soit t fix´e, on a le configuration suivante :
Ainsi on a τψ = inf{t > 0; u(t, Zδ,0
0 ) = 0}. Donc l’information du temps
d’atteinte par un processus de Bessel de la courbe d´elimit´ee par t −→ ψ(t) est
donn´ee par l’´etude de la fonction t −→ u(t, Zδ,0
0 ).
Le th´eor`eme 2.1 de l’article donne une expression g´en´erale pour la densit´e
de la variable al´eatoire τψ.
Th´eor`eme 2.1 Soit u(t,x) telle que u(t, x) = p0(t, x) − 1
a
∞
0
py(t, x)F(dy)
et ψ(t) telle que u(t,ψ(t)) = 0. Alors la densit´e de τψ est donn´ee par :
fτψ
(t) = −1
2
∂u
∂x
|x=ψ(t) + 1
2
∂u
∂x
|x=0 − δ−1
2x
u(t, x)|x=0
4

5. Figure 2: Repr´esentation des valeurs prises par u `a t fix´e
On retrouve la mˆeme structure de d´emonstration que dans le cas vu dans
le cours et dans [3].
1) Les auteurs montrent que P(τψ > t, Zδ,0
t ∈ dx) = u(t, x)dx
2) Par ailleurs on a P(τψ > t) = R+
P(τψ > t, Zδ,0
t ∈ dx)
3) On remarque par d´efinition de τψ que :
{τψ > t} ⊂ {Zδ,0
t < ψ(t)} donc P(τψ > t) =
ψ(t)
0
u(t, x)dx
4) On prend l’oppos´e de la d´eriv´ee en t. Puis on utilise l’´equation v´erifi´ee
par u ainsi que sa valeur sur la courbe (t,ψ(t)). Enfin on int`egre et on utilise
encore la nullit´e de u sur cette mˆeme courbe :
fτψ
(t) = −ψ (t)u(t, ψ(t)) −
ψ(t)
0
∂u
∂t
fτψ
(t) = 0 −
ψ(t)
0
1
2
∂2u
∂x∂x
− δ−1
2
∂
u(t,x)
x
∂x
fτψ
(t) = −1
2
∂u
∂x
|x=ψ(t) + 1
2
∂u
∂x
|x=0 − δ−1
2x
u(t, x)|x=0
5

6. Ce r´esultat est la brique fondamentale de la m´ethode des images. L’id´ee
de cette m´ethode c’est que pour des F(dy) explicites on peut trouver des
formules explicites de temps d’atteinte. Dans l’article, les auteurs donnent
trois formules explicites:
1. F(dy) = y2ν+1
dy
2. F(dy) = p0(s, y)dy
3. F(dy) = y2ν+1
exp{−λy2
}dy
Ces formules explicites donnent respectivement (en respectant l’ordre des
lignes) les fonctions ψa(t) et fτψ
(t) pr´esentes dans le tableau `a la fin du rap-
port.
Remarque : Nous n’avons pas r´eecrit les supports des fonctions. Ce tableau
est donc valables pour es valeurs de t sur lesquelles les fonctions sont bien
d´efinies.
3 Etude de l’algorithme
3.1 Probl´ematique
Les auteurs souhaitent construire une proc´edure pour simuler le premier
temps d’arrˆet d’un processus de Bessel pour une ligne de niveau donn´ee.
Ils d´efinissent donc τl = inf{t > 0; Zδ,x
t ) = l}. On peut caract´eriser ce temps
d’arrˆet par sa trnsform´ee de Laplace, on obtient alors les expressions suiv-
antes :
Ex[eλτl ] = x−ν Iν (x
√
2λ)
l−ν Iν (l
√
2λ)
, x > 0
E0[eλτl ] = (l
√
2λ))ν Iν
2ν Γ(ν+1)
1
Iν (l
√
2λ)
Dans [1] Ciesielski et Taylor ont prouv´e l’expression de la queue de dis-
tribution pour τl,
6

7. P0(τl > t) = 1
2ν−1Γ(ν+1)
∞
k=1
jν−1
ν,k
Jν+1(jν,k)
e
−j2
ν,kt
2l2
Ou Jν est la fonction de Besssel de premi`ere esp`ece et (jν,k)ν,k sont la suite
ses zeros positifs. L’id´ee de l’article est de construire une m´ethode num´erique
efficace car l’inversion d’une transform´ee de Laplace est extrˆement couteuse
d’un point de vue num´erique et il n’est pas possible de calculer l’inverse de
la fonction de r´epartition.
3.2 Cas particulier : temps d’atteinte d’un niveau donn´e
par des processus de Bessel avec une dimension
enti`ere
Nous avons vu dans la section 2.1, le lien entre le mouvement brownien et
les processus de Bessel de dimensions enti`eres : un processus de Bessel de
dimension enti`ere n corrpespond `a la norme d’un mouvement brownien de
dimension n Pour l’algorithme, les auteurs exploitent ce lien en adaptant la
m´ethode introduite par Milstein en 1997 dans [4] pour approximer le temps
de sortie d’un domaine convexe par brownien bi-dimensionnel.
3.3 Origine de la m´ethode WoS (Walking on sphere
algorithm)
On consid`ere le probl`eme de Dirichlet :
∂2u
∂x∂x
= 0(Ω)
u(x) = h(x)(dΩ), avec h born´ee
On a alors ∀x ∈ Ω : u(x) = Ex[h(Wτ )]
Avec W mouvement brownien et τ premier temps de sortie de Ω
Preuve :
Soit Wt mouvement brownien issu de x, par Itˆo on a :
u(Wt) = u(x) +
t
0
∂u
∂x
dWs +
t
0
1
2
∂2u
∂x∂x
ds
u(Wt∧τ ) = u(x) +
t∧τ
0
∂u
∂x
dWs +
t∧τ
0
1
2
∂2u
∂x∂x
ds
u(Wt∧τ ) = u(x) +
t∧τ
0
∂u
∂x
dWs + 0
7

8. Le second terme est une martingale car le crochet est born´e, donc en prenant
l’esp´erance, on trouve : Ex[u(Wt∧τ )] = u(x)
On prend la limite quand t tend vers +∞ et on conclut.
Pour calculer l’esp´erance, on utilise la loi des grands nombres. Pour se
faire il faut simuler des mouvements browniens ind´ependants et arrˆet´es en τ.
La m´ethode WoS fournit un moyen efficace d’´echantillonner le premier
point de sortie d’un mouvement brownien du domaine, en remarquant que
pour toute sph`ere centr´ee sur x, le premier point de sortie de W de la sph`ere
a une distribution uniforme sur sa surface. Ainsi, on commence par x(0)
´egal `a x, et dessine la plus grande sph`ere centr´e sur x(0) et contenue dans le
domaine. Le premier point de sortie x(1) est uniform´ement distribu´e sur sa
surface. En r´ep´etant cette ´etape par induction, le WoS fournit une s´equence
(x(n)) de positions du mouvement brownien.
Selon l’intuition, le processus convergera vers le premier point de sortie du
domaine. Cependant, cet algorithme prend presque certainement un nombre
infini d’´etapes pour se terminer. Pour la mise en œuvre informatique, le
processus est g´en´eralement arrˆet´e lorsqu’il s’approche suffisamment de la
fronti`ere et renvoie la projection du processus sur la fronti`ere. [5]
Figure 3: Illustration de la m´ethode WoS
3.3.1 Etude de l’algorithme pour δ = 2
On d´efinit ρ(x) , la distance au bord,
ρ(x) = inf{|x − y|; y ∈ Dc
} = l − |x| et ∀ > 0, on d´efinit D =
8

9. x ∈ D; ρ(x) ≥
Enfin on d´efinit la fonction φa(t) = 2tlog(a
t
) qui va permettre de calculer
le rayon des cercles succesifs pour l’algorithme.
Algorithm 1 cas particulier : δ = 2
Require: 0 < γ < 1
X1(0) = 0
X2(0) = 0
θ(0) = 0
Θ(0) = 0
A0 = γ2l2e
2
while (X1(n − 1), X2(n − 1)) = X(n − 1) ∈ D do
(Un, Vn, Wn) ← 3 independant random variables uniformly distributed
θn ← An−1UnVn
Θn ← Θn−1 + θn
(X1(n), X2(n))T
= X(n − 1)T
φAn−1 (θn)(cos(2πWn), sin(2πWn)T
An ← γ2ρ(X(n))2e
2
end while
A la fin de la boucle, le r´esultat est donn´e par le couple de valeurs (Θn, X(n)
qui donnent respectivement le temps d’atteinte et la position de sortie.
Remarque : La diff´erence fondamentale entre l’algorithme de WoS e l’algorithme
WoMS est la dimension al´eatoire du rayon de la sph`ere dans le second. En
effet, dans une it´eration de l’algorithme WoS, pour trouver X(n), on cherche
uniform´ement sur le cercle de centre X(n-1) et de rayon γρ(X(n − 1)), donc
sachant X(n-1) ce rayon est d´eterministe. Dans l’algorithme WoMS, au con-
traire, le rayon est donn´e par l’expression : γρ(X(n − 1)) eUnVnlog( 1
UnVn
).
3.3.2 Programmation de l’algorithme pour tester les r´esultats de
l’article
Apr`es avoir pass´e du temps `a essayer de comprendre aux mieux les r´esultats
pr´esent´es dans cet article. J’ai souhait´e tester par moi mˆeme l’algorithme
WOMS. Je l’ai impl´ement´e sur python. D’une part pour mieux comprendre
l’article, pour mieux appr´ehender les r´esultats et d’autre part pour faire un
premier contrˆole simple sur les r´esultats.
9

10. Figure 4: Illustration de la m´ethode WOMS impl´ement´e sur python
J’ai ensuite compar´e mes r´esultats `a ceux pr´esent´es dans l’article avec les
mˆemes param`etres que ceux utilis´es par les auteurs id est l = 1, N = 20 000
(nombre de simulations), gamma = 0.9.
Figure 5: R´esultats personnels obtenus avec le code en python
On observe qu’avec mon code je retrouve des r´esultats tr`es similaires `a
ceux observables dans l’article. Cela montre que mon code correspond bien
a l’algorithme WoMS d´evelopp´e par les auteurs.
Remarques : l’interpr´etation du param`etre gamma n’est pas explicit´e
dans l’article. Apr`es avoir effectuer diff´erents tests sur les param`etres avec
mon code, j’ai juste pu observer (comme on le voit directement avec la formule
) que celui-ci influe sur le nombre dincr´ements (nombre de cercles) pour
sortir du cercle initial. On pourrait donc l’interpr´eter comme un pas de
quantification pour l simulation du processus.
4 Conclusion
J’ai vraiument appr´eci´e ´etudier cet article. Il m’a permis de voir une ap-
plication plus complexe de la methode des images introduite en cours pour
10

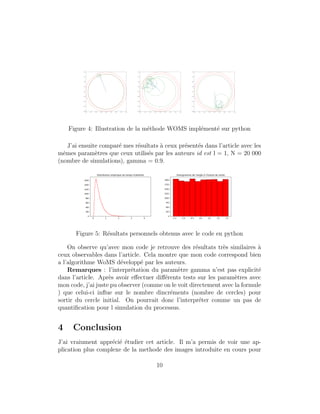
11. des processus browniens. En outre, il m’a amen´e `a parcourir d’autres sources
d’informations grˆace auxquelles j’ai pu me faire un id´ee claire de l’algorithme
WoS. Enfin, j’ai pu impl´ementer moi mˆeme l’algorithme WoMS. cette impl´ementation
a ´et´e un ´el´ement clef de compr´ehension pour apprhender les concepts pr´esent´es
dans l’article. Et j’ai pu l’effectuer car la seconde partie de l’article d´edi´ee `a
la m´ethode num´erique est tr`es bien structur´ee.
References
[1] Z. CIESIELSKI and S. J. TAYLOR. First passage times and sojourn
times for brownian motion in space and the exact hausdor measure of the
sample path. 1962.
[2] Madalina Deaconu and Samuel Herrmann. Hitting time for bessel pro-
cesses walk on moving spheres algorithm (woms). The Annals of Applied
Probability, 23(6):2259–2289, 2013.
[3] LERCHE. Boundary crossing of brownian motion. Lecture Notes in
Statistics 40. Springer, Berlin, 1986.
[4] G. N. MILSTEIN. Weak approximation of a diusion process in a bounded
domain. Stochastics, 62:147–200.
[5] Wikipedia. Walk on spheres method. 2019.
11

12. ψa(t)fτψ
(t)
2tloga
Γ(ν+1)tν+12ν
1
2at
(2tloga
Γ(ν+1)tν+12ν)ν+1
2t(t+s)
s
[(ν+1)log(1+s
t
)+log(a)]1
Γ(ν+1)
1
t
(t+s
s
)ν
[log(a(t+s
t
)ν+1
)]ν+1
exp−t+s
s
log(a(t+s
t
)ν+1
)
λt
1+2λt
+t(λt
1+2λt
)2+2
t
loga(1+2λt)ν+1
2νtν+1Γ(ν+1)
(λt
1+2λt
)2+2
t
loga(1+2λt)ν+1
2νtν+1Γ(ν+1)
p0(t,ψ(t))
12