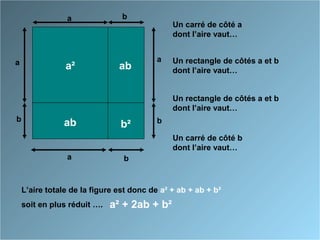
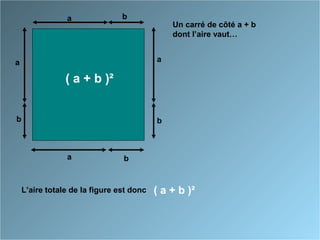
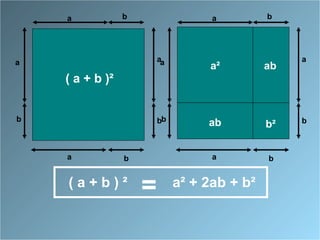
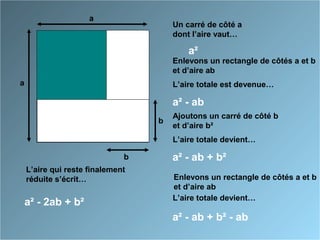
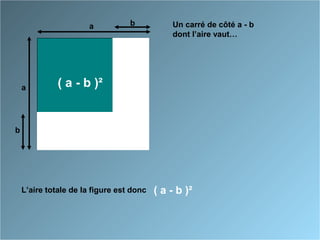
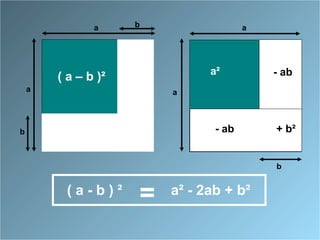
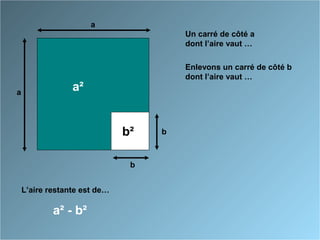
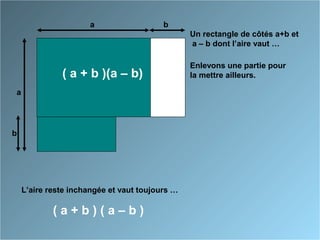
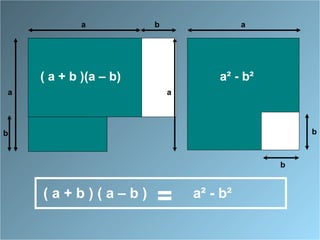
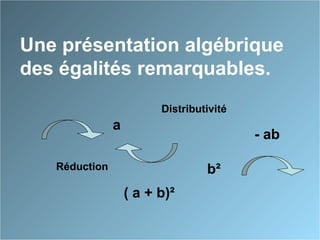
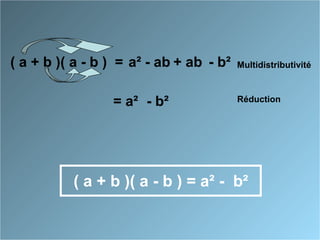
Le document présente des identités remarquables à travers des approches géométriques et algébriques. Il décrit comment développer et factoriser les formules associées aux carrés de sommes et de différences, ainsi que la différence des carrés. Les formules incluent (a + b)², (a - b)² et (a + b)(a - b), avec des démonstrations pour chacune.

1. Chapitre : identités remarquables
Titre :
Une présentation géométrique des
égalités remarquables.
Classe: EB8
Année Scolaire :2018/2019.

2. a
a
b
b
Une présentation géométrique
des égalités remarquables.

3. a
a a
b
a
b
b
b
Un carré de côté a
dont l’aire vaut…
Un rectangle de côtés a et b
dont l’aire vaut…
Un carré de côté b
dont l’aire vaut…
Un rectangle de côtés a et b
dont l’aire vaut…
a² ab
ab b²
L’aire totale de la figure est donc de a² + ab + ab + b²
soit en plus réduit …. a² + 2ab + b²

4. Un carré de côté a + b
dont l’aire vaut…
L’aire totale de la figure est donc ( a + b )²
a
a a
b
a
b
b
b
( a + b )²

5. a
a a
b
a
b
b
b
( a + b )²
a
a a
b
a
b
b
b
a² ab
ab b²
( a + b ) ² a² + 2ab + b²=

6. Un carré de côté a
dont l’aire vaut…
a
a
a²
b
Enlevons un rectangle de côtés a et b
et d’aire ab
L’aire totale est devenue…
a² - ab
Ajoutons un carré de côté b
et d’aire b²
a² - ab + b²
L’aire totale devient…
b
Enlevons un rectangle de côtés a et b
et d’aire ab
L’aire totale devient…
a² - ab + b² - ab
L’aire qui reste finalement
réduite s’écrit…
a² - 2ab + b²

7. Un carré de côté a - b
dont l’aire vaut…
L’aire totale de la figure est donc ( a - b )²
a
a
b
b
( a - b )²

8. a
a
b
b a
a
b
( a – b )² a² - ab
+ b²- ab
( a - b ) ² a² - 2ab + b²=

9. ( a - b )²
a² - b²
L’aire restante est de…
a
a
Un carré de côté a
dont l’aire vaut …
b
b
Enlevons un carré de côté b
dont l’aire vaut …
a²
b²

10. ( a - b )²
( a + b ) ( a – b )
L’aire reste inchangée et vaut toujours …
Un rectangle de côtés a+b et
a – b dont l’aire vaut …
a
a
b
b
Enlevons une partie pour
la mettre ailleurs.( a + b )(a – b)

11. ( a - b )²
a
a
b
b
( a + b )(a – b)
a
a
b
b
a² - b²
=( a + b ) ( a – b ) a² - b²

12. Une présentation algébrique
des égalités remarquables.
Distributivité
Réduction b²
- ab
a
( a + b)²

13. ( a + b ) ² = Réécriture( a + b ) ( a + b)
Multidistributivité= a² + ab + ab + b²
Réduction= a² + 2ab + b²
( a + b )² = a² + 2ab + b²

14. ( a - b ) ² = Réécriture( a - b ) ( a - b)
Multidistributivité= a² - ab -ab + b²
Réduction= a² - 2ab + b²
( a - b )² = a² - 2ab + b²

15. ( a + b )( a - b ) = Multidistributivitéa² - ab + ab - b²
Réduction= a² - b²
( a + b )( a - b ) = a² - b²

16. Les trois égalités remarquables
dans le sens développement
Des produits
( a + b )² =
( a - b )² =
( a + b )(a - b ) =
Des sommes
a² + 2ab +b²
a² - 2ab +b²
a² - b²
Développement

17. Les trois égalités remarquables
dans le sens factorisation
Des sommes
a² + 2ab + b² =
a² - 2ab + b² =
a² - b² =
Des produits
( a + b )²
( a – b )²
( a + b) ( a – b)
Factorisation