Le document aborde la théorie des séries de Fourier et leurs applications, notamment dans la synthèse sonore et le traitement des signaux numériques. Il explique comment les sons peuvent être produits par l'addition d'ondes fondamentales et d'harmoniques, et met en lumière les concepts de périodicité et de convergence des séries trigonométriques. Des applications pratiques telles que la transformation de Fourier rapide (FFT) et la compression JPEG sont également discutées.

1. Dédramathisons
TFE
Séries de Fourier et applications
Rédacteurs :
Antoine Etesse
Frederic Jacobs
Jie-Fang Zhang
1er avril 2011

2. Sommaire
I Introduction et théorie 2
1 Situation problème 3
1.1 Approximation de cette sinusoïde . . . . . . . . . . . . . . . . . . . . . . . 6
1.2 Vers les séries de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2 Elaborer une théorie à partir de l’exemple 8
2.1 Construction de la théorie . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.1.1 Périodicité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.1.2 Calcul d’intégrales intéressantes . . . . . . . . . . . . . . . . . . . . 10
2.1.3 Calcul des coefficients . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.1.4 Exemple : Fonction carrée . . . . . . . . . . . . . . . . . . . . . . . 14
2.1.5 Ecriture complexe des séries de Fourier . . . . . . . . . . . . . . . 20
2.2 Convergence des séries trigonométriques, des séries de Fourier, et Théorème
de Dirichlet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.2.1 Convergence simple . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.2.2 Convergence uniforme . . . . . . . . . . . . . . . . . . . . . . . . . 27
2.2.3 Convergence normale . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.2.4 Convergence des séries trigonométriques . . . . . . . . . . . . . . . 29
2.2.5 Théorème de Dirichlet. . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.2.6 Analyse d’une fonction qui répond aux hypothèses du théorème de
Dirichlet. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
2.3 Phénomène de Gibbs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
II Applications de l’analyse harmonique 37
1 Synthèse numérique d’un son à partir de l’addition des séries de Fourier 38
1

3. 2 Applications informatiques 39
2.1 FFT : Fast Fourier Transform . . . . . . . . . . . . . . . . . . . . . . . . . 39
2.2 Compression JPEG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
2.2.1 Pourquoi Fourier ? . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
2.2.2 Le JPEG, c’est quoi . . . . . . . . . . . . . . . . . . . . . . . . . . 43
2.2.3 Quelle couleur ? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
2.2.4 Alors quelle avancée l’analyse de Fourier a-t-elle permis ? . . . . . 48
3 Digital Signal Processing, un large domaine d’applications 51
3.1 Applications en télécommunications . . . . . . . . . . . . . . . . . . . . . 51
3.1.1 Confondre l’information. Sans la mélanger. . . . . . . . . . . . . . 52
3.1.2 Compression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
3.1.3 Suppression de l’écho . . . . . . . . . . . . . . . . . . . . . . . . . . 52
3.1.4 La Blue Box . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
A Joseph Fourier et ses précurseurs 54
A.1 Les précurseurs de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
A.2 Biographie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
A.3 Son oeuvre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
2

4. Première partie
Introduction et théorie
3

5. Chapitre 1
Situation problème
Comment peut-on produire un son particulier ?
Tout d’abord, on sait qu’un son est une onde sonore, plus ou moins périodique, qui se
propage dans l’air. C’est d’ailleurs ce qui le différencie de ce qu’on appelle communément
un bruit.
Figure 1.1 – Un son, caractérisé par une certaine répétition.
Figure 1.2 – Du bruit, rien n’est ordonné ou répétitif.
Ainsi, la réponse à notre question initiale se déduit aisément : il nous suffit de créer
4

6. des déformations périodiques dans l’air. Cependant, la question s’avère être plus complexe
car nous désirons obtenir un son spécifique. Par exemple, le son la 440Hz correspond en
réalité à 440 déformations par seconde.
Pourtant, il existe des milliers de la 440Hz différents, empreints de leur spécificité, et
tout le monde peut, par exemple distinguer un son d’une fréquence de 440Hz issu d’un
diapason de celui provenant d’un piano. Cette différence sonore que l’on perçoit découle
de la dissimilitude du timbre des deux notes.
L’illustration graphique de ces deux sons (amplitude-fréquence), témoigne de la dissemblance
des deux notes en questions. Voici la même note jouée sur des instruments différents.
Figure 1.3 – Une note jouée sur un Piano UNSW c
Figure 1.4 – Même note jouée sur une guitare UNSW c
Remarquez la forte corrélation entre les deux instruments jouant la même note.
Ainsi émerge une nouvelle question, de loin plus intéressante : comment peut-on
produire un timbre particulier ?
La réponse est en fait relativement simple, et facilement imaginable. Pour commencer,
on peut se pencher sur les instruments de musique. Nous savons que lorsqu’on joue une
note sur un instrument, on produit non seulement la note jouée, mais également ce qu’on
appelle les harmoniques de la note. On dira que la note a une fréquence fondamentale f ,
5

7. et que ses harmoniques possèdent des fréquences multiples de celle-ci, nf avec n ∈ Z. Il va
de soi que l’amplitude des harmoniques peut être nulle, ou non-nulle. On peut représenter
la note sous un graphique (amplitude-fréquence). Comme ceux utilisés pour représenter
les deux sons ci-dessus .
Nous pouvons facilement déduire que dans ce cas, les notes que l’on peut entendre
correspondent bien à la superposition de l’onde fondamentale et ses harmoniques. La
forme de l’onde, donc son timbre, concorde avec la somme des amplitudes de toutes les
harmoniques de l’onde. Aussi la fréquence de deux sons peut-elle très bien être similaire,
chacun possédant ses harmoniques spécifiques, la forme de l’onde diffèrera clairement.
Figure 1.5 – Concept d’addition de sinusoïdes par Denis Auquebon
La méthode expérimentale de représentation d’un son quelconque consiste donc à
ajouter à l’onde sonore fondamentale de fréquence déterminée f , les ondes harmoniques
de fréquence 2f , 3f , 4f ,... et ainsi de suite. La combinaison de la fondamentale et des
harmoniques forment le son, parfois simple, souvent compliqué, dont la fréquence est
évidemment celle du son fondamental. Nous pouvons ainsi créer tout une gamme de sons,
suivant que l’on omette l’harmonique de fréquence 2f , 5f ,... ou que l’on prenne deux fois
l’harmonique de fréquence 3f quatre fois celle de fréquence 8f ,...
Nous arrivons donc à la conclusion que nous pouvons créer toute une série de son
à l’aide d’une addition d’onde fondamentale et des ses harmoniques. Mais inversement,
peut-on décrire tout son comme la somme d’harmoniques ? Afin d’apporter une réponse,
nous devons nous pencher sur les séries de Fourier.
6

8. Figure 1.6 – My normal approach is useless here
1.1 Approximation de cette sinusoïde
1.2 Vers les séries de Fourier
Revenons quelque peu à l’historique, afin d’en savoir un peu plus sur l’émergence de
cette idée géniale.
Joseph Fourier, qui travaillait sur la propagation de la chaleur sur des corps solides,
a remarqué que la propagation de la chaleur sur un anneau ressemble à un mouvement
harmonique. En physique, nous donnons une expression plus générale à ce phénomène
2πx 2πt
y(x, t) = A sin( − + φ)
λ T
où y est le déplacement périodique de la vibration de l’objet , λ la période dans l’espace,
T la période dans le temps et φ la phase, qui est constante.
En fait, lors d’une expérience simple, il a remarqué que la source de chaleur passe
cycliquement, mais brusquement, d’une valeur extrême à une autre. Il a été ainsi amené
à soupçonner le rôle très important des fonctions trigonométriques et admettre qu’elles
pouvaient être les constituants élémentaires de tout Si nous fixons la variable x, nous avons
ici une fonction f (t) périodique de période T . L’idée de Fourier fut alors d’approximer
le phénomène observé par une somme finie, constituée des harmoniques de la période
fondamentale T .
7

9. L’approximation est
N
2πn
An sin( t + φn )
n=1
T
où N un naturel et An et φn deux constantes qui varient en fonction de n.
Nous pouvons développer le sinus, ce qui nous donne :
2πn 2πn 2πn
An sin( t + φn ) = An (sin( t) cos(φn ) + cos( t) sin(φn ))
T T T
2πn 2πn
= An sin(φn ) cos( t) + An cos(φn ) sin( t)
T T
2πn 2πn
= an cos( t) + bn sin( t)
T T
puisque An sin(φn ) et An cos(φn ) sont constantes, on peut alors poser que
a0
an = An sin(φn ) et bn = An cos(φn ), et si on ajoute un terme constant , on obtient,
2
N
a0 2πn 2πn
+ (an cos( t) + bn sin( t))
2 n=1
T T
a0
On a choisi le terme constant comme étant pour une raison bien précise que l’on
2
détaillera au moment convenu.
8

10. Chapitre 2
Elaborer une théorie à partir de
l’exemple
2.1 Construction de la théorie
2.1.1 Périodicité
Tout d’abord, nous devons définir ce qu’est la périodicité d’une fonction.
Une fonction est périodique de période p s’il existe un nombre réel positif le plus petit
possible p tel que f (x) = f (x + p). Le nombre p doit être le plus petit possible parce que
pour satisfaire cette relation, il nous suffit de prendre tous les multiples entiers de p, ce
qui nous donne f (x + np) = f (x) où n ∈ Z.
Penchons-nous à présent sur la somme des fonctions périodiques.
1
Si on a trois fonctions périodiques de période π, 2π et 4π respectivement, alors la somme
4
de ces trois fonctions sera-t-elle périodique ? Si oui, quelle est sa période ?
Afin de faciliter la compréhension, nous pouvons représenter cette fonction somme (s(x) =
1
sin(4x) + sin(x) + sin( x)) et ainsi voir facilement que s(x) est périodique de période de
4
4π.
Ainsi, nous déduisons que la période de la somme correspond à la plus grande période de
ses fonctions initiales, dans ce cas-ci, 4π.
Cependant, la somme des fonctions périodiques n’est pas toujours périodique. On peut
prendre comme exemple s(x) = sin x+sin(πx). Bien que les deux fonctions initiales soient
périodiques de période respectives 2π et 2, s(x) n’est pas périodique. Pour ce genre de
cas, on peut approximer s(x) par s (x) = sin x + sin(3, 1415x), qui est périodique.
Mais ne nous tracassons pas trop, étant donné que nous allons travailler avec des périodes
9

11. simples et entières.
Démontrons un lemme sur la périodicité, qui nous sera utile par la suite.
Soit f une fonction continue par morceau périodique de T .
a+T
L’intégrale f (x) dx ne dépend pas du réel a. Autrement dit,
a
T
a+T T 2
f (x) dx = f (x) dx = f (x) dx = · · ·
−T
a 0 2
Pour démontrer ceci, nous allons exploiter l’additivité de l’intégrale.
a+T 0 T a+T
f (x) dx = f (x) dx + f (x) dx + f (x) dx
a a 0 T
Changeons de variable. Soit x = y + T , ce qui implique dx = dy.
a+T a a
Alors on a f (x) dx = f (y + t) dy = f (y) dy puisque f (y + T ) = f (y).
T 0 0
0 a
On peut voir que f (x) dx + f (y) dy = 0, ce qui nous donne :
a 0
a+T T
f (x) dx = f (x) dx
a 0
Cette dernière expression est indépendante de a
En vue de ce que l’on a pu dire dans l’introduction, peut-on dire qu’une fonction f (x)
périodique de période T peut s’écrire sous la forme d’une somme
N
a0 2πn 2πn
f (x) = + (an cos( x) + bn sin( )x)?
2 n=1
T T
Certainement pas, car nous n’avons pas encore montré les conditions pour que les
deux membres soient équivalents. De plus, on n’a pas encore trouvé les expressions des
a0
constantes , an et bn , qui différencient une série d’une autre.
2
Pour trouver les expressions de ces constantes, nous allons utiliser les outils d’intégrale
sur la période de la fonction que l’on désire étudier.(Et de par le lemme que nous avons
démontré, on voit bien que la restriction à une période suffit).
Pour faciliter la compréhension, nous allons d’abord faire les démonstrations avec une
fonction f (x) qui a une période 2π, puis ensuite étendre la démonstration pour des
périodes quelconques.
10

12. 2.1.2 Calcul d’intégrales intéressantes
Avant de déterminer les expressions de ces constantes, nous devons déterminer certaines
relations qui nous seront très utiles par la suite.(Mentionnons au préalable que nous
utilisons la parité des fonctions sinus et cosinus dans notre développement.)
π
cos nx cos kx dx
−π
π
sin nx sin kx dx
−π
et
π
cos(nx) sin(kx) dx où n, k ∈ Z
−π
Si n = k :
π π
cos nx cos kx dx = 2 cos nx cos kx dx
−π 0
π
1
=2 (cos((n + k)x) + cos((n − k)x) dx
0 2
1 1
=( sin((n + k)x) + sin((n − k)x))|π
0
n+k n−k
1 1
=( sin((n + k)π) + sin((n − k)π)
n+k n−k
=0
π π
sin nx sin kx dx = 2 sin nx sin kx dx
−π 0
π
−1
=2 (cos((n + k)x) − cos((n − k)x) dx
2
0
−1 −1
=( sin((n + k)x) − sin((n − k)x))|π
0
n+k n−k
−1 −1
=( sin((n + k)π) − sin((n − k)π)
n+k n−k
=0
11

13. Si n = k
π π
cos nx cos kx dx = 2 cos2 nx dx
−π 0
π
1 + cos(2nx)
=2 dx
0 2
1 1
= 2( x + sin(2nx))|π
0
2 4n
1
=2× π
2
=π
π π
sin nx sin kx dx = 2 sin2 nx dx
−π 0
π
1 − cos(2nx)
=2 dx
0 2
1 1
= 2( x − sin(2nx))|π
0
2 4n
1
=2× π
2
=π
Et enfin, on voit que cos(nx) sin(kx) est impaire car cos(nx) sin(kx) = − cos(−nx) sin(−kx)
π
Donc, dans tous les cas, cos(nx) sin(kx) dx = 0
−π
En résumé, (n, k ∈ Z)
π
0 si n = k
cos nx cos kx dx =
−π π si n = k
π
0 si n = k
sin nx sin kx dx =
−π π si n = k
π
cos(nx) sin(kx) dx = 0
−π
2.1.3 Calcul des coefficients
Sans avoir montré l’existence, on suppose qu’une fonction périodique de période 2π,
continue sur R et dérivable sur R est égale à sa série de Fourier. Alors,
N
a0
f (x) = + (an cos(nx) + bn sin(nx))
2 n=1
12

14. Pour trouver a0 , on va prendre l’intégrale de −π à π (une période entière) dans les
deux membres, ce qui nous donne
π π π N
a0
f (x) dx = dx + (an cos(nx) + bn sin(nx)) dx
−π −π 2 −π n=1
π π π N
a0
f (x) dx = dx + (an cos(nx) + bn sin(nx)) dx
−π −π 2 −π n=1
l’intégrale d’une somme est égale à la somme de l’intégrale
π N π N π
a0
= dx + an cos(nx) dx + bn sin(nx) dx
−π 2 n=1 −π n=1 −π
N N
a0 π an −bn
= x|−π + sin(nx)|π +
−π cos(nx)|π
−π
2 n=1
n n=1
n
a0
= × 2π
2
= a0 π
On a alors,
π
1
a0 = f (x) dx
π −π
Pour trouver an , on va multiplier les deux membres de l’égalité par cos(kx) où k un entier
positif.
N
a0
f (x) cos(kx) = cos(kx) + cos(kx) (an cos(nx) + bn sin(nx))
2 n=1
N
a0
= cos(kx) + (an cos(nx) cos(kx) + bn sin(nx) cos(kx))
2 n=1
Ensuite, nous prendre l’intégrale de −π à π dans les deux membres, ce qui nous donne
π π π N
a0
f (x) cos(kx) dx = cos(kx) dx + (an cos(nx) cos(kx) + bn sin(nx) cos(kx)) dx
−π −π 2 −π n=1
π N π N π
a0
= cos(kx) dx + an cos(nx) cos(kx) dx + bn sin(nx) cos(kx) dx
−π 2 n=1 −π n=1 −π
π N π N π
a0
= cos(kx) dx + an cos(nx) cos(kx) dx + bn sin(nx) cos(kx) dx
2 −π n=1 −π n=1 −π
13

15. parmi les n, il existe un et un seul n égal à k tel que
N π N π π
an cos(nx) cos(kx) dx = (an cos(nx) cos(kx) dx) + ak cos2 (kx) dx
n=1 −π n=1,n=k −π −π
Par conséquent, la somme s’annule sauf pour terme k qui donne ak π.
N
a0 π π
De plus, cos(kx) dx et bn sin(nx) cos(kx) dx donnent aussi 0
2 −π n=1 −π
π
On obtient donc f (x) cos(kx) dx = ak π pour tout k entier positif ce qui revient à dire
−π
π
1
que ak = f (x) cos(kx) dx, et de façon générale nous avons ainsi :
π −π
π
1
an = f (x) cos(nx) dx
π −π
Pour bn , on va réaliser le même procédé en multipliant les deux membres par sin(kx)
où k est un entier positif.
N
a0
f (x) sin(kx) = sin(kx) + sin(kx) (an cos(nx) + bn sin(nx))
2 n=1
N
a0
= sin(kx) + (an cos(nx) sin(kx) + bn sin(nx) sin(kx))
2 n=1
De même en prenant l’intégrale définie de −π à π, nous avons
π π π N
a0
f (x) sin(kx) dx = sin(kx) dx + (an cos(nx) sin(kx) + bn sin(nx) sin(kx)) dx
−π −π 2 −π n=1
π N π N π
a0
= sin(kx) dx + an cos(nx) sin(kx) dx + bn sin(nx) sin(kx) dx
−π 2 n=1 −π n=1 −π
π N π N π
a0
= sin(kx) dx + an cos(nx) sin(kx) dx + bn sin(nx) sin(kx) dx
2 −π n=1 −π n=1 −π
En considérant les résultats qu’on a montré auparavant, on peut constater que
N π N π π
bn sin(nx) sin(kx) dx = (bn sin(nx) sin(kx) dx) + bk sin2 (kx) dx
n=1 −π n=1,n=k −π −π
π
2
la somme s’annule sauf pour bk sin (kx) dx qui donne bk π.
−π
π N π
a0
et sin(kx) dx et an cos(nx) sin(kx) dx donnent 0.
2 −π n=1 −π
14

16. π
1
Par conséquent, nous avons pour tout k entier positif, bk = f (x) sin(kx) dx
π −π
Et donc π
1
bn = f (x) sin(nx) dx
π −π
Résumons quelque peu. Si une fonction périodique de période 2π peut s’écrire sous
forme de série de Fourier, alors
N
a0
f (x) = + (an cos(nx) + bn sin(nx))
2 n=1
Alors,
π
1
a0 = f (x) dx
π −π
π
1
an = f (x) cos(nx) dx
π −π
π
1
bn = f (x) sin(nx) dx
π −π
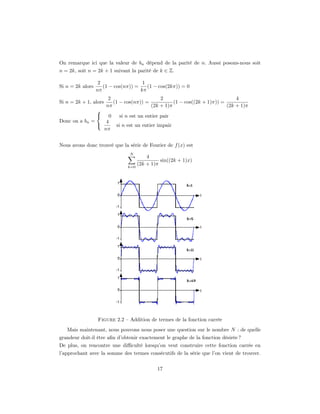
On peut tout de suite appliquer ce que l’on vient de voir sur exemple.
2.1.4 Exemple : Fonction carrée
Prenons l’exemple d’une fonction carrée périodique de période 2π.
1 si 0 ≤ x < π
Alors sur l’intervalle [−π; π], on a f (x) =
−1 si −π ≤ x < 0
Puisqu’elle est définie dans R et est périodique de 2π, on peut alors écrire
1 si 2kπ ≤ x < (2k + 1)π
f (x) = où k ∈ Z
−1 si (2k + 1)π ≤ x < 2kπ
Si cette fonction peut être écrite sous la forme de série de Fourier, alors cette série est
N
a0
égale à + (an cos(nx) + bn sin(nx)).
2 n=1
Maintenant, il faut qu’on détermine les coefficients a0 , an et bn .
Pour cela, nous pouvons directement appliquer ce que nous avons trouvé auparavant,
mais on doit traiter les deux parties séparément, puisque f (x) est définie différemment
15

17. Figure 2.1 – Graphique de la fonction carrée
sur l’intervalle [−π, π].
0 π
1
a0 = ( f (x) dx + f (x) dx)
π −π 0
0 π
1
= ( −1 dx + 1 dx)
π −π 0
1
= (π − π) = 0
π
π
1
an = f (x) cos(nx) dx
π −π
0 π
1
= ( − cos(nx) dx + cos(nx) dx)
π −π 0
1 −1 1
= ( sin(nx)|0 + sin(nx)|π )
−π 0
π n n
1 −1 1
= ( (sin(0) − sin(−nπ)) + (sin(nπ) − sin(0)))
π n n
=0
π
1
bn = f (x) sin(nx) dx
π −π
0 π
1
= ( − sin(nx) dx + sin(nx) dx)
π −π 0
1 1 −1
= ( cos(nx)|0 +
−π cos(nx)|π )
0
π n n
1 1 −1
= ( (cos(0) − cos(−nπ)) + (cos(nπ) − cos(0)))
π n n
1 1 −1
= ( (1 − cos(−nπ)) + (cos(nπ) − 1))
π n n
2
= (1 − cos(nπ))
nπ
16

18. On remarque ici que la valeur de bn dépend de la parité de n. Aussi posons-nous soit
n = 2k, soit n = 2k + 1 suivant la parité de k ∈ Z.
2 1
Si n = 2k alors (1 − cos(nπ)) = (1 − cos(2kπ)) = 0
nπ kπ
2 2 4
Si n = 2k + 1, alors (1 − cos(nπ)) = (1 − cos((2k + 1)π)) =
nπ (2k + 1)π (2k + 1)π

 0 si n est un entier pair
Donc on a bn = 4
 si n est un entier impair
nπ
Nous avons donc trouvé que la série de Fourier de f (x) est
N
4
sin((2k + 1)x)
(2k + 1)π
k=0
Figure 2.2 – Addition de termes de la fonction carrée
Mais maintenant, nous pouvons nous poser une question sur le nombre N : de quelle
grandeur doit-il être afin d’obtenir exactement le graphe de la fonction désirée ?
De plus, on rencontre une difficulté lorsqu’on veut construire cette fonction carrée en
l’approchant avec la somme des termes consécutifs de la série que l’on vient de trouver.
17

19. En effet, comment peut-on construire une fonction discontinue à chaque x = kπ (où k est
un entier) à l’aide de la somme de fonctions continues en tout point dans R et dérivables
dans tous ses degrés (ses fonctions dérivées de degré 1, 2, 3,...,etc. sont toutes continues,
car les fonctions sinus et cosinus sont de classe C n ).
Cependant, nous pouvons observer que plus on ajoute de termes dans cette somme, donc
plus le nombre N croît, plus la fonction a l’air de coller au graphe de la fonction carrée.
Mais elle ne deviendra jamais carrée puisqu’il existe toujours des courbes aux extrémités.
Par cette idée intuitive, on peut déduire que la série de Fourier associée à cette fonction
∞
4
carrée f (x) est sin((2k + 1)x)
(2k + 1)π
k=0
De même, on peut étendre la série de Fourier vers une écriture plus générale. Si une
fonction f (x) périodique de période 2π peut être écrite sous forme de série de Fourier,
alors cette série est égale à
∞
a0
+ (an cos(nx) + bn sin(nx))
2 n=1
Par cet exemple, nous pouvons aussi observer une chose étonnante. Cette fonction carrée
peut être simplement écrite par la somme de sinus. En effet, la raison pour laquelle son
expression est uniquement sous forme de termes en sinus est simplement due à sa parité.
Cette "propriété de parité" nous dit que :
– si la fonction est paire, alors sa série de Fourier est une somme de cosinus
– si la fonction est impaire, sa série de Fourier est une somme de sinus
Rappelons-nous d’abord de certaines propriétés liées a la parité d’une fonction.
Si une fonction est paire, alors f (x) = f (−x)
et on peut simplifier l’expression de l’intégrale sur des intervalles symétriques :
π π
f (x) dx = 2 f (x) dx.
−π 0
Si une fonction est impaire alors, f (x) = −f (−x).
π
et f (x) dx = 0
−π
Finalement, le produit d’une fonction paire et d’une fonction impaire est impaire, et
le produit de deux fonctions de la même parité est paire.
18

20. Ainsi, si f (x) est paire, alors f (x) sin nx est impaire et f (x) cos nx est paire.
π
2
a0 = f (x) dx
π 0
π
2
an = f (x) cos(nx) dx
π 0
π
1
bn = f (x) sin(nx) dx = 0
π −π
Si f (x) est impaire, alors f (x) sin nx est paire et f (x) cos nx est impaire.
π
1
a0 = f (x) dx = 0
π −π
π
1
an = f (x) cos(nx) dx = 0
π −π
π
2
bn = f (x) sin(nx) dx
π 0
Par conséquent, on voit que
∞
a0
Si f (x) paire, la serie = + an cos(nx)
2 n=1
∞
Si f (x) impaire, la serie = bn sin(nx)
n=1
Maintenant qu’on est familier avec la série de Fourier pour une fonction de période
2π, on peut se demander quelle sera la forme de la série de Fourier pour une fonction
périodique de période T quelconque. Étudions cela :
Soit f (x) une fonction périodique de période T . On veut la développer en série de Fourier,
mais on ne connait que le la série pour une période de 2π. Nous allons donc effectuer un
T T
changement de variable x = u tel que f ( u) soit périodique de période 2π.
2π 2π
T T
On le voit facilement car f (x) = f ( u) et f (x + T ) = f ( (u + 2π)).
2π 2π
T T T
Et puisque f (x) = f (x + T ) ⇔ f ( u) = f ( (u + 2π)) donc f ( u) est bien périodique
2π 2π 2π
de 2π.
19

21. On connait ainsi la forme de cette série de Fourier et de ses coefficients
∞
a0
+ (an cos nu + bn sin nu)
2 n=1
T T
Et on applique le changement de variable x = 2π u ⇒ dx = 2π du, ce qui va nous donner
comme expression
π
1 T
a0 = f( u) du
π −π 2π
T
1 2 2π
= f (x) dx
π −T
2
T
T
T
2 2 2
= f (x) dx = f (x) dx
T −T
2
T 0
π
1 T
an = f( u) cos(nu) du
π −π 2π
T
1 2 2πnx 2π
= f (x) cos( ) dx
π −T
2
T T
T
T
2 2 2πnx 2 2πn
= f (x)cos( ) dx = f (x) cos( ) dx
T −T
2
T T 0 T
π
1 T
bn = f( u) sin(nu) du
π −π 2π
T
1 2 2πnx 2π
= f (x) sin( ) dx
π −T
2
T T
T
T
2 2 2πnx 2 2πn
= f (x) sin( ) dx = f (x) sin( ) dx
T −T
2
T T 0 T
Et la série de Fourier d’une fonction de période quelconque T sera
∞
a0 2πn 2πn
+ (an cos x + bn sin x)
2 n=1
T T
Et cela satisfait également toutes les autres propriétés démontrées auparavant.
20

22. 2.1.5 Ecriture complexe des séries de Fourier
Cette manière d’écrire la série de Fourier avec la somme de sinus et cosinus n’est pas
l’unique représentation des séries de Fourier : nous pouvons aussi écrire la somme de
Fourier sous la forme exponentielle, ce qui simplifiera l’écriture et les calculs.
Tout d’abord, nous devons montrer la relation d’Euler qui nous sera très utile pour la
suite.
eiπ + 1 = 0
Par les séries de Taylor (plus précisément par la série de Maclaurin), on peut écrire la
fonction ex sous la forme suivante :
x2 xn
ex = 1 + x + + ··· + + ···
2! n!
Nous pouvons faire la même chose pour sin x et cos x, ce qui nous donne :
x2 x4 x6 x3 x5 x7
cos x = 1 − + − + · · · et sin x = x − + − + ···
2! 4! 6! 3! 5! 7!
Et vu que
(iθ)2 (iθ)3 (iθ)4 (iθ)n
eiθ = 1 + iθ + + + + ··· + + ···
2! 3! 4! n!
−θ2 −iθ3 θ4
= 1 + iθ + + + + ···
2! 3! 4!
2 4
θ θ θ3 θ5
= (1 − + − · · · ) + i(θ − + )
2! 4! 3! 5!
= cos θ + i sin θ
Nous obtenons alors que
eiθ = cos θ + i sin θ
ce qui veut aussi dire que eiπ = cos π + i sin π = −1 ou encore eiπ + 1 = 0
Comme corollaire de la relation eiθ = cos θ + i sin θ, nous pouvons déduire que
eiθ + e−iθ
cos θ =
2
eiθ − e−iθ
sin θ =
2i
a0
Ainsi, on pourrait, sans se préoccuper du terme constant , remplacer ces expressions
2
21

23. dans la série de Fourier trigonométrique.
∞ ∞
einx + e−inx einx − e−inx
(an cos(nx) + bn sin(nx)) = (an + bn )
n=1 n=1
2 2i
∞
an inx ibn inx
= ( (e + e−inx ) − (e − e−inx ))
n=1
2 2
∞ ∞
an ibn an ibn
= einx ( − )+ e−inx ( + )
n=1
2 2 n=1
2 2
Au lieu de prendre tous les termes n de 1 à ∞, on
peut penser qu’on peut inverser ceci sans pour autant changer
le sens de la somme en prenant tout les n de−∞ à −1.
∞ −1
an ibn a−n ib−n
= einx ( − )+ einx ( + )
n=1
2 2 n=−∞
2 2
Nous avons envie de grouper les deux sommes, pour ça, il faut qu’on trouve une
relation entre les deux.
Puisque la série trigonométrique donne une fonction réelle, alors la somme de ces deux
sommes doit aussi donner quelque chose de réel. La somme des deux doit donc satisfaire la
symétrie complexe : si on veut que la somme de deux nombres complexes soit un nombre
réel il faut alors que si l’un est z, l’autre soit son conjugué z.
an − ibn
Si l’on pose que Cn = , donc on peut aussi déduire que
2
a−n − ib−n an + ibn
C−n = , alors on a besoin que le terme correspondant de Cn soit Cn =
2 2
a−n + ib−n
et que celui de C−n soit C−n =
2
Pour montrer cela nous devons d’abord montrer la relation entre les constantes trigonométriques
et a−n et b−n .
π
1
On a vu que an = f (x) cos(nx) dx alors,
π −π
π
1
a−n = f (x) cos(−nx) dx
π −π
π
1
= f (x) cos(nx) dx
π −π
= an
22

24. π
1
bn = f (x) sin(nx) dx
π −π
π
1
b−n = f (x) sin(−nx) dx
π −π
π
1
=− f (x) sin(nx) dx
π −π
= −bn
Par ces deux relations, nous pouvons constater que,
a−n − ib−n
C−n =
2
an + ibn
=
2
an − ibn
=
2
= Cn
Ceci nous montre bien que la somme des deux est bien réelle puisqu’elles satisfont Cn =
C−n . Par la même procédure, on peut aussi montrer que C−n = Cn .
Mais avant de pouvoir les écrire sous une seule somme, on peut constater qu’il nous
manque le terme n = 0.
Puisqu’on sait que Cn = C−n , alors C0 = C−0 = C0 . Ca montre que C0 est un terme
a0
particulier car il est toujours réel est égale a . C’est la raison pour laquelle on a choisi,
2
a0
dans la série de Fourier trigonométrique, d’introduire la constante comme étant .
2
Finalement, nous pouvons continuer notre raisonnement, et poser que
an − ibn a−n + ib−n
Cn = et Cn =
2 2
∞ ∞ −1
a0 a0 an − ibn a−n + ib−n
+ (an cos(nx) + bn sin(nx)) = + einx ( )+ einx ( )
2 n=1
2 n=1
2 n=−∞
2
∞ −1
a0
= + Cn einx + Cn einx
2 n=1 n=−∞
et Cn = C−n et C0 = C−0 = C0 , donc
∞
= Cn einx
−∞
Nous avons donc que si une fonction peut être écrite sous forme de série de Fourier
23

25. exponentielle, alors sa série de Fourier sera
∞
Cn einx
n=−∞
Il nous faut maintenant trouver les expressions du coefficient Cn , à l’instar de ce qu’on a
pu réalisé précédemment.
an − ibn a−n − ib−n
N’oublions pas qu’on a défini que Cn = , C−n = et C−0 = C0 .
2 2
Par ailleurs, nous avons aussi montré les expressions de an et bn , donc pour trouver Cn ,
il nous suffit de substituer les expressions.
an − ibn
Cn =
2
1 1 π i π
= ( f (x) cos(nx) dx − f (x) sin(nx) dx)
2 π −π π −π
π
1
= f (x)(cos(nx) − isin(nx)) dx
2π −π
Par la relation d’Euler, on peut voir directement que cos(nx) − isin(nx) = e−inx
π
1
= f (x)e−inx dx
2π −π
Cependant, cette méthode pour trouver le coefficient Cn dépend fortement de an et
bn qu’on a trouvé auparavant. Donc cette méthode n’est pas très pratique.
Dans ce cas, nous pouvons aussi montrer un autre moyen pour trouver l’expression du
coefficient Cn . Supposons que
∞
f (x) = Cn einx
n=−∞
alors si on multiplie les deux côtés par e−ikx ou k est un entier quelconque, on obtient
∞
f (x)e−ikx = e−ikx Cn einx
n=−∞
Pour la partie de droite, on a
∞
e−ikx Cn einx = e−ikx (· · · + C−2 e−2ix + · · · + C1 eix + · · · + Ck eikx + · · · )
n=−∞
nous remarquons qu’il existe un et un seul terme où n = k qui nous donnera
24

26. Ck eix(k−k) = Ck
donc nous pouvons écrire de façon équivalente :
∞ ∞
e−ikx Cn einx = Cn ei(n−k)x + Ck
n=−∞ n=−∞,n=k
∞
Donc on a Ck = f (x)e−ikx − Cn ei(n−k)x
n=−∞n=k
On peut intégrer sur une période des deux côtés,
π π π ∞
Ck = f (x)e−ikx dx − Cn ei(n−k)x dx
−π −π −π n=−∞,n=k
Prenons un terme dans la somme que nous devons intégrer,
π π
Cn eix(n−k) dx = Cn eix(n−k) dx
−π −π
Cn
= ei(n−k)x |π
−π
i(n − k)
Cn
= (eiπ(n−k) − e−iπ(n−k) )
i(n − k)
par la relation d’Euler, on sait que pour m entier, eiπm = 1
Puisque n et k sont tous les deux entiers, leur différence l’est également
=0
π π
Finalement, on a Ck dx = f (x)e−ikx dx
−π −π
π
2πCk = f (x)e−ikx dx
−π
π
1
Pour tout k entier, on peut avoir Ck = f (x)e−ikx dx.
2π −π
Donc si on peut écrire
∞
f (x) = Cn einx
−∞
alors,
π
1
Cn = f (x)e−inx dx
2π −π
On obtient bien le même expression que ce qu’on a trouve par la première méthode.
Tout comme les séries de Fourier trigonométriques, on peut écrire les séries de Fourier
exponentielles d’une fonction f (x) de période quelconque T .
25

27. T T
On utilisera aussi le changement de variable x = u pour rendre f ( u).
2π 2π
Finalement on obtient que la série de Fourier d’une fonction périodique de T est
∞
2πinx
f (x) = Cn e T
n=−∞
où le coefficient de Fourier
T
T
1 2 −2πinx 1 −2πinx
Cn = f (x)e T dx = f (x)e T dx
T −T
2
T 0
2.2 Convergence des séries trigonométriques, des séries
de Fourier, et Théorème de Dirichlet
Jusqu’à présent, nous avons toujours utilisé soit l’hypothèse "si la fonction égale à
sa série" ou soit le terme "la série de Fourier d’une fonction" parce qu’on a pas encore
montre de manière rigoureuse, l’équivalence entre la fonction et sa série de Fourier. Pour
cela, nous devons montrer la convergence de la série de Fourier vers la fonction.
La convergence est sans conteste l’aspect le plus compliqué dans la description mathématique
des séries de Fourier. Aussi pouvons-nous seulement, avec notre modeste niveau, en
aborder qu’une mince partie.
Avant toute chose, il convient d’introduire certaines notions en ce qui concerne la
convergence, afin que le vocabulaire utilisé, qui peut somme toute paraître anodin, prenne
tout son sens. En premier lieu, nous devons distinguer les différentes formes de convergence :
la convergence simple, la convergente uniforme, la convergence en norme ainsi que la
convergence "presque partout". Nous ne nous occuperons pas des deux derniers cas, car
trop complexes.
2.2.1 Convergence simple
Définition :
Soient I un intervalle de R, (fn )n∈Z une suite de fonctions définies sur I, et f définie
sur I. On dit que (fn ) converge simplement vers f sur I si ∀x ∈ I, la suite (fn (x))
converge vers f (x). Autrement dit :
∀x ∈ I, ∀ > 0, ∃n0 ( , x) ∈ N, ∀n ≥ n0 ⇒ |fn (x) − f (x)| <
Où la notation ( , x) signifie que le choix du n0 dépend et de , et du x déterminé.
Exemple : Soit sur [0, 1], fn (x) = xn . Il est clair que la fonction fn converge
simplement vers la fonction définie par f (x) = 0 si x est dans [0,1[ et f (1) = 1.
26

28. Figure 2.3 – Illustration de la convergence simple
On constate dèjà ici l’insuffisance de la convergence simple pour les fonctions continues :
chaque fonction (fn ) est continue, la suite (fn ) converge simplement vers f , et pourtant
f n’est pas continue. Ainsi la continuité n’est pas toujours préservée par la convergence
simple, d’où par la suite l’idée de convergence uniforme.
Une autre insuffisance d’une telle notion est que l’intégrale de la limite d’une suite
fonctions intégrables n’est pas forcément égale à la limite de l’intégrale de la suite de
fonctions intégrables.
Soit la suite de fonctions définie sur [0,1] par

1
 fn (x) = n2 x,
 0≤x≤ 2n
1 1 1
f (x) = n2 ( n − x), ≤x ≤n
 n 2n
1
fn (x) = 0, x≥

n
Montrons la convergence simple de la suite fn (x) sur [0,1].
1 1
Soit x>0. n →0 lorsque n → ∞, donc à partir d’un certain rang N , on a : n < x.
On en déduit donc qu’à partir du même rang N , fn (x) = 0 et donc fn (x) → 0 lorsque
n → ∞. Ainsi, la suite (fn (x)) converge simplement vers la fonction nulle sur [0,1].
1 1
1 2n n
D’un autre côté, fn (x) = n2 xdx + n − n2 xdx = 1/4 (L’intégrale est donc
1
0 0 2n
1
indépendante de n). Ceci prouve que la suite ( fn ) ne tend pas vers 0. Aussi cette
0
intégrale n’est-elle pas égale à l’intégrale de la fonction nulle, qui est bien entendu nulle,
1 1 1
et donc, lim fn (x)dx = lim fn (x)dx = f (x)dx = 0.
n→∞ 0 0 n→∞ 0
Ces insuffisances motivent donc une nouvelle notion de convergence.
27

29. Figure 2.4 – Illustration de la convergence uniforme
2.2.2 Convergence uniforme
Définition :
Soient I un intervalle de R, (fn )n∈Z une suite de fonctions définies sur I, et f définie
sur I. On dit que (fn ) converge uniformément vers f sur I si :
∀ > 0, ∃n0 ( ) ∈ N, ∀x ∈ I, ∀n ≥ n0 , |fn (x) − f (x)| < .
La convergence uniforme est donc une forme de convergence beaucoup plus exigeante
que la convergence simple, qui ne demandait que, pour chaque point x, la suite (fn (x)) ait
une limite. La convergence uniforme veut que toutes les suites (fn (x)) avancent vers leur
limite respectives avec un certain mouvement d’ensemble, autrement dit, la convergence
a lieu à la même vitesse pour chaque point x, d’où le fait que l’on puisse déterminer une
valeur unique n0 à partir de laquelle toutes les fn (x) dont le n est supérieur à n0 soient
inférieures à un donné, ce indépendamment de x. A l’inverse, pour la convergence
simple, le rang à partir duquel la distance devient très petite peut fortement varier d’un x à
l’autre. De façon imagée, on peut dire que pour que la convergence uniforme, il est possible,
selon le n0 , de former un tube plus ou moins petit autour de la fonction vers laquelle la
suite converge dans lequel tous les fn , n > n0 se trouvent. Pour la convergence simple,
on aurait, toujours de façon imagée, certaines fonctions qui ferait des pics, dépassant ce
tube imaginaire, pour ensuite revenir vers la fonction vers laquelle la suite tend. Ceci se
retrouve bien entendu dans la définition ci-dessus avec |fn (x) − f (x)| < .
28

30. Figure 2.5 – Exemple de convergence uniforme vers la fonction y = |x|
Il semble assez intuitif que toute suite de fonction qui converge uniformément converge
simplement. Nous n’allons pas le démontrer formellement. La réciproque est en général
fausse, sauf cas exceptionnels.
Réglons de suite la seconde insuffisance pour les fonctions intégrables : la définition de
convergence uniforme nous permet une majoration indépendante de x, d’où nous obtenons
l’inégalité suivante :
b
|fn (x) − f (x)|dx ≤ (b − a)max|fn − f |
a
Ceci nous permet dès lors de permuter la position de limite sans affecter le résultat, et la
limite de l’intégrale est bien égale à l’intégrale de la limite. (Quand n tend vers l’infini, le
second membre tend vers 0, d’où le premier également - du fait de la valeur absolu - et
b b
lim fn (x)dx = f (x)dx )
n→∞ a a
Mais qu’en est-il de la première insuffisance en ce qui concerne les fonctions continues :
si une suite de fonction (fn ) continues sur I converge uniformément vers f , f est-elle
continue sur I ? La réponse est oui (on s’en doute), en voici la preuve :
Nous savons que :
∀ > 0, ∃n0 ( ) ∈ N, ∀x ∈ I, ∀n ≥ n0 ⇒ |fn (x) − f (x)| < .
Prenons x0 ∈ I, qui répond donc à l’inégalité, et fixons un nombre entier N qui
caractérise la fonction fN . Nous savons d’autre part que (fN ) est continue en x0 , donc :
∀x ∈ I, ∃δ( , x) > 0, |x − x0 | < δ ⇒ |fN (x) − fN (x0 )| <
Et l’inégalité triangulaire achève la démonstration puisque
|f (x) − f (x0 )| < |f (x) − fN (x)| + |fN (x) − fN (x0 )| + |fN x0 − f (x0 )| < 3 .
29

31. 2.2.3 Convergence normale
Soient I un intervalle de R et (fn )n∈Z une suite de fonctions définies sur I. On dit que
∞
(fn ) converge normalement sur I si la série sup|fn (x)|, x ∈ I est convergente.
n≥0
La convergence normale est encore plus exigeante que la convergence uniforme, dans
le sens où toute fonction qui converge normalement converge uniformément. Nous ne le
démontrerons pas.
2.2.4 Convergence des séries trigonométriques
Proposition 1
Si les séries numériques |an | et |bn | co,nvergent, alors la série trigonométriques
2πn 2πn
S(t) = an cos( t) + bn sin( t) converge normalement (et donc uniformément)
T T
n≥0
sur R
Preuve
Cela découle directement de l’inégalité : |an cos( 2πn t) + bn sin( 2πn )t)| ≤ |an | + |bn |
T T
Corollaire
Si les séries numériques |an | et |bn | convergent, alors la série trigonométrique
S(t) est continue sur R.
Si les séries n |an | et n |bn | convergent, alors la somme S(t) est continue sur R,
à dérivée continue.
Proposition 2
Si les suites numériques (an ) et (bn ) sont décroissantes et tendent vers 0, alors la série
trigonométrique S(t) est convergente pour t = k.T où k ∈ Z
Nous ne démontrons pas cette proposition.
2.2.5 Théorème de Dirichlet.
Avant d’entamer la démonstration, il convient de repréciser les différents types de
convergence qui interviennent dans le cadre des séries de Fourier : la convergence simple,
que traite le théorème de Dirichlet, la convergence uniforme, la convergence en norme,
et la convergence presque partout. Chacune de ces notions de convergence requiert des
hypothèses différentes sur la fonction f (x), ainsi que différents types de preuves. Les
preuves des trois derniers cas de convergence cités sont inabordables car elles nécessitent
des notions d’analyse fonctionnelle très avancées.
Quelques notations et définitions
30

32. Notation
Nous noterons pour la suite f (a+ ) la limite à droite en a et f (b− ) la limite à gauche
en b.
Fonction continue par morceau
Une fonction f : [a, b] → C est dite continue par morceau sur [a,b] si f est continue sur
[a,b] sauf éventuellement en un nombre fini de points qui admettent des limites à gauche
et à droite. En particulier, f (a+ ) et f (b− ) existent.
Fonction lisse par morceaux
Une fonction f : [a, b] → C est dite lisse par morceau sur [a,b] si f et f sont continues
par morceaux sur [a,b]. En particulier, f (a+ ) et f (b− ) existent.
Extension sur R
Une fonction f : R → C est continue (respectivement lisse) par morceau sur R si elle
est continue (respectivement lisse) par morceaux sur tout intervalle borné [a,b]∈ R
Introduction au théorème
n
Expression du noyau de Dirichlet : Dn (x) = eikx
k=−n
Nous allons calculer cette somme dans un cas général afin d’alléger l’écriture. Soit
donc la somme symétrique (car allant de −n à n) de termes d’une suite géométrique de
raison q. Nous allons utiliser la symétrie de la somme afin de modifier l’écriture :
n 2n
q 2n+1
qk = q −n q k = q −n
q−1
k=−n k=0
1
Pour obtenir un terme plus homogène, multiplions numérateur et dénominateur par q − 2 ,
1 1 1
q −n− 2 q 2n+1 − 1 q n+ 2 − q −n− 2
ce qui nous donne : −1 = 1 −1
q 2 q−1 q2 − q 2
En remplaçant maintenant q par eix , nous trouvons :
1 1
ei(n+ 2 )x − e−i(n+ 2 )x
1 1
ei( 2 )x − e−i( 2 )x
Et en utilisant les formules d’Euler, nous pouvons transformer l’expression en :
sin((n + 1 )x)
2
sin( x )
2
Cependant, nous aurons besoin pour notre démonstration de l’intégrale de −π à π
(qui équivaut soit disant passant au double de l’intégrale de 0 à π, la fonction déterminé
par le noyau étant paire) de la fonction Dn (x). La primitive de l’expression trouvée étant
extrêmement ardue, nous devons trouver une autre expression du noyau.
Sachant que le noyau est une fonction réelle, il nous suffit en fait de prendre en compte
n
uniquement les parties réelles de la somme eikx , ce qui nous donne :
k=−n
31

33. k=n
Dn (x) = 1 + 2 cos(kx)
k=1
(Deux fois la somme car cosx est paire, 1 car nous considérons à part le cas où k=0)
π
Aussi trouvons-nous aisément que : Dn (x)dx = 2π, les termes en cosinus devenant
−π
des sinus, qui s’annulent pour x = k.π.
En résumé,
n n 1
sin((n + 2 )x)
Dn (x) = eikx = 1 + 2 cos(kx) =
sin( x )
2
k=−n k=1
Et son intégrale de 0 à π équivaut à π. Passons maintenant au théorème de Dirichlet en
lui-même.
Théorème(Dirichlet, 1824) Si f : R → C est 2π-périodique et lisse par morceau sur
R, alors :
f 1
lim SN (x) = (f (x+ ) + f (x− )) pour tout x.
N →∞ 2
En particulier,
f
lim SN (x) = f (x)
N →∞
f
pour tout x où f est continue, avec SN (x) la série de Fourier correspondant à la fonction.
Nous pouvons dès lors dire qu’une fonction qui vérifie les hypothèses du théorème de
Dirichlet converge simplement. Remarque :Il peut exister des fonctions continues dont la
série de Fourier associée diverge pour certaines valeurs de x.
Preuve
Nous allons utiliser la notation complexe, et choisir le cas particulier T = 2π afin
p
d’alléger l’écriture. Notons Sp (x) = ck eikx la somme partielle de la série de Fourier
k=−p
en un point x fixé.
1
1. Calcul de Sp (x) − (f (x+ ) + f (x− ))
2
Calculons la somme partielle Sp (x), et précisons que f (t) correspond à la fonction que
l’on a représenté sous forme de série. x étant fixé, nous utilisons la variable t afin de ne
pas prêter à confusion ; il ne s’agit en quelque sorte que d’une variable muette :
p 2π
1
Sp (x) = eikx e−ikt f (t)dt
2π 0
k=−p
32

34. 2π p
1
= eik(x−t) f (t)dt
2π 0 k=−p
2π
1
= Dp (x − t)f (t)dt
2π 0
2π−x
1
= Dp (u)f (u + x)du
2π −x
[Changement de variable (t=u+x) + utilisation du fait que le noyau de Dirichlet est
pair.]
π
1
= Dp (u)f (u + x)du
2π −π
2π π k+2π
f périodique de période 2π, donc, comme on a pu le démontrer, = =
0 −π k
Ceci nous permet dès lors d’écrire en se souvenant que l’intégrale du noyau sur la
période est π :
π π
1 1 1
Sp (x) − (f (x+ ) + f (x− )) = Dp (u)f (u + x)du − Dp (u)f (x+ )du −
2 2π −π 4π −π
π
1 −
Dp (u)f (x )du
4π −π
Ce qui nous donne en utilisant la parité du noyau de Dirichlet :
π π 0
1 1 1
Dp (u)f (u + x)du − Dp (u)f (x+ )du − Dp (u)f (x− )du
2π −π 2π 0 2π −π
0 π
=
1
2π
( −π
Dp (u)(f (u + x) − f (x− ))du +
0
Dp (u)((f (u + x) − f (x+ ))du )
Il ne nous reste donc plus qu’à prouver que ces deux intégrales tendent vers 0 lorsque
p tend vers l’infini, et nous aurons gagné. La démonstration étant quasi identique pour
chaque intégrale, nous ne le démontrerons que pour une seule.
π
2. Calcul de lim Dp (u)((f (u + x) − f (x+ ))du
p→∞ 0
1
sin((p + 2 )x)
Nous avons vu dans l’introduction au théorème que Dp (x) = x
sin( 2 )
Choisissons α, 0 < α < π, tel que f soit lisse par morceau sur ]x; x + α[ (sans oublier
π α π
que x est fixé), et décomposons en +
0 0 α
α
2.1 Traitons d’abord le cas de la première intégrale
0
33

35. Notons M la borne supérieure de f sur [0; α] et remarquons que u ≤ πsin( u ) pour
2
tout u ∈ [0, π] Nous appliquons le théorème des accroissements finis à f sur [x; x + u] :
|f (u + x) − f (x+ )| ≤ M u.
Et donc, en réinjectant dans l”intégrale dont on a pris la valeur absolu, tout en se
rappelant que u ≤ πsin( u ) , nous obtenons :
2
α
|sin((p + 1 )u)| α
|sin((p + 1 )u)|
2
|((f (u + x) − f (x+ ))|du ≤ 2
M udu ≤ M πα
0 sin( u )
2 0 sin( u )
2
Ainsi, l’intégrale peut être rendue arbitrairement petite pour autant que l’on choisisse
bien α.
π
2.2 Cas de la seconde intégrale
α
Nous allons utiliser le lemme suivant afin de démontrer cela (remarquons que ce lemme
marche tout aussi bien pour le premier cas) :
Lemme
Toute fonction f lisse par morceau sur [a, b] vérifie :
b
lim f (x)sin(nx)dx = 0
n→∞ a
b
lim f (x)cos(nx)dx = 0
n→∞ a
Preuve
b n−1 αk+1
Il nous suffit d’intégrer par partie : f (x)sin(nx)dx = f (x)sinxdx =
a k=0 αk
n−1 αk+1 n−1
1 + − 1
(f (αk )cos(nαk ) − f (αk+1 )) + f (x)cos(nx)dx
n n αk
k=0 k=0
Et l’on constate bien que lorsque n → ∞, l’expression → 0 (Rappelons-nous bien que
l’hypothèse de départ est que f est lisse par morceau, d’où le fait que sa dérivée soit
continue, et a fortiori bornée, ce qui justifie le fait que la seconde partie de l’expression
tende vers 0.)
Revenons-en au traitement de notre second cas.
f (x+u)−f (x+ )
Posons g(u) = sin( u ) . Il suffit maintenant simplement de constater que g(u) est
2
lisse par morceau sur [α; π], ce qui implique que
π
1
lim g(u)sin((p + )u) = 0 d’après le lemme précédent, ce que l’on cherchait à
p→∞ α 2
34

36. démontrer.
3.Synthèse de la démonstration du théorème de Dirichlet.
1
Nous avons donc démontré que lim Sp (x) − (f (x+ ) + f (x− )) = 0, pour une fonction
p→∞ 2
f lisse par morceau, ce qui nous assure que qu’en tout point de discontinuité, la fonction
converge vers une valeur, et qu’en tout autre point où f est continue, la limite de la série
de Fourier correspondant à la fonction pour p très grand tend vers la fonction.
2.2.6 Analyse d’une fonction qui répond aux hypothèses du théorème
de Dirichlet.
On se propose d’étudier la fonction f (x) = ex si x ∈] − π; π[, fonction qu’on étend par
la suite sur l’ensemble des réels. D’après ce qu’on a pu démontrer sur la périodicité, nous
pouvons nous contenter d’étudier la fonction sur ] − π; π[
Figure 2.6 – Graphique de f (x) = ex si x ∈] − π; π[, fonction qu’on étend par la suite
sur l’ensemble des réels.
Remarquons tout de suite que la fonction est discontinue aux points x = π + k.2π,
qu’elle est de période de 2π et qu’elle vérifie les hypothèses du théorème de Dirichlet
puisqu’elle est clairement lisse par morceau. Ainsi, nous pouvons légitimement écrire
∞
a0
cette fonction sous forme de série de Fourier, c’est-à-dire f (x) = 2 + (an cos(nx) +
n=0
bn sin(nx))
Calcul de a0
1 π x eπ − e−π
a0 = e dx =
π −π π
Calcul de an
1 π x
an = e cos(nx)dx.
π −π
π
Pour trouver ex cos(nx)dx, deux méthodes-entre autres- s’offrent à nous : la double
−π
π
intégration par partie, ou ex(ni+1) , en considérant ensuite la partie réelle de l’intégrale.
−π
Nous allons utiliser la première pour la recherche de an et la seconde pour la recherche de
35

37. bn . ( A la seule différence près que cos(nx) étant subsitué par sin(nx) pour la recherhce
de bn , nous devrons considérer la partie imaginaire de l’intégrale.)
Soit I = ex cos(nx)dx. Après la première intégration par partie, nous trouvons :
ex sin(nx) 1
I= − ex sin(nx)
n n
Intégrons maintenant par partie J = ex sin(nx) ; nous trouvons :
−ex cos(nx) 1 π x
J= + e cos(nx)
n n −π
ex sin(nx) 1 −ex cos(nx) 1
Ainsi, I = − ( + I)
nx n n n
1 e sin(nx) ex cos(nx)
⇔ I(1 + 2 ) = +
nx n x n2
n.e sin(nx) + e cos(nx)
⇔I=
n2 + 1
π
eπ .cos(nπ) e−π .cos(nπ) cos(nπ) π
Dès lors, ex cos(nx)dx = 2+1
− 2+1
= 2 (e − e−π )
−π n n n +1
1 cos(nπ) π
Et finalement, an = ( (e − e−π ))
π n2 + 1
Calcul de bn
1 π x 1 π
bn = e sin(nx)dx = ( ex(ni+1) )
π −π π −π
1 π x(ni+1) eπ(ni+1) e−π(ni+1)
⇒ e = −
π −π ni + 1 ni + 1
−ni + 1 π nπi −π −nπi
= 2 (e e −e e )
n +1
En prenant uniquement la partie imaginaire, en considérant bien que sin(nπ) est de
toute façon nul, nous trouvons :
1 −n
bn = ( 2 (eπ cos(nπ) − e−π cos(nx)))
π n +1
1 ncos(nπ) −π
Et finalement, bn = ( (e − eπ ))
π n2 + 1
Et en groupant le tout, nous trouvons l’expression de la série. (En considérant bien
que suivant que n est pair ou impair, cos(nπ) équivaudra à 1 ou -1)
Série de Fourier associée à la fonction
∞
eπ − e−π (−1)n
f (x) = + (eπ − e−π )(cos(nx) − nsin(nx))
2π n=1
π(n2 + 1)
36

38. ∞
eπ − e−π (−1)n
=
π
(1 +
2 π(n2 + 1)
)
(cos(nx) − nsin(nx)
n=1
2.3 Phénomène de Gibbs
Nous avons vu lors de l’analyse de la fonction carrée qu’au plus on additionne des
termes trigonométriques, au plus la fonction tend vers une forme carrée. Mais nous
remarquons aussi que sur les points anguleux de la fonction, bien qu’on puisse ajouter un
grand nombre de termes, défaut d’approximation persistera.
Figure 2.7 – Illustration du phénomène de Gibbs
Etant donné que tout terme de la série de Fourier est une fonction continue, il
est normal que la série ne puisse approcher uniformément la fonction aux points de
discontinuité. Des études ont déjà montré que l’amplitude d’oscillation autour des discontinuités
est toujours plus importante. Quantitativement, il en ressort que très régulièrement,
l’oscillation y est 18% plus importante que sur le reste la fonction continue. C’est le cas
dans la fonction carrée. Nous verrons dans la partie traitant des applications l’importance
de cette fonction carrée qui est incontournable en électronique lorsque l’on manipule des
informations binaires qui ne s’expriment qu’à l’aide de deux valeurs uniques.
37

39. Deuxième partie
Applications de l’analyse
harmonique
38

40. Chapitre 1
Synthèse numérique d’un son à
partir de l’addition des séries de
Fourier
Nous allons voir comment l’on peut modéliser des signaux à l’aide des séries de Fourier
par addition de termes en sinus et cosinus. Nous avons développé une application qui
montre visuellement et auditivement l’importance de l’addition de termes dans les séries
de Fourier pour modéliser par exemple la fonction carrée. Il faut cependant différencier
plusieurs types de signaux. Les signaux harmoniques, les signaux périodiques qui correspondent
à la composition de différents signaux harmoniques et les signaux non périodiques. Chacun
de ces signaux seront analysés à l’aide d’outils différents. Pour les signaux harmoniques,
une analyse sinusoïdale suffit. Pour des signaux composés de plusieurs harmoniques, on
utilisera les séries de Fourier. Et finalement pour les signaux non périodiques on peut
utiliser les transformées de Fourier.
39

41. Chapitre 2
Applications informatiques
2.1 FFT : Fast Fourier Transform
Nous avons vu que les séries de Fourier sont des outils très pratiques afin de pouvoir
modéliser des signaux sous forme d’addition de sinusoïdes et cosinuoïdes. Il est donc
pratique de disposer de ces séries mais le calcul n’est pas toujours simple et efficace.
C’est pourquoi avec le développement de l’informatique sont apparus des algorithmes qui
permettent de calculer les coefficients selon une méthode linéaire. Ainsi, nos processeurs
binaires savent traiter bien plus rapidement l’information. Jusqu’ici on s’était intéressé
à l’approche temporelle du son, c’est-à-dire que l’on se contentait de considérer le signal
comme une grandeur évoluant au fil du temps. C’est la vision la plus directe mais pas
nécessairement la plus intuitive. Lorsque l’on écoute un son, l’analyse la plus simple,
la plus primitive c’est, d’une part, de savoir s’il est fort ou faible en terme de volume
sonore et par ailleurs s’il est grave ou aigu. 1 Nos oreilles sont essentiellement sensibles à
la fréquence et à l’amplitude du son. A partir de là, il parait évident que la représentation
temporelle n’est pas la plus triviale pour “visualiser” un son de la même manière qu’on
l’écoute. Nous allons donc recourir à une opération qui suit cette logique, la transformée de
Fourier. Une transformée est une opération consistant à faire correspondre une fonction
à une autre pour représenter la même information d’une façon différente. Dans le cas
de Fourier, l’idée est d’exprimer le son comme dépendant de la fréquence et non plus
du temps le tout à partir de l’hypothèse que tout signal est fondamentalement composé
d’une somme de sinusoïdes de fréquences différentes. On peut distinguer assez clairement
l’évolution du volume sonore mais on n’a aucune information visible sur la hauteur du
son joué.
1. Pour l’oreille humaine, des sons très graves oscillent autour des 16Hz alors que des sons très aigus
oscillent autour des 16kHz
40

42. Figure 2.1 – Représentation temporelle d’un son
Figure 2.2 – Représentation fréquentielle d’un son
Comparons les graphes.
Sur la Figure 2.2 on a donc plus le temps comme abscisse mais la fréquence. Tout
de suite, le graphique est nettement moins massif. Pourquoi ? On distingue clairement
que le son est très simple car composé essentiellement d’une seule fréquence (788, 5Hz,
c’est presque un sol) plus deux petits pics à dans les hautes fréquences ( 3000Hz et
7000Hz). Par contre il est difficile de savoir comment le son évolue au fil du temps.
41

43. Les deux représentations ont clairement leurs avantages respectifs en fonction de ce que
l’on recherche. Nous allons maintenant énoncer la formule de base de la transformée de
Fourier, sans la démontrer.
ˆ +∞
F (f ) : ν → f (ν) = −∞
f (t) e−i2πνt dt
La transformée ainsi calculée est un signal complexe, c’est à dire en deux dimensions.
Là où chaque échantillon du signal d’origine était composé d’une grandeur (l’amplitude),
sa transformée associe à chaque fréquence à la fois l’amplitude 2 et la phase. 3
Nous allons maintenant analyser ce qu’il se passe lorsque nous composons un son d’un
la (440Hz) et d’un ré (294Hz), respectivement déphasés de 0.7 et -0.2. L’équation de ce
son est :
x(t) = 0.5 cos((2π)500t + 0.7) + 0.25 cos((2π)294t − 0.2)
Voici ce que donne cette addition graphiquement :
Figure 2.3 – Addition du signal du La et du Ré
Traçons le graphe de la transformée de cette fonction maintenant. Deux traits sont à
nouveau présents sur le graphe de la transformée. En lisant le graphique nous pouvons
donc retrouver les deux fréquences avec leur amplitude et phase respective. Il est important
de remarquer que l’amplitude nous donne une indication sur le volume sonore de chaque
fréquence alors que la phase nous renseigne sur le positionnement dans le temps. Nous
2. L’amplitude c’est le volume sonore associé à chaque fréquence
3. La phase est un concept un peu plus abstrait, il s’agit du “retard” de chaque fréquence.
42

44. Figure 2.4 – Transformée des signaux additionnés
voyons l’utilité des transformées de Fourier dans le but d’analyser un signal, par exemple
un son. Les transformées de Fourier ont pris un essor incroyable ces dernières années grâce
à la révolution en électronique. Beaucoup d’appareils doivent être capables d’effectuer
des transformées de Fourier pour analyser des signaux. C’est alors que les électriciens et
informaticiens se sont penchés sur la question afin optimiser le temps de calcul de ces
coefficients, et permettre ainsi de réduire la puissance des processeurs pour effectuer ces
calculs. L’algorithme le plus connu et le plus répandu est sans aucun doute l’algorithme
baptisé F F T , issu de l’anglais Fast Fourier Transform. Nous ne pouvons pas développer
les opérations qui se cachent derrière cette transformation rapide étant donné la complexité
de celles-ci. Cet algorithme a été mis au point par deux ingénieurs américains. D’une part,
J. W. Cooley d’IBM et John W. Tukey de l’université de Princeton en 1965, après avoir
redécouvert les travaux de Gauss qui avait déjà travaillé sur le problème sans apporter de
réponse reconnue publiquement.
2.2 Compression JPEG
L’appareil photo a connu une grande révolution au virage des années 2000 et l’appareil
photo numérique domine maintenant largement le marché. Il faut savoir que la mise en
place et le développement aussi rapide de cette nouvelle technologie n’aurait pas été
possible sans l’analyse de Fourier. En effet, lorsqu’on déclenche l’appareil photo, il produit
43

45. automatiquement des transformées de Fourier.
2.2.1 Pourquoi Fourier ?
Il faut savoir qu’un appareil photo stocke les images sur une carte mémoire. Au plus
de photos je stocke sur mon appareil photo, au plus de pixels sont conservés sur la carte
mémoire. Pour avoir des capteurs de plus en plus précis 4 (en ayant plus de points de
détection), il faut aussi une augmentation proportionnelle de la mémoire. Bien entendu,
on serait quand même parvenu à utiliser un appareil photo numérique sans se tracasser
des séries de Fourier car il ne s’agit que de la compression du format de stockage et de
traitement postérieur d’image. Mais le développement de la qualité des appareils photo
numériques aurait été plus lente. Nous quantifierons cette observation par la suite.
2.2.2 Le JPEG, c’est quoi
Il s’agit d’un format de stockage de photos numériques largement adopté car il a la
caractéristique d’encoder une image de même résolution en moins de bits 5 que un autre
format. Comment cela ce fait-il ? Il compresse les données reçues du capteur par le F F T . Il
faut savoir que le capteur numérique de l’appareil photo est composé de micro-détecteurs
qui enregistrent chacun une couleur.
2.2.3 Quelle couleur ?
Le tas d’informations reçu du capteur est stocké
sous forme de matrice. La référence des couleurs
de chaque pixel est stocké sous forme de code
hexadécimal. Grâce à Newton, on sait que la lumière
blanche peut se décomposer en 3 couleurs qui sont le
bleu, rouge et vert. C’est ce système tri-chromatique là
que les ordinateurs utilisent. Baptisé RGB, acronyme
de l’anglais pour "Red, Green, Blue", ces trois couleurs
sont les couleurs primaires en synthèse additive. Elles Figure 2.5 – Système RGB
correspondent en fait à peu près aux trois longueurs
d’ondes auxquelles répondent les trois types de cônes
de l’œil humain.
4. Certains appareils atteignent maintenant des capteurs de 30 mégapixels. C’est à dire 30 × 106 pixels
5. Le bit est un chiffre binaire, c’est-à-dire 0 ou 1. Il est donc aussi une unité de mesure en informatique,
celle désignant la quantité élémentaire d’information représentée par un chiffre du système binaire. On
en doit l’invention à John Tukey (qui était aussi derrière la découverte du F T T !).
Définition de Wikipédia
44

46. Figure 2.6 – Adapté d’un document de Vincent Bockaert/123di.com
Un capteur photosensible CCD ou CMOS est constitué d’une seule matrice photosensible
qui est recouverte d’un filtre coloré appelé une grille de Bayer. Contenant des éléments
de différentes couleurs, elle permet de sensibiliser les pixels aux 3 couleurs primaire : le
rouge, le vert ou le bleu.
Le processeur d’image associé au capteur photosensible combine ensuite ces trois
couleurs primaires RGB pour créer par synthèse additive une image couleur et lui associe
une valeur hexadécimale 6 . Nous voilà donc avec une matrice pixelshorizontaux ×pixelsverticaux .
Pour simplifier les calculs nous allons prendre une matrice carrée 8 × 8 en décimales. Nous
avons 64 données différentes 7 relatives aux 64 pixels. A la place d’utiliser une échelle des
couleurs 24 bits, nous allons utiliser les niveaux de gris (communément appelé "Noir et
blanc") qui ne prennent que 8 bits 8 alors que une photo couleur en RGB prend 24 bits 9 .
Pourquoi avoir choisi une matrice 8 × 8 ? Parce que le JPEG sépare une image de plus
grande taille en plusieurs matrices 8 × 8. Quand le standard JPEG a été mis au point,
l’ordinateur ne pouvait que traiter 8 bytes 10 à la fois.
Prenons l’image élémentaire :
C’est à dire la matrice sous forme décimale :
6. Sur ce site internet, vous pouvez convertir une couleur en sa valeur hexadécimale http://
html-color-codes.com
7. Les valeurs hexadécimales sont par convention notées par le préfixe "0×"
8. Pour un pixel en 8 bits il existe alors 28 = 256 possibilités d’encodage. Cette combinaison de 8 bits
est tellement fréquente qu’elle définit une nouvel unité, le byte
9. Pour un pixel en 24-bit, il existe 224 possibilités d’encodage
10. La distinction entre byte et octet est utilisée dans certains textes techniques. Ainsi la description
formelle d’un langage de programmation utilisera sciemment le mot byte si le langage ne nécessite pas
qu’un byte ait une taille d’un octet. C’est par exemple le cas du langage C, où un byte peut contenir plus
de huit bits. Source : Wikipédia
45

47. Figure 2.7 – Une image de 64 pixels correspondant à la matrice
 
53 51 55 60 66 70 64 73
 
63 59 54 89 110 85 69 71
 
63 60 68 113 144 104 66 73
 
 
63 58 71 122 154 106 70 69
 
66 60 68 103 127 88 68 70
 
 
79 65 60 70 77 68 58 75
 
85 71 65 59 55 61 65 83
 
87 79 69 69 65 76 78 95
Dans cette balance des gris, 255 correspondrait à du noir et 0 à du blanc. Toutes les
valeurs intermédiaires ne sont que des mélanges de ces deux couleurs.
Afin de compresser l’images on utilise les coefficients des séries de Fourier mais aussi
le DCT 11 .
Nous allons transformer la matrice de la balance des gris (8 × 8) en une matrice de
coefficients de DCT (toujours 8 × 8). Cette matrice ne représente plus l’image en soi.
11. La transformée en cosinus discrète ou TCD (de l’anglais : DCT ou Discrete Cosine Transform) est
une transformation proche de la transformée de Fourier discrète (DFT). Le noyau de projection est un
cosinus et crée donc des coefficients réels, contrairement à la DFT, dont le noyau est une exponentielle
complexe et qui crée donc des coefficients complexes. On peut cependant exprimer la DCT en fonction
de la DFT, qui est alors appliquée sur le signal symétrisé.
46

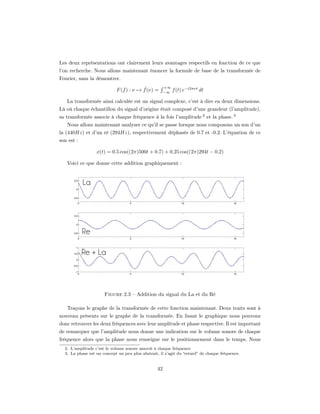
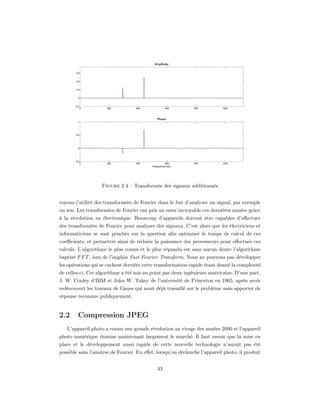
48. Chaque coefficient définit l’amplitude d’une fonction de base. L’image est compressée et
l’ordinateur doit connaître l’algorithme de décompression pour pouvoir lire l’image. Pour
chaque pixel de la matrice de départ nous allons effectuer le calcul suivant. x et y sont
les indices spatiaux qui font référence à un certain pixel. L’index u et v font partie du
spectre fréquentiel qu’on a vu précédemment dans ce chapitre. Puisqu’on travaille sur un
octet, les valeurs de tous les indices peuvent varier de 0 à 7 seulement.
(2x + 1)uπ (2y + 1)vπ
b[x, y] = cos cos (2.1)
16 16
Pour calculer le spectre avec le DCT, on calcule la fonction de base appropriée par
la matrice 8 × 8 et on additionne ensuite les produits. Ensuite, il faut multiplier les 15
valeurs dans le premier rang et dans la première colonne par deux. Finalement, on divise
toutes les données par 16.
47

49. Le résultat est le suivant
Figure 2.8 – Voici les résultats de la transformée discrète des cosinus
Chacun de ces coefficients DCT représentent l’amplitude d’une fonction de base par
rapport aux index v et u en cosinus.
Figure 2.9 – Illustration des différentes fonctions de la DCT. Extrait de The Scientist
and Engineer’s Guide to DSP
Les coefficients des basses fréquences se trouvent dans le coin supérieur gauche alors
que les hautes fréquences se retrouveront dans le coin inférieur droit.
L’algorithme inverse du DCT est calculé en faisant correspondre chacune des amplitudes
à la fonction de base et on additionne à nouveau les termes afin de retrouver des données
similaires à celles de base. La colonne de gauche montre l’effet de réduire le nombre de
48

50. bits utilisés pour représenter le spectre de la fréquence. Cette marge d’erreur est obtenue
en prenant la DCT inverse de la fonction et en soustrayant l’image reconstruite de l’image
originale. Au moins de bits sont utilisées, au plus cette marge d’erreur sera importante et
la qualité d’image reconstruite mauvaise.
Nous remarquons que les chiffres sont nettement moins important après une transformée
et nous pouvons remarquer que la matrice contient des nombres beaucoup plus petits.
Jusque 10 fois plus petits parfois. La taille de l’image est par conséquent divisée par 10 !
Nous avons perdu les plus hautes fréquences en chemin car elles sont les plus atteintes
par la transformée en DCT mais l’aspect général de l’image est le même. Le rendu reste
excellent.
La troisième colonne représente la marge d’erreur présente à cause de la transformation.
Il faut aussi remarquer que cet algorithme est présent partout. Que ce soit l’histogramme
de visualisation sur Windows Media Player ou sur la chaîne Hi-Fi, ils utilisent tous cet
algorithme de transformée rapide de Fourier.
2.2.4 Alors quelle avancée l’analyse de Fourier a-t-elle permis ?
On l’a vu, la compression grâce aux transformées de Fourier permet de diviser par
un facteur 10 la taille de stockage sur les appareils photos (entre autres). Mais cette
observation est aussi valable pour les sons. Sur nos baladeurs MP3, iPods ou ordinateurs
portables, nous stockons des sons au format MP3. Ce format utilise lui aussi les transformations
de Fourier afin de garantir une compression sans trop de pertes. On pourrait se poser la
question suivante : combien d’années plus tard l’appareil photo serait-il apparu si l’analyse
de Fourier n’existait pas ? En 1965, le co-fondateur d’Intel, Gordon Moore prédit que la
capacité de stockage binaire allait doubler tous les ans. A l’époque ce n’était qu’une
prévision aveugle. Un développement similaire serait exponentiel et donc infini. Pourtant
avec une quarantaine d’années de recul, nous pouvons admettre que cette prévision est
assez proche de la réalité. 10 Ans après avoir proposé ce pari risqué, un professeur de
Caltech 12 donne le terme Moore’s Law à cette prédiction. On remarque aussi que cette
évolution est inversement proportionnelle au prix. Donc pour la même capacité, mon
disque dur coûtera 2 fois moins cher l’année prochaine !
Revenons à Fourier. Nous avons vu que la taille de stockage d’une image peut être
réduite d’un facteur 10. La transformée de Fourier nous a donc permis une évolution
de 2t = 10. Autrement dit, t = log2 10 3.3. C’est à dire que si je voulais avoir un
appareil photo qui n’utilise pas la transformée de Fourier, je devrais attendre plus de
trois ans afin d’avoir la même capacité de photo. Ou je devrai débourser deux fois moins
cher pour acheter un iPod de la même capacité un an plus tard (si on admet que les
12. Caltech est l’institut universitaire technologique de Californie
49

51. Figure 2.10 – Illustration de la prédiction de Moore. Le l’échelle de l’axe vertical est
bien entendu logarithmique. Les croix représentent la capacité de stockage des produits
sortis aux années respectives. Source : Wikimédia Foundation
autres composants suivent la même évolution, ce qui n’est pas le cas). D’ailleurs, c’est
ce que Kodak a compris. On retrouve sur leur site internet une page réservée à attirer
de nouveaux investisseurs. Ils illustrent à l’aide d’un graphique que c’est un marché en
pleine évolution où le prix du pixel diminue chaque année de moitié !
50

52. Figure 2.11 – Graphique avec une échelle logarithmique de l’évolution du prix du pixel.
Source : Kodak Australia
51

53. Chapitre 3
Digital Signal Processing, un
large domaine d’applications
Les séries de Fourier ont été pendant longtemps qu’un modeste outil de mathématiques
et thermodynamique 1 . Les séries vont prendre leur véritable essor lors de la révolution
en électronique. La nécessité de traitement d’un signal va faire redécouvrir l’œuvre de
Fourier, peu enseignée jusque là. Le traitement des signaux est omniprésent. Du sonar à
la conquête spatiale tout en passant par la neurologie. Nous avons décidé de montrer la
diversité de son utilisation au sein d’un même domaine : les télécommunications. Nous
n’aborderons pas de manière détaillée son application mais ceci montre son large spectre
d’application.
3.1 Applications en télécommunications
Que sont les télécommunications ? Les télécommunications permettent de transférer
de l’information d’un endroit à un autre. Cette information peut avoir diverses formes :
conversations téléphoniques, chaînes de télévision, fichiers informatiques ... Pour transférer
cette information entre ces deux lieux, il faut une passerelle : un câble de cuivre, un
signal radio, une fibre optique ... Ces câbles sont posés par des sociétés qui ont intérêt à
transmettre le plus d’information possible à travers chaque câble. C’est ici qu’intervient
l’analyse de Fourier.
1. Fourier a travaillé sur des séries trigonométriques à partir d’un problème de propagation de la
chaleur dans les solides.
52

54. 3.1.1 Confondre l’information. Sans la mélanger.
Nous avons actuellement plusieurs milliards de téléphones à l’échelle mondiale. Chacun
de ceux-ci peut-être connecté en quelques secondes à un autre. Jusqu’aux années 60, les
connections téléphoniques nécessitaient des switch manuels et chaque connexion nécessitait
un câble ! La quantité de câbles requis était donc considérable. Heureusement le système a
changé depuis grâce à la numérotation numérique. Désormais, les signaux sont transformés
en un flux de données numériques. Puisque ces bits 2 peuvent être facilement mélangés et
séparés par la suite. Cela permet de transmettre plusieurs signaux à travers le même câble
et présente donc un avantage considérable au niveau économique pour le déploiement du
réseau. De plus, les portes logiques ne coûtent pas cher par rapport aux kilomètres de
câbles qui auraient dû être placés. On verra par la suite comment ces signaux peuvent
être retrouvés par une analyse fréquentielle du signa à l’aide des transformées de Fourier.
3.1.2 Compression
En général, une signal téléphonique est composé de 64 kbits/s, mais grâce aux algorithmes
de la transformée de Fourier, nous pouvons compresser ce signal à 32 kbits/s sans perte
significative de qualité auditive. Cela s’explique par la petite différence entre deux sons
fortement rapprochés vu que le téléphone enregistre le son environ 8000 fois par secondes.
3.1.3 Suppression de l’écho
L’écho est un sérieux problème lors d’appels téléphoniques sur de longues distances.
Lorsque l’on parle au téléphone, le signal transmettant notre voix voyage jusqu’à l’interlocuteur
où une partie du son retourne en écho. Si j’appelle à une centaine de kilomètres, l’écho
n’est pas audible car il n’a un retard que de quelques millisecondes. L’oreille humaine n’est
pas capable de s’apercevoir de si petits retards. Dès lors on ne perçoit rien de dérangeant
et inhabituel. Mais lorsque la distance devient plus importante, l’écho devient également
de plus en plus considérable. Sur des appels intercontinentaux, la distance peut atteindre
les centaines de millisecondes. Heureusement, on peut maintenant mesurer digitalement
le retard de l’écho et par conséquent générer un anti-signal qui va rendre l’écho inaudible.
Cette technologie est indispensable sur des téléphones utilisant des haut-parleurs, car
l’importance du signal retourné est largement plus important. Depuis 2008, de nombreux
téléphones portables sont dotés de deux microphones. Un est situé à proximité de la
bouche de l’interlocuteur et l’autre à l’arrière du téléphone. Cette technologie permet de
2. Le bit est un chiffre binaire, c’est-à-dire 0 ou 1. Il est donc aussi une unité de mesure en informatique,
celle désignant la quantité élémentaire d’information représentée par un chiffre du système binaire. On
doit cette invention à à John Tukey
53

55. supprimer le bruit ambiant répétitif comme le bruit de fond dans un métro, voiture, rue
...
3.1.4 La Blue Box
Un utilisateur était seulement identifié sur le réseau téléphonique à l’aide d’un signal
qu’il envoie à l’opérateur. Ce signal est comme nous l’avons vu une addition de termes
trigonométriques qui contient une information. L’opérateur facturait les appels grâce à
ce procédé d’identification.
Une anecdote à ce sujet. Avant de pouvoir fonder Apple, Steve Jobs et Steve Wozniak
avaient besoin d’argent. Ils ont décidés de construire une petite machine, appelée la Blue
box. Celle-ci permettait de moduler le signal pour faire croire à l’opérateur que l’utilisateur
était un autre, en modulant un signal différent. Le résultat était que l’on pouvait appeler
aux quatre coins du monde gratuitement grâce à cette Blue Box. Steve Jobs a aussi dit
que c’est grâce à la vente de ces dispositifs que lui et son ami ont pu fonder Apple.
54

56. Annexe A
Joseph Fourier et ses précurseurs
Les séries de Fourier constituent la branche la plus ancienne de l’analyse harmonique
et est en évolution permanente. L’étude de leurs particularités s’est développée de pair
avec les progrès de la théorie de l’intégration. Afin de comprendre ce que Joseph Fourier a
apporté de neuf en la matière commençons par reprendre chronologiquement les évènements
qui ont influencé Fourier dans l’élaboration de ses séries.
A.1 Les précurseurs de Fourier
C’est en 1400 qu’apparaissent chez l’indien Madhava, les premières formes de séries
trigonométriques. Ces séries n’apparaitront qu’au 17e siècle en Occident chez James
Gregory et un siècle plus tard chez Brook Taylor qui décrit dans son ouvrage "Methodus
Incrementorum Directa et Inversa" l’étude systématique des cordes vibrantes et de la
propagation du son.
Quelques années plus tard éclate une controverse entre trois grands mathématiciens
du 18e siècle. D’Alembert, Euler et Bernouilli se penchent tous trois sur le problème des
cordes vibrantes. L’équation de l’onde ainsi que les solutions analytiques de celle-ci sont
déterminées par D’Alembert. Bernouilli obtient les même réponses mais en ayant utilisé
un procédé tout à fait différent. Il présente ses solutions sous forme de décomposition en
séries pour superposer des solutions élémentaires. La controverse porte sur la nécessité de
concilier ces points de vue différents.
C’est alors que Fourier intervient.
A.2 Biographie
55

57. Joseph Fourier naît en 1768 à Auxerre. A 10 ans
il est orphelin. Il est interné dans un pensionnat.
L’évêque d’Auxerre le pousse aux études et Joseph
Fourier rentre à l’école militaire d’Auxerre tenue alors
par des Bénédictins. Il réussit brillamment et à l’age de
16 ans, il est déjà promu professeur de mathématiques
à l’école militaire d’Auxerre, ce qui lui permet de
commencer ses recherches personnelles. A 17 ans, il
rédige un mémoire sur les équations algébriques à
haut degré. Il lit notamment les 6 tomes du cours
de mathématiques de Bezout ainsi que l’intégralité de
l’œuvre de Alexis Claude Clairaut. 1 Il rentre ensuite
au séminaire, mais n’a pas vraiment de vocation. A 26
ans, il intègre la prestigieuse Ecole normale supérieure
Figure A.1 – Joseph Fourier. de Paris. Il y rencontre de nombreux mathématiciens
c Wikimedia renommés tels que Joseph-Louis Lagrange, Gaspard
Monge ou encore Pierre-Simon de Laplace. Mais
Joseph Fourier n’a pas que des ambitions mathématiques. Il participe à la révolution
de 1789 manquant de peu de se faire guillotiner durant le régime de la Terreur. Il occupe
ensuite plusieurs postes diplomatique importants en Égypte et en Isère. Alors préfet de
l’Isère, il s’intéresse à la théorie des probabilités. Il se pose notamment la question de savoir
quelle ampleur un sondage doit avoir pour être qualifié de fiable. En 1810, il retourne dans
le secteur académique pour devenir recteur de l’université de Grenoble. Il accumule les
titres honorifiques et devient notamment membre élu de l’Académie des sciences et de
l’Académie française. Il est également le précurseur de l’interprétation de l’effet de serre.
En 1822, il publie son œuvre majeure la théorie analytique de la chaleur. Il meurt en 1830
à Paris où il sera enterré au cimetière du Père Lachaise. Il fait partie des septante-deux
savants dont le nom est inscrit sur la Tour Eiffel.
A.3 Son oeuvre
Retournons à l’oeuvre de Fourier dans son contexte historique. Il introduit en 1803
l’équation de la chaleur dans un premier mémoire. Ces premiers travaux furent tellement
contestés sur le plan de l’analyse qu’ils ne furent pas publiés. Vingt ans plus tard, il expose
ses séries et sa transformation dans son traité Théorie analytique de la chaleur. Fourier
décompose une fonction mathématique unique, mais difficile à décrire mathématiquement,
1. Aspects de l’œuvre de Fourier : les transformées Jean-Pierre Demailly
56

58. en une somme infinie de fonctions en sinus et en cosinus. Il est alors plus facile de décrire
au cours du temps l’évolution de chacune de ces fonctions, et de retrouver la température
au temps t en refaisant la somme.
Cette hypothèse audacieuse est contestée par ses contemporains Laplace, Poisson et
Lagrange ; ce dernier se lève même en pleine séance de l’Institut des sciences et déclare
qu’il tient pour fausse la théorie de Fourier. Il faut dire que, même pour les critères
de rigueur de l’époque, les conclusions de Fourier étaient hardies. Par exemple, dans
un langage moderne, Fourier ne s’intéresse jamais à la convergence de ses séries. Pour les
anciens, ce qui les tracassait était plutôt le phénomène inverse : il leur semblait impossible
qu’une superposition, même infinie, de fonctions continues, puisse donner une fonction
discontinue.
En 1829, Dirichlet donne un premier énoncé correct de convergence limité aux fonctions
périodiques continues par morceaux ne possédant qu’un nombre fini de discontinuités.
Dirichlet considérait que les autres cas s’y ramenaient ; l’erreur sera corrigée par Jordan
en 1881. 2
En 1848, Wilbraham est le premier à mettre en évidence le phénomène de Gibbs en
s’intéressant au comportement des séries de Fourier au voisinage des points de discontinuité.
2. Wikipédia, http://fr.wikipedia.org/wiki/Serie_de_Fourier
57

59. Bibliographie
[1] Brad Osgood The Fourier Transform and Its Applications EE261 , The Fourier
transform is ubiquitous in engineering and science and this course is appropriate
for students from across the engineering and science disciplines. This course will
emphasize relating the theoretical principles to solving practical engineering and
science problems.
[2] Jean-Pierre Kahane et Pierre-Gilles Lemarié-Rieusset Séries de Fourier et ondelettes,
Cassini, 1998
[3] Wikipédia, l’encyclopédie libre http://tinyurl.com/633sda9
[4] MatLab Documentation Mathematical Programming Solutions
[5] Wolfram Documentation Mathematical and Programming Solutions
[6] Jean-Pierre Demailly Aspects de l’œuvre de Fourier : les transformées
[7] Wikipedia, the Free Encyclopedia Moore’s Law http://en.wikipedia.org/wiki/
Moore’s_law
[8] Wikipedia, the Free Encyclopedia Fourier’s Series, Transform, FTT, Cooley and
Tukey http://en.wikipedia.org/wiki/Fourier
[9] Vincent Thilliez Cours de Math 2e licence math sur les séries de Fourier
58