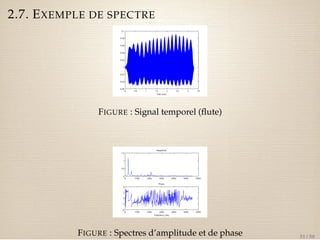
Le document traite des séries de Fourier, des transformées de Fourier et de la théorie des distributions, avec un accent sur l'analyse harmonique des fonctions périodiques et non périodiques. Il aborde également des concepts comme la convolution, l'impulsion de Dirac et les propriétés des spectres d'amplitude et de phase. Enfin, il illustre des applications pratiques et des résultats théoriques, notamment la formule de Parseval-Plancherel.

1. MA3 (GEII - S3)
B - REPRÉSENTATION DE FOURIER ET CONVOLUTION
F. Morain-Nicolier
frederic.nicolier@univ-reims.fr
2014 - 2015 / URCA - IUT Troyes
1 / 50

2. OUTLINE
1. SÉRIES DE FOURIER COMPLEXES
2. DES SÉRIES DE FOURIER AUX INTÉGRALES DE FOURIER
3. IMPULSION DE DIRAC ET DISTRIBUTIONS
4. PRODUIT DE CONVOLUTION
2 / 50

3. 1.1 RAPPELS SUR LES SÉRIES DE FOURIER
Fourier à découvert (comme Euler, Lagrange et Bernouilli
avant lui) qu’une fonction :
I définie sur R,
I à valeurs complexes,
I P-périodique,
I et suffisamment régulière ( ? ! ?)
peut-être synthétisée à l’aide de sinusoïdes (cosinus et sinus).
3 / 50

4. 1.1 RAPPELS SUR LES SÉRIES DE FOURIER
Le développement en série de Fourier (DSF) d’une telle
fonction f s’écrit :
f (t) = a0 +
¥å
n=1
(an cos(nwt) + bn sin(nwt))
I Les coefficients an et bn sont des constantes qui
caractérisent f .
I Cette équation est une équation de synthèse.
4 / 50

5. 1.1 RAPPELS SUR LES SÉRIES DE FOURIER
Les coefficients an et bn peuvent être obtenus à partir des
intégrales suivantes :
a0 =
1
P
Z P
0
f (t)dt,
an =
2
P
Z P
0
f (t) cos(nwt)dt,
bn =
2
P
Z P
0
f (t) sin(nwt)dt.
I Ce sont les équations d’analyse.
5 / 50

6. 1.1 RAPPELS SUR LES SÉRIES DE FOURIER
Le DSF d’une fonction périodique réelle
f (t) = a0 +
¥å
n=1
(an cos(nwt) + bn sin(nwt))
peut également s’écrire uniquement sous la forme d’une
somme de cosinus déphasés :
f (t) =
¥å
n=0
An cos(nwt + fn).
Il est alors possible de tracer deux graphes :
I le spectre d’amplitude An
I le spectre de phase fn
6 / 50

7. 1.1 RAPPELS SUR LES SÉRIES DE FOURIER
Chaque harmonique est donc caractérisée par :
I An un module et
I jn une phase.
) un nombre complexe
7 / 50

8. 1.2 FORME COMPLEXE DU DSF
Le développement en série de Fourier (DSF) d’une fonction
périodique réelle peut également s’écrire :
f (t) =
¥å
n=¥
cneinwt.
(cette équation s’obtient aisément à l’aide des formules d’Euler.
Voir exercice TD 1).
Les coefficients cn sont obtenus par :
cn =
1
P
Z P
0
f (t)einwtdt.
8 / 50

9. 1.2 FORME COMPLEXE DU DSF
Les coefficients complexes cn peuvent s’obtenir à l’aide des
coefficients réels :
cn =
an ibn
2
et
cn =
an + ibn
2
= cn.
I Nombre de coefficients ?
9 / 50

10. 1.2 FORME COMPLEXE DU DSF
QUESTION 1 1 - Par rapport aux coefficients an et bn, le nombre
de coefficients cn non redondants est :
1. plus grand
2. identique
3. plus petit
1. http://lc.cx/WJe
10 / 50

11. 1.3 SPECTRES
I Spectre d’amplitude jcnj (pair)
I Spectre de phase arg cn (impair) - (attention à l’obtention
de l’angle d’un complexe)
11 / 50

12. 1.4 PROPRIÉTÉS : TRANSLATION
En posant
g(t) = f (t a),
montrons que
cn[g] = cn[f ].einwa
et
jcn[g]j = jcn[f ]j.
12 / 50

13. 1.5 PROPRIÉTÉS : DILATATION
En posant
g(t) = f (lt),
montrons que
cn[g] = cn[f ].
I La dilatation n’a aucun effet sur les coefficients du DSF
d’une fonction.
13 / 50

14. 1.6 PROPRIÉTÉS : DÉRIVATION
En posant
g(t) = f 0(t),
montrons que
cn[g] = inwcn[f ].
14 / 50

15. 1.7 FORMULE DE PARSEVAL-PLANCHEREL
En S2, nous avons montré que
1
P
Z P
0
f 2(t)dt = a20+
¥å
k=1
(a2
n + b2
n).
Ce qui, avec des coefficients complexes, s’écrit :
1
P
Z P
0
f 2(t)dt =
¥å
k=¥
c2
n.
) L’énergie totale d’un signal ne dépend pas de la
représentation choisie.
15 / 50

16. OUTLINE
1. SÉRIES DE FOURIER COMPLEXES
2. DES SÉRIES DE FOURIER AUX INTÉGRALES DE FOURIER
3. IMPULSION DE DIRAC ET DISTRIBUTIONS
4. PRODUIT DE CONVOLUTION
16 / 50

17. 2. DES SÉRIES DE FOURIER AUX INTÉGRALES DE
FOURIER
I DSF : Analyse harmonique (fonction périodiques)
I TF : généralisation aux fonctions non-périodiques
17 / 50

18. 2.1. EN PREMIÈRE APPROCHE
18 / 50

19. 2.1. EN PREMIÈRE APPROCHE
I Toutes les fréquences sont présentes dans le spectre
d’une fonction non-périodique
19 / 50

20. 2.2. OBTENTION DES INTÉGRALES DE LA TF
20 / 50

21. 2.2. OBTENTION DES INTÉGRALES DE LA TF
I Équation de synthèse :
f (t) =
1
2p
Z ¥
¥
F(w)eiwtdw.
I Équation d’analyse
F(w) =
Z ¥
¥
f (t)eiwtdt.
21 / 50

22. 2.2. OBTENTION DES INTÉGRALES DE LA TF
I Équation de synthèse :
f (t) =
1
2p
Z ¥
¥
F(w)eiwtdw.
I Équation d’analyse
F(w) =
Z ¥
¥
f (t)eiwtdt.
Pour mémoire, pour une fonction périodique :
f (t) =
¥å
n=¥
cneinwt
et
cn =
1
T
Z
T
f (t)einwtdt.
I Les propriétés du DSF sont (en général) retrouvée avec la
TF.
22 / 50

23. 2.3. DIVERSES RÉPARTITIONS DE LA CONSTANTE
I La constante 2p peut se répartir différemment entre les
deux équations, selon la communauté.
23 / 50

24. 2.4. EXISTENCE
F(w) =
Z ¥
¥
f (t)eiwtdt.
24 / 50

25. 2.4. EXISTENCE
F(w) =
Z ¥
¥
f (t)eiwtdt.
Pour que F(w) existe, il faut que
lim
x!¥
f (x) = 0.
C’est une condition très restrictive !
25 / 50

26. 2.5. CONVERGENCE
26 / 50

27. 2.5. CONVERGENCE
Si f (t) est absolument intégrable sur R, sa représentation
fréquentielle converge vers
f (t+) + f (t)
2
, 8x 2 R.
I La représentation fréquentielle de f (t) converge donc vers
f (t) si f (t) est continue.
27 / 50

28. 2.6. UN EXEMPLE : CRÉNEAU RECTANGULAIRE
SYMÉTRIQUE
Soit c défini par
c(x) =
(
A si jxj t
0 sinon.
I Cherchons sa transformée de Fourier
28 / 50

29. 2.6. UN EXEMPLE : CRÉNEAU RECTANGULAIRE
SYMÉTRIQUE
Soit c défini par
c(x) =
(
A si jxj t
0 sinon.
Sa représentation fréquentielle est
C(w) =
2A
w
sin(wt).
29 / 50

30. 2.7. SPECTRES
De façon analogue au DSF, les spectres sont donnés par :
I spectre d’amplitude : jF(w)j
I spectre de phase : arg F(w)
I le spectre d’énérgie jF(w)j2 donne la répartition de
l’énergie en fonction de w.
30 / 50

31. 2.7. EXEMPLE DE SPECTRE
FIGURE : Signal temporel (flute)
FIGURE : Spectres d’amplitude et de phase 31 / 50

32. 2.7. EXEMPLE DE SPECTRE
QUESTION 2 2 - Qui contient le plus d’information sur le
signal ?
1. Le spectre d’amplitude
2. Le spectre de phase
3. L’un autant que l’autre
2. http://lc.cx/WJe
32 / 50

33. 2.7. MANIPULATION SONORE
33 / 50

34. 2.7. EXEMPLE : SPECTRE D’ÉNERGIE DU CRÉNEAU DE
LARGEUR 2t
Soit c défini par
c(x) =
(
A si jxj t
0 sinon.
Sa représentation fréquentielle est
C(w) =
2A
w
sin(wt).
I Cherchons (et représentons) jF(w)j2.
34 / 50

35. 2.8. RELATION D’INDÉTERMINATION
I Relation d’indétermination ou d’incertitude (cf.
Heisenberg) :
Dt.Dn = Cte
I Plus un signal est court temporellement, plus sa représentation
fréquentielle est large.
I exemple : notes de musique.
35 / 50

36. 2.9. THÉORÊME DE PARSEVAL-PLANCHEREL
L’énergie de la fonction f :
Z ¥
¥
jf (t)j2dt
peut être calculée dans le domaine fréquentiel :
Z ¥
¥
jf (t)j2dt =
1
2p
Z ¥
¥
jF(w)j2dw.
36 / 50

37. OUTLINE
1. SÉRIES DE FOURIER COMPLEXES
2. DES SÉRIES DE FOURIER AUX INTÉGRALES DE FOURIER
3. IMPULSION DE DIRAC ET DISTRIBUTIONS
4. PRODUIT DE CONVOLUTION
37 / 50

38. 3.1. UN CRÉNEAU PARTICULIER : L’IMPULSION DE
DIRAC
38 / 50

39. 3.1. UN CRÉNEAU PARTICULIER : L’IMPULSION DE
DIRAC
d(t) vérifie :
i) 8t, d(t) 0
ii) d(t) = 0 si t6= 0
iii)
R
R d(t)dt = 1
QUESTION 3 3 - l’objet mathématique d (impulsion de dirac)
est-il une fonction ?
1. oui
2. non
3. http://lc.cx/WJe
39 / 50

40. 3.1. UN CRÉNEAU PARTICULIER : L’IMPULSION DE
DIRAC
Les théoriciens de la physique des particules vers 1920–30
(dont Paul Dirac, 1902–1984), on introduit la “fonction” d(t)
vérifiant “de gré ou de force” :
8
:
d(t) = 0 si t6= 0
dR(t) = ¥ si t = 0
R d(t)dt = 1.
I Représentation graphiquement
I Formalisme facilement exploitable
40 / 50

41. 3.2. EXEMPLE : CALCUL DE L’INTÉGRALE DU PRODUIT
D’UN DIRAC ET D’UNE FONCTION
41 / 50

42. 3.3. DÉRIVATION “NEW LOOK”
42 / 50

43. 3.3. DÉRIVATION “NEW LOOK”
I 1946 : proposition d’une théorie complète (théorie des
distributions) par Laurent Schwartz (1915 - 2002)
43 / 50

44. OUTLINE
1. SÉRIES DE FOURIER COMPLEXES
2. DES SÉRIES DE FOURIER AUX INTÉGRALES DE FOURIER
3. IMPULSION DE DIRAC ET DISTRIBUTIONS
4. PRODUIT DE CONVOLUTION
44 / 50

45. 4.1. CELLULE RC
R
i(t)
x(t) C v(t)
FIGURE : Circuit RC
Ri(t) + v(t) = x(t)
i = C
dv
dt
) RCv0(t) + v(t) = x(t)
Montrons que
v(t) =
1
RC
Z t
¥
ets
RC x(s)dt
45 / 50

46. 4.1. CELLULE RC : EXPRESSION DE LA SORTIE
En posant
h(t) =
1
RC
e t
RC u(t),
u(t) étant l’échelon de Heaviside, la sortie v(t) peut s’écrire
sous la forme
v(t) =
Z +¥
¥
h(t s)u(s)ds.
46 / 50

47. 4.2. DÉFINITION DU PRODUIT DE CONVOLUTION
La convolution de deux fonctions f et g est une fonction notée
f g et définie par
(f g)(t) =
Z +¥
¥
f (t u)g(u)du.
47 / 50

48. 4.3. UNE DÉFINITION “MANUELLE”
48 / 50

49. 4.4. PROPRIÉTÉS DU PRODUIT DE CONVOLUTION
(f g)(t) =
Z +¥
¥
f (t u)g(u)du.
I Commutativité :
(f g)(t) = (g f )(t)
I Associativité :
f (g h) = (f g) h
I Distributivité :
f (g + h) = f g + f h
I Élément neutre d :
f d = d f = f
49 / 50

50. 4.4. THÉORÈME DE CONVOLUTION
Montrons que
TF[f g] = TF[f ].TF[g]
50 / 50