Téléchargé 94 fois
Téléchargé parMoussa Maarouf
09 lignes d'influence
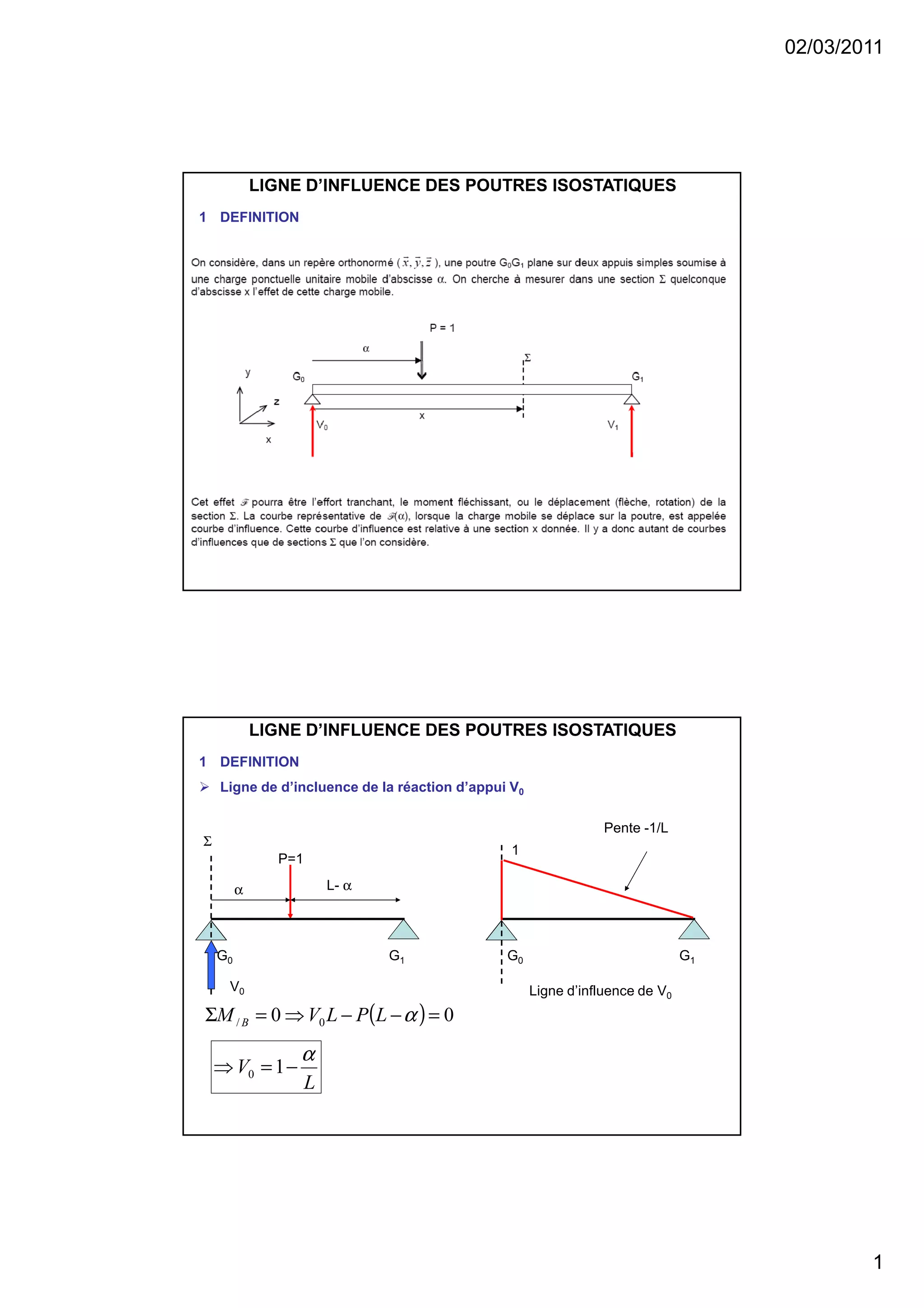
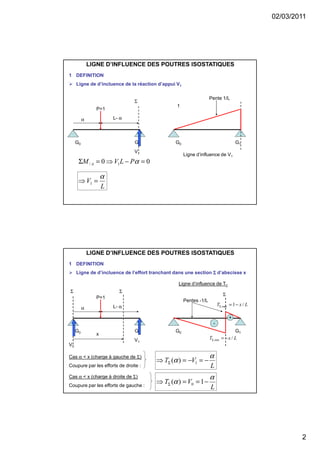
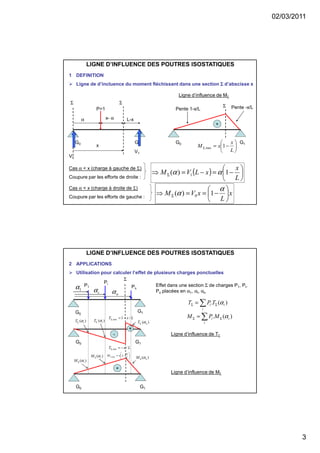
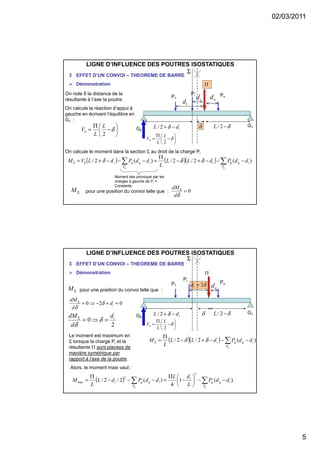
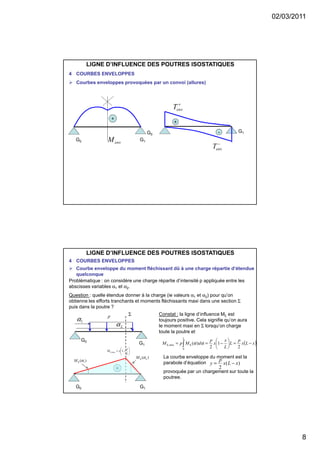
Le document traite des lignes d'influence pour les poutres isostatiques, en expliquant leur définition et leur utilisation pour déterminer les efforts internes, tels que les efforts tranchants et les moments fléchissants, en fonction des charges ponctuelles ou distribuées. Il décrit également le théorème de barre lié aux convois de charges et les courbes enveloppes des effets maximaux sur une poutre. Les applications pratiques et les calculs associés sont illustrés par des exemples spécifiques et des démonstrations mathématiques.
09 lignes d'influence
- 1. 02/03/2011 1 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 1 DEFINITION LIGNE D’INFLUENCE DES POUTRES ISOSTATIQUES 1 DEFINITION Ligne de d’incluence de la réaction d’appui V0 G0 G1 P=1 Σ α L- α ( ) 00 0/ =−−⇒=Σ αLPLVM B L V α −=⇒ 10 G0 G1 1 Ligne d’influence de V0 Pente -1/L V0
- 2. 02/03/2011 2 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 1 DEFINITION Ligne de d’incluence de la réaction d’appui V1 G0 G1 P=1 Σ α L- α 00 1/ =−⇒=Σ αPLVM A L V α =⇒ 1 G0 G1 1 Ligne d’influence de V1 Pente 1/L V1 LIGNE D’INFLUENCE DES POUTRES ISOSTATIQUES 1 DEFINITION Ligne de d’incluence de l’effort tranchant dans une section ΣΣΣΣ d’abscisse x G0 G1 P=1 Σ α L- α L VT α α −=−=⇒ Σ 1)( G0 G1 Ligne d’influence de TΣ Pentes -1/L V1 Σ x V0 Cas α < x (charge à gauche de Σ) Coupure par les efforts de droite : L VT α α −==⇒ Σ 1)( 0 Cas α < x (charge à droite de Σ) Coupure par les efforts de gauche : LxT /min, −=Σ LxT /1max, −=Σ - + Σ
- 3. 02/03/2011 3 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 1 DEFINITION Ligne de d’incluence du moment fléchissant dans une section ΣΣΣΣ d’abscisse x G0 G1 P=1 Σ α ( ) −=−=⇒ Σ L x xLVM 1)( 1 αα G0 G1 Ligne d’influence de MΣ Pente 1-x/L V1 Σ x V0 Cas α < x (charge à gauche de Σ) Coupure par les efforts de droite : x L xVM −==⇒ Σ α α 1)( 0 Cas α < x (charge à droite de Σ) Coupure par les efforts de gauche : −=Σ L x xM 1max, + Σ x- α L-x Pente -x/L LIGNE D’INFLUENCE DES POUTRES ISOSTATIQUES 2 APPLICATIONS Utilisation pour calculer l’effet de plusieurs charges ponctuelles Ligne d’influence de MΣ G0 G1 −=Σ L x xM 1max, + G0 G1 LxT /min, −=Σ LxT /1max, −=Σ - + Σ G0 G1 1α P1 Pi iα nα Pn )( 1αΣT )( iT αΣ )( nT αΣ )( 1αΣM )( iM αΣ )( nM αΣ Ligne d’influence de TΣ Effet dans une section Σ de charges P1, Pi, Pn placées en α1, αi, αn ∑ ΣΣ = i ii TPT )(. α ∑ ΣΣ = i ii MPM )(. α
- 4. 02/03/2011 4 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 2 APPLICATIONS Utilisation pour calculer l’effet d’une charge répartie quelconque G0 G1 −=Σ L x xM 1max, + G0 G1 LxT /min, −=Σ LxT /1max, −=Σ - + Σ G0 G1 0α α 1α )( 0αΣT )(αΣT )( 1αΣT )( 0αΣM )(αΣM )( 1αΣM Effet dans une section Σ d’une charge répartie quelconque p(α) entre les abscisses α0 et α1 ∫ ΣΣ = 1 0 )().( α α ααα dTpT )(αp ∫ ΣΣ = 1 0 )().( α α ααα dMpM Si p est constant, TΣ correspond à p x l’aire délimitée par la courbe TΣ (α) entre α0 et α1 Si p est constant, MΣ correspond à p x l’aire délimitée par la courbe MΣ (α) α0 et α1 LIGNE D’INFLUENCE DES POUTRES ISOSTATIQUES 3 EFFET D’UN CONVOI – THEOREME DE BARRE Définition Un convoi est un ensemble de charges Pi dont les distances entre elles restent fixes (exemples : camions, trains). Le convoi peut être caractérisé par sa résultante La position de chaque charge Pi peut être caractérisée par sa distance di à la résultante Π Pn Π 1d P1 Pi id nd ∑=Π iP Objectif L’objectif est de déterminer la position du convoi qui donne le moment fléchissant maximal dans la poutre sur 2 appuis simples que parcourt le convoi et la valeur de ce moment maximal.
- 5. 02/03/2011 5 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 3 EFFET D’UN CONVOI – THEOREME DE BARRE Démonstration − Π = δ 2 0 L L V On note δ la distance de la résultante à l’axe la poutre. On calcule la réaction d’appui à gauche en écrivant l’équilibre en G1 : Pn Π 1d P1 Pi id nd δ δ−2/LidL −+δ2/ Σ G0 G1 − Π = δ 2 0 L L V On calcule le moment dans la section Σ au droit de la charge Pi ( ) ( )( ) )(2/2/)(2/0 ig P giig P gi ddPdLL L ddPdLVM gg −−−+− Π =−−−+= ∑∑Σ δδδ Moment des provoqué par les charges à gauche de Pi = Constante ΣM pour une position du convoi telle que : 0=Σ δd dM LIGNE D’INFLUENCE DES POUTRES ISOSTATIQUES 3 EFFET D’UN CONVOI – THEOREME DE BARRE Démonstration − Π = δ 2 0 L L V Pn Π P1 Pi δ2=id nd δ δ−2/LidL −+δ2/ Σ G0 G1 ΣM pour une position du convoi telle que : 020 =+−⇒=Σ id d dM δ δ ( )( ) )(2/2/ ig P gi ddPdLL L M g −−−+− Π = ∑Σ δδ 2 0 id d dM =⇒=Σ δ δ Le moment est maximum en Σ lorsque la charge Pi et la résultante Π sont placées de manière symétrique par rapport à l’axe de la poutre. Alors, le moment maxi vaut : ( ) )(1 4 )(2/2/ 2 2 max ig P g i ig P gi ddP L dL ddPdL L M gg −− − Π =−−− Π = ∑∑
- 6. 02/03/2011 6 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 3 EFFET D’UN CONVOI – THEOREME DE BARRE Exemples de convois (EC1-3) Convois routiers Convoi ferroviaire UIC 71 Depends on judgement of designer. ~400mm Maximum moment occurrs here 1.8m 1.0m 1.0m 1.0m 1.8m 1.5m 1.5m 3.0m cL of HB cL of bridge 1.0m 1.0m 1.0m cL of bridge A A Section A-A Position of HB Load to produce Maximum Moment LIGNE D’INFLUENCE DES POUTRES ISOSTATIQUES 3 EFFET D’UN CONVOI – THEOREME DE BARRE Exemples de convois (BS)
- 7. 02/03/2011 7 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 4 COURBES ENVELOPPES Définition La courbe enveloppe de l’effet F est la courbe des effets maximaux dans l’ensemble des sections Σ de la poutre lorsque la charge P=1 mobile évolue sur la poutre (ie c’est la courbe des maximums des lignes d’influence). Courbe enveloppe du moment fléchissant dû a une charge ponctuelle G0 G1 Ligne d’influence de MΣ Pente 1-x/L −=Σ L x xM 1max, + Σ Pente -x/L Dans une section Σ d’abscisse x, le moment maximum en Σ vaut : −=Σ L x xM 1max, La courbe enveloppe du moment fléchissant provoqué par P=1 est donc une parabole d’équation : . Le maximum de la courbe enveloppe donne le moment maximum absolu dans la poutre. −= L x xMenv 1 G0 G1 4 max, L Menv = + Enveloppe des moments fléchissants LIGNE D’INFLUENCE DES POUTRES ISOSTATIQUES 4 COURBES ENVELOPPES Courbe enveloppe de l’effort tranchant dû à une charge ponctuelle Ligne d’influence de TΣ Enveloppe des efforts tranchants positifs G0 G1 Pentes -1/L LxT /min, −=Σ LxT /1max, −=Σ - + G0 G1 LxTenv /1−=+ + G0 G1 LxTenv /−=− - Enveloppe des efforts tranchants négatifs 2 courbes enveloppes : -Courbe enveloppe des efforts tranchants positifs : - Courbe enveloppe des efforts tranchants négatifs 1max −=− T 1max =+ TLxTenv /1−=+ LxTenv /−=+ 1 -1
- 8. 02/03/2011 8 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 4 COURBES ENVELOPPES Courbes enveloppes provoquées par un convoi (allures) G0 G1envM + G0 - − envT G1 + + envT LIGNE D’INFLUENCE DES POUTRES ISOSTATIQUES 4 COURBES ENVELOPPES Courbe enveloppe du moment fléchissant dû à une charge répartie d’étendue quelconque Problématique : on considère une charge répartie d’intensité p appliquée entre les abscisses variables α1 et α2. Question : quelle étendue donner à la charge (ie valeurs α1 et α2) pour qu’on obtienne les efforts tranchants et moments fléchissants maxi dans une section Σ puis dans la poutre ? G0 G1 1α 2α p G0 G1 −=Σ L x xM 1max, + )( 1αΣM )( nM αΣ Σ Constat : la ligne d’influence MΣ est toujours positive. Cela signifie qu’on aura le moment maxi en Σ lorsqu’on charge toute la poutre et ( )xLx p L L x x p dMpM L −= −== ∫ ΣΣ 2 1 2 )( 0 max, αα La courbe enveloppe du moment est la parabole d’équation provoquée par un chargement sur toute la poutree. )( 2 xLx p y −=
- 9. 02/03/2011 9 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 4 COURBES ENVELOPPES Courbe enveloppe de l’effort tranchant T+ dû à une charge répartie d’étendue quelconque G0 G1 1α 2α p Σ Constat : la ligne d’influence TΣ est positive si on applique une charge à droite de Σ. Cela signifie qu’on aura l’effort TΣ+ maxi en Σ lorsqu’on charge toute la poutre à droite de Σ et ( ) ( )2 max, 2 1 2 )( xL L p xL L xp dTpT L x −=− −== ∫ Σ + Σ αα La courbe enveloppe du moment est la parabole d’équation : 2 )( 2 xL L p Tenv −=+ G0 G1 LxT /min, −=Σ LxT /1max, −=Σ - + )( 1αΣT )( 2αΣT G0 ( )2 2 xL L p Tenv −=+ + 2 max, pL Tenv =+ G1 LIGNE D’INFLUENCE DES POUTRES ISOSTATIQUES 4 COURBES ENVELOPPES Courbe enveloppe de l’effort tranchant T- dû à une charge répartie d’étendue quelconque G0 G1 1α 2α p Σ Constat : la ligne d’influence TΣ est négative si on applique une charge à gauche de Σ. Cela signifie qu’on aura l’effort TΣ- maxi en Σ lorsqu’on charge toute la poutre à gauche de Σ et 2 0 max, 22 )( x L p x L xp dTpT x −= −== ∫ Σ − Σ αα La courbe enveloppe du moment est la parabole d’équation : 2 2 x L p Tenv −=− G0 G1 LxT /min, −=Σ LxT /1max, −=Σ - + )( 1αΣT )( 2αΣT G0 2 2 x L p Tenv −=− - 2 max, pL Tenv −=− G1
- 10. 02/03/2011 10 LIGNE D’INFLUENCE DESPOUTRES ISOSTATIQUES 4 COURBES ENVELOPPES Courbes enveloppes de l’effort tranchant dû à une charge répartie d’étendue quelconque On remarquera que, contrairement au moment fléhissant, on n’obtient pas les effets maximaux de T en chargeant la poutre sur toute la longueur, mais en la chargeant en partie (à droite ou à gauche). En particulier, au milieu de la poutre : 82 pLL Tenv = + 82 pLL Tenv −= − G0 2 2 x L p Tenv −=− - 2 max, pL Tenv −=− G1 + ( )2 2 xL L p Tenv −=+ 2 max, pL Tenv =+ obtenu par le chargement de la moitié gauche obtenu par le chargement de la moitié droite Alors que si l’on charge toute la poutre, 0 2 = L T