Le document est un polycopié du tutorat associatif toulousain pour l'année universitaire 2010-2011, fournissant des compléments de cours sur la physique, notamment la mécanique quantique, les interactions fondamentales et la thermodynamique. Il explique les concepts de quantification de l'énergie, d'opérateurs en mécanique quantique, ainsi que l'indiscernabilité des particules et les relations d'indétermination de Heisenberg. L'ensemble vise à aider les étudiants à mieux comprendre les bases de la biophysique et des méthodes d'exploration des systèmes.

1. Tutorat Associatif Toulousain
Année universitaire 2010-2011
PACES
UE 3 : Organisation des appareils et systèmes : bases
physiques des méthodes d'exploration – aspects
fonctionnels
Biophysique
Commentaires de cours et QCM
Partenaire du Tutorat Associatif Toulousain
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 1

2. Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 2

3. ATTENTION
Ce polycopié a été relu sur la base des cours dispensés à
la faculté de Rangueil pour l'année 2009-2010.
Cependant, suite à la réforme de la PACES, le
programme de Biologie Cellulaire a été allégé. Par
conséquent, certains éléments présents dans ce polycopié
peuvent ne plus être d'actualité.
A vous de trier parmi les différents items proposés ceux
qui restent en accord avec les cours dispensés par mesdames
et messieurs les professeurs.
N'hésitez pas à signaler toutes les erreurs éventuelles
ou remarques concernant ce polycopié sur tutoweb dans la
rubrique « Forum polycopiés » ou lors de l'une des
permanences du tutorat.
En aucun cas le contenu de ce polycopié ne
pourra engager la responsabilité de la faculté de
médecine ou de mesdames et messieurs les
professeurs.
Ce polycopié a été réalisé par :
Elise Birague-Cavallie, Djaouad Berkach
Salim Kanoun, Jean Christophe Lecomte
Marine Weyl, Romain Dupont
Florent Ginestet
Compilé par Guillaume Gilbert
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 3

4. Sommaire
Compléments au cours de Physique du noyau
I - Notions de mécanique quantique Page 6
II - Les interactions fondamentales Page 14
III - Stabilité du noyau Page 20
IV - Instabilité du noyau Page 32
Formulaire Page 49
Correction détaillée de certains exercices du
polycopié du Dr Victor Page 53
Thermodynamique : Fiches Page 69
Chapitre 1 : Forces, Vecteurs, Travaux
Chapitre 2 : Température, Chaleur
Chapitre 3 : 1er principe
Chapitre 4 : 2nd principe
Entraînement aux QCM : Page 111
Chapitre 1 : Forces, Vecteurs, Travaux
Chapitre 2 : Température, Chaleur
Chapitre 3 : Transformations thermodynamiques
Chapitre 4 : Calculs de l’évolution des systèmes
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 4

5. Compléments au cours
de Physique du noyau
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 5

6. I - Notions de mécanique quantique
Introduction:
La mécanique quantique va remplacer la mécanique classique à l’échelle des objets
très petits (de l'ordre de grandeur du nanomètre) ou hyperdenses (trou noir…).
Pourquoi une autre théorie de la mécanique ? Parce qu’on observe dans ces
conditions des phénomènes qui ne répondent à aucune loi de la théorie classique:
quantification de l’énergie, aspect corpusculaire et ondulatoire des particules
élémentaires.
En effet, des expériences sur la lumière mettent en évidence l'apect corpusculaire de
la lumière, qui serait composée de photons, en plus de son aspect ondulatoire. Cette
dualité va à l'encontre de la physique classique qui ne considère la lumière que comme
une onde.
D'autre part, l'énergie au sein de l'atome, et par exemple l'énergie des électrons, ne
prend que des valeurs bien précises: c'est l'idée de la quantification, opposée à l'idée du
continuum d'énergie de la physique classique.
Rappel : p est une variable qu'on ne voit plus au lycée, qui représente la quantité de
mouvement. p=mv.
1 - Hypothèse fondamentale de la mécanique ondulatoire :
1.1 Hypothèse de Maxwell:
La physique classique connaissait l'aspect ondulatoire de la lumière. On associait à
une onde de fréquence υ une énergie E telle que E = h . υ, h étant la constante de
Planck.
L’hypothèse de Maxwell est la suivante : la lumière présente aussi un aspect
corpusculaire, elle est composée de « grains » appelés photons. Par conséquent, on
peut attribuer à chaque photon une quantité de mouvement p et une énergie E telle que
E = p . c, c étant la vitesse de la lumière dans le vide.
L’équation E=h.υ était connue, E=p.c venait d’être postulée.
Par λ=c/υ , on trouve υ=E/h et λ=h/p
υ et λ sont des paramètres que l’on associe à une onde, et E et p sont des paramètres
que l’on associe à une particule.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 6

7. Or par ces relations, ces paramètres corpusculaires et ondulatoires sont liés, et par
quoi ? Par la constante de Planck, qui est LA constante de la mécanique quantique.
On dit que c’est la constante unificatrice de (p, E) qui correspond à l’aspect
corpusculaire, et de (λ, υ) qui correspond à l’aspect ondulatoire.
h = 6,62 . 10 -34 J.s
1.2 Hypothèse de Louis de Broglie:
Louis de Broglie émet l’hypothèse que ces relations s’appliquent à toute matière et
associe à une particule d’énergie E = ½ . m . v2 et p = m . v , une onde de fréquence υ
= E / h et de longueur d’onde λ = h / p.
En liant ces relations par une démonstration que vous n’avez pas besoin de savoir
(sauf si ça vous aide à retrouver la formule), on obtient : p = √2 m E.
C'est-à-dire que si on vous demande la quantité de mouvement d’une particule de
masse m et d’énergie E, vous utiliserez cette formule et non p = m . v. En fait, la
formule p = √2 m E est une formule plus générale que la formule p = m . v, c'est
pourquoi il faut utiliser p = √2 m E systématiquement.
Faites bien attention à utiliser les bonnes unités: la masse m en kg (et non en u),
l'énergie E en J (et non en eV).
De plus, il faut noter que lorsqu'on a affaire à une particule, on n'utilise pas la
formule de l'onde: λ = c / υ mais seulement les deux relations fondamentales de la
mécanique quantique: λ = h / p et υ = E / h.
Remarque :
Une autre petite chose à savoir : la manifestation de l’aspect ondulatoire correspond à
une question d’échelle ; on peut dire que toute particule possède une onde associée
(comme le postule de Broglie) mais celle-ci ne se manifeste que si la longueur d’onde
λ est de l’ordre de grandeur de l’environnement.
Exemple :
Une balle de tennis a une longueur d’onde de 10-34 m alors que son environnement est
de l’ordre du mètre : elle manifeste seulement son aspect corpusculaire, mais elle
pourrait manifester son aspect ondulatoire si son environnement était de l’ordre de 10-
34
m.
En revanche, un électron a un environnement de la taille du Fermi, et sa longueur
d'onde associée est aussi de cet ordre de grandeur: il peut donc manifester son aspect
corpusculaire ou ondulatoire.
Pour une particule, exprimer son aspect corpusculaire n’est pas un problème ; par
contre, l’expression de l’aspect ondulatoire sera limitée par la valeur de λ.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 7

8. Si une particule peut manifester les deux aspects, elle ne pourra pas exprimer les
deux simultanément: cela dépendra des conditions d’observation. Seul un des deux
aspects sera observé à un instant t. Nous y reviendrons avec les relations
d'indétermination de Heisenberg.
2 - Notion d’opérateur :
Un opérateur est une expression mathématique qui traduit l’opération que l’on doit
effectuer sur une fonction. De la même façon qu'une fonction quelconque peut etre
notée f, un opérateur quelconque est noté Ô.
Exemples :
▪ L’opérateur d / dx , appliqué à une fonction f, indique que l’on doit dériver
la fonction par rapport à x.
▪ L’opérateur ∫ indique que l’on doit intégrer la fonction.
Si après l’application d’un opérateur Ô à une fonction u, cette fonction reste
inchangée à un facteur multiplicateur λ près, on dit que u est fonction propre de
l’opérateur Ô (ce dernier peut lui être appliqué sans qu’elle ne change).
On obtient ainsi l’équation suivante, qui est l’équation aux valeurs propres de
l’opérateur Ô :
Ôu = λ u
On dit que λ est la valeur propre associée à la fonction propre u de l’opérateur Ô.
L'ensemble des valeurs que peut prendre λ est appelé le spectre de l'opérateur. Le
spectre peut-etre continu ou discret. L'ensemble [0; + ∞ [ est un spectre continu.
L'ensemble {0, 1, 2, 3} est un spectre discret.
Exemple 1: d2 (sin kx) = - k2 (sin kx)
dx2
▪ sin x est la fonction propre de l’opérateur d2/dx2 : elle est inchangée à une
constante près, après application de cet opérateur.
▪ - k2 est la valeur propre associée à la fonction propre de l’opérateur d2 / dx². Le
spectre de l'opérateur est R, c'est un spectre continu.
Exemple 2: d exp (kx) = k . exp(kx)
dx
▪ exp(kx) est la fonction propre de l'opérateur d/dx: elle est inchangée à une
constante près, après application de cet opérateur.
▪ k est la valeur propre associée à la fonction propre de l’opérateur d / dx . Le
spectre l'opérateur est R, c'est un spectre continu.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 8

9. Exemple 3: │kx2n│ = kx 2n
▪ kx 2n est la fonction propre de l'opérateur valeur absolue. Elle est inchangée à
une constante près, après application de cet opérateur.
▪ k est la valeur propre associée à la fonction propre de l’opérateur valeur
absolue. Le spectre de l'opérateur est R+, c'est un spectre continu.
Exemple 4: l’opérateur dont la température absolue (exprimée en Kelvin) est la
fonction propre a fait apparaître un spectre continu de valeurs uniquement positives.
3 - Postulat de la mécanique quantique, système en état
stationnaire :
Tout ce que l’on connaît d’un système de particules, c’est sa fonction d’onde Ψ , qui
n’a aucune signification physique. Lorsqu’on élève son module au carré, elle
représente la probabilité de présence du système de particule autour d’un point x
à un instant t.
On a cherché l’opérateur dont Ψ serait la fonction propre : il s’agit de l’Hamiltonien
que l’on note Ĥ. (ce que vous découvrez à travers la démonstration du Dr Victor dans
son cours)
Appliquer cet opérateur à une fonction équivaut à multiplier la dérivée de cette
−h −h d
fonction par 2 i  . On peut écrire Ĥ =  2 i ∗ dt 
−h du
On a : Ĥ u= ∗ 
2 i  dt
Cette équation n'est pas l'équation aux valeurs propres de l'opérateur Ĥ, il s'agit
seulement de la réécriture de Ĥ u qui explicite Ĥ.
Si on applique Ĥ à Ψ, on a : Ĥ Ψ = E Ψ (même modèle qu’avec l’opérateur Ô et
la fonction u). On obtient cette fois l'équation aux valeurs propres de H. E désigne
l’ensemble des valeurs propres associées à la fonction d’onde Ψ.
Que voit-on ? E correspond à un spectre discret de valeurs énergétiques : on a ainsi
une énergie quantifiée à l’échelle quantique ! On retrouve cette notion de
quantification en chimie. En effet, en chimie, on apprend que chaque électron
appartenant à une case quantique a une énergie bien précise. Chaque case quantique
correspond à une orbitale, c'est à dire à un certain volume autour du noyau dans lequel
on a 99% de chances de trouver l'électron en question. L'orbitale est définie grâce au
module de la fonction d'onde élevée au carré; par conséquent, l'énergie de l'électron
appartenant à cette orbitale sera bien définie.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 9

10. La quantification est associée à la notion d’opérateur : la fonction d’onde Ψ n’est
définie que pour les valeurs propres E qui correspondent aux seuls états énergétiques
possibles du système.
4 - Indiscernabilité des particules :
A l’échelle de la mécanique classique, les particules sont considérées comme
discernables.
A l'échelle de la mécanique quantique, les particules sont considérés comme
indiscernables. Par exemple, prenons deux électrons e−1 ou un e−2, qui font partie du
cortège électronique d'un atome quelconque, et qui appartiennent à deux cases
quantiques différentes. Ces deux particules sont strictement identiques, à l'exception de
leur position, qui, d'après le postulat de la mécanique quantique, n'est définie que par
une probabilité de présence. On considère ces deux électrons ensemble, comme un
système de deux électrons. On définit donc la position des deux électrons considérés
ensemble; celle-ci est définie comme une probabilité de présence. Intervertir l'électron
e-1 avec l'électron e-2 ne change en rien la situation physique: le système de deux
électrons est identique, la position des deux électrons considérés ensemble n'a pas
changé. Les deux électrons sont donc indiscernables.
Cette situation se traduit par l’égalité suivante :
| Ψ (1,2) |2 = | Ψ (2,1) |2
Pour satisfaire cette hypothèse d’indiscernabilité, il y a deux solutions :
| Ψ (1,2) | = | Ψ (2,1) | la fonction d’onde sera la même → symétrique
| Ψ (1,2) | = − | Ψ (2,1) | la fonction d’onde sera opposée → antisymétrique (si
deux particules sont échangées, le signe de la fonction d’onde est changée)
(Il ne faut pas chercher à vous le représenter, on a dit que Ψ n’avait pas de
signification physique)
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 10

11. Cela va permettre de distinguer deux types de particules selon les propriétés de leur
fonction d’onde :
Fonction d’onde symétrique : Fonction d’onde antisymétrique :
Ces particules obéissent à la loi de Bose- Ces particules obéissent à la loi de
Einstein. Fermi-Dirac.
Ce sont des bosons. Ce sont des fermions.
Leur spin est entier ou nul. Leur spin est à ½ entier.
Exemple : photons, mésons, noyaux avec Exemple : nucléons, électrons, noyaux
un A pair… avec un A impair…
Ils peuvent se trouver dans le même état Ils ne peuvent pas se trouver dans le même
(laser, superfluidité de l’He…). état (principe d’exclusion de Pauli).
Quand on vous parle de noyaux A pair ou impair, il s’agit bien de noyaux et non de
l’atome en entier !
Exemple : le 12C n’a pas de propriétés quantiques, MAIS le noyau lui-même,
séparés de ses électrons, oui (comme la particule α qui est un noyau d’He).
5 - Relations d’indétermination d’Heisenberg :
Δp . Δx ≥ ħ
Cette relation montre que la quantité de mouvement et la position d’une particule
quantique ne sont pas indépendantes l’une de l’autre : si une particule bouge beaucoup,
on pourra toujours calculer sa quantité de mouvement ; par contre, pour savoir où elle
est…
De même, si une particule reste immobile, il sera très difficile de connaître sa
quantité de mouvement (comme elle ne fait pas la course, on ne peut pas la
chronométrer). Par contre on sait avec précision où elle est (toujours sur la ligne de
départ).
Δp et Δx peuvent etre compris comme, respectivement, la dispersion des mesures
sur la quantité de mouvement, et la dispersion des mesures sur la position.
On pourrait énoncer la relation de cette façon: « la dispersion des mesures sur la
quantité de mouvement multipliée par la dispersion des mesures sur la position est
supérieure ou égale à ħ ». Autrement dit: la précision des mesures sur la position et la
précision des mesures sur la quantité de mouvement ne sont pas indépendantes.
On peut ajouter, au regard de cette forme de l'équation: Δp ≥ ħ / Δx que si la
mesure de la position est précise (c'est à dire si Δx tend vers 0), alors la mesure de la
quantité de mouvement sera imprécise (Δp tend vers +∞).
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 11

12. Cette relation exprime donc d'une façon particulière la dualité onde/particule des
objets quantiques, et l'impossibilité d'observer les deux aspects simultanément. La
position représente içi l'aspect corpusculaire, alors que la quantité de mouvement
représente l'aspect ondulatoire.
On peut aussi prendre le problème dans un sens différent: on peut considérer que
c'est l'observateur qui influence l'objet quantique. En effet, l'observateur, en décidant
de mettre en évidence l'aspect ondulatoire ou corpusculaire de l'objet quantique,
influence l'objet et le fait effectivement apparaître comme une onde ou comme une
particule. Ce que l'objet n'est pas, en réalité: il est à la fois une onde et une particule.
A partir de cette idée d'influence de l'observateur, on peut aller plus loin.
L'observateur influence la manifestation de l'aspect ondulatoire ou corpusculaire de
l'objet quantique considéré, mais il influence aussi la position de l'objet quantique
considéré: lorsque l'objet n'est pas observé, sa position est définie comme une
probabilité de présence, et lorsqu'on veut déterminer sa position, on influence l'objet
quantique et sa position se précise. On peut ainsi dire qu'avant l'observation, les états
quantiques sont superposés: l'objet quantique est à la fois à un endroit et à un autre.
On peut se servir de ce concept dans d'autres situations. Si l'on prend l'exemple de
la désintégration des noyaux radioactifs, on peut définir un instant pour lequel il y a 1
chance sur 2 qu'un noyau soit désintégré; c'est l'observateur qui influencera la situation
et déterminera l'état du système. A cet instant, et en l'absence d'observateur, le noyau
est à la fois intact et désintégré.
Remarque : Δp et Δλ sont équivalents, ainsi que Δx et Δυ. Donc, on considère que la
proposition Δλ . Δx ≥ ħ est vraie. Par contre, la proposition Δp . Δλ ≥ ħ est fausse (Δp
et Δλ sont équivalents).
ΔE . Δt ≥ ħ
Pour cette relation, le même raisonnement va être établi : si une particule a une
énergie très stable, connue avec précision, sa durée de vie sera infinie (atome). Par
contre, si son énergie est très instable (grande dispersion donc difficilement connue),
sa durée de vie va être courte et connue (ce sont les périodes radioactives).
L’idée de ce ≥ ħ c’est de considérer ħ comme la limite du monde quantique.
Si une particule a Δp . Δx ≥ ħ , elle sera réelle et obéira à des lois (principe de
conservation de l’énergie…)
Si par contre une particule a Δp . Δx < ħ , elle sera virtuelle (ce qui ne veut pas
dire qu’elle n’existe pas !) et donc non observable. Du coup, elle peut peut-être violer
une ou plusieurs lois, mais comme on ne la voit pas, ce n’est pas un problème.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 12

13. Pour conclure, on peut opposer physique classique et physique quantique sur bien
des points.
▪ Le continuum d'énergie de la physique classique s'oppose à la quantification
de l'énergie des objets quantiques.
▪ Alors qu'en physique classique les objets peuvent etre localisés précisément,
les objets quantiques ne peuvent etre localisés que par des probabilités de présence, et
ce à cause de la dualité onde-particule et de la fonction d'onde. De plus, les objets
quantiques peuvent etre dans des états superposés.
▪ La séparabilité de la physique classique est niée par l'indiscernabilité des
objets quantiques, mais aussi par l'influence de l'observateur sur l'objet observé.
▪ Enfin, l'ensemble des principes de la physique quantique s'opposent au
principe de causalité de la physique classique.
Le paradoxe du Chat de Schrodinger
On conçoit mal quelle est la limite à partir de laquelle les lois de la physique
quantique sont valables, et la limite au-delà de laquelle ces lois ne le sont plus.
Cette interrogation est remarquablement exprimée par le paradoxe du chat de
Schrodinger: on place un chat dans une boite, close, inaccessible à l'observation. On
installe un mécanisme qui, lorsqu'il est déclenché, a 1 chance sur 2 de tuer le chat. Ce
mécanisme est particulier, et il dépend de la désintégration de noyaux radioactifs.
Cette désintégration dépend des lois quantiques que l'on a vues auparavant. Ainsi, la
survie du chat est directement liée avec un phénomène quantique.
Que se passe–t il alors ? Eh bien on ne sait pas si le mécanisme s'est déclenché ou
pas, c'est à dire si les noyaux radioactifs se sont désintégrés ou non; ne sachant pas, on
considère que ces noyaux sont à la fois intacts et désintégrés. C'est là que le paradoxe
intervient: le chat se retrouve dans la meme situation que les noyaux radioactifs, alors
qu'il ne répond pas aux lois quantiques. On ne sait pas si le chat est mort ou vivant,
donc on considère que le chat est mort ET vivant. Et si on veut ouvrir la boite, pour
savoir ? Eh bien on va effectivement influencer le chat et déterminer s'il est mort ou
vivant.
Ce paradoxe montre qu'il nous est difficile de considérer les lois de la physique
quantique comme applicables au monde macroscopique.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 13

14. II - Les interactions fondamentales
Introduction
« Interaction » = « Action entre »
Une interaction est un échange mutuel de forces sans qu’il y ait un objet seul qui
exerce une force sur l’autre.
Par exemple pour un objet qui tombe au sol il y a une interaction entre cet objet et la
terre ; la masse de la terre étant bien supérieure à celle de l'objet, celui-ci semble subir
l’interaction.
Si cet objet est la Lune par contre, on voit bien qu’il y a une interaction : aucune des
deux sphères ne tombe sur l’autre mais elles se maintiennent à distance.
Pour rendre concrète l’idée d’interaction, on imagine un support à cette interaction,
une sorte de message qui sera émis et reçu par deux objets en interaction : émis pour
dire « j’ai de quoi interagir avec toi, moi j’ai des électrons, et toi des protons, on est
faits pour s’entendre ! », et reçu par l’objet chargé de H+ (protons) en question : c’est
la théorie quantique d’un champ d’interaction qui s’établit entre deux objets à la
vitesse du boson-vecteur.
Généralités sur les bosons-vecteurs
Les bosons vecteurs ou quanta d’interaction s’occupent de cette communication. La
fonction d’onde du boson-vecteur est symétrique et leur spin est entier ou nul.
- Si le spin est nul ou pair, le boson médie une interaction attractive entre deux
particules identiques.
- Si le spin est impair, le boson médie une interaction de répulsion entre deux
particules identiques.
En utilisant la relation d’Heisenberg ΔE . Δt < ħ, les relations c = Δr / Δt et
E=mc², on obtient :
Δr = ħ/(mc)
La portée d’une interaction est inversement proportionnelle à la masse de son
boson vecteur, donc si on demande « la portée d’une interaction est proportionnelle à
la masse du boson vecteur » → FAUX
(Vous ferez attention plus tard à l’exception des gluons!)
Remarque: les bosons vecteurs sont situés en dessous de la limite ħ dans la relation
d'indétermination de Heisenberg, ils sont donc virtuels et non observables.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 14

15. Connaître les propriétés du boson vecteur permet de connaître l’interaction ; les
principales interactions sont les quatre suivantes :.
I. Forte > I. Electro magnétique > I. Faible > I. Gravitationnelle
Intensité 1 10-3 10-14 10-36
Il est dit de ces 4 interactions qu’elles ont la même forme : ce sont toutes des
interactions fondamentales.
1 - Interaction gravitationnelle (IG)
Les théories de Galilée et Kepler sont unifiées par la loi de gravitation de Newton.
F = G. (m1.m2)/d²
Elle agit sur des systèmes de masse élevée donc elle n’aura aucune importance à
l’échelle des particules quantiques.
Son boson vecteur est l’hypothétique graviton (Il n’a pas été clairement identifié à
ce jour) dont la masse est nulle (d’où portée infinie) et le spin est égal à 2 (interaction
attractive donc).
2 - Interaction électromagnétique (IEM)
Il fut un temps où les sciences étudiant les ondes radios, la lumière, le magnétisme,
l’électrostatisme et les rayons X étaient toutes dissociées : Maxwell les unifie par ses
équations en un seul phénomène : l'interaction électromagnétique.
Cette interaction peut être attractive ou répulsive : on en fait une force unique en
introduisant la notion de charge électrique positive (+) ou négative (-). Cette
interaction n'intervient que pour les particules chargées.
Son médiateur est le photon : (NB ce photon est différent de la particule qui
constitue la lumière, c'est un photon virtuel; les photons sont un terme générique qui
désigne à la fois les photons lumineux, les photons bosons, les photons gamma, les
photons de fluorescence X, comme vous le reverrez par la suite)
Sa masse m est nulle donc sa portée est infinie !
Son spin est s=1, donc le photon est le médiateur d'une interaction répulsive entre
deux particules identiques (par exemple deux protons), mais il peut aussi etre le
médiateur d'une interaction attractive entre deux particules différentes (proton et
électron). On retrouve le fait que l'interaction électromagnétique est soit attractive, soit
répulsive.
Sa seule expression à l’échelle macroscopique est la foudre. Elle n’a donc pas
qu’une expression microscopique, bien que la matière soit neutre à notre échelle. La
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 15

16. neutralité de la matière doit être assimilée à un équilibre plutôt qu’à une absence de
force. Par exemple, le sel de table, le chlorure de sodium, est un cristal composé d'ions
Na+ et d'ions Cl-. Les charges des ions se compensent, et le cristal macroscopique est
neutre.
3 - Interaction faible (If)
Dans la frénésie de réunir toutes les interactions dans l'interaction
électromagnétique, on a tenté d’y rattacher la radioactivité β (voir plus loin).
Le problème, c’est que le neutrino est insensible à l’interaction électromagnétique ;
on introduit donc l’interaction faible.
Ses 3 bosons vecteurs sont : W+ , W- et Z0. Ils n’ont qu’une faible portée (10-3 F)
liée à leur lourdeur.
Rappel : 1F = 1 Fermi
= 1 fm
= 1 femtomètre
= 10-15m
à différencier de l’Angström = 0,1 nm = 10-10 m.
4 - Interaction forte (IF)
Tout comme l’interaction électromagnétique se fait par des charges électriques
positives (+) et négatives (-), l’interaction se fait ici par des charges de couleur.
L'interaction forte agit entre les quarks, qui portent chacun une charge de couleur:
rouge, bleu ou vert.
NB: les quarks portent aussi une charge électrique. Cependant, cette charge
électrique n'intervient pas dans l'interaction forte qui s'établit entre eux.
Le boson vecteur est le gluon de masse m=0 et dont la portée d’interaction est de
1,5 F.
On voit donc l’exception à la règle établie par ∆r = ħ/(mc),(toute interaction est
inversement proportionnelle à la masse de son boson vecteur) qui ne s’applique pas au
système des gluons.
Les particules composites liées par l'interaction forte sont des hadrons, composées
de quarks. Ils n'expriment pas de charge de couleur, car les charges de couleur des
quarks qui les composent se neutralisent:
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 16

17. -Les baryons sont qqq (composés de 3quarks) avec R+V+B = pas de couleur
(couleur blanche, si vous préférez)
-Les mésons sont eux composés d’un quark et de son antiparticule (voir plus loin):
la charge de couleur du quark est annulée par la charge de couleur de l'antiquark qui
lui est associé; c'est comme si on avait « Rouge moins Rouge » = pas de couleur.
NB: en revanche, les hadrons peuvent avoir une charge électrique. Les protons, qui
sont des baryons, ont une charge électrique q = |e-|
En résumé, et pour ne pas s’embrouiller : on a des quarks chargés de couleur, et
des gluons qui les lient par interaction forte : les quarks sont liés en particules
d’interaction forte composites qui, elles, ne portent pas de charge de couleur.
Par analogie : on a des électrons chargés – et des protons chargés + (et des neutrons
non chargés) avec des photons qui les lient par interaction électromagnétique : le tout
est lié en un atome, qui, lui n’est pas chargé.
Remarque: Il existe 8 sortes de gluons. Ceux-ci ont une charge de couleur. Le cas
des gluons est différent de celui des photons, qui médient l'interaction électro-
magnétique. En effet, ceux-ci ne portent pas de charge électrique + ou -, alors qu'ils
médient l'interaction entre deux particules chargées. En revanche, les gluons portent
une charge de couleur, et médient une interaction entre deux particules qui portent une
charge de couleur: les quarks.
Expressions de l'IEM et de l'IF
L’interaction électromagnétique va agir entre l’électron et le noyau pour maintenir la
cohésion atomique.
L’interaction forte va agir entre quarks d’un neutron ou d’un proton pour maintenir
la cohésion de chaque nucléon (neutron ou proton). L'interaction forte étant très
intense, les quarks ne peuvent jamais se séparer: ils n'existent pas à l'état libre, et sont
confinés à l'intérieur du nucléon.
De ces deux interactions on va observer des résiduels, liés à une portée de leur
boson un peu supérieure à celle nécessaire, c'est à dire supérieure à l'atome pour l'IEM
et supérieure au nucléon pour l'IF.
L’interaction électromagnétique, en plus de faire interagir proton et électron, va
créer un résiduel qui permettra aux atomes d’interagir entre eux pour créer des
architectures moléculaires ou une réactivité chimique.
L’interaction forte, en plus de faire interagir les quarks, aura un résiduel qui
permettra aux nucléons d’interagir entre eux : c’est la cohésion nucléaire.
Il est dit de ces deux interactions : de cohésion nucléaire et de cohésion moléculaire,
qu’elles ont la même forme : ce sont des résiduels d’interaction fondamentale.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 17

18. Interaction forte Interaction Electro-
Magnétique
Mediateur Gluon Photon virtuel
Action Cohésion des nucléons Cohésion de l'atome
Forme Interaction fondamentale Interaction fondamentale
Résiduel d'IF = interaction Résiduel d'IEM
de cohésion nucléaire
Médiateur Méson (cette information n'est pas
dans le cours)
Action Cohésion du noyau Cohésion de la molécule
Forme Résiduel d'Interaction Résiduel d'Interaction
fondamentale fondamentale
Remarque: le reve des physiciens est d'unifier les quatre interactions fondamentales en
une seule. Une de leurs théories vise à unifier l'interaction électromagnétique et
l'interaction faible en une interaction appelée électrofaible. Celle-ci serait médiée par
le boson de Higgs.
A retenir :
▪ Le neutrino est insensible à l’interaction électromagnétique.
▪ Les leptons sont insensibles à l’interaction forte(et notamment l’électron).
NB: le neutrino n'est donc sensible qu'à l'interaction faible (puisqu'il est un lepton)
▪ Les hadrons sont sensibles à toutes les interactions.
▪ Les mésons sont les médiateurs de l’interaction de cohésion nucléaire (Résiduel de
l’I.F), (et non pas les gluons!)
▪ Ne pas confondre, pour les quarks, la charge de couleur et la charge électrique up
(u) ou down (d).
La charge électrique u ou d permet de déterminer le caractère du nucléon : le
neutron est formé de udd et la somme des charges électriques portés par ses quarks est
donc neutre, tandis que le proton formé de uud aura une charge totale positive = 1.
▪ A deux exceptions près, chaque particule du tableau de la classification des
particules possède une antiparticule. Par exemple, l'antiparticule de l'électron est le
positon ou positron, qui possède une charge électrique égale à l'opposée de celle de
l'électron. De meme, le neutrino possède une antiparticule appelée antineutrino.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 18

19. L'antiparticule est notée avec une barre au dessus du symbole de la particule. Les deux
exceptions sont le pion π0 et le photon hv, qui sont leur propre antiparticule.
Classification des particules *:
Particules ponctuelles Particules composites =
Hadrons
Leptons Baryons
(6 types regroupés en 3 générations)
FERMIONS - l’électron e- - Nucléons
- et son neutrino électronique νe
- le muon m- Proton avec uud
- et son neutrino muonique nm. (Donc ayant comme charge
- le tau t- +2/3+2/3-1/3 = 1)
- et son neutrino nt.
Neutron avec udd
Quarks (Donc ayant comme charge
+2/3-1/3-1/3 = 0)
(6 types regroupés en 3 générations)
- u et d (up and down)
de charge respective +2/3 et -1/3 - Hypérons
- s et c (strange et charmed)
- b et t (bottom et top)
Bosons d’interaction Mésons (formés de q et de son
antiparticule).
- photon
BOSONS - Z0, W+ et W- -pions
- gluon -mésons
- (graviton ?)
*Ce qui est en gras est à bien savoir.
Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 19

20. III - Stabilité du noyau
1 - Echelles de taille et d’énergie
Plus la taille du système diminue, plus l’énergie de liaison augmente, plus le
système concerné est composé de particules indissociables : il est plus facile de
dissocier les électrons du noyau d’un atome que de séparer des quarks. En fait, la
séparation des quarks est impossible, du fait de l'intensité de l'interaction forte; par
conséquent, il n'existe jamais de quarks à l'état libre. En revanche, il peut exister des
nucléons ou des électrons libres.
2 - Fiche signalétique du noyau
Découverte du noyau : on diffuse des particules α sur une cible constituée d’un film
monoatomique d’or.
▪ La plupart des α ne sont pas déviés : la matière est constituée de vide
▪ Quelques uns sont fortement déviés : la matière est concentrée en de petits volumes.
Avec des cibles aux noyaux plus légers et avec des α plus énergétiques, on peut
mesurer la distance d’effleurement constituée du rayon de la particule α et du rayon du
noyau = Rα + RN et ainsi calculer le rayon d’un noyau.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 20

21. Découverte du proton et du neutron :
Le noyau est composé de A nucléons, de Z protons et de N=A-Z neutrons.
IsotoPes : même nombre de Proton (Z identique), donc même élément donc même
propriétés chimiques (peut se lier aux mêmes atomes pour créer des molécules) mais
propriétés physiques différentes. Il peut ainsi être plus stable ou plus instable que
l’élément associé.
Deux isotopes ont les memes propriétés chimiques, puisqu'ils ont le meme nombre
d'électrons, et que la réactivité chimique est liée au cortège électronique. En revanche,
ils ont des propriétés physiques différentes, car leurs noyaux ne contiennent pas le
meme nombre de neutrons et sont donc plus ou moins stables. Par exemple, le 14C est
radioactif, c'est à dire qu'il est instable, alors que le 12C ne l'est pas. Ils peuvent
cependant faire partie des mêmes molécules: le CO2 peut etre constitué de 12C ou de
14
C.
IsotoNes : même nombre de Neutrons.
IsobAres : même nombre de nucléons A ; ex : les émissions β+ et β- donnent des
pères et fils isobares.
Isomères : deux isomères sont identiques mais ils ont des états énergétiques
différents : ils se désexciteront vers un état stable par isomérisme nucléaire ou
conversion interne (voir plus loin).
Remarque : Le genre de questions que l’on peut vous poser = soit « X ou Y avec
Z=, N=, A=, et sont des isotones/isotopes/isomères…. Vrai ou faux ? ».
3 - Système des masses atomiques
Le système des masses atomiques est un système arbitraire : les masses dont on
parle sont trop petites pour pouvoir être mises dans une balance et mesurées.
La seule chose que l’on soit capable de faire, c’est de calculer les rapports des masses
molaires des éléments à l’état gazeux. Or on a vu que deux opérations sont nécessaires
pour pouvoir faire une échelle absolue. Les rapports donnent le pas de cette échelle. Il
faut ensuite une référence, pour que de repérable, la grandeur devienne mesurable.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 21

22. La référence va donc être fixée et l’on dit que :
m (1 mole) (12C) = 12 g m (1 mole) (12C) représente la masse d'une mole de 12C.
Or m (1 mole) (12C) = M (12C) * N M (12C) représente la masse d'un atome de 12C.
Donc M (12C) = m (1 mole) (12C) / N
= 12 / N
= 12 / (6,02 . 10^23) g
= 12 . 10-3 / (6,02 . 10^23) kg
= 2 . 10-26 kg.
On pose 1 u = M (12C) / 12
Donc 1 u = m (1 mole) (12C) / ( N * 12 )
= 12 / ( N * 12 ) g
=1/Ng
= 10^-3 / N kg
= 1,66 . 10^-27 kg.
1 u = 1,66 . 10-27 kg.
D'une façon littérale: 1 u = 10-3 / N kg.
↔ 1 u * N = 1 g.
1 u = 1 / N g.
En français:
 1 mole de l’isotope 12 du carbone 12C pèse 12g
 1 mole contient N atomes soit 6x1023 atomes donc un atome de 12C pèse 12g/ N
soit 12g/(6x1023)
 M (12C) = 0,012/6x1023 = 0,002x10-23 kg.
Cela ne veut rien dire ! 2x10-26 kg ne nous représente rien !
On crée donc une nouvelle unité, à l’échelle des particules étudiées : c’est l’unité de
masse atomique, uma, qui est égale au 1/12ème de la masse d’un atome de 12C.
 1u = 1/12 M (12C) = 1,66x10-27 kg
De même pour l’énergie, on crée une unité représentative des énergies à cette
échelle, l’électronvolt ou eV : 1 eV = 1,6x10-19 J
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 22

23. Ces deux valeurs sont à savoir par cœur : plus vous ferez d’exercices, plus elles
rentreront facilement et seront faciles à appliquer.
En équivalent énergétique, on a donc 1u qui vaut :
E=mc²
E (1u) = uc²
= 1,66 x 10-27 x (3x108)²
= 15x10-11 J (pas à connaitre)
= 15x10-11/1,6x10-19 eV
= 931,5 MeV
1 u = 931,5 MeV / c²
Retenez bien cette opération : E(J)/1,6.10-19=E(eV) : vous en aurez souvent besoin,
mais soyez vigilant lors des manipulations des unités : les unités internationales sont le
J, ou le kg, et on vous demande souvent des eV ou des uma.
Masse des nucléons, de l'électron, masse de l'atome:
mp= 1,00728u
mn= 1,00866u
me= 5,5x10-4u : cette masse est négligeable par rapport à celle des nucléons. On peut
aussi exprimer me en Mev/c²:
me = 0,511 Mev/c²
En faisant une approximation sur la masse du proton et du neutron, qui sont un peu
supérieures à 1 u, on considère que m nucléon = 1u.
En faisant une seconde approximation sur le défaut de masse (voir paragraphe
suivant), on considère que la masse du noyau M est égale à la masse de la somme des
nucléons: M ≈ A * m nucléon ≈ A u.
En faisant une troisième approximation sur la masse des électrons (voir plus loin),
on considère que la masse de l'atome M est égale à la masse du noyau M:
M ≈ M ≈ A u.
On en déduit:
M≈Au
↔ M*N ≈Au*N et, en sachant que m (1 mole) = M * N et que 1 u * N = 1 g
↔ m (1 mole) ≈ A g
Par exemple, pour le 12C: un atome de 12C pèse 12u, une mole de 12C pèse 12g.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 23

24. Si dans un exercice vous n’avez pas la masse en uma d’un atome, vous pouvez
prendre la masse molaire et vice versa.(vous aurez au moins une approximation). Cela
permet d'avoir une idée de ce sur quoi vous devez tomber avant de commencer vos
calculs précis.
Donc : pour un atome possédant A nucléons, je peux prendre M (AX) = A x 1u
Ex : masse d’un atome d'azote = 14 u
Attention, ces valeurs ne sont là que pour se faire une idée : les masses mn, mp et me
vous seront données dans les exercices où vous devrez calculer M ou M avec
précision.
4 - Masse et énergie de liaison du noyau
En physique nucléaire, il faut avoir complètement intégré E=mc², c'est-à-dire que
masse et énergie sont équivalentes. C'est pour mettre en évidence l'équivalence masse-
énergie que les masses sont souvent exprimées en MeV/c². La conservation lors de
« réactions » est une conservation masse+énergie et non une conservation de masse
strictement ou d'énergie strictement.
Ainsi la somme de la masse des nucléons qui constituent un noyau est
supérieure à la masse de ce noyau lui-même (et on respire et on ne panique pas)
La stabilité, c’est être au niveau d’énergie le plus bas (ici E2) : les nucléons
s’assemblent en noyau car ils constituent alors un système de plus basse énergie donc
plus stable.
Si vous êtes en équilibre en haut d’une montagne, votre énergie potentielle
(=possibilité de tomber) est élevée : vous préférez perdre de l’énergie en descendant,
jusqu’à ce que vous ne puissiez plus tomber (Ep nulle) et ainsi être plus stable; la
matière raisonne de même.
La différence d’énergie est l’énergie de liaison des nucléons; son équivalent en
termes de masse est le défaut de masse.
DDM : Le défaut de masse
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 24

25. Le calcul que fait tout le monde dans la vie en général est : final - initial.
Dans le cas présent, les systèmes étudiés perdent de l’énergie : comme nous, c’est
cette énergie qui nous intéresse (connaître l’énergie d’un rayon C émis lors d’un
examen radiologique pour ne pas trop irradier le patient par exemple), on préfère la
compter en positif.
 On calcule donc : - ΔMIF = DDM = initial - final
Le défaut de masse représente la masse « perdue » ou libérée lors de la formation du
noyau. On pourrait écrire la réaction de cette façon:
Z protons + N neutrons → Noyau ( + DDM)
Z mp + N mn = M + DDM
DDM = Z mp + N mn – M
M = Z mp + N mn – DDM
Ici l’énergie de liaison B (B pour bind = lier) vaut DDMc² (pour défaut de masse
2
c ). Le DDM peut etre exprimé en u, mais l'exprimer en MeV/c² permettra d'avoir
directement accès à l'énergie de liaison.
B = DDM c²
L'excès de masse
Il y a une légère différence entre la masse (A u) théorique et la masse M(A,Z)
réelle. L'excès de masse représente cette différence entre la masse théorique, qui est
sensiblement donnée par le même chiffre que le nombre A de nucléon (voir
précédemment) : M ≈ A u, et la masse réelle.
En effet, comme vu précédemment, on fait d'abord une première approximation
concernant la masse du nucléon, puis une deuxième sur le défaut de masse, et une
troisième sur la masse de l'atome M.
En réalité, M = M + Zme- – | El |
M = Z mp + N mn – DDM + Zme- – | El |
Dans cette formule, El représente l'énergie de liaison des électrons au noyau. (pour la
justification, cf chapitre IV - Instabilité du noyau).
L'excès de masse EM rend compte de l'ensemble des approximations sur la masse de
l'atome.
EM = [M(A,Z) - A] u
= [M(A,Z) - A] * 931,5 MeV / c²
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 25

26. Pourquoi vous dire tout ça ? Parce que dans les exercices qui concerneront le
chapitre instabilité, l’énergie libérée par une désintégration d’un père en un fils se
calculera en faisant la différence entre M(père) et M(fils).
Parfois (pour rigoler) on ne vous donnera pas M(père) et M(fils) mais EM(père) et
EM(fils). Il faut les utiliser de la même façon.
Exemple: pour une désintégration X(A,Z) → Y(A,Z+1) + β-
DDEM = EM(X) - EM(Y)
= ( [ M X(A,Z) - A] - [ M Y(A,Z+1) - A] )
= [ M X(A,Z) - M Y(A,Z+1)]
= DD M
Les A s’annulent, en effet dans β+/-, les A du père et du fils sont égaux, ils sont
isobares !
DDEM est la différence des excès de masse entre l'atome père et l'atome fils, et
DD M la différence des masses des atomes.
Attention: le DDM (défaut de masse du noyau) est toujours positif, alors que le
DDEM (ou le DDM , c'est pareil) peut etre positif ou négatif.
5 - Force de cohésion nucléaire
C’est le résiduel de l’interaction forte à l’extérieur des nucléons, comme on l’a vu
dans le second chapitre.
Elle est plus liante pour une paire neutron/proton où les spins sont parallèles que
pour une paire proton/proton ou encore neutron/neutron où les spins sont antiparallèles
(du fait du principe d'exclusion de Pauli).
Elle est médiée par les mésons (qui sont des bosons) :
Les mésons de spin impair vont provoquer la répulsion entre nucléons qui
s’approchent à moins de 0,5 Fermi. Les mésons de spin pair vont provoquer une
attraction entre nucléons qui s’éloignent de plus de 1Fermi.
Ceci permet de garder une distance constante de 0,5 à 1 Fermi entre les nucléons !
Remarque : Comme on l’a dit précédemment, la cohésion nucléaire et la cohésion
des atomes dans une molécule ayant la même forme de résiduel d’interaction, elles
vont agir de la même manière (répulsion entre 2 atomes trop proches ; attraction s' ils
sont trop loin, d’où la stabilité de longueur des liaisons interatomiques dans une
molécule ; seule différence, l’interaction forte étant plus forte que l’interaction
électromagnétique, l’architecture d’une molécule sera plus labile que celle d’un
noyau).
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 26

27. 6 - Energie de liaison moyenne par nucléon
Courbe B/A en fonction de A (voir le polycopié du Dr Victor)
▪ Pour A<16, B/A = kA donc B = kA². B est proportionnel à A².
▪ Pour A>16, B/A = k donc B = kA. B est proportionnel à A.
Que peut-on en conclure ?
Lorsque le nombre de nucléon est faible (c'est à dire A<16), les nucléons sont très
fortement liés, puisque l'energie de liaison est proportionnelle au carré de A; l'énergie
de liaison augmente très vite avec le nombre de nucléons, jusqu'à A=16. Lorsque
A>16, les nucléons sont moins fortement liés, car l'énergie de liaison augmente moins
rapidement avec le nombre de nucléons, elle est seulement proportionnelle à A.
C’est pour cela que l’on dit qu’à A<16, les effets individuels des nucléons
prédominent: dans ces conditions, chaque nucléon y met du sien pour rester avec les
autres, et se lie fortement avec ses voisins. En revanche, lorsque A>16, les effets
collectifs prédominent: les nucléons ne se lient plus autant avec leurs voisins.
Pour faire une métaphore douteuse, imaginez vous une soirée. Lorsque le nombre
de personnes n'est pas trop grand, chaque personne garde encore son esprit critique, et
il est possible d'avoir un discussion avec tout le monde. En revanche, lorsque le
nombre de personne est trop grand, les gens sont submergés par l'effet de groupe, et on
n'arrive plus à s'entendre ou à se faire entendre.
Pour accéder à plus de stabilité (la nature tend toujours à plus de stabilité, c'est-à-
dire un état énergétique plus bas), il y a deux moyens.
 La fusion de noyaux légers
 La fission de noyaux lourds
Dans les deux cas, il y a libération d’énergie : On utilise la fission pour l’Energie
nucléaire et que l’on cherche à faire de la fusion pour éviter les déchets radioactifs
(Voir cours de Mr Pradère)
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 27

28. 7 - Modélisation du noyau
a) Justification
Une explication complexe vous est ici exposée : ce qu’il faut en retenir, c’est la
conséquence à savoir que le volume du noyau est proportionnel au nombre de
nucléons (puisque ceux-ci restent tous à distance à peu près égale comme nous l’avons
vu, de 0,5 à 1 Fermi).
V = kA or V = kR3 donc R = kA1/3 → R = roA1/3
On retiendra surtout la formule suivante : R= 1,3 A1/3
Il s’agit du rayon du noyau : le rayon de l’atome dépend du nombre de couches du
cortège électronique et du nombre d'électrons qui se trouvent dans cette couche,
puisque, comme vous l’avez vu en chimie, plus il y a d’électrons dans une couche,
plus ils se tassent.
Notion d’épaisseur de peau : e = 2,4 +/- 0,3 F (Fermi) : Il s’agit de la couche de
nucléons qui va se trouver en surface. Pour un noyau à 4 nucléons (He), tous les
nucléons sont en surface ; pour un noyau de 100 nucléons, la proportion sera moindre
→ cette notion n’est pas négligeable, nous verrons pourquoi quand nous parlerons de
l’énergie superficielle.
b) Composantes de B (voir le polycopié du Dr Victor)
B = av A - as A2/3 - ac (Z2 / A1/3) - aa [(N-Z)2/A] + c
Cette relation est à connaître par cœur !
Dans cette relation, tous les av, as,... sont des constantes qu'on arrange un peu pour que
la relation fonctionne: le reste de la formule est explicable par la logique.
Moyen mnémotechnique : « Avahasa de Troie en a assez des Zèbres carrés sur
les arbres tiers. Ah, ah ! La haine moindre des zèbres carrés sur les arbres. »
Sachant qu’ av A est le seul nombre positif, (avec éventuellement c, mais qui n'est pas
très important numériquement) tout le reste est perdu et est donc en négatif. Nous
allons voir pourquoi.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 28

29. -Energie de liaison en volume : av A
Plus il y a de nucléon, plus il y a de résiduel d’Interaction forte et donc plus il y a de
cohésion ou d’énergie de liaison (quand on l’évalue, on a une constante à 14 millions
d’électronvolts)
A partir de là apparaissent des facteurs limitants la cohésion des nucléons.
-Energie superficielle : - as A2/3
Revenons à notre épaisseur de peau…
Imaginez une assemblée de pingouins : tout le monde se communique de la chaleur
sauf ceux qui sont en bordure (l’épaisseur de peau), qui perdent plein de chaleur par la
partie de leur corps exposée au blizzard.
Il en est de même pour les nucléons : Ceux qui sont en bordure perdent de l’énergie
d’interaction, ce qui fait perdre de l’énergie de liaison à l’ensemble des nucléons.
Plus il y a de pingouins, moins il y en a proportionnellement qui sont exposés au
froid !
Et si il n’y en a que 3 ou 4 par exemple, tout le monde a froid ! (perd de l’énergie)
La correction par la surface de la sphère est donc, proportionnellement au nombre
de nucléons, plus importante quand A est petit, et s’atténue quand A augmente. En
valeur absolue, cependant, la correction par la surface de la sphère augmente avec A.
-Energie coulombienne (répulsive) : ac (Z2/A1/3)
Il s’agit de l’énergie perdue durant les querelles électromagnétiques entre protons
(Z). Comme la portée de l’interaction électromagnétique est infinie (m=0 pour le
photon), les protons n’ont pas besoin d’être côte à côte pour se repousser, d’où Z². Ce
Z² fait référence à l'expression de la force électromagnétique:
q1 q2
F =k
r²
On écrit que cette force est proportionnelle au produit des charges des éléments en
interaction. Ici il s'agit d'une interaction entre protons, c'est pourquoi l'énergie
coulombienne s'écrit en fonction de Z².
Cette énergie va aussi dépendre des neutrons qui sont là pour faire « tampon » :
Donc plus il y a de protons, plus il y a répulsion ; mais plus il y a de neutrons, c'est-à-
dire plus A augmente, plus R et plus A1/3 augmentent, et plus cette répulsion est
temporisée.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 29

30. -Energie d’asymétrie : -aa [(N-Z)²/A]
L’idéal est de faire des couples de nucléons (N-P) (voir 5- Force de cohésion
nucléaire), donc si N = Z, N-Z = 0 et l’énergie de liaison n’est pas diminuée.
Pour des noyaux plus gros, il y a plus de neutrons (voir ligne de stabilité page 29)
donc N-Z > 0
En le rapportant à A, on se dit que « d’accord, il n’y a pas autant de n que de p,
mais vous comprenez bien, monsieur, qu’avec un gros noyau comme ça je ne peux pas
contenir tous mes protons (qui se repoussent) sans un minimum de neutrons
excédentaires ! »…
En divisant par A, je relativise le nombre de neutrons excédentaires par rapport à la
taille du noyau : Pour un nombre de A moyen, l’énergie de liaison est maximisée par
N = Z, puis quand A dépasse un certain seuil, l’énergie de liaison est maximisée par N
> Z.
Tout cela explique 99% de l’énergie de liaison B : le reste s’éclaircit grâce à :
-Energie d’appariement c :
Quand les nucléons identiques peuvent se coupler par paire, de l’énergie de liaison
est récupérée : ces deux nucléons vont tourner l’un autour de l’autre, perdant ainsi de
l’énergie cinétique, récupérée en énergie de liaison.
Il faut en fait remarquer que dans l’énergie d’asymétrie ci-dessus, les couples n-p
s’établissent en fait sous la forme 2n-2p.
On parle de noyaux pair/pair par exemple. Cette appellation fait référence
respectivement à Z/N (Z pair / N pair).
Pour les noyaux pair/pair, Z/2 protons s’apparient à Z/2 protons, idem pour les
neutrons.
On obtient Z/2 couples de protons et N/2 couples de neutrons, qui vont s’apparier
pour faire baisser l’énergie d’asymétrie.
Pour les noyaux pair/impair et impair/pair, il y aura dans le premier cas un neutron
solitaire, dans le 2ème cas un proton solitaire.
Enfin, dans les noyaux impair/impair il y aura 1 neutron et 1 proton solitaires, ce qui
est très déstabilisant : seuls 5 noyaux vont adopter cette configuration (il s’agit de
H(2,1) Li(6,3), B(10,5), N(14,7) et Ta(180,73) : cette configuration marche tout de
même pour ces cinq, puisqu’ils peuvent faire des paires n-p au lieu des paires 2n-2p)
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 30

31. Enfin, une contribution moins importante :
-Energie de couche :
Il s’agit là de « magie » qui donne une surstabilité aux noyaux de Z ou N (pas A !!!)
ayant pour valeur 2, 8, 20, 28, 50, 82 et 126 : ce sont des nombres dits « magiques ».
Cette surstabilité est expliquée par le remplissage des couches nucléaires de ces
noyaux (et pas couches électroniques, on parle ici du noyau. On peut par contre faire
l’analogie avec le système des remplissages des couches électroniques que vous
apprenez en chimie pour vous faire une idée : les couches électroniques bien remplies
vous donnent des gaz rares, ici les couches nucléaires bien remplies vous donnent des
noyaux surstables !).
Cette notion explique bien des choses, par exemple, que remarque-t-on ? Que le Pb,
produit final de diverses désintégrations radioactives a Z=82 et N=126, qui sont des
nombres magiques !
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 31

32. IV – Instabilité du noyau
Introduction
La radio activité consiste en l’évolution d’un état initial instable ou excité vers un
état final de plus basse énergie, et donc plus stable.
C’est la désintégration d’un noyau père en un noyau fils avec émission d’une ou
plusieurs particules, ou encore la désexcitation d’un noyau de l'état excité vers son état
fondamental.
Pour que ce processus ait lieu, il faut que le noyau père X ait une masse supérieure à
celle du fils Y. Ainsi, la désintégration de X en Y doit libérer de la matière.
Du fait de l'équivalence masse-énergie, donnée par la relation E=mc2, on peut aussi
dire que la réaction doit libérer de l'énergie, ou que l'énergie disponible doit etre
positive. A cette condition seulement, la réaction est possible. Si vous voulez savoir si
X1 peut devenir X2 par exemple, il faut déjà vérifier cette condition. Si la différence
d’énergie (ou différence de masse, c'est pareil) entre ces deux noyaux est négative,
alors le passage de X1 à X2 par désintégration est impossible.
Pour une désintégration : X → Y + particules + Q
Q est l'énergie disponible à la fin de la désintégration
Q = initial - final
Q = M(X)c² - [M(Y)c² + M(particule)c²]
Q>0
Remarque: on peut aussi parler de différence de masse, c'est équivalent. On a alors:
DDM = M(X) – [M(Y) + M(particules)]
Q = DDM c²
Attention: içi, DDM représente la différence de masse entre l'état initial et l'état final,
et non le défaut de masse.
Cette énergie disponible Q va se répartir en énergie de recul du noyau fils (on la
néglige), en énergie cinétique des particules, et essentiellement en énergie d’excitation
du noyau fils (en effet, la plupart du temps, les noyaux fils naissent à l'état excités, ils
vont ensuite se desexciter en perdant encore de l'énergie).
En fait, on estime qu’une source radioactive (SRA) est constituée d’atomes et
non de noyaux : on écrit le bilan en fonction des masses atomiques M et plus en
fonction des masses nucléaires M:
M (A,Z) = M(A,Z) + Zme - | El |
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 32

33. La masse d'un atome est égale à la somme du noyau et des électrons, moins
l'énergie de liaison du cortège électronique au noyau.
En effet, les électrons sont liés au noyau de la même façon que les nucléons sont
liés entre eux: la masse d'un noyau est inférieure à la somme des masses des nucléons,
la masse de l'atome est inférieure à la somme de la masse du noyau et du cortège
électronique. Toujours ce même principe de s'assembler pour connaitre une plus
grande stabilité, en libérant de l'énergie.
El est donc l’énergie de liaison du cortège électronique au noyau. La plupart du
temps, l'énergie de liaison est négligée.
Maintenant nous allons voir les différentes opérations responsables de la
radioactivité, à savoir les desexcitations par IEM, puis les desintégrations, par
interaction forte puis par interaction faible.
1 - Désexcitation par interaction électromagnétique
Avant de parler des phénomènes un peu plus en détail, un petit résumé:
Lorsque le noyau est excité : une couche nucléaire comporte une lacune. La
désexcitation est une désexcitation par interaction électromagnétique, elle peut
s'effectuer par deux phénomènes: l'isomérisme nucléaire et la conversion interne.
Lorsque l'atome est excité : le cortège électronique comporte une lacune. La
désexcitation peut s'effectuer par deux phénomènes: fluorescence X et émission d'
électron Auger.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 33

34. La désexcitation du noyau et de l'atome sont comparables:
-lors de l'isomérisme nucléaire ou lors de la fluorescence X, l'énergie
d'excitation est émise sous forme d'un rayonnement (rayonnement γ pour l'isomérisme
nucléaire, rayonnement X pour la fluorescence X)
-lors de la conversion interne ou lors de l'émission Auger, l'énergie d'excitation
est transmise directement à une électron, par couplage quantique. L'électron de
conversion interne est plutot proche du noyau, alors que l'électron Auger est un
électron périphérique. Ces deux électrons sont monoénergétiques.
-les deux phénomènes de désexcitation sont indépendants l'un de l'autre. Un
noyau peut se désexciter par isomérisme nucléaire OU conversion interne, un atome
peut se désexciter par fluorescence X OU émission d'un électron Auger.
L'atome est dans un état excité si son cortège électronique comporte une lacune. De
ce fait, l'atome sera dans un état excité
-après capture électronique (voir plus loin)
-après l'émission d'un électron de conversion interne. Autrement dit, toute
désexcitation du noyau par conversio interne est suivie d'une désexcitation de l'atome
par fluorescence X OU émission d'un électron Auger
Nous allons maintenant détailler un peu la désexcitation du noyau.
Le noyau fils est émis dans un état excité :
X → Y* → Y Y* = fils excité Y = fils à l’état fondamental
La transformation qui nous intéresse dans ce paragraphe est la transition Y* → Y .
a) Isomérisme nucléaire
Le noyau se désexcite par l’émission d’un photon γ (qu'on dit photon gamma) qui
va emporter l’excédent d’énergie en une seule fois, ou par l’émission de plusieurs
photons d’énergies différentes, passant par plusieurs états d’excitation intermédiaires
avant d’arriver à l’état fondamental. (voir schéma du polycopié du Dr Victor)
Par convention, l’état fondamental est au niveau d’énergie 0.
On peut écrire que la transformation s'effectue ainsi:
Y* → Y + γ
Si la transformation s'effectue en deux fois, on a:
Y*0 → Y*1 + γ 1 → Y + γ1 + γ 2
Eγ = { EI - EF}
Ces états intermédiaires d’excitation ont une durée de vie très courte. L’état excité est
un isomère de l’état fondamental, c'est à dire que Y* et Y sont des isomères.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 34

35. -Si l' état excité a une durée de vie très courte (10-15 ~ 10-10s), on parle
simplement d'émission γ.
-Si l’état excité a une durée de vie supérieure à 0,1seconde, on parle de
radioactivité γ . Cet état excité de durée de vie « longue » est dit métastable.
Exemple: le Technétium, 99mTc, utilisé dans la scintigraphie, a une durée de vie de
6h et les γ ont une énergie de 140 keV: le petit m en exposant signifie métastable, c'est
un isomère du 99Tc, c'est à dire le même élément à un état d'excitation différent.
b) Conversion interne
Elle a lieu elle aussi lorsqu’un noyau excité veut perdre son énergie. Ce processus
est indépendant de l’isomérisme nucléaire; autrement dit, pour que Y* se désexcite en
Y, il peut soit utiliser l'isomérisme nucléaire, soit la conversion interne.
L’énergie d’excitation du noyau est transmise directement à un électron du cortège
électronique qui se trouve soit excité à une énergie précise, soit ionisé s'il reçoit une
énergie suffisante:
Ee- = { Ei - Ef } - | El |
L’énergie de l’électron est celle émise par le noyau pour se désexciter, à laquelle on
enlève l’énergie de liaison de l’électron à sa couche électronique.
L’énergie d’excitation transférée va d’abord servir à décrocher l’électron, le reste va
à l’énergie cinétique de l’électron qui quitte le cortège.
L’électron à qui l’énergie est transférée est presque toujours l’électron de la couche
K puisque c'est celui qui est le plus près, mais la probabilité que le transfert se fasse
sur des électrons de la couche L, M… n’est pas nulle.
Etant donné que Eγ = { Ei - Ef }
et Ee-CI = { Ei - Ef } - | El |,
on peut écrire
Ee-CI = Eγ - | El |
À l’issue de cela, l’atome fils se retrouve à un état excité, du fait de la lacune, créée
par le départ de l’électron dans le cortège électronique.
La désexcitation de l'atome débute par une transition électronique. Les électrons des
couches supérieures vont « descendre » combler la lacune des couches plus proches du
noyau. Comme ils changent de couche d’énergie, ils perdent de l’énergie. L'énergie de
la transition électronique peut etre libérée sous deux formes:
▪ Emission d'un photon X: l'énergie est émise sous forme de photons X. Ces
photons X portent une énergie égale à la différence d'énergie entre les couches
électroniques. On peut l'écrire ainsi:
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 35

36. EX= { Ei – Ef}
Par exemple, si ce photon est émis suite à la désexcitation d'un électron de couche
M à la couche K, le photon émis aura une énergie EX = EM – EK. Ces photons X vont
faire de la fluorescence, c’est pourquoi on parle de fluorescence X.
▪ Emission d'un électron Auger: l'énergie libérée par la transition électronique est
directement transmise à l'électron Auger, par couplage quantique, ce qui entraine
l'éjection de l'électron. Cette désexcitation est indépendante de l'émission d'un photon
X: autrement dit, la désexcitation d'un atome passe toujours par la transition d'un
électron d'une couche d'énergie élevée à une couche d'énergie plus faible, mais
l'énergie est libérée soit par l'émission d'un photon X, soit par l'émission d'un électron
Auger.
L'electron Auger est émis avec une énergie: Ee-Auger= { Ei - Ef } - | El |
Etant donné que Ee-Auger= { Ei - Ef } - | El |
et EX = { Ei - Ef },
on peut écrire
Ee-Auger= EX - | El |
Donc, pour résumer la conversion interne: Y* → Y + e-CI (+/- photons X et électron
Auger)
c) Remarques :
Les photons, qu’ils soient γ ou X, sont identiques.
On les différencie parce que leur énergie n’a pas le même ordre de grandeur : en
général, EX < E γ
On ne vous demande pas de savoir où est la limite entre les 2, mais seulement de
retenir que les photons γ proviennent de l’isomérisme nucléaire, tandis que le
réarrangement du cortège électronique donne des photons X.
De même, l’électron de conversion interne, l’électron Auger, les β - : ce sont tous
des électrons, on les différencie parce que l’on sait d’où ils viennent…mais si vous les
croisez sur un graphique de Mr Victor (par exemple sur l’examen blanc 2005/2006),
ils ont tous la même tête : à vous de deviner qui est qui…
Lors de la désexcitation de l'atome, le cortège électronique est réarrangé: il reste la
dernière couche qui n’a pas d’électron des couches supérieures pour venir combler sa
lacune, me direz-vous ! Rassurez-vous, la matière est bourrée d’électrons libres qui
n’hésiteront pas à venir combler une couche. On précise que l’électron Auger est un
électron périphérique: il sera remplacé par un électron libre.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 36

37. 2- Désexcitation par interaction forte
a) Emission α
Ce qu’il vous faut savoir :
Que va devenir l'énergie libérée par la désexcitation ? Elle se répartira, comme nous
l'avons vu en introduction,
-en énergie de recul du noyau fils (négligée),
-en énergie d'excitation du noyau fils; dans ce cas le noyau fils se désexcitera par
isomérisme γ ou CI (+/- photon X et électron auger),
-et énergie cinétique des particules.
Dans le cas de l'emission α, une seule particule est émise: la particule α. Celle-ci va
donc récupérer la totalité de l'énergie libérée par la désexcitation; ou bien, si le noyau
fils est émis à l'état excité, elle prendra l'énergie restante. Son énergie ne peut donc
prendre que certaines valeurs bien précises: les α sont monoénergétiques. Vous verrez
la différence avec les béta, où le spectre est continu du fait de la présence de deux
particules, qui se partagent l'énergie.
Les α sont donc monoénergétiques. Un noyau qui émet α émettra plus de 90% de
ses α avec la même énergie (comprise entre 4 et 9 MeV).
Plus l’énergie de l’ α émis est forte, plus la demi-vie de l'émetteur alpha est courte:
c'est comme si le noyau emetteur se retrouvait avec, à l'intérieur, une particule alpha
qui cognerait très fort aux murs pour sortir: Il ne tiendra pas longtemps et se
désintègrera beaucoup plus vite.
Au contraire, lorsque l'énergie de la particule alpha est faible, la particule à
l'intérieur du noyau toque à la porte seulement de temps en temps, ce que le noyau
pourra supporter plus longtemps.
Il y a deux étapes simultanées :
- L’interaction forte assemble la particule α dans le noyau
- La particule α frappe les bords du noyau
Pour en sortir : par cette méthode elle en a pour 4,5x109 années (âge de la terre)…
En fait, sa fonction d’onde (ou plutôt le carré de sa fonction d'onde) nous indique
que sa probabilité de présence à l’extérieur du noyau n’est pas nulle. Elle peut donc
passer, tel le passe muraille à travers la barrière de potentiel, sans avoir à la frapper :
c’est l’effet tunnel.
Il n’y a pas vraiment d’α préformé dans un noyau radioactif α: les deux phénomènes
sont simultanés.
Remarque: l’effet tunnel n’est PAS un processus d’interaction forte, car il peut tout
aussi bien se produire pour des électrons par exemple, qui sont -je vous le rappelle-
insensibles à l'interaction forte. C'est un phénomène quantique. L'effet tunnel des
électrons est à la base du principe du fonctionnement du Microscope à Effet Tunnel.
b) Fission spontanée
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 37

38. C’est un processus d’interaction forte (voir chapitre 3) pour désexciter un noyau
ayant un nombre de nucléons et de protons trop élevé: l'interaction forte est donc
responsable de la fission nucléaire!
Dans ce type de transformation, on a par exemple: X → Y + Z, Y et Z étant des
noyaux fils et non de petites particules comme les α ou les β-.
3- Désexcitation par interaction faible
a) Emission β-
A A ___ 0
X → Y + β + νe (notation de l'antineutrino= l'antiparticule
-
Z Z+1 -1 du neutrino)
L’électron et l’antineutrino sont créés puisqu’ils ne préexistent pas dans le noyau.
Le neutron libre est émetteur β - : n → p + e- , car la masse du neutron est
supérieure à celle du proton.
Ce qu’il se passe : A (nombre de nucléon) restant identique (transformation
isobarique), un neutron devient proton dans le noyau.
La composition en quarks du boson change : udd devient uud : un d devient u sous
l’influence du boson intermédiaire W - (β -), c'est à dire que le neutron devient proton;
ceci provoque l’émission d’un électron et d’un antineutrino.
Le noyau, passe de Z protons à Z+1 protons.
Z+1 est le nouveau numéro atomique, qui indique le nombre de protons et d’électrons.
Mais le cortège électronique n'est pas encore affecté par ce changement:
L’atome fils va donc être temporairement ionisé:
M (Y) = M [Y(A, Z+1)] + Zme (et non (Z+1)me)
masse de l'atome fils = masse du noyau à Z+1 protons + masse des Z électrons
(l'énergie de liaison du cortège électronique au noyau est négligée)
Donc M (Y) = M (A,Z+1) - me
Il manque un électron à l’atome fils.
Si l’on fait le bilan :
Noyau X + électrons de X → Noyau Y + électrons de Y + β-
M(A,Z)c² + Zmec² → M(A,Z+1)c² + Zmec² + mec²
Q β- = M(A ,Z)c² - M(A,Z+1)c² - mec² Q β- = DDMc² - mec²
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 38

39. Noyau X + électrons de X → Noyau Y + électrons de Y + β-
M(A,Z)c² + Zmec² → M(A,Z+1)c² + Zmec² + mec²
M(A,Z)c² → M(A,Z+1)c² – mec² + mec²
M(A,Z)c² → M(A,Z+1)c²
Q β- = M(A,Z)c² - M(A,Z+1)c² Q β- = DD M c²
Le noyau fils peut être émis à l’état excité; il se désexcitera par isomérisme γ ou CI
(+/- photon X et électron auger)
Que va devenir l'énergie libérée par la désexcitation ? Elle se répartira, comme nous
l'avons vu en introduction,
-en énergie de recul du noyau fils (négligée),
-en énergie d'excitation du noyau fils; dans ce cas le noyau fils se désexcitera par
isomérisme γ ou CI (+/- photon X et électron auger),
-et énergie cinétique des particules.
Dans l'émission β-, deux particules sont émises: un électron et un antineutrino.
L'énergie cinétique va donc se répartir entre le β- et l'antineutrino. La plupart du
temps, elle se répartit également: moitié-moitié, mais il peut aussi arriver que le β-
prenne plus d'énergie et l'antineutrino moins, et vice-versa.
On peut tracer le diagramme d'énergie des β- représentant le nombre de particules
possèdant une certaine énergie. Le meme diagramme peut etre tracé pour
l'antineutrino. Comme le β- et l'antineutrino peuvent prendre toutes les valeurs de
l'énergie entre 0 et Q β- MAX, on dit que leur spectre est continu. Ceci s'oppose aux
particule alpha émises lors de l'émission alpha, ainsi qu'aux neutrinos émis lors de la
capture électronique, qui sont monoénergétiques parce qu'ils sont seuls: aucune autre
particule n'est là pour les aider à rétablir la continuité dans le spectre énergétique.
(voir schéma du polycopié du Dr Victor)
De plus, leur spectre est généralement centré sur Q β- MAX/2 (ou E β- MAX/2, c'est
équivalent), c'est à dire que la plupart des désexcitations se soldent par un partage
équitable de l'énergie entre β- et antineutrino.
Parfois, le spectre des β- n'est pas centré sur E β- MAX/2. Il s'agit de l'effet
coulombien: les protons du noyau, qui portent une charge positive, ont tendance à
retenir les β-, et donc à diminuer leur énergie cinétique, à les ralentir. Le spectre des β-
va donc se décaler vers la gauche du graphique.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 39

40. b) Emission β+
A A 0
X → Y + β+ + νe
Z Z-1 1
1 1 0
Attention p
+ →
n + e+ + νe
1 0 +1
mn > mp donc un proton libre ne peut pas être émetteur β+ comme le neutron pouvait
être émetteur β-.
Cette transformation est elle aussi isobarique, c'est à dire que le père et le fils ont le
même nombre de nucléons.
Le noyau, de Z protons passe à (Z-1) protons : là encore le cortège électronique
n’est pas directement affecté par ce changement.
L’atome fils va donc avoir temporairement un électron de trop.
M(Y) = M(A,Z-1) + Zme (et non (Z-1)me)
M(Y) = M(A,Z-1) + me
(on néglige les énergies de liaison du cortège électronique au noyau, là encore)
Il y a un électron de trop à l’atome fils.
Si l’on fait le bilan :
Noyau X + électrons de X → Noyau Y + électrons de Y + β+
M(A,Z)c²+Zmec² → M(A,Z-1)c² + Zmec² + mec²
Qβ+ = M(A,Z)c² - M(A,Z-1)c² - mec² Qβ+ = DDMc² – mec²
Noyau X + électrons de X → Noyau Y + électrons de Y + β+
M(A,Z)c²+Zmec² → M(A,Z-1)c² + Zmec² + mec²
→ M(A,Z -1)c² + (Z-1)mec² + mec² +mec²
M(A,Z)c² → M(A,Z-1)c² + mec² + mec²
→ M(A,Z-1)c² + 2mec²
Qβ+ = M(A,Z)c² - M(A,Z-1) - 2mec² Qβ+ = DD M c² – 2mec²
= DD M c² – 1,022 MeV
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 40

41. Le noyau fils peut être émis à l’état excité; il se désexcitera par isomérisme γ ou CI
(+/- photon X et électron auger)
Attention : Qβ+ doit être positif Qβ+ > 0
DD M c² - 2mec² > 0
DD M c² > 2mec²
Pour pouvoir faire une émission β+ , il FAUT POUVOIR S’AFFRANCHIR
D’ABORD de CETTE ENERGIE de 2mec² = 1,022 MeV
La différence de masse entre atome père et atome fils doit toujours être ≥1,022
MeV pour que l’émission β+ ait lieu.
Le β+ est de l’antimatière : à peine émis, il va rencontrer un électron ; ces deux vont
s’annihiler, créant 2 photons de 0,511 MeV.
Que va devenir l'énergie libérée par la désexcitation ? Elle se répartira, comme nous
l'avons vu en introduction,
-en énergie de recul du noyau fils (négligée),
-en énergie d'excitation du noyau fils; dans ce cas le noyau fils se désexcitera par
isomérisme γ ou CI (+/- photon X et électron auger),
-et énergie cinétique des particules.
Dans l'émission β+, deux particules sont émises: un positon et un neutrino.
L'énergie cinétique va donc se répartir entre le positon et le neutrino. La plupart du
temps, elle se répartit également: moitié-moitié, mais il peut aussi arriver que le
positon prenne plus d'énergie et le neutrino moins, et vice-versa.
On peut tracer le diagramme d'énergie des positons représentant le nombre de
particules possèdant une certaine énergie. Le meme diagramme peut etre tracé pour le
neutrino. Comme le positon et le neutrino peuvent prendre toutes les valeurs de
l'énergie entre 0 et Q β+ MAX, on dit que leur spectre est continu. Ceci s'oppose aux
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 41

42. particule alpha émises lors de l'émission alpha, ainsi qu'aux neutrinos émis lors de la
capture électronique, qui sont monoénergétiques.
(voir schéma du polycopié du Dr Victor)
De plus, leur spectre est centré sur Q β+ MAX/2 (ou E β+ MAX/2, c'est équivalent), c'est
à dire que la plupart des désexcitations se solde par un partage équitable de l'énergie
entre positon et neutrino. .
Parfois, le spectre des β+ n'est pas centré sur E β+ MAX/2. Là aussi, il s'agit de l'effet
coulombien: les protons du noyaux, qui portent une charge positive, ont tendance à
repousser les positons, et donc à les accélérer, à augmenter leur énergie cinétique. Le
spectre des β+ va donc se décaler vers la droite du graphique.
c) Capture électronique
Certains noyaux ont une instabilité β+ mais ne peuvent s’affranchir du seuil de
1,022 MeV. Ils vont donc utiliser la capture électronique (CE).
NB : Les noyaux qui peuvent s’affranchir du seuil et faire du β+, peuvent également
faire la CE. Ceux qui ne peuvent s’affranchir du seuil ne pourront eux faire QUE de la
CE.
A A
X + e → Y + νe
-
Z Z-1
Au bilan QCE = M(A,Z)c² - M(A,Z-1)c² - | El |
= DD M c² - | El |
(El étant l’énergie de liaison de l’électron capturé)
Il y a donc là aussi un seuil, correspondant à l'énergie de liaison de l'électron capturé
à sa couche, mais ≤100keV, très faible : un très petit nombre de noyaux ne peuvent
s’en affranchir.
Pour les noyaux à instabilité β+:
Lorsque seule la CE est possible, il n’y a que de la CE.
Quand β+ et CE sont possibles dans les noyaux légers, les deux se produisent à égale
probabilité.
Quand β+ et CE sont possibles dans les noyaux lourds, la CE l’emporte : Z augmente,
la densité des électrons augmente tout comme leur probabilité d’être dans le noyau.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 42

43. L'énergie libérée peut se répartir:
-en énergie de recul du noyau fils (négligée),
-en énergie d'excitation du noyau fils; dans ce cas le noyau fils se désexcitera par
isomérisme γ ou CI (+/- photon X et électron auger),
-et énergie cinétique des particules.
Dans le cas de la capture électronique, une seule particule est émise: le neutrino.
Celui-ci va donc récupérer la totalité de l'énergie libérée par la désexcitation; ou bien,
si le noyau fils est émis à l'état excité, il prendra l'énergie restante. Son énergie ne peut
donc prendre que certaines valeurs bien précises: il est dit monoénergétique.
Dans tous les cas, l’atome fils Z-1 Y est émis à l’état excité, avec une lacune
profonde dans son cortège : Il y a donc rayonnement X et électron Auger par cascade
lors du réarrangement.
Le noyau fils peut être émis à l'état excité, il s’en suivra alors les phénomènes
d’isomérisme γ et de conversion interne (+ électron auger et fluorescence X).
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 43

44. 4 - Ligne de stabilité
Il faut savoir s’y repérer, savoir ou est présenté N,A, Z…
Ici si l’on prend un noyau père X (N,Z) :
la case en haut à gauche correspond au noyau Y(N+1,Z-1)
la case en haut à droite Y(N+1,Z+1)
la case en bas à gauche Y(N-1,Z-1)
la case en bas à droite Y(N-1,Z+1)
Ex : un atome X subit une désintégration β-:
Il gagne un proton : Z+1
Il perd un neutron : N-1
Isobarique: même nombre de nucléons : reste sur la même diagonale.
Même chose pour β+.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 44

45. A BIEN SAVOIR POUR CE CHAPITRE :
Qβ- = (DDM - me) c² Qβ+ = (DDM - me) c²
Qβ- = (DDM ) c² Qβ+ = (DD M- 2me) c²
Emission β- Emission β+ CE
X/Auger
X/Auger X/Auger X/Auger X/Auger
(2 photons γ de 0,511 MeV)
Ne pas oublier le seuil de 1,022 MeV en β+!
Explication des cas:
- un noyau X se désintègre par β-: il passe d'un niveau d'énergie Qmax, à un niveau
d'énergie 0, soit directement, soit en passant par un état intermédiaire où le noyau fils
est excité; celui ci atteindra l'état fondamental par émission de photons γ ou par
conversion interne, en transmettant son énergie à un électron, qui, après avoir été
décroché (voir le seuil), part avec l'énergie d'excitation du noyau.
- un noyau se désintègre par β+:
- par émission β+: il s'affranchit de son seuil de 1,022 MeV, puis donne
l'énergie restante, Qmax - 1,022, au positon; il peut également passer par des états
excités intermédiaires, où le noyau se débarasse de son excitation par CI ou γ, les CI
occasionnant fluorescence X et Auger. Parallèlement, il y a aura toujours émission de
2 photons d'annihilation de 0,511 MeV.
- par capture électronique: il s'affranchit du seuil qui correspond à
l'énergie de liaison de l'électron à sa couche, puis donne l'énergie restante Qmax - EL,
au neutrino; il peut passer par des états excités intermédiaires, où le noyau se
débarasse de son excitation par CI ou γ, les CI occasionnant fluorescence X et Auger.
Dans tous les cas, il y aura toujours une fluorescence X, et éventuellement des
électrons Auger, à cause de la capture électronique.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 45

46. © Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 46

47. Formulaire de physique
du noyau
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 47

48. I - Notions de mécanique quantique
Quantité de mouvement en physique classique: p=mv
Quantité de mouvement d'un objet quantique: p= 2mE
c
Lien entre longueur d'onde et fréquence: =

Energie d'une onde: E=h∗
Energie d'une particule: E= p∗c
E h
Relations fondamentales de la mécanique quantique: = et =
h p
Equation aux valeurs propres: Ôu=λ u
−h d
Opérateur Hamiltonien: Ĥ= ∗ 
 2 i dt
Equation de Schrodinger: Ĥ Ψ=EΨ
Relations d'indétermination de Heisenberg: Δp . Δx ≥ ħ et ΔE . Δt ≥ ħ
II - Interactions fondamentales
ħ
Portée d'une interaction:  r = mc
III - Stabilité du noyau
Unités et conversions
Unité de masse atomique: 1 u = M (12C) / 12
Unité de masse atomique et nombre d'Avogadro: 1 u = 1 / N g
1 eV = 1,6x10-19 J
1 u = 1,66 . 10-27 kg
1 u = 931,5 MeV / c²
Masses du noyau, de l'atome, de la mole
Masse approchée du noyau et de l'atome: M ≈ M ≈ A u
Masse approchée d'une mole: m (1 mole) ≈ A g
Masse exacte du noyau: M(A,Z) = Z mp + N mn – DDM
Masse exacte de l'atome: M(A,Z) = M(A,Z) + Zme- – | El |
M(A,Z) = Z mp + N mn – DDM + Zme- – | El |
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 48

49. Défaut et excès de masse
Défaut de masse: DDM = Z mp + N mn – M
Excès de masse: EM = [M(A,Z) - A] u
= [M(A,Z) - A] * 931,5 MeV / c²
Différence des excès de masse: DDEM = DD M
Rayon du noyau, énergie de liaison
Rayon du noyau: R = roA1/3 = 1,3A1/3
Energie de liaison: B = DDM c²
= avA - as A2/3 - ac (Z2 / A1/3) - aa [(N-Z)2/A] + c
IV - Instabilité du noyau
Généralités
Différence de masse: DDM = masse des particules à l'état initial – masse des particules
à l'état final
Energie libérée par la réaction: Q = DDM c²
Désexcitation de l'atome
Photon X: EX= { Ei – Ef}
Electron Auger: Ee-Auger= { Ei - Ef } - | El |
Donc Ee-Auger= EX - | El |
Désexcitation par interaction électromagnétique
Isomérisme nucléaire Eγ = { EI – EF}
Conversion interne: Ee- = { Ei - Ef } - | El |
Donc Ee-CI = Eγ - | El |
Désexcitation par interaction forte
Emission α : Qα = E(α) + Erecul (négligée)
= DDM c²
Désexcitation par interaction faible
Emission β- : Qβ- = (DDM - me) c²
= (DD M ) c²
Emission β+ :Qβ+ = (DDM - me) c²
= (DDM- 2me) c²
Capture électronique: QCE = DD M c² - | El |
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 49

50. © Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 50

51. Correction détaillée de
certains exercices du
polycopié du Dr Victor
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 51

52. Dans ces corrections détaillées, seules les formules ont été écrites, pour éviter
d’encombrer les pages de calculs fastidieux, avec des nombres à rallonge … à vous de
faire les calculs.
Les formules fondamentales sont écrites le plus souvent une fois, en gras ; elles sont
ensuite directement utilisées dans la forme qui est intéressante pour l’item.
Remarque : dans ces formules, tous les c2 ont été mentionnés, pour éviter de perturber
ceux qui trouvent que sans eux les formules sont fausses. Ceux-là ont raison,
cependant force est de reconnaître que cette pléthore de c2 encombre un peu les
équations, et qu’il est plus facile de les oublier, sans se tromper pour autant à la fin du
calcul sur le résultat, que d’y penser à chaque fois. Ainsi, il n’est pas impossible qu’au
détour d’un QCM de concours, un c2 passe à la trappe … et que l’item soit juste. N’y
faites pas attention, et habituez vous plutôt à les sous-entendre.
Pour tous les exercices, on a 1u = 931,5 MeV/c2 ; n'oubliez pas que B est exprimée en
Mev!
A2 :
M = M + me
M = mn + mp - DDM + me
= mn + mp – B/(931,5 * c2) + me
mn = M – mp – B/(931,5 * c2) – me.
A3 : A
M= mn + mp – DDM
= mn + mp – B/(931,5 * c2)
= mn + mp – ((B/A) / (931,5 * c2)) * A
B1
M = mn + mp – DDM + me
DDM = mn + mp + me – M
B2 : C
DDM = Zmp + Nmn – M
B/A = (Nmn + Zmp – M) u * 931,5 * c2 / A
C1 : A
2 H → He + Q
2 M(H) – M(He) – Q/(931,5 * c2) = 0
M(H) = ( M(He) + Q/(931,5 * c2) ) /2
C2 : C
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 52

53. On note x le nombre d’atomes de tritium dans 1mg de tritium. On note Q(1mg) et
Q(1atome) l’énergie libérée pour une réaction mettant en jeu 1mg ou 1atome de
tritium respectivement.
On note m(échantillon) la masse de 1mg de tritium et m(1atome) la masse de l’atome
de tritium en mg (il faut convertir cette masse de u au mg)
Q(1mg) = Q(1atome) * x
= Q(1atome) * m(échantillon) / m(1atome)
C3 : ADE
A,B : Q/A = Q/5
C,D : Q(1g) = Q(1atome) * m(échantillon) / m(1atome)
E : le noyau est défini par Z. Z = 2 donc c’est de l’hélium.
D1 : C
On note x le nombre de fissions engendrées par seconde.
On a : Puissance = rendement * nombre de réactions* Energie d'une fission* temps
On a T=1s car 1Watt=1 Joule*seconde
Donc P = ro * x * Q(1fission) * Δt
x = P /( ρ * Q(1fission)*1,6.109*Δt)
E1 :
Q = (M(S) + M(He) – M(Cl) – m(proton) ) * 931,5 * c2
F1 : E
(cf schéma page suivante)
Q = E(γ) + E(βmax)
Q = DD M c2 – 1,022
DD M c2 – 1,022 = E(γ) + E(βmax)
DD M = (E(γ) + E(βmax) + 1,022) / (c2 * 931,5)
M(B)= M(A) - (E(γ) + E(βmax) + 1,022) / (c2 * 931,5)
F2 : C
(cf schéma page suivante)
E(βmax) = DD M c2 – 1,022 - E(γ)
F3 : CD
(cf schéma page suivante)
Q = DD M c2 – | El |
F4 : B
(cf schéma page suivante)
M(A) = M(B) + (E(γ) + E(βmax) + 1,022) / (c2 * 931,5)
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 53

54. F5 : CD
E(γ) = DD M c2 – 1,022 - E(βmax)
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 54

55. G1 : BD
A. Ce sont des radioéléments lourds.
C. Transformation d’un neutron en proton.
E. Des éléments instables
G2 : B
A. Inférieure à celle de ses constituants.
C. Le nucléon a une masse d’environ 1u. Les neutrinos sont bien plus légers, on ne les
prend même pas en compte dans les bilans de masse dans les transformations béta+ ou
béta-.
D. Inversement proportionnelle.
E. C’est la valeur de 1 eV.
G3 : BDE
A. Des noyaux d’Hélium.
C. 4 fois : leur masse est d’environ 4 fois la masse du nucléon.
G4 : BCE
A. Certains seulement : ceux qui peuvent s’affranchir du seuil de 1,022 MeV.
D. Une différence supérieure au seuil de 1,022 MeV.
G5 : ABCD
E. Attention, il s’agit de M(A,Z+1) et non M(A,Z-1).
G6 : B
A. voir G2 C.
C. C’est la valeur du nombre d’Avogadro.
D. ?
E. Elle est inférieure.
G7 : AC
B. Même nombre de nucléons.
D. De l’énergie est libérée.
E. Elle est de loin supérieure, sans quoi il n’y aurait pas de cohésion nucléaire.
G8 : A
B. C’est un spectre monoénergétique.
C. Non pas l'inverse d'un nombre de noyaux radioactifs.
D. C’est une transformation isomérique.
E. C’est le phénomène de capture électronique.
G9 : BCD
A.L'activité est proportionnelle au nombre de noyaux non désintégrés.
E. C’est un transformation isobare.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 55

56. Correction détaillée de certains QCM d'annales
Énoncé commun aux QCM 2, 3 et 4 (annales 2004-2005)
On donne le schéma de désintégration du cuivre 64.
64
29 Cu35
64 Ni *
1
-

γ 2 + 64
Zn stable

64 Ni stable
E.M. 64Cu  = −65 423 keV / c²
• Les excès de masse de ces éléments sont : E.M. 64Zn  = −66 001 keV /c² ;
E.M. 64 Ni  = −67 098 keV /c²
• L'énergie de liaison des électrons de la couche K du cuivre est de -9 keV ;
• ε1 et ε2 sont des captures électroniques ;
• E  = 1346 keV.
QCM 2 :
A. Le zinc 64 a 30 neutrons et 34 protons
B. Le nickel 64 a 28 protons et 34 neutrons
C. 64Cu  64 Zn  +   e
29 30
D. 64Cu  64 Ni  +  e
29 28
E. 29Cu  e -  64 Ni   e
64
28
QCM 3 :
A. Le cuivre 64 est un noyau impair-pair
B. La différence d'excès de masse entre le cuivre 64 et le nickel 64 est 1346 keV/c²
C. La différence d'excès de masse entre le cuivre 64 et le zinc 64 est 578 keV/c²
D. L'énergie maximale du spectre β+ est de 653 keV
E. L'énergie maximale de spectre β- est 329 keV
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 56

57. QCM 4 :
A. La transmutation du Cuivre en Zinc s'effectue par transformation d'un neutron en
proton
B. Cette transformation d'un neutron en proton est médiée par un boson intermédiaire
W-
C. La désintégration du cuivre 64 produit aussi des neutrinos monoénergétiques de 320
keV
D. Le spectre γ du cuivre 64 comporte 2 raies : l'une à 511 keV et l'autre à 1 346 keV
E. B Cu − B  Ni = 2675 keV
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 57

58. Correction
QCM 2 : DE
A. Le zinc est obtenu par émission β- du cuivre 64, il possède donc le même nombre de
nucléons A et un proton de plus , soit Z(Cu) + 1 = 30. De plus, le nombre de neutrons
est 35.
B. Même raisonnement en β+, ici le nickel possède le même A mais un proton en
moins, soit Z(Cu) – 1 = 28. Le nombre de neutrons est 36.
C. La désexcitation du cuivre en zinc est une émission β- et non β+.
QCM 3 : CD
A. A = 64 et Z = 29 donc N = 64 -29 = 35, le cuivre 64 est donc un noyau impair-
impair.
E.M. 64Cu  = −65 423 keV /c²
B. donc DDEM(Cu–Ni) = (-65423) - (-67098) = +
E.M. 64 Ni  = −67 098 keV /c²
1675 keV/c².
C. VRAI. Même méthode qu'en B.
D. Pour une émission β+, E  max = DDEM − 1022 keV et
+
E  max = 653 keV /c² .
+
E. Pour une émission β-, E  max = DDEM donc E  max = 578 keV / c² .
+ +
QCM 4 : ABCD
A et B. VRAI. Le modèle des quarks est explicite pour l'émission β-, cf poly du Dr.
Victor.
C. VRAI. On sait que Eγ = +1346 keV/c². Or, DDM(Cu-Ni) = +1675 keV/c²,
donc DDM(Cu-Ni*) = Eε1 = 1675 – 1346 = 329 keV.
QCE = Eν = DDM(Cu-Ni*)c² - |El| = 329 – 9 = 320 keV.
D. VRAI. Un photon d'énergie Eγ = 1346 keV pour la capture électronique, et deux
photons d'énergie Eγ = 511 keV émis lors de l'annihilation du positon issu de la
désexcitation β+.
E. B(Cu) – B(Ni) = [29mp + 35mn + 29me – M(Cu)] - [28mp + 36mn + 28me -
M(Ni)]
= mp – mn + me – DDEM ≈ - 2450 keV.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 58

59. Janvier 2006
Au spectre β+ se superpose une raie d'électrons négatifs monoénergétiques de
0,501 keV. Le spectre électromagnétique comporte un rayonnement γ de 511 keV
et un rayonnement Xk de 0,525 keV.
Données:
EM (18F) = 873,40 keV / c²
EM (18O) = - 782,20 keV / c²
Energies de liaison des électrons atomiques de l'oxygène 18: Couche K: - 0,532
keV Couche L1: - 0,024 keV Couche L2: - 0,007 keV
QCM 3:
A. Le noyau de fluor 18 possède 9 neutrons et 9 protons.
B. Il n'existe que peu de noyaux impair-impair stables.
C. La relation de transformation β+ du fluor 18 s'écrit: 189F → 188O + e- + νe
D. L'autre tranformation possible du fluor 18 est une conversion interne.
E. L'autre tranformation possible du fluor 18 s'écrit: 189F + 0-1e → 188O + νe
QCM 4:
A. Par convention, l'état fondamental du fils représente le zéro des énergies.
B. Eβ+max = DDMc² – mec²
C. La différence des masses atomiques entre le fluor et l'oxygène est 1655,6 keV / c².
D. L'énergie maximale du spectre β+ est 633,6 keV.
E. Le rayonnement γ de 511 keV correspond à des photons d'isomérisme de l'oxygène.
QCM 5:
A. Lors de la capture électronique, l'atome fils est temporairement ionisé.
B. La capture électronique crée une lacune profonde dans le cortège électronique de
l'atome fils.
C. Le rayonnement Xk de 0,525 keV correspond à la transition électronique L1K de
l'oxygène.
D. Les électrons monoénergétiques de 0,501 keV sont des électrons de conversion
interne.
E. Les électrons monoénergétiques de 0,501 keV sont des électrons Auger L2 de
l'oxygène.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 59

60. Correction
QCM 3: ABE
B. VRAI. Leur énergie d'appariement c est négative. Seuls 5 noyaux impair-impair
sont stables.
C. C'est un positon qui est émis, et non un électron.
D. Tout émetteur β+ est capable de se transformer par capture électronique. La
conversion interne correspond à une désexcitation par interaction électromagnétique,
sans modification de la composition du noyau.
E. VRAI. C'est justement l'équation de la capture électronique.
QCM 4: ACD
B. Eβ+max = DDMc² – 2mec².
C. On a DDM = DDEM = EM(F) – EM(O) = 873,4 + 782,2 = 1655,6 keV.
D. Eβ+max = DDMc² – 2mec² = 1655,6 – 1022 = 633,6 keV.
E. Le rayonnement γ de 511 keV correspond à des photons issus de l'annhilation du
positron émis lors de la désintégration β+ avec un électron.
QCM 5: BE
A. L'atome fils est temporairement excité, et non pas ionisé: un proton et un électron
forment un neutron, donc le noyau et le cortège du noyau fils contiennent le meme
nombre de charges.
B. VRAI. C'est pourquoi l'atome fils est temporairement excité.
C. Le rayonnement X provient de la transition d'un électron du cortège d'une couche à
l'autre. Pour la série de Lyman (rappelez vous la chimie ...), on a deux transitions
possibles: L1-K et L2-K. Pour la série de Balmer, on a une transition possible: L2-L1.
L'énergie des rayonnements X émis lors de ces transitions sont: 0,508keV pour la
transition L1-K, 0,525keV pour la transition L2-K, et 0,017 keV pour la transition L2-
L1. Il semble donc que le rayonnement Xk observé corresponde à la transition
électronique L2K de l'oxygène.
D. et E. Il nous reste maintenant à définir l'origine des électrons monoénergétiques de
0,501 keV. Ces électrons pourraient etre des électrons de conversion interne de
l'oxygène, ou bien des électrons Auger de l'oxygène. On peut éliminer l'hypothèse de
la conversion interne: si cette hypothèse était vraie, on observerait des rayonnements γ
d'isomérisme nucléaire, d'énergie voisine.
Il s'agit donc d'un électron Auger. Le plus probable est que cet électron provienne de la
couche L2. Le but est donc de trouver de quelle transition électronique l'énergie
donnée à l'électron Auger est issue. D'après la formule Ee-Auger= { Ei - Ef } - | El | ,
on écrit
0,501 = { Ei - Ef } - 0,07, donc { Ei - Ef } = 0,508 keV. L'énergie de la transition
électronique recherchée est donc 0,508 keV. Cette transition est donc la transition L1-
K. Au final, on a une transition d'un électron de la couche L1 vers la couche K;
l'énergie libérée par cette transition (0,508 keV) est transmise par couplage quantique à
un électron de la couche L2, qui est éjecté avec une énergie de 0,501 keV.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 60

61. Janvier 2007
QCM 1 : Toute « particule » quantique :
A. a une fonction d'onde non nulle
B. obéit au principe d'exclusion de Pauli
C. possède un spin
D. obéit au principe de causalité
E. peut vérifier des états superposés
QCM 2 : L'interaction forte :
A. est indépendante de la charge électrique
B. est répulsive à très courte distance
C. est très fortement attractive sur des distance supérieures à 3F
D. est médiée par les mésons
E. permet d'expliquer la cohésion des hadrons
QCM 3 : Selon le modèle de la goutte liquide et en supposant les noyaux
sphériques :
A. le rayon du noyau est proportionnel au nombre de nucléons
B. le volume du noyau est proportionnel au cube du rayon
C. le rayon du noyau d'aluminium 27 est juste un peu supérieur au double du rayon du
noyau de tritium.
D. l'énergie de surface est proportionnelle à la puissance ¾ du nombre de nucléons
E. l'énegie coulombienne est proportionnelle à la puissance 1/3 du nombre de nucléons
QCM 4 : On donne la masse des noyaux de 3 isobare A = 14
M  14 N  = 13 040,2 MeV /c²
7
14
M  6C  = 13 041,7 MeV /c²
M  14O  = 13 045,6 MeV /c²
8
La masse totale de 7 protons et 7 neutrons indépendants est 13 144,9
MeV/c²
On rappelle que (mn – mp) = 1,3 MeV/c²
A. le noyau d'azote est impair/impair
B. le noyau d'oxygène a un neutron de plus et un proton de moins que le noyau d'azote
C. l'énergie de liaison de l'azote 14 est 104,7 MeV
D. l'énergie de liaison du carbone 14 est 104,7 MeV
E. l'énergie de liaison par nucléon de l'oxygène 14 est 7,46 MeV
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 61

62. QCM 5 : Pour ces 3 isobares on donne maintenant les excès de masse :
14
E.M. 7 N  = 2,864 MeV / c²
E.M. 14C  = 3,020 MeV /c²
6
14
E.M. 8O  = 8,006 MeV /c²
A. ces trois isobares se répartissent sur une seule parabole des masses
B. parmi ces trois isobares c'est quand même l'azote qui est l'élément stable
C. le carbone 14 produit l'azote 14 en émettant un β- d'énergie maximale 0,156 MeV
D. l'oxygène 14 produit du carbone 14 par l'émission d'un β+
E. le spectre β+ de l'oxygène 14 a une énergie maximale de 4,12 MeV
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 62

63. Correction
QCM 1: ACE
B. Seuls les fermions obéissent au principe d'exclusion de Pauli.
D. Le principe de causalité est niée par la physique quantique.
QCM 2: AE
B. L'interaction forte est attractive à très courte distance.
C. Sa portée est d'environ 1,5 F.
D. Elle est médiée par les gluons.
QCM 3: BC
A. Le rayon du noyau est proportionnel au nombre de nucléons à la puissance 1/3.
B. VRAI. Rappel: le volume de la sphère est 4/3 πR3.
C. VRAI. Simple application numérique à partir de la formule: R = r0 A1/3
D. L'énergie de surface est proportionnelle à la puissance 2/3 des nucléons.
E. Elle est inversement proportionnelle à la puissance 1/3 du nombre de nucléons.
Pour se rappeler des puissances du nombre de nucléons, il faut bien comprendre qu'en
termes de dimensions, le nombre de nucléons, A, est homogène à un volume [L]3. On
peut écrire A = A3/3 . A partir de là, on retrouve que A1/3 a la dimension d'une longueur,
et A2/3 la dimension d'une surface.
QCM 4: ACD
B. Le noyau d'oxygène a 8 protons soit un de plus que l'azote. Il a 6 neutrons (14-8)
soit un de moins que l'azote.
C. VRAI. On a M(N) = 7mn + 7mp – Bc² donc B = 13144,9-13040,2 = 104,7MeV
D. VRAI. On a M(C) = 6mp + 8mn – B = 7mp + 7mn + mn – mp donc B =
13144,9+1,3-13041,7=104,5MeV
E. On a B = 7mp + 7mn – (mn-mp) – M(O) = 13144,9-1,3-13045,6= 98MeV
donc B/A = 98/14 = 7 MeV.
QCM 5: BCE
A.Une parabole de masse représente une courbe où Z est placé en abscisse et EM en
ordonnée. On aura une parabole correspondant aux noyaux pair-pair et une autre
correspondant aux noyaux impairs-impairs. Ici on a donc deux paraboles : une où sont
présents le carbone 14 et l'oxygène 14 qui sont pairs-pairs; et une avec l'azote 14 qui
est impair-impair.
B. VRAI. L'élément le plus stable a l'excès de masse le plus petit : il s'agit bien de
l'azote.
C. VRAI. L'énergie disponible est : E = ( EM(C) – EM(N) ) * c² = 3,020 – 2,864 =
0,156 MeV
D. VRAI. L'oxygène 14 produit de l'azote 14 par émission β+ .
E. L'énergie disponible est alors égale à : E = ( EM(O) – EM(N) – 1,022 ) * c² =
8,006-2,864-1,022 = 4,12 MeV.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 63

64. CCB 2007
QCM 2: A propos des bosons vecteurs
A. Ils ont une masse nulle.
B. Ils sont indétectables expérimentalement.
C. La fonction d'onde d'un boson vecteur est symétrique.
D. L'interaction électromagnétique s'effectue par courant neutre
E. Le médiateur de l'interaction forte a un spin demi entier.
QCM 3: Excès, défaut ou différence ?
A. L'excès de masse est toujours négatif.
B. Le défaut de masse est toujours positif.
C. L'équivalent énergétique de l'unité de masse atomique est: 1,66.10-27.(3.108)² MeV
/ c²
D. L'équivalent énergétique de l'unité de masse atomique est: 1,66.10-27.(3.108)²
Joules
E. L'opposé de l'excès de masse donne l'énergie de liaison d'un noyau.
QCM 4: On a préparé 24.1020 noyaux de Phosphore 3015P de masse atomique M
= 29,978 u ou 27 924,5 MeV / c². On utilisera me = 0,5 MeV / c² et (mp + mn + me)
= 2,016 u et N = 6.1023 mol-1
A. En utilisant le nombre de masse comme arrondi de la masse atomique, on peut
calculer qu'on a obtenu 120 mg de Phosphore.
B. M(3015P) = 27 917 MeV / c²
C. EM(3015P) = -20 493 keV / c²
D. La masse totale des nucléons indépendants qui composent ce noyau est 27 852
MeV / c².
E. B/A (3015P) = 8,135 MeV
QCM 5: Dans une série d'isobares A = 30 et Z consécutifs, on donne les excès de
masse (EM) suivants en keV:
Magnésium E.M.  30Mg  = − 9 100 keV /c²
12
Aluminium E.M. 30 Al  = − 15 890 keV /c²
13
30
Silicium E.M. 14 Si  = − 24 433 keV /c²
Phosphore E.M.  30 P  = − 20 200 keV /c²
15
30
Soufre E.M.  16S  = − 14 063 keV /c²
A. Ces isobares se répartissent sur deux paraboles des masses
B. Dans cette liste, l'élément stable est le Silicium
C. Le Phosphore 30 peut donner du Soufre 30 par transition β+.
D. Le Magnésium 30 peut donner de l'Aluminium 30 par capture électronique.
E. La différence d'excès de masse du Silicium au Phosphore est – 4 233 keV / c²
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 64

65. Correction
QCM 2: BCD
A. La masse de certains bosons vecteurs (le photon, les gluons, le graviton) est nulle,
mais la masse d'autres bosons vecteurs n'est pas nulle (les bosons W+, W- et Z0, les
mésons).
B. VRAI. Ils doivent etre détectables expérimentalement, sinon ce ne sont que de purs
produits théoriques.
C. VRAI. Ils obéissent à la statistique de Bose-Einstein.
D. VRAI. Le photon ne porte pas de charge électrique.
E. Les bosons vecteurs ont un spin entier ou nul.
QCM 3: BD
A. L'excès de masse peut etre positif, nul, ou négatif.
C. et D. L'équivalent énergétique de l'unité de masse atomique s'écrit E(u) = uc² (en
Joules).
E(u) = 1,66.10-27.(3.108)² Joules, ou bien E(u) = 1,66.10-27.c² . 1,6.10-19 eV= 981,5
MeV/c²
E. L'opposé de l'excès de masse ne donne rien du tout. Excès de masse et énergie de
liaison n'ont aucun lien.
QCM 4: ABCE
Amasseéchantillon = M * 24.1020
= 30 u * = 30 * 1,66 . 10-27 * 24.1020 kg = 30 * 1,66 . 10-21 * 24.1020
mg
B. M = M + 15me, donc M = M – 15 me (utiliser les données en MeV / c²).
C. EM = M (u) – A = 29,978 u – 30 = - 0,022 . 931 500 keV / c².
D. massenucléons = 15 (mp + mn + me) * 931,5 - 15 me
E. M = 15 (mp + mn + me) – DDM, donc DDM = [ 29,978 – 15 * 2,016 ] * 931,5
MeV / c²
B = DDM c² = [ 29,978 – 15 * 2,016 ] * 931,5 MeV.
B/A = [ 29,978 – 15 * 2,016 ] * 931,5 / 30 MeV.
QCM 5: ABE
A. VRAI. Ils se répartissent sur la paraboles des noyaux pairs-pairs et impairs-impairs.
B. VRAI. L'élément stable est celui dont l'excès de masse est le plus négatif.
C et D. Les transitions indiquées sont des désintégrations β-.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 65

66. Janvier 2008
QCM 2: la masse atomique du carbone 14 est 14,003242 u. Soit N le nombre
d'Avogadro.
A. La masse molaire du carbone 14 est 14,003242 kg.
B. La référence de l'échelle des masses molaires est la masse d'une mole de l'isotope
12 du carbone prise arbitrairement égale à 0,012 kg.
C. L'excès de masse du carbone 14 est – 0,003242 * 931,5 MeV / c².
D. Dans une masse de 0,003 kg de carbone 14 on pourrait comptabiliser 0,003 * N /
14,003242 noyaux.
E. Dans une massede 0,003 kg de carbone 14, on pourrait comptabiliser 3 * 14,003242
/ N noyaux.
QCM 3: Le bismuth 212 produit du thallium 208 par émission α. Le spectre
comporte 6 raies dont les énergies de désintégration, corrigées de l'énergie de
recul du thallium sont:
Eα0 = Qα = 6207 keV Eα1 = 6167 keV Eα2 = 5879 keV
Eα3 = 5734 keV Eα4 = 5714 keV Eα5 = 5591 keV
Les niveaux d'énergie du noyau de thallium sont à:
A. 40 keV
B. 328 keV
C. 432 keV
D. 576 keV
E. 616 keV
QCM 4: soit la réaction nucléaire α + AZBe → 126C + n
EM (α) = 2,425 MeV / c² EM (n) = 8,071 MeV / c² EM (Be) = 11,351 MeV
/ c²
A. Z = 4
B. A = 8
C. EM (12C) = 0
D. Q = 5,705 MeV
E. M(Be) = 9326,351 MeV / c²
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 66

67. QCM 5:
Dans une série d'isobares A = 30 et Z consécutifs, on donne les excès de masse
(EM) suivants en keV:
Magnésium E.M.  30Mg  = − 9 100 keV /c²
12
Aluminium E.M. 30 Al  = − 15 890 keV /c²
13
Silicium E.M. 30 Si  = − 24 433 keV /c²
14
Phosphore E.M.  30 P  = − 20 200 keV /c²
15
30
Soufre E.M.  16S  = − 14 063 keV /c²
A. Dans une telle série, les noyaux impair-impair sont moins stables que les noyaux
pair-pair.
B. L'aluminium 30 peut émettre un β- (moins) d'énergie maximale 8543 keV.
C. Le phosphore 30 peut émettre un β+ (plus) d'énergie maximale 4233 keV.
D. Le soufre 30 peut émettre un β+ (plus) d'énergie maximale 5115 keV.
E. Le rayon moyen de ces noyaux est de l'ordre de 4 F.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 67

68. Correction
QCM 2: B
A. La masse molaire du carbone 14 est de 14,003242 g /mol.
C. EM = M (u) – A = 0,003242 * 931,5 MeV / c².
D et E. On rappelle que 1u = 1/N g. Prenons le calcul en grammes: dans 3 grammes de
carbone 14, combien peut on comptabiliser de noyaux ? Il suffit de diviser 3g par la
masse de l'atome de carbone 14, en g. Donc 3 / (14,003242 u * 1/N g) = 3N /
14,003242 noyaux.
QCM 3: ABE
L'énergie maximale correspond à la production directe du thallium à l'état stable, elle
est égale à 6207 KeV. Hors le niveau du thallium à l'état stable est le niveau d'énergie
considéré comme égal à 0. Pour calculer les différents niveaux d'énergie du noyau du
thallium, il faut donc soustraire les différentes énergies des émissions alpha à
6207keV. On trouve alors des niveaux α1 α2 α3 α4 α5 respectivement égaux à 40, 328
473 493 et 616 keV.
QCM 4: ACD
A et B. On a 42 He + AZBe → 126C + 10 n donc A = 12-1-4 = 7 et Z = 6-2 = 4
C. VRAI. Par définition, la masse atomique exacte du carbone 12 est de 12 u, donc
l'excès de masse du carbone 12 est nul.
D. Il faut calculer la différence des excès de masse: Q = EM (α) + EM (Be) ( - EM
(C)) - EM (n).
E. on a EM = ( M(Be) – A) * 931,5MeV/c² soit M(Be) = EM/931,5 + A =
11,351/931,5 + 7 = 7,012 MeV/c²
QCM 5: BDE
A. Les excès de masse des noyaux impair-impair, dans cette série, sont plus négatifs
en moyenne que les excès de masse des noyaux pair-pair, donc les noyaux impair-
impair sont aussi stables voire plus stables (le plus stable étant le silicium).
B, C et D. Il faut calculer les différences d'excès de masse, et éventuellement
compléter avec un -2mec² pour les transformations béta+.
La désintégration β- de l'aluminium forme du silicium. Qβ- = DDEM (Al – Si) = EM
(Al) – EM (Si).
La désintégration β+ du phosphore forme du silicium. Qβ+ = DDEM (P – Si) -1,022
meV = EM (P) – EM (Si) – 1,022 MeV.
La désintégration β+ du soufre forme du phosphore. Qβ+ = DDEM (S – P) -1,022
meV = EM (S) – EM (P) – 1,022 MeV.
E. VRAI. Le rayon se calcule avec la formule: R = r0 A 1/3. On remarque que tous ces
noyaux ont le meme nombre de masse, ils ont donc sensiblement le meme rayon.
Astuce de calcul: au lieu de calculer 301/3, on prend un nombre proche: 27, qui est égal
à 33. R = 1,3 * 3 = 3,9. Le rayon est un peu supérieur à 3,9 Fermi.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 68

69. Thermodynamique
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 69

70. © Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 70

71. Partie I
Commentaires de
cours
Chapitre 1 :
Forces,
Vecteurs,
Travaux
Commenté par Elise Birague-
Cavallie
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 71

72. Introduction à la thermodynamique :
Définition :
Etude de la matière et de ses transformations dans tous les cas où intervient la température.
Un corps physique est constitué d’un grand nombre de particules dont l’évolution individuelle
n’est accessible ni à l’expérience ni à la précision théorique.
Cependant, il est possible de caractériser un comportement collectif par des grandeurs
mesurables à notre échelle.
Le lien entre les grandeurs thermodynamiques, à l’échelle macroscopique et les grandeurs
mécaniques, discontinus, à l’échelle moléculaire est de nature statistique : par le calcul
utilisant l’intégration.
Rappels mathématiques :
Scalaire :
Un scalaire est un point défini par une valeur numérique.
Exemple : une distance quantitative du point A au point B
La voiture va de A en B, l’info porte uniquement sur la distance.
Vecteur :
Un vecteur est défini par sa direction, son sens et sa norme. Sa norme est une valeur scalaire.
B est défini par ses coordonnées dans le repère (x, y, z).
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 72

73. On peut écrire que B = Bx .k + B y .i + Bz . j
Ou bien
Bx
B
By
Bz
(Bx,By,Bz) sont les valeurs de la norme de B selon les 3 axes (0x), (0y) et (0z) eux-
mêmes définis par leurs vecteurs directions i , j et k .
Produit scalaire :
Le produit scalaire de 2 vecteurs est égal à la projection orthogonale de v sur la droite ayant
comme direction u multiplié par le module de vecteur u (le résultat est un scalaire).
Dérivée :
La dérivée d’une fonction est la variation de cette fonction par unité de variation de sa
variable (le plus souvent).
f’(x) = df(x)/dx
Différentielle totale exacte (DTE) :
Soit f, une fonction qui varie selon 2 variables x et y : f(x,y).
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 73

74. df ( x, y ) = f ' ( x).dx + f ' ( y ).dy
 ∂f   ∂f 
=   .dx + 
 ∂ y  .dy

 ∂x y  x
∂ : dérivée partielle
Une DTE est définie par la propriété de commutativité:
∂ ² f ( x, y ) ∂ ² f ( x, y )
=
∂ x∂ y ∂ y∂ x
Mécanique classique :
On considère un référentiel (x,y,z).
Le point :
Est défini comme un scalaire.
La vitesse :
v représente la dérivée de la position de ce point par rapport au temps : dx/dt (sur un axe
par exemple)
Quantité de mouvement :
p = m.v
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 74

75. La force :
Est définie par la relation fondamentale de la dynamique : F = m.a
m.d v d p
F= =
dt dt
C’est une variation de quantité mouvement par unité de temps.
Travail d’une force :
Pour un travail infinitésimal, dW = F ⋅ d r
On applique au point une vitesse
v pendant un temps dt.
Le point se déplace d’une distance dr , dans la direction donnée par le vecteur d r .
D’un point A à un point B, il y a une succession d’états infinitésimaux dr, le travail de A en B
(WAB) est la somme des travaux élémentaires sur les trajets.
Le travail élémentaire est noté dW
B
La somme des dW est notée mathématiquement W= ∫ dW .
A
Cela signifie que l’on additionne les différents dW sur un trajet continu du point A au point B.
Le calcul mathématique revient à effectuer une intégration.
Puissance cinétique :
F , force totale appliquée à un point de masse m, de vitesse v , dans un référentiel (x,y,z)
dv
F = m.a = m.
dt
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 75

76. dv
Et F ⋅ v = m.v ⋅
dt
m.v ²
d( )
F⋅v= 2 = dEc
dt dt
1
L’énergie cinétique Ec est égale à m.v ² .
2
dEc
La puissance P est égale à .
dt
Energie cinétique :
Une force peut communiquer un mouvement à un point
Le travail élémentaire de la force pendant la durée élémentaire dt est dW = P .dt = dEc
Déplacement du point matériel M d’une position M1 à la date t1 à un point M2 à la date t2 :
déplacement infinitésimal dM.
W= ∫t1,t2 P .dt= ∫t1,t2 F ⋅ d M = Ec(t2)-Ec(t1)
Le travail dépend généralement du chemin suivi (en effet, il est non conservatif le plus
souvent).
La variation d’énergie cinétique entre 2 temps, dt, est égale au travail de la force qui lui est
appliquée (somme des travaux des forces qui s’exercent sur le système).
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 76

77. Forces conservatives :
- Champ de force :
Une force qui ne dépend que de son point d’application définit un champ de force.
Une ligne de niveau est l’ensemble des points de l’espace pour lesquels la force a une valeur
identique
z
P=m v
grad f
jk
i y
x
- Gradient :
Un gradient est un vecteur de composantes les dérivées partielles de la fonction scalaire f.
C’est la variation de la fonction scalaire suivant les lignes de niveaux, c’est-à-dire la variation
d’une grandeur dans l’espace.
- Travail de la force conservative :
Le travail est indépendant du chemin suivi, la force est conservée pendant le chemin.
W ANB = W AMB
Le travail sur une ligne de niveau est nul.
Dans le référentiel (x,y,z), on considère le point O(x0,y0,z0).
Alors f(A→B)=f(AOB)
W A→B = W A→O→B
f(A,B)= f(A,O) - f(B,O)
La variation de la fonction f entre A et O est égale à une énergie potentielle Ep(A)
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 77

78. - Déterminer si la force est conservative :
F de coordonnées (Fx,Fy) : F = Fx .i + Fy . j
∂ Fx ∂ Fy
On vérifie que: =
∂y ∂x
Soit f (x,y) fonction primitive de la force conservative F
 ∂f   ∂f 
df ( x, y ) =   .dx + 
 ∂ y  .dy

 ∂x y  x
dW = Fx .dx + Fy .dy
La force dérive d’une énergie potentielle :
Notation :
∂ Ep
Fx = −
∂x
∂ Ep
Fy = −
∂y
dW = − dEp pour une force conservative
F c = − grad Ep
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 78

79. Thermodynamique application :
C’est l’ensemble des études microscopiques que l’on additionne pour obtenir une étude
macroscopique.
Grandeurs extensives :
Relatives au système entier, elles sont additives lors la réunion de 2 systèmes.
Exemple : la masse d’un livre est une grandeur extensive: cela correspond à la somme des
masses de chaque page et de la couverture.
Grandeur intensive :
Elles sont définies en un point indépendamment de la quantité de matière.
Exemple : la masse volumique ρ.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 79

80. © Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 80

81. Chapitre 2 :
Chaleur
Température
Commenté par Salim
Kanoun
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 81

82. C’est une partie facile qui donne lieu chaque année à 1 ou 2 QCM (sur 6 ou 7), c’est donc une
partie à ne pas rater.
Vous avez tous plus ou moins des notions abstraites concernant la température, la chaleur,
vous verrez qu’elles sont des notions beaucoup plus concrètes que vous ne le croyez.
Les principaux objectifs de ce chapitre :
 Définir l’équilibre thermique d’un système thermodynamique.
 Comprendre les différences entre échelle Celsius et Kelvin.
 Comprendre les phénomènes d’agitation moléculaire et comprendre d’où provient la
force pressante.
 Définir et calculer l’énergie cinétique moyenne, la vitesse quadratique, l’énergie
interne.
 Différencier chaleur et température, définir la capacité thermique.
 Savoir utiliser l’équation d’état des gaz parfaits.
 Différencier grandeurs extensives et intensives.
 Savoir se placer dans le système étudié et comprendre le sens des échanges.
 Application : comment obtenir une température de 20°C dans un avion ?
1) Définir l’équilibre thermique d’un système thermodynamique :
Pré-requis : un système thermodynamique :
Un système thermodynamique est défini par une quantité de matière connue, limitée par une
paroi aux propriétés connues et exposée à des énergies internes et externes au système.
La paroi et le système peuvent avoir plusieurs caractéristiques :
 Par rapport à la matière :
 Laisse passer la matière : système ouvert.
 Ne laisse pas passer la matière : système fermé.
 Par rapport aux rayonnements :
 Laisse passer les rayonnements : paroi transparente.
 Ne laisse pas passer les rayonnements : paroi opaque.
 Par rapport aux forces mécaniques :
 Transmet les forces mécaniques : paroi souple.
 Ne transmet pas les forces mécaniques : paroi rigide.
 Par rapport à la chaleur :
 Permet les échanges de chaleur : paroi diatherme.
 Ne permet pas les échanges de chaleur : paroi adiabatique.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 82

83. En fonction des propriétés du système et de la paroi, on définit donc une qualité du système :
Transferts de : Oui Non
Matière Système ouvert Fermé
Chaleur Paroi diatherme Adiabatique
Force Paroi souple Paroi rigide
Rayonnement Paroi transparente Opaque
Attention : système isolé = fermé + adiabatique + rigide + opaque donc système isolé
implique système fermé mais pas l’inverse !
L’état d’équilibre thermique : c’est la mise à égalité des températures des deux systèmes en
relation via une paroi diatherme.
Autrement dit : si une paroi séparant deux systèmes n’est pas totalement adiabatique, la
température de deux systèmes est forcément égale au bout d’un certain temps.
Par exemple, c’est le cas de votre appartement, les murs n’étant pas adiabatiques si vous
éteignez votre chauffage la température à l’intérieur va tendre vers la température extérieure.
L’équilibre va être décalé vers la température extérieure : on se doute que la chaleur de votre
appartement ne suffira pas à réchauffer le monde entier…
Plus votre appartement sera isolé plus l’équilibre sera long à réaliser. A l’extrême, on peut
empêcher l’équilibre de se réaliser via une enceinte adiabatique (mais qui coûte bien trop cher
pour être utilisée dans le bâtiment).
L’équilibre thermique est un principe (aussi appelé principe zéro), il n’y a pas
d’exception connue, on le considère comme universel, en tout temps et en tout lieu de
l’espace.
Comment mesure-t-on la température ?
 Soit par comparaison, sans définir le « zéro » via un simple rapport c’est le
thermoscope.
 Soit en définissant un « zéro » et en comparant avec une échelle de nombres c’est
le thermomètre.
2) Comprendre les différences entre échelles Celsius (centigrade) et
Kelvin :
Les deux échelles ont le même « pas », c'est-à-dire qu’il revient exactement au même de dire
« le système a vu sa température augmenter d’un degré Celsius » et « le système a vu sa
température augmenter d’un Kelvin ».
En revanche, l’origine (le « zéro ») est différente.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 83

84. Comment sont calculés les deux zéros ?
 Dans l’échelle Celsius, c’est la température de la glace fondante (ou température de fusion
de l’eau ou température de liquéfaction).
C’est une échelle utile dans la vie de tous les jours, le signe indique par exemple la
présence possible ou non de verglas…
 Dans l’échelle Kelvin, l’approche du zéro est mathématique.
On mesure l’agitation moléculaire à plusieurs températures différentes et on trace
la courbe en fonction de ces valeurs.
On extrapole cette courbe pour obtenir la température pour laquelle les molécules
sont théoriquement immobiles : c’est le zéro absolu.
On tombe sur - 273,15°C (c’est un chiffre très important).
Aucune température ne peut être inférieure (il n’y pas moins mobile qu’immobile).
• En conséquence :
♦ La température en Kelvins n’est JAMAIS négative (sauf erreur de calcul)
♦ Pour trouver la température en Kelvins il faut AJOUTER 273,15 à une
température donnée en Celsius.
♦ L’échelle Kelvin étant basée sur une théorie physique c’est la seule
utilisable en thermodynamique.
Tout calcul en thermodynamique nécessite d’utiliser cette échelle (d’où
l’importance de ce nombre : 273,15 soit environ 273)
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 84

85. 3) Comprendre les phénomènes d’agitation moléculaire et
comprendre d’où provient la force pressante :
La température anime les molécules d’air ou de gaz.
Elles ont un mouvement aléatoire et peuvent donc se percuter entre elles et sur les
parois.
Les chocs sur la paroi provoquent une force normale à la paroi : la force pressante
(qu’il faut bien distinguer de la pression).
C’est une force très intense : D’ailleurs dans les avions où il existe un gradient de
pression entre une cabine pressurisée et l’atmosphère d’altitude à une pression
inférieure cela implique d’avoir une carlingue très rigide.
C’est même un problème de sécurité aérienne, suivant le nombre d’heures de vol, les
variations de vitesse… on détermine les forces qu’a subies l’avion.
Quand le risque de rupture devient supérieur à 1% on change l’avion…
Le terme de pression est abusif car il ne désigne qu’une valeur numérique alors qu’une
force est définie par une direction, un sens et une intensité (valeur en N).
La pression est un scalaire, pas une force ni un vecteur.
4) Définir et calculer l’énergie cinétique moyenne, la vitesse
quadratique, l’énergie interne :
L’énergie du système est contenue dans l’énergie qui provoque le mouvement des molécules.
Ces mouvements sont aléatoires : il n’y a pas de trajectoire ni de vitesse définie.
Ces mouvements étant aléatoires, il en résulte une équirépartition dans tous les plans de
l’espace.
La somme vectorielle de toutes les trajectoires est donc nulle.
Les particules en mouvement ayant une masse non nulle, ce mouvement est porteur d’une
énergie cinétique.
1
Elle s’exprime par la formule : Ec = m.V ² .
2
C’est une relation fondamentale dans la physique. Ainsi, l’énergie cinétique d’une particule
dépend de sa masse et de sa vitesse.
L’énergie Interne : pour un gaz parfait, c’est la somme de toutes les énergies
cinétiques (des différentes particules) (il n’y a pas d’énergie potentielle dans le
modèle du gaz parfait).
n= + ∞
1 1 1 1
On la notera donc : U = m1.V1 ² + m2 .V2 ² + ... + mn .Vn ² = ∑ mn .Vn ²
2 2 2 n= 1 2
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 85

86. En pratique, il faut simplifier cette expression.
i= + ∞
On définit donc la vitesse moyenne d’une molécule du gaz :
∑ Vn
V= n= 1
n.Ν
Rappel sur le nombre d’Avogadro (N) :
• Dire « il y a une mole de produit » revient à dire « il y a
6.02 × 10 23 molécules de ce produit ».
Cela est vrai pour tous les atomes et toutes les molécules.
• La masse molaire correspond en fait au nombre de molécules
contenues dans un gramme d’un élément donné.
On exprime ce nombre en fraction de mole (c'est-à-dire par unité
de 6.02 × 10 23 molécules)
Exemple : si dans un gramme il y a 12,04 × 10 23 molécules
(=2moles) la masse molaire est de 0,5g/mol
• Connaissant les masses molaires de tous les atomes, on déduit
les masses molaires des molécules en additionnant les masses
molaires de chaque atome qui les composent.
• La mole permet donc de passer d’une dimension que l’on a
l’habitude de mesurer (la masse), à celle d’un nombre de
molécules contenues dans un échantillon. Ceci est très utile
en physique- chimie : cette unité permet de savoir le nombre
de réaction qui va se produire, dans quelle proportion…
• Pour conclure, il suffit de multiplier le nombre de moles (n)
par 6.02 × 10 23 (N) pour avoir le nombre de particules
présentes (d’où le produit n.N dans le calcul de la vitesse
moyenne d’une molécule du gaz).
Les mouvements étant aléatoires, la somme vectorielle des vitesses sera nulle et on à donc :
n= + ∞
∑ Vn
V= n= 1
= 0
nΝ
2
Pour s’affranchir de cette contrainte on va chercher à déterminer .
V
2
V (qui peut aussi s’écrire
V2 car c’est un carré scalaire) est forcément positif (le produit
de deux nombres négatifs donne un résultat positif) et la moyenne des carrés des vitesses est
donc non nulle.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 86

87. Il ne faut pas confondre avec le carré de la moyenne des vitesses qui reste nul :
2
 n= + ∞ 
 ∑ Vn 
2
 n= 1  = 0 2 = 0
V =  nΝ  ()
 
 
n= + ∞
Pour s’affranchir de cette contrainte on cherche à calculer :
∑ Vn
V² = n= 1
≠ 0
nN
L’énergie cinétique moyenne pour une particule est alors facilement déterminable :
1
Ec = m.V ²
2
On peut en déduire l’énergie interne du gaz parfait : U = n.N × Ec
La vitesse quadratique moyenne est définie par V * = V²
3RT
Il faut retenir que pour un gaz parfait monoatomique : V* = (formule très
M
importante)
R est la constante des gaz parfaits : R ≈ 8,314 J .K − 1 .mol − 1 .
T est la température (en kelvins comme toujours)
M est la masse molaire en kg/mol (attention aux unités !)
Démonstration d’une autre expression de Ec pour le gaz parfait monoatomique (3 DDL) :
1
On a démontré : Ec = m.V ²
2
M
On sait que m = (masse molaire divisée par nombre d’Avogadro)
N
3RT
De plus : V* = V² =
M
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 87

88. 3RT
D’où : V² =
M
1 M 3RT
On remplace donc dans la formule initiale : Ec = × ×
2 N M
3 R 3
Par simplification : Ec = × × T = kT
2 N 2
R et N étant des constantes leur rapport est aussi une constante que l’on note k (constante de
R
Boltzmann) : k = ≈ 1.38 × 10 − 23 J .K − 1 .
N
3 R 3
Par conséquent : U = n.N × Ec = n.N × × × T = n.R.T
2 N 2
Par analogie, les mathématiciens ont déduit que si le gaz comptait 5 degrés de liberté (gaz
5
parfait diatomique rigide (comme 0² N²), on avait Ec = k .T et que s’il comportait 7 DDL
2
7
(GP diatomique non rigide), on avait Ec = k .T
2
Rigide : distance en deux atomes fixes, pas de mouvement relatif, pas de mouvement
Non rigide : vibration permise car la distance entre deux atomes varie.
DDL
Plus généralement, pour une GP, on a : Ec = k .T avec DDL le nombre de Degrés De
2
Liberté.
5) Différencier chaleur et température. Définir la capacité
thermique :
Dans le langage courant, on confond souvent 2 grandeurs pourtant différentes.
La température (en °C ou K) est le reflet de l’agitation moléculaire.
LA chaleur (en J) est un mode de transfert d’énergie. Pour la chaleur, il vous faut donc
adopter un nouveau concept : celui de la capacité thermique.
Vous pouvez aisément comprendre qu’il faut fournir plus d’énergie (sous forme de chaleur ou
de travail) pour chauffer une piscine olympique à 35°C que pour chauffer un verre d’eau à
35°C. De même, pour un même volume il faut plus d’énergie pour chauffer de l’eau que de
l’air…
La différence réside dans la capacité thermique.
Symboliquement prenons un récipient rempli d’un liquide. La hauteur du liquide symbolise la
température et le volume du liquide symbolise la chaleur.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 88

89. Vous voyez bien que si le récipient est très large il faudra beaucoup de liquide pour avoir une
faible augmentation de hauteur du liquide. (Donc beaucoup de chaleur pour une petite
variation de température).
A l’inverse, si le récipient est très étroit, une petite variation de volume influe grandement sur
la hauteur du liquide…
Le diamètre du récipient est le lien entre les deux : c’est la capacité thermique.
∂Q
Mathématiquement, on a : C=
∂T
Elle s’exprime en Joules/Kelvin
Elle exprime la quantité de chaleur à fournir pour faire varier la température d’un degré.
Pour s’affranchir de la variable d’étendue du système, on définit les capacités thermiques
molaire et massique c'est-à-dire la capacité thermique par mole ou par unité de masse du
système :
C C
c= c' =
n m
Ainsi, ces capacités massiques ou molaires sont spécifiques à un matériau et il suffit de
multiplier par la masse ou le nombre de moles pour déterminer la capacité thermique d’un
système thermodynamique.
 Remarque : nous avons vu que l’équilibre thermique imposait que deux systèmes en
relation via une paroi diatherme aient des températures égales.
Le niveau va donc s’égaliser avant le volume !
Si les deux systèmes n’ont pas la même capacité thermique, la répartition de chaleur
sera inégale mais la température des deux systèmes se stabilisera à une valeur
commune.
Attention : ne pas confondre équilibre et moyenne ! Si vous arrêtez de chauffer votre
appartement qui était à la température de 20°C alors que la température à l’extérieur
est de 0°C l’équilibre thermique ne se fera pas à 10°C mais à 0°C.
En effet, la capacité thermique de l’extérieur est tellement grande que la chaleur que
communiquera votre appartement à l’extérieur aura un effet similaire à la variation du
niveau de la mer provoquée par une goutte d’eau…
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 89

90. Plus généralement, quand vous étudierez les transformations thermiques, on
considérera que la température d’une source de chaleur ne varie pas.
Pour résumer :
 La capacité thermique varie en fonction de l’étendue et de la nature du système.
 Pour s’affranchir de l’étendue du système on peut définir la capacité thermique
molaire (c) ou la capacité thermique massique (c’).
 Pour les calculs :
 Il ne faut jamais utiliser de température en °C (toujours en Kelvins !)
 Pour les calculs de chaleur, si on vous donne une capacité thermique molaire
ou massique, il faut en 1er lieu déterminer la capacité thermique (en multipliant
par la masse ou le nombre de moles).
 Pour calculer la quantité de chaleur contenue dans un corps on utilise la
relation : Q = C× T
 Pour calculer la chaleur échangée, la relation à utiliser est :
Q = C.∆ T
Cette équation n’est valable que si C est constante. Si elle est exprimée en
fonction de T, alors il faut procéder à une intégration (voir dans les QCM en
annexe).
6) Savoir utiliser la formule des gaz parfaits :
Le gaz parfait est un modèle qui sert aux physiciens pour approcher des calculs pour des cas
particuliers.
A partir de relations fondamentales, ils appliquent des facteurs correctifs pour adapter leurs
calculs à un gaz réel étudié.
Le gaz parfait est le seul modèle de gaz étudié en PCEM1.
 Les propriétés d’un gaz parfait
 Les molécules sont animées d’un mouvement incessant (comme tous les gaz).
 Les molécules sont identiques
 Les molécules sont ponctuelles (les plus petites possibles).
 Pas de forces extérieures exercées sur le gaz.
 Faible pression, peu de molécules dans un grand volume donc pas
d’interactions entre les molécules du gaz.
 Répartition des vitesses équivalente dans tous les plans de l’espace : isotrope.
L’équation d’état d’un gaz parfait est p.V = n.R.T (formule très importante)
Avec :
p : pression en Pascal
V : volume en m3
n : nombre de moles
R : constante des gaz parfait : R ≈ 8,314 J .K − 1.mol − 1
T : température en kelvins
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 90

91. 3
Nous avions pour le GPM : Ec = k .T
2
p.V
De l’équation d’état du gaz parfait on déduit T =
n.R
R
Par ailleurs, on rappelle que k =
N
3 R p.V 3 p.V
En injectant ces termes dans l’équation initiale, on obtient : Ec = × × = ×
2 N n.R 2 n.N
2 n.N
D’où : p= × × Ec
3 V
Cette relation p.V = n.R.T a de nombreuses applications dans les 1er et 2nd principes.
7) Différencier grandeur extensive et grandeur intensive :
Leurs noms sont assez explicites.
« Extensive » (= facteur de quantité) signifie que la valeur varie en fonction de l’étendue du
système.
A contrario, « intensif » (facteur de tension) signifie que la valeur de la grandeur est
indépendante de l’étendue du système.
Pour les différencier, il faut imaginer que vous coupez le système en deux. Vous pouvez alors
intuitivement deviner quelles grandeurs sont extensives et quelles grandeurs sont intensives.
 Les grandeurs extensives : e :
 Les plus logiques : longueur, surface, volume, masse, quantité de matière (nombre de
moles).
 Les moins évidentes : énergie, quantité de mouvement, charge, capacité thermique.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 91

92.  Les grandeurs intensives : i :
 Les plus logiques : la densité moléculaire, la vitesse.
 Les moins évidentes : la concentration, la température, la pression, la masse
volumique, les capacités thermiques molaire et massique, le potentiel (énergie divisée
par une grandeur extensive).
e
i× e → e → i
e
Quelques astuces pour bien fixer les idées :
 Souvenez vous des colonnes d’eau : si vous divisez la colonne en deux
(selon un plan sagittal médian), la hauteur du liquide est la même dans
les deux colonnes filles, mais le volume et le diamètre sont réduits.
De même, la température ne change pas mais la capacité thermique et la
chaleur (qui est une énergie) changent.
 Toutes les grandeurs qui sont exprimées par unité d’un facteur extensif
(masse ou quantité de matière) sont des grandeurs intensives.
C’est le cas de la capacité thermique massique ou molaire, de la
concentration, de la pression (pression = norme de la force pressante par
unité de surface).
Toute grandeur qui est accompagnée du terme « massique » ou
« molaire » est donc intensive… (a priori)
8) Savoir se placer dans le système étudié et comprendre le sens
des échanges :
Ici le problème, est avant tout un problème de vocabulaire.
En physique il y a un certain nombre de conventions à respecter.
Il faut bien comprendre ce qu’est une convention dans le cas présent : c’est une méthode
d’analyse des résultats décidée arbitrairement et qui permet aux individus de mieux se
comprendre.
En thermodynamique, vous devez vous souvenir qu’on se place toujours du point de vue du
système.
On note avec une valeur positive toute arrivée d’énergie vers le système
On note avec une valeur négative toute sortie d’énergie hors du système et donc vers le
milieu extérieur.
Si l’on se place du point de vue extérieur, une valeur positive correspond à une perte
d’énergie du milieu extérieur vers le système. Inversement, lorsque la valeur est négative,
c’est le milieu extérieur qui a gagné de l’énergie.
Il faut donc bien faire attention à deux mots dans les libellés des QCM : quelle est la partie
concernée (milieu extérieur ou système) et le verbe (reçoit ou perd de l’énergie).
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 92

93. N.B. : il y a des grandeurs pour lesquelles l’énergie perdue par le système est égale à l’énergie
gagnée par le milieu extérieur. Exemple : la chaleur
Cependant, il y a des grandeurs pour lesquelles le raisonnement est un peu plus
complexe comme l’entropie :
 Pour l’entropie échangée ∆ e S , ce qui est perdu par l’un est gagné par l’autre dans
tous les cas.
 Cependant, la variation d’entropie ∆ S est différente du fait de la création d’entropie au
sein du système ∆ i S : (voir 2ème principe)
 Le système perd moins d’entropie qu’il n’en fournit au milieu
extérieur.
 Le système gagne plus d’entropie qu’il n’en reçoit du milieu extérieur.
9) Comment obtenir une température de 20°C dans un avion ?
 Le défi : passer d’une température extérieure de -50°C à une température de +20°C dans
la cabine.
 Utiliser un chauffage ? Impossible : trop gourmand en énergie et le transfert de chaleur
serait trop lent.
 La solution : dans le moteur, l’air extérieur est comprimé donc sa température s’élève
à plusieurs centaines de degrés Celsius. Par conséquent, il suffit de mêler cet air à un
volume adéquat d’air extérieur pour obtenir de l’air à une température proche de
+20°C. D’où l’importance de connaître les capacités thermiques pour ce calcul.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 93

94. © Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 94

95. Chapitre 3 :
er
1 Principe
Commenté par Salim
Kanoun
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 95

96. Le premier principe :
dU = ∂ W + ∂ Q
Objectif :
 Comprendre le système thermodynamique et ses définitions.
 Savoir comment calculer les travaux suivant le mode réversible ou irréversible.
 Comprendre et définir le 1er principe.
 Comprendre les propriétés des différents modes de transformation.
 Appliquer les relations du 1er principe aux capacités thermiques.
1) Comprendre le système thermodynamique et ses définitions.
Nous avons déjà posé qu’il contenait une quantité de matière définie avec une paroi qui peut
avoir de nombreuses propriétés.
Au cours d’une transformation, le système thermodynamique passe d’un état initial à un état
final.
Les fonctions d’état du système ne sont définies que dans les états d’équilibre du système.
Il y a différents modes de transformations :
 Si la transformation est brutale = transformation irréversible :
 On ne fait des calculs qu’à l’état initial et à l’état final (seuls états d’équilibre
du système).
 Cela correspond au cas de l’ensemble des transformations réelles (qui ont lieu
en pratique dans la vie courante).
 Si la transformation est faite d’étapes intermédiaires = transformation quasi-
statique (TQS) :
 On peut faire des calculs sur les états : initial, final et intermédiaires.
 Si la transformation est théorique = transformation réversible :
 C’est une approche mathématique utilisant les dérivées. La transformation
comporte une infinité d’états d’équilibre infiniment voisins.
Voyons ceci d’une manière plus imagée : comment descendre du 10ème au 1er étage :
 Sauter dans le vide : une fois mort, il sera difficile de remonter. C’est
irréversible.
 Prendre l’escalier. C’est l’équivalent de la TQS (au pire vous risquez de vous
fouler la cheville).
 Emprunter un long plan incliné à petit pas. C’est l’équivalent d’une
transformation réversible.
Entre 2 états d’équilibre, il y a une phase d’échange d’énergie que l’on note avec les
conventions déjà vues (on se place toujours du point de vue du système !).
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 96

97. Vous verrez avec l’étude du 2ème principe que, dans un cycle réversible (aller et retour), le
milieu extérieur revient à l’état initial (avant les échanges).
En revanche, dans un cycle irréversible, le milieu extérieur garde une « cicatrice » de la
transformation.
2) Comment calculer les travaux suivant les modes réversible et
irréversible ?
 Travail des forces pressantes sachant que ∂ W = − p.dV (à savoir +++) :
 Dans la transformation irréversible, on ne s’intéresse qu’aux états initial et final.
La formule est donc simple : W = − p (V − V )
i
AB B B A
avec p B la pression à l’état d’équilibre final (B) et V A et VB désignant les
volumes aux états initial (A) et final (B).
 Dans la transformation réversible, étant donné que les étapes intermédiaires sont
B
W AB = ∫ − p.dV
r
de nombre infini, il faut procéder à une intégrale :
A
 Pour les transferts de chaleur, en se rappelant que ∂ Q = C.dT :
B
Q AB = ∫ C.dT
r
 Suivant le mode réversible :
A
Qi
 Suivant le mode irréversible, il faut connaître ∆ e S , sachant que : ∆ e S =
Tf
3) Comprendre et définir le 1er principe :
dU = ∂ W + ∂ Q
 Remarques :
• dU est une DTE donc dans tous les cas (réversibles et irréversibles) on a :
♦ ∆ U AB = − ∆ U BA
♦ ∫ dU = 0
• ∂ W et ∂ Q ne sont pas des DTE donc les propriétés précédentes ne
s’appliquent pas pour le travail et la chaleur sauf dans des cas très
particuliers que nous allons étudier plus loin (voir 4ème objectif).
 Un système isolé n’échange ni travail, ni chaleur, ni énergie, ni matière.
 On a donc : ∂ W = ∂ Q = 0
 Par conséquent : dU = 0 d’où U est constante
Un système isolé a donc une énergie interne constante.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 97

98.  A partir de p et de U on définit une autre fonction d’état : l’enthalpie H :
 H = U + p.V (à apprendre ainsi)
4) Les propriétés des différents modes de transformation :
 Si transformation à volume constant = ISOchore (dV=0) :
 Alors : ∂W = 0 donc dU = ∂ Q = CV .dT (d’où le nom de
phénomène calorifique pur) (avec CV la capacité thermique à volume
constant).
 De fait, ∂Q prend les propriétés d’une DTE dans ce cas (dQ).
dU
 On peut aussi déduire de précédemment : CV =
dT
 Si paroi adiabatique ( ∂ Q = 0):
 Donc dans ce cas : dU=W∂−p.V
 De fait, ∂ W prend les propriétés d’une DTE dans ce cas.
 Si pression constante pendant toute la transformation = ISObare (dp=0) :
 On sait que : H = U + p.V
D’où : dH = dU + d ( p.V ) = dU + p.dV + V .dp
Or dU = ∂ Q − p.dV car ∂ W = − p.dV
On a donc dH = ∂ Q − p.dV + p.dV + V .dp donc dH = ∂ Q + V .dp
 Ici, comme la pression constante, dp = 0
On a donc dH = ∂ Q = C p .dT
De fait, ∂Q prend les propriétés d’une DTE dans ce cas (dQ).
dH
On peut aussi déduire de précédemment : Cp =
dT
Attention : Ne pas confondre ISObare et MONObare !
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 98

99. - Monobare : système en contact avec une seule « source de pression » qui
modifie la pression du système : p A = pB = p0 .
- Isobare : la pression du système est constante pendant toute la durée de
la transformation : p = p A = pB = p0
5) Appliquer ces relations aux capacités thermiques :
dU
Dans le phénomène thermique pur (dV=0), on a : CV =
dT
dH
Dans le cas isobare (dp=0), on a : C p =
dT
3
Pour les gaz parfaits : U = n.R.T
2
Par simple dérivation on obtient alors :
3
CV = n.R
2
dH d (U + p.V )
Cp = =
dT dT
Or p.V = n.R.T
d (U + n.R.T ) 3
Donc C p = = CV .n.R = n.R + n.R .
dT 2
5
Par conséquent : Cp = n.R
2
5
Il en résulte que : H= n.R.T
2
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 99

100.  Remarques importantes :
o C p et CV pour le gaz parfait ne dépendent que de n (et ne
dépendent ni de la température ni de la nature du gaz parfait)
Cp CV
o Leurs expressions molaires ( et ) donnent deux constantes.
n n
o On observe que C p > Cv : la capacité thermique à volume constant est plus
petite donc la température va augmenter plus vite que dans le cas où la
pression est constante (à transfert de chaleur égal). D’où l’intérêt de mettre un
couvercle à votre casserole.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 100

101. Chapitre 4 :
nd
2 principe,
Transformations
Commenté par
Salim Kanoun
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 101

102. Le deuxième principe :
dS = ∂ e S + ∂ i S
Objectifs :
 Savoir ce qu’est l’entropie.
 Connaître les relations fondamentales de l’entropie.
 Différencier entropie créée et échangée.
 Comprendre et savoir utiliser le second principe dans certaines situations.
 Comprendre les relations entre fonction d’état, fonction conservatrice et DTE.
 Connaître la définition de l’énergie et de l’enthalpie libre.
 Calculs et applications aux gaz parfaits.
 Conclusion : ce qui se passe dans un moteur à explosion.
1) Savoir ce qu’est l’entropie :
C’est une grandeur purement mathématique : on n’a aucun instrument qui permette de la
mesurer, on ne peut que la calculer à partir de relation mathématique.
C’est la grandeur qui détermine l’irréversibilité d’une transformation.
2) Connaître les relations fondamentales de l’entropie :
Elles sont au nombre de trois :
∂ Qr
dS =
T
∂ Qi
∂ eS =
T
∂ Q'
∂ iS =
T
Q’ est la chaleur non compensée de Clausius.
Elle correspond à la différence entre chaleur réversible et chaleur irréversible.
L’entropie est une grandeur extensive.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 102

103. 3) Différencier entropie créée et échangée :
L’entropie échangée est celle qui passe au travers de la paroi du système (dans un sens ou
dans l’autre)
L’entropie échangée supporte le transfert de chaleur, elle est toujours du
même signe que la chaleur échangée.
L’entropie créée est une entropie qui se crée à l’intérieur du système de façon spontanée.
La convention veut qu’elle soit toujours placée à l’intérieur du système et qu’elle
soit toujours positive ou nulle.
De fait, étant donné que l’entropie peut se créer spontanément, elle ne peut répondre à une
loi de conservation.
L’entropie est donc une fonction d’état non conservative (sauf cas particulier, voir plus
loin).
4) Comprendre et savoir utiliser le second principe dans certaines
situations :
dS = ∂ e S + ∂ i S
 Remarques :
• dS est une DTE donc dans tous les cas on a :
♦ ∆ S AB = − ∆ S BA
♦ ∫ dS = 0
• ∂ e S et ∂ i S ne sont pas des DTE donc les propriétés précédentes ne
s’appliquent pas, sauf dans des cas très particulier que nous allons étudier.
 Dans le système isolé (ou comportant une paroi adiabatique) :
 Il n’échange pas de chaleur donc pas d’entropie non plus (car l’entropie est le
« support d’échange » de la chaleur) : ∂ es = 0
 La variation d’entropie est liée seulement à la création d’entropie et on écrit alors :
∂ S = ∂ is : dS perd donc ses propriété de DTE et devient ∂ S .
 ∂ i S étant positive : l’entropie d’un système isolé augmente (sauf dans le cas d’un
cycle réversible qui se produit à l’intérieur du système et qui fait que l’entropie reste
constante).
 Univers = Système + milieu extérieur.
L’univers est un système isolé, s’il était modifié par un autre élément il deviendrait à
son tour un système thermodynamique qui serait modifié par un milieu extérieur…
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 103

104.  Dans une transformation réversible :
 ∂ iS = 0
 ∂ e S = dS
 Ici ∂ e S acquière les propriétés d’une DTE.
 C’est seulement dans ce cas où l’entropie répond à la loi de conservation.
 Dans une transformation irréversible
 dS étant une DTE pour un trajet donné AB cette valeur est toujours la même et est
l’opposé dans le chemin retour BA
 En revanche, suivant les conditions de réversibilité cette variation d’entropie est
partagée inégalement entre ∂ e S et ∂ i S .
 La part portée par ∂ i S sera d’autant plus importante que la transformation
irréversible.
ΔeS
ΔeS ΔeS ΔS
ΔiS
ΔiS
Transfo Transfo
« très Transfo « peu réversible
irréversi irréversible »
ble »
5) Comprendre les relations entre fonction d’état, fonction conservatrice,
DTE :
Il faut faire attention à ne pas confondre ces différents termes.
Les Fonctions d’Etat sont celle que vous avez étudiées dans les différentes formules : Energie
interne (U), Entropie, Enthalpie…
La plupart du temps, elles donnent des dérivées totales exactes mais il existe des exceptions.
La fonction conservative est une propriété réservée aux DTE, elle signifie qu’il n’y a pas de
création spontanée d’une grandeur : seul ce qui est mis à disposition dans l’Univers peut être
mobilisé.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 104

105. Fonction d’Etat
(U, S, H…)
DTE Non DTE
donc conservative (ex : donc non conservative
U, entropie réversible…) entropie irréversible
6) Connaître la définition de l’énergie libre (F) et de l’enthalpie libre (G) :
Deux relations à connaître :
 F = U − TS
Et surtout : ∂ Q r = d [U − F ]
D’où ∂ Q r = dF dans un système isolé dU=0
 G=F+PV
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 105

106. 7) Calculs et application aux gaz parfaits :
Retenir les formules suivantes peut vous faire gagner beaucoup de temps (il vaut mieux le
faire)
Mais au moindre doute, tout peut se retrouver comme ainsi :
Pour le Calcul du Travail :
 Suivant le mode réversible dans une transformation isotherme (T=constante)
 On sait W AB = ∫ − p.dV et p.V= n.R.T
r
n.R.T
D’où : p=
V
B
n.R.T V (On peut sortir n.R.T car se sont des
W r AB = ∫−
A
V
.dV = − n.R.T ln B
VA
constantes)
n.R.T
 Mais également V=
p
n.R.T
r p n.R.T pA p p
W AB = − n.R.T . ln B = − n.R.T . ln( × ) = − n.R.T . ln A = n.R.T . ln B
n.R.T pB n.R.T pB pA
pA
 Suivant le mode irréversible :
 On sait W AB i = − p B (V B − V A ) et p.V = n.R.T
i n.R.T n.R.T 1 1
W AB = − p B (V B − V A ) = − p B ( − ) = − p B .n.R.T ( − )
pB pA pB p A

− pB pB p
= n.R.T ( + ) = n.R.T ( B − 1)
pB pA pA
Pour le calcul d’entropie :
 Variation d’entropie :
 Dans un gaz parfait U ne dépend que de T.
 T étant constante dans le mode réversible isotherme dU=0 et ∂ W = − ∂ Q
r r
Q AB − W Ab p p
dS = = = − n.R. ln B = n.R. ln A
T T pA pB
 Entropie échangée :
i
Q i AB − W AB
 ∂ eS = =
T T
 N.B. : dans le cadre d’une transformation calorifiquement pure (= isochore), on ne
peut utiliser le travail (il n’y en a pas) !
∂ Qr C.dT T
 ∆ S AB = ∫ dS = ∫ = ∫ = C. ln B
T T TA
 Valable aussi pour la transformation isobare.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 106

107. 8) Conclusion : ce qui se passe dans un moteur à explosion :
 Le principe :
 Un piston comprime un peu d’air, du combustible et une étincelle
déclenche la réaction.
 La combustion des hydrocarbures libère beaucoup de chaleur
Le gaz s’échauffe.
Comme p.V = n.R.T quand T augmente la pression augmente dont une
force s’exerce sur le piston mobile qui en se déplaçant va faire augmenter
le volume (et diminuer la pression).
Ensuite le piston remonte et se produit un nouveau cycle.
 Un peu de Thermodynamique.
 D’après le premier principe on sait que l’énergie interne du système (qui
est ici le cylindre) est égale à la somme : chaleur échangée et travail
échangé.
 Au sens ALLER :
 Le système par la combustion de l’essence reçoit de la chaleur.
 Le système en repoussant le piston fournit un travail.
 Au sens RETOUR (qui n’existe pas tout à fait ainsi dans un vrai moteur)
 Le système reçoit une énergie mécanique.
 Le système émet de la chaleur car l’augmentation de pression produit
une augmentation de température (transfert de chaleur car obligation
de mise en équilibre thermique).
Attention : dans un vrai moteur, il faut évacuer les gaz d’échappement dans la
remontée du piston évacue vers l’extérieur ces gaz (il n’y a pas transfert de
chaleur mais transfert de matière vers le milieu extérieur).
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 107

108. La somme de ces deux termes est la même lors du sens aller et retour.
Car dU = ∂ W + ∂ Q (dU étant une DTE)
Et l’entropie dans tout ça ?
Le moteur est irréversible, ∂ iS est positif non nul, le milieu extérieur ayant une
capacité infinie par rapport au piston on considèrera que T est constante pendant
les phases d’équilibre.
dS se calcule facilement (il suffit de connaître la capacité thermique du gaz
parfait) et ∂ eS se calcule à partir de la chaleur qui a été échangé.
On peut alors grâce au deuxième principe déterminer le degré d’irréversibilité
du moteur.
Les différences entre le sens aller et retour
Si la somme de travail et chaleur est la même, chacune de ces deux
composantes est différente entre le sens aller et retour.
dW
dW
dU
dQ
dQ
Sens 1 Sens 2
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 108

109. De même pour le 2nd principe :
ΔeS
ΔeS
dS
ΔiS
ΔiS
Sens A Sens B
Le degré d’irréversibilité est donc différent dans le sens aller et dans le sens
retour.
A quoi sert tout cela ???
La création d’entropie correspond en fait à l’énergie que vous avez perdue lors
de la transformation.
Pour une même transformation, il vous faudra fournir d’autant plus d’énergie
que la transformation est brutale.
Dans l’idéal, le minimum que l’on puisse atteindre est la chaleur réversible.
3
Comme dU est fixe ( n.R.T ) vous remarquerez que si la chaleur réversible est
2
minimale, il faut annuler le bilan par un échange de travail maximal…
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 109

110. © Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 110

111. Partie II
Entraînement aux
QCM
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 111

112. © Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 112

113. Chapitre 1 :
Forces,
Vecteurs,
Travaux
QCM commentés par Elise
Birague-Cavallie
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 113

114. Question n°1 :
A) Un potentiel est une grandeur extensive.
B) Une énergie est une grandeur intensive.
C) La masse molaire est un paramètre extensif.
D) La pression est une grandeur scalaire.
Question n°2 :
A) Une variation élémentaire de potentiel est une Différentielle Totale Exacte (DTE).
B) Une DTE n’est intégrable que sur un trajet fermé.
C) Un champ scalaire peut être exprimé par un gradient.
D) Une force dissipative dérive d’un potentiel.
Q.C.M. n°3 :
Calculer le travail de la force de composantes f x = ky et f y = kx sur la courbe
Y= 2 x + 4 de xA = 1 à xB = 9 :
A: - 96 k B: 24 k C : 52 k
D: 80 k E : 84 k
Q.C.M. n°4 :
Calculer le travail d’une force de composantes f x = f y = − kxy sur le trajet
y = − 2 x + 3 du point A (0;3) au point B (3;-3).
A: -9k B: - 4,5 k C: 0 k
D: +9k E: + 32 k
Question n°5 :
Calculer le travail d’une force de composantes f x = k ( y + 1) et f y = k ( x − 1) sur
le trajet A (-1;+2)  B (+4;+3) :
A:+4k B:+8k C : + 18 k
D: + 22 k E : + 32 k
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 114

115. Question n°6 :
Calculer le travail d’une force de composante f x = − k et f y = + k sur le trajet
A (-1;2)  B (4;2) :
A:k B:-3k C:+5k
D:-k E:-5k
Question n° 7 :
Calculer le travail d’une force de composantes f x = k ( x − y ) et f y = − kx
sur le trajet A (+1;-1)  B (+ 3, + 2) (k = constante).
A:+4k B : + 11 k C:-k D:-3k E:0k
Question n°8 :
∂3f
Soit la fonction f(x, y) = x2y2 + x2 lny + e2x + 3x y Calculer
∂ x∂ y∂ x
2
A: 8 e2x B: 2xy2 + e2x + y C : 4y + y
2x 2x 3
D: 4y - y2 E: 4xy + y + 2 y
Question n°9 :
Calculer le travail d’une force de composantes f x = f y = − k ( x + y ) .
sur le trajet A (3;-1)  B (2;2) (k = constante).
A : + 13 k B:+6 k C:-5k
D:-6k E : - 13 k
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 115

116. Question n° 10 :
Calculer la DTE de la fonction : f(x, y) = 2 x - x2y + xy.
y
2
A : (-2x Ln y –x2 + x).dy + ( y - 2xy + y). dx.
2x 2
B : (- y2 - x2+x).dx + ( y -2xy +y).dy.
2
C : ( y - 2x + y).dx + (-2x ln y – x2+x). dy.
2 2x
D : ( y - 2xy + y).dx + (- y2 - x2 + x). dy.
2 2x
E : ( y - 2xy + y).dx + ( y2 - x2 + x). dy
Question n°11 :
Calculer le travail d’une force de composantes F x = k (y+1) et Fy = kx sur la droite
A(1,1), B(2,3).
A:3k B: - 7 k C: 6 k
D: - 6 k E : 10 k
Question n° 12 :
A) Le gradient est un vecteur perpendiculaire aux lignes de niveau d’un champ
scalaire.
B) Un gradient d’énergie potentielle est un vecteur qui représente une force
conservative parallèle et de même sens.
C) Une force qui peut s’exprimer par un gradient est une force conservative.
D) Le gradient est une grandeur scalaire qui exprime la variation spatiale d’un vecteur.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 116

117. 1. D
2. AC
3. E
4. B
5. C
6. E
7. D
8. C
9. D
10. D
11. C
12. AC
QCM 1 :
Rappel :
Valeurs extensives : sont relatives au système entier et sont additives lors la réunion de 2
systèmes.
Valeurs intensives : elles sont définies en un point indépendamment de la quantité de matière.
Exemple : la masse volumique ρ.
Calcul : intensif x extensif → extensif
Extensif / extensif → intensif
A) potentiel V=dEp/dq => ext/ext→intensif
B) Energie cinétique Ec = ½ m.v2, masse m, est une valeur extensive, énergie =
grandeur extensive.
C) La masse molaire est définie comme un rapport entre 2 valeurs extensives : unité en
g.mol-1
D) La pression est une grandeur scalaire.
QCM 2 :
B) Un trajet fermé est un cycle. Lorsque l‘on revient au point de départ, A → B → A
Une DTE est indépendant du chemin parcouru. De fait, elle ne dépend que de l’état initial et
de l’état final et est intégrable sur n’importe quel trajet.
Un trajet fermé est un cycle : on revient au point de départ (A → B → A) et on a :
∫ DTE = 0
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 117

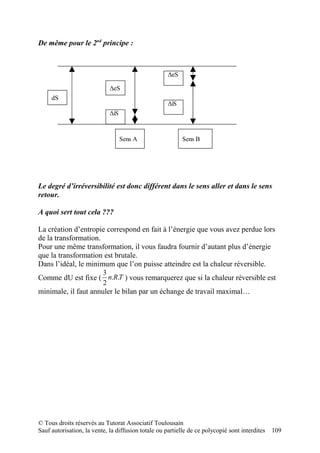
118. D) Une force conservative dérive d’une énergie potentielle.
Q.C.M. n°3 :
Méthode :
1) vérifier que la force est conservative (propriété de commutativité)
2) calcul de la fonction primitive
3) calcul du travail entre 2 points
Correction :
1) La force est-elle conservative ?
∂ fx ∂ f y
=
∂y ∂x
Ici, égal à k
2) Fonction primitive :
∫ f x .dx = kxy
∫ f y .dy = kxy
3) Calcul du travail entre deux points :
[kxy] à intégrer entre 2 points, chacun ayant 2 coordonnées.
Calcul des coordonnées, on résout l‘équation avec x=1, puis avec x=9
Pour x=1 : y=6
Pour x=9 : y=10
Donc W= k (90-6) = 84 k
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 118

119. QCM. 4 :
∂ fx ∂ f y
Force conservative ? = ?
∂y ∂x
∂ fx ∂f
Ici ce n’est pas le cas : = − kx alors que y = − ky donc non DTE.
∂y ∂x
Dans ce cas, la force est dissipative et de fait le travail dépend du chemin suivi.
dy = y ' ( x).dx donc dy = (− 2 x + 3)'.dx = − 2.dx
D’où :
df = f x .dx + f y .dy = − kxy.dx + [ − kxy × (− 2dx)] = − kxy.dx + 2kxy.dx = kxy.dx
= kx × (− 2 x + 3).dx
⇒ df = − 2kx² + 3kx.dx
B B ( 3; − 3)
 2 3 
Donc W AB = ∫ − 2kx ² + 3kx.dx =  − kx 3 + kx ² 
A  3 2  A ( 0; 3)
 2 3   2 3  27 9
⇒ W AB =  − k × 33 + k × 3²  −  − k × 0 3 + k × 0²  = − 18k + k = − k = − 4,5k
 3 2   3 2  2 2
Réponse B
Remarque : la résolution de ce genre de QCM est particulièrement complexe. C’est
pourquoi au concours un tel QCM serait probablement formulé de façon différente.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 119

120. Question n° 5 :
∂ fx ∂ fy
= donc c’est une force conservative.
∂y ∂x
Fx = ∫ f x .dx = ∫ k ( y + 1).dx = [ kxy + kx]
Fy = ∫ f y .dy = ∫ k ( x − 1).dy = [ kxy − ky ]
[
D’où : W AB = kxy + kx − ky ] B(( +− 4;;++ 23))
A 1
⇒ W AB = [ k × (+ 4) × (+ 3) + k × (+ 4) − k × (+ 3)] − [ k × (− 1) × (+ 2) + k × (− 1) − k × (+ 2)]
⇒ W AB = [12k + 4k − 3k ] − [ − 2k − k − 2k ] = 13k − (− 5k ) = + 18k
Réponse C
Question n°6 :
force conservative ? Oui
Wab = [- k(x-y)] à prendre entre (-1,2) et (4,2)
= -k(xb-yb –xa+ya)
Wab = -5k
Question n° 7 :
force conservative ? oui
Wab= [k(x²/2 – xy)]AB
= k (xb²/2 –yb x b – xa²/2 +ya xa )
= -3k
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 120

121. Question n°8 :
On demande de dériver 2 fois par rapport à x ce que l’on fait à la suite
Rappel : ∂ x∂ y∂ x = ∂ x ²∂ y = ∂ y∂ x ²
On commence à dériver par rapport à x :
∂f
= 2 y ² + 2 x ln y + 2e x + 3 y
∂x
∂²f
= 2 y ² + 2 ln( y ) + 4e 2 x
∂ x²
∂3f 2
= 4y +
∂ x²∂ y y
Question n°9 :
force conservative, oui
Wab= [-k(x²/2+xy + y²/2)]AB entre A(3,-1) et B(2,2)
= - k( xb²/2 +xbyb + yb²/2) – (xa²/2 +xaya+ ya²/2)
= -6k
Question n° 10 :
Il s’agit ici de dériver une fonction à 2 variables.
Il faut d’abord dériver par rapport à x, puis dériver par rapport à y.
∂ f ( x, y ) 2
= − 2 xy + y
∂x y
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 121

122. Question n°11 :
Force conservative, oui.
Wab=[kx(y+1)]AB avec A(1,1) et B(2,3)
Wab= k( xb(yb+1)-xa(ya+1) )= 6k
Question n° 12 :
A) Par exemple, une source sonore émet des sons. Chaque onde est une ligne de
niveau où l’on entend le même niveau sonore tant que l’on reste à une distance
constante de la source.
z
grad f P=m v
jk
i y
x
B) attention !!!
L’énergie potentielle a un sens opposé au travail,
Il faut se rappeler que F = − grad Ep
D) le gradient est un vecteur qui exprime la variation spatiale d'un scalaire
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 122

123. Chapitre 2 :
Température,
Chaleur
QCM commentés par
Salim Kanoun
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 123

124. Question n° 1 :
Calculer la vitesse quadratique moyenne des molécules d'un gaz parfait monoatomique
de masse molaire M = 20 g.mol-1 à la température de 102°C.
3R=25 k = 1,38.10-23 J.K-1
0,3 = 0,5
A v* = 1250 m.s-1
B v* = 650 m.s-1
C v* = 1250 km.s-1.
D v* = 20,5 m.s-1
E v* = 1250 km.s-1
Question n°2 :
A : La température est une variable qui mesure la chaleur d'un corps.
B : La capacité thermique ne dépend pas de l’étendue du système.
C : Le principe 0 permet de définir la température en tant que variable d'état
mesurable.
D : La température est l’expression macroscopique de l'intensité de l’agitation
moléculaire.
E : La température est une grandeur intensive.
Question n°3 :
Calculer la vitesse quadratique moyenne des molécules d'un gaz parfait monoatomique
de masse molaire M = 14 g.mol-1 en équilibre.
Thermodynamique à la température de -40 °C 3R = 25
25
= 1,34 23,3 = 4,83
14
A: 20 m.s-1 B: 267 m.s-1 C: 444 m.s-1
D: 544 m.s-1 E: 647 m.s-1
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 124

125. Question n°4:
Quelle est la température d'un gaz parfait monoatomique de masse molaire :
2 g.mol-1 et de vitesse quadratique moyenne 1,8 km.s-1 ?
3R=25
A: 144 K B: 260 K C: 320 K.
D: 1565 K E: 259800 K.
Question n°5 :
Quelle est la vitesse quadratique moyenne des molécules d'un gaz parfait
monoatomique de masse molaire M = 4 g.mol -1 en équilibre thermodynamique à la
température T= 46,85°C 3R = 25 2 = 1,41
A: 1414 m.s-1 B: 44m.s-1 C: 481m.s-1
D: 1,41 km.s-1 E: 1,05 km.s-1
Question n°6 :
Quelle est la vitesse quadratique moyenne des molécules d'un gaz parfait
monoatomique de masse molaire M = 20 g.mol -1 en équilibre thermodynamique à la
température t = 127°C 3R=25 2 = 1,41
A: 401 m.s-1 B: 0.705 Km.s-1 C: 529,6 m.s-1
D: 705 m.s-1 E: 1023 m.s-1
Question n°7:
A : Un système en phase solide doit forcément passer par une phase liquide avant de se
vaporiser.
B : La définition de l’égalité de 2 températures est une condition nécessaire et
suffisante pour en faire une variable mesurable.
C : Une variation de température n'est pas la même dans l'échelle Celsius et dans
l'échelle Kelvin.
D : Deux systèmes en équilibre thermique entre eux sont forcément à la même
température.
E : Deux systèmes en équilibre thermique contiennent forcément la même quantité de
chaleur
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 125

126. Question n°8 :
Quelle est la vitesse quadratique moyenne des molécules d'un gaz parfait
monoatomique de masse molaire M = 40 g.mol-1 en équilibre thermodynamique à la
Température de 7 °C ? On donne 3R = 25 0,7 = 0,84
A: 86 m.s-1 B: 612 m.s-1 C: 420 m.s-1
D: 13,3 m.s-1 E: 177 ,6 m.s-1
Question n°9 :
Quelle est la vitesse quadratique moyenne des molécules d'un gaz parafait
monoatomique de masse molaire M = 30 g.mol -1 en équilibre thermodynamique à la
température de 327 °C ? On donne 3R = 25 2 = 1,41
A: 16 m.s-1 B: 78 km.s-1 C : 83 m.s-1
-1 -1
D : 705 m.s E: 2461 km.s
Question n° 10 :
A : La chaleur est proportionnelle à l'intensité moyenne de l’agitation moléculaire.
B : La capacité molaire est une grandeur intensive.
C : La chaleur est une grandeur intensive.
D : La chaleur est un opérateur de transfert d'énergie.
E : La pression est perpendiculaire à une paroi.
Question n° 11 :
A) L'équation d'état du gaz parfait est vérifiée au cours de toute transformation subie
par ce gaz.
B) La capacité thermique molaire d'un gaz parfait monoatomique dépend de la nature
du gaz parfait.
C) La vitesse quadratique moyenne est le carré de la moyenne des vitesses
moléculaires.
D) L'énergie interne du gaz parfait monoatomique est exclusivement de l'énergie
cinétique de translation des molécules.
E) U = n.N × Ec
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 126

127. Question n° 12 :
A très basse température, la capacité thermique molaire à volume constant du chlorure
de sodium est une fonction linéaire de la température: cv=2000.T (J.mol-1).
Quelle quantité de chaleur faut-il fournir à 10 g de NaCl pour élever sa température de
20 à 40 K.
On donne la masse molaire du NaCl : M = 58,5 g.mol-1.
A : 205 kJ B : 136,7 kJ C: 410 kJ
4
D : 1200.10 J E: 6837 J
Question n° 13 :
Calcul de chaleur dans le cadre d'un phénomène calorifique pur et sans changement
d'état.
La capacité thermique molaire d'un corps pur est:
c = 17+20.10-3T J.mol-1. K-1
Calculer la quantité de chaleur reçue par un système constitué par 2,5 moles de ce
corps pur à la température initiale de 360 K, dans une transformation qui amènera sa
température à 260 K.
2,6² - 3,6² = - 6,2
A: - 4000 J B : - 2320 J C : - 5800 J
D: - 5550 J E : - 2700 J.
Question n° 14 :
La capacité thermique molaire du dioxyde de carbone est :
C = a + b.l0-3. T + c.l0-6.T2 cal.mol-l.K-l
avec a = 7, 70 b = 5,3 c = -0,83.
Calculer la quantité de chaleur que doit recevoir 11g de CO 2 pour que sa température
s'élève de 280 K à 300 K.
Masse molaire du CO2 : M = 44 g.mol-1.
3² − 2.8² = 1.16
33 − 2.8 3 = 5.1
A. 183 cal
B. 31 cal
C. 39 cal
D. 46 cal
E. 9,3 cal
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 127

128. Question n°15:
La capacité thermique massique d'un corps pur est:
C' = A0 - A1 (J.K-1.g-1) A0 = 1,41 A1 = 492.
T
Quelle quantité de chaleur doit recevoir un système constitué par 100g de ce corps pur
dans une transformation calorifique pure modifiant sa température de 250° à 25°C ?
Vous pouvez utiliser une calculatrice
A: 81560 ± 10J B: -59380 ± 10J C: -4060 ± 10J
D: 27800 ± 10J E: -6050 ± 10J.
Question n° 16 :
Calculer l'enthalpie d'une mole d'un gaz parfait monoatomique de masse molaire
M = 40 g.mol-1 dont la vitesse quadratique moyenne est v* = 610 m.s-1
R = 8,314 J.mol-1.K-1
Vous pouvez utiliser une calculatrice
A 12,4.106J B : 10 000 J C :12 403 J D : 5 856 J E : 7 442 J
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 128

129. 1- A
2- DE
3- E
4- B
5- AD
6- BD
7- D
8- C
9- D
10- BD
11- DE
12-A
13-C
14-D
15-C
16-C
Correction :
3RT
Qcm 1 : V * =
M
Attention : M doit être exprimée en kg.mol-1
Ne pas oublier : Toujours convertir la température en kelvin (dans toutes les formules de
thermodynamiques) :
T= 102+273,15= 375,15 kelvin
3RT 25 × 350 5 × 5 × 5 × 75 5 × 5 × 5 × 15
= −3
= = = 5 × 5 3 × 10 3 = 25 × 10 2 0.3 = 1250m / sec
M 20 × 10 4 × 5 × 10 − 3 10 − 3
Qcm 2 :
A : non elle reflète l’agitation moléculaire.
B : Seulement si elle est massique ou molaire
C : Repérable seulement, pour être mesurable il faut définir le « zéro »
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 129

130. QCM 3 :
T= - 40 + 273.15 =233,15 K
3RT 25 × 233 25
V* = = = × 23.3 × 10 4 = 1.34 × 4.83 × 102
M 14 × 10 − 3 14
≈ 624m.s − 1
Pour les calculs limitez vous à un chiffre après la virgule et choisissez la valeur la plus
proche.
QCM 4 :
3RT
1800 =
M
3RT
En élevant l’équation au carré : 324 × 10 4 =
M
D’où :
324 × 10 4 × M 324 × 10 4 × 2 × 10 − 3 324 × 20 324 × 4
T= = = = = 324 × 0,8 = 259,2 K
3R 25 5× 5 5
QCM 5 :
T= 46,85 + 273,15 = 320 K
3RT 25 × 320 25 × 8 × 4 × 10
V* = = =
M 4 × 10 − 3 4 × 10 − 3
= 25 × 8 × 10 4 = 5 × 10 2 × 2 2 = 10 3 2 = 1414m.s − 1
QCM 6 :
T =127 + 273,15 = 400,15 K
3RT 25 × 400 25 × 20
V* = = −3
=
M 20 × 10 10 − 3
= 5 2 × 10 4 = 5 × 102 × 1.41 = 705m.s − 1
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 130

131. QCM 7 :
A : Faux, il peut se sublimer.
B : Repérable, il faut définir le « zéro » pour devenir mesurable
C : Si, le « pas » est identique
E : Non : la quantité de chaleur dépend de la capacité thermique de chaque élément.
QCM 8 :
3RT 25 × 280
V* = = −3
= 25 × 7 × 103 = 5 × 10 2 0.7 = 420m.s − 1
M 40 × 10
QCM 9 :
3RT 25 × 600
V* = = −3
= 25 × 20 × 103 = 5 × 102 2 = 705m.s − 1
M 30 × 10
QCM 10 :
A : C’est la température
C : Extensif
E : C’est la force pressante.
QCM 11 :
A : Définie qu’à l’état d’équilibre
B : Elle ne dépend que de la température
2
C : V = 0 donc V = 0 × 0
QCM 12 :
B B  T²  40² − 20² 
Q AB = ∫A n.c.dT = n ∫ 2000T .dT = n  2000
A
  = n  2000 ×
2   2 

 12 × 10²  10 2400000
= n  2000 ×  = 58.5 × = 205kJ
 2  2
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 131

132. QCM 13 :
B B  T²  260² − 360² 
Q AB = ∫ A
ncdT = n ∫ 17 + 20 × 10 − 3 TdT = n  17T + 20 × 10 − 3  = n  17 × − 100 + 20 × 10 − 3
A
 2  2 

 − 6.2 × 10 4 
= n  − 1700 + 20 × 10 − 3  = 2.5 × − 2320 = − 5800 J
 2 
QCM 14 :
B B  T² T3
Q AB = ∫ A
n.c.dT = n ∫ 7,70 + 5,5 × 10 − 3 T − 0,83 × 10 − 6 T ² dT = n  7,70T + 5,5 × 10 − 3
A
 ²
− 0,83 × 10 − 6 
3 
 300² − 280² 300 3 − 280 3 
= n  7,70(300 − 280) + 5,5 × 10 − 3 − 0,83 × 10 − 6 
 2 3 
 3² × 10 4 − 2,8² × 10 4 33 × 10 6 − 2,83 × 10 6 
= n  7,7 × 20 + 5,5 × 10 − 3 − 0,83 × 10 − 6 
 2 3 
 1,16 × 10 4
5,1× 10  11
6
= n  154 + 5,5 × 10 − 3 − 0,83 × 10 − 6  = [154 + 31,9 − 1,41] = 0,25 × 184,49 = 46cal
 2 3  44
QCM 15 :
492
dt = − m[141T − 492 ln T ]
B A
Q AB = ∫A m.c .dT = − m ∫ 1,41 −
'
B T
= m[1,41× 225 − 492( Ln 298 − Ln523)]
 523 
= − 100 ×  317,25 − 492 Ln ≈ − 100 × 41,73 ≈ − 4173 J
 298 

© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 132

133. QCM 16 :
5
Pour un gaz parfait on a : H = n.R.T
2
Il nous faut donc connaître T
3R.T
V* =
M
25 × T
D’où 610² =
40 × 10 − 3
610² × 40 × 10 − 3
T= = 595,360 K
25
5
H = × 1 × 8,3 × 595 = 12346 J
2
Autre raisonnement pour une réponse plus exacte (précise) :
5
H = nRT
2
3RT
v* =
M
3RT
(v*)² =
M
v * ²M
RT =
3
5 v * ²M 5 5
H = n× = × 1× v * ² M = × 610² × 40 × 10 − 3
2 3 6 6
200 0,2
H= × 10 − 3 × 610² = × 610² = 12403 J
6 6
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 133

134. © Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 134

135. Chapitre 3 :
Transformations
thermodynamiques
QCM commentés par
Djaouad Berkach
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 135

136. Question n°1 :
A) Un système réel évoluant à la surface de la terre dans des conditions
monotherme et monobare évoluera spontanément dans le sens qui minimise son
enthalpie libre.
B) Le 2ème principe permet de calculer de manière parfaitement déterminée le
degré d'irréversibilité d'une transformation réelle.
C) Sans postulat complémentaire, l'entropie d'un système ne peut être connue
qu'à une constante près.
D) Le 2ème principe affirme que dans une transformation monotherme,
irréversible d'un état d'équilibre initial A à un état d'équilibre final B, le système
ne peut que recevoir du travail et fournir de la chaleur.
E) L’entropie est une grandeur accessible à nos sens.
Question n°2 :
A) Une transformation isotherme est une transformation monotherme au cours
de laquelle la température, en tous les points du système, reste égale a celle de la
source de chaleur.
B) Une paroi adiabatique est une paroi qui s'oppose à toute variation de la
température du système.
C) Une variable intensive est une variable qui ne dépend pas de l'étendue du
système.
D) La température d'une source de chaleur ne reste pas constante lors du
transfert d'une grande quantité de chaleur.
E) Un système fermé entouré d’une paroi adiabatique et rigide peut toujours
échanger avec le milieu extérieur.
Question n° 3 :
A) La variation élémentaire d'entropie échangée par un système non isolé est
une DTE.
B) La variation d'entropie d'un système fermé non isolé dans une transformation
quelconque d'un état d'équilibre B à un état d'équilibre A est l'opposée de la
variation d'entropie de ce système dans une transformation réversible AB.
C) L'entropie décrit le système d'un point de vue microscopique.
D) L'entropie est le facteur extensif de la chaleur.
E) L’entropie crée est d’autant moins importante que la vitesse de
transformation est grande.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 136

137. Question n°4 : L'énergie interne :
A: est une fonction d'état.
B: permet de calculer directement le travail adiabatique.
C: permet de calculer directement la chaleur dans une transformation à pression
constante.
D: est une grandeur extensive.
E: peut être calculée à partir d'une seule variable d'état pour une mole d'un gaz
parfait monoatomique en équilibre thermodynamique.
Question n° 5 :
A) La variation d'enthalpie est la chaleur de transformation isobare.
B) La variation d’énergie interne d'un système qui subit une transformation d’un
état initial A à un état final B est indépendante des quantités de travail ou de
chaleur que le système reçoit du milieu extérieur.
C) Un système isolé ne peut évoluer qu'à énergie interne constante.
D) L’entropie de l’univers ne peut qu’augmenter.
E) L’énergie libre est l’énergie minimale que le système doit recevoir sous
forme de travail pour subir une transformation de A vers B.
Question n° 6 :
A) L'enthalpie est la somme de l'énergie interne et du produit de la pression par
le volume.
B) L'enthalpie permet de calculer l’irréversibilité d’une transformation.
C) La variation d’enthalpie est égale à la variation d’énergie interne.
D) La variation d'enthalpie est égale à l'effet thermique d'une réaction
chimique quelconque.
E) L’enthalpie n’est pas une fonction d’état
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 137

138. Question n° 7 : L'énergie libre :
A) est égale à la différence entre l'énergie interne et le produit de la température
thermodynamique par l'entropie.
B) est une grandeur énergétique dont la variation est égale au travail reçu par un
système qui évolue de manière monotherme réversible.
C) est une fonction d'état.
D) joue le rôle de fonction potentiel thermodynamique d'un système qui évolue
selon une transformation monotherme isobare.
E) est supérieure au travail monotherme irréversible.
Q.C.M. n°8 : Un système isolé :
A) ne reçoit ni matière, ni énergie.
B) évolue vers un minimum d'énergie interne.
C) évolue vers un maximum d'entropie.
D) ne peut subir aucune transformation.
E) peut être constitués de plusieurs phases distinctes.
Question n° 9 : La variation élémentaire d'entropie d'un système s’écrit
dS = ∂eS + ∂iS
A) Si la transformation est réversible, la création d'entropie est nulle et
dS = deS
B) Si la transformation est irréversible, S est positif et (dS)irr est plus grand que
(dS)rév.
C) Dans tous les cas la variation d'entropie de l'univers est égale à la création
d'entropie.
D) Si dS est négatif la transformation est interdite.
E) Le fait qu’une transformation s’accomplisse spontanément suffit à prouver
que l’entropie du système a augmenté.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 138

139. Q.C.M. n°10: On fait subir à un système un cycle de transformations
calorifiques pures en l’échauffant de TA à TB puis en le refroidissant de TB à TA,
sans changement d'état ni variation significative du volume.
A) La chaleur reçue par le système dans la transformation AB sera la même quel
que soit le mode, réversible ou irréversible, de l'échauffement.
B) QBA = -QAB et ∆SBA = -∆SAB
C) ∆eSBA et ∆eSAB seront de signes opposés.
D) ∆iSBA et ∆SiAB seront de signes opposés.
E) Le fait que le système revienne à son état initial prouve que la réaction est
réversible.
Q.C.M. n°11: A propos du 2nd principe :
A: Il introduit la fonction d'état entropie du système.
B : Il permet de prévoir l'évolution spontanée de l'état du système.
C : Il postule que l'entropie de l'univers est une fonction d'état.
D : Il permet de différencier évolution réversible et évolution irréversible de
l'état du système.
E: Il montre que l’entropie perdue par le système est reçue par le milieu
extérieur.
Q. C. M. n°12 :
A) Un facteur de quantité est une variable extensive.
B) Une énergie élémentaire s'exprime comme le produit d’un facteur intensif par
la variation de son facteur extensif conjugué.
C) Une capacité thermique molaire est un facteur intensif.
D) Quand on divise le système en B sous-systèmes, le facteur de tension est
modifié.
E) Pour refroidir le système, on aura recours à une source froide.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 139

140. Question n°13 :
A) Un système fermé entouré par une paroi diatherme peut échanger de la
chaleur par convection.
B) Les échelles de températures Kelvin et Celsius coïncideront si elles sont
basées sur les mêmes points fixes.
C) Tous les thermoscopes à gaz fournissent la même échelle de température
indépendamment de la pression.
D) Le principe zéro permet de définir l’égalité de B température en affirmant le
caractère obligatoire de la réalisation de l'équilibre thermique.
E) Toute grandeur échangée entre le système et le milieu extérieur est
considérée du point de vue du système comme un gain pour le système.
Question n°14 :
A) Un système fermé entouré par une paroi diatherme peut échanger de la
chaleur par conduction.
B) La température est une variable intensive.
C) Pour un système fermé où ne s'exercent que des forces de pression, la chaleur
mise en jeu dans une transformation isochore ne dépend que de l'état initial et de
l'état final du système.
D) L'expression ∂ Q signifie que la chaleur élémentaire est une DTE.
E) La durée de la phase de déséquilibre de la transformation se nomme temps de
relaxation.
Q.C.M. n°15 :
A: C’est un principe de conservation de l'énergie.
B: Il postule l'équivalence entre travail et chaleur.
C: Il introduit l'énergie interne qui est dans tous les cas une fonction d'état.
D: Il permet de différencier évolution réversible et évolution irréversible de l'état
du système.
E: Pour un système isolé, la variation d'énergie interne est nulle.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 140

141. 1 ABC
2 AC
3 BD
4 ABDE
5 ABCDE
6 A
7 ABC
8 ACE
9 ACE
10 ABC
11 ABDE
12 ABCE
13 BDE
14 ABCE
15 ABCE
1 A L’enthalpie libre molaire joue le rôle de potentiel thermodynamique d’un
système monobare et monotherme. Par conséquent, le système a tendance à
diminuer son enthalpie libre.
B Le deuxième principe permet de déterminer l’entropie crée, autrement dit : le
degré d’irréversibilité de la transformation. Plus ∂i S est élevé, plus la
transformation est irréversible.
TB
∂ Qr
C ∆ S AB = ∫
TA
T
Etant donné que l’entropie est ici définie par une intégrale, on ne peut la
connaître qu’à une constante près, à moins de disposer d’une information
complémentaire.
D Le 2eme principe dit que c’est le sens spontané des échanges, mais il n’interdit
pas à l’inverse de se produire, à condition de fournir de l’énergie au système.
E L’entropie a beau être une grandeur physique à part entière, elle n’est pas
accessible à nos sens.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 141

142. 2 A C’est la définition même.
B La paroi adiabatique s’oppose aux transferts de chaleur entre le milieu
extérieur et le système. Néanmoins, le système peut toujours évoluer par
transformation interne.
C C’est la définition même. Exemple de variable intensive : p, T…
D C’est la définition même. On peut rajouter que la capacité thermique du
milieu extérieur est très supérieure à celle du système. CME >>> Csystème
E Ce type de système est dit isolé. Il est totalement coupé du milieu extérieur.
3 A La variation totale d’entropie du système est une DTE, pas la variation
d’entropie échangée.
i
QAB
A savoir : ∆ eSAB = et ∂ Q AB n’est pas une DTE.
i
Tf
B L’entropie est une fonction d’état. Par conséquent, elle est indépendante du
mode de transformation.
Donc: ∆SAB = - ∆SBA.
Or ∆SAB = (∆SeAB)rev Donc ∆SBA = - (∆SeAB)rev
Et comme (∆SeAB)rev = (∆SAB)rev ( puisque (∆SiAB)rev = 0 )
Alors ∆SBA = - (∆SAB)rev
C L’entropie est une grandeur macroscopique. Pour s’en souvenir, il suffit de
se rappeler que l’entropie est le support des échanges de chaleur et que la
chaleur se ressent macroscopiquement.
E Plus la transformation est rapide, plus la création d’entropie est grande. Pour
vous vous en souvenir, sachez que plus la transformation est rapide, plus elle est
irréversible.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 142

143. 4 B On a dU = ∂Wr
C Si la transformation est isobare, on a : dQp = Cp dT= dH. C’est l’enthalpie
qui permet de calculer directement la chaleur dans une transformation à pression
constante.
D L’énergie interne dépend de la quantité de matière.
E Si le système est à l’équilibre, pour 1 mole de ce GPM, on a
3 3
U= × 1 × R.T = R.T
2 2
Donc seule compte la température.
5 A Si la transformation est isobare, on a : dQp = Cp.dT= dH. L’enthalpie
permet de calculer directement la chaleur dans une transformation à pression
constante.
B U est une fonction d’état, elle est indépendante du mode de transformation.
C L’énergie interne ne se « crée » pas plus qu’elle ne se « perd ». Si le système
ne peut en échanger, alors son énergie reste constante.
E C’est la définition.
6 A C’est la définition même.
B C’est l’entropie
C Non il y a le facteur PV qu’il faut pendre en compte suivant les différents
modes de transformation.
D dH = ∂Q dans le cas d’une transformation isobare.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 143

144. 7 A C’est la définition même : dF = dU – T.dS
B On a dF = ∂W – T ∂iS. Si le système évolue réversiblement alors ∂iS = o
Donc dF = ∂W
Retenez que : dF = ∂Wr. Le travail monotherme a les propriétés d’une fonction
d’état.
C dF = dU – T.dS. U et S sont des fonctions d’état, donc F est une fonction
d’état.
D C’est l’enthalpie libre qui joue le rôle de fonction potentiel
thermodynamique d'un système qui évolue selon une transformation
monotherme isobare.
E dF = ∂Wr . Et ∂Wirr > ∂Wr. Donc ∂Wirr > dF
8 A Par définition même.
B L’énergie interne d’un système isolé ne peut pas varier.
C Si le système isolé ne peut pas échanger d’entropie, il peut toujours en créer.
Donc s’il ne perd pas de l’entropie et qu’il en crée, son entropie totale ne peut
qu’augmenter.
D Le système peut toujours évoluer par transformation interne. Par exemple :
un système isolé contenant de l’alcool et de l’acide carboxylique peut continuer
d’évoluer vers un mélange d’ester et d’eau.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 144

145. 9 A Par définition même.
B dSirr = dSrev .
Mais si ∂iS > 0 alors ∂eSirr < ∂eSrev
C L’univers est un système isolé, donc ∂eS = 0. Par conséquent dS = ∂ is
D La transformation est possible, mais il faudra lui fournir de l’énergie. Cela
va contre le sens d’évolution spontanée du système, mais ce n’est pas interdit.
E La transformation d’un système se fait spontanément vers l’augmentation
d’entropie.
10 A Si le volume est constant, alors le système ne produit pas de travail. Donc
∂Qv = dU
La chaleur prend les propriétés d’une fonction d’état.
B Puisque la chaleur a les propriétés d’une fonction d’état dans cette
transformation, alors : QBA = - QAB. L’entropie quant à elle est toujours une
fonction d’état.
C Puisque ΔSBA = -ΔSAB et que ΔSAB = ΔeSAB + ΔiSAB
et que ΔSBA = ΔeSBA + ΔiSBA
alors ΔeSAB et ΔeSBA seront de signes opposés.
D ΔiS est toujours positif.
E Pour qu’une réaction soit réversible, il faut que le système et le milieu
extérieur reviennent à leur état initial.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 145

146. 11 B Le deuxième principe permet de connaître la création d’entropie. On peut
ainsi prévoir l’évolution spontanée du système, en sachant que la transformation
qui crée le plus d’entropie sera celle que le système réalisera spontanément.
Par exemple, sortez un pain du four et placer le sur la table. Le pain a deux
possibilités : se réchauffer encore plus, ou se refroidir en donnant sa chaleur au
milieu extérieur. Il se trouve que la création d’entropie lors du refroidissement
est supérieure à celle lors du réchauffement. Par conséquent, le pain aura
spontanément tendance à se refroidir.
C Entropie de l’univers = ∂ iS , ce n’est pas une fonction d’état (seule S l’est)
D Une transformation irréversible est une transformation où le système crée de
l’entropie. Une transformation réversible est une transformation où le système
ne crée pas de l’entropie.
12 A Exemple de variables extensives : n, m. Plus généralement, toutes les
variables qui dépendent de la quantité de matière du système sont des variables
extensives.
B C’est la définition même.
C D’une manière générale, toutes les variables qui sont ramenées à leur valeur
pour une mole (ou une autre quantité) sont des variables intensives. Ex :
Concentration en
g.mol-1, capacité thermique massique en J.K-1.g-1…
D La tension est une variable intensive, par conséquent, elle n’est pas modifiée
lorsqu’on divise le système en deux sous-systèmes.
13 A La convection se définit comme un transfert de chaleur supporté par un
transfert de matière.
C La température et la pression d’un système gazeux sont liées. Par
conséquent une échelle de température ne peut être établie qu’en spécifiant la
pression à laquelle se font les mesures.
D Le caractère obligatoire de la réalisation d’un équilibre entre deux
systèmes mis en contact prolongé par le biais de parois diathermes constitue le
postulat du principe zéro. La température est définie comme la variable qui
atteint cet équilibre.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 146

147. 14 A La conduction se définit comme le transfert de chaleur sans transfert de
matière. C’est le seul type d’échange que peut réaliser un système fermé entouré
d’une paroi diatherme rigide.
C Puisque les transformations s’effectuent à volume constant, alors le travail
des forces de pression est nul. Or dU = ∂W + ∂Q. Donc à pression constante :
dU = ∂Q. La chaleur prend les propriétés d’une fonction d’état, elle ne dépend
plus que de l’état initial et de l’état final.
D ∂Q signifie que la chaleur élémentaire est une dérivée partielle.
E C’est la définition.
15 A Le 1er principe stipule que lors d’échanges de travail et de chaleur dans un
cycle, il existe une variable qui reste constante : c’est l’énergie interne.
B Ce principe explique que le travail et la chaleur sont des opérateurs de
transfert de l’énergie. Il s’agit de deux formes que peut prendre l’énergie.
D C’est le deuxième principe qui permet de faire cette différenciation.
E Un système isolé ne peut échanger ni de la chaleur ni du travail donc
∂W + ∂Q = 0. Donc dU = 0. Cela signifie que la variation d’énergie interne est
nulle.
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 147

148. © Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 148

149. Chapitre 4 :
Calculs de
l’évolution des
systèmes
QCM commentés par
Jean-Christophe Lecomte
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 149

150. Q.C.M n°1:
Un système est constitué par 2 mol d'un gaz parfait en équilibre, thermodynamique à la
température de 300,7 K sous la pression atmosphérique (10 5 Pa). On lui fait subir une
transformation monobare qui l'amène au volume final de 72 litres.
Calculer le travail reçu par le système (R = 8,314 J.K-1.mol-1).
A: -2200 J B: +2200 J C : -2200 kJ
D: +2200 kJ E : -4700 J
Q.C.M. n° 2:
Un système est constitué par 41: d'un gaz supposé parfait, en équilibre
thermodynamique avec une source de chaleur T0= 340K, et sous une pression de 4.105
Pa. On lui fait subir une détente monotherme irréversible qui l'amène à la pression
atmosphérique et au cours de laquelle sa variation d'énergie libre est
∆ F = -2218 J. Quel est le travail reçu par le système dans cette transformation ?
A: 4800 J B: 2218 J C: -1200 J
D: -2380 J E: -2400 J
Q.C.M. n°3 :
La capacité thermique massique d'un corps pur est :
c' = 292 + 2.10-3 T2 (J.K-1.kg-1)
Un système constitué par 100g de ce corps pur initialement en équilibre thermique
avec une source de chaleur à 17°C est mis en contact par une paroi diatherme avec une
source à 80°C. Quelle est la variation d’entropie du système dans cette transformation
calorifique pure entre les états d'équilibre initial et final ?
A: 1,6 J.K-1 B: 9,8 J.K-1 C: 8,9 J.K-1
D: 10,8 J.K-1 E : 13, 7 J.K-1
Question n° 4:
Un corps de pompe à paroi diatherme contient 0,04 mol d'air (gaz parfait) en équilibre
thermodynamique à la pression atmosphérique. La source de chaleur est l'air ambiant à
17 °C.
On effectue une compression qui amène ce système à une pression finale de 3 atm.
Calculer la variation d'énergie libre du système dans cette transformation :
(R = 8,31 J.mol-1.K-1).
A: + 192 J B : +45 J C : +6 J
D: +106J E: -192J.
Enoncé commun aux 2 questions suivantes :
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 150

151. On comprime de manière monotherme, de 2 à 10 atm, un système constitué par 3
moles d'un gaz parfait.
La température de la source de chaleur est ta = 107 °C.
On donne R = 8,31 J.K-1.mol-1
Question 5 :
Calculer la variation d'énergie libre du système.
A: -15247 J B : + 4293 J C : + 6622 J r
D : +15247 J E : + 37894 J
Question 6 :
Calculer la variation d'entropie du système.
A: -99,7 J.K-1 B: -40 J.K-1 C: -17 ,4 J.K-1
D : +40,1 J.K-1 E : +99,7 J.K-1
Enoncé commun aux Questions 7 et 8 :
Soit un corps pur de capacité thermique Cp = 2,3 + 4.10- 4T (J.K-1).
On diminue sa température, sans changement d’état, de 900 à 400 K.
Question n°7 :
Calculer la chaleur reçue par la source de chaleur :
A : +5,26 J.K-1 C : + 10,8 J.K-1 E : + 1410 J
B : + 1280 J D : + 127,7 J.
Question n°8 :
Calculer la création d’entropie ∆ jS.
A : + 5,26 J.K-1 C : +10,8 J.K-1 E: + 1,14 J.K-1
B : +4,86 J.K-1 D : + 3,48 J.K-1
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 151

152. Enoncé commun aux 2 questions suivantes :
Un système constitué par 2 moles d'un gaz parfait est en équilibre thermodynamique,
sous une pression extérieure de 8 atm, avec une source de chaleur à la température t 0 =
257 °C. On effectue une transformation monotherme irréversible au cours de laquelle
la source de chaleur fournit une quantité de chaleur de 8038 J au système.
On donne R = 8,31 J.K-1.mol-1.
Question n°9:
Calculer la pression du système à l'état d'équilibre final.
Une réponse exacte.
A: 3,2 atm B: 0,7 atm C: 15,1 atm.
D: 2 atm E: 0,4 atm.
Question n°10 :
Calculer la création d'entropie dans cette transformation irréversible.
Une réponse exacte
A: + 25,3 J.K-1 B: + 40 J.K-1 C : + 15 J.K-1
-1 -1
D: + 52,2 J.K E: + 55,6 J.K
Enoncé commun aux 4 questions suivantes :
Un système est constitué par 0,6 moles d'un gaz parfait en équilibre thermique avec
une source de chaleur à t0 = 30°C. Sa pression initiale est pA=3.105 Pa. On effectue une
détente monotherme irréversible qui l’amène à la pression finale pB = 105 Pa.
On donne R = 8,31 J.K-1 mol-1
Pour cette transformation irréversible :
Question n°11 :
Calculer le travail reçu par le système.
A: -100 J B : 1007J C:-1678J
D: -721 J E:-1660J.
Question n°12 :
Calculer la variation d'énergie libre du système.
A: -1048J B: -164J C: -1007J
D: -721J E: -1660 J
Question n°13:
Calculer la variation d'entropie du système.
A: +5,5 J.K-1 B: +55 J.K-1 C: +3.3 J.K-1
D: +33 J.K-1 E: +24 J.K-1
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 152

153. Question n°14 :
Calculer la création d'entropie
A: +3,3 J.K-1 B: + 33 J.K-1
-1
D: + 22 J.K E: + 8,8 J:K-1 C: + 2,2 J.K-1
Enoncé commun aux 3 questions suivantes (questions n°18, n°19 et n°20)
La capacité thermique molaire (en J.mol-1.K-1) d'un corps pur est
c = 15,1 + 30,1.10-3 T.
Un système constitué par 2 mol de ce corps pur est initialement en équilibre
thermodynamique avec l'air ambiant à 290 K. On effectue une transformation
calorifique pure qui amène sa température à 460 K, sans changement d'état.
Question n°15 :
Calculer la quantité de chaleur reçue par le système.
Indiquer la seule réponse exacte:
A: +2694 J B : +4480J C: +8972J
D: +9841 J E: +12809 J.
Question n° 16 :
Calculer la variation d'entropie du système dans cette transformation.
Indiquer la seule réponse exacte:
A: +21,1 J.K-1 B: +24,2 J.K-1 C: +30,0 J.K-1
D: +52,5 J.K-1 E: -3,6 J.K-1
Question n°17:
1) La variation d'entropie de la source de chaleur est -19,5 J.K-1
2) L'entropie créée dans le système lors de cette transformation est +4,7 J.K-1.
3) Si on ramène le système à son état initial, la quantité de chaleur reçue par le système
et aussi la variation d'entropie du système seront chacune, par rapport à l'aller,
changées de signe mais égales en valeur absolue.
4) La variation d'entropie de l'univers est -4,7 J.K-1
Indiquer la seule combinaison des propositions exactes:
A:1,2,3 B:1,3 C:2,4 D:4 E: 1,2,3,4
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 153

154. Réponses :
1–A
2–C
3–B
4–D
5–D
6–B
7–B
8–E
9–B
10– A
11– B
12– E
13– A
14– C
15– C
16– B
17– A
QCM 1 :
Il s’agit d’un gaz parfait (GP).
Wmonobare = − p 0 (V B − V A )
Par hypothèse : p 0 = 10 Pa et V B = 72 L = 72.10 − 3 m 3 (en effet, il faut exprimer les volumes
5
en unités du système international : m 3 !)
Il faut déterminer V A :
D’après l’équation d’état des GP : p.V = n.R.T
n.R.T A 2 X 8,314 X 300,7
⇒ VA = = 5
≈ 50.10 − 3 m 3
p0 10
⇒ Wmonobare = − 10 5 (72.10 − 3 − 50.10 − 3 ) = − 22.10 − 2 = − 2200 J
Réponse A
QCM 2 :
Le gaz est supposé parfait.
p
Wmonotherme = n.R.T0 ( B − 1)
pA
Par hypothèse : p A = 4.10 5 Pa et p B = 10 5 Pa puisqu’il s’agit de la pression atmosphérique.
Il faut déterminer n :
D’après l’équation d’état des GP : p.V = n.R.T
⇒ n.R.T0 = p A .V A = 4.10 5 X 4.10 − 3 = 16.10 2 U .S .I . (en effet, il faut exprimer les volumes en
unités du système international : V A = 4 L = 4.10 − 3 m 3 !)
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 154

155. 10 5 −3
Donc Wmonotherme = 16.10 2 ( 5
− 1) = 16.10 2 X ( ) = − 1200 J
4.10 4
Réponse C
QCM 3 :
∂ Qr
dS =
T
∂ Qr m.c' (T )
⇒ ∆S = ∫ T .dT = ∫ T .dT
Attention : il faut exprimer toutes les données dans les unités adéquates :
m = 100 g = 10 − 1 kg , T A = 17° C = 17 + 273 = 290 K et TB = 80° C = 80 + 273 = 353K
10 − 1 X ( 292 + 2.10 − 3 T ²) 29,2 2.10 − 4 T ²
Donc : ∆ S AB = ∫ T
.dT = ∫
T
.dT + ∫
T
.dT
29,2 T²
⇒ ∆ S AB = ∫ .dT + ∫ 2.10 − 4 T .dT = [29,2 ln T ] B + [2.10 − 4 X ] B
A A
T 2
T
⇒ ∆ S AB = 29,2 X (ln TB − ln T A ) + 10 − 4 X (TB2 − T A2 ) = 29,2 ln B + 10 − 4 X (TB2 − T A2 )
TA
353
⇒ ∆ S AB = 29,2 ln + 10 − 4 X (353² − 290²) ≈ 9,8 J .K − 1
290
Réponse B
QCM 4 :
∆F = Wr
Le gaz est supposé parfait.
pB
⇒ ∆ F = Wisotherme = n.R.T0 . ln
pA
Attention de bien exprimer les données dans les unités adéquates :
T0 = 17° C = 17 + 273 = 290 K (il est ici possible de laisser p A et p B en atm car ces valeurs
vont être employées dans un rapport).
3
⇒ ∆ F = 0,04 X 8,31X 290 X ln ≈ 106 J
1
Réponse D
(normalement, ln3 vous sera donné dans l’énoncé le jour du concours)
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 155

156. QCM 5 :
∆F = Wr
Il s’agit d’un gaz parfait.
pB
⇒ ∆ F = Wisotherme = n.R.T0 . ln
pA
Attention : la température doit être exprimée en kelvins !
T0 = 107° C = 107 + 273 = 380 K (il est ici possible de laisser p A et p B en atm car ces valeurs
vont être employées dans un rapport).
10
⇒ ∆ F = 3 X 8,31X 380 X ln ≈ 15247 J
2
Réponse D
(normalement, ln3 vous sera donné dans l’énoncé le jour du concours)
QCM 6 :
∂ Qr
dS =
T
∂ Qr ∂ Qr 1 Qisotherme
⇒ ∆S = ∫ .dT = ∫ .dT = ∫ ∂ Q .dT = T0
r
T T0 T0
Or il s’agit d’un gaz parfait donc : Wisotherme = − Qisotherme
⇒ Qisotherme = − ∆ F = − 15247 J
− 15247
⇒ ∆S = ≈ − 40,1J .K − 1 (attention au signe !)
380
Réponse B
QCM 7 :
Attention : il s’agit de la chaleur reçue par la source de chaleur !
C’est donc l’opposé de la chaleur reçue par le système : QSC = − Q
Q= ∫ C (T ).dT
⇒ Q = − ∫ 2,3 + 4.10
SC
−4
T.dT = − [2,3T + 2.10 − 4 T ²]900
400
⇒ QSC = − [2,3 X (400 − 900) + 2.10 − 4 (400² − 900²)]
⇒ QSC = − [230 X (− 5) + 2.10 − 4 X 10 4 (16 − 81)] = − [− 1150 + 2 X (− 65)]
⇒ QSC = − [− 1150 + 2 X (− 65)] = − (− 1280) = + 1280 J (attention au signe !)
Réponse B
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 156

157. QCM 8 :
D’après le second principe : dS = ∂ e S + ∂ i S
⇒ ∆ iS = ∆ S − ∆ eS
δ Qr C (T ) 2,3 + 4.10 − 4 T
∆S = ∫ T .dT = ∫
T
.dT = ∫
T
.dT
2,3
⇒ ∆S = ∫ .dT + ∫ 4.10 − 4.dT = [2,3 ln T ]900 + [ 4.10 − 4 T ]900
400 400
T
400  2 2
⇒ ∆ S = 2,3 ln + 4.10 X (400 − 900) = 2,3 X ln     + 4.10 − 4 X (− 500)
−4
900  3 
 
⇒ ∆ S = 4,6 X (ln 2 − ln 3) − 0,2 ≈ 4,6 X (0,7 − 1,1) − 0,2 ≈ − 2,04 J .K − 1
Qi Q − QSC − 1280
∆ eS = = = = = − 3,2 J .K − 1
Tf Tf Tf 400
⇒ ∆ i S = − 2,04 − (− 3,2) = − 2,04 + 3,2 = 1,16 ≈ 1,14 J .K − 1 (approximation due aux arrondis pris
pour les calculs de ln)
Réponse E
QCM 9 :
Il s’agit d’un gaz parfait.
p
Wmonotherme = n.R.T0 ( B − 1)
pA
p W
⇒ B − 1 = monotherme
pA n.R.T0
W 
⇒ p B = p A X  monotherme + 1
 n.R.T 
 0 
Attention : la température doit être exprimée en kelvins !
T0 = 257° C = 257 + 273 = 530 K
p A et p B ont laissées en atm car ces valeurs vont être employées dans un rapport.
La source de chaleur fournit QSC = 8038 J donc le système reçoit Qmonotherme = 8038 J .
Or il s’agit d’un gaz parfait donc Wmonotherme = − Qmonotherme .
 − 8038 
⇒ pB = 8X  + 1 ≈ 0,7 atm
 2 X 8,31X 530 
Réponse B
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 157

158. QCM 10 :
D’après le second principe : dS = ∂ e S + ∂ i S
⇒ ∆ iS = ∆ S − ∆ eS
∂ Qr
dS =
T
∂ Qr ∂ Qr 1 Qisotherme
⇒ ∆S = ∫ T .dT = ∫ .dT = ∫ ∂ Q .dT = T0
r
T0 T0
Or il s’agit d’un gaz parfait donc : Wisotherme = − Qisotherme
pB
De plus, Wisotherme = n.R.T0 . ln
pA
p
− n.R.T0 . ln B
pA p
⇒ ∆S = = − n.R. ln B
T0 pA
0,7
⇒ ∆ S = − 2 X 8,31X ln ≈ 40,5 J .K − 1
8
Q i Qmonotherme 8038
∆ eS = = = ≈ 15,2 J .K − 1
Tf T0 530
⇒ ∆ i S = 40,5 − 15,2 = 25,3 J .K − 1
Réponse A
QCM 11 :
Il s’agit d’un gaz parfait.
p
Wmonotherme = n.R.T0 ( B − 1)
pA
Attention de bien exprimer la température en kelvins !
T0 = 30° C = 30 + 273 = 303K
10 5
⇒ Wmonotherme = 0,6 X 8,31X 303 X ( − 1)
3.10 5
− 2
⇒ Wmonotherme = 0,6 X 8,31X 303 X ( ) ≈ − 1007 J
3
Réponse B
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 158

159. QCM 12 :
∆F = Wr
Il s’agit d’un gaz parfait.
pB
⇒ ∆ F = Wisotherme = n.R.T0 . ln
pA
10 5
⇒ ∆ F = 0,6 X 8,31X 303 X ln = 0,6 X 8,31X 303 X (− ln 3) ≈ − 1660 J
3.10 5
Réponse E
QCM 13 :
∂ Qr
dS =
T
∂ Qr ∂ Qr 1 Qisotherme
⇒ ∆S = ∫ T .dT = ∫ .dT = ∫ ∂ Q .dT = T0
r
T0 T0
Or il s’agit d’un gaz parfait donc : Wisotherme = − Qisotherme
De plus, Wisotherme = W = ∆ F
r
− ( − 1660) 1660
⇒ ∆S = = ≈ 5,5 J .K − 1
303 303
Réponse A
QCM 14 :
D’après le second principe : dS = ∂ e S + ∂ i S
⇒ ∆ iS = ∆ S − ∆ eS
Q i Qmonotherme
∆ eS = =
Tf T0
Or il s’agit d’un gaz parfait donc : Qmonotherme = − Wmonotherme
− (− 1007) 1007
⇒ ∆ eS = = ≈ 3,3 J .K − 1
330 303
⇒ ∆ i S = 5,5 − 3,3 = 2,2 J .K − 1
Réponse C
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 159

160. QCM 15 :
Q= ∫ n.c(T ).dT
⇒ Q = ∫ 2 X (15,1 + 30,1.10 −3
T ).dT = 2 X [15,1T + 15,05.10 − 3 T ²] 460
290
⇒ Q = 2 X [15,1X (460 − 290) + 15,05.10 − 3 (460² − 290²)]
⇒ Q = 2 X [151X 17 + 15,05.10 − 3 X 10² X (46² − 29²)]
⇒ Q = 2 X [2567 + 15,05.10 − 1 X (2116 − 841)] ≈ 8972 J
Réponse C
QCM 16 :
∂ Qr
dS =
T
δ Qr n.c(T ) 2 X (15,1 + 30,1.10 − 3 T )
⇒ ∆S = ∫ T .dT = ∫
T
.dT = ∫
T
.dT
2 X 15,1
⇒ ∆S = ∫ .dT + ∫ 2 X 30,1.10 − 3.dT = 30,2 X [ln T ] 460 + 60,2.10 − 3 [T ] 460
290 290
T
460
⇒ ∆ S = 30,2 X ln + 60,2.10 − 3 X (460 − 290)
290
46
⇒ ∆ S = 30,2 X ln + 60,2.10 − 3 X 170 ≈ 24,2 J .K − 1
29
Réponse B
QCM 17 :
1) ∆ S SC = − ∆ e S
Q
Or ∆ e S =
Tf
8972
⇒ ∆ S SC = − ≈ − 19,5 J .K − 1
460
Vrai
2) D’après le second principe : dS = ∂ e S + ∂ i S
⇒ ∆ iS = ∆ S − ∆ eS
Or ∆ e S = − ∆ S SC donc ∆ e S = 19,5 J .K
−1
⇒ ∆ i S = 24,2 − 19,5 = 4,7 J .K − 1
Vrai
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 160

161. 3) Vrai car il s’agit d’une transformation calorifique pure.
Démonstration :
- D’après le 1er principe :
dU = ∂ W + ∂ Q
Or c’est une transformation calorifique pure donc ∂ Wisochore = 0
⇒ dU = ∂ Qisochore = dQisochore : la chaleur isochore prend les propriétés d’une fonction d‘état.
Or ∆ U BA = − ∆ U AB . Par conséquent : ∆ QisochoreBA = − ∆ QisochoreAB
- La variation d’entropie du système à toujours les propriétés d’une fonction d’état.
⇒ ∆ S BA = − ∆ S AB
4) L’Univers est un système isolé : ∆ SUnivers = ∆ i S
⇒ ∆ SUnivers > 0
Faux
Réponse A (ce format de QCM ne vous sera pas proposé au concours : tous les QCM du
concours sont sans patrons de réponse).
© Tous droits réservés au Tutorat Associatif Toulousain
Sauf autorisation, la vente, la diffusion totale ou partielle de ce polycopié sont interdites 161