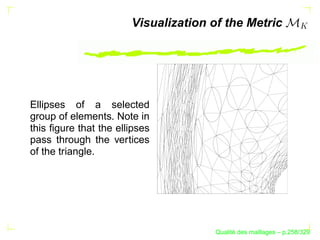
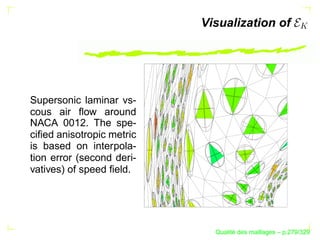
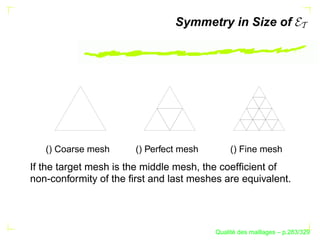
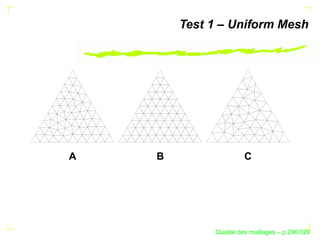
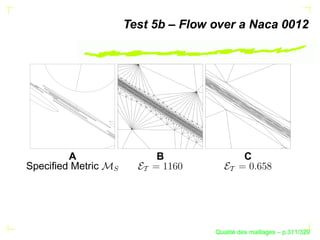
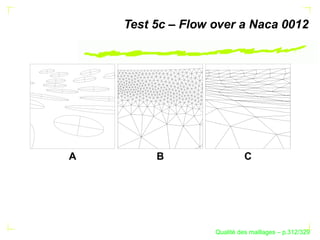
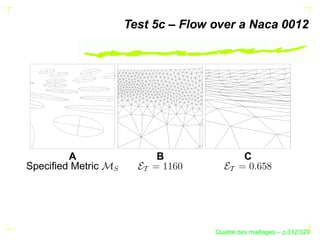
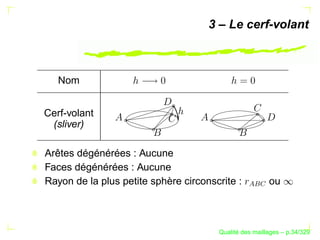
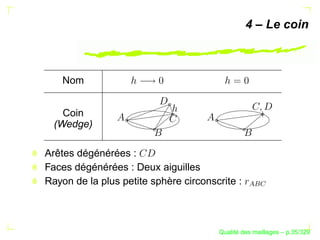
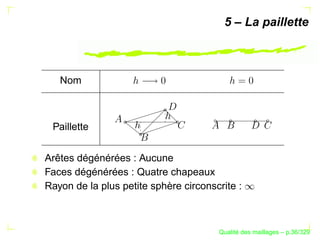
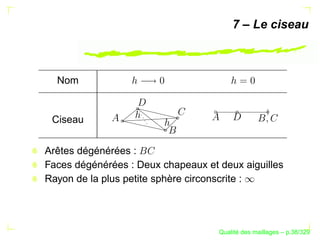
Le document traite de la qualité des maillages en recherche appliquée, en abordant des critères de qualité pour les maillages simpliciaux et non simpliciaux. Il fournit une introduction aux concepts fondamentaux tels que la définition d'un simplexe, la dégénérescence de ceux-ci, ainsi que des techniques d'optimisation des maillages dans des contextes tridimensionnels. Les références citées soulignent l'importance des travaux précédents sur le sujet.

1. Qualité des maillages
Julien Dompierre
julien@cerca.umontreal.ca
´
Centre de Recherche en Calcul Applique (CERCA)
´ ´
Ecole Polytechnique de Montreal
´
Qualite des maillages – p.1/329

2. Auteurs
Professionnels de recherche
Julien Dompierre
Paul Labbé
Marie-Gabrielle Vallet
Professeurs
François Guibault
Jean-Yves Trépanier
Ricardo Camarero
´
Qualite des maillages – p.2/329

3. Références – 1
J. D OMPIERRE , P. L ABBÉ ,
M.-G. VALLET, F. G UIBAULT
ET R. C AMARERO, Critères
de qualité pour les maillages
simpliciaux. Dans Maillage et
adaptation, Hermès, octobre
2001, Paris, pages 311–348.
´
Qualite des maillages – p.3/329

4. Références – 2
A. L IU et B. J OE, Relationship between
Tetrahedron Shape Measures, Bit, Vol. 34,
pages 268–287, (1994).
´
Qualite des maillages – p.4/329

5. Références – 3
P. L ABBÉ, J. D OMPIERRE, M.-G. VALLET, F.
G UIBAULT et J.-Y. T RÉPANIER, A Universal
Measure of the Conformity of a Mesh with
Respect to an Anisotropic Metric Field,
Submitted to Int. J. for Numer. Meth. in Engng,
(2003).
´
Qualite des maillages – p.5/329

6. Références – 4
P. L ABBÉ, J. D OMPIERRE, M.-G. VALLET, F.
G UIBAULT et J.-Y. T RÉPANIER, A Measure of
the Conformity of a Mesh to an Anisotropic
Metric, Tenth International Meshing Roundtable,
Newport Beach, CA, pages 319–326, (2001).
´
Qualite des maillages – p.6/329

7. Références – 5
P.-L. G EORGE ET H. B OROU -
CHAKI, Triangulation de De-
launay et maillage, applica-
tions aux éléments finis. Her-
mès, 1997, Paris.
´
Qualite des maillages – p.7/329

8. Références – 6
P. J. F REY AND P.-L.
G EORGE, Maillages. Ap-
plications aux éléments finis.
Hermès, 1999, Paris.
´
Qualite des maillages – p.8/329

9. Table des matières
1. Introduction 8. Éléments non simpli
2. Définition d’un sim- ciaux
plexe 9. Représentation des
3. Dégénérescence des critères de forme
simplexes 10. Équivalence des cri
4. Qualité de forme des tères de forme
simplexes 11. Qualité globale e
5. Formules pour les optimisation
simplexes 12. Qualité en taille des
6. Voronoï, Delaunay et simplexes
Riemann 13. Qualité universelle
7. Critères de formes et 14. Conclusions – p.9/329
´
Qualite des maillages

10. Introduction et justifications
On travaille sur la génération, l’adaptation et
l’optimisation de maillages.
Comment choisir la configuration qui donne les
plus beaux triangles ? Il faut un critère de qualité
des triangles.
´
Qualite des maillages – p.10/329

11. Retournement d’une face
Comment choisir la configuration qui donne les
plus beaux tétraèdres ? Il faut un critère de
qualité des tétraèdres.
´
Qualite des maillages – p.11/329

12. Retournement d’une arête
S4 S3 S4 S3
S5 S5
A A
B B
S2 S2
S1 S1
Comment choisir la configuration qui donne les
plus beaux tétraèdres ? Il faut un critère de
qualité des tétraèdres.
´
Qualite des maillages – p.12/329

13. Optimisation de maillages
Soit et , deux ptimiseurs de maillages
tridimensionnels tétraédriques non structurés.
´
Qualite des maillages – p.13/329

14. Optimisation de maillages
Soit et , deux ptimiseurs de maillages
tridimensionnels tétraédriques non structurés.
Quelle est la norme d’un optimiseur de
maillage ?
´
Qualite des maillages – p.13/329

15. Optimisation de maillages
Soit et , deux ptimiseurs de maillages
tridimensionnels tétraédriques non structurés.
Quelle est la norme d’un optimiseur de
maillage ?
Comment peut-on affirmer que ?
´
Qualite des maillages – p.13/329

16. Mais c’est très simple !
Soit , un banc d’essai (un benchmark).
´
Qualite des maillages – p.14/329

17. Mais c’est très simple !
Soit , un banc d’essai (un benchmark).
Soit , le maillage optimisé obtenu
avec l’optimiseur .
´
Qualite des maillages – p.14/329

18. Mais c’est très simple !
Soit , un banc d’essai (un benchmark).
Soit , le maillage optimisé obtenu
avec l’optimiseur .
Soit , le maillage optimisé obtenu
avec l’optimiseur .
´
Qualite des maillages – p.14/329

19. Mais c’est très simple !
Soit , un banc d’essai (un benchmark).
Soit , le maillage optimisé obtenu
avec l’optimiseur .
Soit , le maillage optimisé obtenu
avec l’optimiseur .
La sagesse populaire dit : “On juge un arbre à
ses fruits”.
´
Qualite des maillages – p.14/329

20. Mais c’est très simple !
Soit , un banc d’essai (un benchmark).
Soit , le maillage optimisé obtenu
avec l’optimiseur .
Soit , le maillage optimisé obtenu
avec l’optimiseur .
La sagesse populaire dit : “On juge un arbre à
ses fruits”.
Si alors .
´
Qualite des maillages – p.14/329

21. Bancs d’essais d’optimisation de maill
J. D OMPIERRE, P. L ABBÉ, F. G UIBAULT et
R. C AMARERO.
Proposal of Benchmarks for 3D Unstructured
Tetrahedral Mesh Optimization.
7th International Meshing Roundtable, Dearborn,
MI, octobre 1998, pages 459–478.
´
Qualite des maillages – p.15/329

22. Le piège...
Parce qu’on ne connaît pas la norme d’un
optimiseur, on a remplacé la comparaison de
deux optimiseurs par la comparaison de deux
maillages.
´
Qualite des maillages – p.16/329

23. Le piège...
Parce qu’on ne connaît pas la norme d’un
optimiseur, on a remplacé la comparaison de
deux optimiseurs par la comparaison de deux
maillages.
Quelle est la norme d’un maillage ?
´
Qualite des maillages – p.16/329

24. Le piège...
Parce qu’on ne connaît pas la norme d’un
optimiseur, on a remplacé la comparaison de
deux optimiseurs par la comparaison de deux
maillages.
Quelle est la norme d’un maillage ?
Comment peut-on affirmer que ?
´
Qualite des maillages – p.16/329

25. Le piège...
Parce qu’on ne connaît pas la norme d’un
optimiseur, on a remplacé la comparaison de
deux optimiseurs par la comparaison de deux
maillages.
Quelle est la norme d’un maillage ?
Comment peut-on affirmer que ?
C’est ce que vous saurez bientôt, ou vous
serez remboursés !
´
Qualite des maillages – p.16/329

26. Ce qu’il faut retenir
Cet exposé portera sur les notions de qualité
des éléments d’un maillage et sur la qualité de
tout un maillage.
´
Qualite des maillages – p.17/329

27. Ce qu’il faut retenir
Cet exposé portera sur les notions de qualité
des éléments d’un maillage et sur la qualité de
tout un maillage.
La notion de qualité des éléments est
nécessaire pour les algorithmes de
retournement d’arêtes et de faces.
´
Qualite des maillages – p.17/329

28. Ce qu’il faut retenir
Cet exposé portera sur les notions de qualité
des éléments d’un maillage et sur la qualité de
tout un maillage.
La notion de qualité des éléments est
nécessaire pour les algorithmes de
retournement d’arêtes et de faces.
La notion de qualité de tout un maillage est
nécessaire dans la recherche sur l’optimisation
des maillages.
´
Qualite des maillages – p.17/329

29. Table des matières
1. Introduction 8. Éléments non simpliciaux
2. Définition d’un simplexe 9. Représentation des cri-
3. Dégénérescence des sim- tères de forme
plexes 10. Équivalence des critères
4. Qualité de forme des sim- de forme
plexes 11. Qualité globale et optimi-
5. Formules pour les sim- sation
plexes 12. Qualité en taille des sim-
6. Voronoï, Delaunay et Rie- plexes
mann 13. Qualité universelle
7. Critères de formes et de 14. Conclusions
Delaunay
´
Qualite des maillages – p.18/329

30. Définition d’un simplexe
Les maillages en deux et trois dimensions sont
constitués de polygones ou de polyèdres appelés
éléments.
´
Qualite des maillages – p.19/329

31. Définition d’un simplexe
Les maillages en deux et trois dimensions sont
constitués de polygones ou de polyèdres appelés
éléments.
Les plus simples d’entre eux, les simplexes, sont ceux
qui ont le nombre minimal de sommets.
´
Qualite des maillages – p.19/329

32. Définition d’un simplexe
Les maillages en deux et trois dimensions sont
constitués de polygones ou de polyèdres appelés
éléments.
Les plus simples d’entre eux, les simplexes, sont ceux
qui ont le nombre minimal de sommets.
Le segment en une dimension.
´
Qualite des maillages – p.19/329

33. Définition d’un simplexe
Les maillages en deux et trois dimensions sont
constitués de polygones ou de polyèdres appelés
éléments.
Les plus simples d’entre eux, les simplexes, sont ceux
qui ont le nombre minimal de sommets.
Le segment en une dimension.
Le triangle en deux dimensions.
´
Qualite des maillages – p.19/329

34. Définition d’un simplexe
Les maillages en deux et trois dimensions sont
constitués de polygones ou de polyèdres appelés
éléments.
Les plus simples d’entre eux, les simplexes, sont ceux
qui ont le nombre minimal de sommets.
Le segment en une dimension.
Le triangle en deux dimensions.
Le tétraèdre en trois dimensions.
´
Qualite des maillages – p.19/329

35. Définition d’un simplexe
Les maillages en deux et trois dimensions sont
constitués de polygones ou de polyèdres appelés
éléments.
Les plus simples d’entre eux, les simplexes, sont ceux
qui ont le nombre minimal de sommets.
Le segment en une dimension.
Le triangle en deux dimensions.
Le tétraèdre en trois dimensions.
Le hypertétraèdre en quatre dimensions.
´
Qualite des maillages – p.19/329

36. Définition d’un simplexe
Les maillages en deux et trois dimensions sont
constitués de polygones ou de polyèdres appelés
éléments.
Les plus simples d’entre eux, les simplexes, sont ceux
qui ont le nombre minimal de sommets.
Le segment en une dimension.
Le triangle en deux dimensions.
Le tétraèdre en trois dimensions.
Le hypertétraèdre en quatre dimensions.
Les quadrilatères, les pyramides, les prismes, les
hexaèdres et autres bizarreries sont des éléments non
simpliciaux.
´
Qualite des maillages – p.19/329

37. Définition d’un -simplexe dans
£
Soient points ,
¡
¢
£
, non situés dans le même hyperplan,
c’est-à-dire tel que la matrice d’ordre ,
¡¡
¡¢
¥¡
£
¦¡
¤
¢¡
¢¢
¤ ¢
£
¦¡
.
. .
. ... .
.
. . .
£¡
£¢
¤ £
£
¦¡
soit inversible. On appelle -simplexe des points ,
l’enveloppe convexe des points .
´
Qualite des maillages – p.20/329

38. Un simplexe engendre
£
©§ £
Tout point , de coordonnées cartésiennes
§
¡
¨
est caractérisé par la donnée des scalaires
définis comme solution du système linéaire
£
¦¡
§ pour
§
£ ¨
¡
¦¡
¨
¡
dont la matrice est .
´
Qualite des maillages – p.21/329

39. Ce qu’il faut retenir
En deux dimensions, le simplexe est le triangle.
´
Qualite des maillages – p.22/329

40. Ce qu’il faut retenir
En deux dimensions, le simplexe est le triangle.
En trois dimensions, le simplexe est le tétraèdre.
´
Qualite des maillages – p.22/329

41. Ce qu’il faut retenir
En deux dimensions, le simplexe est le triangle.
En trois dimensions, le simplexe est le tétraèdre.
£
Les sommets d’un simplexe dans engendrent
£
vecteurs qui forment une base de .
´
Qualite des maillages – p.22/329

42. Ce qu’il faut retenir
En deux dimensions, le simplexe est le triangle.
En trois dimensions, le simplexe est le tétraèdre.
£
Les sommets d’un simplexe dans engendrent
£
vecteurs qui forment une base de .
£
Les coordonnées d’un point dans la base
engendrée par le simplexe sont les coordonnées
barycentriques.
´
Qualite des maillages – p.22/329

43. Table des matières
1. Introduction 8. Éléments non simpliciaux
2. Définition d’un simplexe 9. Représentation des cri-
3. Dégénérescence des sim- tères de forme
plexes 10. Équivalence des critères
4. Qualité de forme des sim- de forme
plexes 11. Qualité globale et optimi-
5. Formules pour les sim- sation
plexes 12. Qualité en taille des sim-
6. Voronoï, Delaunay et Rie- plexes
mann 13. Qualité universelle
7. Critères de formes et de 14. Conclusions
Delaunay
´
Qualite des maillages – p.23/329

44. Dégénérescence des simplexes
Un -simplexe formé de sommets est dégénéré si
ses sommets sont situés dans le même hyperplan,
c’est-à-dire, si la matrice est non inversible.
´
Qualite des maillages – p.24/329

45. Dégénérescence des simplexes
Un -simplexe est dégénéré si ses sommets
£
n’engendrent pas l’espace .
´
Qualite des maillages – p.25/329

46. Dégénérescence des simplexes
Un -simplexe est dégénéré si ses sommets
£
n’engendrent pas l’espace .
C’est le cas si les sommets sont contenus dans
un espace de dimension inférieure à .
´
Qualite des maillages – p.25/329

47. Dégénérescence des simplexes
Un -simplexe est dégénéré si ses sommets
£
n’engendrent pas l’espace .
C’est le cas si les sommets sont contenus dans
un espace de dimension inférieure à .
Un triangle est dégénéré si ses sommets sont
colinéaires ou confondus.
´
Qualite des maillages – p.25/329

48. Dégénérescence des simplexes
Un -simplexe est dégénéré si ses sommets
£
n’engendrent pas l’espace .
C’est le cas si les sommets sont contenus dans
un espace de dimension inférieure à .
Un triangle est dégénéré si ses sommets sont
colinéaires ou confondus.
Un tétraèdre est dégénéré si ses sommets sont
coplanaires, colinéaires ou confondus.
´
Qualite des maillages – p.25/329

49. Dégénérescence des simplexes
Un -simplexe est dégénéré si ses sommets
£
n’engendrent pas l’espace .
C’est le cas si les sommets sont contenus dans
un espace de dimension inférieure à .
Un triangle est dégénéré si ses sommets sont
colinéaires ou confondus.
Un tétraèdre est dégénéré si ses sommets sont
coplanaires, colinéaires ou confondus.
Notez qu’à strictement parler, un simplexe dégénéré
n’est plus un simplexe au sens de la définition.
´
Qualite des maillages – p.25/329

50. Critère de dégénérescence
Un -simplexe est dégénéré si la matrice est non
inversible. Une matrice est non inversible si son
déterminant est nul.
´
Qualite des maillages – p.26/329

51. Critère de dégénérescence
Un -simplexe est dégénéré si la matrice est non
inversible. Une matrice est non inversible si son
déterminant est nul.
La mesure d’un simplexe est son aire en deux
dimensions et son volume en trois dimensions.
´
Qualite des maillages – p.26/329

52. Critère de dégénérescence
Un -simplexe est dégénéré si la matrice est non
inversible. Une matrice est non inversible si son
déterminant est nul.
La mesure d’un simplexe est son aire en deux
dimensions et son volume en trois dimensions.
La mesure d’un -simplexe formé de
sommets est donnée par
´
Qualite des maillages – p.26/329

53. Critère de dégénérescence
Un -simplexe est dégénéré si la matrice est non
inversible. Une matrice est non inversible si son
déterminant est nul.
La mesure d’un simplexe est son aire en deux
dimensions et son volume en trois dimensions.
La mesure d’un -simplexe formé de
sommets est donnée par
Un triangle est dégénéré si son aire est nulle.
´
Qualite des maillages – p.26/329

54. Critère de dégénérescence
Un -simplexe est dégénéré si la matrice est non
inversible. Une matrice est non inversible si son
déterminant est nul.
La mesure d’un simplexe est son aire en deux
dimensions et son volume en trois dimensions.
La mesure d’un -simplexe formé de
sommets est donnée par
Un triangle est dégénéré si son aire est nulle.
Un tétraèdre est dégénéré si son volume est nul.
´
Qualite des maillages – p.26/329

55. Taxonomie des simplexes dégénérés
Cette taxonomique repose sur les différents états
dégénérés possibles des simplexes.
´
Qualite des maillages – p.27/329

56. Taxonomie des simplexes dégénérés
Cette taxonomique repose sur les différents états
dégénérés possibles des simplexes.
Il y a trois cas de triangles dégénérés.
´
Qualite des maillages – p.27/329

57. Taxonomie des simplexes dégénérés
Cette taxonomique repose sur les différents états
dégénérés possibles des simplexes.
Il y a trois cas de triangles dégénérés.
Il y a dix cas de tétraèdres dégénérés.
´
Qualite des maillages – p.27/329

58. Taxonomie des simplexes dégénérés
Cette taxonomique repose sur les différents états
dégénérés possibles des simplexes.
Il y a trois cas de triangles dégénérés.
Il y a dix cas de tétraèdres dégénérés.
Dans ce catalogue, les quatre symboles
, , et représentent des sommets de
multiplicité simple, double, triple et quadruple
respectivement.
´
Qualite des maillages – p.27/329

59. 1 – Le chapeau
Nom
Chapeau
(cap)
Arêtes dégénérées : Aucune
Rayon du plus petit cercle circonscrit :
´
Qualite des maillages – p.28/329

60. 2 – L’aiguille
Nom
Aiguille
,
(needle)
Arêtes dégénérées :
Rayon du plus petit cercle circonscrit :
´
Qualite des maillages – p.29/329

61. 3 – Le Big Crunch
Nom
Big , ,
Crunch
Arêtes dégénérées : Toutes
Rayon du plus petit cercle circonscrit :
Le Big Crunch est la théorie inverse du Big Bang.
´
Qualite des maillages – p.30/329

62. Dégénérescence des tétraèdres
Il y a un cas de dégénérescence en quatre sommets
confondus.
Il y a cinq cas de dégénérescence en quatre sommets
colinéaires.
Il y a quatre cas de dégénérescence en quatre
sommets coplanaires.
d
a
b
c
´
Qualite des maillages – p.31/329

63. 1 – L’aileron
Nom
Aileron
Arêtes dégénérées : Aucune
Faces dégénérées : Un chapeau
Rayon de la plus petite sphère circonscrite :
´
Qualite des maillages – p.32/329

64. 2 – Le chapeau
Nom
Chapeau
(Cap)
Arêtes dégénérées : Aucune
Faces dégénérées : Aucune
Rayon de la plus petite sphère circonscrite :
´
Qualite des maillages – p.33/329

65. 3 – Le cerf-volant
Nom
Cerf-volant
(sliver)
Arêtes dégénérées : Aucune
Faces dégénérées : Aucune
Rayon de la plus petite sphère circonscrite : ou
´
Qualite des maillages – p.34/329

66. 4 – Le coin
Nom
Coin
(Wedge)
Arêtes dégénérées :
Faces dégénérées : Deux aiguilles
Rayon de la plus petite sphère circonscrite :
´
Qualite des maillages – p.35/329

67. 5 – La paillette
Nom
Paillette
Arêtes dégénérées : Aucune
Faces dégénérées : Quatre chapeaux
Rayon de la plus petite sphère circonscrite :
´
Qualite des maillages – p.36/329

68. 6 – Le fuseau
Nom
Fuseau
Arêtes dégénérées :
Faces dégénérées : Deux chapeaux et deux aiguilles
Rayon de la plus petite sphère circonscrite :
´
Qualite des maillages – p.37/329

69. 7 – Le ciseau
Nom
Ciseau
Arêtes dégénérées :
Faces dégénérées : Deux chapeaux et deux aiguilles
Rayon de la plus petite sphère circonscrite :
´
Qualite des maillages – p.38/329

70. 8 – Le berlingot
Nom
Berlingot
Arêtes dégénérées : et
Faces dégénérées : Quatre aiguilles
Rayon de la plus petite sphère circonscrite :
´
Qualite des maillages – p.39/329

71. 9 – L’aiguille
Nom
Aiguille
(needle)
Arêtes dégénérées : , et
Faces dégénérées : Trois aiguilles et un Big Crunch
Rayon de la plus petite sphère circonscrite :
´
Qualite des maillages – p.40/329

72. 10 – Le Big Crunch
Nom
Big
Crunch
Arêtes dégénérées : Toutes
Faces dégénérées : Quatre Big Crunchs
Rayon de la plus petite sphère circonscrite :
´
Qualite des maillages – p.41/329

73. Ce qu’il faut retenir
Un triangle est dégénéré si ses sommets sont
colinéaires ou confondus, et donc si son aire est nulle.
´
Qualite des maillages – p.42/329

74. Ce qu’il faut retenir
Un triangle est dégénéré si ses sommets sont
colinéaires ou confondus, et donc si son aire est nulle.
Il y a trois cas de dégénérescence des triangles.
´
Qualite des maillages – p.42/329

75. Ce qu’il faut retenir
Un triangle est dégénéré si ses sommets sont
colinéaires ou confondus, et donc si son aire est nulle.
Il y a trois cas de dégénérescence des triangles.
Un tétraèdre est dégénéré si ses sommets sont
coplanaires, colinéaires ou confondus, et donc si son
volume est nul.
´
Qualite des maillages – p.42/329

76. Ce qu’il faut retenir
Un triangle est dégénéré si ses sommets sont
colinéaires ou confondus, et donc si son aire est nulle.
Il y a trois cas de dégénérescence des triangles.
Un tétraèdre est dégénéré si ses sommets sont
coplanaires, colinéaires ou confondus, et donc si son
volume est nul.
Il y a dix cas de dégénérescence des tétraèdres.
´
Qualite des maillages – p.42/329

77. Table des matières
1. Introduction 8. Éléments non simpliciaux
2. Définition d’un simplexe 9. Représentation des cri-
3. Dégénérescence des sim- tères de forme
plexes 10. Équivalence des critères
4. Qualité de forme des sim- de forme
plexes 11. Qualité globale et optimi-
5. Formules pour les sim- sation
plexes 12. Qualité en taille des sim-
6. Voronoï, Delaunay et Rie- plexes
mann 13. Qualité universelle
7. Critères de formes et de 14. Conclusions
Delaunay
´
Qualite des maillages – p.43/329

78. Qualité en forme des simplexes
Une façon habituelle de quantifier la qualité d’un
maillage est faite par le biais de la qualité des éléments
qui le composent.
´
Qualite des maillages – p.44/329

79. Qualité en forme des simplexes
Une façon habituelle de quantifier la qualité d’un
maillage est faite par le biais de la qualité des éléments
qui le composent.
Un critère de qualité couramment utilisé pour quantifier
la qualité d’un élément est le critère de forme.
´
Qualite des maillages – p.44/329

80. Qualité en forme des simplexes
Une façon habituelle de quantifier la qualité d’un
maillage est faite par le biais de la qualité des éléments
qui le composent.
Un critère de qualité couramment utilisé pour quantifier
la qualité d’un élément est le critère de forme.
Cette section fait le tour des différents critères de forme
utilisés pour les simplexes.
´
Qualite des maillages – p.44/329

81. Le simplex régulier
Définition : Un élément simplicial est régulier s’il
maximise sa mesure pour une mesure donnée de sa
frontière.
´
Qualite des maillages – p.45/329

82. Le simplex régulier
Définition : Un élément simplicial est régulier s’il
maximise sa mesure pour une mesure donnée de sa
frontière.
Le triangle équilatéral est régulier car c’est celui qui a
l’aire optimale pour un périmètre donné.
´
Qualite des maillages – p.45/329

83. Le simplex régulier
Définition : Un élément simplicial est régulier s’il
maximise sa mesure pour une mesure donnée de sa
frontière.
Le triangle équilatéral est régulier car c’est celui qui a
l’aire optimale pour un périmètre donné.
Le tétraèdre équilatéral est régulier car c’est celui qui a
le volume optimal pour une surface donnée de ses
faces.
´
Qualite des maillages – p.45/329

84. Critère de forme simplicial
Définition A : Un critère de forme simplicial est une
fonction continue qui évalue la forme d’un simplexe, et qui
est invariante par translation, rotation, réflexion et
homothétie du simplexe. Il est dit valide s’il est maximal
uniquement pour le simplexe régulier et s’il est minimal
pour tous les simplexes dégénérés. Les critères de forme
simpliciaux sont normalisés dans l’intervalle , avec
pour le simplexe régulier et pour tous les simplexes
dégénérés.
´
Qualite des maillages – p.46/329

85. Remarques
L’invariance par translation, rotation et réflexion signifie
que les critères de forme simpliciaux doivent être
indépendants du système de coordonnées.
´
Qualite des maillages – p.47/329

86. Remarques
L’invariance par translation, rotation et réflexion signifie
que les critères de forme simpliciaux doivent être
indépendants du système de coordonnées.
L’invariance par une homothétie valide signifie qu’ils
doivent être adimensionnels (indépendants du système
d’unités).
´
Qualite des maillages – p.47/329

87. Remarques
L’invariance par translation, rotation et réflexion signifie
que les critères de forme simpliciaux doivent être
indépendants du système de coordonnées.
L’invariance par une homothétie valide signifie qu’ils
doivent être adimensionnels (indépendants du système
d’unités).
La continuité signifie que les critères de forme varient
continûment en fonction de la position des sommets du
simplexe.
´
Qualite des maillages – p.47/329

88. Le rapport des rayons
Le rapport des rayons d’un simplexe est un critère de
forme défini par , où et sont les rayons
des cercles (sphères en 3D) inscrit et circonscrit à , et
est la dimension de l’espace.
´
Qualite des maillages – p.48/329

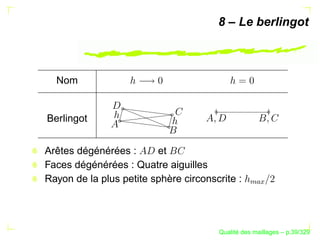
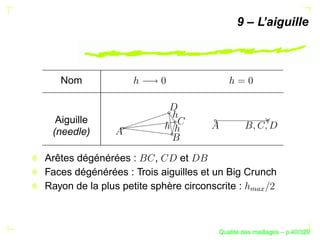
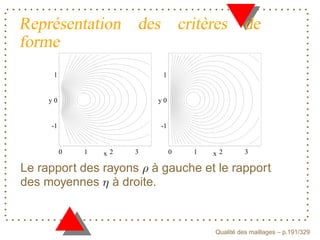
89. La rapport des moyennes
Soit ¡
, un simplexe équilatéral ayant le
¢
même [aire|volume] que le simplexe . Soit
¡
¢
, la matrice de la transformation affine de vers , i.e.
, , où est un vecteur de
§
§
translation.
´
Qualite des maillages – p.49/329

90. La rapport des moyennes
Alors, le rapport des moyennes d’un simplexe est le
rapport de la moyenne géométrique sur la moyenne
algébrique des valeurs propres , [, ] de la matrice
¡
¢
.
!
¡
¢
en D
£
§ ¢
¡
¢
§
¡
§
©§
¡
¨
£
£ ¡
¢
#
#
§
¡
¢
en D
©§
¡
¨
§ ¢
¡
¢
¡
§
´
Qualite des maillages – p.50/329

91. Le conditionnement
F ORMAGGIA et P EROTTO (2000) utilisent l’inverse du
conditionnement de la matrice.
§
¡
§
§
£
§
si les valeurs propres sont ordonnées en ordre croissant.
´
Qualite des maillages – p.51/329

92. Le norme de Frobenius
Freitag et Knupp (1999) utilise la norme de Frobenius de la
¡
matrice pour définir un critère de forme.
¡
£
£
¡
§
§
©§
¡
©§
¡
¨
¨
où les sont les valeurs propres du tenseur .
§
´
Qualite des maillages – p.52/329

93. Le minimum des angles solides
Le critère de forme simplicial basé sur le minimum des
%§
$
angles solides du -simplexe est défini par
¡
%§
§
$
¡
§
£
¦¡
Le coefficient est la valeur de chaque angle solide du
-simplexe régulier, soit en deux dimensions
et en trois dimensions.
´
Qualite des maillages – p.53/329

94. Le sinus de
Un critère de forme simplicial moins coûteux du point de
vue numérique est le sinus minimum. On évite ainsi le
calcul de la fonction dans le calcul de en 2D et
§
de en 3D.
§
¡
%§
§
$
¡
§
£
¦¡
où en 2D et en 3D. est la valeur
§
§
§
§
de pour tous les angles solides du simplexe régulier,
§
soit en 2D et en
3D.
´
Qualite des maillages – p.54/329

95. Angles des faces
On pourrait définir un critère de forme basé sur le minimum
des douze angles des quatre faces du tétraèdre. Cet angle
est de pour le tétraèdre régulier.
Mais ce n’est pas un critère de forme valide au sens de la
Définition A car il ne détecte pas les tétraèdres dégénérés
qui n’ont pas de faces dégénérées (le cerf-volant et le
chapeau).
´
Qualite des maillages – p.55/329

96. Angles dièdres
L’angle dièdre est l’angle entre l’intersection des deux faces
adjacentes à l’arête avec le plan perpendiculaire à l’arête.
§
§
Le minimum des six angles dièdres est utilisé comme
%§
$
critère de forme.
´
Qualite des maillages – p.56/329

97. Angles dièdres
%§
§
§
¡
§
¢
$
¡
§
¡
§
où et sont les normales aux deux faces adjacentes
§
¡
§
¢
à l’arête , et où est la valeur des
§
six angles dièdres du tétraèdre régulier.
Ce n’est pas un critère de forme valide au sens de la
Définition A. Le plus petit angle dièdre de l’aiguille, du
fuseau et de la paillette peut être aussi grand que .
´
Qualite des maillages – p.57/329

98. Le coefficient de l’erreur
d’interpolation
En éléments finis, l’erreur d’interpolation d’une fonction sur
un élément est bornée par un coefficient fois la
semi-norme de la fonction. Ce coefficient est le
rapport où est le diamètre de l’élément et
est la rondeur de l’élément .
en D
en D
´
Qualite des maillages – p.58/329

99. Le rapport des arêtes
Rapport de la plus petite arête sur la plus grande
%§
$
Le rapport des arêtes est un critère de forme non valide
selon la Définition A, car il est non-nul pour certains
simplexes dégénérés. En 2D, il peut être aussi grand
que pour le chapeau. En 3D, il peut valoir pour le
cerf-volant, pour l’aileron, pour le chapeau et
pour la paillette.
´
Qualite des maillages – p.59/329

100. Autres critères de forme – 1
, le rapport du diamètre du tétraèdre sur le
rayon de la sphère circonscrite, dans B AKER, (1989). Ce
critère de forme est non valide.
, le rapport de la plus petite arête du tétraèdre
%§
$
sur le rayon de la sphère circonscrite, dans M ILLER et al
(1996). Ce critère de forme est non valide.
, le rapport entre le volume du tétraèdre et le
rayon de la sphère circonscrite, dans M ARCUM et
W EATHERILL, (1995).
´
Qualite des maillages – p.60/329

101. Autres critères de forme – 2
§ ¢
, le rapport entre le volume du tétraèdre
©§
¡
¨
et l’aire de ses faces, dans D E C OUGNY et al (1990).
L’évaluation de ce critère de forme, ainsi que sa validité,
sont assez problématiques pour les tétraèdres
dégénérés en quatre sommets colinéaires.
, le rapport entre le volume du
§
¡
§
tétraèdre et la moyenne de ses six arêtes, dans
DANNELONGUE et TANGUY (1991), Z AVATTIERI et al
(1996) et W EATHERILL et al (1993).
´
Qualite des maillages – p.61/329

102. Autres critères de forme – 3
¢
§
¡¢
¡
¢
¢
¡
§
§ ¢
¡
¢
¡
§
le rapport entre le volume du tétraèdre et une somme, à la
puissance trois demis, de plusieurs termes homogènes à
des carrés de longueurs d’arêtes, dans B ERZINS (1998).
´
Qualite des maillages – p.62/329

103. Autres critères de forme – 4
§ ¢
, le rapport entre le volume du
¡
§
tétraèdre et la moyenne quadratique de ses six arêtes,
dans G RAICHEN et al (1991).
Etc... Cette liste n’est pas exhaustive.
´
Qualite des maillages – p.63/329

104. Il y a une infinité de critères de forme
¦
Si et sont deux critères de forme valides, si ,
alors
,
' ©(
¡0
)
avec ,
)
£
avec ,
'£
'
sont aussi des critères de forme simpliciaux valides.
´
Qualite des maillages – p.64/329

105. Ce qu’il faut retenir
Un simplexe régulier est un simplexe équilatéral, ie,
dont toutes les arêtes sont de même longueur.
´
Qualite des maillages – p.65/329

106. Ce qu’il faut retenir
Un simplexe régulier est un simplexe équilatéral, ie,
dont toutes les arêtes sont de même longueur.
Un critère de forme mesure le rapport à l’équilatéralité.
´
Qualite des maillages – p.65/329

107. Ce qu’il faut retenir
Un simplexe régulier est un simplexe équilatéral, ie,
dont toutes les arêtes sont de même longueur.
Un critère de forme mesure le rapport à l’équilatéralité.
Les critères de forme non valides ne sont pas nuls pour
tous les simplexes dégénérés.
´
Qualite des maillages – p.65/329

108. Ce qu’il faut retenir
Un simplexe régulier est un simplexe équilatéral, ie,
dont toutes les arêtes sont de même longueur.
Un critère de forme mesure le rapport à l’équilatéralité.
Les critères de forme non valides ne sont pas nuls pour
tous les simplexes dégénérés.
Il existe des zillions de critères de formes valides.
´
Qualite des maillages – p.65/329

109. Ce qu’il faut retenir
Un simplexe régulier est un simplexe équilatéral, ie,
dont toutes les arêtes sont de même longueur.
Un critère de forme mesure le rapport à l’équilatéralité.
Les critères de forme non valides ne sont pas nuls pour
tous les simplexes dégénérés.
Il existe des zillions de critères de formes valides.
Le but de la recherche n’est pas d’en trouver un autre
bien meilleur que les autres.
´
Qualite des maillages – p.65/329

110. Table des matières
1. Introduction 8. Éléments non simpliciaux
2. Définition d’un simplexe 9. Représentation des cri-
3. Dégénérescence des sim- tères de forme
plexes 10. Équivalence des critères
4. Qualité de forme des sim- de forme
plexes 11. Qualité globale et optimi-
5. Formules pour les sim- sation
plexes 12. Qualité en taille des sim-
6. Voronoï, Delaunay et Rie- plexes
mann 13. Qualité universelle
7. Critères de formes et de 14. Conclusions
Delaunay
´
Qualite des maillages – p.66/329

111. Formules pour le triangle
La donnée de la longueur des trois arêtes d’un triangle le
détermine entièrement.
Donc, les grandeurs mesurables telles les rayons des
cercles inscrit et circonscrit, les angles, la surface, etc,
peuvent s’écrire en fonction de la longueur des trois arêtes
d’un triangle.
Soit un triangle non dégénéré de sommets , et .
¡
¢
Les longueurs des arêtes de sont
§
notées , .
§
§
´
Qualite des maillages – p.67/329

112. Le demi-périmètre
Le demi-périmètre est donné par
¡¢
¡
¢
´
Qualite des maillages – p.68/329

113. Formule de Héron
L’aire d’un triangle peut aussi s’exprimer en terme de
longueurs d’arête, à l’aide de la formule de Héron :
¢
¡¢
¡
¢
´
Qualite des maillages – p.69/329

114. Rayon du cercle inscrit
Le rayon du cercle inscrit au triangle est donné par
´
Qualite des maillages – p.70/329

115. Rayon du cercle circonscrit
Le rayon du cercle circonscrit au triangle est donné
par
¡¢
¡
¢
´
Qualite des maillages – p.71/329

116. Diamètre de l’élément
Le diamètre d’un élément est la plus grande distance
euclidienne entre deux points de l’élément. Pour un
triangle, c’est aussi la longueur de la plus grande
arête
¡¢
¡
¢
La longueur de la plus petite arête est notée
%§
$
%§
¡¢
¡
¢
$
´
Qualite des maillages – p.72/329

117. Angle solide
L’angle au sommet du triangle est la longueur de
§
§
l’arc de cercle obtenu en projetant l’arête du triangle
opposée à sur un cercle unitaire de centre . Il
§
§
s’exprime en terme de longueurs d’arête comme
¡
§
§
§B
A 1@ 3762 154
@# 8
4
9
´
Qualite des maillages – p.73/329

118. Formules pour le tétraèdre
La donnée de la longueur des six arêtes d’un tétraèdre le
détermine entièrement.
Donc, les grandeurs mesurables telles les rayons des
sphères inscrite et circonscrite, les angles, le volume, etc,
peuvent s’écrire en fonction de la longueur des six arêtes
d’un tétraèdre.
´
Qualite des maillages – p.74/329

119. Formules pour le tétraèdre
Soit un tétraèdre non dégénéré de sommets , ,
¡
¢
et . Les longueurs des arêtes de sont notées
§
, . Les aires des faces du
§
§
tétraèdre, , , et , sont
¢
¡
¡
¢
¡
¢
désignées par , , et . Enfin, est le volume du
¡
¢
tétraèdre .
´
Qualite des maillages – p.75/329

120. Formule de “Héron” 3D
Soit , , , , et , les longueurs des six arêtes du
tétraèdre de manière à ce que les arêtes , et soient
connectées à un même sommet, soit l’arête opposée à ,
l’arête opposée à et l’arête opposée à . Alors le
volume est
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
´
Qualite des maillages – p.76/329

121. Rayon de la sphère inscrite
Le rayon de la sphère inscrite au tétraèdre est donné
par
¡
¢
´
Qualite des maillages – p.77/329

122. Rayon de la sphère circonscrite
Le rayon de la sphère circonscrite au tétraèdre est
donné par
où , et sont les produits
¡¢
¡
¢
¡
¢
des longueurs des arêtes opposées de (deux arêtes
sont opposées si elles n’ont pas de sommet commun).
´
Qualite des maillages – p.78/329

123. Diamètre de l’élément
Le diamètre d’un élément est la plus grande distance
euclidienne entre deux points de l’élément. Pour un
tétraèdre, c’est aussi la longueur de la plus grande
arête
¡¢
¡
¡
¢
¢
La longueur de la plus petite arête est notée
%§
$
%§
¡¢
¡
¡
¢
¢
$
´
Qualite des maillages – p.79/329

124. Angle solide
L’angle solide au sommet d’un tétraèdre, est l’aire du
§
§
secteur sphérique obtenue en projetant la face opposée
à sur la sphère unitaire centrée en .
§
§
¡
¡
¢
´
Qualite des maillages – p.80/329

125. Angle solide
L IU et J OE (1994) donnent la formule pour calculer l’angle
solide en fonction de la longueur des arêtes :
¡
¢
¢
B ¢
§
§
§B
A 1@ 3762 154
C@ 8
4
9
´
Qualite des maillages – p.81/329

126. Table des matières
1. Introduction 8. Éléments non simpli
2. Définition d’un sim- ciaux
plexe 9. Représentation des
3. Dégénérescence des critères de forme
simplexes 10. Équivalence des cri
4. Qualité de forme des tères de forme
simplexes 11. Qualité globale e
5. Formules pour les optimisation
simplexes 12. Qualité en taille des
6. Voronoï, Delaunay et simplexes
Riemann 13. Qualité universelle
7. Critères de formes et 14. Conclusions – p.82/329
´
Qualite des maillages

127. Quel est le plus beau triangle ?
´
Qualite des maillages – p.83/329

128. Quel est le plus beau triangle ?
A
´
Qualite des maillages – p.83/329

129. Quel est le plus beau triangle ?
A B
´
Qualite des maillages – p.83/329

130. Si vous avez choisi le triangle A...
´
Qualite des maillages – p.84/329

131. Si vous avez choisi le triangle A...
A
Vous avez tort !
´
Qualite des maillages – p.84/329

132. Si vous avez choisi le triangle B...
´
Qualite des maillages – p.85/329

133. Si vous avez choisi le triangle B...
B
Vous avez encore tort !
´
Qualite des maillages – p.85/329

134. Quel est le plus beau triangle ?
A B
Aucune de ces réponses !
´
Qualite des maillages – p.86/329

135. Quelle est la plus belle femme ?
´
Qualite des maillages – p.87/329

136. Quelle est la plus belle femme ?
A
´
Qualite des maillages – p.87/329

137. Quelle est la plus belle femme ?
A B
´
Qualite des maillages – p.87/329

138. Vous avez probablement choisi...
´
Qualite des maillages – p.88/329

139. Vous avez probablement choisi...
A B
La femme A.
´
Qualite des maillages – p.88/329

140. Et si on demandait à ces messieurs...
´
Qualite des maillages – p.89/329

141. Et si on demandait à ces messieurs...
´
Qualite des maillages – p.89/329

142. Ces messieurs choisiraient...
´
Qualite des maillages – p.90/329

143. Ces messieurs choisiraient...
A B
La femme B.
´
Qualite des maillages – p.90/329

144. Quelle est la plus belle femme...
Il n’y a pas de réponse dans l’absolue car la
question est incomplète.
On n’a pas spécifié qui allait juger les
candidates, quel était le barême d’évaluation,
quelles étaient les mesures utilisées, etc.
´
Qualite des maillages – p.91/329

145. Quel est le plus beau triangle ?
´
Qualite des maillages – p.92/329

146. Quel est le plus beau triangle ?
A B
´
Qualite des maillages – p.92/329

147. Quel est le plus beau triangle ?
A B
La question est incomplète. Il manque une façon
de mesurer la qualité d’un triangle.
´
Qualite des maillages – p.92/329

148. Diagramme de Voronoï
Georgy Fedoseevich VORO -
NOÏ. 28 avril 1868, Ukraine
– 20 novembre 1908, Var-
sovie. Nouvelles applications
des paramètres continus à
la théorie des formes qua-
dratiques. Recherches sur
les parallélloèdes primitifs.
Journal Reine Angew. Math,
Vol 134, 1908.
´
Qualite des maillages – p.93/329

149. La médiatrice
Soit et , deux som-
mets dans . La mé-
diatrice est le
lieu des points équi-
distants de et .
où est la distance
euclidienne entre deux
points de l’espace.
´
Qualite des maillages – p.94/329

150. Un nuage de sommets
Soit , un nuage de sommets.
´
Qualite des maillages – p.95/329

151. Cellule de Voronoï
Définition : La cellule de Voronoï associée
au sommet est le lieu des points de l’espace
qui sont plus proche de que de tout autre
sommet :
´
Qualite des maillages – p.96/329

152. Diagramme de Voronoï
L’ensemble des cellules de Voronoï associées à
tous les sommets du nuage de sommets forme
le diagramme de Voronoï.
´
Qualite des maillages – p.97/329

153. Propriétés des diagrammes de Vorono
Les cellules de Voronoï sont des polygones en
2D, des polyèdres en 3D, des -polytopes en
D.
Les cellules de Voronoï sont convexes.
Les cellules de Voronoï recouvrent l’espace
sans chevauchement.
´
Qualite des maillages – p.98/329

154. Ce qu’il faut retenir
Les diagrammes de Voronoï sont des
partitions de l’espace en cellules basées sur
la notion de distance.
´
Qualite des maillages – p.99/329

155. Triangulation de Delaunay
Boris Nikolaevich D ELONE ou
D ELAUNAY. 15 mars 1890,
Saint Petersbourg — 1980.
Sur la sphère vide. À la mé-
moire de Georges Voronoi,
Bulletin de l’Académie des
Sciences de l’URSS, Vol. 7,
pp. 793–800, 1934.
´
Qualite des maillages – p.100/329

156. Triangulation d’un nuage de points
Le même nuage de points peut se trianguler de
beaucoup de façons différentes.
...
´
Qualite des maillages – p.101/329

157. Triangulation d’un nuage de points
...
...
´
Qualite des maillages – p.102/329

158. Triangulation d’un nuage de points
...
...
´
Qualite des maillages – p.103/329

159. Triangulation de Delaunay
Parmi toutes ces façons, il y en a une (ou parfois
plusieurs) triangulation de l’enveloppe convexe
du nuage de point qui est dite de Delaunay.
´
Qualite des maillages – p.104/329

160. Critère de la sphère vide de Delaunay
Critère de la sphère vide : Un simplexe
satisfait le critère de la sphère vide si la boule
ouverte circonscrite au simplexe est vide (ie,
ne contient aucun sommet de la triangulation).
´
Qualite des maillages – p.105/329

161. Critère de la sphère vide violé
Un simplexe ne satisfait pas le critère de la
sphère vide si la boule ouverte circonscrite au
simplexe n’est pas vide (ie, contient un ou
plusieurs sommets de la triangulation).
´
Qualite des maillages – p.106/329

162. Triangulation de Delaunay
Triangulation de Delaunay : Si tous les
éléments d’une triangulation satisfont le
critère de la sphère vide, alors la triangulation est
dite de Delaunay.
´
Qualite des maillages – p.107/329

163. Algorithme de Delaunay
Il faut trouver la
sphère circonscrite
à un simplexe.
Cela revient à
trouver son centre.
Le centre est le
point à égale dis-
tance des som-
mets du simplexe.
´
Qualite des maillages – p.108/329

164. Algorithme de Delaunay
Comment savoir si un point viol le critère de la
sphère vide d’un simplexe ?
Il faut trouver le centre et le rayon de la
sphère circonscrite au simplexe .
Il faut trouver la distance entre le point et
le centre .
Si la distance est supérieure au rayon , le
point n’est pas dans la sphère circonscrite
au simplexe .
´
Qualite des maillages – p.109/329

165. Ce qu’il faut retenir
Le diagramme de Voronoï d’un nuage de
points est une partition de l’espace en
cellules basée sur la notion de distance.
Une triangulation de Delaunay d’un nuage de
points est une triangulation basée sur la
notion de distance.
´
Qualite des maillages – p.110/329

166. Dualité Delaunay-Voronoï
Le diagramme de Voronoï est le dual de la
triangulation de Delaunay et vice versa.
´
Qualite des maillages – p.111/329

167. Voronoï et Delaunay dans la nature
Les diagrammes de Voronoï et les triangulations
de Delaunay ne sont pas juste un trip de
matheux, ce sont des structures qu’on retrouve
dans la nature.
´
Qualite des maillages – p.112/329

168. Voronoï et Delaunay dans la nature
´
Qualite des maillages – p.113/329

169. Une tortue
´
Qualite des maillages – p.114/329

170. Un ananas
´
Qualite des maillages – p.115/329

171. La Tour Du Diable
´
Qualite des maillages – p.116/329

172. Boue séchée
´
Qualite des maillages – p.117/329

173. Nids d’abeilles
´
Qualite des maillages – p.118/329

174. Ailes de libellule
´
Qualite des maillages – p.119/329

175. Maïs soufflé
´
Qualite des maillages – p.120/329

176. Yeux de mouches
´
Qualite des maillages – p.121/329

177. Nanotubes de carbone
´
Qualite des maillages – p.122/329

178. Bulles de savon
´
Qualite des maillages – p.123/329

179. Un dôme geodésique
´
Qualite des maillages – p.124/329

180. Biosphère de Montréal
´
Qualite des maillages – p.125/329

181. Rue de Paris
´
Qualite des maillages – p.126/329

182. Routes de la Sarthe
´
Qualite des maillages – p.127/329

183. Routes dans la Loire
´
Qualite des maillages – p.128/329

184. Où s’en va le gars en avant ?
Un critère de forme d’un simplexe mesure le
rapport à l’équilatéralité.
´
Qualite des maillages – p.129/329

185. Où s’en va le gars en avant ?
Un critère de forme d’un simplexe mesure le
rapport à l’équilatéralité.
Le diagramme de Voronoï d’un nuage de
points est une partition de l’espace en cellules
basée sur la notion de distance.
´
Qualite des maillages – p.129/329

186. Où s’en va le gars en avant ?
Un critère de forme d’un simplexe mesure le
rapport à l’équilatéralité.
Le diagramme de Voronoï d’un nuage de
points est une partition de l’espace en cellules
basée sur la notion de distance.
Une triangulation de Delaunay d’un nuage de
points est une triangulation basée sur la notion
de distance.
´
Qualite des maillages – p.129/329

187. Où s’en va le gars en avant ?
Un critère de forme d’un simplexe mesure le
rapport à l’équilatéralité.
Le diagramme de Voronoï d’un nuage de
points est une partition de l’espace en cellules
basée sur la notion de distance.
Une triangulation de Delaunay d’un nuage de
points est une triangulation basée sur la notion
de distance.
On généralise la notion de distance.
´
Qualite des maillages – p.129/329

188. Où s’en va le gars en avant ?
Un critère de forme d’un simplexe mesure le
rapport à l’équilatéralité.
Le diagramme de Voronoï d’un nuage de
points est une partition de l’espace en cellules
basée sur la notion de distance.
Une triangulation de Delaunay d’un nuage de
points est une triangulation basée sur la notion
de distance.
On généralise la notion de distance.
On généralise ainsi les notions de critère de
forme, de diagramme de Voronoï et de
triangulation de Delaunay.
´
Qualite des maillages – p.129/329

189. Nikolai Ivanovich Lobachevsky
N IKOLAI I VANOVICH
LOBACHEVSKY, 1
décembre 1792, Nizhny
Novgorod — 24 février
1856, Kazan.
´
Qualite des maillages – p.130/329

190. János Bolyai
J ÁNOS BOLYAI, 15 dé-
cembre 1802 à Kolozsvár,
Empire Austrichien (Cluj,
Roumanie) — 27 janvier
1860 à Marosvásárhely,
Empire Austrichien (Tirgu-
Mures, Roumanie).
´
Qualite des maillages – p.131/329

191. Bernhard RIEMANN
G EORG F RIEDRICH B ERN -
HARD RIEMANN, 7 sep-
tembre 1826, Hanovre — 20
juillet 1866, Selasca. Über die
Hypothesen welche der Geo-
metrie zu Grunde liegen. 10
juin 1854.
´
Qualite des maillages – p.132/329

192. Géométrie non euclidienne
Riemann a généralisé la géométrie euclidienne
sur le plan à la géométrie riemannienne sur une
surface.
Il a définit la distance entre deux points sur une
surface comme étant la longueur du plus court
chemin entre ces deux points (géodésique).
Il a introduit le métrique riemannienne qui définit
la courbure de l’espace.
´
Qualite des maillages – p.133/329

193. Définition d’une métrique
Soit un ensemble quelconque, alors la fonction
est appelée une métrique sur si elle satisfait
(i) pour tous , dans ;
(ii) si et seulement si ;
(iii) pour tous , dans ;
(iv) pour tous , ,
dans .
´
Qualite des maillages – p.134/329

194. La distance euclidienne est une métriq
Dans la définition précédente de la métrique,
supposons que soit , alors la fonction
est une métrique sur .
´
Qualite des maillages – p.135/329

195. Le produit scalaire est une métrique
Soit un espace vectoriel muni d’un produit
scalaire . Alors la norme du produit scalaire
de la différence de deux éléments de l’espace
vectoriel est une métrique.
´
Qualite des maillages – p.136/329

196. Le produit scalaire est une métrique
Si l’espace vectoriel est , alors la norme du
produit scalaire du vecteur est la distance
euclidienne.
´
Qualite des maillages – p.137/329

197. Tenseur métrique
Un tenseur métrique est une matrice
symétrique définie positive
en 2D,
en 3D.
´
Qualite des maillages – p.138/329

198. Longueur dans la métrique
La longueur d’une arête entre les
sommets et dans la métrique est donnée
par
´
Qualite des maillages – p.139/329

199. Longueur euclidienne avec
´
Qualite des maillages – p.140/329

200. Longueur métrique avec
´
Qualite des maillages – p.141/329

201. Longueur dans une métrique variable
D’une façon générale, la métrique n’est pas
constante mais varie continûment en tout point
de l’espace. La longueur d’une courbe
paramétrée
est évaluée dans la métrique par
où est un point de la courbe et est le
vecteur tangent à la courbe en ce point.
´
Qualite des maillages – p.142/329

202. Aire et volume dans une métrique
Aire du triangle dans la métrique :
Volume du tétraèdre dans la métrique :
´
Qualite des maillages – p.143/329

203. Métrique et maillage de Delaunay
´
Qualite des maillages – p.144/329

204. Quel est le plus beau triangle ?
A B
La question est incomplète. Il manque une façon
de mesurer la qualité d’un triangle.
´
Qualite des maillages – p.145/329

205. Quel est le plus beau triangle ?
A B
´
Qualite des maillages – p.146/329

206. Quel est le plus beau triangle ?
A B
´
Qualite des maillages – p.147/329

207. Exemple d’un maillage adapté
Maillage adapté et solution pour un écoulement
compressible visqueux transonique à Mach 0.85
et Reynolds = 5 000.
´
Qualite des maillages – p.148/329

208. Zoom couche limite–choc
´
Qualite des maillages – p.149/329

209. Ce qu’il faut retenir
La beauté, la qualité, la forme, est une
notion toute relative.
´
Qualite des maillages – p.150/329

210. Ce qu’il faut retenir
La beauté, la qualité, la forme, est une
notion toute relative.
Il faut d’abord être capable de définir qu’est-ce
qu’on veut pour pouvoir juger ce qu’on a
obtenu.
´
Qualite des maillages – p.150/329

211. Ce qu’il faut retenir
La beauté, la qualité, la forme, est une
notion toute relative.
Il faut d’abord être capable de définir qu’est-ce
qu’on veut pour pouvoir juger ce qu’on a
obtenu.
“Qu’est-ce qu’on veut” s’écrit sous forme
d’une métrique.
´
Qualite des maillages – p.150/329

212. Ce qu’il faut retenir
La beauté, la qualité, la forme, est une
notion toute relative.
Il faut d’abord être capable de définir qu’est-ce
qu’on veut pour pouvoir juger ce qu’on a
obtenu.
“Qu’est-ce qu’on veut” s’écrit sous forme
d’une métrique.
Un critère de forme est une mesure de
l’équilatéralité d’un simplexe dans la métrique.
´
Qualite des maillages – p.150/329

213. Critère de forme dans la métrique
Première méthode (métrique constante)
Sur le simplexe , évaluer la métrique en
plusieurs points (de Gauss) et trouver une
métrique moyenne.
Supposer que cette métrique moyenne est
constante sur tout le simplexe et évaluer le
critère de forme avec cette métrique.
´
Qualite des maillages – p.151/329

214. Critère de forme dans la métrique
Deuxième méthode (métrique constante)
Sur le simplexe , évaluer la métrique en un
point (de Gauss), supposer que cette métrique
est constante sur tout le simplexe et évaluer le
critère de forme en ce point avec cette métrique.
Répéter cette opération en plusieurs points et
faire la moyenne des critères de forme.
C’est ce qui est fait à l’INRIA.
´
Qualite des maillages – p.152/329

215. Critère de forme dans la métrique
Troisième méthode (métrique variable)
Exprimer le critère de forme en fonction
seulement de longueurs d’arêtes.
Évaluer les longueurs d’arêtes dans la métrique.
C’est ce qui est fait dans OORT.
´
Qualite des maillages – p.153/329

216. Critère de forme dans la métrique
Quatrième méthode (métrique variable)
Exprimer le critère de forme en fonction de
longueurs d’arêtes, d’aire et de volume.
Évaluer longueurs, aire et volume dans la
métrique.
´
Qualite des maillages – p.154/329

217. Critère de forme dans la métrique
Cinquième méthode (métrique variable)
Savoir évaluer des quantités telles le rayon du
cercle inscrit, du cercle circonscrit, un angle
solide, etc, dans une métrique variable.
D’une façon générale, la métrique variable ne
satisfait pas l’inégalité triangulaire, la somme des
angles n’est pas 180 degrés, etc.
L’évaluation d’un critère de forme dans une
métrique variable, dans toutes sa généralité, est
un problème ouvert. Dans l’immédiat, on se
contente d’approximations.
´
Qualite des maillages – p.155/329

218. Table des matières
1. Introduction 8. Éléments non simpli
2. Définition d’un sim- ciaux
plexe 9. Représentation des
3. Dégénérescence des critères de forme
simplexes 10. Équivalence des cri
4. Qualité de forme des tères de forme
simplexes 11. Qualité globale e
5. Formules pour les optimisation
simplexes 12. Qualité en taille des
6. Voronoï, Delaunay et simplexes
Riemann 13. Qualité universelle
7. Critères de formes et 14. Conclusions – p.156/329
´
Qualite des maillages

219. Critères de formes et de Delaunay
Les maillages de Delaunay ont plusieurs
propriétés de régularité.
Le maximum des rayons des sphères minimales
associées aux éléments de la triangulation est minimum
si la triangulation est de Delaunay.
Si tous les simplexes d’une triangulation contiennent le
centre de leur sphère circonscrite, alors cette
triangulation est de Delaunay.
Dans une triangulation de Delaunay, la somme des
carrés des longueurs d’arêtes pondérées par le volume
des éléments partageant ces arêtes est minimal.
´
Qualite des maillages – p.157/329

220. Delaunay 3D et dégénérescence
En trois dimensions, il est bien connu que les
maillages de Delaunay peuvent contenir de
éléments dégénérés du type cerf-volant.
Pourquoi ?
Comment y remédier ?
´
Qualite des maillages – p.158/329

221. Critère de la sphère vide de Delaunay
Le critères de la sphère vide de Delaunay n’est
pas un critère de forme, mais il peut être utilisé
comme un critère de forme dans un algorithme
de retournement d’arêtes.
´
Qualite des maillages – p.159/329

222. Retournement d’arêtes et critère
Dans le retournement d’arêtes, appliquer le
critère de la sphère vide (critère de Delaunay)
Appliquer le critère (maximiser le minimum
des angles).
´
Qualite des maillages – p.160/329

223. Ce qu’il faut comprendre
Le critère de la sphère vide de Delaunay n’est
pas un critère de forme mais il peut être utilisé
comme un critère de forme.
´
Qualite des maillages – p.161/329

224. Ce qu’il faut comprendre
Le critère de la sphère vide de Delaunay n’est
pas un critère de forme mais il peut être utilisé
comme un critère de forme.
En deux dimensions, dans l’algorithme de
retournement d’arêtes (méthode de Lawson),
le critère de la sphère vide de Delaunay est
équivalent au critère de forme .
´
Qualite des maillages – p.161/329

225. Ce qu’il faut comprendre
Le critère de la sphère vide de Delaunay n’est
pas un critère de forme mais il peut être utilisé
comme un critère de forme.
En deux dimensions, dans l’algorithme de
retournement d’arêtes (méthode de Lawson),
le critère de la sphère vide de Delaunay est
équivalent au critère de forme .
Il y une multitude de critères de forme valides,
et donc une multitude de généralisations du
maillage de Delaunay.
´
Qualite des maillages – p.161/329

226. Delaunay et sphère circonscrite
Plus la sphère circonscrite d’un tétraèdre est
grande, plus il a de chance qu’un autre sommet
du maillage soit dans cette sphère, et moins il y a
de chance que ce tétraèdre et le maillage
satisfasse le critère de Delaunay.
Plus la sphère circonscrite d’un tétraèdre est
petite, moins il a de chance qu’un autre sommet
du maillage soit dans cette sphère, et plus il y a
de chance que ce tétraèdre et le maillage
satisfasse le critère de Delaunay.
´
Qualite des maillages – p.162/329

227. Sphère circonscrite de rayon infini
Les tétraèdres qui dégénèrent en aileron, en
chapeau, en paillette, en fuseau et en ciseau
ont une sphère circonscrite de rayon infini.
´
Qualite des maillages – p.163/329

228. Sphère circonscrite de rayon borné
Les tétraèdres qui dégénèrent en cerf-volant, en
coin, en berlingot, en aiguille et en Big Crunch
ont une sphère circonscrite de rayon borné.
´
Qualite des maillages – p.164/329

229. Ce qu’il faut comprendre
Le critère de la sphère vide de
Delaunay n’est pas un critère de
forme valide sensible à tous les cas
de dégénérescence des tétraèdres.
´
Qualite des maillages – p.165/329

230. Sphère circonscrite de rayon borné
Parmi les tétraèdres dégénérés qui ont une
sphère circonscrite de rayon borné, on peut
éliminer le coin, le berlingot, l’aiguille et le
Big Crunch
car ils ont plusieurs sommets confondus.
´
Qualite des maillages – p.166/329

231. Le cerf-volant
Or, il reste le cerf-volant,
un tétraèdre dégénéré, dont les quatre sommets
sont disjoints, dont la sphère circonscrite est de
rayon bornée, et qui est donc
“Delaunay-admissible”.
´
Qualite des maillages – p.167/329

232. Quadrilatère non convexe
Il est interdit de retourner une arête d’un
quadrilatère non convexe.
´
Qualite des maillages – p.168/329

233. Quadrilatère non convexe
Deux triangles adja-
cents qui forment un
quadrilatère concave
satisfont nécessaire-
ment le critère de la
sphère vide de Delau-
nay.
´
Qualite des maillages – p.169/329

234. Perte de la propriété de convexité en 3
´
Qualite des maillages – p.170/329

235. Ce qu’il faut retenir
Le critère de la sphère vide de Delaunay est
plus ou moins un critère de forme simplicial.
´
Qualite des maillages – p.171/329

236. Ce qu’il faut retenir
Le critère de la sphère vide de Delaunay est
plus ou moins un critère de forme simplicial.
Le critère de la sphère vide de Delaunay n’est
pas sensible à tous les cas de
dégénérescence des tétraèdres en 3D.
´
Qualite des maillages – p.171/329

237. Ce qu’il faut retenir
Le critère de la sphère vide de Delaunay est
plus ou moins un critère de forme simplicial.
Le critère de la sphère vide de Delaunay n’est
pas sensible à tous les cas de
dégénérescence des tétraèdres en 3D.
Un critère de forme valide, et donc sensible à
tous les cas de dégénérescence des
tétraèdres, dans un algorithme de
retournement d’arêtes et de faces, devrait
mener à un maillage qui n’est pas de
Delaunay, mais qui est de meilleure qualité.
´
Qualite des maillages – p.171/329

238. Table des matières
1. Introduction 8. Éléments non simpli
2. Définition d’un sim- ciaux
plexe 9. Représentation des
3. Dégénérescence des critères de forme
simplexes 10. Équivalence des cri
4. Qualité de forme des tères de forme
simplexes 11. Qualité globale e
5. Formules pour les optimisation
simplexes 12. Qualité en taille des
6. Voronoï, Delaunay et simplexes
Riemann 13. Qualité universelle
7. Critères de formes et 14. Conclusions – p.172/329
´
Qualite des maillages

239. Éléments non simpliciaux
Cette section propose une façon de généraliser
les notions de régularité, dégénérescence et
critère de forme des simplexes aux éléments non
simpliciaux, les quadrilatères en deux
dimensions, les prismes et les hexaèdres en trois
dimensions.
´
Qualite des maillages – p.173/329

240. Éléments non simpliciaux
On Element Shape Measures for Mesh
Optimization
PAUL L ABBÉ , J ULIEN D OMPIERRE , F RANÇOIS
G UIBAULT ET R ICARDO C AMARERO
Presenté à la 2nd Symposium on Trends in
Unstructured Mesh Generation, Fifth US National
Congress on Computational Mechanics, 4–6
août 1999 University du Colorado à Boulder.
´
Qualite des maillages – p.174/329

241. Généralisation de la régularité
Un quadrilatère équilatéral, ie ayant quatre
arêtes de même longueur, n’est pas
nécessairement un carré...
´
Qualite des maillages – p.175/329

242. Généralisation de la régularité
Un quadrilatère équilatéral, ie ayant quatre
arêtes de même longueur, n’est pas
nécessairement un carré...
Définition : Un élément, simplicial ou non,
est régulier s’il maximise sa mesure pour une
mesure donnée de sa frontière.
´
Qualite des maillages – p.175/329

243. Généralisation de la régularité
Un quadrilatère équilatéral, ie ayant quatre
arêtes de même longueur, n’est pas
nécessairement un carré...
Définition : Un élément, simplicial ou non,
est régulier s’il maximise sa mesure pour une
mesure donnée de sa frontière.
Le triangle équilatéral est régulier car c’est
celui qui a l’aire optimale pour un périmètre
donné.
´
Qualite des maillages – p.175/329

244. Généralisation de la régularité
Un quadrilatère équilatéral, ie ayant quatre
arêtes de même longueur, n’est pas
nécessairement un carré...
Définition : Un élément, simplicial ou non,
est régulier s’il maximise sa mesure pour une
mesure donnée de sa frontière.
Le triangle équilatéral est régulier car c’est
celui qui a l’aire optimale pour un périmètre
donné.
Le tétraèdre équilatéral est régulier car c’est
celui qui a le volume optimal pour une surface
donnée de ses faces.
´
Qualite des maillages – p.175/329

245. Éléments non simpliciaux réguliers
Le quadrilatère régulier est le carré.
L’hexaèdre régulier est le cube.
Le prisme régulier est ... Le prisme régulier !
Les deux faces triangulaires du prisme régulier
sont équilatérales avec des arêtes de longueur
notée . Les trois faces quadrilatérales du
prisme régulier sont des rectangles plans
ayant une base de longueur et une hauteur
de longueur .
´
Qualite des maillages – p.176/329

246. Qualité des éléments non simpliciaux
Définition : Le critère de forme d’un élément non
simplicial est donné par le minimum du critère de
forme des simplexes construits à partir de
chaque sommet de l’élément non simplicial et de
ses sommets voisins.
´
Qualite des maillages – p.177/329

247. Critère de forme d’un quadrilatère
Le critère de forme d’un quadrilatère est le
minimum du critère de forme des quatre triangles
de coin construits à partir de ses quatre
sommets.
´
Qualite des maillages – p.178/329

248. Critère de forme d’un prisme
Le critère de forme d’un prisme est le minimum
du critère de forme des six tétraèdres de coin
construits à partir de ses six sommets.
´
Qualite des maillages – p.179/329

249. Critère de forme d’un hexaèdre
Le critère de forme d’un hexaèdre est le
minimum du critère de forme des huit tétraèdres
de coin construits à partir de ses huit sommets.
´
Qualite des maillages – p.180/329

250. Forme du simplexe de coin
Les simplexes de coin construits sur les
éléments non simpliciaux réguliers ne sont pas
des simplexes réguliers.
Pour le carré, les quatre triangles de coin sont
des triangles rectangles isocèles.
Pour le cube, les huit tétraèdres de coin sont
des tétraèdres rectangles et isocèles.
Pour le prisme régulier, les six tétraèdres de
coin sont des tétraèdres avec une base faite
d’un triangle équilatéral de côté , avec une
quatrième arête perpendiculaire à la base et
de longueur . ´
Qualite des maillages – p.181/329

251. Forme du simplexe de coin
Chaque critère de forme doit être normalisé pour
obtenir un critère de forme égal à l’unité pour les
éléments non simpliciaux réguliers.
Carré
Prisme
DD
Cube
´
Qualite des maillages – p.182/329

252. Éléments non simpliciaux dégénérés
Définition :Un élément non simplicial est
dégénéré si au moins un de ses simplexes de
coin est dégénéré.
Si au moins un des simplexes de coin est plus
que dégénéré, c’est-à-dire qu’il est devenu
inversé (de mesure négative), alors l’élément
non simplicial est concave et est aussi considéré
dégénéré.
´
Qualite des maillages – p.183/329

253. Éléments non simpliciaux tordus
En trois dimensions, la définition du critère de
forme des éléments non simpliciaux a un défaut :
elle est peu sensible à la torsion des éléments.
´
Qualite des maillages – p.184/329

254. Torsion des faces quadrilatérales
Un critère utilisé pour mesurer la torsion d’une
face quadrilatérale est de considérer
l’angle dièdre entre les triangles et
d’une part, et les triangles et d’autre
part.
Si ces angles dièdres sont de , alors la face
quadrilatérale est plane (non tordue). Plus ces
angles s’éloignent de , plus la face
quadrilatérale est tordue.
´
Qualite des maillages – p.185/329

255. Torsion des faces quadrilatérales
Définition :Étant donné un critère de forme
simplicial valide, la torsion d’une face
quadrilatérale est égale à la valeur de ce critère
pour le tétraèdre engendré par les quatre
sommets de la face quadrilatérale.
Ainsi, une face plane a une torsion nulle car les quatre
sommets forment un tétraèdre dégénéré et tous les
critères de forme valides sont nuls.
Plus une face quadrilatérale est tordue, plus ses sommets
s’éloignent de la coplanarité, plus le critère de forme du
tétraèdre engendré est grand.
´
Qualite des maillages – p.186/329

256. Ce qu’il faut retenir
La forme, la dégénérescence, la convexité, la
concavité et la torsion peuvent se réécrire en
fonction de simplexes.
Un avantage de cette approche est qu’une fois
que la mesure et les critères de forme pour les
simplexes sont programmés, en euclidien
comme avec une métrique riemannienne,
l’extension aux éléments non simpliciaux est
directe.
´
Qualite des maillages – p.187/329

257. Table des matières
1. Introduction 8. Éléments non simpli-
2. Définition d’un sim- ciaux
plexe 9. Représentation des
3. Dégénérescence des critères de forme
simplexes 10. Équivalence des cri-
4. Qualité de forme des tères de forme
simplexes 11. Qualité globale et
5. Formules pour les optimisation
simplexes 12. Qualité en taille des
6. Voronoï, Delaunay et simplexes
Riemann 13. Qualité universelle
7. Critères de formes et 14. Conclusions
de Delaunay ´
Qualite des maillages – p.188/329

258. Représentation des critères de
forme
1
0.5
2
1
y 0
-1 3
2
-2 1 x
0
Position des trois sommets , et du
triangle pour construire le graphe d’un critère
de forme triangulaire.
´
Qualite des maillages – p.189/329

259. Représentation des critères de
forme
1 1 1
y0 y0 y0
-1 -1 -1
0 1 x 2 3 0 1 x2 3 0 1 x2 3
Le rapport des arêtes à gauche. Le minimum
des angles solides au centre. Le coefficient
d’erreur d’interpolation à droite.
´
Qualite des maillages – p.190/329

260. Représentation des critères de
forme
1 1
y0 y0
-1 -1
0 1 x2 3 0 1 x2 3
Le rapport des rayons à gauche et le rapport
des moyennes à droite.
´
Qualite des maillages – p.191/329

261. Quel critère de forme est le meilleur
1 n’est pas un critère de
forme valide.
y0
et sont continus
-1 mais non différentiables.
et sont continus et dif-
0 1 x2 3
férentiables.
est instable numérique-
ment.
est le moins coûteux.
a des isovaleurs circu-
laires.
´
Qualite des maillages – p.192/329

262. Représentation en trois dimensions
En 3D, 5 paramètres sont nécessaires. On en
fixe 2 et on voit l’influence des 3 autres.
´
Qualite des maillages – p.193/329

263. Représentation avec une métrique
1
y0
-1
0 1 x 2 3
Rapport des moyennes
´
Qualite des maillages – p.194/329

264. Représentation avec une métrique
1
y0
-1
0 1 x 2
Rapport des moyennes
´
Qualite des maillages – p.195/329

265. Représentation avec une métrique
1
y0
-1
0 1 x 2 3
Rapport des moyennes
´
Qualite des maillages – p.196/329

266. Représentation avec une métrique
1
y0
-1
0 1 x2 3
Rapport des moyennes
´
Qualite des maillages – p.197/329

267. Ce qu’il faut retenir
Rapport des moyennes est le critère de
forme privilégié.
´
Qualite des maillages – p.198/329

268. Ce qu’il faut retenir
Rapport des moyennes est le critère de
forme privilégié.
Des cercles en euclidien deviennent des
ellipses dans le cas général.
´
Qualite des maillages – p.198/329

269. Ce qu’il faut retenir
Rapport des moyennes est le critère de
forme privilégié.
Des cercles en euclidien deviennent des
ellipses dans le cas général.
La forme d’un triangle est un critère de qualité
relatif.
´
Qualite des maillages – p.198/329

270. Ce qu’il faut retenir
Rapport des moyennes est le critère de
forme privilégié.
Des cercles en euclidien deviennent des
ellipses dans le cas général.
La forme d’un triangle est un critère de qualité
relatif.
Un beau triangle pour une métrique n’est pas
beau pour une autre.
´
Qualite des maillages – p.198/329

271. Ce qu’il faut retenir
Rapport des moyennes est le critère de
forme privilégié.
Des cercles en euclidien deviennent des
ellipses dans le cas général.
La forme d’un triangle est un critère de qualité
relatif.
Un beau triangle pour une métrique n’est pas
beau pour une autre.
On ne peut juger la qualité d’un triangle que si
on a défini une métrique.
´
Qualite des maillages – p.198/329

272. Table des matières
1. Introduction 8. Éléments non simpli-
2. Définition d’un sim- ciaux
plexe 9. Représentation des
3. Dégénérescence des critères de forme
simplexes 10. Équivalence des cri-
4. Qualité de forme des tères de forme
simplexes 11. Qualité globale et
5. Formules pour les optimisation
simplexes 12. Qualité en taille des
6. Voronoï, Delaunay et simplexes
Riemann 13. Qualité universelle
7. Critères de formes et 14. Conclusions
de Delaunay ´
Qualite des maillages – p.199/329

273. Équivalence des critères de forme
´
Qualite des maillages – p.200/329

274. Équivalence des critères de forme
1
Superposition des
isolignes des critères
y0
de forme triangu-
laires , , et
-1 .
0 1 x2 3
´
Qualite des maillages – p.201/329

275. Équivalence des critères de forme
Définition B (de L IU et J OE, 1994) : Soient
et , deux critères de forme simpliciaux différents
ayant des valeurs dans l’intervalle . On dit
que est équivalent à s’il existe des
constantes positives , , et telles que
E
F
´
Qualite des maillages – p.202/329

276. Bornes optimales
Dans l’équation d’équivalence des critères de
forme
´
Qualite des maillages – p.203/329

277. Bornes optimales
Dans l’équation d’équivalence des critères de
forme
la borne inférieure est dite optimale si est le
plus petit exposant possible,
´
Qualite des maillages – p.203/329

278. Bornes optimales
Dans l’équation d’équivalence des critères de
forme
la borne inférieure est dite optimale si est le
plus petit exposant possible,
et la borne supérieure est dite optimale si est
le plus grand exposant possible.
´
Qualite des maillages – p.203/329

279. Bornes serrées
Dans l’équation d’équivalence des critères de
forme
E
F
´
Qualite des maillages – p.204/329

280. Bornes serrées
Dans l’équation d’équivalence des critères de
forme
E
F
la borne inférieure est dite serrée si est la plus
grande constante possible,
´
Qualite des maillages – p.204/329

281. Bornes serrées
Dans l’équation d’équivalence des critères de
forme
E
F
la borne inférieure est dite serrée si est la plus
grande constante possible,
et la borne supérieure est dite serrée si est la
plus petite constante possible.
´
Qualite des maillages – p.204/329

282. Relation d’équivalence
Il s’agit effectivement d’une relation
d’équivalence, c’est-à-dire une relation
réflexive,
symétrique,
transitive.
´
Qualite des maillages – p.205/329

283. Relation symétrique
Si est équivalent à avec
E
F
alors est équivalent à avec
G
D
F
E
où , , et .
´
Qualite des maillages – p.206/329

284. Relation transitive
Si est équivalent à et si est équivalent à
avec E
F
G
D
alors est équivalent à avec
H
I
où , , et .
E
F
´
Qualite des maillages – p.207/329

285. Équivalence entre , et
L’équivalence entre les critères de forme
tétraédriques , et a été prouvée dans L IU
et J OE, 1994, avec une conjecture sur trois
bornes supérieures serrées
´
Qualite des maillages – p.208/329

286. Équivalence entre , , et
On peut encore démontrer que les critères de
forme , , et font partie de la même classe
d’équivalence, du moins en deux dimensions
pour .
en D
en D
en D
en D
en D
´
Qualite des maillages – p.209/329

287. Classes d’équivalence des critères
de forme
La relation d’équivalence Définition B définit
des classes d’équivalence.
´
Qualite des maillages – p.210/329

288. Classes d’équivalence des critères
de forme
La relation d’équivalence Définition B définit
des classes d’équivalence.
Tous les critères de forme satisfaisant la
Définition A et couramment utilisés sont
équivalents entre eux suivant la Définition B.
´
Qualite des maillages – p.210/329

289. Classes d’équivalence des critères
de forme
La relation d’équivalence Définition B définit
des classes d’équivalence.
Tous les critères de forme satisfaisant la
Définition A et couramment utilisés sont
équivalents entre eux suivant la Définition B.
La classe d’équivalence de la relation
d’équivalence Définition B est-elle formée de
tous les critères de forme simpliciaux qui
satisfont la Définition A ? ? ?
´
Qualite des maillages – p.210/329

290. Classes d’équivalence des critères
de forme
La relation d’équivalence Définition B définit
des classes d’équivalence.
Tous les critères de forme satisfaisant la
Définition A et couramment utilisés sont
équivalents entre eux suivant la Définition B.
La classe d’équivalence de la relation
d’équivalence Définition B est-elle formée de
tous les critères de forme simpliciaux qui
satisfont la Définition A ? ? ?
Non ! L IU m’a donné un contre-exemple.
´
Qualite des maillages – p.210/329

291. Contre-exemple
Soit , un critère de forme qui satisfait
Définition A, alors
est aussi un critère de forme. Cependant, on ne
peut pas prouver que et sont équivalents au
sens de la Définition B car il n’y a pas de
constantes et telles que quand
P
tend vers zéro car le comportement
asymptotique exponentiel de tend vers zéro
plus vite que n’importe quel comportement
asymptotique polynômial.
´
Qualite des maillages – p.211/329

292. Ce qu’il faut retenir
Tous les critères de forme satisfaisant la
Définition A et couramment utilisés sont
équivalents entre eux suivant la Définition B.
´
Qualite des maillages – p.212/329

293. Ce qu’il faut retenir
Tous les critères de forme satisfaisant la
Définition A et couramment utilisés sont
équivalents entre eux suivant la Définition B.
Ils sont tous sensibles à tous les cas de
dégénérescence des simplexes.
´
Qualite des maillages – p.212/329

294. Ce qu’il faut retenir
Tous les critères de forme satisfaisant la
Définition A et couramment utilisés sont
équivalents entre eux suivant la Définition B.
Ils sont tous sensibles à tous les cas de
dégénérescence des simplexes.
De ce point de vue, il n’y en a pas un meilleur
que les autres.
´
Qualite des maillages – p.212/329

295. Table des matières
1. Introduction 8. Éléments non simpliciaux
2. Définition d’un simplexe 9. Représentation des cri-
3. Dégénérescence des sim- tères de forme
plexes 10. Équivalence des critères
4. Qualité de forme des sim- de forme
plexes 11. Qualité globale et optimi-
5. Formules pour les sim- sation
plexes 12. Qualité en taille des sim-
6. Voronoï, Delaunay et Rie- plexes
mann 13. Qualité universelle
7. Critères de formes et de 14. Conclusions
Delaunay
´
Qualite des maillages – p.213/329

296. Qualité globale et optimisation
On évalue la qualité globale de tout un maillage par le biais
de la qualité de chacun des éléments qui le composent.
En pratique, la comparaison entre des maillages issus de
différentes publications est souvent impossible : les
statistiques présentées, les critères de forme et les
échelles utilisées varient d’une publication à l’autre. Il faut
définir des bancs d’essai avec des sorties standards.
´
Qualite des maillages – p.214/329

297. Banc d’essai
Cube unitaire avec une
carte de taille uniforme
et isotrope de .
´
Qualite des maillages – p.215/329

298. Histogramme
30
Rapport des moyennes
Rapport des rayons
25
Pourcentage des tétraèdres
20
Histogramme du rap-
15
Q
port des moyennes et
10 du rapport des rayons
.
5
0
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Critère de forme des tétraèdres
´
Qualite des maillages – p.216/329

299. Histogramme
30
Angle solide minimum
Angle dièdre minimum
25
20
Histogramme du mini-
15 mum des angles so-
lides et du mi-
%§
$
10 nimum des angles di-
èdres .
%§
$
5
0
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Critère de forme des tétraèdres
´
Qualite des maillages – p.217/329

300. Histogramme
30
Coefficient d’erreur
Rapport des arêtes
25
20
Histogramme du rap-
15
port des arêtes et
10 du coefficient de l’er-
reur d’interpolation .
5
0
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Critère de forme des tétraèdres
´
Qualite des maillages – p.218/329

301. Statistiques sur tous les tétraèdres
min max
Rap. rayons 0.5151 0.9067 0.9978 0.0602
Rap. moyennes 0.6559 0.9222 0.9979 0.0468
Rap. arêtes 0.5696 0.7375 0.9504 0.0641
Erreur d’inter. 0.4862 0.8058 0.9741 0.0709
solide 0.2962 0.7115 0.9697 0.0996
%§
$
dièdre 0.4207 0.7657 0.9768 0.0852
%§
$
´
Qualite des maillages – p.219/329

302. Moyenne des critères de forme
Pour un maillage donné, la moyenne dépend beaucoup du
critère de forme utilisé. L IU et J OE (1994) ont constaté que
%§
$
On a constaté numériquement sur plusieurs maillages que
%§
%§
$
$
´
Qualite des maillages – p.220/329

303. Moyenne des critères de forme
La moyenne, sur tous les tétraèdres du maillage, d’un
critère de forme semble être un indice assez significatif de
la qualité globale du maillage.
En effet, si on prend plusieurs maillages de différente
qualité et si on les classe en fonction de la moyenne d’un
critère de forme, on obtient le même classement, à
quelques permutations près, quelque soit le critère de
forme utilisé.
´
Qualite des maillages – p.221/329

304. Maximum des critères de forme
C’est une donnée non significative car quelque soit le
maillage ou le critère de forme utilisé, le maximum est
presque toujours 1.
C’est significatif seulement si c’est loin de l’unité ce qui
démarque un très mauvais maillage.
´
Qualite des maillages – p.222/329

305. Minimum des critères de forme
C’est une donnée peu significative. C’est significatif
seulement si c’est près de zéro ce qui démarque un très
mauvais maillage.
Sur une série de tests, le classement de maillages en
fonction du minimum du critère de forme donne un
classement chaotique. Il n’est pas bon de caractériser tout
un maillage par la valeur d’un seul de ses éléments.
´
Qualite des maillages – p.223/329

306. Écart type des critères de forme
C’est une donnée assez significative. Plus l’écart type est
petit, plus le maillage est de qualité.
Sur une série de test, le classement de maillages en
fonction de l’écart type donne un classement significatif
mais un peu chaotique.
´
Qualite des maillages – p.224/329

307. Ce qu’il faut retenir
Des statistiques sur la forme des éléments d’un
maillage sont des données significatives sur la qualité
du maillage.
´
Qualite des maillages – p.225/329

308. Ce qu’il faut retenir
Des statistiques sur la forme des éléments d’un
maillage sont des données significatives sur la qualité
du maillage.
N’importe quel critère de forme valide semble faire
l’affaire.
´
Qualite des maillages – p.225/329

309. Ce qu’il faut retenir
Des statistiques sur la forme des éléments d’un
maillage sont des données significatives sur la qualité
du maillage.
N’importe quel critère de forme valide semble faire
l’affaire.
Il n’y a pas un seul chiffre unique qui semble pouvoir
caractériser entièrement la qualité d’un maillage.
´
Qualite des maillages – p.225/329

310. Ce qu’il faut retenir
Des statistiques sur la forme des éléments d’un
maillage sont des données significatives sur la qualité
du maillage.
N’importe quel critère de forme valide semble faire
l’affaire.
Il n’y a pas un seul chiffre unique qui semble pouvoir
caractériser entièrement la qualité d’un maillage.
La moyenne semble être le chiffre le plus significatif.
´
Qualite des maillages – p.225/329

311. Optimisation de maillages
Un maillage peut être décrit par l’ensemble
¨ $
§
©§
¡
¡
¨
où est le nombre de sommets du maillage,
£
sont les coordonnées dans du
§
¡§
¢§
£§
ème sommet, est le nombre de simplexes du maillage,
et est la connectivité du ème
¡
¢
£
£
¤¥¦ ¡
simplexe du maillage composé de pointeurs vers des
sommets du maillage
´
Qualite des maillages – p.226/329

312. Optimisation et critères de forme
Quelle est l’influence de choix d’un critère de forme dans
l’optimisation d’un maillage ?
Le banc d’essai est un domaine
en forme de triangle équilatéral
avec une métrique uniforme et iso-
trope qui spécifie une taille d’arête
de de la longueur du côté du
domaine. Le maillage optimal existe
dans ce cas particulier.
´
Qualite des maillages – p.227/329

313. Influence du critère de forme
%§
$
´
Qualite des maillages – p.228/329

314. Optimisation et critères de forme
Quelle est l’influence de choix d’un critère de forme dans
l’optimisation d’un maillage ?
Le banc d’essai est un domaine en
forme de carré équilatéral avec une
métrique uniforme et isotrope qui
spécifie une taille d’arête de de
la longueur du côté du domaine. Le
maillage optimal n’existe pas dans
ce cas.
´
Qualite des maillages – p.229/329

315. Influence du critère de forme
%§
$
´
Qualite des maillages – p.230/329

316. Influence de l’algorithme
On enlève le déplacement de sommets dans l’algorithme
d’optimisation de maillages.
Le banc d’essai est un domaine
en forme de triangle équilatéral
avec une métrique uniforme et iso-
trope qui spécifie une taille d’arête
de de la longueur du côté du
domaine. Le maillage optimal existe
dans ce cas.
´
Qualite des maillages – p.231/329

317. Influence de l’algorithme
%§
$
´
Qualite des maillages – p.232/329

318. Ce qu’il faut retenir
Si le maillage optimal existe, l’optimiseur converge vers
le maillage optimal quel que soit le critère de forme.
´
Qualite des maillages – p.233/329

319. Ce qu’il faut retenir
Si le maillage optimal existe, l’optimiseur converge vers
le maillage optimal quel que soit le critère de forme.
Si le maillage optimal n’existe pas, des critères de
forme différents donnent des maillages différents. Mais
plus le maillage est optimisé, moins la différence de
qualité est grande statistiquement.
´
Qualite des maillages – p.233/329

320. Ce qu’il faut retenir
Si le maillage optimal existe, l’optimiseur converge vers
le maillage optimal quel que soit le critère de forme.
Si le maillage optimal n’existe pas, des critères de
forme différents donnent des maillages différents. Mais
plus le maillage est optimisé, moins la différence de
qualité est grande statistiquement.
Si le maillage est mauvais, ce n’est pas en changeant
le critère de forme qu’on l’améliore, mais en changeant
l’algorithme d’optimisation.
´
Qualite des maillages – p.233/329

321. Table des matières
1. Introduction 8. Éléments non simpliciaux
2. Définition d’un simplexe 9. Représentation des cri-
3. Dégénérescence des sim- tères de forme
plexes 10. Équivalence des critères
4. Qualité de forme des sim- de forme
plexes 11. Qualité globale et optimi-
5. Formules pour les sim- sation
plexes 12. Qualité en taille des sim-
6. Voronoï, Delaunay et Rie- plexes
mann 13. Qualité universelle
7. Critères de formes et de 14. Conclusions
Delaunay
´
Qualite des maillages – p.234/329

322. Qualité en taille des simlexes
Les critères de forme servent à mesurer la forme des
éléments du maillage.
´
Qualite des maillages – p.235/329

323. Qualité en taille des simlexes
Les critères de forme servent à mesurer la forme des
éléments du maillage.
Les critères de forme sont adimensionnels.
´
Qualite des maillages – p.235/329

324. Qualité en taille des simlexes
Les critères de forme servent à mesurer la forme des
éléments du maillage.
Les critères de forme sont adimensionnels.
La forme n’est qu’un aspect de la qualité d’un maillage.
´
Qualite des maillages – p.235/329

325. Qualité en taille des simlexes
Les critères de forme servent à mesurer la forme des
éléments du maillage.
Les critères de forme sont adimensionnels.
La forme n’est qu’un aspect de la qualité d’un maillage.
On recherche un maillage qui respecte aussi, du mieux
possible, la taille spécifiée des éléments.
´
Qualite des maillages – p.235/329

326. Qualité en taille des simlexes
Les critères de forme servent à mesurer la forme des
éléments du maillage.
Les critères de forme sont adimensionnels.
La forme n’est qu’un aspect de la qualité d’un maillage.
On recherche un maillage qui respecte aussi, du mieux
possible, la taille spécifiée des éléments.
Cette section va présenter trois critères de taille.
´
Qualite des maillages – p.235/329

327. Taille cible des simplexes
Dans C UILLIÈRE (1998), on compare la taille des
simplexes avec la taille cible.
La taille cible locale d’un simplexe est celle qu’aurait un
simplexe régulier de côté unitaire.
Pour un triangle, l’aire cible est de .
Pour un tétraèdre, le volume cible est de .
en 2D,
en 3D.
´
Qualite des maillages – p.236/329

328. Critère de taille
Le critère de taille du simplexe s’écrit comme suit :
où est une constante de mise à l’échelle globale pour
tout le maillage.
Si un simplexe est de bonne taille dans la métrique,
alors son critère de taille sera unitaire.
´
Qualite des maillages – p.237/329

329. Indice d’efficacité
Un autre critère pour évaluer la conformité d’un maillage à
une métrique est proposé par F REY et G EORGE (1999).
Ce critère, contrairement au précédent qui évaluait les
aires ou les volumes des éléments, est basé sur les
longueurs d’arêtes dans la métrique.
´
Qualite des maillages – p.238/329

330. Indice d’efficacité
On note § les longueurs dans la métrique
des arêtes d’un maillage.
La longueur optimale des arêtes dans la métrique est ,
et une longueur de signifie que l’arête est deux fois plus
grande que la longueur spécifiée.
Une mesure globale de la conformité du maillage à la taille
spécifiée est l’indice d’efficacité
$
R
¢
§
§
©§
¡
¨
´
Qualite des maillages – p.239/329

331. Indice d’efficacité
Considérons la distribution, sur toutes les arêtes du
maillage, de la variable .
§
§
§
¨ $
Notons sa valeur moyenne
$ ©§ R
§
¡
¢
¢
Notons son écart-type.
¡ R
§
¨©§
Alors
¢
¢
L’indice d’efficacité mesure à la fois la dispersion des
longueurs d’arêtes et leur proximité à la valeur cible.
´
Qualite des maillages – p.240/329

332. Indice d’efficacité
¢
¢
Cette égalité montre que maximiser implique à la fois
minimiser l’écart-type de la distribution, et rapprocher sa
moyenne de la valeur . La valeur optimale est obtenue
lorsque et . Cela n’est possible que si toutes les
arêtes sont de longueur exactement égale à la longueur
locale spécifiée.
Ainsi, l’indice d’efficacité est une bonne mesure globale de
la conformité des longueurs d’arêtes avec les longueurs
spécifiées.
´
Qualite des maillages – p.241/329

333. Table des matières
1. Introduction 8. Éléments non simpliciaux
2. Définition d’un simplexe 9. Représentation des cri-
3. Dégénérescence des sim- tères de forme
plexes 10. Équivalence des critères
4. Qualité de forme des sim- de forme
plexes 11. Qualité globale et optimi-
5. Formules pour les sim- sation
plexes 12. Qualité en taille des sim-
6. Voronoï, Delaunay et Rie- plexes
mann 13. Qualité universelle
7. Critères de formes et de 14. Conclusions
Delaunay
´
Qualite des maillages – p.242/329

334. Un critère universel de qualité de
maillage
Attache ta tuque avec de la broche...
´
Qualite des maillages – p.243/329

335. Un critère universel de qualité de
maillage
Table des matières
1. Introduction
2. La métrique du simplexe
3. La métrique spécifiée
4. La non conformité d’un simplexe
5. La non conformité d’un maillage
6. Généralisation des critères de taille
7. Extension aux éléments non simpliciaux
8. Interrogation orale
9. Ce qu’il faut retenir
´
Qualite des maillages – p.244/329

336. Introduction
Les simplexes peuvent être de la bonne forme sans
pour autant être de la bonne taille.
´
Qualite des maillages – p.245/329

337. Introduction
Les simplexes peuvent être de la bonne forme sans
pour autant être de la bonne taille.
Il existe des critères de qualité en taille des simplexes
et des maillages.
´
Qualite des maillages – p.245/329

338. Introduction
Les simplexes peuvent être de la bonne forme sans
pour autant être de la bonne taille.
Il existe des critères de qualité en taille des simplexes
et des maillages.
En principe, un simplexe dont toutes les arêtes sont de
longueur unité dans la métrique, est aussi de forme
parfaite dans la métrique.
´
Qualite des maillages – p.245/329

339. Introduction
Les simplexes peuvent être de la bonne forme sans
pour autant être de la bonne taille.
Il existe des critères de qualité en taille des simplexes
et des maillages.
En principe, un simplexe dont toutes les arêtes sont de
longueur unité dans la métrique, est aussi de forme
parfaite dans la métrique.
En pratique, les maillages construits ne sont pas
parfaitement de la bonne taille et les simplexes sont
composés d’arêtes plus ou moins trop courtes ou trop
longues.
´
Qualite des maillages – p.245/329

340. Critères de forme et de taille
Or, le rapport de la plus petite arête sur la plus grande
peut être aussi grand que pour qu’un
tétraèdre dégénère en cerf-volant.
´
Qualite des maillages – p.246/329

341. Critères de forme et de taille
Or, le rapport de la plus petite arête sur la plus grande
peut être aussi grand que pour qu’un
tétraèdre dégénère en cerf-volant.
Cela signifie qu’un simplexe ayant des arêtes de taille
convenable n’implique pas que ce simplexe est aussi
forme convenable car il peut être totalement dégénéré.
´
Qualite des maillages – p.246/329

342. Critères de forme et de taille
On peut faire une combinaison linéaire d’un critère de
forme et d’un critère de taille, mais c’est assez arbitraire.
´
Qualite des maillages – p.247/329

343. Critères de forme et de taille
On peut faire une combinaison linéaire d’un critère de
forme et d’un critère de taille, mais c’est assez arbitraire.
Le but de cet exposé est d’introduire un critère universel
qui mesure la taille et la forme en même temps.
´
Qualite des maillages – p.247/329

344. Un critère universel de qualité de
maillage
Table des matières
1. Introduction
2. La métrique du simplexe
3. La métrique spécifiée
4. La non conformité d’un simplexe
5. La non conformité d’un maillage
6. Généralisation des critères de taille
7. Extension aux éléments non simpliciaux
8. Interrogation orale
9. Ce qu’il faut retenir
´
Qualite des maillages – p.248/329

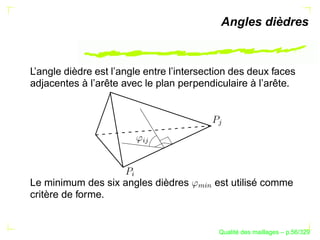
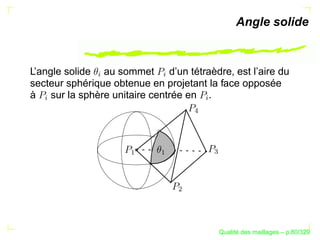
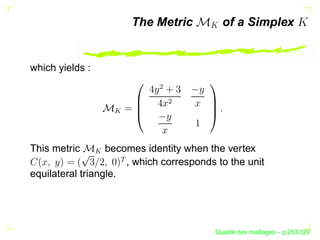
345. The Metric of a Simplex
How to compute the metric of the transformation that
transforms a simplex into a unit equilateral element ?
Let , , [, ], the vertices of the simplex
£ ¡
¢
in .
Let , , the edges of the simplex.
§
´
Qualite des maillages – p.249/329

346. The Metric of a Simplex
£
In , or , the components of the metric
are found by solving the following system of Eqs :
for
§
§
which yields one equation per edge of the simplex.
All the edges of measure 1 in .
´
Qualite des maillages – p.250/329

347. The Metric of a Simplex
For example in two dimensions, if the vertices of triangle
are located at ,
and , then this system of Eqs gives :
¢
¢
¡¡
¡¢
¢¢
¢
¢
¡¡
¡¢
¢¢
¢
¢
¡¡
¡¢
¢¢
which has a unique solution for all non-degenerate
triangles.
´
Qualite des maillages – p.251/329

348. The Metric of a Simplex
For instance, recall the triangle where vertices and are
located at , and where the
vertex free to move in the half-plane .
The system of Eqs. reduces to the system
¡¡
¢ ¡ ¢ ¡
¢ ¡ ¢ ¡
¢
¢
¡¢
¢
¢
¢¢
´
Qualite des maillages – p.252/329

349. The Metric of a Simplex
which yields :
¢
¢
This metric becomes identity when the vertex
, which corresponds to the unit
equilateral triangle.
´
Qualite des maillages – p.253/329

350. Visualization of the Metric
It is usual to visualize the metric tensor as an ellipse.
Indeed, the metric tensor can be written as
¡
, where the matrix is the diagonal
matrix of the eigenvalues of , i.e., .
¡
¢
The eigenvalues are the length of the axes of the ellipse
§
and is the rotation matrix of the ellipse about the origin.
´
Qualite des maillages – p.254/329

351. Visualization of the Metric
However, it is more telling to draw ellipses of size ,
this ellipse will go through the vertices of the triangle.
´
Qualite des maillages – p.255/329

352. Visualization of the Metric
Ellipses of a selected
group of elements. Note in
this figure that the ellipses
pass through the vertices
of the triangle.
´
Qualite des maillages – p.256/329

353. Visualization of the Metric
Ellipses of a selected
group of elements. Note in
this figure that the ellipses
pass through the vertices
of the triangle.
´
Qualite des maillages – p.257/329

354. Visualization of the Metric
Ellipses of a selected
group of elements. Note in
this figure that the ellipses
pass through the vertices
of the triangle.
´
Qualite des maillages – p.258/329

355. Un critère universel de qualité de
maillage
Table des matières
1. Introduction
2. La métrique du simplexe
3. La métrique spécifiée
4. La non conformité d’un simplexe
5. La non conformité d’un maillage
6. Généralisation des critères de taille
7. Extension aux éléments non simpliciaux
8. Interrogation orale
9. Ce qu’il faut retenir
´
Qualite des maillages – p.259/329

356. The Specified Metric
A size specification map can be constructed from a
posteriori error estimators, from geometrical properties of
the domain (e.g. curvature), from user defined inputs, etc.
Isotropic size specification map ( size of the elements)
can be constructed by making the metrics diagonal
¢
matrices whose diagonal terms are .
´
Qualite des maillages – p.260/329

357. The Specified Metric
Whatever its origin, the size specification map contains the
information of the prescribed size and stretching of the
mesh to be built as an anisotropic metric field.
An anisotropic metric field is given as input.
S
´
Qualite des maillages – p.261/329

358. The Average Specified Metric
Let be the specified Riemannian metric value at
S
point . Let be the averaged specified
S
Riemannian metric over a simplex as computed by :
S
S
This integral can be approximated by a numerical
quadrature.
´
Qualite des maillages – p.262/329

359. Visualization of
The specified metric is de-
fined in G EORGE and B O -
ROUCHAKI (1997). It is an
analytical function that de-
fines an isotropic metric.
Note that the triangles do
not fit exactly the specified
metric.
´
Qualite des maillages – p.263/329

360. Visualization of
The specified metric is de-
fined in G EORGE and B O -
ROUCHAKI (1997). It is an
analytical function that de-
fines an anisotropic metric.
Note that the triangles do
not fit exactly the specified
metric.
´
Qualite des maillages – p.264/329

361. Visualization of
Supersonic laminar vs-
cous air flow around
NACA 0012. The specified
anisotropic metric is based
on the interpolation error
(second derivatives) of the
speed field.
Note that the triangles do
not fit exactly the specified
metric.
´
Qualite des maillages – p.265/329

362. Un critère universel de qualité de
maillage
Table des matières
1. Introduction
2. La métrique du simplexe
3. La métrique spécifiée
4. La non conformité d’un simplexe
5. La non conformité d’un maillage
6. Généralisation des critères de taille
7. Extension aux éléments non simpliciaux
8. Interrogation orale
9. Ce qu’il faut retenir
´
Qualite des maillages – p.266/329

363. Simplex Conformity
When the metric of the simplex corresponds exactly
to the averaged specified Riemannian metric for
S
that simplex, the following equality holds :
S
However, in practice, there is usually some discrepancy
between these two metrics and this section presents a
method to measure this discrepancy.
´
Qualite des maillages – p.267/329

364. Simplex Conformity
This equality of metrics can be rewritten in the two
following ways :
¡
S
and
¡
S
where is the identity matrix.
´
Qualite des maillages – p.268/329

365. Simplex Residuals
When a perfect match between what is specified and what
is realized does not happen, a residual for each of the two
previous equations yields the two following tensors :
¡
S
T
and
¡
U
S
where will detect the degeneration of the simplex as
T
it’s volume tends to zero and as it’s volume tends to
U
infinity.
´
Qualite des maillages – p.269/329

366. Example – Triangle
Recall the triangle with two fixed vertices, one
at and one at , and that the
third vertex was free to move. Furthermore, if the specified
triangle is the unit equilateral triangle, then the averaged
specified Riemannian metric is equal to the identity matrix,
ie :
¡
S
S
´
Qualite des maillages – p.270/329

367. Example – Triangle
The residuals and can be written as
U
T
¢
¢
¢
¢
T
¢
¢
U
¢
¢
´
Qualite des maillages – p.271/329

368. Example – with
If the third vertex is restricted to the axis , then all
but the first term of these tensors vanish.
The two curves intersect at , where the residuals
become null.
20
Residual
15
V
Rs Rb
10
5
0
0.5 1 2 3 x
´
Qualite des maillages – p.272/329

369. Total Residual
The total residual is defined to be the sum of the two
W
residuals and , ie,
U
T
¡
¡
U
S
S
W
T
´
Qualite des maillages – p.273/329

370. The Non-Conformity of a
Simplex
Définition : The non-conformity of a simplex with
respect to the averaged specified Riemannian metric is
defined to be the Euclidean norm of the total residual ,
W
W
W
W
The Euclidean norm of a matrix amounts to the square
root of the sum of each term of the matrix individually
squared.
´
Qualite des maillages – p.274/329

371. Example – Triangle
For the triangle described above with two fixed vertices
and a free vertex and for which the specified Riemannian
metric was the identity matrix, the coefficient of
non-conformity is expressed as,
¢
¢
¢
¢
¢
´
Qualite des maillages – p.275/329

372. Example – Triangle
Logarithm base of
when the target
metric is the identity 1
matrix. It is minimum
and equal to zero for
y0
the equilateral triangle,
and increases very ra-
pidly as the third vertex -1
moves away from the
optimal position. It is in-
0 1 x 2 3
finite for all degenerate
¡
X
,
S
a
triangles.
Y`
X
¡
´
Qualite des maillages – p.276/329

373. Visualization of
The specified metric is
defined in G EORGE and
B OROUCHAKI (1997). It
is an analytical function
that defines an isotropic
metric.
´
Qualite des maillages – p.277/329

374. Visualization of
The specified metric is
defined in G EORGE and
B OROUCHAKI (1997). It
is an analytical function
that define an anisotro-
pic metric.
´
Qualite des maillages – p.278/329

375. Visualization of
Supersonic laminar vs-
cous air flow around
NACA 0012. The spe-
cified anisotropic metric
is based on interpola-
tion error (second deri-
vatives) of speed field.
´
Qualite des maillages – p.279/329

376. Un critère universel de qualité de
maillage
Table des matières
1. Introduction
2. La métrique du simplexe
3. La métrique spécifiée
4. La non conformité d’un simplexe
5. La non conformité d’un maillage
6. Généralisation des critères de taille
7. Extension aux éléments non simpliciaux
8. Interrogation orale
9. Ce qu’il faut retenir
´
Qualite des maillages – p.280/329

377. The Non-Conformity of a Mesh
Définition : The coefficient of non-conformity of a
mesh is defined as :
$
b
8
©§
¡
¨
which is the average value of the coefficient of
non-conformity of the simplices of the mesh.
´
Qualite des maillages – p.281/329

378. Properties of
The perfect mesh is obtained when the coefficient of
non-conformity of the mesh vanishes.
And if one simplex of the mesh degenerates, then
tends to infinity.
The coefficient of non-conformity of a mesh is
insensitive to compatible scaling of both the mesh and
the specified Riemannian metric.
´
Qualite des maillages – p.282/329

379. Symmetry in Size of
() Coarse mesh () Perfect mesh () Fine mesh
If the target mesh is the middle mesh, the coefficient of
non-conformity of the first and last meshes are equivalent.
´
Qualite des maillages – p.283/329

380. Properties of
It is possible to compare the quality of the mesh of two
vastly different domains, such as the mesh of a galaxy and
the mesh of a micro-circuit. In both cases, the measure
gives a comparable number that reflects the degree to
which each mesh satisfies its size specification map.
This coefficient therefore poses itself as a unique and
dimensionless measure of the non-conformity of a mesh
with respect to a size specification map given in the form of
a Riemannian metric, be it isotropic or anisotropic.
´
Qualite des maillages – p.284/329

381. Un critère universel de qualité de
maillage
Table des matières
1. Introduction
2. La métrique du simplexe
3. La métrique spécifiée
4. La non conformité d’un simplexe
5. La non conformité d’un maillage
6. Généralisation des critères de taille
7. Extension aux éléments non simpliciaux
8. Interrogation orale
9. Ce qu’il faut retenir
´
Qualite des maillages – p.285/329

382. Generalisation of Size Quality
Measures
The non-conformity between the metric of a simplicial
element and the specified metric , ie,
S
S
is a generalisation of the size criterion and the
efficiency index .
´
Qualite des maillages – p.286/329

383. Generalisation of the Size
Criterion
S
S
and then
S
is an integral form of the conformity between the
metric of the simplex and the specified metric .
S
´
Qualite des maillages – p.287/329

384. Generalisation of Efficiency Index
Let , a simplex and , an edge of this simplex. Then
the pointwise conformity between the metric of the
simplex and the specified metric
S
S
can be evaluated in an integral form over the edge of the
simplex as
S
S
´
Qualite des maillages – p.288/329

385. Generalisation of Efficiency Index
This relation
S
can be rewritten as two residual :
or
¡
¢
S
S
which is the efficiency index . This index is an integral
form of the conformity between the metric of the
simplex and the specified metric evaluated over the
S
edges of the mesh.
´
Qualite des maillages – p.289/329

386. Un critère universel de qualité de
maillage
Table des matières
1. Introduction
2. La métrique du simplexe
3. La métrique spécifiée
4. La non conformité d’un simplexe
5. La non conformité d’un maillage
6. Généralisation des critères de taille
7. Extension aux éléments non simpliciaux
8. Interrogation orale
9. Ce qu’il faut retenir
´
Qualite des maillages – p.290/329

387. Extension to Non-Simplicial
Elements
Non-Simplicial elements are quadrilaterals in two
dimensions and prisms and hexahedra in three
dimensions.
In order to extend this measure to non-simplicial elements,
it has to be understood that the metric tensor of
non-simplicial elements is not a constant and varies for
every point of space.
In other words, the Jacobian of a simplex is constant but
the Jacobian of a non-simplicial element depends of the
point of evaluation.
´
Qualite des maillages – p.291/329

388. Non-Simplicial Element Conformity
The conformity between the metric of a non-simplicial
element and the specified metric takes on a pointwise
S
nature can be rewritten as :
S
´
Qualite des maillages – p.292/329

389. Non-Simplicial Element Conformity
Residue
The total residue become a pointwise value
W
¡
¡
S
W
S
Then the non-conformity of an element with respect
to the specified Riemannian metric is defined to be
averaged over the element by an integration of the
Euclidean norm of the total residue :
W
¡
¡
S
S
´
Qualite des maillages – p.293/329

390. Un critère universel de qualité de
maillage
Table des matières
1. Introduction
2. La métrique du simplexe
3. La métrique spécifiée
4. La non conformité d’un simplexe
5. La non conformité d’un maillage
6. Généralisation des critères de taille
7. Extension aux éléments non simpliciaux
8. Interrogation orale
9. Ce qu’il faut retenir
´
Qualite des maillages – p.294/329

391. Test 1
The domain is a unit regular tri-
angle.
The size specification map is uni-
form and isotropic.
The target edge length is .
´
Qualite des maillages – p.295/329

392. Test 1 – Uniform Mesh
A B C
´
Qualite des maillages – p.296/329

393. Test 1 – Uniform Mesh
A B C
´
Qualite des maillages – p.296/329

394. Test 2 – Isotropic Mesh
This test case is defined in G EORGE and B OROUCHAKI
(1997).
The domain is a rectangle.
This test case has an isotropic Riemannian metric defined
by : ¢
¡
S
¢
¢
´
Qualite des maillages – p.297/329

395. Test 2 – Isotropic Mesh
where is given by :
¡
¢
if
c%¢ (
d0
e
if
d(
e 0
c¢
if
f
e ¡
e
c
if
¢
´
Qualite des maillages – p.298/329

396. Test 2 – Isotropic Mesh
View of the size specification map as a field of tensor
metrics and view of a mesh that fits rather well these
tensor metrics.
´
Qualite des maillages – p.299/329

397. Test 2a – Isotropic Mesh
A B C
´
Qualite des maillages – p.300/329

398. Test 2a – Isotropic Mesh
A B C
´
Qualite des maillages – p.300/329

399. Test 2b – Isotropic Mesh
A B C
´
Qualite des maillages – p.301/329

400. Test 2b – Isotropic Mesh
A B C
´
Qualite des maillages – p.301/329

401. Test 3 – Anisotropic Mesh
This test case is defined in G EORGE and B OROUCHAKI
(1997).
The domain is a rectangle.
This test case has an anisotropic Riemannian metric
defined by : ¢
¡
S
¢
¢
´
Qualite des maillages – p.302/329

402. Test 3 – Anisotropic Mesh
where is given by :
¡
if
¢(
f0
if
¡
f(
0
¢
if
e ¡
e
¢ e
if
´
Qualite des maillages – p.303/329

403. Test 3 – Anisotropic Mesh
and ¢ is given by :
if
c ¢(
d0
e
if
¢
d(
e 0
%¢
if
c
f
e ¡
e
c
if
¢
´
Qualite des maillages – p.304/329

404. Test 3 – Anisotropic Mesh
View of the size specification map as a field of tensor
metrics and view of a mesh that fits rather well these
tensor metrics.
´
Qualite des maillages – p.305/329

405. Test 3 – Anisotropic Mesh
A B C
´
Qualite des maillages – p.306/329

406. Test 3 – Anisotropic Mesh
A B C
´
Qualite des maillages – p.306/329

407. Test 4 – Bernhard Riemann
The size specification map is
deduced from an error esti-
mator based on the second
derivatives of the grey level of
the picture.
´
Qualite des maillages – p.307/329

408. Test 4 – Bernhard Riemann
A B C
´
Qualite des maillages – p.308/329

409. Test 4 – Bernhard Riemann
A B C
´
Qualite des maillages – p.308/329

410. Test 5 – Flow over a Naca 0012
Supersonic laminar flow at Mach 2.0, Reynolds 1000 and
an angle of attack of 10 degrees. An a posteriori error
estimator is deduced from this solution.
´
Qualite des maillages – p.309/329

411. Test 5a – Flow over a Naca 0012
A B C
´
Qualite des maillages – p.310/329

412. Test 5a – Flow over a Naca 0012
A B C
Specified Metric
S
´
Qualite des maillages – p.310/329

413. Test 5b – Flow over a Naca 0012
A B C
´
Qualite des maillages – p.311/329

414. Test 5b – Flow over a Naca 0012
A B C
Specified Metric
S
´
Qualite des maillages – p.311/329

415. Test 5c – Flow over a Naca 0012
A B C
´
Qualite des maillages – p.312/329

416. Test 5c – Flow over a Naca 0012
A B C
Specified Metric
S
´
Qualite des maillages – p.312/329

417. Un critère universel de qualité de
maillage
Table des matières
1. Introduction
2. La métrique du simplexe
3. La métrique spécifiée
4. La non conformité d’un simplexe
5. La non conformité d’un maillage
6. Généralisation des critères de taille
7. Extension aux éléments non simpliciaux
8. Interrogation orale
9. Ce qu’il faut retenir
´
Qualite des maillages – p.313/329

418. What to Retain
This lecture presented a method to measure the
non-conformity of a simplex and of a whole mesh with
respect to a size specification map given in the form of a
Riemannian metric.
This measure is sensitive to discrepancies in both size and
shape with respect to what is specified.
Analytical examples of the behavior were presented and
numerical examples were provided.
´
Qualite des maillages – p.314/329

419. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
´
Qualite des maillages – p.315/329

420. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
´
Qualite des maillages – p.315/329

421. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
´
Qualite des maillages – p.315/329

422. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
It is sensitive to discrepancies in shape and in size.
´
Qualite des maillages – p.315/329

423. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
It is sensitive to discrepancies in shape and in size.
It is also defined for non-simplicial elements.
´
Qualite des maillages – p.315/329

424. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
It is sensitive to discrepancies in shape and in size.
It is also defined for non-simplicial elements.
It gives a unique number for the whole mesh.
´
Qualite des maillages – p.315/329

425. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
It is sensitive to discrepancies in shape and in size.
It is also defined for non-simplicial elements.
It gives a unique number for the whole mesh.
It characterizes a whole mesh, coarse or fine, in a small
or a big domain.
´
Qualite des maillages – p.315/329

426. Mesh Optimization
This measure poses itself as a natural measure to use in
the benchmarking process. Indeed, since the measure is
able to compare two different meshes, it can help to
compare the algorithms used to produce the meshes.
This measure of the non-conformity of a mesh seems to be
an adequate cost function for mesh generation, mesh
optimization and mesh adaptation. This measure could be
used for each step such that each step minimizes the
same cost function.
´
Qualite des maillages – p.316/329

427. Table des matières
1. Introduction 8. Éléments non simpliciaux
2. Définition d’un simplexe 9. Représentation des cri-
3. Dégénérescence des sim- tères de forme
plexes 10. Équivalence des critères
4. Qualité de forme des sim- de forme
plexes 11. Qualité globale et optimi-
5. Formules pour les sim- sation
plexes 12. Qualité en taille des sim-
6. Voronoï, Delaunay et Rie- plexes
mann 13. Qualité universelle
7. Critères de formes et de 14. Conclusions
Delaunay
´
Qualite des maillages – p.317/329

428. Conclusions
Enfin, il achève ! ! !
´
Qualite des maillages – p.318/329

429. Simplexes dégénérés
Un simplexe est dégénéré si sa mesure est nulle.
´
Qualite des maillages – p.319/329

430. Simplexes dégénérés
Un simplexe est dégénéré si sa mesure est nulle.
La dégénérescence est indépendante de la métrique.
´
Qualite des maillages – p.319/329

431. Simplexes dégénérés
Un simplexe est dégénéré si sa mesure est nulle.
La dégénérescence est indépendante de la métrique.
Un critère de forme est valide s’il est sensible à tous les
cas de dégénérescence.
´
Qualite des maillages – p.319/329

432. Simplexes dégénérés
Un simplexe est dégénéré si sa mesure est nulle.
La dégénérescence est indépendante de la métrique.
Un critère de forme est valide s’il est sensible à tous les
cas de dégénérescence.
Un critère de forme est non valide s’il est non-nul pour
certain simplexes dégénérés.
´
Qualite des maillages – p.319/329

433. Critères de forme
La beauté, la qualité, la forme, est une notion toute
relative.
´
Qualite des maillages – p.320/329

434. Critères de forme
La beauté, la qualité, la forme, est une notion toute
relative.
Il faut d’abord être capable de définir qu’est-ce qu’on
veut pour pouvoir juger ce qu’on a obtenu.
´
Qualite des maillages – p.320/329

435. Critères de forme
La beauté, la qualité, la forme, est une notion toute
relative.
Il faut d’abord être capable de définir qu’est-ce qu’on
veut pour pouvoir juger ce qu’on a obtenu.
“Qu’est-ce qu’on veut” s’écrit sous forme d’une
métrique.
´
Qualite des maillages – p.320/329

436. Critères de forme
La beauté, la qualité, la forme, est une notion toute
relative.
Il faut d’abord être capable de définir qu’est-ce qu’on
veut pour pouvoir juger ce qu’on a obtenu.
“Qu’est-ce qu’on veut” s’écrit sous forme d’une
métrique.
Un critère de forme est une mesure de l’équilatéralité
d’un simplexe dans la métrique.
´
Qualite des maillages – p.320/329

437. Critères de forme
La moyenne d’un critère de forme valide sur tous les
simplexes du maillage est un critère de qualité
significatif.
´
Qualite des maillages – p.321/329

438. Critères de forme
La moyenne d’un critère de forme valide sur tous les
simplexes du maillage est un critère de qualité
significatif.
Les critères de forme sont plus ou moins équivalents
dans la caractérisation d’un maillage.
´
Qualite des maillages – p.321/329

439. Critères de forme
La moyenne d’un critère de forme valide sur tous les
simplexes du maillage est un critère de qualité
significatif.
Les critères de forme sont plus ou moins équivalents
dans la caractérisation d’un maillage.
Les critères de forme sont plus ou moins équivalents
dans l’optimisation d’un maillage.
´
Qualite des maillages – p.321/329

440. Critères de taille
Les simplexes peuvent être de la bonne forme sans
pour autant être de la bonne taille.
´
Qualite des maillages – p.322/329

441. Critères de taille
Les simplexes peuvent être de la bonne forme sans
pour autant être de la bonne taille.
Il existe des critères de qualité en taille des simplexes
et des maillages.
´
Qualite des maillages – p.322/329

442. Critères de taille
Les simplexes peuvent être de la bonne forme sans
pour autant être de la bonne taille.
Il existe des critères de qualité en taille des simplexes
et des maillages.
En principe, un simplexe dont toutes les arêtes sont de
longueur unité dans la métrique, est aussi de forme
parfaite dans la métrique.
´
Qualite des maillages – p.322/329

443. Critères de taille
Les simplexes peuvent être de la bonne forme sans
pour autant être de la bonne taille.
Il existe des critères de qualité en taille des simplexes
et des maillages.
En principe, un simplexe dont toutes les arêtes sont de
longueur unité dans la métrique, est aussi de forme
parfaite dans la métrique.
En pratique, les maillages construits ne sont pas
parfaitement de la bonne taille et les simplexes sont
composés d’arêtes plus ou moins trop courtes ou trop
longues.
´
Qualite des maillages – p.322/329

444. Critères de taille
Or, le rapport de la plus petite arête sur la plus grande
peut être aussi grand que pour qu’un tétraèdre
dégénère en cerf-volant.
´
Qualite des maillages – p.323/329

445. Critères de taille
Or, le rapport de la plus petite arête sur la plus grande
peut être aussi grand que pour qu’un tétraèdre
dégénère en cerf-volant.
Cela signifie qu’un simplexe ayant des arêtes de taille
convenable n’implique pas que ce simplexe est aussi
forme convenable car il peut être totalement dégénéré.
´
Qualite des maillages – p.323/329

446. Critère universel
Ceci amène naturellement le problème dans toute sa
généralité :
Quelle serait un critère de qualité simplicial qui mesurait
simultanément taille et forme, qui serait sensible à tous
les cas de dégénérescence des simplexes, qui serait
optimal pour le simplexe régulier et unitaire, dans une
métrique euclidienne ou riemannienne, isotrope ou
anisotrope, en deux et en trois dimensions.
´
Qualite des maillages – p.324/329

447. Prochainement sur vos écrans
P. L ABBÉ, J. D OMPIERRE, M.-G. VALLET, F. G UIBAULT et
J.-Y. T RÉPANIER . A Measure of the Conformity of a Mesh
to an Anisotropic Metric, Tenth International Meshing
Roundtable, Newport Beach, CA, octobre 2001, pages
319–326,
proposent un tel critère qui mesure la conformité en taille
et forme entre le maillage qui a été construit et le maillage
qui avait été spécifié par la métrique.
´
Qualite des maillages – p.325/329

448. The Non-Conformity of a Mesh
A method to measure the non-conformity of a simplex and
of a whole mesh with respect to a size specification map
given in the form of a Riemannian metric was given.
This measure is sensitive to discrepancies in both size and
shape with respect to what is specified.
Analytical examples of the behavior were presented and
numerical examples were provided.
´
Qualite des maillages – p.326/329

449. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
´
Qualite des maillages – p.327/329

450. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
´
Qualite des maillages – p.327/329

451. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
´
Qualite des maillages – p.327/329

452. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
It is sensitive to discrepancies in shape and in size.
´
Qualite des maillages – p.327/329

453. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
It is sensitive to discrepancies in shape and in size.
It is also defined for non-simplicial elements.
´
Qualite des maillages – p.327/329

454. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
It is sensitive to discrepancies in shape and in size.
It is also defined for non-simplicial elements.
It gives a unique number for the whole mesh.
´
Qualite des maillages – p.327/329

455. The Non-Conformity is Universal
The coefficient of non-conformity of a mesh, , is a
universal measure in the following sense :
It is defined in two and three dimensions.
It is sensitive to all simplex degeneracies.
It takes into account an Euclidean or Riemannian
metric, isotropic or anisotropic.
It is sensitive to discrepancies in shape and in size.
It is also defined for non-simplicial elements.
It gives a unique number for the whole mesh.
It characterizes a whole mesh, coarse or fine, in a small
or a big domain.
´
Qualite des maillages – p.327/329

456. Mesh Optimization
This measure poses itself as a natural measure to use in
the benchmarking process. Indeed, since the measure is
able to compare two different meshes, it can help to
compare the algorithms used to produce the meshes.
This measure of the non-conformity of a mesh seems to be
an adequate cost function for mesh generation, mesh
optimization and mesh adaptation. This measure could be
used for each step such that each step minimizes the
same cost function.
´
Qualite des maillages – p.328/329

457. La fin
´
Qualite des maillages – p.329/329

458. La fin
´
Qualite des maillages – p.329/329