statistique descriptive

GROUPE MIAGE Pr Hammoucha Yassine
- 1 -
- 1 -

Sommaire
Les statistiques descriptives……………………………………………………...……….…….…....4
I-Terminologie.……………………………………………………......………………….…...…….4
II- Types de critères, de caractères ou de variables……………………..………………….……….6
1.Caractères quantitatifs……………………………………………………….……...…………….6
2. Caractère qualitatif………………………………………..….………...…………...…………….9
En résumé…………………………………………………...…...…………………….………….12
III- Tableaux statistiques……...…...…………...…...………...…...……...…...……………………12
A- les tableaux à un seul caractère……...…...…………...…...………...…...……...….……………14
B- Les tableaux à deux caractères……...…...…………...…...………...…...………………………18
C- Les différentes distributions statistiques……...…...…………...…...………....…………………21
IV- Représentations graphiques……...…...…………...…...………...…...……...…………………25
1. Représentations des distributions à une dimension……...…...…………...…...…...……………25
2.Représentations des distributions à deux dimensions……...…...…………...…...………………34
3.Autres représentations graphiques……...…...…………...…...………...…...……………………37
V- Caractéristiques de tendance centrale et de position……...…...…………...…...………………38
A- Mode……...…...…………...…...………...…...……...…...…………………….………………39
B- Médiane……...…...…………...…...………...…...……...………………....……………………41
C- Moyenne arithmétique……...…...…………...…...………...…...…….........……………………44
D- Moyenne géométrique……...…...…………...…...………...…...……...…......…………………48
E- Moyenne harmonique……...…...…………...…...………...…...……...…...……...….…………49
F- Moyenne quadratique……...…...…………...…...………...…...……...…...……………………50
G- Quantiles……...…...…………...…...………...…...……...…...……………….……...…………51
H- Le choix d’une caractéristique de tendance centrale……...…...…………......…………………52
VI- Caractéristiques de dispersion……...…...…………...…...………...……..……………………53
Introduction……...…...…………...…...………...…...…….........................…...……………………53
Les écarts simples……...…...…………...…...…………...…...…...……...…...……………………53
A- l’étendue……...…...…………...…...………...……………….....……...…...……………………53
B- Intervalle inter-quartile……...…...…………...….....………...…...……...…...……………………54
C- L’écart absolu moyen……...…...…………...…...…………...…...……...…...……………………54
D - Variance et écart-type……...…...…………...…...………...…......……...…...……………………55
E- Coefficient de variation……...…...…………...…...………...….....……...…...……………………56
VII- La concentration……...…...…………...…...………...…...……...……....……………………56
A- Valeurs globales……...…...…………...…...………...…...……...…...………….………………56
B-Médiale……...…...…………...…...………...…...……...…...…………………………………...56
C- Courbe de concentration (ou de LORENZ) ……...…...…………...…...………...……………57
D- Indice de GINI……...…...………..………...…...………...…...……...…...……………………58
VIII- Les séries à double entrées : régression linéaire (corrélation) ……...…...…………...………59
1- notion de tableau de contingence……...…...…………...…...………...…...……………………59
A. une distribution statistique double……...…...…………...…...………...……..……………………59
B. distributions marginales……...…...…………...…...………...…...……...…...……………….……59
C. Les distributions conditionnelles……...…...…………..……...…...……...…...……………………60
2- généralisation du tableau de contingences……...…...…………...…...………...…...……....……60
3- La régression linéaire……...…...…………...…...………...…...……...…...………………..……61
A. Présentation du problème……...…...…………...…...………...…...……...…...………….………61
B. la méthode des moindres carrés……...…...…………...…...………...…...……...…...……….……62
- 2 -

C. Calcul des paramètres de la droite de régression……...…...…………...…...………....…………….63
4- la corrélation linéaire……...…...…………...…...………...…...…….....…...…………..……...…65
IX- Analyse Des Séries Chronologiques……...…...…………...…...………...……………………69
1 – Généralités……...…...…………...…...………...…...……...….....................……………………69
A. Définition……...…...…………...…...………...…...……...…...…………………………………69
B. les différentes composantes d’une série chronologique……...…...…………...…...………...………69
C. intérêt d’une analyse d’une série chronologique……...…...…………...…...………...…...…………70
2 – l’analyse de la tendance longue : « trend » ……...…...…………...…...………...…...…………70
A. la méthode des moyennes mobiles……...…...…………...…...………...…...…….......……………70
B. Opérations sur les matrices……...…...…………...…...………...…...……...…...…………………70
X- Les Probabilités et l’analyse combinatoire……...…...…………...…...…....……………………71
1- Le modèle probabiliste……...…...…………...…...………...…...……...…...………………...…71
A- Evènements……...…...…………...…...………...…...……...…...………………………….……71
B- Loi de probabilité, espace de probabilité……...…...…………...…...………...……………………72
C- Le cas où les évènements élémentaires sont équiprobables……...…...………...……………………74
D- Exercices……...…...…………...…...………...…...……...….........................……………………75
2- Probabilités conditionnelles……...…...…………...…...………...…...…….……………………76
A- Définition……...…...…………...…...………...…...……...…...…………………………………76
B- Deux résultats de décomposition……...…...…………...…...………...…...…….…………………76
C- Evènements indépendants……...…...…………...…...………...…...……...…....…………………78
D- Exercices……...…...…………...…...………...…...……...………………....……………………79
XI- Les variables aléatoires……...…...…………...…...………...…...……...…...….………………80
1- Généralités……...…...…………...…...………...…...……...…...……………..…………………80
A- Définitions……...…...…………...…...………...…...……...…...………………...………………80
B- Variables aléatoires discrètes, variables aléatoires à densité……...…...…………...…...……..………82
C- Couples de variables aléatoires……...…...…………...…...………...…...……...…...........…………83
D- Variables aléatoires indépendantes……...…...…………...…...………...…..........…………………84
E- Exercices……...…...…………...…...………...…...……...……………….....……………………85
2- Caractéristiques numériques des variables aléatoires….....…………………………...…………86
A- Espérance….....…………………………………………………………………………….……86
B- Variance, covariance……...…...……………....…...………...…...……...…...……………………87
C- Exercices……...…...…………...…...…………………..…...…...……...…...……………………90
3-Variables aléatoires usuelles……...…...…………...…...………...…...……...…...………………90
A- Loi de bernoulli……...…...…………...…...………...…...……...…...……………………...……90
B- Loi Binomiale……...…...…………...…...………...…...……...…...…………………………..…91
C- Loi uniforme……...…...…………...…...………...…...……...…...………………………………91
D- Loi exponentielle……...…...…………...…...………...…...……...…...………………….………91
E- Loi de Poisson……...…...…………...…...………...…...……...…...……………………..………92
F- Loi Normale……...…...…………...…...………...…...……...…...…………………….…………92
G-Exercices……...…...…………...…...………...…...……...…...…………………………..………93
4-Caractéristiques des lois usuelles……...…...…………...…...………...…...……...…....…………94
A-Variables aléatoires réelles discrètes……...…...…………...…...………...…...……..………………94
B-Variables aléatoires réelles continues……...…...…………...…...………...…...……………………94
Exercices corrigés……...…...…………...…...………...…...…………......…...……………………96
Exercices……...…...…………...…...………...…...……...…...………………...…………………141
Bibliographie……...…...…………...…...………...…...……...…...………………………………
- 3 -

Chapitre I- Les statistiques descriptives
I-Terminologie :
1. Statistique :
La statistique est une méthode scientifique dont l’objet est de recueillir, d’organiser,
de résumer et d’analyser les données d’une enquête, d’une étude o d’une expérience,
aussi bien que de tirer les conclusions logiques et de prendre les décisions qui
s’imposent à partir des analyses effectuées.
Les statistiques se sont des données chiffrées relatives à un phénomène étudié
collectés par la statistique.
Exemple : des statistiques du chômage.
Statistique descriptive: classification des données et leur traitement afin de les rendre
utilisables et permettre leur interprétation.
2. Population :
Ensemble d'individus définis par une propriété commune donnée.
Exemple : *si l’on veut étudier la durée de vie des ampoules électriques fabriquées par
une compagnie, la population considérée est l’ensemble de toutes les ampoules
fabriquées par cette compagnie.
*Age des étudiants de 1
ère
année : l’ensemble étudié c’est l’âge.
3. Echantillon :
Sous-ensemble de la population. Exemple : pour établir la durée de vie des ampoules
électriques produites par une machine, on peut prélever au hasard un certain nombre
d’ampoules - un échantillon- parmi toutes les celles produites par cette machine.
L’échantillonnage représente l’ensemble des opérations qui ont pour objet de
prélever un certain nombre d’individus dans une population donnée.
4. Individu ou unité statistique :
Chaque élément de la population ou de l’échantillon.
Exemple : dans l’exemple précédant, chaque ampoule constitue un individu ou une
unité statistique.
5. La taille :
Représente le nombre d’individus d’un échantillon ou d’une population. Elle est
symbolisée par « n » dans le cas d’un échantillon et par « N » dans le cas d’une
population.
6. Le caractère :
- 4 -

C’est l’aspect particulier que l’on désire étudier.
Exemple : concernant un groupe de personnes, on peut s’intéresser à leur âge, leur sexe
leur taille…
7. Les modalités :
Les différentes manières d’être que peut présenter un caractère.
Exemple 1 : le sexe est un caractère qui présente deux modalités : féminin ou masculin
Exemple 2 : quant au nombre d’enfants par famille, les modalités de ce caractère
peuvent être 0,1, 2,3…,20.
8. Caractère qualitatif :
Ses modalités ne s’expriment pas par un nombre
Exemple : la religion, le sexe, l’opinion…
9. Caractère quantitatif :
Ses modalités sont numériques.
Exemple : l’age, la taille, le poids…
10. Caractère quantitatif discret ou discontinu
L’ensemble des valeurs que peut prendre le caractère est fini ou dénombrable. Le plus
Souvent, ces valeurs sont entières.
Exemple :le nombre d’enfant dans une famille, le nombre de téléviseurs par foyer et la
pointure des souliers.
11. Caractère quantitatif continu :
Le caractère peut prendre théoriquement n’importe quelle valeur dans un intervalle
donné de nombres réels.
Exemple : la taille d’un individu, le poids…
12. Série statistique :
L’ensemble des différentes données associées à un certain nombre d’individus.
Exemple : la série suivante résulte d’une courte enquête auprès de quelques personnes
pour connaître leur âge :
18 21 19 19 17 22 27 18 18 17 20 20 23
13. Les recensemen s
t
- 5 -

Sont des opérations issues du dénombrement, qui consistent à étudier de façon
exhaustive et en fonction de plusieurs critères tous les éléments d’une population
Ne pas confondre «dénombrement» et «recensement»
*Le dénombrement: comptage des individus d’une population
*Le recensement: chiffrer les données selon plusieurs aspects (âge, sexe,
chiffred’affaires, etc.)
Exemple Explicatif Des Notions Importants
II- Types de critères, de caractères ou de variables
Population urbaine marocaine par groupe d’âge et sexe (en
millier)
Population: Population urbaine marocaine en 2005 et 2006
Individu: Population urbaine
Caractère: Groupe d’âge et sexe
1. Caractères quantitatifs
Variables numériques et mesurables exprimant une quantité
Exemple: Chiffre d’Affaires d’une entreprise; taux de chômage; taille; PIB, etc
Les variables quantitatives peuvent être classées en :
a. Variables quantitatives discrètes ou discontinues
b. Variables quantitatives continues
a. Variable quantitative discrète (discontinue)
Elle est représentée par un nombre fini de valeurs (Ex: nombre d’enfant par ménage;
nombre d’hospitalisation par patient, etc.)
Les modalités de la variable peuvent être traitées mathématiquement (par des
opérations mathématiques de base)
- 6 -

Exemple: enquête réalisée auprès de 20 femmes casablancaises nées en 1970 sur le
nombre d’enfants qu’elles ont eus
Nombre d’enfants/femmes
Nombre d’enfants Effectif de femmes
0 1
1 3
2 5
3 5
4 4
5 2
Total 20
b. Variable quantitative continue
Elle peut prendre un nombre infini de valeurs dans son intervalle de définition (Ex:
taille, revenus, CA, poids, etc.)
Il s’agit de grandeurs liées à l’espace(longueur, surface), au temps(âge, durée, vitesse), à
la masse(poids, teneur), à la monnaie(salaire, CA)
Les variables continues peuvent être regroupées en classe: un individu qui pèse 76,5
Kg sera repéré dans une classe de poids de [76-77]
Lorsque les données sont regroupées en classe, il faut définir les extrémités de classe
r la «borne inférieure» et la «borne supérieure» des classes
I t inclues ou non dans
les classes
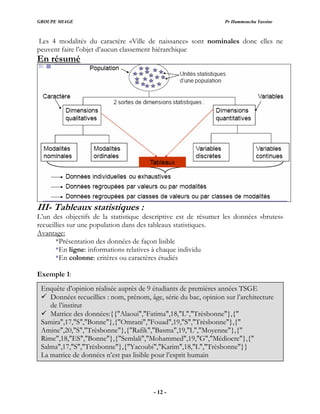
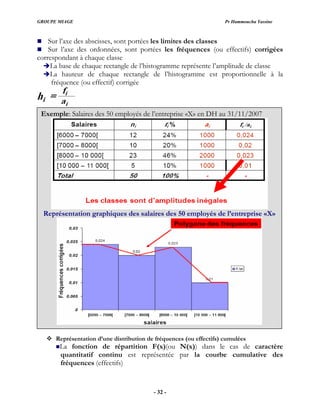
Exemple 1:
Il faut précise
l faut préciser sans ambiguïté si les valeurs des extrémités son
nombre d’enfants par femme
[
ignifie que la valeur «2» est inclue dans la classe
ue la valeur «4» est exclue de la classe
To
et une
Classe [2 –4
«[2 –» s
« –4 [» signifie q
us les éléments de la population étudiée (femmes) doivent se retrouver dans une
seule classe
- 7 -

Exemple 2:
Pour des raisons pratiques, on retient généralement comme extrémités de classes des
valeurs «rondes» afin d’effectuer aisément des calculs sur les extrémités de classes
plitude des classes et du centre des classes.
comme pour le calcul de l’am
b.1- L’amplitude de classe
L’amplitude de classe=la différence entre la valeur de l’extrémité supérieure et la
L’amplitude a d’une classe i sera donnée par la formule suivante :
valeur de l’extrémité inférieure
Exemple 1:
xemple 2:
Salaires mensuels des employés d’une entreprise «X» en DH au 31/12/2006
classes de salaires :
-De 6000 à moins de 7000 DH: [6000 –7000[
Cette classe comprendra un employé dont le salaire = 6999 ta dis qu’un
salarié dont le revenu = 7000 s’en trouvera exclu
moins de 9000 DH: [7000 –9000[
DH: [9000
3
n
-De7000 à
-De9000 à moins de 12 000 –12 000[
L’amplitude ai de la classe [6000 –7000[
E
Nombre d’enfants par femme
- 8 -

Exemple 3:
b.2- Le centre de classe
classe=la moyenne des extrémités de classe
L
Le centre de
e centre c d’une classe i sera donnée par la formule suivante :
Exemple 1:
Exemple 2:
A Ne Pas Oublier
Salaires des employés de l’entreprise «X» en DH
L’amplitude de la deuxième classe est 2 fois plus grande que celle de la première
classe
L’amplitude de la troisième classe est 3 fois plus grande que celle de la première
classe
Cas où les amplitudes sont égales (Nombre d’enfants par femme)
Cas de classes d’amplitudes inégales (Salaires des employés de l’entreprise «X» en
DH)
- 9 -

2.Caractère qualitatif:
Ne peut faire l’objet d’une mesure car il ne se présente pas sous forme numérique.(Ex:
u; section du bac; catégorie socio-professionnelle; etc.)
• On ne peut pas effectuer d’opérations arithmétiques sur les caractères qualitatifs
Les caractères qualitatifs se déclinent en plusieurs Modalités:
Modalités:: les différentes valeurs prises par un caractère qualitatif
Exemple 1: la variable«sexe» à deux modalités «Masculin» «Feminin»
Exemple 2: la variable «couleurs des yeux» peut prendre comme modalités «Noir»
«Brun» «Bleu» «Vert» «Gris»
Exemple 3:
couleur de pea
(on ne peut additionner les couleurs de peau des êtres humains)
- 10 -
Si la population est décrite selon le caractère «CSP agrégées», les différentes
modalités seront

2.a- Les mod ent
alités d’un caractère qualitatif sont exhaustives et mutuellem
incompatibles
Exhaustives: à chaque individu doit correspondre une modalité du caractère
Exemple: enquête sur l’état matrimonial d’un groupe d’individu
modalités du caractère «Etat matrimonial» : Célibataire, Marié, Veuf,
Pour satisfaire la condition d’exhaustivité, on doit avoir quatre
Divorcé
: Un individu ne peut être à la fois «célibataire» et «marié»
voir être classé dans une et une seule
2.b- Les modalités d’un caractère qualitatif peuvent être ordinales ou
Incompatibles: Chaque individu doit pouvoir être classé dans une seule
modalité du caractère
Exemple
Chaque individu d’un caractère doit pou
modalité
nominales
Les modalités ordinales: peuvent être classées ou hiérarchisées
Exemple: Enquête réalisée en 2006 par l’association «Maroc Entrepreneur» sur
Pas
le degré de satisfaction des marocains ayant vécu à l’étranger et franchi le cap du
retour au Maroc
- Le Caractère: «Degré de satisfaction»
- Les :
modalités du Caractère «Satisfait», «Assez Satisfait», «Peu Satisfait», «
Satisfait»
L
Le classement effectué va de l’opinion «Satisfait» à l’opinion «
es modalités sont ordinales car on peut les classer :
Pas Satisfait»
d’une préférence positive à une préférence de plus en plus négative
Les modalités ordinales ne peuvent faire l’objet d’aucune opération
arithmétique
On passe
- 11 -
Les modalités nominales: ne peuvent pas être classées (hiérarchisées)
Exemple: Classement d’un groupe de 15 étudiants selon leur ville de naissance

Les 4 modalités du caractère «Ville de naissance» sont nominales donc elles ne
peuvent faire l’objet d’aucun classement hiérarchique
En résumé
leaux statistiques :
umer les données «brutes»
.
III- Tab
L’un des objectifs de la statistique descriptive est de rés
recueillies sur une population dans des tableaux statistiques
Avantage:
*Présentation des données de façon lisible
ne: informations relatives à chaque individu
E
*En lig
*En colonne: critères ou caractères étudiés
xemple 1:
Enquête d’opinion réalisée auprès de 9 étudiants de premières années TSGE
rchitecture
yenne"},{"
Rime",18,"ES","Bonne"},{"Semlali","Mohammed",19,"G","Médiocre"},{"
Salma",17,"S","Trèsbonne"},{"Yacoubi","Karim",18,"L","Trèsbonne"}}
umain
Données recueillies : nom, prénom, âge, série du bac, opinion sur l’a
de l’institut
Matrice des données:{{"Alaoui","Fatima",18,"L","Trèsbonne"},{"
Samira",17,"S","Bonne"},{"Omrani","Fouad",19,"S","Trèsbonne"},{"
Amine",20,"S","Trèsbonne"},{"Rafik","Basma",19,"L","Mo
La matrice de données n’est pas lisible pour l’esprit h
- 12 -

n des données dans un tableau
Présentatio
Tab 1: Résultat de l’enquête effectuée auprès des étudiants de l’institut
Exemple 2:
Nombre d’enfants par famille observé dans un échantillon de 56 familles
enquête auprès d’un échantillon de 56 familles marocaines sur le nombre d’enfant
par ménage
Données brutes: 0 0 0 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 4 4 4 4 4
4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 7 7 8 9
Les données brutes ne sont pas lisibles
Regroupement des données dans un tableau pour faciliter le
traitement et les interprétations
- 13 -

La première colonne du tableau reprend les différentes modalités (xi) prises par la
variable ou le caractère nombre d’enfants/ménage
La deuxième colonne présente les effectifs (ni) (fréquences absolues): le nombre
d’individus correspondant à chaque modalité du caractère
haque cas du tableau dénombre les individus considérés comme équivalents face au
ion
C
phénomène étudié
L’ensemble des modalités et des effectifs d’un caractère forment une distribut
statistique ou une série statistique
e doit respecter des principes généraux:
ter des intitulés de lignes et de colonnes clairement définis
Le tableau doit préciser les unit ndre le mètre avec le
mètre carré, le millier avec le million, le
Le tableau doit préciser la source nnées sont
empruntées à une publication ou à un o
Les tableaux statistiques peuvent être à ns
À «une dimension» si un seul carac ié (nombre d’enfants/ménage)
À «deux dimensions» si l’on retient deux caractères (nombre et sexe des
enfants/ménage)
La présentation d’un tableau statistiqu
Le tableau doit porter un titre précisant son contenu : le phénomène étudié , la
façon dont il est étudié ,le lieu, la date, etc.
Le tableau doit por
és utilisées : ne pas confo
DH avec l’Euro, etc.
des informations lorsque les do
rganisme
une ou à plusieurs dimensio
tère est étud
A- les tableaux à un seul caractère
onsidérons une population statistique de n individus décrite selon le caractère x dont
C
les k modalités sont x1, x2, ..., xi, ...., xk
représente le nombre
ou «fréquence absolue», présentant
La somme des «effectifs partiels»
ni est «l’effectif total» n de la
ni
d’individus, appelé «effectif partiel»
la modalité xi
population
- 14 -

La «fréquence relative» ou «fréquence» fi est la proportion d’individus présentant
la même modalité dans la population
La «fréquence» fi est obtenue en divisant chaque effectif par l’effectif total
La «fréquence» fi peut être exprimée en pourcentage%
La somme des fréquences relatives i est égale à 1 et a somme des fréquences
Dé
f l
exprimées en % est égale à 100
monstration
L atistique initiale se présen sous la forme suivante :
e tableau st tera
Exemple d’application : Compléter le tableau en calculant les fréquences relatives et les
fréquences en pourcentages ?
Nombre d’enfants par famille
bre d’ amille (xi) Effectif (ni) Fréquence (fi)%
Nom enfants/f
0 3 5.36
1 5 8.92
2 8 14.29
3 7 12.5
4 14 25
5 9 16.08
6 6 10.72
7 2 3.57
8 1 1.78
9 1 1.78
Total 56 100
- 15 -

A.1- Les tableaux à caractères qualitatifs
tableaux à caractères qualitatifs ne posen
Les t pas de problèmes particuliers
1. re à modalités nominales
2. Tableaux de caractère à modalités ordinales
Tableaux de caractè
A.2- Les tableaux à caractères quantitatifs peuvent contenir plus d’informations
que les tableaux à caractères qualitatifs :
Effectifs cumulés
Fréquences cumulées
Les effectifs cumulés notés N(x)
Exemple : Nombre d’enfants par famille : Combien de familles ont plus de
quatre enfants? Combien de familles ont moins de quatre enfants?
Les fréquences cumulées notées F (x)
Exemple1: Répartition des salariés de l’entreprise M selon la CSP au 31/12/06
Les modalités des CSP (xi) Effectifs (ni) fréquences (fi) fi en %
Cadre Supérieur 10 0.071 7.1
Contremaitres 5 0.036 3.6
Employés 30 0.214 21.4
Ouvriers spécialisés 90 0.643 64.3
Autres catégories 5 0.036 3.6
Total 140 1 100
Exemple 2: Répartition des étudiants du groupe A selon leur lieu de naissance
Lieu de naissance (xi) Effectifs (ni) fréquences (fi) fi en %
Casablanca 98 0.392 39.2
Mohammedia 53 0.212 21.2
Rabat 47 0.188 18.8
Kenitra 32 0.128 12.8
Autres 20 0.080 8
Total 250 1 100
Exemple: enquête effectuée auprès d’un éc antillon de 9 étudiants de sciences
économiques sur leur opinion concernant l’architecture de l’institut
Opinion (xi) Effectifs (ni) fréquences (fi) fi en %
h
Très bonne 5 0.556 55.6
Bonne 2 0.222 22.2
Moyenne 1 0.111 11.1
Médiocre 1 0.111 11.1
Total 9 1 100
- 16 -

Q
prop
Le c s effectifs cumulés et des fréquences cumulées se fait en cumulant
(s
uelle est la proportion de familles ayant plus de quatre enfants? Quelle est la
ortion de familles ayant moins de quatre enfants?
alcul de
ommant) les effectifs et les fréquences relatives dans une colonne du tableau
1. Cas de caractères quantitatifs discrets
Exemple: Nombre d’enfants (xi) observés dans un échantillon de 55 familles
- 17 -

2. Cas de caractères quantitatifs continus
Remarque importante
Le calcul des fréquences et des effectifs cumulés n’est pas affecté par l’amplitude des
classes
B- Les tableaux à deux caractères
Une population statistique peut être décrite à l’aide de deux caractères simultanément
B.1- Présentation générale des tableaux de contingence
Il y a 15 ménages dans l’échantillon qui ont «moins de» 3 enfants. On peut dire
aussi qu’il y a 15 ménages dans l’échantillon qui ont «au plus» 2 enfants.
Il y a 40 ménages dans l’échantillon qui ont «plus de» 2 enfants. On peut dire
ages dans l’échantillon qui ont «au moins» 3 enfants
ants
lon ont «plus de» 3 enfants ou «au moins» 4
aussi qu’il y a 40 mén
40% des ménages de l’échantillon ont «moins de» 4 enfants ou «au plus» 3
enf
60% des ménages de l’échantil
enfants
Exemple: Répartition des salaires mensuels d’une entreprise X au 31/12/06
Interprétation des résultats
88% des salariés gagnent moins de 10000 DH par mois (260 personnes)
80% des salariés de gagnent plus de 9000 DH par mois (235 personnes)
Exemple 1: la population des ménages peut être décrite selon son revenu et ses
dépenses simultanément
ion de la CSP
tion
Exemple 2: la population active marocaine peut être décrite en fonct
et du niveau de forma
Les tableaux statistiques correspondant sont à deux dimensions
Les tableaux de contingence ou croisés dynamiques ou à double entrées
Considérons une population statistique décrite selon deux caractères :
Un caractère X dont les n modalités xisont x1, x2, ..., xi, ...., xn
Un caractère Y dont les k modalités yjsont y1, y2, ..., yj, ...., yk
- 18 -

Le tableau de contingence obéit à une notation conventionnelle
1. Le tableau contient :
Dans la 1ère
colonne les n modalités x1, x2, ..., xi, ...., xn du caractère X
Dans la 1èreligne les k modalités y1, y2, ..., yj, ...., ykdu caractère Y
2. L’effectif nij correspond à l’intersection d’une ligne i et d’une colonne j
s effectifs de la ième ligne, j=1, ..., K est remplacé par «.»
.j: somme des effectifs de la jème colonne, i=1, ..., n’est remplacé par «.»
tif général marginal de X est noté «ni.»et celui de Y«n.j»
5. L’effectif total du tableau est noté «n..»:il s’agit de l’effectif total de la population
étudiée
Exemple:
L’effectif de la population présentant à la fois la modalité xi et la modalité yj
3. Pour les effectifs marginaux ni. Et n.j, on remplace l’indice qui varie par «.»
ni.: somme de
n
4. L’effec
- 19 -
Répartition des salariés d’une entre
formation
prise X selon le sexe (xi) et le niveau de
(yj)

B.2- Propriétés des tableaux de contingence
a xi et yj étant incompatibles et exhaustives, on peut écrire plusieurs
séries d’égalités
) Les modalités de
Pour yj
Pour xi
L’effectif total de la population n...
Apparaît à l’intersection de la dernière ligne et de la dernière colonne
Est égal à la somme de la dernière ligne ou de la dernière colonne
En remplaçant ni. et n.j par les expressions précédentes, on obtient
b) Les fré
Rappor
*La fréquence partielle des modalités xi, yj est égale à :
quences partielles
t de l’effectif partiel sur l’effectif total
*Proportion d’individus satisfaisant à la fois la modalité xi et la modalité yj
La somme des fréquences partielles est égale à 1
- 20 -

Démonstration
C- Les différentes distributions statistiques
Plusieurs distributions statistiques peuvent être définies dans un tableau à double
entrées
Les distributions marginales
Les distributions conditionnelles
1. Les distributions marginales
Un tableau de contingence compte deux distributions marginales: la distribution
marginale du caractère X et la distribution marginale du caractère Y
C.1.a- La distribution marginale du caractère X
Est composée des modalités du caractère X et des effectifs correspondant quelles que
soit les modalités du caractère Y.
La distribution marginale du caractère X est donnée par le tableau suivant
Exemple: Répartition des salariés d’une entreprise M selon le sexe (xi) et le niveau de
formation (yj)
1.
2. Interpréter les résultats
C lculer f22, f31, f12
a
8% des salariés sont des hommes de niveau Bac + 5
- 21 -

- 22 -
C.1.b - La distribution marginale du caractère Y
Est composée des modalités du caractère Y et des
t les modalités du caractère X
effectifs correspondant quelles que
soi
La fréquence marginale de la modalité yj est égale à :

2. Les distributions conditionnelles
Deux séries de distributions conditionnelles
Celle du caractère X conditionnellement au caractère Y
C.2.a Distributions conditionnelles du caractère X liées par yj, j=1, ..., k
Exemple d’application :Répartition des salariés d’une entreprise
M selon le sexe (xi) et le niveau de formation (yj)
Celle du caractère Y conditionnellement au caractère X
e sont les modalités de X et des effectifs de chacune de ces modalités dans la sous
p
Distribution conditionnelle du caractère X liée par yj (j=1à k) est la suivante :
C
opulation présentant la modalité yj de Y:
Exemple : Répartition de la sous population des femmes de l’entreprise M selon leur
niveau de formation
- 23 -

C.2.b Distributions conditionnelles du caractère Y liées par xi, i=1, ..., n
n conditionnelle du aractère Y liées par xi(i=1, ..., n) est la suivante
Ce sont les modalités de et des effectifs d
Y e chacune de ces modalités dans la sous
population présentant la modalité xi de X
Distributio c
Exemple : Répartition de la sous population de l’entreprise M ayant un niveau de
formation «Bac+3» selon le sexe
- 24 -
Exemple d’application : Répartition des salariés d’une entreprise M selon le sexe
(xi) et le niveau de formation (yj)

- 25 -
3. Relation entre les fréquences marginales et les fréquences conditionnelles
On peut démontrer que le produit des fréquences marginales par les fréquences
conditionnelles est égal aux fréquences partielles
I
Les graphiques permettent de donner une synthèse visuelle de la distribution d’une variable. Ils
apparaissent comme plus «parlants»que les tableaux Ils donnent, au sens propre,
une image des réalités observées
Les représentations graphiques sont spécifiques à un type de variables ou de
caractères.
*Qualitatif : ordinal / nominal
*Quantitatif : discret / continu
1. Représentations des distributions à une dimension
Le choix des représentations graphiques dépend de la nature du caractère statistique
étudié
V- Représentations graphiques
A- Représentations des caractères qualitatifs
Les variables qualitatives peuvent être représentées graphiquement de différentes
manières
Diagrammes en bâtons
Diagrammes en barres (ou en tuyaux d’orgue)
Diagrammes circulaires (ou en camembert ou en secteurs)
A.1 Diagrammes en bâtons
Un diagramme en bâtons est constitué d’une suite de «bâtons»
A chaque modalité xi du caractère, on associe un «bâton» de longueur hi
La longueur hi doit être proportionnelle à la fréquence ou à l’effectif n
es bâtons peuvent être verticaux ou horizontaux
fi
L

A.2 Diagrammes en barres (ou en tuyaux d’orgue)
Même principe que pour les diagrammes en bâtons
Exemple : Répartition des salariés de l’entreprise X selon la CSP
Représenter graphiquement la distribution étudiée
A.3 Diagrammes circulaires (camembert ou secteurs)
Cercle divisé en secteurs représentant l’ensemble de la population
-
- 26 -

- Les différentes modalités du caractères ont représentées par des secteurs dont la
surface est proportionnelle aux effectifs ou fréquences
- L’angle de chaque secteur αi est proportionnel à la fréquence fi: αi= 360 x fi
atifs discrets
B- Représentations des caractères quantitatifs
B.1.Représentation graphique des caractères quantit
Exemple : Répartition des salariés de l’entreprise X selon la CSP
Représenter graphiquement la distribution étudiée
ces cumulées (ou effectifs
bâtons
ibution des fréquences (ou effectifs)
Représentation d’une distribution des fréquen
Représentation d’une distr
cumulés)
Représentation d’une distribution des fréquences (ou effectifs)
Les fréquences (ou effectifs) sont représentées par les diagrammes en
- 27 -

Exemple: Nombre d’enfants des 40 salariés d’une entreprise
Représentation d’une distribution de fréquences cumulées (ou eff. cum.)
*Pour représenter une distribution de fréquences (effectifs) cumulées, il faut d’abord
définir la fonction de répartition F(x)
*Considérons une population statistique décrite selon un caractère quantitatif discret X
dont les n modalités xi sont : x1, x2,..., xi,...., xn
Où x1<x2<xi<...<xn
La fonction de répartition F(x) est définie comme suit:
Distribution des fréquences des salariés selon leur nombre d’enfants
*
Il y
consid
*F(x) représentant les fréquences cumulées «moins de» x:
a plusieurs définitions possibles d’une fonction de répartition F(x) selon que sont
érées les fréquences (effectifs) cumulées «moins de», «plus de»
- 28 -

*F(x) représentant les fréquences cumulées «plus de» x:
*La fonction de répartition F(x) (ou N(x)) est représentée par la courbe
cumulative des fréquences (effectifs)
Représentation graphique de la courbe cumulative croissante
Exemple: Nombre d’enfants des 40 salariés d’une entreprise
- 29 -

Représentation graphique de la courbe cumulative décroissante
B.2.Représentation graphique des caractères quantitatifs continus
Représentation d’une distribution des fréquences (ou effectifs)
Représentation d’une distribution des fréquences cumulées (ou effectifs cumulés)
Représentation d’une distribution de fréquences (ou effectifs)
Les fréquences (ou effectifs) des variables quantitatives continues sont représentées
graphiquement par les histogrammes
- À chaque classe de valeurs, on fait correspondre un rectangle dont l’air est
proportionnelle à la fréquence (ou l’effectif) de chaque classe
- Deux cas de figures doivent être envisagés selon que les amplitudes de classes
sont égales ou inégales
Cas de classes d’amplitudes égales
Sur l’axe des abscisses , sont portées les limites des classes
Sur l’axe des ordonnées, sont portées les fréquences (ou effectifs) correspondant à
chaque classe
Chaque fréquence (ou effectif) est représentée par un rectangle dont la base représente
l’amplitude de classe et dont la hauteur est proportionnelle à la fréquence (ou effectif)
- 30 -

- 31 -
On obtient le polygone des fréquences en joignant les milieux des segments
périeurs de chaque rectangle de l’histogramme.
La propriété fondamentale du polygone des fréquences est qu’il conserve l’aire ou la
rface de l’histogramme.
L’aire comprise entre le polygone des fréquences et l’axe des abscisses est la même
ue l’aire comprise dans l’histogramme
as de classes d’amplitudes inégales
*
su
*
su
*
q
C
Exemple: Salaires des 50 employés de l’entreprise «X» en DH au 31/11/2007
Représentation graphiques des salaires des 50 employés de l’entreprise «X»
L’histogramme ne peut plus être construit exactement de la même manière
Les fréquences (effectifs) se rapportant à des classes d’amplitudes inégales ne
ction se fait en calculant les fréquences (ou effectifs)
sont plus comparables
Il faut dans ce cas effectuer une correction pour tenir compte des
différences d’amplitude
Généralement, la corre
par unité d’amplitude

Sur l’axe des abscisses, sont portées les limites des classes
r l’axe des ordonnées, sont port
Su ées les fréquences (ou effectifs) corrigées
ogramme représente l’amplitude de classe
istogramme est proportionnelle à la
fréquence (ou effectif) corrigée
correspondant à chaque classe
La base de chaque rectangle de l’hist
La hauteur de chaque rectangle de l’h
Représentation d’une distribution de fréquences (ou effectifs) cumulées
F(x)(ou N(x)) dans le cas de caractère
umulative des
Exemple: Salaires des 50 employés de l’entreprise «X» en DH au 31/11/2007
Représentation graphiques des salaires des 50 employés de l’entreprise «X»
La fonction de répartition
quantitatif continu est représentée par la courbe c
fréquences (effectifs)
- 32 -

des caractères quantitatifs continus possèdent
s des fonctions de répartition des caractères dis « La
fonctions de répartition des caractères quantitatifs continus sont
droite
ans
Les fonctions de répartition
toutes les propriété
continuité»
Les
continues à gauche et à
D chaque classe, on fait une interpolation linéaire: on relie les points extrêmes de
haque classe par un segment de droite
c
La courbe cumulative est donc continue
xemple: Salaires des 50 employés de l’entreprise «X» en DH au 31/11/2007
E
Représenter gra
F(x) «moins de» :On prend pour abscisses les limites supérieures des
classes et, pour ordonnées, les fréquences cumulées correspondantes
F(x) «plus de»: On prend pour abscisses les limites inférieures des classes
et, pour ordonnées, les fréquences cumulées correspondantes
eprésentation graphique des courbes cumulatives des fréquences
phiquement les fréquences cumulées
R
- 33 -

2. Représentations des distributions à deux dimensions
es distributions statistiques à deux dimensions peuvent être représentées de
ifférentes manières.
Diagramme en tuyaux d’orgue
Diagramme circulaire
Stéréogramme
Etc.
ctère qualitatif
.1 Représentation graphique des distributions conditionnelles
L
d
A. Cas de cara
Exemple: Répartition des élèves d’une classe selon le sexe et le groupe
Méthode de calcul
Répartition des élèves selon le sexe et le groupe
A
- 34 -
Exemple1: Distributions de la variable GROUPE conditionnellement à la variable SEXE

- 35 -
Diagramme des fréquences de la variable GROUPE conditionnellement à la variable SEXE
E
G
xemple 2: Distributions de la variable SEXE conditionnellement à la variable
ROUPE
Diagramme des fréquences de la variable SEXE conditionnellement à la variable GROUPE

B. Cas de cara
Les dist
graphiquement sous forme de nuage de points dans un plan
Les points sont obtenus en représentant chaque couple d'observation (xi;yi) par un
point dans le plan
ctère quantitatif
ributions statistiques à deux dimensions peuvent être représentées
Exemple 1:Distributions d’un groupe d’étudiants selon les notes de statistique et de
mathématiques
Représentation par nuage de points des étudiants selon leurs notes de statistique et de
mathématiques
- 36 -

On peut remplacer chaque point par un cercle délimitant une aire proportionnelle à
utres représentations graphiques
l'effectif ou à la fréquence
Représentation des étudiants selon leurs notes de stat et de math
A
Stéréogramme
Le stéréogramme permet de faire des représentations 3D
graphiques.
- 37 -

Pyramide des âges
Nous n’avons présenté que les représentations graphiques les plus courantes
Au-delà de cette présentation non exhaustive, il existe des représentations appelées
cartogrammes qui consistent à utiliser des cartes géographiques pour exprimer des
distributions d’individus dans l’espace
Il existe également des graphiques figuratifs où les phénomènes sont représentés par
des objets en rapport avec le caractère étudié (Voiture pour la production de voitures ;
des sacs pour la production de blé, etc.)
V- Caractéristiques de tendance centrale et de position :
• Ici, il s’agit de faire une synthèse de l’information, contenue dans la séri brute, par le
c rale, qui caractérisent
l’
• Dans ce chapitre, on analysera trois de ces paramètres qui sont : les moyennes, le
mode et la médiane.
e
hiffre; et ce en calculant des paramètres dits de tendance cent
ordre de grandeur des observations.
- 38 -

A- Mode
A.1 Définition
Le mode, noté Mo, d’une série statistique est la valeur de cette série, dont l’effectif (ou
la fréquence) est plus grand que les effectifs (ou les fréquences) des valeurs voisines.
Exemple :
A.2 Cas d’un caractère discret
Calculer le mode de la distribution statistique suivante représentant les notes en
statistique d’une classe de 35 élèves :
12-15-14-13-19-20-16-8-9-17-16-15-16-14-7-8-9-12-16-17-13-16-20-16-6-12-14-16-
19-20-16-5-6-14-15
La note qui se répète le plus (08 fois) est 16 qui représente le mode
Exemple
La distribution statistique suivante donne le nombre d’enfants par famille pour un échantillon
de 500 familles.
Nombre d’enfants Nombre de familles
0 50
1 70
2 70
3 50
4 80
5 90
6 et plus 70
Total 500
Représentation graphique des nombre d'enfants par
famille
50 50
90
0
20
40
0
1
2
3
4
5
6
et
Nombre d'enfants
nombre
de
e
70 70
80
70
60
80
famill
100
Nombre de familles
Quel est le mode de cette distribution et quelle est sa signification ?
Le mode
C’est 5 enfants par famille parce que l’effectif correspondant est égal à 90
Cela veut dire qu’il y a 90 familles sur 500 qui ont 5 enfant c’est les familles qu’on rencontre le
plus.
- 39 -

- 40 -
Dans le cas d'une variable statistique discrète. la détermination du mode est immédiate
à partir du tableau statistique ou du diagramme en bâtons.
Ci-dessous on donne trois diagrammes en bâtons associés respectivement, à une
distribution unimodale (qui a un seul mode), et à une distribution bimodale
(qui a deux modes ), et à une distribution qui a un intervalle modal.
A.3 Cas d’un caractère continu
Le mode se trouve dans la classe modale, c'est la classe qui correspond à
l réquence corrigée.
a plus grande f
On peut démontrer que l’expression algébrique du mode est comme suit :
B : est la borne inferie
1 ure de la classe modale
B2 : est l
e
a borne supérieure de la classe modale
n : est l’effectif de la classe modale
en-1 : est l’effectif de la classe qui se trouve avant la classe modale
e l’effectif de la classe qui se trouve après la classe modale
n+1 : est

Exemple
On considère 75 ateliers d’artisans classés en fonction du nombre des heures
travaillées :
Calculez le mode, et interpréter le résultat.
Mo= 130 +(23-15) (150-130)
(23-15)+ (23-17)
Mo= 130 +160
14
Mo= 130 +160=141.42
14
Alors le mode est de 141.42
C’est le nombre fréquent d’heures travaillées dans les 75 ateliers.
B- Médiane
B.1 Définition
La Médiane, notée Me, d’une série statistique, est la valeur de la série qui partage la
population en deux parties d’effectifs égaux. Par conséquent, on aura autant
’observations inférieures à Me que d’observations supérieures à M.
d
B.2 Détermination de la médiane
(a) Cas d’une série brute
Soit la série ordonnée (par ordre croissant) de n observations : x1 , x2 , ..., xn .
, mais on a un
_Si n est impaire, alors la valeur médiane est l’observation qui occupe le rang (n+1)/2.
_Si n est paire, on ne peut plus déterminer exactement la médiane
intervalle médian ( ) [ ]
(b)Cas d’une distribution
Cas d’une Variable Statistique Discrète
Soit X une Variable Statistique Discrète . de distribution Pour déterminer sa
médiane, on utilise les fréquences cumulées croissantes Fi.
Procédure à suivre
Si " i Fi ¹0,5 ; autrement dit, si aucune fréquence cumulée Fi n’est égale à 0,5,
dans ce cas la médiane est la modalité xi qui correspond à la plus petite fréquence
Cumulée dépassant strictement 0,5.
- 41 -

S'il existe une modalité xi pour laquelle Fi = 0,5, dans ce cas on parle d’un
intervalle médian : [xi , xi+1].
Exemple 1 :
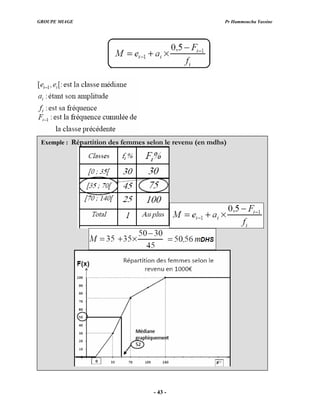
Dans le cas continue, la médiane toujours unique : c’est la valeur qui partage
exactement la population deux parties égales. En d'autres termes, Me est la solutio
de l’équation :
Cas d’une Variable Statistique continue
n
Où F est la fonction de répartition de X.
On a deux méthodes pour déterminer la médiane :
(a) Détermination graphique :
-La médiane correspond à l’abscisse du point de la courbe cumulative qui admet pour
ordonnée la valeur 0,5 (ou 50%). (Voir Graphique de l’exemple)
(b) Détermination par interpolation :
-D'après le tableau ou la courbe cumulative, on détermine la classe contenant la
médiane Me ; c’est la classe [ ei-1 , ei [telle que, Fi-1 £ 0,5 < Fi; puis on détermine
Me par interpolation linéaire. donc on a :
Classement des 20 femmes selon le nombre d’enfants
- 42 -

- 43 -
Exemple : Répartition des femmes selon le revenu (en mdhs)

C- Moyenne arithmétique
•(a) Définition :
La moyenne arithmétique, notée , d’une variable statistique X de distribution
Est la quantité :
Où, n est la taille de la population, et les xi sont les modalités dans le cas d'une
variable statistique discrète. et les centres des classes dans le cas d'une variable
statistique continue.
Exemple 1 : On reprend l’exemple des 20 femmes selon le nombre d’enfants
- 44 -

Exemple 2 : Pour les revenus des femmes
Exemple 3 : soit les séries suivantes : répartition selon l’âge
Selon la règle de la moyenne arithmétique
- 45 -

(b) moyenne arithmétique globale
Pour plusieurs populations d'effectifs n1, n2, ....., nk, de moyennes
Respectives
Moyenne globale = moyenne des moyennes
(c)Méthode des simplifications des calculs
Lorsque les calculs sont compliqués, on peut les simplifier en précédant à un
changement de variable Par changement d’échelle : Tout variable Xi peut s’écrire :
X
a= nouvelle échelle Xi= nouvelle variable
Par changement d’origine et d’échelle : tout variable Xi peut s’écrire
i= a X’i
= nouvelle origine a : n.é ’i : n. va
X0 chelle X riable
Exemple
Exemple
- 46 -

Si on pose :
La moyenne arithmétique :
- 47 -
On utilise cette relation pour simplifier les calculs de la manière suivante
On prend pour X0 la valeur de caractère la plus fréquente
O classes sont égaux
n prend « a » l’intervalle des classes lorsque les
Application
l’
: reprenant l’exemple 3 : soit les séries suivantes : répartition selon
âge
Age effictifs
20-25 8
25-30 10
30-35 20
35-40 25
40-45 15
45-50 10
total 88
On calcule :
1- le centre xi de chaque intervalle ex : 20+25/2=22.5
2- on calcul la nouvelle échelle a
Ex : 22.5=2.5+(5*4)
37.5=2.5*(5*6)
De ce fait la n.échelle est a=5
3- Calculez la moyenne avec changement du variable x0 = 37,5 c’est le centre de
classe modale dont l’effectif (25)est le plus élevé la classe (35-40)
Age effectifs xi x’i= (xi-x0)/a ni*x’i
20-25 8 22,5 -24=(-3*8)
25-30 10 27,5 -20= (-2*10)
30-35 20 32,5 -20
35-40 25 37,5 0
40-45 15 42,5 15
45-50 10 47,5
- 3 =(22.5-37.5)/5
-2
-1
0
1
2 20
total 88 -29

D- Moyenne géométrique
(a) Définition :
On appelle moyenne géométrique de la distribution que l’on note G. la
racine niéme
du produit de x ni
i
C’est plus pratique d’utiliser le logarithme
Exemple : Calculer la moyenne géométrique
xi ni
2 1
6 2
10 3
12 2
Total 8
Méthode 1
On utilise a la calculatrice la commande X Y
ou Y X
- 48 -

(b) Domaines d’application :
On utilise la moyenne géométrique dans le calcul du taux d’accroissement moyen et
dans le calcul de certains indices statistiques.
E- Moyenne harmonique
Méthode 2
xi ni Log xi ni log xi
2 1 0..301 0.301
6 2 0.778 1.556
10 3 1 3
12 2 1.079 2.158
Total 8 7.015
On utilise a la calculatrice la commande log x
On utilise a la calculatrice la commande X Y
ou Y X
Définition et propriété :
La moyenne harmonique, notée H, d’une distribution est l’inverse de la
m istribution :
oyenne arithmétique de la d
- 49 -

Domaines d’application
On utilise cette moyenne dans le calcul des durées moyennes, dans le calcul des
moyennes de rapports et de pourcentages et dans les études du pouvoir d’achat
(inverse du MGP)...etc.
F- Moyenne quadratique
éfinition et propriété
D
La moyenne quadratique, notée Q , d’une distribution est l
arrée de la
a racine
moyenne arithmétique de la distribution
c
Exemple : Calculer la moyenne harmonique
xi ni
2 1
6 2
10 3
12 2
Total 8
xi ni fi 1/x ni 1/x fi 1/x
2 1 0.125 0.5 0.5 0,0625
6 2 0.25 0.166 0.332 0,0415
10 3 0.375 0.1 0.3 0,0375
12 2 0.25 0.083 0.166 0,02075
Total 8 1 1,298 0,16225
- 50 -

Domaines d’application
e
:
• La moyenne quadratique intervient dans le calcul de certains paramètres d
dispersion.
G- Quantiles
La détermination des quantiles:
i) Détermination Graphique : elle est pratiquement la même que celle de la
Exemple : Calculer la moyenne quadratique
xi ni
2 1
6 2
10 3
12 2
Total 8
xi ni fi X2
ni X2
fi X2
2 1 0.125 4 4 0.5
6 2 0.25 36 72 9
10 3 0.375 100 300 37.5
12 2 0.25 144 288 36
Total 8 1 664 83
Ou bien
- 51 -

Médiane, il suffit de remplacer 0,5 par α.
ii) Détermination par Interpolation :
Elle correspond à la plus petite fréquence cumulée dépassant
strictement α.
H-
e
E )
Fi%
xemple : On reprend les revenus des 20 femmes (mdhs
Classes ni fi %
[0 ; 35[ 6 30 30
[35 ; 70[ 9 45 75
[70 ; 140[ 5 25 100
TOTAL 20 100
Le choix d’une caractéristique de tendance central
1 : Les conditions de Yule :
- 52 -

1ère conditions : Une modalité caractéristique doit être : définie de façon
doivent trouver le même résultat)
2
5 Doit se prêter au calcul algébrique
2 : Comparaison des différentes cara tiques de tendance centrale
objective. (2 personnes différentes
éme conditions : Tenir compte de toutes les observations
3éme conditions : être facile à comprendre
4éme conditions : être facile à calculer
éme conditions :
ctéris :
La moyenne :
Elle répond par nt au ndition Yule ; pour cela qu’elle est la
caractéristique la tilisée, mais il y a des cas ou il faut lui préférer la médiane
quand elle risque nflu e des va extrêm
La médiane :
Elle ne satisfait p ondi de Yul
leur
itions de Yule, mais il y a des cas ou il est utile, en
VI- Caractéristiques de dispersion :
Introduction
faiteme x co s de c’est
plus u
d’être i encé leurs es.
as les c tions e.
En effet, la valeur de la médiane ne change pas quand on augmente la va
d’une observation qui lui est inférieure
Le mode :
Ne remplit pas les cond
particulier quand on cherche la valeur la plus typique d’une série :
Ex : un vendeur de chaussures ne va pas stocker des chaussures de pointure
moyenne, mais va stocker les chaussures les plus vendues.
es paramètres de dispersion servent à mesurer la dispersion des observations
Au tour d'une tendance centrale.
On considère deux catégories de paramètres de dispersion :
• 1- Les écarts simples :
étendue- écart interquantile.
• 2-L'écart-type, la variance et le coefficient de variation.
1- Les écarts simples :
L
A- l’étendue
∆= 3
- 53 -

el que : 25%
des observations lui sont inférieurs et 75% lui sont supérieurs. 25% < ; 75%>
2éme quartile Q2= Me 50% < 50%>
émé quartile Q3= 75%< 25%>
On appelle inter quartile : Q3 – Q1 différence entre 1ér quartile et 3éme quartile.
N.B : Intervalle Inter quartile contient 50% des observations
B-3. Application
Salaires Effectifs fi % Fi%
B
B-1.Définition des quartiles :
- Intervalle inter-quartile
On appelle 1ér quartile Q1 la valeur du caractère t
3
B-2. Définition inter quartile :
10-15 9 11 11
15-20 25 30.5 41.5
20-25 32 39 80.5
25-30 16 19.5 100
Total 82 100
Ecart I. Inter quartile Q3 – Q1 =24,3 - 17,3 = 7DH
Signification : pour 50% des effectifs l’écart Maximum de salaire est de 7 DH
C- L’écart absolu moyen :
C-1 Définition
On appelle écart absolu moyen que l’on désigne par la moyenne arithmétique des
écarts absolus entre les valeurs du caractère et la moyenne arithmétique.
Application :
Quelle est l étendue de la série statistique suivante : 10- 390- 395- 405- 410- 1000
léments de réponse : Etendue = 990
E
C-2 Application
Soit le tableau suivant :
- 54 -
Signification : Ca = 4.42 Kg signifie qu’en moyenne, chaque individu s’éloigne de
la moyenne (67.75 Kg) de 4.42 Kg.

Remarque : Pour dire si une dispersion est grande ou non, pour comparer deux
séries entre elles, on se sert de l’indice de dispersion relatif = Ca / X *100
D - Variance et écart-type
D-1. Définition :
On appelle une variance la moyenne arithmétique des carrés des écarts entre les
valeurs du caractère et la moyenne arithmétique.
On appelle pe (ou écart quadratique moyen) la racine carré de
écart-ty
D
Poids ni xi ni * xi
-2. Application : Le même tableau précédent
ni
55-60 12 57,5 690 -10,25 105,0625 1260,75
60-65 17 62,5 1062,50 -5,25 27,5625 468,5625
65-70 36 67,5 2430 -0,25 ,0625 2,25
0
70-75 24 72,5 1740 4,75 22,5625 541,5
75-80 11 77,5 852,50 9,75 95,0625 1045,6875
Total 100 6775 3318,75
Signification : En moyenne chaque individu s’écarte du poids moyen (67.5 Kg) de
5.76 kg.
- 55 -

E- Coefficient de variation :
C'est un coefficient qui permet de relativiser l'écart type en fonction de la taille des
valeurs. Il permet ainsi de comparer la dispersion de séries de mesures exprimées dans
des unités différentes.
VII- La concentration :
L'objectif est de mesurer les inégalités dans la répartition d'une variable à l'intérieur
d'une population. Cette notion n'a d'intérêt que dans la mesure où les valeurs globales
xi représentent les valeurs ponctuelles ou les centres des classes, ni les effectifs
la sér
-Médiale :
ition :
caractère qui partage la masse
a médiale de la série (xi, gi)
édiane
çant les Fi par les F’i
suivantes ont une signification concrète
A- Valeurs globales
correspondants.
Les valeurs globales de ie (xi , ni) sont les quantités gi = ni xi
B
B-1. Défin
Application : Le même tableau précédent
Poids ni xi gi=ni * xi
55-60 12 57,5 690
60-65 17 62,5 1062,50
65-70 36 67,5 2430
70-75 24 72,5 1740
75-80 11 77,5 852,50
Total 100 6775
La médiale de la série statistique X est la valeur du
globale en deux parties égales. On la note Ml , et on a :
G(Ml) =0,5 =50 %.
La médiane de la série (xi, ni) est l
B-2. Détermination de la médiale
La procédure de la détermination de la médiale est similaire à celle de la m
En rempla
- 56 -

B-3. L’écart absolu médiale- médiane
noté
Poids ni xi fi% Fi%
cr
gi=ni *
xi
f’i% F’i%
cr
55-60 12 57,5 12 12 690 10.1 10.1
60-65 7
1 62,5 17 29 1062,50 15.7 25.8
65-70 36 67,5 36 65 2430 35.9 61.70
70-75 24 72,5 24 89 1740 25.7 87.4
75-80 11 77,5 11 100 852,50 12.6 100
Total 100 100 6775 100
Me= 65+5(50-29)/36=67,91
Classe médiale 65-70 amplitude a=05
M est un indicateur de concentration
• Si ∆Mr = 0alors M = Ml donc on a une distribution parfaitement égalitaire
• Plus ∆Mr est grand plus la concentration est forte, et inversement.
C- C nce n (ou RENZ
Dans un repère orthonormé, on trace les points de coordonnées (Fi, F’i) et on les
joint par Segments de droite.
• la courbe ainsi obtenue est appelée courbe de co entration ou urbe de
Lorenz.
&
ourbe de co ntratio de LO )
des
nc co
- 57 -

D- Indice de G
D-1. Définiti
L'indice de concentration ou indice de Gini, que l'on note IC est donné par :
INI
on
A
cr xi cr
pplication : Le même tableau précédent
Poids ni xi fi% Fi% gi=ni * f’i% F’i% fi
55-60 12 57,5 12 12 690 10.1 10.1 0.101 0.012
60-65 17 62,5 17 29 1062,50 15.7 25.8 0.3590 0.061
65-70 36 67,5 36 65 2430 35.9 61.70 0.875 0.315
70-75 24 72,5 24 89 1740 25.7 87.4 1.4910 0.358
75-80 11 77,5 11 100 852,50 12.6 100 1.8740 0.206
Total 100 100 6775 100 0.952
- 58 -

VIII Le ries oubl e régre i ire
r lat )
no able e co c
n dist tion statistique
ne d ution ’obser ff e selon èr
n la taille et l’âge
ents selon le nbre de pièces et superficie
total
- s sé à d e entré s : ssion l néa
(co ré ion
1- tion de t au d ntingen e :
A. u e ribu double
C’est u istrib ou l vation s’e ectu 2 caract es.
EX : Répartition des étudiants selo
Répartition des logem
superficie 10-30 30-50 50-70 70-80
nbr de piece
1 3 1
2 1 14 3 18
3 1 7 4 12
4 10 7 17
5 6 6 6
total 4 16 20 17 57
B. distributi marginales
e sont les distributions relatives à la seul variable X ou Y
- la répartition des logements selon le nombre de pièces (X)
Nbre de pièces (x) Nbre de logement
ons
C
a
1 4
2 18
3 12
4 17
5 6
total 57
Cette distribution qui concerne la seule variable x est appelée distribution marginale
on la tro à la marge du tableau statistique)
peut calc la moyenne de cette distribution, (et sa signification est le nbre de
es moyen ar logement)
oyenne ap lée moy.marginale notée
(car uve
On uler
pièc ne p
M pe
b- la réparti des logements selon la superficie :
superficie y Nbre de logemen
tion
ts
10-30 4
30-50 16
50-70 20
70-80 17
- 59 -

total 57
Cette distribution qui concerne la seule variable ‘ y’ est appelée distribution marginale
on peut calculer la moyenne (qui exprime la surface moy des logements) appllée
moy.marginal notée
C. Les distributions conditionnelles :
On appelle distribution Conditionnelle la distribution ou l’on a posé une condition sur
l’une des variables.
lles relatives au caractère x que
Ex : Réparation de logements de 30-50m
Cette distribution est appelée Distribution Conditionnelle parce que l’on ne s’intéresse
qu’aux logements qui satisfont la condition de surface 30-50 m2.
On peut calculer la moyenne de cette distribution (c-a-d le nombre moyen de pièces
des logts de 30-50 m2) on appelle cette moyenne : moyenne conditionnelle.
Dans cet exercice on calcule
ns conditionne
Remarque il existe autant de distributio
le caractère y a de modalités
2- généralisation du tableau de contingences :
x y Y1 Y2 ………. Yj ………. Ym total
X X X
11 12 ………. X1j
1 ………. X1m X1.
X2 X21 … ………. X2j ………. X2m X2.
… … ………. … ………. … …
Xi Xi1 Xi2 ………. Xij ………. Xim Xi.
… … … ………. … ………. … …
Xk Xk1 Xk2 ………. Xkj ………. Xkm Xk.
total x.1 x.2 ………. x.j ………. x.m x..
x1 x2 . . . xk = les modalités de x
1 y2 . . . yk = les modalités de y
y
x1 .effectifs pour la 1ére modalités de x et pour toutes les modalités de y
La distribution marginale de X :
X(xi) Xi.
X1 X1.
X2 X2.
. .
. .
Xi Xi.
Xk Xk.
Total X..
- 60 -

La distribution marginale de y :
Distribution conditionnelle relatif à X et à Y
Dist. Conditionnelle relative à X Dist. Conditionnelle relative à Y
X Xij
X1 X1j
X2 X2j
. .
. .
Xi Xij
Xk Xkj
Total X.j
3- La régression linéaire
A. Présentation du problème :
Soit le tableau suivant :
Ce tableau est un tableau de contingence ou les observations sont connues
individuellement,
On peut présenter plus simplement ce tableau de la manière suivante :
y Xij
y1 Xi1
y2 Xi2
. .
. .
yi Xij
ym Xim
Total Xi.
- 61 -

Nous avons un ensemble de points « un nuage statistique »qui nous indique que les
prix estles quantités évoluent selon la même tendance.
i sont inconnus et qu’il
de régression
ssion c’est le fait de relier y à x par une fonction
Calcule des paramètres de la droite de régression :
B. la méthode des moindres carrés
Il est possible de schématiser ce nuage :
-Par une fonction simple : la fonction linéaire (Droite) qu
faudra trouver.
a=pente de droite
b=ordonnée à l’origine
Une telle droite est appelée droite de régression D(x)
fficient
A=coe
a régre
L
Notion de moindres carrés :
Partons d’un nuage statistique théorique :
- 62 -

C. Calcul des paramètres de la droite de régression.
- 63 -

- 64 -

ans le paragraphe précédent, nous avions estimé y en fonction de x, et nous avions
btenu la droite de régression Dy(x)
atistique estimer x en fonction de y, et trouver la droite
de régression Dx(y) lui aura pour équation.
4- la corrélation linéaire :
D
o
On peut pour le même nuage st
Pour toute yi, nous avons une valeur observée xi.
Pour toute yi, nous avons une valeur estimée sur la droite x’i
Pour toute yi, nous avons une erreur d’estimation égale à | xi – x’i |
ve
Dx(y) idéale est tel que : ∑ | xi – x’i | minimum ou encore ∑ (xi – x’i) 2 minimum
En procédant de la même manière que dans le paragraphe précédent, on trou
l’équation de
Dx(y).
- 65 -

- 66 -

Si on appelle coéff de corrélation la Quantité r tel que : r2
= a . a’, on peut écrire :
• Si r = ±1 on a une corrélation parfaite.
• Si r = +1 on a une corrélation parfaite positive.
• Si r = -1 on a une corrélation parfaite.
d les variables varient dans le même sens.
• Si r = 0 = corrélation nulle.
Application : calculer le coefficient de corrélation d’une autre façon (existe-t-il
un lien entre y et x).
Corr. positive : c à
• Si r = -1 = corrélation parfaite négative.
rient en sens inverse.
C à d les deux phénomènes va
Par exemple Prix et Quantité
, e le est d’a
• Si 0 < r < 1 = la corrélation est positive l utant plus forte que l’on se
rapproche de 1.
• Si -1 < r < 0 = la corrélation est négative, et elle est d’autant plus forte que l’on se
rapproche de -1.
- 67 -

On a une très forte corrélation car r = 0.975 tend vers 1
Remarque : lorsqu’on écrit r2
= a. a’ r = racine a .a’, nous avons une expression très
positif. Comment trouver alors le signe d’une corrélation ?
Réponse : le sens de la corrélation est donnée par le signe de a et a’.
• Si a et a’ sont >0 le produit a.a’ >0 : corrélation positive.
• Si a et a’ sont <0 le produit a.a’>0 :corrélation négative.
On peut dire d’une corrélation qu’elle est très satisfaisante à partir 0.86.
On peut dire d’une corrélation qu’elle parfaite à partir de 0.96.
Formule développée
– Autre formule de r :
- 68 -

Si on appelle : covariance de x et de y l’expression :
IX- Analyse Des Séries Chronologiques.
A. Définition :
B. les différentes composantes d’une série chronologique.
1 – Généralités :
Une série chronologique est une série où les observations de la variable sont faites à
des intervalles réguliers de temps.
Soit la série chronologique suivante : Evolution trimestrielle du chiffre d’affaire d’une
entreprise
trimètres 1 2 3 4
1998 120 148 155 120
1999 130 162 169 132
2000 144 178 186 145
2001 157 196 210 160
Représentation graphique de la série :
- 69 -

L’examen d’une série chronologique révèle l’existence de différences composantes :
Un mouvement de tendance longue (à long terme), appelée « trend ».
Un mouvement saisonnier qui est les variations saisonnières.
:
s variations
ge » de la série est appelée Ajustement. Les 2
stement les plus utilisés sont :
A. la méthode des moyennes mobiles :
1
Des variations accidentelles : ce sont des variations imprévisibles dues à des
circonstances exceptionnelles.
C. intérêt d’une analyse d’une série chronologique
L’analyse des séries chronologiques permet de séparer le mouvement de long terme du
mouvement saisonnier, ce qui nous permettra de faire des calculs de prévision.
2 – l’analyse de la tendance longue : « trend »
Déterminer le trend, cela revient à «
saisonnières, cette technique de « lissa
lisser » la série pour éliminer le
méthodes d’aju
La méthode des moyennes mobiles.
L’ajustement analytique.
Elle consiste à diviser un nuage statistique en « sous – nuages » comprenant chacune
(n–1) données du sous nuages précédent, et à remplacer chaque sous nuage par un
point tel que : x’i = médiane des xi – yi = moyenne des valeurs yi
B. Opérations sur les matrices :
– matrices transposées :
2 – L’addition :
- 70 -

3- Multiplication par un réel :
X- Les Probabilités et l’analyse combinatoire
1- Le modèle probabiliste
Voici les premières phrases d'un manuel : "La théorie des probabilités est une science
mathématique étudiant les lois régissant les phénomènes aléatoires. Un phénomène est
aléatoire si, reproduit maintes fois, il se déroule chaque fois un peu différemment, de
sorte que le résultat de l'expérience change d'une fois à l'autre d'une manière aléatoire,
imprévisible."
L'usage même du mot expérience sous-entend que le phénomène aléatoire est observé
t être
hacun
des résultats possibles est observé avec une certaine fréquence dont la valeur se
aléatoire, on note W l'ensemble de tous les résultats
s A, on dit que A est réalisé.
par le biais d'un critère bien défini, et que le résultat de cette observation peu
décrit sans ambiguïté. L'expérience peut aussi être répétée, et on suppose que c
stabilise si on répète l'expérience maintes et "maintes fois". C'est cette "loi" que
présuppose l'existence d'un modèle probabiliste.
Ce premier chapitre est une rapide présentation du cadre formel des modèles
Probabilistes.
A- Evènements
Etant donnée une expérience
possibles de cette expérience.
Un singleton de Ω est appelé évènement élémentaire.
Un sous-ensemble A de Ω est appelé un évènement. Un évènement A est donc un
Ensemble constitué de résultats possibles de l'expérience. Si le résultat d'une
expérience est dan
- 71 -

On tire une boule dans une urne contenant 2 boules blanches, 1 noire, 4 vertes, 5
rouges, et on regarde sa couleur. Si on répète cette expérience, la fréquence avec
B- Loi de probabilité, espace de probabilité
- 72 -

laquelle on obtient une boule rouge se stabilise peu à peu sur une valeur, égale ici à
5/12. On dit couramment qu'on a 5 chances sur 12 de tirer une boule rouge. Dans le
cadre d'un modèle mathématique de cette expérience aléatoire, on dira que
t
L'additivité
'on a 5 chances sur 12 de tirer une boule rouge et 2
ule soit
t seulement que si on tire une boule, on a 100% de
l'évènement "tirer une boule rouge" a la probabilité 5/12. Plus généralement, dans un
modèle probabiliste, chaque évènement est pondéré par un nombre compris entre 0 e
1, sa probabilité. Ces probabilités doivent respecter certaines règles de compatibilité,
naturelles si on les interprète en termes de "nombre de chances sur 100".
est la principale de ces règles. Appliquée à un cas particulier dans notre exemple, elle
exprime simplement que, puisqu
chances sur 12 de tirer une blanche, on a 5+2 chances sur 12 de tirer une bo
rouge soit blanche. L'autre règle di
chances de …tirer une boule…
Définition 1 Soit Ω un ensemble. Une loi de probabilité P sur Ω est une fonction qui à
tout évènement A associe un nombre réel P(A), et qui a les trois propriétés :
Exemple 1 : On lance un dé et on observe la face du dessus. On posera :
et on supposera que le dé est parfaitement équilibré, de sorte que la probabilité d
chaque face est la même :
e
Remarquo le en utilisant la
propriété des trois
ensemble
ns qu'alors, la probabilité de tout évènement est calculab
c) de la définition. Par exemple, comme {1, 3, 4} est la réunion
s 2 à 2 incompatibles {1}, {3} et {4}, on a :
Plus généralement, soit Ω un ensemble fini :
Définir une loi de probabilité P sur Ω revient à se donner n réels positifs ou nuls p1,
p2, ...., pn tels que et à poser, pour tout indice k, P({wk}) = pk. La loi de
probabilité sur Ω est alors complètement déterminée car, étant donné un évènement
osent A.
A, P(A) est calculable en additionnant les probabilités pk de chacun des évènements
élémentaires {wk} qui comp
- 73 -

Il en est de même si Ω est un ensemble dénombrable, les sommes finies sont alors
remplacées par les sommes de séries.
Exercice 2 : Soit (Ω, P) un espace de probabilité. Répondre aux questions en utilisant la
définition 1 :
a) Si A est un évènement de probabilité P(A) connue, que vaut P(Ac) ?
et P(B).
Montrer que P(A ou B) £ P(A)+P(B). Généraliser cette inégalité à un nombre fini
d'évènements.
On pourrait aussi démontrer les propriétés suivantes :
b) Si A B, comparer P(A) et P(B).
c) Calculer P (A ou B) en fonction de P(A et B), P(A)
d)
C- Le cas où les évènements élémentaires sont équiprobables
Soit (W, P) un espace de probabilité correspondant à une expérience aléatoire dont
l'ensemble des résultats possibles est fini :
Supposons que chaque résultat "a autant de chances d'être réalisé qu'un autre", soit, en
termes probabilistes, que P est telle que :
Comme la somme de ces n nombres est 1, leur valeur commune est égale à 1/n . Soit
maintenant un évènement A. Sa probabilité est :
Cette loi de probabilité est souvent appelée loi uniforme sur Ω. Calculer des
ient donc à dénombrer des
e sait pas lire prend les 6 jetons d'un jeu de
osaient le mot "CARTON". Il réaligne ces jetons au hasard. Avec
ecompose-t-il ce mot ? Même question s'il a pris les 8 jetons qui
ot "INSTITUT".
p
e
robabilités par une méthode directe dans ce cas rev
nsembles.
Exercice 3 : Un jeune enfant qui n
Scrabble qui comp
quelle probabilité r
composaient le m
- 74 -

Exercice 4 : 20 sujets sont au programme d'un oral d'examen. Le candidat tire au sort
3 de ces sujets et traite l'un de ces trois. Combien doit-il avoir révisé de sujets pour
avoir au moins 9 chances sur 10 de pouvoir traiter un sujet qu'il a révisé ?
Remarque sur le choix du modèle probabiliste
Comme dans tout problème de modélisation, il n'y a pas d'automatisme qui permette
reprenons l'exemple de l'urne
introduisant le paragraphe 2. Deux modèles peuvent être considérés comme naturels :
- On peut distinguer les 12 boules contenues dans l'urne en posant :
d'associer un espace de probabilité à une expérience aléatoire "concrète". Même dans
des cas d'école, il n'y a jamais un seul "bon" choix :
D- Exercices
Exercice 5 : Soit (Ω, P) un espace de probabilité, et soient A et B deux évènements.
Montrer que si P(A) = P(B) = 0,9 , alors, P(A B) ≥ 0,8 .
groupe de n personnes, auxquelles on a
b) Avec quelle probabilité sont-ils distants de r places, c'est-à-dire séparés par r-1
personnes. Représenter ces probabilités par un diagramme en bâtons.
Dans le cas général, montrer que P(A B) ≥ P(A)+ P(B) - 1 .
Exercice 6 Deux personnes sont tirées au sort dans un groupe de 30 composés de 10
femmes et 20 hommes. Avec quelle probabilité ces deux personnes sont-elles des
hommes ? Avec quelle probabilité sont-elles des femmes ?
font partie d'un
Exercice 7 Deux amis
distribué au hasard des numéros d'ordre pour constituer une file d'attente.
a) Avec quelle probabilité sont-ils les deux premiers ?
- 75 -

Exercice 8 Un tiroir contient en vrac les 20 chaussettes de 10 paires différentes. On
en sort au hasard 4 chaussettes. Avec quelle probabilité obtient-on :
a) 2 paires b) au moins une paire
2- Probabilités conditionnelles
A- Définition
Lançons un dé parfaitement équilibré. Un bon modèle probabiliste en est donné par :
muni de la loi de probabilité P uniforme.
cette nouvelle expérience, l'évènement A est réalisé quand on obtient un 5, et c'est
Notons A l'évènement "le dé donne au moins 4 points" et B l'évènement "le résultat
est impair". Supposons qu'on ne retienne le résultat du lancer que s'il est dans B. Dans
avec la probabilité relative
Plus généralement la probabilité relative de A sous la
condition que B est réalisé est . On l'appelle aussi probabilité de A sachant
que B, ou probabilité conditionnelle de A relative à B, etc…
Définition : Soit (Ω, P) un espace de probabilité, et soit B un évènement tel que
P(B) ≠ 0. La probabilité de A sachant que B est notée P(A | B), et est définie par :
Exercice 9 : a) Soit B un évènement tel que P(B) ≠ 0. Montrer que l'application qui
à A associe P( A | B ) est une loi de probabilité sur Ω.
0,
b) Donner une propriété de A qui implique P(A | B) = 1, qui implique P(A | B) =
qui implique
Exercice 10 : Un couple a deux enfants. Sous l'une des conditions suivantes :
ants est un garçon,
avec quelle probabilité le couple a-t-il un fils et une fille ?
B- Deux résultats de décomposition
Les deux résultats de ce paragraphe utilisent "à l'envers" la définition 2-1, c'est-à-dire
donnent un moyen de calcul de probabilités connaissant des probabilités conditionnelles.
Ils sont très utiles dans la pratique.
a) l'aîné est un garçon,
b) l'un des enf
Exemple: Une urne contient deux boules blanches et une boule noire. Une personne
tire une boule et la garde, une deuxième personne tire une boule. Avec quelle probabilité
les deux boules tirées sont-elles blanches ? On peut répondre à cette question en utilisant
la définition.
- 76 -

En effet, notons A l'évènement "la première personne a tiré une boule blanche" et B
l'évènement "la deuxième personne a tiré une boule blanche". D'après la définition, P (A
et B) = P (B | A) P(A). Mais P(A) est connue, c'est 2/3. P(B | A) est aussi connue : c'est
ière personne ayant tiré une boule blanche, la deuxième personne tire une
oule au hasard dans une urne qui contient une boule blanche et une boule noire. Ainsi,
P(A et B) vaut (2/3).(1/2) = 1/3 .·
alise
ce procédé de calcul :
Proposition
1/2 car, la prem
b
La proposition suivante, parfois appelé "théorème des probabilités composées", génér
: Soit (Ω, P) un espace de probabilité, et soient A1, A2,…, An des
évènements. On a :
Cet énoncé est constamment utilisé dans le contexte des "chaînes de Markov", qui
Interviennent naturellement dans les problèmes concrets où A1, A2,…, An représente une
succession (temporelle) d'évènements, la probabilité de réalisation du n-ième évènement
An étant conditionnée par "le passé" (probabilité sachant que A1 et … et An-1 ont eu
lieu).
En voici un exemple simple :
Exercice 11: On sait que si le flash d'un appareil photo n'a pas eu panne durant les n
premiers déclenchements (n entier positif ou nul), la probabilité pour qu'il fonctionne au
(n+1)-ième est égale à p (0 < p <1 ).
a) Quel est la probabilité pour qu'il n'ait pas de panne au cours des 100 premiers
déclenchements ?
b) Sachant qu'il a fonctionné n fois, avec quelle probabilité fonctionnera-t-il au moins 100
fois de plus ?
ossibles Ω. En termes ensemblistes, {C1, C2, …, Cn} est
donc une partition de Ω ; en termes probabilistes, on l'appelle un système complet
d’évènements. Soit A un évènement. On a bien sûr :
Soient C1, C2, …, Cn n évènements deux à deux disjoints et dont la réunion est
l'ensemble de tous les résultats p
et en utilisant la définition, on obtient le résultat :
Proposition: Soit (Ω, P) un espace de probabilité, et soit {C1, C2, …, Cn} un système
complet d'évènements. Soit A un évènement. On a :
(Remarquons sans démonstration que ce résultat se généralise à un système complet
INSEE 1994), la population active en
dénombrable d'évènements.)
Exercice 12: En mars 1994 (enquête sur l'emploi
- 77 -

France comprend 44,7% de femmes. Le taux de chômage chez les hommes est 10,8% ; il
est chez les femmes 14,3% . On tire au sort une personne parmi les actifs.
a) Avec quelle probabilité est-elle au chômage ?
b) Sachant qu'elle est au chômage, avec quelle probabilité est-ce une femme ?
C- Evènements indépendants
Définition :
Exercice 13
mpatibles sont-ils indépendants ?
c) Par un diagramme donner un exemple d'évènements A, B, C deux à deux
indépendants
Mais qui ne sont pas indépendants dans leur ensemble.
Remarque
: a) Montrer que si A et B sont indépendants, A et Bc, Ac et B, Ac et Bc
le sont aussi. Généraliser cette remarque au cas d'une famille finie d'évènements
indépendants dans leur ensemble.
b) Deux évènements A et B inco
: Lançons deux dés, chacun parfaitement équilibré. L'ensemble des résultats
Possibles est :
Notons A l'évènement "le premier dé donne 4". Comme le premier dé est
parfaitement équilibré, la probabilité de A est 1/6. Notons B l'évènement "le deuxième
dé donne 6".
Comme le deuxième dé est parfaitement équilibré, la probabilité de A est 1/6. De plus,
nous pouvons sans difficulté supposer
D
que les évènements A et B sont indépendants.
la loi uniforme sur Ω pour représenter l'expérience
odèle
n fois de façon indépendante, on choisira
onc, la probabilité de (A et B), c'est-à-dire de l'évènement élémentaire (4, 6), est égale
à (1/6).(1/6) = 1/36, et de même bien sûr pour tout autre couple (i, j). Ce
e le choix de
raisonnement confirm
aléatoire du lancer de deux dés.
lle probabilité la somme des points
Exercice 14 : On lance deux dés. Avec que
obtenus est-elle égale à 11 ? à 10 ?
ent, considérons une expérience aléatoire dont (Ω, P) est un m
Plus généralem
probabiliste. Si cette expérience est répétée
- 78 -

comme ensemble de résultats ~Ω = Ωn , qu'on munira de la probabilité produit ~P, c'est
à- dire telle que, quels que soient les sous-ensembles A1, A2,…, An de Ω :
D- Exercices
Exercice 15 : Avec quelle probabilité une famille de 3 enfants comporte-t-elle au
moins un garçon ?
Exercice 16 : Dans un groupe de 20 personnes, quelle est la probabilité pour qu'il n'y
ait jamais plus d'un anniversaire par jour ? Et dans un groupe de 50 personnes ? (on
fera comme si toutes les années avaient 365 jours).
Exercice 17 : Une expérience est conduite pour étudier la mémoire des rats. Un rat est
mis devant trois couloirs. Au bout de l'un d'eux se trouve de la nourriture qu'il aime,
au bout des deux autres, il reçoit une décharge électrique. Cette expérience élémentaire
est répétée jusqu'à ce que le rat trouve le bon couloir. Sous chacune des hypothèses
s
enir des expériences antérieures,
abilité la première tentative réussie est-elle la k-ième ? Représenter
graphiquement les réponses.
Exercice 18 : Pour décider d'un traitement thérapeutique, on utilise un test qui est
positif 99 fois sur 100 si une personne est effectivement malade. Mais si une personne
n'est pas malade, le test est positif une fois sur 100. On sait par ailleurs que 5
personnes sur 100 ont cette maladie.
a) Si le test d'une personne est positif, avec quelle probabilité cette personne est-elle
effectivement malade ?
b) Si le test d'une personne est négatif, avec quelle probabilité cette personne n'est-elle
effectivement pas malade ?
Calculer ces probabilités quand on sait que 5 personnes sur 1000 ont cette maladie.
Exercice 19 : La probabilité de fermeture du relai i des circuits décrits ci-dessous est
pi.
B ?
uivantes :
(H1) le rat n'a aucun souv
(H2) le rat se souvient de l'expérience immédiatement précédente,
(H3) le rat se souvient des deux expériences précédentes,
avec quelle prob
Tous les relais
est la probabilit
fonctionnent indépendamment. Dans chacun des cas suivants, quelle
é pour que le courant passe entre A et
a) A et B sont séparés par n relais reliés en série.
b) A et B sont séparés par n relais reliés en parallèle.
c)
- 79 -

d)
Exercice 20 : On transmet un message composé de n symboles binaires '0' ou '1'. Lors de
la transmission, chaque symbole est perturbé avec la probabilité p et se transforme alors
en symbole opposé. Par précaution, le message est transmis deux fois. Si les deux
messages transmis coïncident, l'information est considérée comme correcte.
a) Avec quelle probabilité le i-ième symbole du premier message transmis est-il identique
robabilité les deux messages transmis sont-ils identiques ?
c) Trouver la probabilité pour que, malgré la coïncidence des deux messages,
l'information s'avère erronée. (Application numérique : n = 100 p = 0,001).
Exercice 21 : Un candidat d'un jeu télévisé américain est face à trois portes. Derrière
l'une d'elles se trouve le prix, - une voiture -. Le candidat se place devant la porte de son
choix. Le présentateur de l'émission, qui lui sait où se trouve la voiture, ouvre alors l'une
des deux autres portes et indique au candidat que la voiture ne s'y trouve pas. Le candidat
peut à son tour ouvrir une porte. S'il découvre la voiture, il la gagne.
Un candidat décide d'adopter l'une des trois stratégies suivantes :
a) ouvrir la porte devant laquelle il s'est placé à l'issu de son premier choix,
b) ouvrir l'autre porte,
c) tirer à pile ou face et, s'il obtient pile, ouvrir la porte devant laquelle il s'est placé à
l'issu de son premier choix, ouvrir l'autre porte s'il obtient face.
L'une de ces trois stratégies est-elle préférable aux autres ?
X
A
Dans beaucoup de situations, le détail du résultat d'une expérience aléatoire ne nous
intéresse pas, mais seulement une valeur numérique fonction de ce résultat. Par
exemple, on peut se demander quel est le nombre de pannes d'un ordinateur sur une
du lancer des deux dés :
au i-ième symbole du deuxième message transmis ?
b) Avec quelle p
I- Les variables aléatoires
1- Généralités
- Définitions
durée d'un an, sans être intéressé par les dates auxquelles ont lieu ces pannes. Etudions
un exemple plus simple :
Exemple: On lance deux dés, et on regarde la somme des points obtenus. On choisit
pour modèle probabiliste
- 80 -

muni de la loi de probabilité P uniforme, qui affecte à chaque évènement élémentaire
(i, j) la probabilité P{(i, j)} = 1/36. Avec quelle probabilité la somme des points
obtenus est elle égale, par exemple, à 5 ? C'est la probabilité de l'ensemble des
évènements élémentaires (i, j) qui réalisent cette condition.
par :
La question posée est le calcul de la probabilité de l'évènement { (i, j)∈Ω / S(i, j) = 5
},c'est-à-dire de l'évènement { (1, 4), (2, 3), (3, 2), (4, 1) }. On notera cet évènement, de
façon simplifiée, { S = 5 }. On trouve :
Remarquons que S prend ses valeurs dans {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} et que, par
conséquent :
Abordons maintenant le cas général, dans lequel l'ensemble des valeurs prises par une
variable aléatoire n'est pas forcément fini ou dénombrable :
Définition: On appelle variable aléatoire une application X définie sur un espace de
probabilité (Ω, P) et à valeurs réelles.
Exercice 22 : Représenter la fonction de répartition de la variable aléatoire S de
l'exemple
Exercice 23 : Soit X une variable aléatoire, e soit F sa fonction de répartition. Pour a et
b réels (a < b), exprimer en fonction de F :
P( X > a ), P( a < X ≤ b ),
P(X < a ) (utiliser la proposition 1-1-b), P( X ≥ a), P( X = a ), P( a ≤ X < b ), …
t
- 81 -

Exercice 24: Soit X une variable aléatoire. On suppose que sa fonction de répartition
F est donnée par :
B- Variables aléatoires discrètes, variables aléatoires à densité
- 82 -

Exercice 25: On fait tourner une aiguille autour d'un axe et on repère la position sur
laquelle elle s'arrête par un angle Θ de [0, 2π[.
a) Quelles valeurs proposer pour P( 0 ≤ Θ < π ), P( π ≤ Θ < 2π ), P( π/2 ≤ Θ < 3π/2 ) ?
Et pour P(Θ∈I) lorsque I est un sous-intervalle de [0, 2π[ ?
b) Peut-on proposer une fonction f qui soit la densité de la loi de Θ ?
Remarquons que si X est une variable aléatoire à densité, la densité f vérifie
nécessairement :
Exercice 26 : Soit X une variable aléatoire à densité f définie par :
Exercice 27 : Reprendre l'exemple de l'exercice 24, et montrer qu'on peut écrire :
où f est une fonction à déterminer.
C- Couples de variables aléatoires
- 83 -

Exercice 28 : Soient (X, Y) un couple de variables aléatoires dont la loi est telle que, si
i et j sont deux entiers tels que
D- Variables aléatoires indépendantes
Définition: Soient X et Y deux variables aléatoires définies sur un espace de probabilité
(Ω, P). On dit qu'elles sont indépendantes si pour tout couple (A, B) de sous
Exercice 29 : a) Soient (X, Y) un couple de variables aléatoires de loi donnée par :
X et Y sont-elles indépendantes ?
b) même question avec les données de l'exercice 28
ercice 30
Ex
- 84 -

Dans le cas général, on montre la proposition :
bles aléatoires définies sur un espace de
FY. X et Y sont indépendantes si et
seulement si, pour tout couple (x, y) de réels :
Proposition 1: Soient X et Y deux varia
probabilité (Ω, P), de fonctions de répartitions FX et
Le résultat suivant est utile :
Enonçons enfin une extension de la définition :
E- Exercices
: On équipe un local souterrain de 5 ampoules électriques. On suppose
ue les durées de vie de ces ampoules sont des variables aléatoires indépendantes, et
e même densité f donnée par :
Exercice 31
q
d
On contrôle l'état des ampoules après 300 heures d'utilisation. Avec quelle probabilité
sont-elles hors d'usage.
: Une boîte contient 5 transistors, dont on sait que 3 sont défectueux. On
ste l'un après l'autre les transistors et on les met de côté, jusqu'à avoir trouvé les
éfectueux. On note N1 le nombre de tests effectués pour trouver le premier
deux (exactement) des ampoules
Exercice 32
te
d
- 85 -

transistor défectueux, et N2 le nombre de tests complémentaires effectués pour
ouver le deuxième.
écrire la loi conjointe de N1 et N2.
: Soient X1,…, Xn des variables aléatoires indépendantes et suivant toutes
loi uniforme sur [0, 1]. On pose :
= max (X1,…, Xn)
) Quelle est la fonction de répartition de M ? Quelle est la densité de la loi de M ?
es questions avec min (X1,…, Xn).
- Caractéristiques numériques des variables aléatoires
- Espérance
tr
D
Exercice 33
la
M
a
b) Mêm
2
A
Exercice 34: Quelle est l'espérance de la variable aléatoire qui représente le nombre de
: Quelle est l'espérance de la variable aléatoire de l'exercice 3-4 ?
: Dans chacun des deux cas suivants, calculer E(X), décrire la loi de X2 et
Calculer E(X2) :
points obtenus en lançant un dé ?
Exercice 35
Exercice 36
- 86 -

Exercice 37 : Reprendre les exemples de l'exercice 4-3 et calculer E(X2) en utilisant la
L'énoncé suivant ser r la suite :
éatoires sur un espace de probabilité
proposition 1.
a très utilisé pa
Proposition 2 : Soient X et Y deux variables al
(Ω, P), et soient a et b deux réels. Alors :
Exercice 38 : Montrer la deuxième égalité de cette proposition dans le cas où les lois
s, et on note S la varia eprésente la
somme des points obtenus. Quelle est l'espérance de S ?
de X et Y sont discrètes.
Exercice 39 : On lance deux dé ble aléatoire qui r
B- Variance, covariance
Exemple: Considérons les quatre variables aléatoires :
X1 = 0, c'est-à-dire la variable "aléatoire" constante et nulle
e sur [-1, 1]
X3 de loi uniforme sur [-100, +100]
(T=2000) = P(T=4000) = ¼
pour espérance 0, mais leurs lois sont clairement différentes. Une
tingue est l'étalement, la dispersion, des valeurs qu'elles prennent
,
X2 de loi uniform
X4 telle que P(T=-3000) = 1/2 P
Elles ont toutes quatre
caractéristique qui les dis
autour de leur valeur moyenne E(Xi) = 0. Une façon de mesurer cette dispersion est de
regarder la valeur moyenne de la distance entre Xi et E(Xi). Pour des raisons pratiques, on
- 87 -

préfère choisir la valeur moyenn ntre Xi et E(Xi), qu'on appelle
la variance.
Définition
e du carré de la distance e
: Soit X une variable aléatoire sur un espace de probabilité (Ω, P). La variance
ν(X) de X est :
Exercice 40 : Calculer les variances des variables aléatoires Xi de l'exemple Précédent
Exercice 41 : On lance un dé, et aléatoire qui représente le
nombre de points obtenus. Quelle est la variance de X ?
Proposition 3 : Soit X une variable aléatoire.
on note X la variable
Appelle la variable aléatoire centrée réduite associée à X. Le passage de l'une des variables à
l'autre se fait tout simplement par un changement d'origine et d'unité dans l'ensemble
rises par X.
iance d'une variable aléatoire n'est manifestement pas linéaire. De
Exemple 2: Soit par exemp e non nulle, - c'est-à-dire
qui n'est pas presque sûrement constante -. On a :
des valeurs p
L'expression de la var
fait, si X et Y sont deux variables aléatoires sur (Ω, P), en général, la variance de la
somme X+Y n'est pas égale à la somme des variances de X et de Y :
le X une variable aléatoire de varianc
Calculons dans le cas général ν(X+Y). Comme :
- 88 -

Proposition 4 : Soient X et Y deux variables aléatoires sur (Ω, P). Si X et Y sont
indépendantes, alors :
Exercice 42: Démontrer la proposition dans le cas où les lois de X et Y sont discrètes.
Exercice 43 : On lanc qui représente la
somme des points obtenus. Quelle est la variance de S ?
Une caractéristique souvent utilisée en statistiques est un coefficient appelé coefficient de
corrélation de deux variables aléatoires X et Y. C'est par définition, - et si ni X ni Y n'est
presque sûrement constante - :
e deux dés, et on note S la variable aléatoire
- 89 -

C- Exercices
Exercice 44 : Calculer l'espérance et la variance de la variable aléatoire M de l'exercice
33
Exercice 45 : Les transistors fournis par une usine sont défectueux dans la proportion
p. On teste un transistor après l'autre jusqu'à en obtenir un bon. On note N le nombre
de tests effectués. Quelle est la loi de N ? Calculer l'espérance de N.
és fonctionnent. Le procédé de construction des sous-unités est
tel qu'elles sont défect amment les unes des
autres.
i
constituée. Si elle ne marche pas, on la jette, et on recommence jusqu'à obtenir une
bonne machine.
On note : cu le coût de construction d'une sous-unité,
tu le coût du test d'une sous-unité,
tm le coût du test d'une machine,
t on suppose pour simplifier que le coût d'assemblage des unités est nul.
1) On note C le coût de construction d'une bonne machine. Calculer l'espérance de C
dans les deux cas a) et b).
Exercice 46 : Une machine est constituée de n sous-unités identiques. Elle fonctionne
si toutes ses sous-unit
ueuses dans la proportion p, et indépend
Pour construire une machine sans défaut, deux procédés sont envisagés :
a) On construit une sous-unité, on la teste, si elle est bonne, on la monte, sinon, on la
jette, etc… On continue jusqu'à avoir monté les n sous-unités de la machine. On
suppose pour simplifier qu'il n'y a pas de problème de montage. La machine ainsi
construite est donc bonne.
b) On construit et monte sans les tester n sous-unités, et on teste la machine ains
e
3-Variables aléatoires usuelles
ropriétés d es lois con pourra trouver beaucoup
dans la "litté : les loi étriques (exercice 45),
ue, multinomiale, gamma, etc…, et nous en in s d'autres dans la partie
Voici une liste de définitio
classiques
ns et p e quelqu nues. On
d'autres lois
iq
rature" s géom
hypergéométr
"statistiques"
troduiron
de ce cours.
A-
- 90 -

B-
Exercice 47 : On lance 4 fois un dé. On note X le nombre de fois où on obtient 6.
a) Pour k = 0, 1, 2, 3, 4, calculer P(X = k).
b) On note Xi la variable de Bernoulli qui vaut 1 si on tire un 6 au i-ième lancer, 0 si
on ne tire pas 6 à ce lancer. Ecrire X en fonction des Xi , et en déduire la valeur de
E(X) et de n(X).
C- Loi uniforme
Exercice 48: Soit X une variable aléatoire de loi uniforme sur [0, 1].
a) Calculer directement E(X) et n(X).
b) On pose Y = a + (b-a) X . Que valent E(Y) et n(Y) ? Quelle est la loi de Y ? Qu'en
conclut-on ?
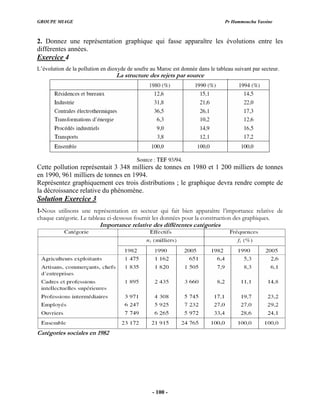
D- Loi exponentielle
Si X suit cette loi :
- 91 -

On peut remarquer aussi que pour tout t positif ou nul :
E-
F-
- 92 -

G-Exercices
- 93 -

4-Caractéristiques des lois usuelles
A-Variables aléatoires réelles discrètes
A-Variables aléatoires réelles continues
- 94 -

- 95 -

- 96 -

Exercice 1
aractères ci-dessous ?
Quelle est la nature des c
Nombre d’actions vendues chaque jour à la bourse
Indicateur du moral de
Écart de rémunération entre hommes et femmes
Les pays de l’Union européenne
Les niveaux de formation des salariés
Les formes de contrat de travail
Taux de croissance du PIB
Prix à la consommation
Solde commercial
Nombre de personnes par ménages
Exercice 2
Rémunérations des enseignants d’un lycée
s ménages
Fréquences des appels téléphoniques
1. Construisez le graphique des effectifs des appels.
2. Construisez le diagramme cumulatif.
Solution Exercice 1
Le caractère La nature
Nombre d’actions vendues chaque jour à la bourse variable discrète
Rémunérations des enseignants d’un lycée variable quantitative continue
Indicateur du moral des ménages variable qualitative
Écart de rémunération entre hommes et femmes variable quantitative continue
Les pays de l’Union européenne variable qualitative
- 97 -

Les niveaux de formation des salariés variable qualitative
Les formes de contrat de travail variable qualitative
Taux de croissance du PIB variable quantitative
Prix à la consommation variable quantitative
Solde commercial variable quantitative
Nombre de personnes par ménages variable discrète
Solution Exercice 2
1. Nous construisons un diagramme en bâtons appelé diagramme différentiel car il représente les
différentes modalités avons une variable
discrète.
Nombre d’appels par jour
de la variable. Ce diagramme s’impose puisque nous
2. Le diagramme cumulatif est également appelé diagramme intégral au sens de l’intégration
mathématique. Il représente le graphe des fréquences cumulées.
escalier », les valeurs ne sont connues q
C’est un graphique « en
même de la nature de la v
ue sur des intervalles en raison
ariable.
Tableau des appels cumulés
- 98 -

Diagramme cumulatif
Exercice 3
Les tableaux suivants fournissent des informations sur l’importance des professions et
catégories sociales dans la population active occupée en 1982, en 1990 et en 2005.
Les professions et catégories sociales
1. Donnez des représentations graphiques qui fassent apparaître l’importance relative des
différentes catégories sociales pour l’année 1982, pour l’année 1990 et pour l’année 2005.
- 99 -

2. Donnez une représentation graphique qui fasse apparaître les évolutions entre les
différentes années.
ercice
Ex 4
L’évolution de la pollution en dioxyde de soufre au Maroc est donnée dans le tableau suivant par secteur.
La structure des rejets par source
Cette pollution représentait 3 348 milliers de tonnes en 1980 et 1 200 milliers de tonnes
en 1990, 961 milliers de tonnes en 1994.
Représentez graphiquement ces trois distributions ; le graphique devra rendre compte de
la décrois
Solution Exercice 3
sance relative du phénomène.
1-Nous utilisons une r mportance relative de
chaque catégorie. Le tableau ci-dessous fournit les données pour la construction des graphiques.
Importance relative des différentes catégories
eprésentation en secteur qui fait bien apparaître l’i
Catégories sociales en 1982
- 100 -

2-Nous utilisons un diagramme qui fait apparaître les évolutions des différentes catégories sociales
pour les années étudiées.
Évolution des différentes catégories sociales
- 101 -

Ce graphique montre bien la diminution absolue du nombre des indépendants « Agriculteurs exploitants »,
« Artisans, commerçants et chefs d’entreprise », en particulier des agriculteurs, ainsi que de la catégorie «
Ouvriers ». La catégorie sociale modale en France en 2005 est celle des employés, dont nous savons par
ailleurs que le taux de féminisation est élevé. Ce graphique illustre également l’importance croissante de
la catégorie des « Professions intermédiaires » presque aussi nombreuse que celle des « Ouvriers » ainsi
que la place croissante des « Cadres ».
Solution Exercice 4
Les quantités de rejet
1980 1990 1994
Résidences et bureaux 421,8 181,2 139,3
Industrie 1064,7 259,2 211,4
Centrales électrothermiques 1222,0 313,2 166,3
Transformations d’énergie 210,9 122,4 121,1
Procédés industriels 301,3 178,8 158,6
Transports 127,2 145,2 165,3
Ensemble 3348,0 1200,0 961,0
- 102 -

Le premier graphique retenu est en « tuyaux d’orgue », il montre la forte décroissance du
volume de la pollution en dioxyde de soufre. Les modifications de l’importance relative
des sources de pollution est peu lisible.
Évolution du volume des rejets
Le volume de la pollution s’est considérablement réduit entre 1980 et 1994. Parmi les
raisons expliquant cette évolution, nous pouvons évoquer la lutte contre la pollution ,et la
diminution des activités industrielles sur le territoire Du Maroc
Pour mettre en lumière les modifications de la structure des diverses sources de rejets de
dioxyde de soufre nous utiliserons des graphiques en secteurs.
- 103 -

- 104 -

Cet ensemble de graphiques permet de voir que la réduction de la pollution n’est pas
homothétique. Très globalement, les activités de consommation (transports, résidences)
voient leur importance augmenter relativement aux rejets industriels.
La réduction importante de la pollution se traduit par une répartition différente des
principales sources de production.
Exercice 5
Soit la répartition des revenus d’une population présentée dans le tableau suivant en
Répartition des revenus
milliers de Dhs
1. Représentez cette distribution à l’aide de la fonction « histogramme » d’un tableur.
2. Construisez l’histogramme statistique de la série.
- 105 -

Exercice 6
1. À quel type de représentation graphique fait appel la pyramide des âges ?
2. Quelles réflexions vous inspirent la comparaison entre les deux pyramides ?
es à celles des femmes en 1998 ? Vos conclusions sont-
4. La population est-elle en croissance ? Justifiez votre réponse.
5. La population est-elle vieillissante ? Justifiez votre réponse.
des tranches d’âge sur la période 1970/2020.
Solution Exercice 5
3. Comparez la distribution des homm
elles les mêmes en 2020 ?
6. Représentez l’évolution
1. Nous allons tout d’abord construire l’ « histogramme » avec cette fonction d’un tableur.
Données pour « l’histogramme » du tableur
- 106 -

Nous obtenons le graphi
En quoi cette représenta
que ci-contre.
tion est-elle insatisfaisante ?
La première raison tient au fait que la représentation donne une image d’une variable
discrète, or nous avons une variable continue. La contradiction entre le caractère continu
de la variable et sa représentation graphique sous forme discrète rend sans intérêt une telle
« représentation » qui justement ne représente pas la nature de la variable.
La seconde raison du caractère insatisfaisant de cette représentation s’explique par
l’absence de prise en compte des différences dans l’amplitude des classes.
« Histogramme » selon un tableur
Cette fois encore le graphique est infidèle à ce qu’il veut représenter.
ntinu de la variable et des
mplitudes différentes.
Tableau statistique pour la construction de l’histogramme statistique
2. L’histogramme statistique va rendre compte du caractère co
a
- 107 -

Le graphique suivant rend compte du caractère continu de la variable et du fait que les classes ont
des amplitudes différentes. Cet histogramme est également construit à l’aide d un tableur mais
pas en utilisant la fonction histogramme.
Solution Exercice 6
1. Les variables représentées sont les âges des hommes et des femmes, vivant à une
date donnée. Il s’agit donc de variables continues. Les pyramides sont des
histogrammes horizontaux.
2. La comparaison entre la pyramide des âges au 1er janvier 1998 et celle qui est
prévue en 2020 montre un épaississement de la courbe des plus de 50 ans accompagné
de la disparition du creux de la génération 1915, le creux de la génération 1940 étant
encore perceptible. Les jeunes générations sont beaucoup plus lisses dans la pyramide
de 2020 car les chiffres utilisés sont des prévisions de population. On ne projette pas
une augmentation du nombre de naissances en 2020.
3. En janvier 1998, on constate qu’il naît légèrement plus de garçons que de filles mais
que, plus on avance en âge, et plus la pyramide des femmes s’épaissit par rapport à
- 108 -

celle des hommes. Les creux des deux guerres sont aussi perceptibles chez les hommes
que chez les femmes.
Ces tendances se maintiennent en 2020. On voit, toutefois, d’une façon plus nette
l’épaississement de l’histogramme des femmes pour les tranches âgées de la
population.
4. Le tableau présentant la projection de la population indique une croissance prévue
de la population à l’horizon 2020.
de des âges que globalement la population est en
ses tranches vieillissantes. Ce qui est confirmé par les chiffres
des tableaux. Nous constatons une proportion croissante des personnes de plus de 60
e la part de la population jeune (moins de 20 ans). Ce
e également par l’élévation continue de l’âge moyen de la
population.
6. Le graphique ci-contre, en bandes superposées, illustre l’analyse numérique.
Tranches d’âges sur la période 1970-2020
5. Nous voyons sur la pyrami
croissance du fait des
ans, une réduction d
vieillissement s’appréci
Exercice 7
La répartition d’une population de salariés par établissement au sein d’un bassin
d’emploi est donnée par le tableau ci-dessous.
Répartition des salariés par établissement
- 109 -

1. Construisez l’histogramme.
2. Construisez le polygone des fréquences.
Exercice 8
Nous connaissons la valeur des subventions versées à une population d’agriculteurs.
Répartition des subventions par exploitation
1. Construisez l’histogramme.
2. Construisez le polygone des fréquences.
Solution Exercice 7
1. Pour construire l’histogramme, nous élaborons le tableau statistique nécessaire.
Calculs pour l’histogramme
- 110 -

Histogramme de la distribution
2. Nous construisons l es milieux de chaque
sommet des rectangles. Les ordonnées sont les fréquences par unité d’amplitude, les
abscisses sont des centres de classe si les classes sont d’amplitude égale. Pour fermer la
courbe nous avons pris le point origine et un point qui se trouve à une distance égale à la
moitié de l’amplitude de la dernière classe. Un tableau explicite les valeurs prises.
Valeurs pour le polygone des fréquences
e polygone des fréquences en joignant l
- 111 -

Polygone des fréquences
Le polygone des fréquences donne une vision plus réaliste de la distribution en éliminant
les ruptures entre les classes. Il permet également de percevoir la dissymétrie de la
distribution.
Ce polygone de fréquences ne respecte pas le principe de la conservation des aires. Il
n’est donc pas rigoureusement satisfaisant du point de vue statistique.
Néanmoins, compte tenu de la diversité de l’amplitude des classes et de leur étendue, il
permet de fournir une première image de la distribution des fréquences.
Solution Exercice 8
1. Pour construire l’histogramme, nous élaborons le tableau statistique nécessaire.
Calculs pour la construction de l’histogramme
- 112 -

Histogramme de la distribution
2. Le polygone des fréquences représente la distribution des fréquences. Nous le
construisons en joignant les points de chaque milieu des segments de l’histogramme.
Les ordonnées sont les fréquences par unité d’amplitude, les abscisses sont des centres de
classe si les classes sont d’amplitude égale. Pour fermer la courbe nous avons pris le point
origine et un point qui se trouve à une distance égale à la moitié de l’amplitude de la
dernière classe. Un tableau explicite les valeurs prises.
Fréquences par unité d’amplitude
L’unité d’amplitude est de 10. Pour la dernière classe dont l’amplitude est de deux unités,
nous n’avons pas retenu le centre de classe, nous avons subdivisé cette classe en classes
- 113 -

ayant l’amplitude unitaire, ce qui nous conduit à créer deux classes. Nous considérons
qu’entre 65 et 75, la répartition est stable.
L’objectif est de faire en sorte que la surface du polygone des fréquences soit identique à
celle de l’histogramme.
Polygone des fréquences
Le polygone des fréquences donne une vision plus réaliste de la distribution en éliminant
la dissymétrie de la
distribution.
ercice 9
les ruptures entre les classes. Il permet également de percevoir
Ex
Les catégories socioprofessionnelles en 1989 (en milliers)
Le tableau suivant donne la répartition de la population active par catégorie
socioprofessionnelle (C.S.P.) des individus et par sexe pour une population donnée en
1989.
1. Représentez graphiquement cette double distribution.
2. Représentez les distributions conditionnelles selon diverses possibilités.
Exercice 10
Répartition des entreprises par nombre de salariés et activités au 1/1/1998 (en milliers)
- 114 -

1. Quelles sont les variables étudiées ? Quel est leur type ?
2. Proposez une représentation graphique permettant de visualiser la répartition des
activités au sein de chaque groupe de moyennes entreprises.
Solution Exercice 9
La représentation en tuyaux d’orgue est dans le cas de variables qualitatives la meilleure
représentation graphique. Plusieurs solutions sont possibles.
1. Nous représentons côte à côte les deux distributions en tenant compte des effectifs de
chaque catégorie.
Distribution des catégories selon le sexe
- 115 -

2. Dans la deuxième représentation, nous utilisons des cartouches superposées rendant
une
mieux compte de l’importance relative des actifs masculins et féminins, en gardant
représentation des valeurs absolues.
Distribution selon le sexe et la CSP
Par rapport au graphique précédent, nous constatons, entre autres, qu’il y a plus d’ouvriers
phique superposé pour représenter les distributions
ramme à cumul
Tableau des fréquences relatives
que d’employés en 1989 sans distinction de genre.
3. Nous utilisons un gra
conditionnelles suivant la catégorie sociale et le genre dans un diag
interne.
Part des femmes dans chacune des CSP
- 116 -

Cette rep entation rend sens fait que la très majorité des em s sont des
employée alors que dans les s catégories les h s sont majoritai
Solution Exercice 10
rés ible le grande ployé
s, autre omme res.
1. Nous avons un tableau croisant une variable qualitative (une nomenclature des
activités) et une variable quantitative continue (le nombre de salariés). Cette variable est
continu en équivalent plein, toutes les valeurs de la variable peuvent être
2.
bleau de la prises pour construire le graph
e car, temps
atteintes.
ique (en %)
Ta répartition des entre
Répartition des moyennes entre e en fonction
pris taill
es par du secteu ivités
r d’act
- 117 -

Répartition de toutes prises selon
les entre les secteurs
Il est clair que les très grandes entreprises n’apparaissent pas sur le graphique.
Exercice 11
Soit les éléments de l’exécution du budget ne université grenoblois
d’u e.
Donnez une représentation graphique de ces deux distributions.
- 118 -

Pour représenter cette double distribution nous utilisons deux formes de représentation :
les barres pour les recettes, et une courbe pour les dépenses.
Les taux d’exécution budgétaires
Exercice 12
Exercice 13
- 119 -

- 120 -

- 121 -

Exercice 14
- 122 -

Exercice 15
Les renseignements f 100 res sociation sortie ont été consignés
dans les tableaux suivants :
Tableau N° 01
ournis par 0 memb d’une as
:
Tableau N° 02
T ° 03
ableau N
- 123 -

1/ Préciser la population étudiée et sa taille.
2/Préciser le caractère, la nature de caractère, le nombre de modalité dansles tableaux ci-
valeur 51, 114,105 ?
dessus.
3/Interpréter la
4/ Calculer les fréquences pour les trois tableaux ?
Exercice 16
- 124 -

olutio ice 15
S n Exerc
Solution E cice
xer 16
- 125 -

Qualification socioprofessionnelle
Exercice 17
- 126 -

Exercice 18
Exercice 19
- 127 -

- 128 -

Histogramme
- 129 -

Courbe Cumulative croissante et décroissante
Exercice 20
Soit le tableau suivant relatif au nombre d’enfants par famille:
- 130 -

Exercice 21
Exercice 22
- 131 -

- 132 -

- 133 -

Exercice 23
- 134 -

Exercice 24
Exercice 25
- 135 -

Évolution des entrées entre 2000 et 2010
Evolution des ventes trimestrielles pendant les 7 Années
- 136 -

Tableau des calculs
- 137 -

- 138 -

Exercice 26
Le poids des tomates produites par un jardini béit à une loi normale de moyenne
200 gr et d'écart type 40 gr.
a. Calculez la prob que le poids d'une tomate excède 250 gr.
b. Calculez la prob que le poids d'une tomate soit inférieur à 100 gr.
c. Calculez la prob que le poids d'une tomate soit inférieur à 230 gr.
d. Calculez la prob que le poids d’un mate ne s’écarte pas de la valeur
moyenne de plus de 20 gr.
Solution Exercice 2
er o
abilité
abilité
abilité
abilité e to
6
a.
gr
50
200
250 =
−
=
δ
%
6
,
10
106
,
0
Prob
25
,
1
40
50
0 =
=
=
=
=
σ
δ
z
b. la loi normale est symétrique on ne s'occupe pas du signe
→
5
,
2
40
100
0 =
=
=
σ
δ
z
c. 230 −
= gr
30
200
δ =
75
,
0
40
30
0 =
=
=
σ
δ
z
L’intervalle (< 230 gr) considéré contient la valeur moyenne (200 gr) → on prend 1
– Prob(table):
- 139 -

%
3
,
77
773
,
0
227
,
0
1
Prob =
=
−
=
d. on calcule d’abord la probabilité que le poids s’écarte de plus de 20 gr, vers le
haut ou vers le bas :
%
9
,
30
309
,
0
Prob
5
,
0
40
20
40
gr
20
0
=
=
=
=
=
=
=
σ
δ
σ
δ
z
On doit multiplier par 2 car on considère les deux côtés → Prob = 2 × 0,309 =
e 0,618 que le poids s'écarte de µ de plus de 20 gr, et donc
0,618
On a donc une prob. d
une prob. 1-0,618 que le poids ne s'écarte pas de plus de 20 gr.
Réponse: 0,382 = 38,2%
- 140 -

- 141 -

Exercice 1
Dans une commune rurale, où aucune exploitation agricole n’atteint 123 Ha. La distribution
des 100 exploitants en fonction de la superficie se présente comme suit :
Superficie en Ha : xi Le pourcentage des propriétaires
:fi
fonciers
Moins de 5 15
5 – 10 20
10 – 15 15
15 – 20 10
20 – 30 10
30 – 50 12
50 et plus 18
Total 100
Qu
1- quelle est la population cible ?
quel est le caractère étudié ?
quel est le nombre de modalités ?
2- représentez graphiquement la distribution étudiée (simple et cumulative)
3- déterminez les différentes caractéristiques de tendance centrale
4- qu’en est-il de la dispersion ?
5- est-ce que la répartition des terres au
estions :
sein de cette commune est équitable ?
Exercice 2
On considère la distribution définie par le tableau ci-dessus
mensuel en DH Nombre d’appartements
Loyer
150-179 3
180-209 8
210-239 10
240-269 13
270-299 33
300-329 40
330-359 35
360-389 30
Total 172
Questions :
a- quelles sont les born érieures et supérieures de la 1ere classe ?
b- quelles sont les vrai 1ere classe ?
c- l’intervalle de classe e est identique pour chaque classe ? quelle est sa taille ?
- quel est le centre de e classe ?
- q
f- q
mensue
es inf
es limites de la
utilisé
la 1er
d
e uels sont les vraies limites de la classe correspondant à l’effectif le plus élevé ?
uelles sont les bornes de la classe à l’intérieur de laquelle s’est trouvé recensé un loyer
l de 239.50 DH ?
- 142 -

g- c
h- cons ées du tableau.
onstruisez un histogramme exprimant les données du tableau.
truisez une courbe d’effectifs pour les donn
Exercice 3
Une agence d’urbanisme a effectué une étude sur la structure des
habiter une ville nouvelle dont elle est chargée d’établir le projet.
familles susceptibles de venir
Trois types de familles ont été
définis selon la présence et l’activité du conjoint. D’après cette étude, les distributions de
:
fréquences de ces familles selon le nombre d’enfants sont les suivantes
Chef de famille…
Nombre d’enfants
…sans conjoint … avec femme
active
…avec femme
inactive
0 33.3 16.2 8.4
1 39.3 26.6 16.4
2 16.6 26.6 25.2
3 6 .6
.4 15.6 20
4 2 .3
.5 9.3 15
5 1.1 4.5 12.2
6 0.8 1.2 1.9
7 0.0 0.0 0.0
Total 100.0 100.0 100.0
Les trois types de familles considérés se repartissent en pourcentage comme ci-après :
Chef de famille…
Total
…sans conjoint … avec femme …avec femme
active
inactive
100 5.8 52.9 41.2
Questio
1- déter r chaque type de ur l’ensemble, le mode de la distribution selon
le nombre d’enfants.
2- déter r chaque type de ur l’ensemble, la médiane de la distribution
selon le nombre d’enfants.
ns :
minez pou famille et po
minez pou famille et po
3- calculez pour chaque type de fam pour l’ensemble, le nombre m d’enfants .
Exercice 4
ille et oyen
Au cours de la d
production nette de charbon ont
écennie 1990-2000, les effectifs employés au fond d’une houillère et la
évolué de façon suivante :
Année Effectifs du fond (milliers
de
Production nette de
charbon
personnes (millions de tonnes)
1990 71.3 40.1
1991 65.3 35.8
1992 57.6 32.7
1993 50.4 28.4
1994 47.1 25.7
- 143 -

1995 5 .6
4 .8 25
1996 2 5.1
4 .4 2
1997 38.6 24.4
1998 35.9 22.4
1999 32.7 21.1
2000 30.8 20.7
1- n d su iq r e
de l’autr n à mettre dence tence de covariations
hique de corrélation correspondant au tableau précédant.
représentez l’évolutio e ces deux séries r deux graph ues à coo données arithmétiqu s
présentés l’un au dessous e faço en évi l’exis
éventuelles dans le temps.
2- quels sont les inconvénients de cette présentation ?
graphique permettrait d’y remédier ?
3- quel type de
4- tracer le grap
5- comment interprétez-vous ce graphique ?
Exercice 5
Un sondage sur la capacité pulmonaire de idus nous a donné sultats suivants :
Age e C
s indiv les ré
Sex apacité pulmonaire (litre)
54 2.94
F
19 4.03
M
18 3.75
F
26 M 6.04
19 F 4.92
22 M 6.57
18 M 5.28
20 M 5.19
20 F 4.08
18 M 4.68
17 5.38
M
29 4.71
M
17 5.20
M
43 4.50
M
30 4.93
M
18 3.92
F
25 6.54
M
38 5.35
M
19 4.21
F
26 M 5.40
20 M 6.66
18 M 5.14
16 F 3.49
19 M 5.82
20 M 5.25
21 M 4.89
19 M 6.07
19 F 3.82
19 M 6.71
- 144 -

30 M 5.93
24 M 6.22
17 F 3.86
Questions:
1- Construisez une distribution d’effectifs pour chacune des variables
2- donner une représentation graphique pour chacun des cas
l’écart type de la distribution de la capacité pulmonaire
3- donnez la mesure de tendance centrale la plus appropriée, pour chacune des variables
4- calculez
Exercice 6
Des étudiants de 1ere année TCE ont eu les résultats en statistiques et en mathématiques
6 7 56 47
financières (/100)
x (notes de 66 64 9 93 80 1 87 73 79
statistiques)
Y(notes de 72 70 60 94 82 68 86 82 90 55 64
math.fin.)
Questions :
1- tracez le nuage statistique
2- ajustez la droite des moindres carrés
e mathématiq
3- quelle note d
qui a eu 75 en s
ues financières pouvez-vous prédire à un étudiant de ce niveau
tatistiques ?
Exerci
4- calculez le coefficient de corrélation ?
ce 7
ES
Les caractères suivants sont qualitatifs quantitatifs
TERMINOLOGIE ET TABLEAUX STATISTIQU
1-
- Le tour de ceinture d'une personne
- Le code postal de io
français
l'habitat n d'un foyer
- La superficie d'une exploitation agricole
- Le groupe sanguin d'un individu
2- Les classes suivantes sont-elles bien définies?
- 145 -

3- La fréquence d'une classe s'obtient en divisant l'effectif de la classe par
4- Le caractère quantitatif discret x admet le tableau de distribution suivant
5- Quelle est la fréquence cumulée croissa p
nte our x = 3
6- Pour une distribution continue, l'effectif total s'obtient en multipliant l'effectif de chaque
t les nombres ainsi obtenus
vrai faux
classe par le centre de la classe et en ajoutan
7- Le tableau ci-dessous (notes obtenues par 40 étudiants à un examen de statistique) est un
bleau
ta
- 146 -

8- Les caractères quantitatifs suiv omme des variables
statistiques continues
ants peuvent-ils être considérés c
9- Le é le tableau suivant
s tudiants de formation continue sont répartis selon leur âge dans
Quelle limite doit-on donner à la dernière classe si l'on veut que toutes les classes aient la
même a
50 55 34
mplitude
Quel
3
est le centre de la classe [30 ; 35[
3 35 37,5
autre
réponse
Quell e de 35 ans
e st la proportion d'étudiants âgés de moins
53,3% 79,12% 92,31% 25,82%
10- La fréquence cumulée croissante est définie par
- propo dont la valeur du caractère est
inférieure à x
rtion d'individus
- prop
supérieure à x
ortion d'individus dont la valeur du caractère est
- ensemble des modalités que peut prendre le caractère
- autre réponse
11- On a pu regrouper les individus d’une population par classes dont les centres sont les
suivants : 52, 60, 68, 76, 84, 92. Quelle plitude des classes
est l’am
- 147 -

Exercice 8
A partir du tableau ci-dessous, 3 graphiques ont été établis. Indiquez celui (unique) de ces
raphiques qui ne constitue pas une représentation correcte du phénomène
g
1 2
- 148 -

- 149 -
Exercice 9
Lequel des graphiques ci-dessous correspond à l'histogramme des données suivantes
- 149 -

Exercice 10
Le caractère quantitatif X admet la distribution suivante:
classes [0 ; 1[ [1 ; 2[ [2 ; 4[
effectifs 40 30 30
Quelle est la représentation graphique des fréquences qui convient?
Exercice 11
Le caractère quantitatif X admet la distribution suivante:
classes [0 ; 1[ [1 ; 2[ [2 ; 4[
effectifs 40 30 30
Quelle représentation graphique des fréquences cumulées croissantes convient?
Exercice 12
La représentation graphique ci-dessous est un diagramme
- 150 -

Exercice 13
Un histogramme est une représentation graphique de la distribution des fréquences d'une
variable statistique continue
Exercice 14
Dans un diagramme à secteurs, la modalité n° 2 du tableau ci-dessous serait représentée par
un secteur d'angle
Exercice 15
Le tableau suivant donne la répartition des ménages d'une population selon le nombre de
véhicules possédés
nombre 0 1 2 3 4 et plus
d'automobiles
nombre de 528 2463 906 156 12
ménages
La représentation graphique qui convient le mieux est
- 151 -

- 152 -
Exercice 16
1- Quelle est la moyenne des valeurs ci-dessous
2- La médiane d'une distribution est toujours égale au second quartile
3- Dans une série statistique, il est possible de déterminer dix déciles
4- On observe pendant 79 jours ouvrables, le nombre de lettres recommandées émises au cours de
la journée, par le service des approvisionnements. L'évolution de ces envois au cours de cette
période est fournie dans le tableau suivant. Déterminer le premier et le troisième quartile de cette
série d'expéditions quotidiennes de lettres recommandées.
rang nbre
lettres
rang nbre
lettres
rang nbre
lettres
rang nbre
lettres
rang nbre
lettres
1 1 17 6 33 7 49 8 65 11
2 3 18 6 34 7 50 8 66 11
3 3 19 6 35 7 51 9 67 11
4 4 20 6 36 7 52 9 68 11
5 4 21 6 37 7 53 9 69 11
6 5 22 6 38 7 54 9 70 11
7 5 23 6 39 8 55 9 71 11
8 5 24 6 40 8 56 9 72 12
9 5 25 7 41 8 57 9 73 12
10 5 26 7 42 8 58 9 74 12
11 5 27 7 43 8 59 10 75 12
12 6 28 7 44 8 60 10 76 13
13 6 29 7 45 8 61 10 77 13

- 153 -
14 6 30 7 46 8 62 10 78 14
15 6 31 7 47 8 63 10 79 15
16 6 32 7 48 8 64 10
5- Cocher la nature des indicateurs numériques suivants
6- Soit le tableau suivant

- 154 -
7- Il existe 100 centiles qui partagent une série statistique
OUI NON
8- On donne la série statistique suivante : 14, 16, 12, 9, 11, 18, 7, 8, 9, 16, 7, 9, 18. La
médiane est égale à
9- La moyenne géométrique d'une série statistique est
10- Quand les classes d'une série statistique sont d'amplitudes inégales, il faut obligatoirement
corriger les effectifs ou les fréquences pour calculer la médiane
11- La moyenne harmonique d'une série statistique est égale à l'inverse de la moyenne
arithmétique des inverses des valeurs
12- La médiane partage l'histogramme en deux surfaces égales
13- Soit la série suivante
1,92 2,78 357
la moyenne quadratique est égale à 4,86 5,04 15
1,87 2,15 3,57
la moyenne géométrique est égale à 6,25 autre réponse
6,25 215 1,92
la moyenne harmonique est égale à
1,87 autre réponse

- 155 -
14- La répartition des célibataires selon leur âge est fournie par le tableau suivant
Sachant que l'âge moyen est égal à 28,8 ans, la valeur manquante est
Sachant que l'âge moyen est égal à 28,8 ans, la valeur manquante est
L’âge médian est
Exercice 17
1- Complétez le tableau suivant pour calculer la variance
La variance vaut
2- Calculez le coefficient de variation des données suivantes:
3- La synthèse d'un ensemble d'observations relatives à une variable quantitative peut s'effectuer
par des paramètres de tendance centrale et de dispersion.
L'une des quatre réponses suivantes n'a rien à voir avec ce type de synthèse:
4- On observe sur un tronçon d'autoroute, pendant 51 jours, le nombre x de dépannages effectués
au cours de la journée. Calculer l'intervalle inter-quartile des observations

- 156 -
ran
g
nbre
dépannages
rang nbre
dépannages
rang nbre
dépannages
rang nbre
dépannages
rang nbre
dépannage
s
1 1 11 3 21 4 31 4 41 6
2 1 12 3 22 4 32 4 42 6
3 1 13 3 23 4 33 5 43 6
4 1 14 3 24 4 34 5 44 6
5 1 15 3 25 4 35 5 45 6
6 2 16 3 26 4 36 5 46 6
7 2 17 3 27 4 37 5 47 7
8 2 18 3 28 4 38 5 48 8
9 2 19 3 29 4 39 5 49 9
10 3 20 4 30 4 40 5 50 10
51 11
L'intervalle inter-quartile vaut
3 4 5 6
autre
réponse
5- La variance est toujours positive ou nulle
OUI NON
6- Une entreprise E possède 3 établissements A, B, C. Les effectifs et les salaires moyens pour
les ouvriers, les employés , et les cadres , sont donnés dans le tableau suivant

- 157 -
Exercice 18
1- Si, pour un caractère quantitatif continu et positif, la médiane est très peu différente de la
Médiale, alors l'indice de concentration de Gini est peu différent de
2- Dans un diagramme de concentration on porte généralement en ordonnées les valeurs des
fréquences cumulées des valeurs globales. Comment s'écrivent ces valeurs
Exercice 19
1- Pour justifier un ajustement affine (y = ax + b) , on a calculé le coefficient de corrélation
Linéaire r. Dans les cas suivants, le résultat est
2- Quand on ajuste linéairement x et y par la méthode des moindres carrés, on obtient deux
droites de régression. L'équation de la droite D de y par rapport à x est
3- Dans le cas d'indépendance totale, le coefficient de corrélation linéaire est égal à
0 1 -1
autre
réponse
4- Une valeur élevée du coefficient de corrélation linéaire est signe d'une réelle relation causale,
dans le cas

- 158 -
5- Utiliser les calculs effectués dans le tableau ci-dessous pour calculer la covariance entre les
variables x et y
6- D'après les données et le graphique du tableau ci-dessous, indiquer laquelle des propositions
s'applique correctement à ces informations

- 159 -
7- Calculer la pente a de l'équation de régression y = ax + b , pour les données du tableau suivant
8- Calculer l'ordonnée à l'origine b de l'équation de régression y = ax + b , pour les données du
tableau suivant
422,4
-
13,25 756,14 687,4
autre
réponse
Exercice 20
1-On considère la série chronologique
Trimestre 1 Trimestre 2 Trimestre 3 Trimestre 4
1995 10 12 13 14
1996 11 15 16 13
1997 12 17 18 15
1998 13 17 19 16
2- Si une série suit un modèle multiplicatif et qu'on divise les valeurs de la série brute par les
valeurs des coefficients saisonniers, on obtient

- 160 -
3- Soit la série chronologique suivante, qui suit un modèle multiplicatif
Le trend, à la date t = 3, calculé par les moyennes mobiles d'ordre 4 est égal à
La valeur à la même date de la série CVS est
4- Soit la série chronologique
La série suit un modèle de type
5- Soit Yt la série du chiffre d'affaires mensuel d'une entreprise de janvier 1987 à décembre
1991. L'équation du trend est Tt = 3,76 t + 700 ; (t = 1,....,60)
Les coefficients saisonniers sont :
janvier S1 = -16 mai S5 = 11 septembre S9 = - 60
février S2 = -51 juin S6 = 64 octobre S10 = -1
mars S3 = -80 juillet S7 = 0,09 novembre S11 = 62
avril S4 = -81 août S8 = -69 décembre S12 = 222
Sachant qu'on a un modèle additif, une estimation de la valeur future de juin 1993 est
6- Soit la série chronologique ci-après qui suit un modèle de type additif
- La moyenne mobile d'ordre 4 du 3° trimestre 1997 est
- La valeur du coefficient saisonnier brut S' du 1° trimestre est

- 161 -
- Le coefficient saisonnier S du 1° trimestre est
- La valeur de la série CVS au 2° trimestre de l'année 1996 est
Exercice 21
On considère les notes sur 20 de 16 candidats :
Exercice 22
Le tableau suivant donne la répartition des abonnés à la bibliothèque municipale selon
l’âge (en année) :
1)- Définir la population, le caractère et la nature de ce caractère.
2)- Représenter le tableau statistique ci-dessus par un histogramme.
3)- Tracer le polygone de fréquence.
4)- Calculer la proportion des abonnés âgés entre 20 et 50 ans.
5)- Calculer le mode et la médiane.
6)- Déterminer l’étendue et le cinquième décile.
7)- Calculer l’écart type.
Exercice 23
Le tableau suivant donne l’observation des prix Y (en DH) et des quantités disponibles
X d’un produit sur un marché :

- 162 -
Exercice 24
Le tableau suivant donne la répartition de 200 salariés selon le salaire net (en milliers
de DH) : X en mDH :
Exercice 25
Le responsable logistique s’intéresse à l a corrélation pouvant exister entre le temps de
préparation d’une commande Y (en minutes) et le nombre de colis à préparer X. Il a
effectué 5 observations de la statistique double (X, Y) :
Exercice 26
Soient X le nombre d’accidents et Y le nombre d’accidentés dans ces accidents :
On a ainsi obtenu les couples suivants

- 163 -
Exercice 27
Dans une entreprise A travaillent 752 hommes et 248 femmes. Dans l'entreprise B, ces
effectifs sont respectivement 363 et 637. Les salaires moyens (en DH) sont donnés par
le tableau suivant
Quelle entreprise offre le salaire moyen le plus élevé ? Interpréter.
Exercice 28
Exercice 29
Dans une entreprise, la répartition des salariés selon le salaire mensuel est la suivante :

- 164 -
Exercice 30
Le service de recouvrement de l’entreprise E s’intéresse à l’étude du nombre de
chèques « de montant élevé : supérieur à 50 000 DH » traités quotidiennement au
cours des 25 jours d’observations :
Exercice 31
Le chef de service d’une grande surface dispose des données ci-dessous concernant, pour
différents produits, le temps mis par un employé à installer les rayons en fonction du nombre
d’articles à ranger.
Soient X le nombre d’articles et Y le temps en mn (minute) :

- 165 -
Exercice 32
Dans une entreprise E, la répartition de 42 salariés selon le poste occupé est comme
suit :
Exercice 33
On reprend les 42 salariés de l’exercice 32, mais cette fois-ci on s’intéresse à leur
niveau de rémunération mensuelle en cdh (centaines de dirhams):
Exercice 34
Une enquête a été réalisée sur une population selon deux variables X et Y et a donnée
le tableau suivant :
Exercice 35

- 166 -
On donne le tableau suivant dénombrant le nombre moyen de véhicules entrés par
jour dans un parking entre 1997 et 2001 :
Exercice 36
On a effectué une enquête auprès de 20 ménages d’un quartier. Quatre types
d’informations ont été recueillies : le revenu annuel net (en DH), le statut
matrimonial (Ménage avec un seul parent veuf, Ménage avec un seul parent divorcé,
Couple marié) ; le nombre d’enfants du ménage et l’opinion du ménage sur la qualité
du voisinage (Mauvaise, Passable, Moyenne, Bonne).
- De quels types de critères s’agit-il : (Qualitatif (ordinal, nominal) ; quantitatif
(discret, continu) ?
Exercice 37
Une étude concernant une population de femmes selon le nombre d’enfants et le
revenu annuel (en Milliers de dirhams : mdh) a donnée le tableau suivant :
Exercice 38

- 167 -
Le tableau statistique ci-dessous donne la répartition de 100 ouvriers selon le salaire
mensuel en centaines de dirhams :cdh):
Exercice 39
Un étudiant du département des Sc.E.G. se rend tous les matins à pied à la faculté.
Passionné par son cours de statistique, l'étudiant compte le nombre de véhicules "4
roues" qu'il croise sur son chemin à la faculté. A la fin du premier semestre, il a
obtenu les résultats suivants:
Exercice 40
Dans une entreprise de télécommunications, le salaire annuel moyen de 16 hommes
possédant entre 2 et 5 ans d’expérience est de 28000 € et l’écart type est de 4500 €. Les
salaires (exprimés en millier d’euros) d’une population de 9 femmes possédant entre
2 et 5 ans d’expérience sont les suivants : 27, 24, 31, 21, 19, 26, 30, 22, 34.
Exercice 41
Préciser la population, sa taille, le caractère et sa nature. Représenter par le
diagramme circulaire.

- 168 -
Exercice 42
Sachant que dans 3 régions également peuplées d’un pays, il y a respectivement 1
médecin pour 300, 500, 1000 habitants. Quel est le nombre moyen d’habitant par
médecin dans le pays ?
Exercice 43
Dans une entreprise de télécommunications, le salaire annuel moyen de 16 hommes
possédant entre 2 et 5 ans d’expérience est de 28000 € et l’écart type est de 4500 €. Les
salaires (exprimés en millier d’euros) d’une population de 9 femmes possédant entre
2 et 5 ans d’expérience sont les suivants : 27, 24, 31, 21, 19, 26, 30, 22, 34.
a)- Donner le salaire annuel moyen pour l’ensemble des deux sexes.
b)- Donner l’écart type du salaire annuel pour l’ensemble des deux sexes.
Exercice 44
Le tableau statistique ci-dessous donne la répartition de 100 ouvriers selon le salaire
mensuel en centaines de dirhams :cdh):
1) Tracer l’histogramme (échelle : sur X : 1 unité → 0,2 cm ; sur Y : 0,02 →1 cm)
2) Calculer le mode, la moyenne et la médiane.
3) Tracer la courbe de concentration.
4) Commenter globalement la distribution.
Exercice 45
1) On donne ici la distribution des salaires mensuels des salariés de l’entreprise E
Représenter graphiquement cette distribution et en déterminer le mode et la
médiane.
2) Tracer la fonction de répartition. Construire la courbe de concentration et calculer
l’indice de GINI. Calculer la médiale. (Rep : 3567,4 DH, 15.2%)

- 169 -
3) Calculer le salaire mensuel moyen ainsi que la masse salariale de E1.(Rep : 3,54
KDH ; 354KDH)
4) Deux formules d’augmentation de salaire sont proposées :
a) une augmentation forfaitaire de 75 DH par mois ;
b) une augmentation de 2% du salaire mensuel.
Déterminer pour chacune de ces possibilités, le salaire moyen et la masse salariale.
Quelle possibilité aura la préférence de la direction ?Justifier.
5) Calculer par interpolation, le pourcentage de salariés ayant un salaire inférieur à
3750 DH. En déduire le pourcentage de salariés optant pour une augmentation de 2%
de leur salaire.
Exercice 45
Dans une entreprise de 80 salariés on a enregistré les salaires mensuels suivants :
• 54 salariés gagnent 6 000 dirhams ou plus ;
1. Présenter ces données dans un tableau avec des classes de même amplitude en
sachant qu’aucun salarié ne gagne plus de 14 000 DH.
2. Calculer la moyenne et donner sa signification.
3. Calculer la médiane et donner sa signification.
4. Calculer le mode graphiquement, algébriquement et donner sa signification.
5. Combien gagnent les 20% des salariés les mieux payés.
Exercice 46
La répartition des salariés d’une entreprise de confection selon leurs gains mensuels
(en milliers de dirhams) se présente comme suit :
1. déterminer graphiquement le salaire modal
2. calculer le coefficient de variation
3. calculer l’étendue
4. calculer algébriquement et graphiquement la médiane.
Exercice 47
La répartition par âge d’une population d’un centre de vacances est comme suit :

- 170 -
1. tracer l’histogramme de cette distribution
2. calculer l’écart type et donner sa signification
3. on désire rajeunir cette population en invitant au centre des vacances des
personnes de la classe [25-35[.combien faudrait-il en faire venir pour que la moyenne
de la population soit de 35 ans.
Exercice 48
Dans une commune urbaine, on a relevé la répartition en pourcentages de 10 000
contribuables selon le montant des impôts payés.
Classes d’impôts Fréquences relatives en pourcentages
1-3 8
3-6 12
6-L2 20
L2-12 26
12-18 F6
18-22 10
22-30 6
1. Trouver les valeurs manquantes de ce tableau sachant que la moyenne est égale à
11,42
2. tracer la courbe cumulative croissante
3. déterminer graphiquement et algébriquement l’impôt médian. Donner sa
signification
4. quel est le pourcentage des contribuables qui paient un impôt annuel supérieur à
20 000dh ?cela représente combien de personnes ?
Exercice 49
Soit la distribution statistique suivante qui donne la répartition des propriétaires
terriens selon la superficie des terres cultivables dans une certaine région agricole

- 171 -
Partie I :
1. préciser le caractère étudié et préciser sa nature.
2. donner la signification de du centre de la 2ème classe.
3. déterminer rapidement la médiane et donner sa signification
4. déterminer algébriquement le mode et donner sa signification
5. calculer la superficie moyenne et l’écart type. Que peut-on conclure ?
6. déterminer le 1er et le 9ème décile et donner leurs significations
Partie II :
1. déterminer graphiquement la concentration foncière dans cette région agricole,
Calculer l’indice de GINI
2. déterminer algébriquement la concentration
3. déterminer graphiquement le pourcentage des propriétaires dont la superficie des
terres est inférieure à la médiale.
Exercice 50
Pendant 9 années les bénéfices d’une entreprise ont augmenté :
de 4% par an pendant les 3 premières années.
de 7% par an pendant les 4 années suivantes.
De 10% par an pendant les 2 dernières années de la période considérée.
Quelle est l’augmentation moyenne des bénéfices de cette entreprise sur les 9 années ?
Exercice 51
Le tableau suivant donne la répartition des salaires mensuels des cadres d’une
entreprise:
Salaires en 1000DH Nombre des cadres
6-8 50
8-10 70
10-16 80
16-22 50
22-30 50
30-34 80
34-38 20
total 400
1. préciser le caractère étudié et sa nature
2. représenter graphiquement cette distribution, tracer le polygone des fréquences
3. déterminer rapidement :

- 172 -
• le salaire médian des cadres donner sa signification.
• Le 3ème quartile (Q3). donner sa signification.
4. donner graphiquement le salaire modal des cadres.
5. calculer le salaire moyen des cadres.
6. Calculer le coefficient de variation et donner sa signification
7. Pour motiver davantage ses cadres, l’entreprise décide une augmentation générale
des salaires de 20%. Calculer la nouvelle moyenne et le nouveau coefficient de
variation.
Exercice 52
Une entreprise a présenté ses dépenses de publicité et ses chiffres pour les 6
dernières années dans le tableau suivant (en 10P
6P DH)
1. L’entreprise pense qu il y’a un lien entre dépenses de publicité (X) et le chiffre
d’affaire(Y).pouvez vous le confirmer ?
2. établir par la méthode des moindres carrés la relation liant le chiffre d’affaires et les
dépenses de publicité
3. combien l’entreprise peut-elle espérer réaliser comme chiffre d’affaires avec des
dépenses de publicité de 30 ?
Exercice 53
On a observé une population en retenant 2 caractères : le nombre d’enfants(X) et la
taille du logement (Y).les résultats sont les suivants :
Exercice 54

- 173 -
Le tableau suivant donne la répartition des salariés d’une entreprise de bâtiment
selon le nombre d’enfants à charge X et les salaires mensuels perçus y en milliers de
DH
1. donner la distribution marginale de la variable X
2. donner la distribution conditionnelle de la variable Y liée à la modalité 4 de X.
3. que signifient les valeurs 16 et 3 soulignée dans le tableau
4. vérifier de deux manières différentes que les deux variables sont indépendantes.
Dites dans ce cas à est égal le coefficient de corrélation linéaire : r (sans le calculer.
5. calculer la variance marginale de Y.
Exercice 55
Une étude réalisée dans un club sportif concernant le poids et la taille de 124
adhérents a fourni les informations suivantes :
poids en Kg Y
taille en mètres X
50-60 60-65 65-75 75-80
1,60-1,70 12 7 6 4
1,70-1,75 ? 6 8 3
1,75-1,80 9 8 8 4
1,80-1,90 ? 7 5 6
1,90-2,00 3 5 3 3
Exercice 56
Une entreprise commerciale a présenté ses ventes xi et ses frais de publicité yi au
cours du premier semestre de l’année 2003 comme suit (en 1000 DH)
Mois Ventes Frais de publicité
Janvier 40 1.1
Février 30 0.8

- 174 -
Mars 42 1.2
Avril 46 1.4
Mai 44 1.3
juin 38 1.1
1. Déterminer une fonction linéaire qui donne le montant des ventes lorsqu’on
connaît les frais de publicité.
2. Quel serait le montant des ventes si les frais de publicité atteindront 3500DH.
3. Déterminer s’il y a ou non une liaison entre les ventes et les frais de publicité.
Exercice 57 :
Au poste de péage, on compte le nombre de voitures se présentant sur une période de
5mn. Sur 100 observations de 5mn, on obtient les résultats suivants :
Nombre de voitures 1 2 3 4 5 6 7 8 9 10 11 12
Nombre d’observations 2 8 14 20 19 15 9 6 2 3 1 1
1) Construire la table des fréquences et le diagramme en bâtons en fréquences de
la série du nombre de voitures.
2) Calculer la moyenne et l’écart-type de cette série.
3) Déterminer la médiane, les quartiles et tracer le box-plot.
4) Etudier la symétrie de la série.
Exercice 58 :
On donne la série unidimensionnelle suivante, correspondant à la répartition des
entreprises du secteur automobile en fonction de leur chiffre d’affaire en millions
d’euros.
a) Calculer le chiffre d’affaire moyen et l’écart-type de la série.
b) Construire l’histogramme des fréquences
c) Construire les deux polygones des fréquences cumulées
d) Calculer la médiane et la proportion d’entreprises dont le chiffre d’affaire est
supérieur à 3 millions d’euros.
Exercice 59 :
La distribution des demandeurs d’emploi selon le sexe et la classe d’âge dans une
localité est la suivante :

- 175 -
a) Tracer les deux courbes de fréquences cumulées croissantes.
b) Déterminer les quartiles de la variable X associant à chaque demandeur
d’emploi masculin son âge. Même question pour les demandeurs d’emploi de
sexe féminin.
c) Conclusions.
Exercice 60 :
On cherche à étudier la relation entre le nombre d’enfants d’un couple et son salaire.
On dispose des séries bidimensionnelles suivantes :
Salaire en euros (Y) Nombre d’enfants (X)
510 4
590 3
900 2
1420 1
2000 0
600 5
850 6
1300 7
2200 8
a) Calculer le coefficient de corrélation linéaire entre ces deux variables
statistiques. Conclusion ?
b) Un expert en démographie affirme que les deux caractéristiques sont
indépendantes. Qu’en pensez-vous ?
Exercice 61:
L’indice moyen d’un salaire a évolué de la façon suivante :
a) Représenter cette série statistique par un nuage de points.
b) En utilisant la méthode des moindres carrées, calculer l’équation de la droite
représentant l’indice en fonction de l’année.
c) Comment pourrait-on prévoir l’indice à l’année 9 ?

- 176 -
Exercice 62
On observe le nombre d’enfants Y sur un ensemble de 12 individus répartis entre les
sexes (variable X) :
F 3 4 5 4 2 5
H 10 7 6 3 4 2
1) Représenter graphiquement cette série.
2) Calculer les moyennes arithmétiques dans chaque classe
3) Calculer les variances inter et intra-catégories.
4) Calculer et interpréter le rapport de corrélation entre X et Y. Conclusion ?
Exercice 63
Ce tableau donne la distribution selon l’âge de la population de l’île de la Réunion et
de la métropole.
âge La Réunion ( en pourcentage) métropole ( en pourcentage)
[0 ;15[ 29 20
[15 ;30[ 30 22
[30 ;50[ 25 28
[50 ;70[ 12 20
[70 ;90[ 4 10
Tracer les histogrammes correspondants à ces deux séries sur le même graphique.
Donner la valeur de la médiane et celle de la moyenne correspondant à ces deux
séries.
Exercice 64
Les salaires ont augmenté de 15 et les prix de 12. Sachant que le pouvoir d’achat se
calcule en faisant le quotient du salaire par le prix, de combien a varié le pouvoir
d’achat.
Exercice 65
Calculer la médiane, la moyenne et l’écart-type des notes obtenus à un devoir par une
classe de 32 élèves.
notes 5 6 7 8 9 10 11 12 13 14 15
effectifs 1 3 1 4 3 9 4 1 2 1 2
Exercice 66
Le tableau suivant donne la répartition des entreprises du secteur de l’automobile en
fonction de leur chiffre d’affaires en millions d’euros.
chiffres d’affaires moins de 0,25 [0,25 ;0,5[ [0,5 ;1[ [1 ;2,5[ [2,5 ;5[ [5 ;10[
nombre d’entreprises 137 106 112 154 100 33
Tracer l’histogramme correspondant à cette répartition. Déterminer le chiffre
d’affaire médian. Calculer la moyenne et l’écart-type.

- 177 -
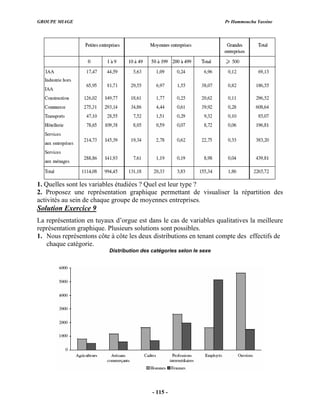
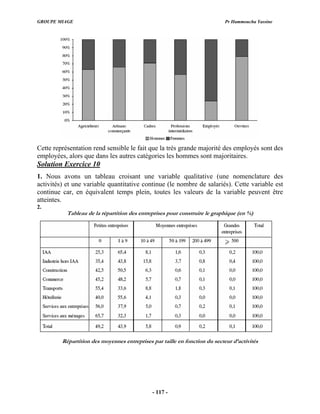
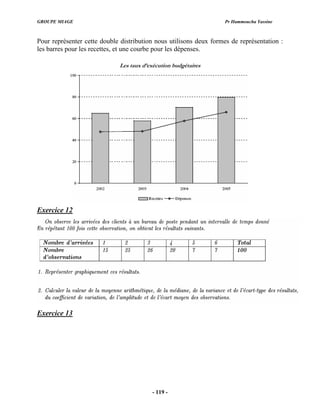
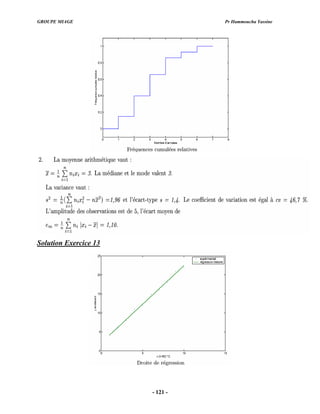
Exercice 67
La distribution des demandeurs d’emploi selon le sexe et la classe d’âge dans une
localité est la suivante :
âge Hommes Femmes
[16 ;26[ 280 160
[26 ;40[ 310 360
[40 ;50[ 240 120
[50 ;60[ 420 530
[60 ;65[ 70 50
a) Tracer les deux courbes de fréquences cumulées croissantes.
b) Déterminer les quartiles de la variable X associant à chaque demandeur d’emploi
masculin son âge. Même question pour les demandeurs d’emploi de sexe féminin.
Exercice 68
Une étude sur le chiffre d’affaires d’une population de PME a permis d’obtenir les
résultats suivants ( en milliers d’euro)
minimum 3500
moyenne 4900
Ecart-type 650
mode 4550
Ecart interquartile 1100
médiane 4600
premier quartile 4100
étendue 5000
a) Classer ces paramètres en deux catégories (position, dispersion).
b) Quel est le chiffre d’affaires le plus grand dans cette population de PME?
c) Calculer le troisième quartile. Placer sur un axe les paramètres caractérisant cette
série.
Exercice 69
On étudie les revenus (mensuels en euros) d’un ensemble de familles d’un quartier
de Montpellier.
Revenus [700 ;900[ [900 ;1100[ [1100 ;1300[ [1300 ;1400[ [1400 ;1500[ [1500 ;1600]]
Effectifs 13 219 20 46 50 82
a) Quel est le nombre de familles dont les revenus sont compris entre 700 et 900 ?
b) Quelle est la proportion de familles dont les revenus sont compris entre 900 et 1500 ?
c) Quelle est la moyenne des revenus ? (Préciser la formule utilisée)
d) Quel est l’écart-type des revenus ? (Préciser la formule utilisée)
e) Que mesurent la moyenne et la variance ?
f) Dans quel intervalle se trouve la médiane ? Calculer la en faisant une interpolation
linéaire.
g) Faire l’histogramme correspondant à cette distribution et placer sur cet histogramme
la médiane en abscisse. Que remarquez-vous ?

- 178 -
Exercice 70
Une population statistique se présente comme suit :
valeur de la variable [0 ;4[ [4 ;10[ [10 ;20[ [20 ;40[
effectifs 4 20 14 2
a) Calculer la moyenne et la variance.
b) Chacune des classes de la distribution précédente est divisée en deux classes de
même amplitude, auxquelles on fait correspondre un effectif moitié de l’effectif initial
de la classe qui a été divisée. Faire un nouveau tableau. Comment sont modifiées la
moyenne et la variance ?
Exercice 71
Le tableau suivant donne la répartition d’une population par tranches d’âge.
classes [0 ; 10[ [10 ;20[ [20 ;30[ [30 ;40[ [40,50[ [50,60[ [60,70[ [70,80[
effectifs 18 44 68 54 42 36 16 10
Calculer les quartiles de cette série statistique.
Exercice 72
On a relevé la recette d’un hypermarché le lundi et le samedi.
semaine 1 2 3 4 5 6 7 8 9 10
lundi 57 60 52 49 56 46 51 63 49 57
samedi 86 93 77 69 81 70 71 91 67 82
Déterminer l’équation de la droite de régression linéaire de la recette du samedi en
fonction de celle du lundi. A partir de cette hypothèse quelle pourrait être la recette
du samedi sachant que celle du lundi est de 55 ?
Exercice 73
L’indice moyen d’un salaire a évolué de la façon suivante :
année 1 2 3 4 5 6 7
indice 165 176 193 202 222 245 253
a) Représenter cette série statistique par un nuage de points.
b) En utilisant la méthode des moindres carrées, calculer l’équation de la droite
représentant l’indice en fonction de l’année.
c) Peut-on prévoir l’indice à l’année 9 ?
Exercice 74
Le tableau suivant donne la distance de freinage d’un véhicule roulant sur route
sèche en fonction de sa vitesse.
vitesse en km/h 40 50 60 70 80 90 100 110
distance en m 8 12 18 24 32 40 48 58
a) Représenter cette série statistique par un nuage de points. Calculer la vitesse
moyenne et la distance moyenne.
b) En utilisant la méthode des moindres carrées, déterminer l’équation de la droite
représentant la distance en fonction de la vitesse.

- 179 -
c) Estimer, à l’aide de cette équation, la distance de freinage d’un véhicule roulant à
120km/h ?
Exercice 75
On désigne par X la variable associée à la proportion d’actifs occupés dans le secteur
primaire (donnée en pourcentage) et Y la variable associée à la part du secteur
primaire dans le PIB (donnée en pourcentage) .
Etats Allemagne Belgique Espagne France Grèce Irlande
X 3,4 2,7 11,8 6 24,5 15
Y 2 2 5 4 15 10
a) Représenter cette série statistique par un nuage de points. Calculer les deux
moyennes.
b) En utilisant la méthode des moindres carrées, déterminer l’équation de la droite
représentant Y en fonction de X.
c) Calculer le coefficient de corrélation linéaire.
Exercice 76
Dans une banque, on considère un échantillon de 10 clients choisis au hasard. On
note X le nombre de chèques émis et Y le nombre de visites à la banque de chaque
client durant le trimestre.
X 34 42 53 30 50 60 46 57 32 24
Y 12 14 15 10 15 17 12 14 10 9
a) Après avoir dessiné le nuage de points, déterminer la droite d’ajustement de Y en
fonction de X et celle de X en fonction de Y (méthode des moindres carrées).
b) Placer ces droites sur le graphique.

- 180 -
Bibliographie
Méthodes Quantitatives : Cours Et Epreuves Dr Driss Touijar
Statistiques : Fkairat Abdelmoutaleb /Biborchi Nassera
Probabilités et statistiques : cours et exercices C. REDER
Principes Et Méthodes Statistiques : Notes De Cours : Olivier Gaudoin
Statistique Descriptive : Samira Oukarfi
Statistiques Descriptives : Exercices : Pierre Bailly Et Christine Carrere
HThttp://www.univ-montp3.fr/miap/ens/AES/L1/optionmath/index.htmlTH
Twww.larrun.iut.bayonne.univ-pau.fr
Probabilités et statistiques : Audet, Boucher, Caumartin et Skeene : Gaëten
morin, 1983
Manuel de statistiques descriptives : Omar Rajaâ :El Wataniya, 2001
Mémento pratique statistiques : Rachid Boutti : Collection Expertise, 1996
Gestion prévisionnelle et mesure de la performance : Brigitte Doriath et
christian Goujet : Dunod, 2002
L’essentiel du marketing : Eric Vernette : Editions d’Organisation, 2002
Statistiques descriptives : Niveau technicien O.F.P.P.T : Mars 1993

- 181 -

- 182 -

- 183 -

- 184 -

statistique descriptive

Contenu connexe

Tendances

Similaire à statistique descriptive

Plus de YassineHammoucha

statistique descriptive