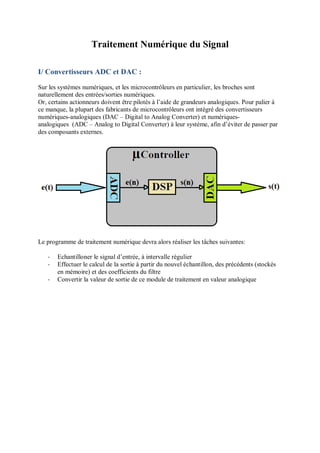
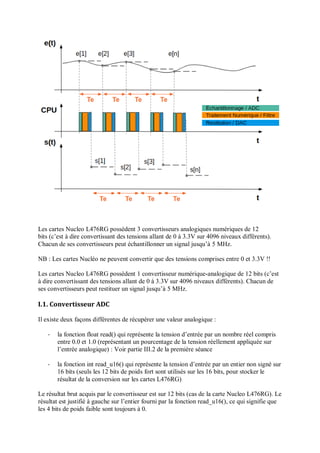
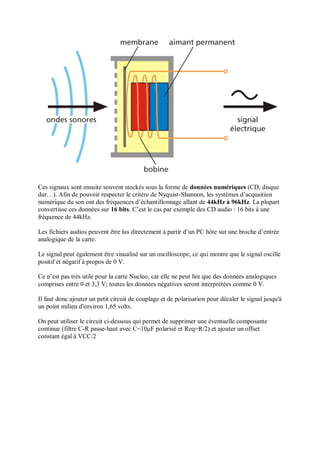
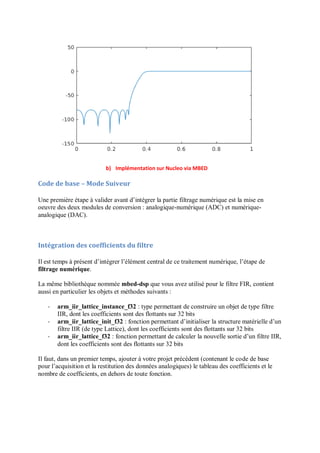
Le document présente la carte STM32 Nucleo-L476RG et son utilisation avec l'environnement de développement Mbed Compiler, en détaillant ses caractéristiques matérielles et les étapes nécessaires pour programmer la carte. Il aborde également la récupération de signaux numériques et analogiques, ainsi que l'utilisation de timers matériels et logiciels pour créer des routines d'interruption. Des exemples de code sont fournis pour illustrer comment manipuler les entrées et sorties de la carte, et comment afficher des données sur un ordinateur.

1. Initialisation
Objectifs :
- Se familiariser avec la carte STM32 Nucleo et l’environnement MBED Compiler
- Acquisitions des signaux numériques et analogiques.
I/ Présentation de La carte STM32 Nucléo-L476RG
La carte de développement que nous allons utiliser est une carte Nucléo-L476RG, conçue
par ST MicroElectronics (société franco-italienne – ex Thomson Semiconducteurs).
Elle possède les éléments suivants :
 Processeur : STM32L476RGT6 / ARM®32-bit Cortex®-M4 CPU
 Fréquence maximale : 80 MHz
 Alimentation : 3.3 V
 Mémoire programme : 1 MB Flash
 Mémoire données :128 KB SRAM
 Ressources :
o Entrées/Sorties Numériques : 51, dont 1 LED présente sur la carte
(sortie D13 ou PA_5) et un bouton-poussoir (entrée PC_13)
o ADC 12 bits / 5 MHz (x 3)
o DAC 12 bits / 2 canaux
o Timers
o Interruptions externes
 Communications :
o SPI / I2C
o USART / UART / CAN
o USB OTG Full Speed
Pour accéder aux broches de la carte, il existe deux types de connecteurs différents :
 Connecteurs compatibles Arduino Uno
 Connecteurs ST Morpho
II/ Programmer la carte Nucléo sous MBED Compiler
Un IDE, pour integrated development environment, ou EDI en français (Environnement de
Développement Intégré) est un ensemble d’outils proposés pour aider les programmeurs dans
leur travail.

2. Il comporte (souvent) :
 un éditeur de texte destiné à la programmation
 un compilateur pour transformer le code écrit en langage de haut niveau vers du code
assembleur
 un éditeur de liens, qui permet de compacter dans un même fichier binaire l’ensemble
des fonctions utiles au projet
 un débogueur en ligne, qui permet d’exécuter ligne par ligne le programme en cours de
construction
Certains environnements sont dédiés à un langage de programmation en particulier ou/et à une
cible particulière (microprocesseur généraliste ou microcontroleur).
L’IDE utilisé durant les séances de TP s’appelle MBED Compiler. Il est dédié aux
microcontrôleurs de type ARM-M qui se code en C et C++. Il est intégralement en ligne et
accessible de ce lien : https://os.mbed.com/
Les différentes étapes à suivre afin de pouvoir programmer notre carte avec MBED
Compiler sont:
- Création de compte
- Choix de la carte de développement
- Création d’un projet
- Ecriture du code
- Compilation du code
- Téléversement du code dans la carte
Applicaion :
Ecrire, compiler et téléverser un programme qui permet de clignoter le LED de test de la
carte « LED1 » .
III/ Récupération des signaux Analogiques et Numériques
1) récupérer une information numérique
Pour rappel, une entrée numérique permet de récupérer une information numérique (‘0’ ou
‘1’) provenant de l’extérieur vers l’intérieur du composant. Dans le cas de la carte Nucléo, un
‘0’ est codé par une tension de 0V et un ‘1’ est codé par une tension de 3.3V.
L’intérêt d’utiliser une entrée numérique est de pouvoir récupérer une information provenant
de l’extérieur dans son programme.
La première étape est la déclaration au compilateur de cette broche en entrée. Il faut la placer
après la déclaration des ressources externes (bibliothèques) et avant toute définition de
fonction :
DigitalIn inte(PB_9);

3. Dans l’exemple précédent, on configure la broche PB_9 (du connecteur Morpho) en entrée
numérique (ou digital en anglais). Dans ce code, il y a trois notions importantes :
 ‘DigitalIn‘, la classe qui définit le type de la broche, ici une entrée numérique
 ‘inte‘, le nom de la variable qui va être associée au port donné dans les parenthèses
 ‘PB_9‘, le nom de la broche que l’on va associer sur le composant
Pour pouvoir utiliser les sorties déclarées précédemment sur la carte, on passe par les
variables qu’on a associé à chacune de ces sorties. On pourra ensuite stocker cette information
dans une variable interne au microcontroleur.
int a;
a = inte.read();
La fonction read() permet de récupérer la valeur de l’entrée associée. La variable a, de type
entier, vaudra alors :
 0 si l’entrée inte (PB_9, d’après la déclaration d’avant) est à 0V
 1 si l’entrée inte est à 3.3V
Il est alors possible de tester la variable a pour connaitre son état et faire une action en
conséquence.
int a;
a = inte.read();
if (a == 1){
// ACTIONS A FAIRE SI L'ENTREE PB_9 EST A 3.3V / 1 LOGIQUE
}
else{
// ACTIONS A FAIRE SI L'ENTREE PB_9 EST A 0V / 0 LOGIQUE
}
Application : Afin de pratiquer l’utilisation d’une entrée numérique et d’une sortie numérique,
essayez d’écrire un code qui permet d’allumer la lED (LED1) de la carte si le bouton poussoir
de la carte (USER_Button) est appuyé et vice versa.

4. 2) Récupérer un signal analogique :
Certaines broches du composant (notée AnalogIn sur les connecteurs de la carte) peuvent être
reliées à ce convertisseur analogique-numérique.
La première étape est la déclaration au compilateur de cette broche en entrée analogique. Il faut
la placer après la déclaration des ressources externes (bibliothèques) et avant toute définition
de fonction
AnalogIn myInput(PC_2);
Dans l’exemple précédent, on configure la broche PC_2 (du connecteur Morpho) en entrée
analogique (ou analog en anglais). Dans ce code, il y a trois notions importantes :
 ‘AnalogIn‘, la classe qui définit le type de la broche, ici une entrée analogique
 ‘myInput‘, le nom de la variable qui va être associée au port donné dans les
parenthèses
 ‘PC_2‘, le nom de la broche que l’on va associer sur le composant
L’intérêt d’utiliser une entrée analogique est de pouvoir récupérer une information analogique
provenant de l’extérieur dans son programme (par exemple la sortie d’un capteur).
Dans l’exemple ci-dessous, nous utilisons la conversion à l’aide de la fonction read().
double meas, tension;
meas = analog_in.read();
tension = meas * 3.3;
Dans l’exemple précédent, on stocke dans la variable meas le résultat de la conversion sous
forme d’un nombre réel compris entre 0 et 1. A la seconde ligne, on multiplie par 3.3 afin
d’obtenir un nouveau nombre réel nommé tension égale à une tension comprise entre 0 et 3.3V,
image de la tension présente sur la broche A0.
Il est alors possible de faire une action selon la mesure obtenue :
double meas, tension;
meas = analog_in.read();
tension = meas * 3.3;
if(tension < 1){
// ACTIONS A FAIRE SI LA TENSION MESUREE A L'ENTREE PC_2 EST SUPERIEUR A 1V
}

5. else{
// ACTIONS A FAIRE SI LA TENSION MESUREE A L'ENTREE PC_2 EST INFERIEURE A 1V
}
Application :
Ecrire un code qui permet d’allumer la LED de la carte si la tension mesurée au niveau du
connecteur A0 est supérieure ou égale à 1.5V et de l’éteindre dans le cas échéant.
Au moins deux méthodes peuvent être utilisées pour tester le code développé :
 La première solution est d’utiliser une source de tension continue réglable de la façon
indiquée sur la Figure (à droite). En modifiant la tension de sortie de cette
alimentation, on pourra alors vérifier le bon fonctionnement du code développé.
 Étant donné que la carte Nucléo possède déjà une alimentation stabilisée de 3.3V,
accessible sur le connecteur Arduino sous le nom 3V3. La deuxième solution consiste
alors à relier un potentiomètre de la façon montrée sur la Figure (à gauche) pour
obtenir une tension variable à sa sortie entre 0 et 3.3V.
Affichage des données de la carte STM32 Nucleo à l'écran d'un ordinateur
Lorsque vous programmez d'autres microcontrôleurs, toutefois, il peut arriver que vous soyez
obligé d'utiliser un environnement de développement qui ne comporte pas un moniteur série
intégré. C'est le cas, par exemple, pour l'IDE Pinguino, et pour mbed (IDE en ligne utilisé
pour programmer les cartes STM32 Nucleo). Il demeure alors parfaitement possible
d'afficher à l'écran de l'ordinateur des informations qui proviennent du microcontrôleur, à la
condition d'utiliser un autre logiciel.
Cet autre logiciel peut être, par exemple, TeraTerm ou PuTTY (si vous utilisez Windows)
ou Moserial (si vous utilisez Linux). Mais, si vous le désirez, vous pouvez tout simplement
utiliser le moniteur série de l'IDE Arduino.
Le moniteur série (ou "serial monitor") de l'environnement Arduino est drôlement utile
lorsque vous avez besoin de déboguer un sketch, ou simplement d'afficher à l'écran d'un
ordinateur des valeurs mesurées par des capteurs branchés à l'Arduino.

6. Pour qu'une carte STM32 Nucleo envoie des informations à l'ordinateur par le câble USB, on
utilise la fonction "pc.printf", qui utilise la syntaxe habituelle de "printf" comme le montre
l'exemple ci-dessous, qui sera installé dans le Nucleo au moyen de l'IDE en ligne mbed.
#include "mbed.h"
Int compteur = 0 ;
Serial pc(USBTX,USBRX) ;
Int main() {
While(1) {
Compteur ++ ;
Pc.printf("Valeur du compteur: %irn", compteur) ;
Wait (0.5) ;
}
}

7. Notions « Timer » et « Interruption »
Objectifs
 Mettre en œuvre un timer matériel dans le cadre d’une interruption
 Créer des routines d’interruption
 Mettre en œuvre des timers logiciels basés sur un timer matériel
 Comprendre le principe d’interruption externe
 Mettre en œuvre les interruptions externes sur un microcontroleur STM32
 Mesurer le temps de calcul d’un traitement numérique
I/ Timer matériel
I.1. Principe de fonctionnement et Déclaration
Basé sur l’horloge interne de la carte de développement, ce module permet de générer une
interruption à intervalle de temps donné. Pour cela, il utilise un composant de
l’électronique numérique séquentielle : un compteur.
A chaque front montant d’un signal d’horloge, le compteur s’incrémente d’un pas de 1 entre 0
et une valeur limite N−1. A chaque passage par N−1, une interruption est générée sur le
microcontroleur et le compteur se réinitialise à 0. Il recommence à compter.
Ainsi, en connaissant parfaitement la période d’application de l’horloge, on peut en déduire le
temps qui s’est écoulé entre l’instant où le compteur valait 0 et le moment où il arrive à N−1:
ΔT=N⋅ TH.
la déclaration au compilateur de cet timer matériel se fait de la manière suivante
Ticker toggle_led_ticker;
Avec :
 ‘Ticker‘, la classe qui définit les objets de type timer matériel
 ‘toggle_led_ticker‘, le nom de la variable qui va être associée à cet objet
I.2. Routine d’interruption
Ce type d’objet génère ce qu’on appelle une interruption, c’est à dire un arrêt des
instructions en cours d’exécution puis un déroutement vers un bloc d’instructions à
exécuter à intervalle régulier. On appelle ce bloc d’instructions une routine d’interruption.
Cette routine est une fonction spécifique qu’il faut déclarer et définir dans le code.
Par exemple, on peut déclarer le fonction suivante :

8. void toggle_led(void); // Déclaration de la fonction d'interruption du ticker
void toggle_led() { // Fonction d'interruption du ticker
led1 = !led1;
}
Elle ne sera appelée nulle part dans le code. Elle sera exécutée lors d’un événement provoqué
par le débordement du timer matériel associé.
I.3. Paramètrage du timer matériel
Enfin, il est nécessaire d’initialiser ce ticker. Cette initialisation permet d’attacher la routine
d’interruption à laquelle il faut faire appel en cas de débordement du timer et également la
période de répétition de cet événement (i.e. les paramètres temporels du timer matériel :
fréquence d’horloge, valeur de N… pour avoir la meilleure approximation de la valeur
souhaitée).
Pour cela il faut utiliser la fonction attach().
Dans l’exemple ci-dessous on associe la fonction toggle_led() au ticker toggle_led_ticker
avec interruption chaque seconde.
toggle_led_ticker.attach(&toggle_led, 1);
I.4. Exemple
Voilà ci-dessous le code complet résultant des différentes parties de la description :
#include "mbed.h"
Ticker toggle_led_ticker; // Déclaration du ticker
DigitalOut led1(LED1); // Déclaration de la sortie numérique
void toggle_led(void); // Déclaration de la fonction d'interruption du ticker
int main() {
// Initialisation du ticker attaché à la fonction (toggle_led) et l'intervalle de temps (en
s)
toggle_led_ticker.attach(&toggle_led, 1);
while (1) {
// Boucle Infinie
}

9. }
void toggle_led() { // Fonction d'interruption du ticker
led1 = !led1;
}
On remarque dans ce code que la boucle infinie est vide. Elle est cependant essentielle pour
limiter l’exécution d’une zone de la mémoire programme qui ne nous appartient pas…
II/ Timer logiciel
Les modules matériels de gestion du temps ne sont pas en nombre suffisant pour certaines
applications afin de pouvoir traiter indépendamment toutes les actions à réaliser à intervalle
régulier. Il est parfois nécessaire de passer par des timers dits logiciels.
II.1. Principe de fonctionnement
Un timer logiciel est une variable du programme qui va servir de compteur. Celle-ci sera
décrémentée à chaque interruption d’un timer matériel (voir tutoriel Faire une action à
intervalle régulier). A l’aide de cette variable, on pourra alors compter le nombre de périodes
réalisées du timer matériel (dont on connait la période de répétition – TM). Ainsi, en
paramétrant bien la valeur initiale du compteur, à une valeur N, on pourra obtenir un temps
précis : ΔT=(N+1).TM
.
On peut ainsi déclarer une grande quantité de variables “timers”.
II.2. Fonctionnement en mode astable
Dans le cas où l’on souhaite réaliser une action à intervalle régulier dans le temps et de
manière répétée indéfiniment, on parle d’un fonctionnement astable. Le code suivant permet
d’obtenir un tel fonctionnement sur deux sorties différentes avec des périodes d’allumage et
d’extinction différentes, multiples d’un quantum de temps (1 ms dans cet exemple).
#include "mbed.h"
#define TIMER1 54
#define TIMER2 221
Ticker log_timer; // Déclaration du ticker
DigitalOut led1(LED1); // Déclaration de la sortie numérique
DigitalOut led2(D10); // Déclaration de la sortie numérique

10. int timer1, timer2; // variables compteurs
void toggle_cpt() {
if(timer1 != 0) timer1--;
if(timer2 != 0) timer2--;
}
int main() {
timer1 = TIMER1;
timer2 = TIMER2;
log_timer.attach(&toggle_cpt, 0.001);
while (1) {
if(timer1 == 0){
timer1 = TIMER1;
led1 = !led1;
}
if(timer2 == 0){
timer2 = TIMER2;
led2 = !led2;
}
// Boucle Infinie
}
}
Dans cet exemple, on paramètre un timer matériel à une période de 1. La routine
d’interruption associée à ce timer permet de décrémenter l’ensemble des compteurs
logiciels (variables entières) jusqu’à 0. Dans la boucle infinie du programme principal, on
teste en permanence le passage par 0 de ces compteurs logiciels. Lorsqu’ils arrivent à 0, on
les recharge à une valeur particulière (correspondant à la période associée à l’ensemble des
actions à réaliser).

11. Ici la sortie nommée LED1 “clignotera” à la période de 2 x 54 ms et la sortie nommée LED2
à la période de 2 x 221 ms.
II.3. Fonctionnement en mode monostable
On peut aussi avoir de déclencher une action pendant un temps donné : allumage d’une sortie
durant un temps prédéfini, temporisation d’une cage d’escalier… On parle alors d’un
fonctionnement en mode monostable.
La fin de l’action sera fixée par la durée de la temporisation et le début de l’action par un
événement extérieur : le passage d’une variable à une valeur particulière, l’appui sur un
bouton poussoir.
Dans l’exemple suivant, on déclenche une minuterie de 500 ms à partir de l’appui sur le
bouton-poussoir USER_BUTTON.
#include "mbed.h"
#define TIMER1 50
Ticker log_timer; // Déclaration du ticker
DigitalOut led1(LED1); // Déclaration de la sortie numérique
InterruptIn bp_int(USER_BUTTON); // Déclaration d'une entrée numérique /
interruption
int timer1; // variable compteur
void toggle_cpt() {
if (timer1 != 0) timer1--;
}
void routine_bp(){
timer1 = TIMER1;
led1 = 1;
}
int main() {
timer1 = TIMER1;
bp_int.fall(&routine_bp);
log_timer.attach(&toggle_cpt, 0.01);

12. while (1) {
if(timer1 == 0){
// FIN ACTION
led1 = 0;
}
// Boucle Infinie
}
}
Dans cet exemple, on paramètre un timer matériel à une période de 10 ms.
On paramètre également l’entrée USER_BUTTON comme entrée d’interruption, que l’on
attache à la fonction routine_bp. Celle-ci permet d’initialiser le compteur logiciel et de
réaliser l’action à faire sur l’appui sur le bouton poussoir (ici mettre à ‘1’ la sortie led1). Dans
la boucle infinie, dès que le compteur timer1 arrive à 0, on réalise une seconde action (ici
mettre à ‘0’ la sortie led1).
III/ Interruption externe
III.1. Généralité
Afin de pouvoir interagir plus rapidement avec son environnement et prendre en compte
des événements extérieurs dès qu’ils arrivent, la plupart des microcontrôleurs sont dotés d’une
capacité à interrompre l’exécution d’un programme pour se détourner vers une fonction
particulière à exécuter lors de l’arrivée de cet événement extérieur. On appelle cela une
interruption Externe.
Pour cela, le microcontrôleur possède plusieurs entrées particulières qui permettent
d’interrompre le programme principal. On verra dans des tutoriaux ultérieurs que d’autres
modules du microcontrôleur (timers, ADC,…) peuvent également venir interrompre
l’exécution du programme principal.
Cette méthode a pour intérêt qu’une sollicitation extérieure est prise en compte uniquement
quand elle intervient. Le calcul associé à ce changement est alors réalisé que si une
évolution dans les signaux d’entrée intervient.
Cette stratégie est la base des systèmes embarqués dits temps réel. Lors du développement
d’une telle application, les concepteurs assurent que toute sollicitation extérieure aura une
réponse dans un temps donné et défini à l’avance (en fonction des performances des
systèmes matériels choisis).

13. III.2. Déclaration d’une entrée d’interruption
Toutes les broches du microcontroleur présent sur les cartes Nucléo L476RG sont utilisables
comme source externe d’interruption.
La première étape est la déclaration au compilateur de cette broche en entrée d’interruption.
Cela peut se faire de la manière suivante :
InterruptIn mon_int(PA_12);
Dans l’exemple précédent, on configure la broche PA_12 (du connecteur Morpho) en entrée
numérique d’interruption. Dans ce code, il y a trois notions importantes :
 ‘InterruptIn‘, la classe définit le type de la broche, ici une entrée numérique
d’interruption
 ‘mon_int‘, le nom de la variable qui va être associée au port donné dans les
parenthèses
 ‘PA_12‘, le nom de la broche que l’on va associer sur le composant
III.3. Routine d’interruption
Une routine est une fonction appelée automatiquement par le microcontroleur. Dans le cas
des interruptions externes, on peut associer une fonction spécifique à une broche d’entrée
d’interruption.
Avant de pouvoir l’affecter à telle ou telle interruption, il faut d’abord écrire cette fonction
d’interruption. Cette fonction doit se trouver en dehors de toute autre fonction. Son prototype
doit être rappelé avant la fonction main.
#include "mbed.h"
void fonction_interruption1(void);
void main(void){
...
while(1){
...
}
}
/* Routine d'interruption */
void fonction_interruption1(void)

14. {
// ACTIONS A REALISER LORS DE L'ACTIVATION DE L'INTERRUPTION 1
La plupart du temps, on cherche à détecter un changement d’état d’une entrée. Deux
événements sont alors possibles avec une entrée numérique :
 un front montant, le passage d’un ‘0’ à un ‘1’
 un front descendant, le passage d’un ‘1’ à un ‘0’
Il est alors possible d’attacher à la broche d’interruption déclarée précédemment deux actions
différentes en fonction de l’événement que l’on cherche à détecter. Pour cela, il existe deux
fonctions dans la classe InterruptIn associée à la gestion des interruptions externes :
 rise() : détection d’un front montant
 fall() : détection d’un front descendant
N.B. La détection d’un niveau constant (‘0’ ou ‘1’) peut se faire sans l’utilisation des
interruptions. C’est pourquoi ces fonctions ne sont pas implémentées dans la partie gestion
des interruptions externes.
Pour associer une fonction à un changement d’état de type front montant, il faut utiliser la
fonction suivante sur l’entrée à associer :
mon_int.rise(&fonction_interruption1);
Pour associer une fonction à un changement d’état de type front descendant, il faut utiliser la
fonction suivante sur l’entrée à associer :
mon_int.fall(&fonction_interruption1);
Dans les deux cas précédents, on associe la fonction nommée fonction_interruption1 à un
changement d’état de l’entrée mon_int (associée à la broche PA_12).
III.4. Exemple d’application :
On propose l’exemple suivant :
#include "mbed.h"
InterruptIn mybutton(USER_BUTTON); // Déclaration de l'interruption
DigitalOut myled(LED1); // Déclaration de la sortie numérique
void pressed(void); // Déclaration de la fonction d'interruption 1
void released(void); // Déclaration de la fonction d'interruption 2
int delay = 1000000; // 1 sec ou 10^6 us

15. void pressed(){ // fonction d'interruption 1
delay = delay>>3;
}
void released(){ // fonction d'interruption 2
delay = delay<<3;
}
int main(){
mybutton.fall(&pressed); // association de l'interruption 1 a un front descendant sur
l'entree USER_BUTTON
mybutton.rise(&released); // association de l'interruption 2 a un front montant sur
l'entree USER_BUTTON
while(1) {
myled=!myled;
wait_us(delay);
}
}
VI/ Utilisation du Timer pour mesurer le temps de calcul d’un traitement
numérique
Ce type de système doit souvent répondre à des sollicitations extérieures (prise
d’information sur des capteurs…) le plus rapidement possible (systèmes dits temps réel).
Pour cela, le programme embarqué dans un tel système utilise des instructions qui prennent
chacune un certain temps pour être exécuté.
Il est intéressant de pouvoir mesurer le temps de calcul d’une chaîne de traitement
numérique afin de pouvoir caractériser son système, en particulier pour connaître le temps de
réponse à une sollicitation extérieure.
VI.1. Principe
Les modules Timer sont basés sur un compteur interne au microcontroleur, sur lequel on
peut modifier la fréquence d’entrée à laquelle ce compteur s’incrémente. Ainsi, il est possible
de déterminer le temps qu’il s’est écoulé entre un instant t0 où ce compteur aura une valeur
N0 et un instant t1 où ce compteur sera arrivé à une valeur N1.

16. En effet, chaque pas d’incrémentation a pour durée la période du signal d’horloge associée au
module Timer. Ainsi, Δt= t1–t0 =(N1–N0)⋅ TH (où TH est la période du signal d’horloge).
VI.2. Méthode de mesure
C’est à partir de l’un de ces modules de Timer (au nombre de 3 différents sur les cartes
Nucléo L476RG) que se base la méthode proposée ici.
En premier lieu, il est nécessaire de déclarer le module Timer grâce à la ligne de code ci-
dessous :
Timer t;
Par la suite, il faut l’initialiser avec la ligne de code suivante.
t.reset();
Enfin, il s’utilise de la façon suivante :
t.start();
... // bloc à caractériser
t.stop();
Une fois le module Timer démarré (start) puis arrêté (stop), il est intéressant de pouvoir lire
la valeur obtenue entre ces deux instants. Pour cela, il existe une fonction nommée read() qui
retourne un nombre réel correspondant au nombre de secondes écoulées.
A travers la liaison série, il est possible de l’afficher de cette façon :
float t_ecoule = t.read();
pc.printf("The time taken was %f secondsn", t_ecoule);
N.B. Il existe deux autres fonctions de lecture read_ms() et read_us() qui renvoie un nombre
entier correspondant respectivement au nombre de millisecondes écoulées et au nombre de
microsecondes écoulées.
Voici ci-dessous un exemple complet de mesure de temps par Timer.
#include "mbed.h"
Timer t;
Serial pc(SERIAL_TX, SERIAL_RX);
int main()
{

17. while(1) {
t.reset();
t.start();
pc.printf("Hello World!n");
t.stop();
pc.printf("The time taken was %f secondsn", t.read());
pc.printf("The time taken was %d millisecondsn", t.read_ms());
pc.printf("The time taken was %d µsecondsn", t.read_us());
VI.3. Application :
Ecrire un programme qui affiche le temps écoulé pour traiter une seule lecture du signal
transmis par le capteur de luminosité relié à la broche A0 de la carte STM32.

18. Traitement Numérique du Signal
I/ Convertisseurs ADC et DAC :
Sur les systèmes numériques, et les microcontrôleurs en particulier, les broches sont
naturellement des entrées/sorties numériques.
Or, certains actionneurs doivent être pilotés à l’aide de grandeurs analogiques. Pour palier à
ce manque, la plupart des fabricants de microcontrôleurs ont intégré des convertisseurs
numériques-analogiques (DAC – Digital to Analog Converter) et numériques-
analogiques (ADC – Analog to Digital Converter) à leur système, afin d’éviter de passer par
des composants externes.
Le programme de traitement numérique devra alors réaliser les tâches suivantes:
- Echantilloner le signal d’entrée, à intervalle régulier
- Effectuer le calcul de la sortie à partir du nouvel échantillon, des précédents (stockés
en mémoire) et des coefficients du filtre
- Convertir la valeur de sortie de ce module de traitement en valeur analogique

19. Les cartes Nucleo L476RG possèdent 3 convertisseurs analogiques numériques de 12
bits (c’est à dire convertissant des tensions allant de 0 à 3.3V sur 4096 niveaux différents).
Chacun de ses convertisseurs peut échantillonner un signal jusqu’à 5 MHz.
NB : Les cartes Nucléo ne peuvent convertir que des tensions comprises entre 0 et 3.3V !!
Les cartes Nucleo L476RG possèdent 1 convertisseur numérique-analogique de 12 bits (c’est
à dire convertissant des tensions allant de 0 à 3.3V sur 4096 niveaux différents). Chacun de
ses convertisseurs peut restituer un signal jusqu’à 5 MHz.
I.1. Convertisseur ADC
Il existe deux façons différentes de récupérer une valeur analogique :
- la fonction float read() qui représente la tension d’entrée par un nombre réel compris
entre 0.0 et 1.0 (représentant un pourcentage de la tension réellement appliquée sur
l’entrée analogique) : Voir partie III.2 de la première séance
- la fonction int read_u16() qui représente la tension d’entrée par un entier non signé sur
16 bits (seuls les 12 bits de poids fort sont utilisés sur les 16 bits, pour stocker le
résultat de la conversion sur les cartes L476RG)
Le résultat brut acquis par le convertisseur est sur 12 bits (cas de la carte Nucleo L476RG). Le
résultat est justifié à gauche sur l’entier fourni par la fonction read_u16(), ce qui signifie que
les 4 bits de poids faible sont toujours à 0.

20. Pour obtenir la valeur sur 12 bits retournée par l’ADC à partir de la valeur transmise par la
fonction read_u16, il faut effectuer un décalage de l’information de 4 bits vers la droite :
int valeur_ADC; // valeur entre 0 et 4095 (12 bits)
int valeur_transmise = analog_in.read_u16();
valeur_ADC = valeur_transmise >> 4;
Le programme suivant va récupérer les valeurs sur l’entrée analogique A0 (connecteur
Arduino), transformer l’information pour obtenir une tension en Volt et l’envoyer sur la
liaison série de deux façons : la valeur brute (sur 12 bits positionnés en poids fort d’une
variable entière sur 16 bits) et la valeur convertie en Volt.
#include "mbed.h"
AnalogIn entree_analog(A0);
Serial pc(USBTX, USBRX);
int main()
{
pc.baud(115200);
int meas_int;
double tension;
while(1) {
meas_int = entree_analog.read_u16(); // sur 12 bits MSB
pc.printf("Tension = %d n", meas_int);
tension = meas_int / 65536.0 * 3.3; // en V
pc.printf("Tension = %lf V n", tension);
wait(1.0);
}
}
I.2. Convertisseur DAC
Le convertisseur présent sur ces cartes possède deux sorties indépendantes (notées
AnalogOut sur les connecteurs de la carte).

21. Il existe deux façons différentes de définir la valeur de la sortie analogique :
la fonction void write(float val) qui représente la tension de sortie par un nombre réel compris
entre 0.0 et 1.0 (représentant un pourcentage de la tension réellement appliquée sur la sortie
analogique entre 0 et 3.3V) :
la fonction void write_u16(int val) qui convertit un entier non signé sur 16 bits passé en
paramètre vers une tension entre 0 et 3.3V
Ecriture avec write(double val) :
Dans le code ci-dessous, on incrémente, toutes les microsecondes, la valeur de la variable
value par pas de 0.1, de 0 à 1 (puis on la refait passer à 0). Cette variable est ensuite passée en
paramètre de la fonction write qui l’envoie sur la sortie analogique nommée out (sur la broche
PA_4 du composant).
La tension de sortie vaut alors : VS=value⋅3.3V.
#include "mbed.h"
AnalogOut analog_out(PA_4);
int main()
{
double value=0.00;
while(1) {
value = value + 0.10;
wait_us(1);
if(value>=1.00) {
value =0.00;
}
analog_out.write(value);
}
}

22. Ecriture avec write_u16(int val) :
Dans le code ci-dessous, nous utilisons la conversion à l’aide de la fonction write_u16(int val)
qui prend en paramètre un nombre entier compris entre 0 et 65535.
#include "mbed.h"
AnalogOut analog_out(PA_4);
int main()
{
unsigned short value=0;
while(1) {
value = value + 0.1 * 65535;
wait_us(1);
if(value>=65535) {
value =0;
}
analog_out.write_u16(value);
}
}
Ce code permet d’incrémenter, toutes les microsecondes, la valeur de la variable value par pas
de (0.1⋅65535), de 0 à 65535 (puis on la refait passer à 0) – N.B. 65535=216–1
Cette variable est ensuite passée en paramètre de la fonction write_u16 qui l’envoie sur la
sortie analogique nommée out (sur la broche PA_4 du composant).
NB : La valeur à transmettre est un nombre entier sur 16 bits. Or le convertisseur numérique-
analogique attend une information binaire sur 12 bits. Le paramètre attendu dans la fonction
write_u16(int val) est une valeur de 12 bits justifiée à gauche sur un entier de 16 bits.
Entre la valeur sur 12 bits attendue par le DAC et la valeur à transmettre à la fonction
write_u16, il faut effectuer un décalage de l’information de 4 bits vers la gauche :
int valeur_DAC = 200; // valeur entre 0 et 4095 (12 bits)

23. int valeur_transmise = valeur_DAC << 4;
out.write_u16(valeur_transmise);
I.3. Génération d’un signal sinusoïdale
Dans les 2 exemples suivants, on génère un signal sinusoïdal centré autour de 1.65V :
Exemple 1 :
#include "mbed.h"
/* Tableau contenant les points du sinus */
const int sinu[64] = { 2048, 2149, 2250, 2349, 2445, 2537, 2624, 2706,
2781, 2848, 2908, 2959, 3001, 3033, 3056, 3069,
3071, 3064, 3046, 3018, 2981, 2934, 2879, 2815,
2744, 2666, 2581, 2492, 2398, 2300, 2200, 2099,
1996, 1895, 1795, 1697, 1603, 1514, 1429, 1351,
1280, 1216, 1161, 1114, 1077, 1049, 1031, 1024,
1026, 1039, 1062, 1094, 1136, 1187, 1247, 1314,
1389, 1471, 1558, 1650, 1746, 1845, 1946, 2048};
/* Déclaration de la sortie analogique */
AnalogOut analog_out(PA_4);
/* Programme principal */
void main(void){
int i = 0;
while(1){
for(i = 0; i < 64; i++){
analog_out.write(sinu[i]/4096.0);
wait_ms(10);

24. }
}
}
Exemple 2 :
#include "mbed.h"
AnalogOut analog_value(PA_4);
//DigitalOut led(LED1);
float da;
float Amp = 1.0;
float w = 1.0;
float pi = 3.14159;
float deltaT = 0.01;
int main() {
int i;
while(1) {
for ( i=0; i<(360); i++) {
da = Amp*(sin(w*i/(180)*pi)*0.5+0.5);
analog_value.write(da);
}

25. wait(deltaT); // 10 ms
}
}
Nous pouvons aussi générer un signal sinusoïdale en utilisant les sorties PWM de la carte. Un
exemple d’application est donné par ce lien :
https://os.mbed.com/users/wim/notebook/pwm-to-generate-analog-waveforms-/
II/ Signaux sonores
Les signaux audibles par l’être humain sont compris dans une bande de fréquence de 20 Hz à
20 kHz.
Cette plage de fréquence reste théorique. Elle évolue au cours de la vie d’un être humain,
notamment la fréquence maximale qui a tendance à diminuer avec l’age.
D’autre part, les fréquences entre 1 et 50 Hz sont également difficilement perceptibles par
l’oreille humaine. Par contre, elles peuvent être ressenties par les corps.
II.1. Acquisition d’un signal sonore
Si le son est avant tout une onde vibratoire perceptible par l’oreille humaine, il est souvent
transporté par un signal électrique de même fréquence que l’onde initiale.
Ces ondes sont récupérées à l’aide d’un microphone (par exemple), qui est une membrane
reliée à un système de conversion électrique. Le signal résultant est alors une tension
électrique centrée autour de 0V et dont le signe de la variation dépend du sens de déplacement
de la membrane.

26. Ces signaux sont ensuite souvent stockés sous la forme de données numériques (CD, disque
dur…). Afin de pouvoir respecter le critère de Nyquist-Shannon, les systèmes d’acqusition
numérique du son ont des fréquences d’échantillonnage allant de 44kHz à 96kHz. La plupart
convertisse ces données sur 16 bits. C’est le cas par exemple des CD audio : 16 bits à une
fréquence de 44kHz.
Les fichiers audios peuvent être lus directement à partir d’un PC hôte sur une broche d’entrée
analogique de la carte.
Le signal peut également être visualisé sur un oscilloscope, ce qui montre que le signal oscille
positif et négatif à propos de 0 V.
Ce n’est pas très utile pour la carte Nucleo, car elle ne peut lire que des données analogiques
comprises entre 0 et 3,3 V; toutes les données négatives seront interprétées comme 0 V.
Il faut donc ajouter un petit circuit de couplage et de polarisation pour décaler le signal jusqu'à
un point milieu d'environ 1,65 volts.
On peut utiliser le circuit ci-dessous qui permet de supprimer une éventuelle composante
continue (filtre C-R passe-haut avec C=10μF polarisé et Req=R/2) et ajouter un offset
constant égal à VCC/2

27. Le filtre d’entrée a une fréquence de coupure égale à 1/(π⋅R⋅C).
II.2. Restitution d’un signal sonore :
La restitution d’un son se fait dans le sens inverse de son acquisition. Un signal électrique
vient déplacer une membrane qui elle-même fait vibrer l’air qui l’entoure. Mais faire
déplacer une membrane, aussi petite qu’elle soit, nécessite souvent un courant important et
donc de la puissance.
Si vous regardez de près les signaux audio entrants et sortants de la carte Nucleo, vous verrez
que la sortie DAC a des étapes discrètes. Ceci est plus évident dans le signal haute fréquence
comme il est plus proche de la fréquence d'échantillonnage choisie.
Avec de nombreux systèmes DSP audio, la sortie analogique du DAC est convertie en un
signal reconstruit en mettant en œuvre un filtre de reconstruction analogique, cela supprime
tout pas du signal en laissant une sortie lisse.
Dans les applications audios, un filtre de reconstruction est généralement conçu pour être un
filtre passe-bas avec une fréquence de coupure à environ 20 kHz, car l’audition humaine ne
peux pas traiter les signaux avec des fréquences au-delà de 20 kHz.
Le filtre de reconstruction montré ci-dessous peut être mis en œuvre pour donner un signal de
sortie lisse en supprimant les paliers dus à l’échantillonnage (CNA) et la composante
continue.

28. Notez qu'après le filtre passe-bas, un condensateur de découplage est également ajouté pour
supprimer le DC-offset de 1.65 V.
II.3. Code de test :
Dans cet exemple, le signal de sortie recopie le signal d’entrée. Cela permet de vérifier le bon
fonctionnement des étages de conversion, avant même l’ajout d’un calcul intermédiaire.
La relation entre l’entrée et la sortie est alors du type : s[n]=e[n]
#include "mbed.h"
#define TE 0.00003
#define SAMPLE_RATE 1/TE
void convert(void);
/* E/S */
AnalogIn mesure(A0); // A0 on Arduino Header
AnalogOut analog_out (PA_5);
/* Timer a repetition */
Ticker tik;
float in, out;
int main() {

29. /* Association de la fonction convert à un timer */
tik.attach(&convert, TE);
while(1) {
}
}
void convert(void){
in = mesure.read(); // Lecture de l'entree analogique
out = in;
analog_out.write(out); // Ecriture de la sortie analogique
}
Dans le code précédent, on peut également noter que l’acquisition du signal d’entrée (nommé
mesure) et de la restitution de ce même signal vers la sortie (signal nommé analog_out) se fait
à intervalle régulier (ici 30 us – soit une fréquence d’échantillonnage de 33kHz) grâce à
l’utilisation d’un module de gestion du temps par interruption, le Ticker tik.
III. Filtrage Numerique
Les filtres permettent de sélectionner des intervalles de fréquences à supprimer ou à conserver
dans un signal. On supprime les fréquences aigues d’un signal sonore par exemple.
La Figure ci-dessous montre un signal avec des composants basse fréquence et haute
fréquence à la fois et comment nous pouvons garder seulement la fréquence désirée en
utilisant un filtre Passe-haut ou Passe-Bas.

30. Les premiers filtres que vous avez étudié sont des filtres analogiques, réalisés :
 soit avec des composants uniquement passifs (résistances, inductances, capacités), on
parle de filtres analogiques passifs
 soit avec des composants actifs également (amplificateurs linéaires intégrés), on parle
de filtres analogiques actifs. On peut citer par exemple les structures de Rauch ou de
Sallen-Key (de deuxième ordre) ou bien encore des filtres universels (type UAF42)
 soit avec des composants actifs à capacité commutée, on parle de filtres à capacités
commutées
Les premiers filtres sont difficilement reconfigurables. En effet, le choix des composants
passifs imposent les diverses fréquences caractéristiques et le type de filtre. Les derniers cités,
les filtres à capacités commutées, ont la particularité d’avoir une fréquence de coupure
ajustable en fonction d’un signal d’horloge externe. Cependant, la plupart du temps, ils ne
permettent que de réaliser des filtres passe-bas.
Si l’on souhaite rendre totalement reconfigurable un système de filtrage, il faut alors passer
par le monde du numérique.
Il existe 2 types de filtres numériques permettant de travailler sur des échantillons réels :
- Les filtres non-récursifs ou à réponse impulsionnelle finie (FIR – Finite Impulse
Response) :
- Les filtres récursifs ou à réponse impulsionnelle infinie (IIR – Infinite Impulse
Response)
Avant de concevoir un filtre, il faut définir son gabarit, c’est à dire ses différentes
spécificités : fréquences caractéristiques, atténuation autorisée…
Voici les 4 gabarits associés aux 4 grands types de filtres possibles :

31. Dans le cas de filtres numériques, on parle souvent de fréquence réduite ν. Il s’agit de la
fréquence considérée (f) ramenée à la fréquence d’échantillonnage (Fe ou Fs). Ainsi : ν=f/Fe.
Elle est souvent appelée W sous Matlab.
 G0 : gain (en dB) dans la bande passante (souvent 0 dB)
 FS ou Fe : fréquence d’échantillonnage (en Hz)
 W=f/FS : fréquence réduite (ou normalisée)
 Rpass : variation maximale de gain possible dans la bande passante (en
dB)
 Astop : valeur maximale de gain (par rapport au gain dans la bande
passante) autorisée dans la bande atténuée (en dB)
 Wpx : fréquences caractéristiques de la bande passante
 Wsx : fréquences caractéristiques de la bande atténuée
III.1. Les Filtres FIR :
Ce sont des filtres dits non-récursifs. La sortie est calculée uniquement avec une série
d’échantillons d’entrée. Ils ont une structure de ce type :

32. Chacun des nouveaux échantillons de sortie est calculée en fonction de M
échantillons d’entrée, auxquels on associe des coefficients permettant de donner la réponse
impulsionnelle souhaitée au filtre (i.e. sa réponse en fréquence… tout est qu’une question de
référentiel de travail – temporel ou fréquentiel).
L’ordre d’un tel filtre est M.
a) Conception sous Matlab :
Plusieurs logiciels existent pour concevoir des filtres numériques FIR. Nous utiliserons
Matlab et sa boite à outils Filter Designer.
Nous allons concevoir un filtre de type passe-haut, de fréquence d’échantillonnage de 10kHz,
de fréquence de bande-passante de 4kHz (avec 1dB de différence de gain maximale dans cette
bande), de fréquence de bande atténuée de 3kHz (avec -80dB dans cette bande).
Pour ce faire, il suffit de suivre les étapes suivantes :
- Lancez Matlab. Puis, dans l’onglet APPS, sélectionnez Filter Designer (dans la
rubrique Signal Processing and Communications).
- Saisir les différents paramètres et cliquer sur le bouton Design Filter.
- Vérifier si le filtre créé a un comportement fréquentiel conforme avec celui attendu,
sinon, modifier certaines valeurs et de relancer la conception du filtre (bouton Design
Filter)
Si tout est bien validé, Il est possible à présent obtenir de cette réponse les différents
coefficients du filtre afin de pouvoir l’implémenter dans un calculateur en suivant ces
etapes :
- Aller dans le menu Targets et de sélectionner Generate C Headers
- Choisir un format de type : Single precision float (plus adequat pour limplementation
sur les Nucleo).
- Cliquer sur Generate et stocker le fichier header (extension .h) où vous le souhaitez.
Ceci vous permet d’avoir un code contient un tableau avec les coefficients du filtre, nommé
(par défaut) B, et le nombre de coefficients associés, nommé BL.

33. b) Implementation sur la carte Nucleo :
Une première étape à valider avant d’intégrer la partie filtrage numérique est la mise en œuvre
des deux modules de conversion : analogique-numérique (ADC) et numérique-analogique
(DAC). Pour cela, il peut être intéressant de revenir sur le code de test donné dans la partie
II.3.
Après validation de la chaine d’acquisition et restitution, il est temps d’intégrer l’élément
central de ce traitement numérique, l’étape de filtrage numérique.
Pour cela, une bibliothèque, nommée mbed-dsp, est à votre disposition : vous sera remis par
l’enseignant ou vous pouvez la telecharger directement du site MbedOS:
http://developer.mbed.org/users/mbed_official/code/mbed-dsp/ .
Elle contient tous les objets en lien avec les filtres FIR et les méthodes permettant la mise en
place de la structure matérielle associée à un filtre de type FIR.
Importez-la dans votre projet (Cliquez droit sur votre projet, puis Import Library / From
Import Wizard, puis Upload, sélectionnez le fichier zip contenant la bibliothèque, puis Import
/ Import).
Cette bibliothèque contient en particulier les objets et méthodes suivants :
- arm_fir_instance_f32 : type permettant de construire un objet de type filtre FIR, dont
les coefficients sont des flottants sur 32 bits
- arm_fir_init_f32 : fonction permettant d’initialiser la structure matérielle d’un filtre
FIR, dont les coefficients sont des flottants sur 32 bits
- arm_fir_f32 : fonction permettant de calculer la nouvelle sortie d’un filtre FIR, dont
les coefficients sont des flottants sur 32 bits
Il faut, dans un premier temps, ajouter à votre projet précédent (contenant le code de base
pour l’acquisition et la restitution des données analogiques) le tableau des coefficients et le
nombre de coefficients, en dehors de toute fonction.
/*
* Coefficients du filtre
*/
const int BL = 53;
float32_t B[53] = {
-1.923207674e-05,8.679173334e-05,-0.0001035222012,-9.687029524e-
05,0.0004889828269,
-0.0006440563011,-8.671574244e-19, 0.001367349061,-0.002238002373,
0.000988851185,

34. 0.00250719348, -0.0055896868, 0.004243299831, 0.002845831681, -0.01105924882,
0.01178205013,-3.774590571e-17, -0.0181965474, 0.02652300335, -0.01072031818,
-0.02558417059, 0.05551689863, -0.04286225513, -0.03121924214, 0.1481076032,
-0.2561196983, 0.2999954224, -0.2561196983, 0.1481076032, -0.03121924214,
-0.04286225513, 0.05551689863, -0.02558417059, -0.01072031818, 0.02652300335,
-0.0181965474,-3.774590571e-17, 0.01178205013, -0.01105924882,
0.002845831681,
0.004243299831, -0.0055896868, 0.00250719348, 0.000988851185,-
0.002238002373,
0.001367349061,-8.671574244e-19,-0.0006440563011,0.0004889828269,-
9.687029524e-05,
-0.0001035222012,8.679173334e-05,-1.923207674e-05
};
Il faut ensuite initialiser, en dehors de toute fonction également, les différentes structures qui
accueilleront les résultats intermédiaires des calculs. Pour cela, il faut
float32_t state[BL];
arm_fir_instance_f32 fir;
La première ligne permet de créer un tableau où seront stockées les derniers échantillons
acquis (nécessaires pour le calcul de la sortie du filtre). La seconde ligne permet de créer un
objet de type filtre FIR, dont les coefficients sont des flottants sur 32 bits.
Par la suite, il faut faire appel à la fonction qui va initialiser la structure matérielle, basée sur
le tableau précédent et les coefficients du filtre. Pour cela, il faut faire appel à la fonction
suivante, une seule fois dans le main (par exemple) :
arm_fir_init_f32(&fir, BL, B, state, 1);
Les paramètres à lui fournir sont : l’objet de type filtre FIR (ici fir), le nombre de coefficients
(ici BL), le tableau contenant les coefficients (ici B), le tableau permettant de stocker tous les
échantillons nécessaires (ici state) et le nombre total d’entrées à utiliser (ici une seule entrée,
car un seul filtre calculé).
Enfin, il faut faire appel régulièrement à la fonction qui exécutera le traitement numérique des
données par l’intermédiaire de la fonction suivante :
arm_fir_f32(&fir, &in, &out, 1);

35. Les paramètres à lui fournir sont : l’objet de type filtre FIR (ici fir), le nouvel échantillon (ici
in), la valeur de sortie (ici out) et le nombre total d’entrées à utiliser (ici une seule entrée, car
un seul filtre calculé).
Code Complet :
#include "mbed.h"
#include "dsp.h"
#define TE 0.00003
#define SAMPLE_RATE 1/TE
const int BL = 53;
float32_t B[53] = {
-1.923207674e-05,8.679173334e-05,-0.0001035222012,-9.687029524e-
05,0.0004889828269,
-0.0006440563011,-8.671574244e-19, 0.001367349061,-0.002238002373,
0.000988851185,
0.00250719348, -0.0055896868, 0.004243299831, 0.002845831681, -0.01105924882,
0.01178205013,-3.774590571e-17, -0.0181965474, 0.02652300335, -0.01072031818,
-0.02558417059, 0.05551689863, -0.04286225513, -0.03121924214, 0.1481076032,
-0.2561196983, 0.2999954224, -0.2561196983, 0.1481076032, -0.03121924214,
-0.04286225513, 0.05551689863, -0.02558417059, -0.01072031818, 0.02652300335,
-0.0181965474,-3.774590571e-17, 0.01178205013, -0.01105924882,
0.002845831681,
0.004243299831, -0.0055896868, 0.00250719348, 0.000988851185,-
0.002238002373,
0.001367349061,-8.671574244e-19,-0.0006440563011,0.0004889828269,-
9.687029524e-05,
-0.0001035222012,8.679173334e-05,-1.923207674e-05
};
float32_t state[BL];
arm_fir_instance_f32 fir;

36. void convert(void);
/* E/S */
AnalogIn mesure(A0); // A0 on Arduino Header
AnalogOut analog_out(PA_5);
/* Timer a repetition */
Ticker tik;
float in, out;
int main() {
arm_fir_init_f32(&fir, BL, B, state, 1);
tik.attach(&convert, TE);
while(1) {
}
}
void convert(void){
in = mesure.read();
arm_fir_f32(&fir, &in, &out, 1);
analog_out.write(out);
}
III.2. Filtres IIR :
Ces filtres récursifs ont une structure de ce type :

37. Contrairement à la précédente structure, ces filtres dits récursifs calculent leurs échantillons
de sortie à la fois en se basant sur une série de M échantillons d’entrée, mais en se basant
également sur une série des N précédents échantillons de sortie.
L’ordre d’un tel filtre est donné par le maximum entre N et M.
Il est a noter que ces filtres permettent généralement d’obtenir des ordres bien inférieurs aux
filtres non-récursifs, pour un gabarit quasi-identique (i.e. des fréquences caractéristiques
similaires pour une fréquence d’échantillonnage égale et des gains identiques dans les
différentes zones utiles du gabarit). Ceci permet donc de gagner en temps de calcul.
Cependant, ce type de filtre est plus difficile à mettre en oeuvre par leur rebouclage qui peut
entrainer une instabilité.
a) Conception sous Matlab
Plusieurs logiciels existent pour concevoir des filtres numériques. Nous utiliserons Matlab,
cette fois-ci sans sa boite à outils Filter Designer, car les filtres ainsi conçus n’ont pas la
structure que permet d’implémenter les cartes Nucléo. En effet, ces dernières permettent
l’implantation de structure de type Lattice.
Il est à noter que la démarche proposée ici se base sur les fréquences réduites ν=f/Fe (où f est
la fréquence considérée et Fe la fréquence d’échantillonnage souhaitée).
Nous allons voir ici une méthode permettant de définir le gabarit du filtre de manière non
graphique et d’en afficher sa réponse en fréquence. Ce tutoriel est basé sur la page de
Mathworks : https://fr.mathworks.com/help/signal/ug/iir-filter-
design.html?requestedDomain=true
Il existe 4 grands types de filtres IIR, dits classiques, concevables avec Matlab :
Butterworth : [b,a] = butter(n,Wn,options)
Chebyshev Type I : [b,a] = cheby1(n,Rp,Wn,options)
Chebyshev Type II : [b,a] = cheby2(n,Rs,Wn,options)
Elliptic : [b,a] = ellip(n,Rp,Rs,Wn,options)

38. Matlab propose alors 4 fonctions associées à la conception de ces filtres (voir ci-dessus).
Chacune d’entre elles fournit les coefficients β (b) et α (a) du filtre numérique associé. Par
défaut les filtres réalisés sont de type passe-bas.
Dans tous les cas, il est nécessaire de préciser plusieurs paramètres :
 n : l’ordre du filtre
 Wn : un ensemble de fréquences caractéristiques (normalisées / réduites)
 Rp : le taux d’ondulation autorisée dans la bande passante (en dB)
 Rs : la valeur minimale d’atténuation dans la bande atténuée (en dB)
Remarque : Il est à noter que l’on peut ajouter certaines options à l’ensemble de ces fonctions.
Parmi ces options, il est possible de spéficier le type de filtre que l’on souhaite : ‘high’ pour
un filtre passe-haut (à partir d’un modèle passe-bas) et ‘stop’ pour un filtre coupe-bande (à
partir d’un modèle passe-bande).
Gabarit et conception
Pour pouvoir calculer la réponse en fréquence (par exemple) et les coefficients du filtre qui
seront utilisés pour l’implémentation sur la carte Nucléo, il est donc indispensable de
connaître l’ordre du filtre (noté n) et les fréquences caractéristiques de coupure (notées
Wn).
Pour cela, Matlab propose d’autres fonctions qui permettent à partir du gabarit du filtre de
récupérer ces informations.
Butterworth : [n,Wn] = buttord(Wp,Ws,Rp,Rs)
Chebyshev Type I : [n,Wn] = cheb1ord(Wp,Ws,Rp,Rs)
Chebyshev Type II : [n,Wn] = cheb2ord(Wp,Ws,Rp,Rs)
Elliptic : [n,Wn] = ellipord(Wp,Ws,Rp,Rs)
Filtre passe-bas
Par exemple, on pourra utiliser le code Matlab suivant pour générer un filtre passe-bas de
fréquence d’échantillonnage de 10kHz, de bande passante 0-3.5kHz (variation de 1dB
autorisée) et de bande atténuée 4-5kHz (à 60 dB en dessous du gain dans la bande passante) :
Fs = 10e3;
Fpass = 3.5e3; Wpass = Fpass/Fs;
Fstop = 4e3; Wstop = Fstop/Fs;
Apass = 1;
Astop = 60;

39. [n1, Wn1] = buttord(Wpass, Wstop, Apass, Astop)
[n2, Wn2] = cheb1ord(Wpass, Wstop, Apass, Astop)
[n3, Wn3] = cheb2ord(Wpass, Wstop, Apass, Astop)
[n4, Wn4] = ellipord(Wpass, Wstop, Apass, Astop)
Ce code fournit alors l’ordre n de chacun des types de filtres, ainsi que la fréquence
caractéristique dans Wn .
Filtre passe-bande
Pour concevoir un filtre passe-bande de fréquence d’échantillonnage de 10kHz, de bande-
passante 2-3.5kHz (variation de 3 dB) et de bandes atténuées 0-1.5kHz et 4-5kHz (à 80 dB en
dessous du gain dans la bande passante)
on pourra utiliser le code Matlab suivant pour générer un filtre passe-bas de fréquence
d’échantillonnage de 10kHz, de bande passante 0-3.5kHz (variation de 1dB autorisée) et de
bande atténuée 4-5kHz (à 80 dB en dessous du gain dans la bande passante) :
Fs = 10e3;
Fpass = [2e3 3.5e3]; Wpass = Fpass/Fs;
Fstop = [1.5e3 4e3]; Wstop = Fstop/Fs;
Apass = 1;
Astop = 80;
[n, Wn] = buttord(Wpass, Wstop, Apass, Astop);
Filtres passe-haut et coupe-bande
Pour la conception de filtres passe-haut et coupe-bande, ce sont les mêmes fonctions que
précédemment. Seules les fréquences Fpass et Fstop sont inversées pour coller au gabarit.
C’est lors de la génération des coefficients que l’on choisit définitivement le type de filtre que
l’on souhaite.
Génération des coefficients
Il est maintenant possible de générer les différents coefficients du filtre afin de pouvoir
l’implémenter dans un calculateur et d’en obtenir la réponse en fréquence.
Pour cela, on va s’appuyer sur les fonctions suivantes :

40. Butterworth : [b,a] = butter(n,Wn,options)
Chebyshev Type I : [b,a] = cheby1(n,Rp,Wn,options)
Chebyshev Type II : [b,a] = cheby2(n,Rs,Wn,options)
Elliptic : [b,a] = ellip(n,Rp,Rs,Wn,options)
qui permettent de générer les coefficients α et β du filtre à partir des données obtenues par les
fonctions précédentes.
Par exemple, pour obtenir les coefficients d’un filtre elliptique, on pourra utiliser la fonction
suivante :
[b,a] = ellip(n,Apass,Astop,Wn);
Les coefficients du filtre sont stockés dans les variables b et a.
La structure implémentable sur une carte Nucléo est de type Lattice. Il reste donc une
dernière étape avant de pouvoir récupérer les coefficients, les traduire en structure Lattice via
la fonction tf2latc, qui renvoie les coefficients transformés.
[k v] = tf2latc(b,a);
Pour pouvoir par la suite les implémenter sur une carte Nucléo, il faut pouvoir exporter ces
variables dans un format lisible. On va ici utiliser le format CSV (compatible avec Excel) et
qui sépare les différentes valeurs par des virgules (,). On peut utiliser la fonction suivante :
csvwrite('k_coeff.csv',k')
csvwrite('v_coeff.csv',v')
Les coefficients obtenus s’appellent k et v pour une structure de type Lattice.
Réponse en fréquence et réponse impulsionnelle
A partir des coefficients précédents, on peut obtenir la réponse en fréquence à l’aide de la
fonction suivante (où b et a sont les coefficients du filtre et h la réponse en fréquence
complexe aux points de pulsation réduite w) :
[h, w] = freqz(b, a);
ou la réponse impulsionnelle grâce à la fonction suivante (où b et a sont les coefficients du
filtre et h la réponse impulsionnelle aux instants t) :
[h,t] = impz(b,a)
Dans les deux cas, il est possible de préciser le nombre de points sur lequel on souhaite
réaliser ces opérations.

41. Ainsi pour obtenir la réponse en fréquence du filtre elliptique passe-bas précédent, on peut
utiliser les instructions suivantes :
[h, w] = freqz(b, a, 2048);
plot(w/pi, 20*log10(abs(h)));
Le troisième argument de la fonction freqz permet de préciser le nombre de points sur lequel
calculer la fonction de transfert. On obtient alors la figure suivante :
On peut faire de même avec la réponse impulsionnelle :
[h, t] = impz(b, a, 200);
plot(t, h);
On obtient alors la figure suivante (le troisième paramètre de la fonction impz correspond au
nombre d’échantillons – à la période TE=1/FE) :

42. Exemple d’un passe-haut
Pour un filtre passe-haut, de fréquence d’échantillonnage de 10kHz, de fréquence de bande-
passante de 4kHz (avec 1dB de différence de gain maximale dans cette bande), de fréquence
de bande atténuée de 3kHz (avec -80dB dans cette bande), on obtient :
Fs = 10e3;
Fpass = 4e3; Wpass = Fpass/Fs;
Fstop = 3e3; Wstop = Fstop/Fs;
Apass = 1;
Astop = 80;
[n, Wn] = cheb2ord(Wpass, Wstop, Apass, Astop);
figure;
[b, a] = cheby2(n,Astop,Wn, 'high');
[h, w] = freqz(b, a);
plot(w/pi, 20*log10(abs(h)));
[k v] = tf2latc(b,a);
csvwrite('k_coeff.csv',k')
csvwrite('v_coeff.csv',v')
Les coefficients obtenus s’appellent k et v pour une structure de type Lattice.
On obtient alors la réponse en fréquence suivante (pour un filtre de type Chebyshev 2) :

43. b) Implémentation sur Nucleo via MBED
Code de base – Mode Suiveur
Une première étape à valider avant d’intégrer la partie filtrage numérique est la mise en
oeuvre des deux modules de conversion : analogique-numérique (ADC) et numérique-
analogique (DAC).
Intégration des coefficients du filtre
Il est temps à présent d’intégrer l’élément central de ce traitement numérique, l’étape de
filtrage numérique.
La même bibliothèque nommée mbed-dsp que vous avez utilisé pour le filtre FIR, contient
aussi en particulier les objets et méthodes suivants :
- arm_iir_lattice_instance_f32 : type permettant de construire un objet de type filtre
IIR, dont les coefficients sont des flottants sur 32 bits
- arm_iir_lattice_init_f32 : fonction permettant d’initialiser la structure matérielle d’un
filtre IIR (de type Lattice), dont les coefficients sont des flottants sur 32 bits
- arm_iir_lattice_f32 : fonction permettant de calculer la nouvelle sortie d’un filtre IIR,
dont les coefficients sont des flottants sur 32 bits
Il faut, dans un premier temps, ajouter à votre projet précédent (contenant le code de base
pour l’acquisition et la restitution des données analogiques) le tableau des coefficients et le
nombre de coefficients, en dehors de toute fonction.

44. Coefficients du filtre
Il faut ensuite créer les variables permettant de stocker les coefficients du filtre. Pour cela, il
faut connaîtrer le nombre de coefficients. Pour cela, il faut regarder la taille des variables
contenant les coefficients sous Matlab.
On voit cela dans l’espace de travail (ou Workspace) de Matlab.
Dans le cas du filtre de Chebyshev 2 de type passe-haut, on se retrouve avec des variables de
type double et de taille 13 (pour a et b). C’est la même chose pour les coefficients Lattice k et
v:
Remarques : On peut remarquer que l’un des tableaux est plus petit d’une case que l’autre.
Il va donc falloir créer deux tableaux de float32_t (équivalent à des nombres réels simple
précision) de taille spécifiée précédemment, dans votre projet MBED.
#define NB_POINTS 13
float32_t k_coeff[NB_POINTS-1];
float32_t v_coeff[NB_POINTS];
Remarque : Les coefficients des filtres sont théoriquement constants au cours du temps.
Cependant, les fonctions utilisées par la suite pour calculer les échantillons ont besoin de
variables et non de constantes pour travailler, même si à terme ces tableaux ne seront pas
modifiés.
Il faut ensuite remplir ces tableaux avec les valeurs des coefficients. Pour cela, il faut ouvrir
les fichiers *.csv exportés précédemment sous Matlab avec un éditeur de texte.

45. Il faut ensuite copier l’ensemble des coefficients et les coller dans le tableau déclaré
précédemment sous MBED.
float32_t k_coeff[NB_POINTS-1]; = {-0.7775,0.98328,-0.84677,0.91293,-0.85179,
0.8205,-0.73222,0.5711,-0.32475,
0.11381,-0.021763,0.0017756};
float32_t v_coeff[NB_POINTS]; = {-0.00062406,-0.00071921,-0.00067741,0.012544,
0.038442,0.068748,0.08427,0.074132,0.048655,
0.025367,0.010842,0.0035784,0.00075118};
Structure de stockage
Il faut ensuite initialiser, en dehors de toute fonction également, les différentes structures qui
accueilleront les résultats intermédiaires des calculs. Pour cela, il faut utiliser la suite
d’instruction suivante :
float32_t iir_state[NB_POINTS+1];
arm_iir_lattice_instance_f32 my_iir;
La première ligne permet de créer un tableau où seront stockées les derniers échantillons
acquis (nécessaires pour le calcul de la sortie du filtre). La taille de ce tableau doit être la taille
du tableau v incrémentée de 1. La seconde ligne permet de créer un objet de type filtre IIR,
dont les coefficients sont des flottants sur 32 bits.
Par la suite, il faut faire appel à la fonction qui va initialiser la structure matérielle, basée sur
le tableau précédent et les coefficients du filtre. Pour cela, il faut faire appel à la fonction
suivante, une seule fois dans le main (par exemple) :
arm_iir_lattice_init_f32(&my_iir, NB_POINTS, k_coeff, v_coeff, iir_state, 1);
Les paramètres à lui fournir sont : l’objet de type filtre IIR (ici my_iir), le nombre de
coefficients (ici NB_POINTS), le tableau contenant les coefficients (ici k_coeff et v_coeff), le
tableau permettant de stocker tous les échantillons nécessaires (ici iir_state) et le nombre total
d’entrées à utiliser (ici une seule entrée, car un seul filtre calculé).
Enfin, il faut faire appel régulièrement à la fonction qui exécutera le traitement numérique des
données par l’intermédiaire de la fonction suivante :
arm_iir_lattice_f32(&my_iir, &in, &out, 1);
Les paramètres à lui fournir sont : l’objet de type filtre IIR (ici my_iir), le nouvel échantillon
(ici in), la valeur de sortie (ici out) et le nombre total d’entrées à utiliser (ici une seule entrée,
car un seul filtre calculé).

46. Code complet
Voici un exemple complet d’un filtre IIR de même caractéristiques que le filtre FIR
précédemment développé.
#include "mbed.h"
#include "dsp.h"
/* E/S */
AnalogIn mesure(A0); // A0 on Arduino Header
DigitalOut clk_test(PA_9); // D8
AnalogOut sortie(PA_5); // D13
#define TE 0.0001
// Filtre PASSE-HAUT - Cheby2 - FS = 10kHz, Fp = 4kHz, Fstop = 3.5kHz
#define NB_POINTS 13
float32_t k_coeff[NB_POINTS-1] = {-0.7775,0.98328,-0.84677,0.91293,-0.85179,
0.8205,-0.73222,0.5711,-0.32475,
0.11381,-0.021763,0.0017756};
float32_t v_coeff[NB_POINTS] = {-0.00062406,-0.00071921,-0.00067741,0.012544,
0.038442,0.068748,0.08427,0.074132,0.048655,
0.025367,0.010842,0.0035784,0.00075118};
float32_t iir_state[NB_POINTS+1];
arm_iir_lattice_instance_f32 my_iir;
/* Conversion routine */
void convert(void);
/* Timer a repetition */
Ticker tik;
float in, out;

47. int main() {
arm_iir_lattice_init_f32(&my_iir, NB_POINTS, k_coeff, v_coeff, iir_state, 1);
tik.attach(&convert, TE);
while(1) {
}
}
/*
* ROUTINE DE CONVERSION ET CALCUL
*/
void convert(void){
in = mesure.read()-0.5;
clk_test = 1;
arm_iir_lattice_f32(&my_iir, &in, &out, 1);
clk_test = 0;
sortie.write(out+0.5);
}
IV/ Spectre d’un signal sonore en temps réel
Dans cette partie, on réalise une transformée de Fourier numérique à l’aide d’une carte Nucléo
d’un signal sonore récupéré à l’aide d’un microphone à électret amplifié.
VI.1. Rappel : Transformée de Fourier et échantillonnage
Le passage au numérique impose quelques règles y parmi la nécessité d’échantillonner le
signal analogique en une série de données numériques. Il est donc indispensable de respecter
le critère de Nyquist-Shannon, à savoir que la fréquence d’échantillonnage choisie doit être
deux fois supérieure à la fréquence maximale du signal à analyser.

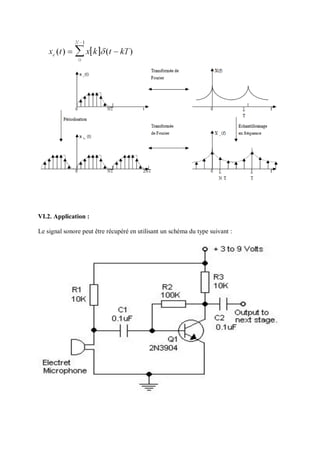
48. Signal et transformée de Fourier
Si x(t) est un signal analogique décrivant l’évolution d’une grandeur physique dans le temps,
sa transformée de Fourier est alors donné de la façon suivante :
On peut remarquer que le spectre d’un signal de ce type – réel à temps continu – est à
symétrie hermitienne (module paire, phase impaire).
Signal échantillonné et transformée de Fourier
L’échantillonnage à une fréquence Fe (ou une période Te) du signal précédent, donne un
nouveau signal contenant des informations numériques discrétisées notées xD, telles que
xD[n]=x(n⋅Te)=xn.
Son spectre est celui du signal initial x(t) périodisé, de période 1 avec ν la fréquence réduite
(ν=f/Fe). Il est donné par :
On peut remarquer que le spectre d’un signal discret est continu et périodique.
Transformée de Fourier échantillonnée
La transformée de Fourrier échantillonnée (ou TFD) d’un signal discret est un échantillonnage
de la transformée de Fourier du signal initial.

49. VI.2. Application :
Le signal sonore peut être récupéré en utilisant un schéma du type suivant :

50. Le code suivant réalise une FFT sur 256 échantillons à une période d’échantillonnage de 20us
sur un signal analogique appliqué sur A0 (signal à valeurs uniquement positives) et donne le
résultat sous forme d’un signal analogique (PA_5), visualisable à l’oscilloscope.
#include "mbed.h"
#include "arm_math.h"
/* Include mbed-dsp libraries */
#include "dsp.h"
#include "arm_common_tables.h"
#include "arm_const_structs.h"
#define SAMPLES 512 /* 256 real party and 256 imaginary parts */
#define FFT_SIZE SAMPLES / 2 /* FFT size is always the same size as we have
samples, so 256 in our case */
float32_t Input[SAMPLES];
float32_t Output[FFT_SIZE];
bool trig=0;
DigitalOut myled(LED1);
AnalogIn myADC(A0);
AnalogOut myDAC(PA_5);
Serial pc(USBTX, USBRX);
Ticker timer;
void sample(){
trig=1;
}

51. int main() {
float maxValue; // Max FFT value is stored here
uint32_t maxIndex; // Index in Output array where max value is
while(1) {
timer.attach_us(&sample,20); //20us 50KHz sampling rate
for (int i = 0; i < SAMPLES; i += 2) {
while (trig==0){}
trig=0;
Input[i] = myADC.read() - 0.5f; //Real part NB removing DC offset
Input[i + 1] = 0; //Imaginary Part set to zero
}
timer.detach();
// Init the Complex FFT module, intFlag = 0, doBitReverse = 1
//NB using predefined arm_cfft_sR_f32_lenXXX, in this case XXX is 256
arm_cfft_f32(&arm_cfft_sR_f32_len256, Input, 0, 1);
// Complex Magniture Module put results into Output(Half size of the Input)
arm_cmplx_mag_f32(Input, Output, FFT_SIZE);
Output[0] = 0;
//Calculates maxValue and returns corresponding value
arm_max_f32(Output, FFT_SIZE, &maxValue, &maxIndex);
myDAC=1.0f; //SYNC Pulse to DAC Output

52. wait_us(20); //Used on Oscilliscope set trigger level to the highest
myDAC=0.0f; //point on this pulse
for(int i=0; i < FFT_SIZE / 2; i++){
myDAC=(Output[i]) * 0.9f; // Scale to Max Value and scale to 90 / 100
wait_us(10); //Each pulse of 10us is 50KHz/256 = 195Hz resolution
}
myDAC=0.0f;
}
}