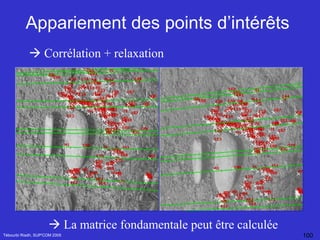
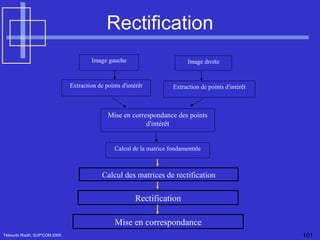
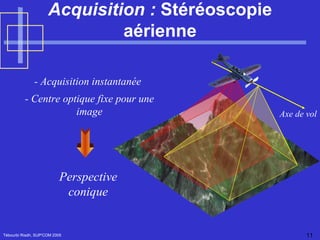
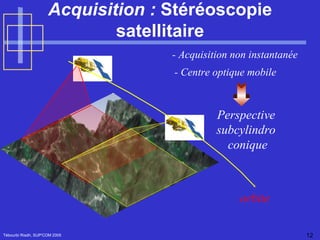
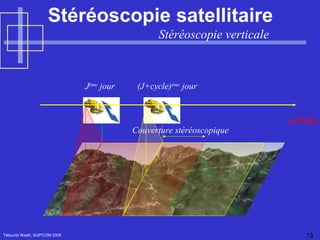
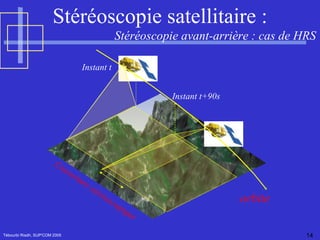
Le document traite de la vision par ordinateur, en se concentrant sur l'imagerie 3D et les méthodes passives et actives pour acquérir des informations tridimensionnelles. Il présente des techniques telles que la stéréovision et l'étalonnage des caméras, ainsi que la modélisation de la géométrie des capteurs. Enfin, il explore des applications pratiques, notamment en imagerie médicale et en stéréoscopie, en décrivant des concepts clés tels que la matrice essentielle et la géométrie épipolaire.

1. Tébourbi Riadh, SUP'COM 2005 IMAGERIE 3D 08/10/2007 Ecole Supérieure des Communications de Tunis Cours Tébourbi Riadh

2. Quelques références Tébourbi Riadh, SUP'COM 2005 - R. Horaud & O. Monga. Vision par Ordinateur : Outils Fondamentaux, Editions Hermès, 1995. http://www.inrialpes.fr/movi/people/Horaud/livre-hermes.html - O livier Faugeras . Three-Dimensional Computer Vision, MIT Press, 1993. - Frederic Devernay. Vision par Ordinateur. INRIA (France). http:// devernay.free.fr/cours/vision - Joshua Gluckman. Computer Vision. Polytechnic University (USA). http://cis.poly.edu/cs664/0

3. Contexte Tébourbi Riadh, SUP'COM 2005 Vision par ordinateur : branche de l’IA dont le but est de permettre à une machine de comprendre ce qu'elle «voit » lorsqu'on la connecte à une ou plusieurs caméras.  ne cherche pas à comprendre ou à reproduire la vision humaine, mais à construire un modèle algorithmique qui, vu de l'extérieur, possède des propriétés semblables.

4. Vision 3D Tébourbi Riadh, SUP'COM 2005 Vision binoculaire Perception 3D Objet 3D 1 er point de vue 2 ème point de vue Problème difficile de la vision artificielle

5. Introduction Tébourbi Riadh, SUP'COM 2005 Vision 3D : Méthodes passives : Méthodes actives : Acquisition directe de la profondeur - Analyse de déphasage ou de distorsion du signal émis - Stéréoscopie (deux images ou plus) - Monoscopie (une seule image) : étude des formes

6. Méthodes actives Tébourbi Riadh, SUP'COM 2005 Méthodes actives : ultra-sons, lumière cohérente, faisceau laser... L ’information 3-D est directement acquise par analyse de déphasage ou de distorsion du signal. Techniques coûteuses. Objets étudiés proches et immobiles . Exemples d’imagerie 3D: Imagerie médicale (Tomographie CT, scanner X, résonance magnétique nucléaire) , Holographie ,…

7. Méthodes passives Tébourbi Riadh, SUP'COM 2005 Une seule image : étude des formes à partir de l’ombrage, analyse de texture… Deux images ou plus : Stéréovision L ’information 3-D est obtenue par recherche de points homologues entre deux images ou plus : la différence de projection du même point physique appelée disparité est directement liée à l ’élévation. Invention du premier stéréoscope (1838). La stéréovision reproduit le processus de la vision binoculaire chez l’homme.

8. Stéréovision: Principe Tébourbi Riadh, SUP'COM 2005 M Image gauche Image droite m1 m2 Reconstruction 3D Mise en correspondance Modèle caméra gauche Modèle caméra droite

9. Etapes de la reconstitution 3D par stéréovision Tébourbi Riadh, SUP'COM 2005 Acquisition stéréoscopique Etalonner les deux caméras: Modélisation des capteurs connaissance du modèle de projection  relation coordonnées 3D/2D Trouver les points correspondants m1/m2 dans les deux images: Mise en correspondance Calculer les coordonnées 3D: Reconstruction 3D

10. Acquisition : Photos Tébourbi Riadh, SUP'COM 2005 2 appareils photos (numériques). H B A

11. Acquisition : Stéréoscopie aérienne Tébourbi Riadh, SUP'COM 2005 - Acquisition instantanée - Centre optique fixe pour une image Perspective conique Axe de vol

12. Acquisition : Stéréoscopie satellitaire Tébourbi Riadh, SUP'COM 2005 orbite - Acquisition non instantanée - Centre optique mobile Perspective subcylindro conique

13. Stéréoscopie satellitaire Tébourbi Riadh, SUP'COM 2005 orbite J ème jour (J+cycle) ème jour Couverture stéréoscopique Stéréoscopie verticale

14. Tébourbi Riadh, SUP'COM 2005 orbite Instant t Instant t+90s Couverture stéréoscopique Stéréoscopie avant-arrière : cas de HRS Stéréoscopie satellitaire :

15. Tébourbi Riadh, SUP'COM 2005 Stéréoscopie satellitaire Jour j Jour j’ Orbite descendante Orbite ascendante Couverture stéréoscopique Stéréoscopie latérale : cas de HRG

16. Exemples d’images stéréoscopiques Tébourbi Riadh, SUP'COM 2005 Photos

17. Tébourbi Riadh, SUP'COM 2005 Aériennes

18. Tébourbi Riadh, SUP'COM 2005 Satellitaires (SPOT5)

19. Tébourbi Riadh, SUP'COM 2005 Satellitaires (IKONOS)

20. Modélisation du capteur Tébourbi Riadh, SUP'COM 2005

21. Modélisation du capteur Tébourbi Riadh, SUP'COM 2005 BUT : Déterminer le modèle géométrique associé au processus de saisie d'une image stéréoscopique à l'aide d'une caméra (capteur)  déterminer les paramètres liés à ce modèle. Déterminer relation coordonnées Image/scène Modéliser

22. Géométrie d’une caméra « sténopé » Tébourbi Riadh, SUP'COM 2005 - Acquisition instantanée - Centre optique fixe pour une image Perspective conique Axe de vol

23. Géométrie du capteur SPOT Tébourbi Riadh, SUP'COM 2005 Barrette CCD Orbite du satellite Sens du défilement balayage push broom Perspective conique par ligne

24. Modélisation du capteur Tébourbi Riadh, SUP'COM 2005 Modèle “ à trou d’épingle” Ou modèle sténopé ou « pinhole model »  Ce modèle considère que la transformation opérée par la caméra est une transformation perspective parfaite, de centre C (le centre optique de la caméra). C P p

25. Modèle “ à trou d’épingle” Tébourbi Riadh, SUP'COM 2005 b) Projection a) Transformation R + T I- Géométrie d’une caméra b) a) R c R w m 2 (u,v) m 1 (u,v) P( X w , Y w , Z w ) C 2 C 1 Z Y X u v S: facteur d’échelle M: matrice 3  4 1 Z Y X M w w w                          s sv su 0 v m m v Z m Z m v Y m Y m v X m X m 0 u m m u Z m Z m u Y m Y m u X m X m 34 24 W 33 W 23 W 32 W 22 W 31 W 21 34 14 W 33 W 13 W 32 W 12 W 31 W 11                

26. Tébourbi Riadh, SUP'COM 2005 b) Une projection qui transforme un point de l’espace 3D dans le repère de la caméra (X,Y, Z) en un point 2D de coordonnées (u,v) de l’image Ku et Kv facteurs d’échelle de l’image respectivement dans la direction de u et de v(pixels/mm), f : focale exprimée en mm et u 0 et v 0 :coordonnées en pixels du centre de l'image u 0 , v 0 ,  u et  v représentent les paramètres intrinsèques de la caméra

27. Remarque Tébourbi Riadh, SUP'COM 2005 Si on pose alors avec et Soit:

28. Tébourbi Riadh, SUP'COM 2005 a) Une transformation qui lie les coordonnées d’un point Pw(Xw,Yw,Zw) de l’espace 3D à ceux dans le repère de la caméra (X,Y,Z). = transformation rigide qui se compose d’une rotation et d’une translation Les termes de R et de T sont appelés les paramètres extrinsèques de la caméra

29. Tébourbi Riadh, SUP'COM 2005 Peut s’écrire: Avec:

30. Tébourbi Riadh, SUP'COM 2005 Et Donnent: M (3  4) appelée la matrice de projection de la caméra

31. Tébourbi Riadh, SUP'COM 2005 Résumé

32. Relation 2D/3D Tébourbi Riadh, SUP'COM 2005 Elimination de s  . Relations linéaires entre (u,v) et (Xw,Yw,Zw). . Si 2 caméras ou plus alors 4 équations ou plus pour 3 inconnues. Trouver les coefficients de M ? 0 v m m v Z m Z m v Y m Y m v X m X m 0 u m m u Z m Z m u Y m Y m u X m X m 34 24 W 33 W 23 W 32 W 22 W 31 W 21 34 14 W 33 W 13 W 32 W 12 W 31 W 11                

33. Etalonnage de la caméra Tébourbi Riadh, SUP'COM 2005 L’étalonnage de la caméra = calcul des coefficients m ij de M A partir des coordonnées 3D: Pwi=(Xwi,Ywi,Zwi) de N points et de leurs projections dans l’image : (ui,vi) N points (N  6 )  2N (2N  12) équations pour 12 inconnues. Nous avons un système a 2N équations linéaires.

34. Etalonnage (suite) Tébourbi Riadh, SUP'COM 2005  Utilisation une mire Contient un ensemble de points dont les coordonnées (3D) sont connues Les Coordonnées 2D sont repérés dans l’image.  GPS Exemple:

35. Etalonnage (suite) Tébourbi Riadh, SUP'COM 2005 Pour chaque point i : 1  i  N Résoudre un système linéaire homogène à 2N équations:

36. Etalonnage (suite) Tébourbi Riadh, SUP'COM 2005 Le système peut être écrit: Il faut éviter la solution évidente mij=0  Poser des contraintes.

37. Etalonnage (suite) Tébourbi Riadh, SUP'COM 2005 Pour pouvoir poser des contraintes sur des mij regardons la matrice M en fonction des paramètres intrinsèques et extrinsèques:  Contrainte m34  0 (m34 = Tz)  2 contraintes :

38. Tébourbi Riadh, SUP'COM 2005 Etalonnage (suite)  R31, R32 et R33 sont les éléments d’une matrice de rotation R : Nous pouvons écrire: Donc contrainte : Or

39. Etalonnage (suite) Tébourbi Riadh, SUP'COM 2005 Utilisation de la contrainte m34  0 : on divise le système d’équations par m34 on obtient: Nous cherchons les qij = mij/m34  Résolution de ce système par la méthode des moindres carrés ( pseudo-inverse ):

40. Etalonnage (suite) Tébourbi Riadh, SUP'COM 2005 Une fois les qij trouvés nous cherchons les mij sachant que: Soit: D’où Et

41. Calcul des paramètres intrinsèques et extrinsèques de la caméra Tébourbi Riadh, SUP'COM 2005 M =(mij) : fonctions des paramètres intrinsèques et extrinsèques. En tenant compte de: - La matrice R est orthogonale - L’origine du repère de la scène Ow est toujours devant la caméra (Tz>0) On obtient:

42. Précision de l’étalonnage Tébourbi Riadh, SUP'COM 2005 Pour vérifier la précision du calibrage nous pouvons calculer deux erreurs : Une erreur commise sur l’orthogonalité de la matrice R : La matrice R est une matrice de rotation et doit vérifier: Une erreur calculée en reconstituant les coordonnées (u i ,v i ) des points de référence (coordonnées de ces points utilisées pour le calcul des coefficients de M). Après calibration nous pouvons recalculer les coordonnées (uc i ,vc i ) de ces points de référence et calculer l’erreur : qui est la moyenne des erreurs résiduelles et: qui est la variance de ces erreurs.

43. Géométrie d’un système stéréoscopique Tébourbi Riadh, SUP'COM 2005 1) Position relative des deux caméras 2) Géométrie épipolaire 3) La matrice essentielle 4) La matrice fondamentale

44. Position relative des deux caméras Tébourbi Riadh, SUP'COM 2005 Pour chaque caméra i P w =(X w ,Y w ,Z w ) t Rappel:

45. Tébourbi Riadh, SUP'COM 2005 Pour les deux caméras, nous pouvons alors écrire En éliminant Pw entre les deux équations, nous obtenons: avec As est une matrice décrivant la transformation rigide « repère caméra gauche/repère caméra droite » et peut être représentée par une matrice de rotation Rs et un vecteur translation Ts

46. Tébourbi Riadh, SUP'COM 2005 En introduisant dans cette dernière équation les coordonnées de la projection de P w dans l'image rétinienne gauche et droite , nous pouvons écrire :

47. Tébourbi Riadh, SUP'COM 2005 En éliminant Z1 Avec:  équation qui décrit l' ensemble des points (x2,y2) de l'image de droite pouvant correspondre à un point (x1,y1) de l'image gauche = une droite appelée droite épipolaire Le correspondant d'un point de l'image gauche se trouve forcément sur une ligne épipolaire dans l'image droite

48. Géométrie épipolaire Tébourbi Riadh, SUP'COM 2005 e1 et e2 sont appelés les épipoles Le faisceau de lignes qui passent par e1 dans image1 et par e2 dans image2 sont appelées les lignes épipolaires Pour chaque point m1 de image1, son correspondant m2 dans image2 se trouve sur une ligne épipolaire Im1 m 1 m 2 e 1 e 2 M C 2 C 1 Image 1 Image 2

49. Contrainte épipolaire Tébourbi Riadh, SUP'COM 2005 Un point dans l’image gauche se situe sur la droite épipolaire correspondante dans l’image droite

50. Exemple Tébourbi Riadh, SUP'COM 2005

51. La matrice essentielle Tébourbi Riadh, SUP'COM 2005 Coefficients de la droite épipolaire: Droite épipolaire qui peut s'écrire, en introduisant la matrice E, sous la forme:

52. La matrice essentielle Tébourbi Riadh, SUP'COM 2005 Equation de la droite épipolaire peut s’écrire: et Donne: p i =(x i ,y i ,1)t avec E est appelée la matrice essentielle E: décrit la transformation épipolaire gauche-droite et donne l'équation de la droite épipolaire droite Transformation épipolaire droite-gauche E t

53. La matrice fondamentale Tébourbi Riadh, SUP'COM 2005 Rappel: pour chaque caméra i: avec et En remplacant dans Nous obtenons = matrice fondamentale (3 x 3) Exprime la relation qui existe entre les coordonnées images (en pixels) gauche (u1,v1) et droite (u2,v2), décrivant, ainsi, la géométrie épipolaire

54. Mise en correspondance Tébourbi Riadh, SUP'COM 2005 (X w ,Y w ,Z w ) (scène)  projections (U 1 ,V 1 ) (image gauche) et (U 2 ,V 2 ) (image droite) i=1,2  Pour chaque pixel dans image gauche: recherche de son correspondant dans image droite: un problème de mise en correspondance ou appariement 0 v m m v Z m Z m v Y m Y m v X m X m 0 u m m u Z m Z m u Y m Y m u X m X m i 34 24 i W 33 W 23 i W 32 W 22 i W 31 W 21 i 34 14 i W 33 W 13 i W 32 W 12 i W 31 W 11                

55. Mise en correspondance (suite) Tébourbi Riadh, SUP'COM 2005 Problème simplifié: a) contrainte épipolaire m 1 m 2 e 1 e 2 M C 2 C 1 Image 1 Image 2 Analytiquement: 0 1 1 1 1 2 2                      v u F v u F: matrice fondamentale (3 x 3)

56. Tébourbi Riadh, SUP'COM 2005 Contrainte épipolaire Image de référence Image de recherche Ligne épipolaire m C 1 C 2 Espace de recherche monodimensionnel (≈ ligne)

57. Mise en correspondance (suite) Tébourbi Riadh, SUP'COM 2005 Problème encore simplifié: b) Rectification des images m 1 m 2 m’ 1 m’ 2 u’ 1 u’ 2 disparité : d = u’ 2 – u’ 1

58. Tébourbi Riadh, SUP'COM 2005 Exemple d d’

59. Géométrie des images rectifiées Tébourbi Riadh, SUP'COM 2005 Paramètres: H B m 1 m 2 u 1 u 2 disparité : d = u’ 2 – u’ 1

60. Géométrie des images rectifiées (2) Tébourbi Riadh, SUP'COM 2005  La géométrie des deux caméras peut être décrite seulement par la distance qui sépare les deux centres optiques B et la hauteur des deux caméras H Matrices de rotation (égales) : Vecteurs de translation: Transformation rigide gauche-droite (simple translation)

61. Géométrie des images rectifiées (3) Tébourbi Riadh, SUP'COM 2005 Matrice essentielle: Matrice fondamentale: Si pour les deux caméras α u = α v Disprité = f(Z w ,B,H)

62. Mise en correspondance Tébourbi Riadh, SUP'COM 2005 Objectif: Trouver, pour un élément géométrique dans une image (résultant d'une projection d'un objet 3D de la scène sur l'image), sont élément homologue ( ou correspondant) dans l'autre image Mise en correspondance de primitives points d’intérêt segments / contours régions Mise en correspondance dense chaque pixel est apparié

63. Tébourbi Riadh, SUP'COM 2005 Mise en correspondance par corrélation p l l fenêtre de corrélation fenêtre de recherche Image gauche Image droite d min d max

64. exemple Tébourbi Riadh, SUP'COM 2005

65. Tébourbi Riadh, SUP'COM 2005 Approche hiérarchique Sous-échantillonnage de facteur 2 Sous-échantillonnage de facteur 2 Reconstruction grossière Reconstruction fine

66. Tébourbi Riadh, SUP'COM 2005 Approche hiérarchique

67. Approche hiérarchique Tébourbi Riadh, SUP'COM 2005 Construction d‘une pyramide Propagation de la disparié Rapidité Intervalle de disparité large

68. Approche par régions Tébourbi Riadh, SUP'COM 2005 Extraction de régions Extraction de régions Mise en correspondance Carte de disparité  Besoin de moyens d’extraction de régions Segmentation par Détecteurs de contours Morphologie mathématique Contours actifs Et Classification A B C

69. Détection de contours Tébourbi Riadh, SUP'COM 2005 Régions  Fermeture de contours Élimination des contours orphelins Buit  pré-filtrage des images A

70. Classification Tébourbi Riadh, SUP'COM 2005 Non connaissance a priori du contenu de la scène Contenu diversifié  tenir compte des zones texturées Méthodes Non supervisées FCM, Agglomération Compétitive, etc. Classification spectrale ou spatiale (texture) Texture: ondelettes complexes, Gabor, etc. A

71. Mise en correspondance des régions Tébourbi Riadh, SUP'COM 2005 À base de contraintes géométriques Contrainte épipolaire Contrainte de domaine de disparité À base du contexte de l’objet Contrainte de rapport de taille Contrainte de similarité Restriction du domaine de recherche B

72. Critère de similarité Tébourbi Riadh, SUP'COM 2005 Attributs spatiaux Attributs de texture a k (R i ) attribut géométrique de la région R i . A = nombre d’attributs utilisés . Moment spatial, taille, nombre de pixels, etc. B

73. Mise en correspondance de régions Tébourbi Riadh, SUP'COM 2005 C

74. Mise en correspondance de régions Tébourbi Riadh, SUP'COM 2005 C

75. Carte des disparités Tébourbi Riadh, SUP'COM 2005 Idéale

76. Difficultés de l’appariement Tébourbi Riadh, SUP'COM 2005 Correspondance difficile (voire impossible) dans les zones faiblement texturées. Ceci quelque soit l’approche utilisée.

77. Difficultés de l’appariement Tébourbi Riadh, SUP'COM 2005 Les points ne sont pas forcément dans le même ordre dans les deux images.

78. Difficultés de l’appariement Tébourbi Riadh, SUP'COM 2005 Les tailles et distances ne sont pas les mêmes d’une image à l’autre.

79. Difficultés de l’appariement Tébourbi Riadh, SUP'COM 2005 Occlusions : des objets ou parties d’objets sont cachés. La correspondance n’existe pas dans ce cas.

80. Carte des disparités Tébourbi Riadh, SUP'COM 2005

81. Interpolation de la carte des disparités Tébourbi Riadh, SUP'COM 2005 Images stéréo Plane Polynomiale Rationnelle Interpolations Nature de la scène Médiane . . . Mise en correspondance Images des disparités calculées

82. Tébourbi Riadh, SUP'COM 2005 Image disparités seuil=0.8 Filtre médian Fenêtre 3*3 Filtre médian Fenêtre 5*5 Filtre médian Fenêtre 7*7 Modèle 3-D Image gauche Interpolation médiane

83. Interpolation rationnelle Tébourbi Riadh, SUP'COM 2005 Image gauche Image des hauteurs: seuil =0.8 Résultat de l’interpolation rationnelle

84. Tébourbi Riadh, SUP'COM 2005 Densification : interpolation médiane Densification : interpolation rationnelle Densification : interpolation plane Carte des disparités

85. Calcul des coordonnées 3D Tébourbi Riadh, SUP'COM 2005 i=1,2 m ij connus (u 1 ,v 1 ), (u 2 ,v 2 ) connus 0 v m m v Z m Z m v Y m Y m v X m X m 0 u m m u Z m Z m u Y m Y m u X m X m i 34 24 i W 33 W 23 i W 32 W 22 i W 31 W 21 i 34 14 i W 33 W 13 i W 32 W 12 i W 31 W 11                 Système de 4 équations 3 inconnues Résolution par moindres carrés.

86. Modélisation 3D Tébourbi Riadh, SUP'COM 2005 Etalonnage Etalonnage

87. Modélisation 3D Tébourbi Riadh, SUP'COM 2005

88. Tébourbi Riadh, SUP'COM 2005 Visualisation 3D

89. Visualisation 3D Tébourbi Riadh, SUP'COM 2005

90. Tébourbi Riadh, SUP'COM 2005 Navigation 3D

91. Influence des paramètres d’acquisition Tébourbi Riadh, SUP'COM 2005 B H H, B Résolutions ?

92. Influence des paramètres d’acquisition Tébourbi Riadh, SUP'COM 2005 B H Compromis 2   H a R R y x    B H ) B , H ( R z     B H 2 A  1  B H

93. Estimation de la matrice fondamental Tébourbi Riadh, SUP'COM 2005 Problème appelé Calcul de la « géométrie épipolaire » ou « Etalonnage faible » Exprime la relation qui existe entre les coordonnées images (en pixels) gauche (u1,v1) et droite (u2,v2), décrivant, ainsi, la géométrie épipolaire Avec étalonnage: Sans étalonnage ?

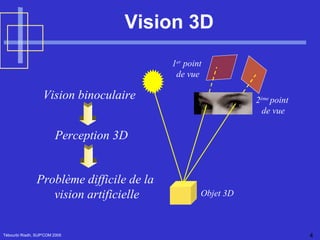
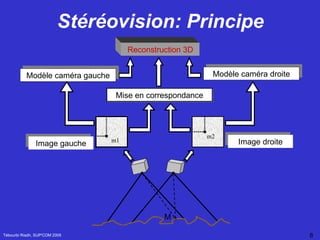
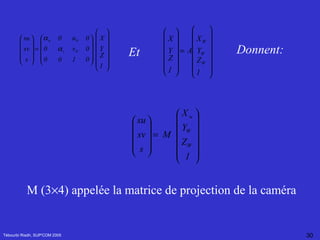
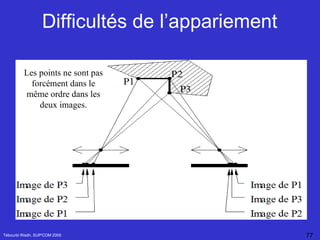
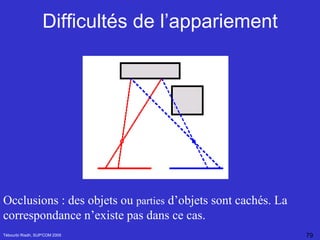
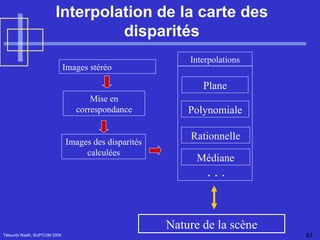
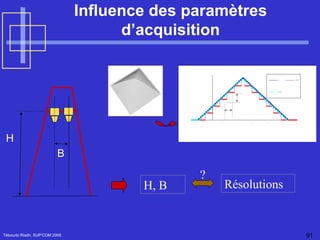
94. Estimation de la matrice fondamental Tébourbi Riadh, SUP'COM 2005 F peut estimée calculée à partir de l'ensemble des points homologues m 1 (u 1 ,v 1 ) et m 2 (u 2 ,v 2 ) K= [u 1 u 2 , v 1 u 2 ,u 2 ,u 1 v 2 ,v 1 v 2 ,v 2 ,u 1 ,v 1 ,1] et F définie à un facteur multiplicatif près On peut poser F 33 = 1 Avec

95. Estimation de la matrice fondamental Tébourbi Riadh, SUP'COM 2005 Pour un couple j de points homologues on peut écrire  Pour n points (n>7) homologues: système linéaire n équations à 8 inconnus. Résolution Méthodes linéaires: pseudo inverse, SVD, etc.. (très sensibles au bruit ) Méthodes non linéaires: Least Median of Squares ou LMedS, RANSAC

96. Estimation de la matrice fondamental par LMedS Tébourbi Riadh, SUP'COM 2005  En entrée: n correspondances extraites des deux images stéréoscopiques  l’utilisation d’une d'optimisation basée sur la distance aux lignes épipolaires de deux points m 1 (u 1 ,v 1 ,1) t et m 2 (u 2 ,v 2 ,1) t : (Fm 1 ) k est le k-ième élément du vecteur Fm 1 .

97. Détection et appariement de points d'intérêts Tébourbi Riadh, SUP'COM 2005 Image gauche Image droite Extraction de points d'intérêt Extraction de points d'intérêt Mise en correspondance des points d'intérêt Calcul de la matrice fondamentale

98. Extraction des points d’intérêt Tébourbi Riadh, SUP'COM 2005  Plusieurs détecteurs « corners detectors » Les méthodes fonctionnant en 2 étapes : détermination de contours chaînés puis détermination des points du contour de courbure maximale Les méthodes opérant directement sur les intensités de l’image et basée sur la mesure du gradient et de la courbure Moravec Susan Harris

99. Exemple résultat Harris Tébourbi Riadh, SUP'COM 2005

100. Appariement des points d’intérêts Tébourbi Riadh, SUP'COM 2005  Corrélation + relaxation  La matrice fondamentale peut être calculée

101. Rectification Tébourbi Riadh, SUP'COM 2005 Image gauche Image droite Extraction de points d'intérêt Extraction de points d'intérêt Mise en correspondance des points d'intérêt Calcul de la matrice fondamentale Calcul des matrices de rectification Rectification Mise en correspondance

102. Rectification Tébourbi Riadh, SUP'COM 2005 Objectif: trouver deux matrices H1 et H2 de rectifications Pour deux points correspondants: Matrice fondamentale des images rectifiées: Une première paire de matrices de rectification H 01 et H 02 , il suffit de décomposer F en valeurs singulières :

103. Famille des matrices de rectification Tébourbi Riadh, SUP'COM 2005 L'ensemble des paires de matrices de rectification (H 1 ,H 2 ) se déduisent de H 01 et H 02 par les relations: Variété de dim. 9  Trouver deux paires de rectification qui distordent le moins possible les images

104. Tébourbi Riadh, SUP'COM 2005 Exemples

105. Calcul d’une paire de matrices de rectification Tébourbi Riadh, SUP'COM 2005  Poser des contraintes 1) d'=u' 2 -u' 1 =d

106. Calcul d’une paire de matrices de rectification Tébourbi Riadh, SUP'COM 2005 2) Conservation des lignes épipolaires  calculer les coins de l’image rectifiée Rectifier l'image revient à transformer les lignes épipolaires en lignes parallèles et horizontales et envoyer l'épipole e 1 à l'infini. Eviter de compresser ou d’allonger les lignes épipolaires lors de la rectification et de déformer ainsi les images, la dimension de l'image rectifiée est d'abord calculée

107. COMPLEMENTS Tébourbi Riadh, SUP'COM 2005

108. Méthode du pseudo-inverse Tébourbi Riadh, SUP'COM 2005  Résoudre le système d’équations linéaires suivant Q = vecteur n (inconnus) K = Matrice m*n C = vecteur n

109. Méthode du pseudo-inverse Tébourbi Riadh, SUP'COM 2005 K.Q-C=e e représente un vecteur erreur La meilleure solution Q est celle qui minimise le module du vecteur erreur On cherche Q tel que soit minimum En différenciant par rapport à Q, on obtient : La matrice (K t K) -1 K t

110. Géométrie des images rectifiées Tébourbi Riadh, SUP'COM 2005 Caméra gauche Caméra droite