Le document traite des méthodes quantitatives en mathématiques économiques avec un focus sur les fonctions trigonométriques et leurs propriétés, les intégrales simples et doubles, ainsi que les limites des fonctions exponentielles et logarithmiques. Il fournit une série de définitions, de propriétés et d'exercices pour chaque thème, permettant une compréhension approfondie des concepts mathématiques. Le contenu est principalement destiné aux étudiants en économie, avec des exemples pratiques et des exercices de résolution.

1. Semestre
Module
Elément
Enseignant
:2
: Méthodes Quantitatives
: Mathématiques Economiques
: Mr BENMOUSSA
Eléments du cours
Les Fonctions
Les Intégrales simples
Les Intégrales doubles
Extrêmes de fonctions de deux variables
Numérisation & Conception
Mr Mohamed-Fadil ZIADI
Le Portail des Etudiant d’Economie
www.e-tahero.net
contact@e-tahero.net

2. Professeur BENMOUSSA
Mathématiques Economiques
PROGRAMME
Les Fonctions :
- Fonctions trigonométriques.
- Fonctions ex.
- Fonction log x.
- Elasticité.
II-
Les Intégrales simples :
- Par parties.
- Par changement de variables.
- Fractions rationnelles.
- Fractions irrationnelles.
- Intégrales impropres.
IIIIV-
Les Intégrales doubles.
Extrêmes de fonctions de deux variables.
© www.e-tahero.net – Z.M.F
I-
Portail des Etudiants d’Economie
-2-

3. Professeur BENMOUSSA
Mathématiques Economiques
Chapitre 1 : FONCTIONS TRIGONOM2TRIQUES.
I-
Définition : cercle trigonométrique :
π/2
Sin
tan
+
Sin α
π
-1
α
cosα
2π
1
Cos
3π
2
Rayon = 1.
R=1 ⇒
α
-1 ≤ cos α ≤ 1
-1 ≤ sin α ≤ 1
- ∞ < tg α < + ∞
0
0
Tg α
-α
1
Sin α
© www.e-tahero.net – Z.M.F
Cos α
0
π
π
π
π
4
2
2
2
2
2
6
3
2
1
2
3
0
1
1
0
Sin (- α) = - sin α
cos (- α) = cos α
tg (- α) = - tg α
Portail des Etudiants d’Economie
π-α
-3-
3
3
½
3
2
3
sin (π - α) = sin α
cos (π - α) = - cos α
tg (π - α) = - tg α

4. Professeur BENMOUSSA
Mathématiques Economiques
sin (π + α) = - sin α
cos (π + α) = - cos α
tg (π + α) = tg α
π+α
sin (
π
2
+α
cos (
π
2
π
2
+ α) = cos α
+α) = - sin α
π
tg ( + α) = 2
II-
1
= - cotg α.
tgα
Formules trigonométriques:
Sin (a + b) = sin a cos b + cos a sin b.
Sin (a – b) = sin a cos b – cos a sin b.
Cos (a + b) = cos a cos b – sin a sin b.
Cos (a – b) = cos a cos b + sin a sin b.
Sin 2a = 2 sin a cos a.
Cos 2a = cos2 a – sin2 a.
Théorème de Pythagore :
A
B
α
O
OA2 = AB2 + OB2
⇒ 12 = sin2 α + cos2 α
⇒ cos2 α + cos2 α = 1
© www.e-tahero.net – Z.M.F
⇒
cos 2 α + sin 2 α
1
=
.
2
cos α
cos 2 α
1
⇒ 1 + tg2 α =
cos 2 α
sin 2α
2 sin α . cos α
=
.
cos 2α
cos 2 α − sin 2 α
2 sin α .2 cos α
cos 2 α
=
cos 2 α − sin 2 α
cos 2 α
tg 2α =
Portail des Etudiants d’Economie
=
-2-
2tgx
.
1 − tg 2α

5. Professeur BENMOUSSA
III-
Mathématiques Economiques
Dérivées des fonctions trigonométriques :
f ′ (x)
f (x)
sin x
cos x
tg x
cos (ax + b)
sin (ax + b)
IV-
V-
1
= 1 + tg2 x
2
cos x
- a . sin ( ax + b)
a . cos (ax + b)
Fonctions réciproques :
Y = cos x
Y = sin x
Y = tg x
cos x
- sin x
⇔
x = arcos y
⇔ x = arc sin y
⇔ x = arc tg y
Etude de la fonction (y = sin x) :
1- Domaine de définition :
Df = ℜ.
2- Parité :
Si f (-x) = f (x). ⇒ la fonction est paire.
Si f (-x) = - f (x) ⇒ la fonction est impaire.
Donc sin (-x) = - sin (x) ⇒ y est une fonction impaire.
3- Périodicité :
© www.e-tahero.net – Z.M.F
Une fonction est périodique de période T.
⇔ f (x + T) = f (x).
y = sin (x)
sin
sin (α + 2π) = sin α.
Sin (α + 4π) = sin α.
Sin (α + kπ) = sinα.
Sin α
α
Donc dans ce cas T = 2π
Portail des Etudiants d’Economie
-2-
cos
cos α

6. Professeur BENMOUSSA
Mathématiques Economiques
4- Dérivée :
cos x ≥ 0 ⇔ -
π
cos x ≤ 0
y ′ = cos x ⇔
π
⇔
2
≤ x ≤
π
2
3π
≤x≤
2
2
5- Tableau de variation :
x
π
0
y′
y
3π
2
2
+
-
2π
+
1
0
0
-1
6- La courbe :
y
1
π
3π
2
2
x
2π
-1
© www.e-tahero.net – Z.M.F
T=2π
VI-
Etude de la fonction (y = cos x) :
La dérivée de cette fonction est la suivante :
y ′ = - sin x.
La table de variation se présente comme suit :
Portail des Etudiants d’Economie
-3-

7. Professeur BENMOUSSA
Mathématiques Economiques
x
y′
y
π
0
2π
-
+
-
1
1
-1
y
1
0


π


π
2

3π
2



2π
-1
VII- Etude de la fonction (y = tg x) :
1- Période :
Tg (α + π) = tg α
⇒ tg α est périodique et T = π.
2- Parité :
tg (-x) = -tg x
⇒
y = tg x est impaire.
© www.e-tahero.net – Z.M.F
3- Dérivée :
y′=
1
cos 2 x
≠ 0.
4- Le tableau de variation :
Portail des Etudiants d’Economie
-4-

x

8. Professeur BENMOUSSA
Mathématiques Economiques
−π
2
x
y′
y
π
2
+
+∞
-∞
5- La courbe :
y
y = tg x
x
Remarque : les asymptotes :
VIII- Exercices :
© www.e-tahero.net – Z.M.F
1/ Calculer le (sin x) et la (tg x), sachant que cos x = 1 2/ Résoudre dans RR les équations :
a2 sin 3 x = 1.
b-
cos 2 x =
3
2
Solution :
1- On sait que sin2x + cos2x = 1
⇒ sin2x = 1- cos2x.
On sait aussi que : cos x = 1- 2 .
Portail des Etudiants d’Economie
-5-
2 .

9. Professeur BENMOUSSA
Mathématiques Economiques
⇒ cos2x = (1- 2 )2 = 1- 2 2 + 2.
⇒ sin2x = 1- (1- 2 2 + 2).
⇒ sin2x = 2 2 - 2 = 2( 2 - 1).
⇒ sin x = ± 2( 2 − 1) = ±
2 −1 × 2
• tg = ?
On sait que 1+ lg2 =
⇒ tg2 x =
⇒ tg x =
2
1
.
cos 2 x
1
-1.
cos 2 x
1
(1 − 2 )
2
-1=
2
⇒ tg2 x = -
(1 − 2 )
(1 − 2 )
2- a- 2 sin (3x) = 1
⇒ sin 3x = 1 2
⇒ sin 3x = sin
π
(1 − 2 )
= ±
© www.e-tahero.net – Z.M.F
2
( 2 − 1)
.
* x = α + 2kπ.
* x = - α + 2kπ.
π
sin 3x = sin .
3x =
π
6
6
+ 2kπ.
; (k∈Ζ)
π
3x = (π - ) + 2kπ.
6
⇒
2kπ
18
3
5π
2kπ
+
x=
18
3
x=
π
(1 − 2 ) 2
* x = α + 2kπ.
* x = (π - α) + 2kπ.
cos x = cos α ⇒
⇒
2( 2 − 1)
.
6
Observation: sin x = sin α ⇒
Donc :
=
2
.
−2
⇒ tg2 x = ±
1 − (1 − 2 ) 2
+
Portail des Etudiants d’Economie
; (k∈Ζ)
-6-
.

10. Professeur BENMOUSSA
b-
Mathématiques Economiques
3
.
2
cos 2x =
⇒ cos 2x = cos
⇒
2x =
π
6
2x = -
6
+ 2kπ.
π
6
x=
; (k∈Ζ)
+ 2kπ.
2kπ
12
2
π
2kπ
x=- +
12
2
⇒
π
π
+
; (k∈Ζ)
Consequences:
Il existe quatre solutions :
• x1 =
• x2 =
π
12
.
π
12
• x3 = -
π
12
π
12
.
+ π.
© www.e-tahero.net – Z.M.F
• x4 = -
+π.
Portail des Etudiants d’Economie
-7-

11. Professeur BENMOUSSA
Mathématiques Economiques
x
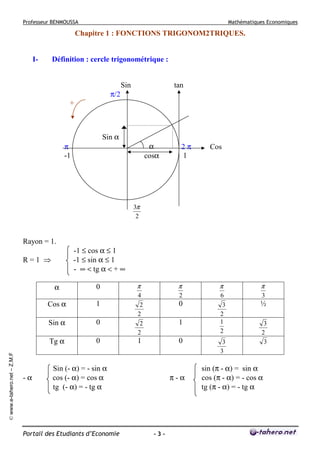
Chapitre 2 : FONCTION « y = e »
I-
Définition :
e0 = 1
e = 2,718.
II-
Propriétés :
1- y’ = ex.
2- ea+b = ea.eb
3- ea.b = (ea)b
4-
ea
eb
III-
= ea-b
Etude de la fonction f(x) = ex :
1- ex est strictement croissante.
2- Df = ℜ = ]− ∞,+∞[
3- lim ex = + ∞ .
+∞
lim
0
en −1
= 1.
h
x
lim e = 0.
−∞
Exercice:
1- Simplifier les expressions suivantes:
a- ex . e-2x
b- (e2x)2 . (e-3x)4.
c- (ex + e-x)2 – (ex – e-x)2.
2- Soit la fonction :
ex −1
.
ex +1
et lim f(x).
f(x) =
a- Calculer lim f(x)
−∞
+∞
e −1
).
3x
© www.e-tahero.net – Z.M.F
x
3- Calculer lim (
0
Solution:
1- a- ex.e-2x = e-x.
b- (e2x)2 . (e-3x)4 = e4x . e-12x = e-8x.
c- (ex + e-x) – (ex – e-x) = 4.
Portail des Etudiants d’Economie
-8-

12. Professeur BENMOUSSA
Mathématiques Economiques
2- On considère que : f(x) =
ex −1
ex +1
lim f(x) = -1.
−∞
ex
lim f(x) = x
+∞
e
[
1− 1
1+ 1
ex
]
ex
1
= 0.
ex
Car on sait que lim
+∞
ex −1
3- lim
0
3x
IV-
= 1.
1
ex −1
= lim
.
3 0
x
1
= .
3
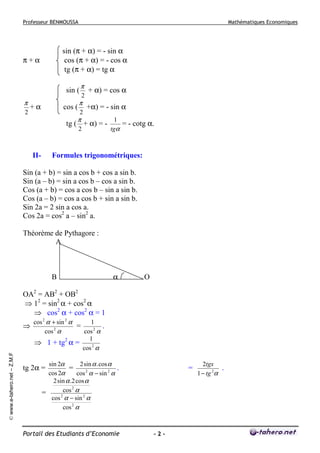
Tableau de variation:
x
y’
y
-∞
0
+
1
+∞
+∞
0
Car on sait que : y’ = ex ≠ 0.
La courbe :
y
y = ex
1
x
© www.e-tahero.net – Z.M.F
0
Vlim
+∞
Autres limites :
ex
x
= +∞.
x
lim x e = 0.
−∞
Portail des Etudiants d’Economie
-9-

13. Professeur BENMOUSSA
VI-
Mathématiques Economiques
Equations et inéquations:
* ea = eb ⇒ a = b.
* ea > eb ⇒ a > b. Car ex est strictement croissante.
VII- Exercices :
1- Calculer lim f(x) = lim (ex – x + 1).
+∞
+∞
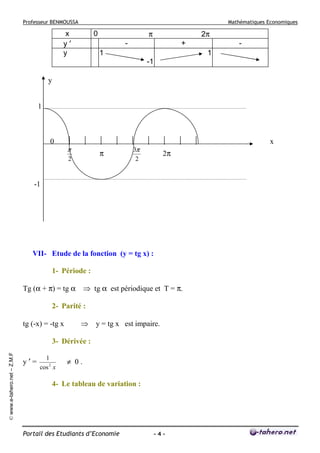
2- Etudier le sens de variation de la fonction : f(x) = (x – 2)ex.
Solution :
1- lim (ex – x + 1) = lim (
+∞
+∞
ex
1
- 1 + ) = +∞.
x
x
2- Df = ℜ = ]− ∞,+∞[ .
On sait qu’au règle générale : (f.g)’ = f’.g + f.g’
f’(x) = ex + (x – 2)ex = ex (1 + x – 2)
= ex (x – 1).
x
f’(x)
f(x)
-∞
1
0
-
+∞
+
0
+∞
y
0
І
1
© www.e-tahero.net – Z.M.F
-e
Portail des Etudiants d’Economie
- 10 -
x

14. Professeur BENMOUSSA
Mathématiques Economiques
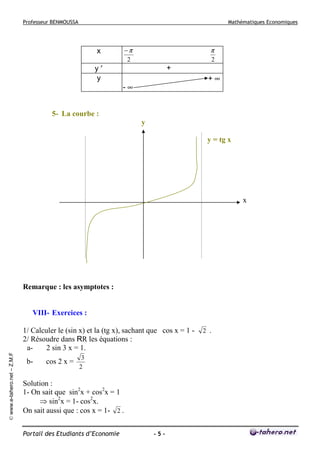
Chapitre 3 : FONCTIONS LOGARITHMES.
I-
Définition :
On appelle logarithmes de base « a » :
y=
log( x)
.
log(a )
Cas particulier : quand a = e ⇒ y = log x (c’est le logarithme népérien).
y = log x =
∫
x
1
1
dx.
x
x > 0.
Pour: x = 1 ⇒ log 1 = 0 =
Pour : x = 0 ⇒ log x = - ∞.
1
∫
1
1
dx.
x
+
1- Dérivée :
y = log x ⇒ y’ =
1
.
x
2- Propriétés:
* log (a.b) = log a + log b.
a
= log a – log b.
b
1
* log = - log a.
a
* log
* log an = n. log a
II-
Etudier la fonction y = log x :
* Df = ]0,+∞[
© www.e-tahero.net – Z.M.F
* y’ =
1
≠0.
x
x
y’
y
0+
1
+
0
-∞
Portail des Etudiants d’Economie
- 11 -
+∞
+∞

15. Professeur BENMOUSSA
Mathématiques Economiques
y
y = log x
0
x
i
1
Exercices :
Etude des fonctions :
a- y = 3 log x + 2.
b- y = log (x – 2).
Solutions :
a- Df = ]0,+∞[
f’(x) =
3
.
x
x
f’(x)
f(x)
0+
1
+
2
+∞
+∞
-∞
b- Df = ]2,+∞[
© www.e-tahero.net – Z.M.F
f’(x) =
1
x−2
x
f’(x)
f(x)
2
3
+
0
-∞
Portail des Etudiants d’Economie
- 12 -
+∞
+∞

16. Professeur BENMOUSSA
III-
Mathématiques Economiques
Limites :
* lim ln x = +∞.
+∞
* lim ln x = -∞.
0+
* lim
+∞
ln x
= 0x
* lim x lnx = 00
ln x
=1
x −1
ln( x + 1)
=1
* lim
0
x
* lim
1
IV-
Exercices:
1
1- Etude de la fonction : y = x2 e x .
Et tracer le graphique.
2- Etude de la fonction : y = x logx – 3x.
−
1
3- Etude de la fonction : y = (x – 2) e x .
Solution :
2
1
x
1- Etude de la fonction : y = x e .
* Df = ℜ * = ]− ∞,0[ ∪ ]0,+∞[
1
x
* y’ = 2x. e + x2 (-
1
). e
x2
car on a (x ≠ 1).
1
x
1
= (2x – 1). e x .
1
On a: y’ = 0 ⇔ 2x – 1 = 0
ou
e x = 0.
1
x
1
⇔ x=
2
1
x
on sait que e > 0 donc : e ≠ 0.
© www.e-tahero.net – Z.M.F
Donc le tableau de variation est le suivant :
x
y’
y
-∞
1
2
0
-
-
+∞
Portail des Etudiants d’Economie
+
+∞
+∞
1 2
e
4
0
- 13 -
+∞

17. Professeur BENMOUSSA
Mathématiques Economiques
1
* lim f(x) = lim (x2. e x ) = +∞
−∞
−∞
2
1
x
2
1
x
* lim f(x) = lim (x . e ) = +∞
+∞
+∞
* lim f(x) = lim (x . e ) = 0
0−
0−
2
1
x
* lim f(x) = lim (x . e ) = 1
0+
0+
y
e2
4
0
1
2
x
2- Etude de la fonction : y = x log x – 3x.
* Df = ]0,+∞[ .
* y’ = (x log x)’ – (3x)’ = log x + x (log x)’ – 3
y’ = log x – 2.
© www.e-tahero.net – Z.M.F
On a : y’ = 0 ⇔ log x – 2 = 0.
⇔ x = e2 .
* Tableau de variation :
x
y’
y
e2
0
0
+∞
+
+∞
e
* lim f(x) = lim x.(log x – 3) = +∞.
+∞
+∞
* lim f(x) = lim x. log x – 3x = 0
0+
0+
Portail des Etudiants d’Economie
+∞
- 14 -
-2

18. Professeur BENMOUSSA
Mathématiques Economiques
* Représentation graphique:
y
y = x log x – 3x.
e2
e3
x
-e2
3- Etude de la fonction : y = (x – 2) e
−
1
x
:
* Df = ℜ * = ]− ∞,0[ ∪ ]0,+∞[
* f’ (x) = e
=e
=e
=e
−
1
x
−
1
x
−
1
x
−
1
x
1
+ (x – 2).
−
1
.e x
2
x
x − 2 −x
+
.e
x2
x+2
(1 + 2 ).
x
2
x + x+2
(
).
x2
1
−
1
On a f’(x) = 0 ⇔ e x (
−
x2 + x + 2
)=0
x2
1
x
© www.e-tahero.net – Z.M.F
On sait que e ≠ 0 et x2 ≠ 0.
Donc x2 + x + 2 = 0
∆ = 9 = 32.
x1 = 1
et x2 = -2.
* Tableau de variation :
x
y’
y
-∞
-2
+
0
-
-
-4 2
-∞
Portail des Etudiants d’Economie
1
0
-∞
- 15 -
+∞
+
+∞

19. Professeur BENMOUSSA
* lim f(x) = lim (x – 2) e
−∞
Mathématiques Economiques
−
1
x
= -∞.
−∞
* lim f(x) = lim (x – 2) e
+∞
+∞
* lim f(x) = lim (x – 2) e
0−
−
1
x
−
1
x
= +∞.
= -∞.
0−
* lim f(x) = lim (x – 2) e
0+
0+
−
1
x
= 0.
* Asymptotes obliques:
f ( x)
( x − 2).e
- lim
= lim
+∞
+∞
x
x
f ( x)
⇒ lim
= 1.
+∞
x
−
1
x
1
−
x
2
= lim . (1 - ) . e x .
+∞ x
x
- lim [f(x) – x] = lim (x – 2). e
+∞
+∞
= lim x e
+∞
−
1
x
= lim x [ e
+∞
On met:
Donc : lim +∞
X=-
−
−
1
x
-2 e
1
x
- x.
−
1
x
- x.
−
1
- 1] – 2 e x .
1
.
x
1
[eX – 1] – 2 eX = -3.
X
* Représentation graphique :
© www.e-tahero.net – Z.M.F
-
1
e
-4 e
Portail des Etudiants d’Economie
- 16 -

20. Professeur BENMOUSSA
Mathématiques Economiques
Chapitre 4 : INTEGRALES
I-
Principes :
1- 1er cas :
Un train roule à la vitesse de v = 70 m s Durant un temps de t = 15 secondes.
Quelle est la distance parcourue par le train ?
On sait que : d = v.t donc : d = 70 * 15 = 1050 m.
v (ms )
v1 = 70
t (secondes)
t1 = 15
d = v.t = aire du rectangle hachuré.
2- 2ème cas :
La vitesse du train n’est pas constante et varie en fonction du temps « t », donc v= v(t).
On sait que : d = v.t.
Donc : d(t) = v(t) . t.
v (ms )
V(t)
v1 = 70
© www.e-tahero.net – Z.M.F
S
0
t (secondes)
t1 = 15
Portail des Etudiants d’Economie
- 17 -

21. Professeur BENMOUSSA
d = ∑ di =
Mathématiques Economiques
15
∫ f (t )
dt = S.
0
C’est la somme des aires des petits rectangles.
II-
Intégrale d’une fonction sur un intervalle :
1- Définition :
f(x)
f(x)
v1 = 70
S
0
x
a
b
b
I=
∫ f ( x)
dx = aire S.
a
Remarque:
L’intégrale (aire) peut être positif ou négatif.
v (ms )
© www.e-tahero.net – Z.M.F
0
t (secondes)
a
Portail des Etudiants d’Economie
b
- 18 -

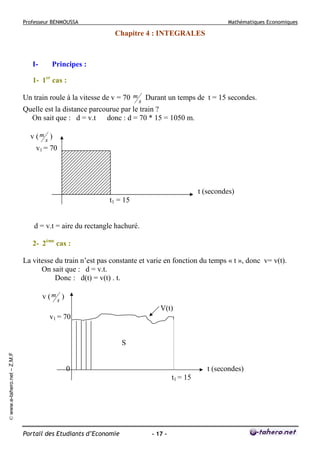
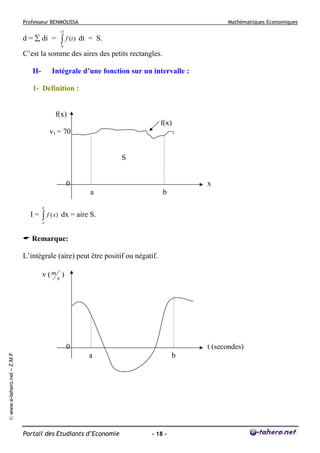
22. Professeur BENMOUSSA
Mathématiques Economiques
2- Propriétés :
Si « f » est constante ⇒ I =
b
∫ kf ( x) dx.
a
I = k (b – a).
3- Valeur moyenne d’une fonction f(x) :
1
M=
(b − a )
III-
b
∫ f ( x) dx.
a
Propriétés générales d’une intégrale :
1- Théorème :
Toute fonction continue sur un intervalle I = [a, b] admet un intégrale.
2- Propriétés :
a
*
∫ f ( x)
dx = 0.
a
b
*
∫ f ( x)
a
dx = - ∫ f ( x) dx.
a
b
b
*
∫
c
f ( x) dx +
a
∫
b
b
*
c
f ( x) dx =
∫ kf ( x) dx
a
∫
dx.
a
b
=k
∫ f ( x) dx.
a
b
*
∫ f ( x)
b
f ( f + g )( x) dx =
a
a
* Si f(x) ≤ g(x) ⇒
IV-
∫
b
f ( x) dx +
∫ g ( x)
dx.
a
∫ f (x)
≤
∫ g (x) .
Primitives d’une fonction :
© www.e-tahero.net – Z.M.F
1- Théorème :
Soit f(x) une fonction continue sur I = [a, b] .
L’application : F : x → F(x) = ∫ f (t ) dt est dérivable sur I, et la dérivé de F(x) est F’(x) =
f(x).
2- Propriétés :
Portail des Etudiants d’Economie
- 19 -

23. Professeur BENMOUSSA
Mathématiques Economiques
Toute fonction f(x) continue sur I possède plusieurs primitives.
Si « f » admet une primitive « F » sur I, alors « G = F + k » est aussi primitive de « f ».
Avec « k » constante.
L’intervalle « I »
ℜ
ℜ
Fonction « f »
a
x
ℜ
xn ; n∈ℵ
+
−
ℜ * ou ℜ *
1
x2
1
xn
1
+
−
ℜ * ou ℜ *
+
ℜ*
ℜ
+
*
r
x
ℜ
1
1+ x2
Cos x
Sin x
ℜ
ℜ
π
 π

 − 2 + kπ ; 2 + kπ 


]kπ ; π + kπ [
« u » est dérivable sur I et
strictement positive sur I
« u » est dérivable sur I et
strictement positive sur I
1
(cos) 2
1
1+ cotan2x =
(sin) 2
1+ tan2x =
u’ × un ; n ∈(Q/ {− 1} )
« u » est dérivable sur I
© www.e-tahero.net – Z.M.F
x
; r∈( Q/ {− 1} )
u'
u
u'
1+ u2
v'
v2
u’ + v’
« v » est dérivable et ne
s’annule pas sur I
« u et v » sont dérivables
sur I
« u et v » sont dérivables
sur I
« u et v » sont dérivables
sur I et v ≠ 0
« v » est dérivable sur I et
« u » est dérivable sur v(I)
ℜ
ℜ
sin (ax + b) ; a ≠ 0
Portail des Etudiants d’Economie
Primitive « F »
ax + b
1 2
x +c
2
1 n+1
x +c
n +1
1
- +c
x
−1
+c
(n − 1) x n −1
2 x +c
1
xr+1 + c
r +1
Artan x + c
Sin x + c
- cos x + c
Tan x + c
- cotan x + c
1
un+1 + c
n +1
2 u +c
Arctan (u) + c
1
+c
v
u+v+c
-
u’v + uv’
u.v + c
u ' v − uv'
v2
u’(v(x)) × v’(x)
u
+c
v
(uov)(x) + c
Cos (ax + b) ; a ≠ 0
( 1 ) sin (ax + b) + c
a
- ( 1 ) cos (ax + b) + c
a
- 20 -

24. Professeur BENMOUSSA
V-
∫ U '.V
Mathématiques Economiques
Intégration par partie :
∫ U .V ' .
= U.V -
Exemples :
Calculer les intégrales suivantes :
π
I = ∫ x. cos x .dx .
1-
0
On pose:
I = [x. sin
V=x
U’ = cos x
V’ = 1
U = sin x
π
x]π0
- ∫ sin x .dx
0
x]π0
= [x. sin
+ [cos x]π0
= (π. Sin π - 0) + (cos π - cos 0).
I = -2.
2
x
I = ∫ ( x 2 + ) dx.
2-
I = ∫ x 2 dx +
I=
2
∫x
dx.
x3
+ 2 log x + k.
3
4
I = ∫ x x 2 + 4 dx.
3-
2
1
I=
2
4
∫ 2 x( x
2
+ 4)
dx.
2
1

2
 x2 + 4 
1

I= 
2  1

 +1 
 2

© www.e-tahero.net – Z.M.F
1
2
+1
3
1
dx . =
( x 2 + 4) 2 .
3
Car on sait que:
4-
I=
∫ 5x
3
m
∫ U '.U =
U m +1
.
m +1
x 4 + 1 dx.
1
I = ∫ 5 x 3 ( x 4 + 1) 2 dx.
Portail des Etudiants d’Economie
- 21 -

25. Professeur BENMOUSSA
1
5 ( x 4 + 1) 2
=
1
4
+1
3
Mathématiques Economiques
+1
3
=
15 3
( x + 1) 2 .
16
e
I = ∫ log x dx.
5-
1
On pose :
U’ = 1
V = log x
I = [x log
U=x
V’ =
x]e1
1
x
e
- ∫ dx = [x log x –x]e1.
1
I = 1.
π
π
2
I = ∫ sin(2 x + ) dx.
6-
4
0
1
cos (ax + b).
a
1
π
1
π
π
Donc: I = [- cos (2x + )] = - [cos (π + ) – cos ].
2
4
2
4
4
∫ sin(ax + b)
On sait que :
On sait que : cos (π +
Donc : I = -
π
4
dx = -
) = -cos
π
4
.
1
2
2
1
[] = .
2
2
2
2
2
1
I = ∫ (2t − 4)e t dt.
7-
0
On pose :
U = (2t – 4)
V’ = et
U’ = 2
V = et .
1
1
0
0
© www.e-tahero.net – Z.M.F
I = ∫ (2t − 4)e t dt = [et (2t – 4)]10 - ∫ 2e t dt.
= [e (-2) – (-4)] – 2 [et]10.
= -4e + 6.
Portail des Etudiants d’Economie
- 22 -

26. Professeur BENMOUSSA
Mathématiques Economiques
e
8-
I=
log x
dx.
2
1 x
∫
On pose : V = log x
U’ =
V’ =
1
x2
1
x
U=-
1
x
e
1
1
.log x]e1 + ∫ 2 dx.
x
1 x
1
1
= [ - . Log e + 1. log 1] – [ - 1].
e
e
2
+ 1.
=e
I = [-
π
9-
I = ∫ 2t sin t dt.
0
On pose :
V = 2t
U’ = sin t
V’ = 2
U = -cos t.
π
I = - [2t.cos t]π0 + ∫ 2 cos t dt.
0
= - [2 π cos π - 0] + 2 [sin t]π0.
= 2 π.
VI-
Décomposition :
1+ x
.
( x + 4) 2 ( x − 1)
1+ x
A
B
C
R(x) =
=
+
+
.
2
2
( x + 4)
( x − 1)
( x + 4) ( x − 1)
( x + 4)
3
* Calculer B : B =
5
2
* Calculer C : C =
25
2
* Calculer A : A = 25
© www.e-tahero.net – Z.M.F
Décomposition de : R(x) =
3- Lorsque d° P(x) ≥ d° Q(x) :
La méthode des calcules est la division euclidienne.
Portail des Etudiants d’Economie
- 23 -

27. Professeur BENMOUSSA
Mathématiques Economiques
P(x)
Q(x)
p(x)
r(x)
P( x)
r ( x)
= p(x) +
Q( x)
Q( x)
avec d° r(x) < d° Q(x).
Exemple :
P( x)
x4
=
.
Q( x)
x( x + 1) 2
On a d° P(x) > d° Q(x).
x (x + 1)2 = x (x2 + 2x + 1).
= x3 + 2x2 + x.
x4
x4 + 2x3 + x2
x3 + 2x2 + x
x-2
3
2
- 2x – x
2x + 4x2 + 2x
3
3x2 + 2x
x4
x4
3x 2 + 2 x
= 3
= (x – 2) + 3
.
x( x + 1) 2
x + 2x
x + 2x 2 + x
3x + 2
= (x – 2) +
.
( x + 1) 2
x4
∫ x(x + 1) 2 dx.
3x + 2
I = ∫ x − 2 dx + ∫
dx.
( x + 1) 2
Calcul de I =
© www.e-tahero.net – Z.M.F
On pose: I1 = ∫ x − 2 dx.
I2 =
I2 =
3x + 2
∫ ( x + 1)
2
3x + 2
∫ ( x + 1)
dx. = 3
=
3
2
2
dx.
x
∫ (x + 1)
2
dx +
2x + 1 − 1
dx +
2
+ 2x + 1
∫x
Portail des Etudiants d’Economie
2
∫ ( x + 1)
2
dx.
2
∫ ( x + 1)
2
- 24 -
dx

28. Professeur BENMOUSSA
Mathématiques Economiques
3
2x + 1
1
[∫
dx - ∫
dx] +
2
2
( x + 1)
( x + 1) 2
3
1
2
=
[log (x + 1) +
].
2
x +1
x +1
=
Donc : I + I1 + I2.
Exercice :
Calculer :
2x + 1
∫ ( x + 1)( x
dx
+ 1)
P( x)
2x + 1
A
Bx + C
=
=
+ 2
.
R(x) =
2
Q( x)
x +1
( x + 1)( x + 1)
( x + 1)
2
* Calculer A :
A = [R(x) × (x+1)]x = -1 = -
1
2
* Calculer B :
2x 2
Ax
=
3
x
x
Bx 2
=A+B=0
x2
1
⇒B=-A= .
2
+
* Calculer C :
On donne à x = 0. Donc 1 = A +
C
⇒ A + C = 1.
1
⇒ C = 1 – A.
⇒C=
3
.
2
3
1
 x+ 
2
2 dx +  2
I= ∫
∫ ( x 2 + 1) dx.
( x + 1)
1
I = - log x + 1 + I2
2
3
1
 x+ 
1 x+3
2
2
I2 = ∫  2
dx = ∫ 2
dx.
2 x +1
( x + 1)
1
x
3
dx
=
∫ x 2 + 1 dx + 2 ∫ x 2 + 1 dx.
2
1
2x
3
dx
=
∫ x 2 + 1 dx + 2 ∫ x 2 + 1 dx.
4
1
3
= log (x2 + 1) +
artang x.
4
2
1
1
3
artang x.
I = - log x + 1 + log (x2 + 1) +
2
4
2
© www.e-tahero.net – Z.M.F
−1
Portail des Etudiants d’Economie
- 25 -
2
∫ ( x + 1)
2
dx.