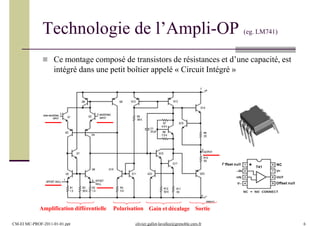
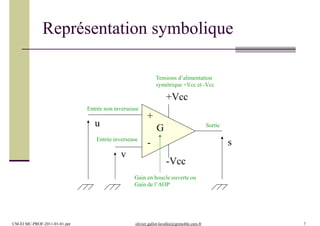
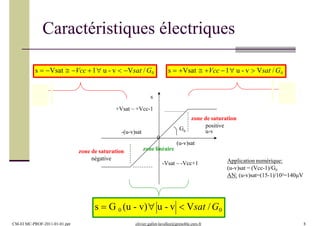
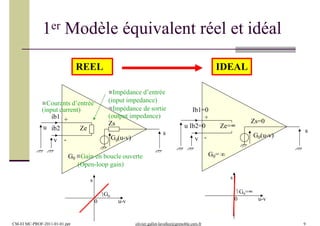
Ce document présente un module de formation en électronique d'instrumentation axé sur les amplificateurs opérationnels, le filtrage actif, et le traitement des signaux, incorporant 12 heures de cours, 24 heures de travaux dirigés, et 32 heures de travaux pratiques. Les étudiants apprendront à connaître les dispositifs électroniques, les montages d'amplification, ainsi que les imperfections des amplificateurs. L'évaluation comprend des devoirs surveillés et un examen pratique.











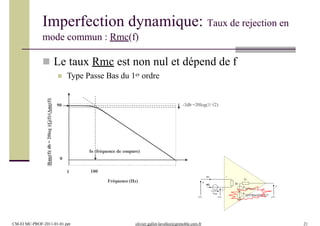










![Filtre actif ou passif ? (Rappel)
Les filtres passifs = composants passifs
F > MHz et Gain ≤ 1
Les filtres actifs = composants actifs
F < MHz et Gain > 1
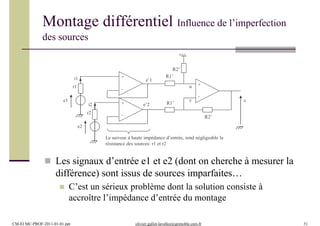
-
+
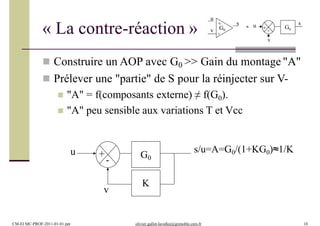
v
u
vs
R1
ve
R2
C
Eg:
R1=5,1[kΩ]
vs(t)ve(t) C=10[nF]
CM-EI MC-PROF-2011-01-01.ppt olivier.gallot-lavallee@grenoble.cnrs.fr 37
Eg:](https://image.slidesharecdn.com/amplificationfiltrage-200131192803/85/Amplification-filtrage-37-320.jpg)




![-30
-20
-10
0
Gain[dB]
102
103
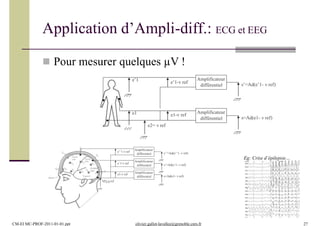
105
106
-90
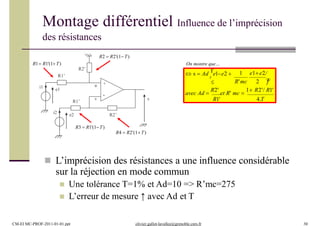
-45
-40
104
Pulsation [rad/s]
Phase[deg]
c=1/RC
-3db
droite à 0db
droite à 0°
droite à -90°
inflexion à -45°
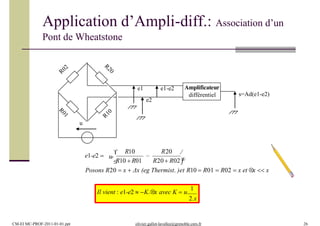
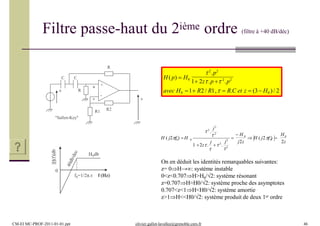
Application… (Rappel)
1 RC.p
Hp
1
(1) p0(2) Hp 1
RC.p
1
p
(3) Hp
= fonction affine de pente -20db /décades et
passant par Hdb=0 en ω =1/RC (dans un
repère ou les abscisses sont log.)
.
(4)
Hdb 20.log(1) 0
H 20.log(
1
) 20.log(
1
) -20.log()
db
RC.ω RC
(5)
dbdb
1
) 20.log(
1
) -3
211
H 20.log(
1 j
1
arg( ) arctg(1) -45
arg(1) 0
) -90
1
j.RC.
arg(
(4)
CM-EI MC-PROF-2011-01-01.ppt olivier.gallot-lavallee@grenoble.cnrs.fr 42](https://image.slidesharecdn.com/amplificationfiltrage-200131192803/85/Amplification-filtrage-42-320.jpg)











![Oscillateur à relaxation (Générateur bistable)
Fréq. =f(Capa.)
Mesurer la dérive d’une capacité
Capteur de pression ou de déformation
RC
-
+
v
u
G
s
R1
R2
a=R1/(R1+R2)
t
+Vsat
+aVsat
0
-aVsat
-Vsat
s(t)
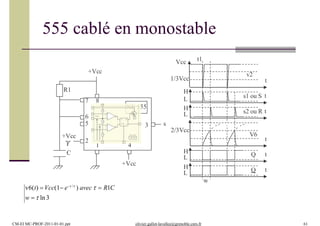
T=2.τ.ln[(1+a)/(1-a)] T
v1(t)
Inverseur
v(t)v2(t)
CM-EI MC-PROF-2011-01-01.ppt olivier.gallot-lavallee@grenoble.cnrs.fr 58
1 a
v2(t) Vsat1(1 a).ett2/
v1(t) Vsat1 (1 a).ett1/
avec a R1/(R1 R2)T 2 ln
1 a
v(t) Vsat(1 et /
) avec RC](https://image.slidesharecdn.com/amplificationfiltrage-200131192803/85/Amplification-filtrage-58-320.jpg)