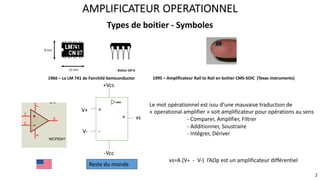
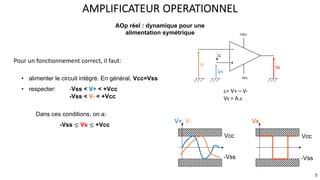
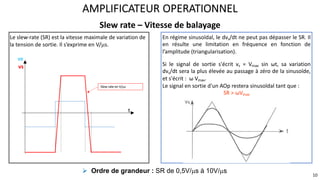
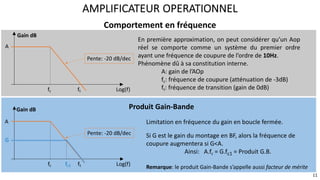
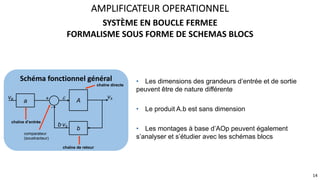
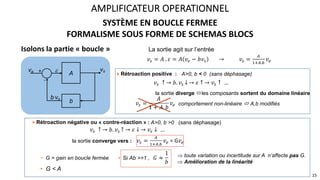
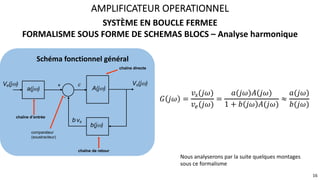
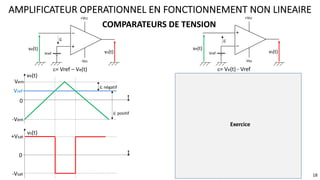
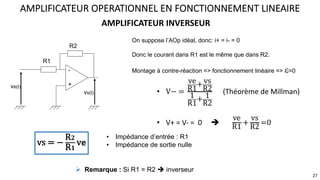
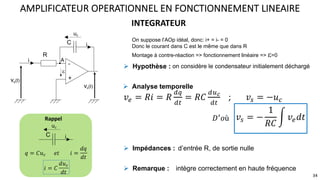
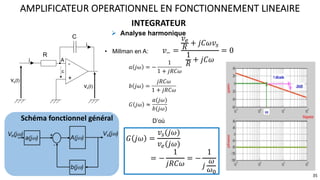
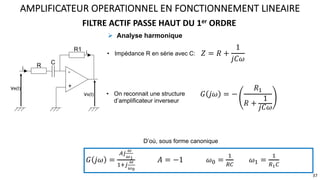
Le document présente une étude approfondie des amplificateurs opérationnels (AOP), discutant de leurs caractéristiques, fonctionnement et différentes configurations telles que les montages à rétroaction négative et positive. Il aborde également des concepts tels que le taux de réjection de mode commun, la vitesse de balayage, et la dynamique des AOP dans des régimes linéaires et non linéaires. Enfin, il fournit des exemples pratiques d'utilisation des AOP dans divers circuits électroniques.

1. 1
Partie 3
AMPLIFICATEUR OPERATIONNEL
Bernard DHALLUIN
Jean-Max DUTERTRE
Année 2021-2022
ISMIN 1A
Electronique Analogique 1
Version du 05/09/2021

2. Types de boitier - Symboles
AMPLIFICATEUR OPERATIONNEL
2
12 mm
8 mm
Boîtier DIP 8
1966 – Le LM 741 de Fairchild Semiconductor 1995 – Amplificateur Rail to Rail en boitier CMS-SOIC (Texas instruments)
vs=A.(V+ - V-) l’AOp est un amplificateur différentiel
3
2
6
7
4
U3
MCP6041
Le mot opérationnel est issu d’une mauvaise traduction de
« operational amplifier » soit amplificateur pour opérations au sens
- Comparer, Amplifier, Filtrer
- Additionner, Soustraire
- Intégrer, Dériver
+Vcc
w∞
+
+
-
e+
e-
vs
-Vcc
Reste du monde
V+
V-

3. • Gain A très grand, de l’ordre de 105 pour
des fréquences allant du continu (0Hz) à
quelques MHz,
• Courants d’entrée très faibles
• Impédance d’entrée très grande (>100MW)
• Impédance de sortie faible (qq 10W).
• Gain A est infini quelque soit la
fréquence
• Courants d’entrée nuls
• Impédance d’entrée infinie
• Impédance de sortie nulle
• Bande passante infinie
AOp idéal
Caractéristiques utilisées lors de l’étude théorique des
montages à AOp.
AOp réel
Choisir un AOp, c’est choisir les caractéristiques de celui-ci telles que l’on puisse le considérer
idéal dans la gamme de tensions et de fréquences de fonctionnement du système étudié.
Caractéristiques principales d’un AOp
AMPLIFICATEUR OPERATIONNEL
3

4. • Gain > 105
• Tension d’alimentation: simple ou symétrique
• Courants d’entrée très faibles ~ 10pA
• Impédance d’entrée >100MW
• Impédance de sortie ~ 10W
• Bande passante ~ 10aine Hz
• Voff ~ 10nV à 1mV
AOp réel
Ordres de grandeur
AMPLIFICATEUR OPERATIONNEL
4

5. Pour un fonctionnement correct, il faut:
• alimenter le circuit intégré. En général, Vcc=Vss
• respecter: -Vss < V+ < +Vcc
-Vss < V- < +Vcc
Dans ces conditions, on a:
-Vss ≤ Vs ≤ +Vcc
V+, V-
Vcc
-Vss
Vs
Vcc
-Vss
AMPLIFICATEUR OPERATIONNEL
_
+
+Vcc
-Vss
e
V- Vs
e= V+ – V-
Vs = A.e
V+
5
AOp réel : dynamique pour une
alimentation symétrique

6. AOp réels : défauts et correction
6

7. La fonction générale d’un AOp est d’amplifier la différence des entrées, soit:
Vs = A.(V+ - V-) = A. e
! Comme A est très grand. Cela se traduit par la fonction
de transfert ci-contre où la pente est très raide.
! Comme la tension de sortie ne peut pas évoluer au delà
des tensions d’alimentation, on a saturation de la
sortie.
! Pour les AOps réels:
" les tensions de saturation sont différentes des tensions
d’alimentation et on a:
+Vsat ¹ Vcc, -Vsat ¹ -Vss et +Vsat ¹|-Vsat|
" Pour la technologie Rail-to-Rail on a +Vsat ~ Vcc et –Vsat ~ -Vss
" Il existe une tension d’offset (Voff), lorsque e=0 Vs≠0
AMPLIFICATEUR OPERATIONNEL
+Vsat
-Vsat
Vcc
-Vss
Vs
e
Fonctionnement linéaire
Fonctionnement en saturation
Voff
7
Saturation et offset

8. Impédances d’entrée et de sortie
AMPLIFICATEUR OPERATIONNEL
8
Source Charge
Modèle de l’AOp
Avi
RL
vS
ve
Ri
vi
R0
Re
Ie+
Ie-
Voff
Pour avoir vi = ve il faut Ri >> Re donc idéalement Ri => ∞
En entrée (on a un diviseur de tension) : e
e
i
i
i v
R
R
R
v
+
=
En sortie (on a un diviseur de tension) : i
L
L
S Av
R
R
R
v
+
=
0
Pour avoir vS = Avi il faut idéalement R0 ~ 0
Conclusion si Ri = ∞ et R0 = 0 :
• les valeurs de Ri et R0 sont
généralement respectivement très
grande ou négligeable devant les
autres résistances du montage
considéré
vs = A . ve
! Remarques :
• Ri = ∞ et R0 = 0 est la meilleure
adaptation d’impédance qu’il soit. Elle
reste théorique

9. Taux de réjection de mode commun
AMPLIFICATEUR OPERATIONNEL
9
On recherche Vs = Ad.(V+ - V-)
Théoriquement si V+ et V- augmentent ou diminuent d’une même valeur, Vs ne change pas…
En pratique, Vs n'est jamais absolument indépendante de la valeur individuelle de V+ et de V-
et on peut écrire:
Ad : gain différentiel
Amc : gain de mode commun
Le gain en mode commun correspond à un effet indésirable (la sortie n'est plus proportionnelle
à la seule différence des entrées), par conséquent il doit être le plus petit possible.
Le gain en mode commun est donné à partir du taux de réjection de mode commun CMRR
(Common Mode Rejection Ratio) défini par:
𝑉𝑠 = 𝐴𝑑 𝑉! − 𝑉
" + 𝐴𝑚𝑐
𝑉! + 𝑉
"
2
𝐶𝑀𝑅𝑅 =
𝐴𝑑
𝐴𝑚𝑐
𝑜𝑢 𝐶𝑀𝑅𝑅#$ = 20 𝑙𝑜𝑔
𝐴𝑑
𝐴𝑚𝑐
! Remarque : comme nous le verrons plus tard, les amplis d’instrumentation ont un CMRR élevé > 100dB

10. Slew rate – Vitesse de balayage
AMPLIFICATEUR OPERATIONNEL
10
t
ve
vs
Slew rate en V/µs
Le slew-rate (SR) est la vitesse maximale de variation de
la tension de sortie. Il s’exprime en V/µs.
En régime sinusoïdal, le dvs/dt ne peut pas dépasser le SR. Il
en résulte une limitation en fréquence en fonction de
l’amplitude (triangularisation).
Si le signal de sortie s'écrit vs = Vmax sin ωt, sa variation
dvs/dt sera la plus élevée au passage à zéro de la sinusoïde,
et s'écrit : ω Vmax.
Le signal en sortie d'un AOp restera sinusoïdal tant que :
SR > ωVmax
! Ordre de grandeur : SR de 0,5V/µs à 10V/µs

11. Comportement en fréquence
AMPLIFICATEUR OPERATIONNEL
11
En première approximation, on peut considérer qu’un Aop
réel se comporte comme un système du premier ordre
ayant une fréquence de coupure de l’ordre de 10Hz.
Phénomène dû à sa constitution interne.
A: gain de l’AOp
fc: fréquence de coupure (atténuation de -3dB)
ft: fréquence de transition (gain de 0dB)
Log(f)
Gain dB
ft
fc
Pente: -20 dB/dec
A
Produit Gain-Bande
Limitation en fréquence du gain en boucle fermée.
Si G est le gain du montage en BF, alors la fréquence de
coupure augmentera si G<A.
Ainsi: A.fc = G.fc1 = Produit G.B.
Remarque: le produit Gain-Bande s’appelle aussi facteur de mérite
Log(f)
Gain dB
ft
fc
Pente: -20 dB/dec
A
fc1
G

12. Montages à AOp
12

13. Deux régimes de fonctionnement
AMPLIFICATEUR OPERATIONNEL
FONCTIONNEMENT LINEAIRE
Prélèvement d’une partie du signal de
sortie pour l’injecter sur l’entrée
inverseuse de l’AOp.
Montage avec rétroaction négative
ou contre-réaction
Dans ces conditions on considère:
V+ = V- donc e = 0
FONCTIONNEMENT NON LINEAIRE
(ou en saturation)
Prélèvement d’une partie du signal de
sortie pour l’injecter sur l’entrée positive
de l’AOp.
Montage avec rétroaction positive
Dans ces conditions la tension de sortie
ne peut prendre que 2 valeurs:
+ Vsat ou - Vsat
13
Utilisation des AOp en boucle fermée (sauf en comparateur)

14. SYSTÈME EN BOUCLE FERMEE
FORMALISME SOUS FORME DE SCHEMAS BLOCS
AMPLIFICATEUR OPERATIONNEL
14
A
b
ve vs
e
b.vs
-
+
a
Schéma fonctionnel général
chaîne de retour
chaîne d’entrée
comparateur
(soustracteur)
chaîne directe
• Les dimensions des grandeurs d’entrée et de sortie
peuvent être de nature différente
• Le produit A.b est sans dimension
• Les montages à base d’AOp peuvent également
s’analyser et s’étudier avec les schémas blocs

15. SYSTÈME EN BOUCLE FERMEE
FORMALISME SOUS FORME DE SCHEMAS BLOCS
AMPLIFICATEUR OPERATIONNEL
15
A
b
ve vs
e
b.vs
-
+
Isolons la partie « boucle » La sortie agit sur l’entrée
𝑣% = 𝐴 . 𝜀 = 𝐴 𝑣& − 𝑏𝑣% → 𝑣% =
'
(!'.*
𝑣&
4Rétroaction positive : A>0, b < 0 (sans déphasage)
la sortie diverge #les composants sortent du domaine linéaire
comportement non-linéaire # A,b modifiés
𝑣% ↑ → 𝑏. 𝑣% ↓ → 𝜀 ↑ → 𝑣% ↑ …
𝑣% =
𝐴
1 + 𝐴. 𝑏
𝑣&
4Rétroaction négative ou « contre-réaction » : A>0, b >0 (sans déphasage)
la sortie converge vers :
• G = gain en boucle fermée
• G < A
• Si Ab >>1 , Þ toute variation ou incertitude sur A n’affecte pas G.
Þ Amélioration de la linéarité
𝑣% ↑ → 𝑏. 𝑣% ↑ → 𝜀 ↓ → 𝑣% ↓ …
𝑣% =
'
(!'.*
𝑣& = G𝑣&
𝐺 ≈
1
𝑏

16. SYSTÈME EN BOUCLE FERMEE
FORMALISME SOUS FORME DE SCHEMAS BLOCS – Analyse harmonique
AMPLIFICATEUR OPERATIONNEL
16
𝐺 𝑗𝜔 =
𝑣@(𝑗𝜔)
𝑣A(𝑗𝜔)
=
𝑎(𝑗𝜔)𝐴(𝑗𝜔)
1 + 𝑏 𝑗𝜔 𝐴(𝑗𝜔)
≈
𝑎(𝑗𝜔)
𝑏(𝑗𝜔)
Schéma fonctionnel général
A(jw)
b(jw)
Ve(jw) Vs(jw)
e
b.vs
-
+
a(jw)
chaîne de retour
chaîne d’entrée
comparateur
(soustracteur)
chaîne directe
Nous analyserons par la suite quelques montages
sous ce formalisme

17. Montages à AOp en fonctionnement non linéaire
17

18. ve(t)
t
Vem
-Vem
0
Vref
e positif
e négatif
vs(t)
t
0
+Vsat
-Vsat
Ve(t)
t
Vem
-Vem
0
Vref
e négatif
e positif
vs(t)
t
0
+Vsat
-Vsat
COMPARATEURS DE TENSION
Vref
_
+
+Vcc
-Vss
e
ve(t)
vs(t)
e= Vref – Ve(t)
+
_
+Vcc
-Vss
Vref
e
ve(t)
vs(t)
e= Ve(t) - Vref
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT NON LINEAIRE
18
E
Exercice

19. ï
î
ï
í
ì
=
-
+
+
=
+
0
2
1
1
*
2
*
V
R
R
R
Vs
R
Ve
V
+
-
ve(t)
vs(t)
R1
R2
On suppose l’AOp idéal, donc: i+ = i- =0
Donc le courant dans R1 est le même que dans R2.
Le circuit permet d’écrire:
COMPARATEUR DE TENSION A HYSTERESIS – TRIGGER DE SCHMITT
Vs(t)
Ve(t)
+Vsat
-Vsat
𝑉𝑠𝑎𝑡
𝑅!
𝑅"
−𝑉𝑠𝑎𝑡
𝑅!
𝑅"
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT NON LINEAIRE
19
Hypothèse 1: état de la sortie: vs=+Vsat. Ce qui se traduit par V+>V-
La sortie basculera donc à –Vsat lorsque ve sera telle que:
c’est-à-dire :
ve∗R2+Vsat∗R1
R1+R2 < 0 ve < -
Vsat∗R1
R2
Hypothèse 2: état de la sortie: vs=-Vsat. Ce qui se traduit par V->V+.
La sortie basculera donc à +Vsat lorsque ve sera telle que:
ve > +
Vsat∗R1
R2
(Théorème de Millman)

20. ï
î
ï
í
ì
=
-
+
+
=
+
0
2
1
1
*
2
*
V
R
R
R
Vs
R
Ve
V
On suppose l’AOp idéal, donc: i+ = i- =0
Donc le courant dans R1 est le même que dans R2.
Hypothèse 1: état de la sortie: vs=+Vsat. Ce qui se traduit par V+>V-
Le circuit permet d’écrire:
La sortie basculera donc à –Vsat lorsque ve sera telle que:
c’est-à-dire :
COMPARATEUR DE TENSION A HYSTERESIS – TRIGGER DE SCHMITT
Hypothèse 2: état de la sortie: vs=-Vsat. Ce qui se traduit par V->V+.
La sortie basculera donc à +Vsat lorsque ve sera telle que:
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT NON LINEAIRE
20
+
-
ve(t)
vs(t)
R1
R2
vref
Vb = Vref+𝑉𝑠𝑎𝑡
#!
#"
Va = Vref−𝑉𝑠𝑎𝑡
#!
#"
Vs(t)
Ve(t)
+Vsat
-Vsat
Vref
Va Vb
ve∗R2+Vsat∗R1
R1+R2 < Vref ve < Vref -
Vsat∗R1
R2
ve > Vref +
Vsat∗R1
R2

21. R1
R2
On suppose l’AOp idéal, donc: i+ = i- =0
Donc le courant dans R1 est le même que dans R2.
Hypothèse 1: état de la sortie: vs=+Vsat. Ce qui se traduit par V+>V-
Le circuit permet d’écrire:
La sortie basculera donc à –Vsat lorsque ve sera telle que:
c’est-à-dire :
COMPARATEUR DE TENSION A HYSTERESIS – TRIGGER DE SCHMITT
Hypothèse 2: état de la sortie: vs=-Vsat. Ce qui se traduit par V->V+.
La sortie basculera donc à +Vsat lorsque ve sera telle que:
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT NON LINEAIRE
+
-
ve(t)
vs(t)
V+ =
R1
R1+R2
vs
V- = ve
𝑅1 𝑣𝑠
𝑅1 + 𝑅2
− 𝑣𝑒 > 0 ve >
Vsat R1
R1+R2
ve <
−Vsat R1
R1+R2 21
Vs(t)
Ve(t)
+Vsat
-Vsat
Vb = +Vsat
R1
R1+R2
Va = −Vsat
R1
R1+R2
Va
Vb

22. COMPARATEUR DE TENSION A HYSTERESIS – TRIGGER DE SCHMITT
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT NON LINEAIRE
22
V+
a =Vref + (Vsat-Vref)
R1
R1+R2
V+b =Vref - (Vsat+Vref)
R1
R1+R2
Vs(t)
Ve(t)
+Vsat
-Vsat
V’a
V’b
Vref
R2
+
-
ve(t)
vs(t)
R1
I
I
Vref
Exercice
On suppose l’AOp idéal, donc: i+ = i- =0
Donc le courant dans R1 est le même que dans R2.
Le circuit permet d’écrire:
V+ = Vref+R1 I= Vref + (Vs-Vref)
R1
R1+R2
V- = ve

23. On suppose l’AOp idéal, donc: i+ = i- =0
Donc le courant dans R1 est le même que dans R2.
Hypothèse 1: état de la sortie: vs=+Vsat. Ce qui se traduit par V+>V-
Le circuit permet d’écrire:
La sortie basculera donc à –Vsat lorsque ve sera telle que:
COMPARATEUR DE TENSION A HYSTERESIS – TRIGGER DE SCHMITT
Hypothèse 2: état de la sortie: vs=-Vsat. Ce qui se traduit par V->V+.
La sortie basculera donc à +Vsat lorsque ve sera telle que:
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT NON LINEAIRE
V+ = Vref+R1 I= Vref + (Vs-Vref)
R1
R1+R2
V- = ve
ve > Vref + (Vsat-Vref)
R1
R1+R2
23
ve < Vref - (Vsat+Vref)
R1
R1+R2
V+
a =Vref - (Vsat-Vref)
R1
R1+R2
V+b =Vref + (Vsat+Vref)
R1
R1+R2
Vs(t)
Ve(t)
+Vsat
-Vsat
V’a
V’b
Vref
R2
+
-
ve(t)
vs(t)
R1
I
I
Vref
Solution

24. Montages à AOp en fonctionnement linéaire
24

25. On suppose l’AOp idéal, donc: i+ = i- = 0
MONTAGE SUIVEUR
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
-
+
ve(t)
vs(t)
25
Montage à contre-réaction => fonctionnement linéaire => e=0
vs= ve
! Adaptateur d’impédance : Impédance d’entrée infinie
Impédance de sortie nulle
! Intérêt : Permet de connecter un 1er étage avec une mauvaise (grande)
impédance de sortie avec un second étage avec une mauvaise
(petite) impédance d'entrée.
! Remarque : montage appelé aussi buffer

26. On suppose l’AOp idéal, donc: i+ = i- = 0
Donc le courant dans R1 est le même que dans R2.
Montage à contre-réaction => fonctionnement linéaire => e=0
AMPLIFICATEUR NON INVERSEUR
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
• V− =
R1
R1+R2 vs
• V+ = V- = ve
26
vs = (1+
R𝟐
R𝟏
)ve • Impédance d’entrée infinie
• Impédance de sortie nulle
Schéma fonctionnel
La chaîne de retour est le
pont diviseur de tension :
b = R1/(R1+R2)
Ab> 1 $ vs/ve = 1 / b
A
b
ve vs
e
b.vs
-
+
-
+
ve(t)
vs(t)
R1
R2
e

27. On suppose l’AOp idéal, donc: i+ = i- = 0
Donc le courant dans R1 est le même que dans R2.
Montage à contre-réaction => fonctionnement linéaire => e=0
AMPLIFICATEUR INVERSEUR
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
• V− =
ve
R1
+vs
R2
1
R1
+ 1
R2
(Théorème de Millman)
• V+ = V- = 0 $
ve
R1 +
vs
R2 =0
27
vs = −
R𝟐
R𝟏
ve
-
+
ve(t)
vs(t)
R1
R2
• Impédance d’entrée : R1
• Impédance de sortie nulle
! Remarque : Si R1 = R2 $ inverseur

28. On suppose l’AOp idéal, donc: i+ = i- = 0
Montage à contre-réaction => fonctionnement linéaire => e=0
ADDITIONNEUR INVERSEUR
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
Les théorèmes de Millman et de superposition conduisent à:
• V− =
v1
R1
+v2
R2
+ …+vn
Rn
+vs
R
1
R1
+ 1
R2
+ … + 1
Rn
+1
R
• V+ = V- = 0
28
• Chaque voie d’entrée possède son impédance propre: Ri
• Impédance de sortie nulle
-
+
v1(t)
vs(t)
R1
R
v2(t)
vn(t) R2
Rn
vs =−R
v1
R1
+
v2
R2
+ … +
vn
Rn

29. ADDITIONNEUR INVERSEUR: APPLICATION
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
29
vs =−R
v1
R1
+
v2
R2
+ … +
vn
Rn
Rappel:
CONVERTISSEUR NUMERIQUE ANALOGIQUE
vs =−Vref 𝑨𝟏+
A2
2
+
𝑨𝟑
𝟒
+
A4
8
Ai : valeur binaire
-
+
vs(t)
R
R
2R
8R
4R
A3
A1
A2
A4
Vref
! Remarque : les interrupteurs peuvent être des MOS

30. On suppose l’AOp idéal, donc: i+ = i- = 0
Donc le courant dans R1 est le même que dans R.
Montage à contre-réaction => fonctionnement linéaire => e=0
SOUSTRACTEUR
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
30
• Impédance d’entrée v1(t) = R1
• Impédance d’entrée v2(t) = R2+R3
• Impédance de sortie nulle
vs =
R1+R
R1
R3
R2+R3
v2 −
R
R1+R
v1
𝑣" =
𝑣(
𝑅1
+
𝑣%
𝑅
1
𝑅1 +
1
𝑅
=
𝑅
𝑅1 + 𝑅
𝑣( +
𝑅1
𝑅1 + 𝑅
𝑣%
• Pont diviseur en B : 𝑣! =
𝑅3
𝑅2 + 𝑅3
𝑣,
• Millman en A:
-
+
v2(t)
vs(t)
R1
R
v1(t) R2
R3
e
A
B
! Remarque : si R=R1=R2=R3 alors vs = v2 – v1

31. SOUSTRACTEUR : Représentation en schéma bloc
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
31
atténuation d’entrée v1
(par definition: affectée du
signe – car entrée inverseuse)
𝑎( = −
𝑅
𝑅1 + 𝑅
atténuation de retour
𝑏 =
𝑅1
𝑅1 + 𝑅
atténuation d’entrée v2
𝑎, =
𝑅3
𝑅2 + 𝑅3
𝒗𝒔 =
𝑨
𝟏 + 𝑨. 𝒃
𝒗𝟐. 𝒂𝟐 + 𝒗𝟏. 𝒂𝟏
Or A.b >> 1 d’où 𝒗𝒔 =
𝟏
𝒃
𝒗𝟐. 𝒂𝟐 + 𝒗𝟏. 𝒂𝟏
𝒗𝒔 =
𝑹𝟏 + 𝑹
𝑹𝟏
𝑹𝟑
𝑹𝟐 + 𝑹𝟑
𝒗𝟐 −
𝑹
𝑹𝟏 + 𝑹
𝒗𝟏
-
+
v2(t)
vs(t)
R1
R
v1(t) R2
R3
e
A
B
Millman en A: 𝑣" =
𝑅
𝑅1 + 𝑅
𝑣( +
𝑅1
𝑅1 + 𝑅
𝑣%
Pont diviseur en B : 𝑣! =
𝑅3
𝑅2 + 𝑅3
𝑣,
Schéma fonctionnel
A
b
v1 vs
e
b.vs
-
+
a1
a2
+
+
v2

32. On suppose l’AOp idéal, donc: i+ = i- = 0
Donc le courant dans R est le même que dans C
Montage à contre-réaction =>
fonctionnement linéaire => e=0
DERIVATEUR
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
32
! Analyse temporelle
𝑣# = 𝑢$ ; 𝑣% = −𝑅𝑖 = −𝑅𝐶
𝑑𝑢$
𝑑𝑡
𝑣% = −𝑅𝐶
𝑑𝑣#
𝑑𝑡
𝐷U𝑜ù
-
+
ve(t)
vs(t)
R
C
i
i
A
e
uc
uR
d’entrée jCw , de sortie nulle
! Impédances :
! Remarque : dérivation correcte en basse fréquence
! Hypothèse : on considère le condensateur initialement
déchargé

33. DERIVATEUR
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
33
! Analyse harmonique
• Millman en A: 𝑣V =
𝑗𝐶𝜔𝑣A +
𝑣@
𝑅
𝑗𝐶𝜔 +
1
𝑅
= 0
D’où
𝐺 𝑗𝜔 =
W!(YZ)
W"(YZ)
= −𝑗𝑅𝐶𝜔 = −𝑗
Z
Z#
𝑎 𝑗𝜔 = −
𝑗𝑅𝐶𝜔
1 + 𝑗𝑅𝐶𝜔
𝑏 𝑗𝜔 =
1
1 + 𝑗𝑅𝐶𝜔
𝐺 𝑗𝜔 ≈
𝑎(𝑗𝜔)
𝑏(𝑗𝜔)
-
+
ve(t)
vs(t)
R
C
i
i
A
e
Schéma fonctionnel général
A(jw)
b(jw)
Ve(jw) Vs(jw)
-
+
a(jw)

34. On suppose l’AOp idéal, donc: i+ = i- = 0
Donc le courant dans C est le même que dans R
Montage à contre-réaction => fonctionnement linéaire => e=0
INTEGRATEUR
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
34
𝑣# = 𝑅𝑖 = 𝑅
&'
&(
= 𝑅𝐶
&)!
&(
; 𝑣% = −𝑢$
𝑣% = −
1
𝑅𝐶
> 𝑣#𝑑𝑡
𝐷U𝑜ù
! Analyse temporelle
R
C
-
+
ve(t)
vs(t)
i
i
A
e
uc
C i
u𝑐
𝑞 = 𝐶𝑢- 𝑒𝑡 𝑖 =
𝑑𝑞
𝑑𝑡
𝑖 = 𝐶
𝑑𝑢-
𝑑𝑡
Rappel
! Hypothèse : on considère le condensateur initialement déchargé
d’entrée R, de sortie nulle
! Impédances :
! Remarque : intègre correctement en haute fréquence

35. INTEGRATEUR
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
35
! Analyse harmonique
• Millman en A: 𝑣) =
𝑣*
𝑅 + 𝑗𝐶𝜔𝑣+
1
𝑅 + 𝑗𝐶𝜔
= 0
D’où
𝐺 𝑗𝜔 =
𝑣+(𝑗𝜔)
𝑣*(𝑗𝜔)
= −
1
𝑗𝑅𝐶𝜔
= −
1
𝑗
𝜔
𝜔,
Schéma fonctionnel général
𝑎 𝑗𝜔 = −
1
1 + 𝑗𝑅𝐶𝜔
𝑏 𝑗𝜔 =
𝑗𝑅𝐶𝜔
1 + 𝑗𝑅𝐶𝜔
𝐺 𝑗𝜔 ≈
𝑎(𝑗𝜔)
𝑏(𝑗𝜔)
R
C
-
+
ve(t)
vs(t)
i
i
A
e
A(jw)
b(jw)
Ve(jw) Vs(jw)
-
+
a(jw)

36. FILTRE ACTIF PASSE BAS DU 1er ORDRE
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
36
! Analyse harmonique
• Impédance R1//C1: 𝑍9 =
𝑅9
𝑗𝐶9𝜔
𝑅9 +
1
𝑗𝐶9𝜔
=
𝑅9
1 + 𝑗𝑅9𝐶9𝜔
D’où, sous forme canonique
𝐺 𝑗𝜔 =
:
9;<
$
$#
𝐴 = −
=%
=
𝜔, =
9
=%>%
-
+
ve(t)
vs(t)
R
C1
i
i
R1
• On reconnait une structure
d’amplificateur inverseur
𝐺 𝑗𝜔 = −
𝑍9
𝑅
= −
1
𝑅
𝑅9
1 + 𝑗𝑅9𝐶9𝜔

37. FILTRE ACTIF PASSE HAUT DU 1er ORDRE
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
37
ve(t)
-
+
vs(t)
R1
C
i
i
R
D’où, sous forme canonique
𝐺 𝑗𝜔 =
:<
$
$%
9;<
$
$#
𝐴 = −1 𝜔, =
9
=>
𝜔9 =
9
=%>
! Analyse harmonique
• Impédance R en série avec C: 𝑍 = 𝑅 +
1
𝑗𝐶𝜔
• On reconnait une structure
d’amplificateur inverseur
𝐺 𝑗𝜔 = −
𝑅9
𝑅 +
1
𝑗𝐶𝜔

38. FILTRE PASSE-BANDE
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
38
D’où, sous forme canonique
𝐺 𝑗𝜔 =
: ?@<
$
$#
9;?@<
$
$#
;
&$
$#
' 𝐴 = −1 𝜔, =
9
=>
m=0,5 (coeff d’amortissement)
! Analyse harmonique
• On reconnait une structure
d’amplificateur inverseur
𝐺 𝑗𝜔 = −
𝑍?
𝑍9
= −
𝑗𝑅𝐶𝜔
1 + 𝑗𝑅𝐶𝜔 ?
ve(t)
-
+
vs(t)
R
C
R
C
• Impédances 𝑍9 = 𝑅 +
1
𝑗𝐶𝜔
R et C en série:
𝑍? =
𝑅
1 + 𝑗𝑅𝐶𝜔
R et C en parallèle:

39. FILTRE DU SECOND ORDRE : STRUCTURE DE RAUCH
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
39
ve(t)
-
+
vs(t)
Y1
Y2
Y3
Y4 Y5
A B
% La structure de RAUCH est donnée ci-contre où les Yi
sont les admittances complexes de chaque branche
(inverse des impédances)
% Par application de la loi des nœuds en A et en B, on
trouve:
𝑣𝑠
𝑣𝑒
=
𝑌9𝑌A
𝑌A𝑌B + 𝑌C 𝑌9 + 𝑌? + 𝑌A + 𝑌B

40. FILTRE DU SECOND ORDRE : STRUCTURE DE RAUCH
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
40
% Par application de la structure de RAUCH les
admittances sont:
FILTRE Passe-Bas
ve(t)
-
+
vs(t)
R1
R3 C2
C1
R2
A B
𝑌( =
1
𝑅(
; 𝑌, = 𝑗𝐶(𝜔 ; 𝑌. =
1
𝑅,
; 𝑌/ =
1
𝑅.
; 𝑌0 = 𝑗𝐶,𝜔
% La fonction de transfert est alors:
𝐺 𝑗𝜔 = −
𝑅.
𝑅(
1 + 𝑗𝑅,𝑅.𝐶,𝜔
1
𝑅(
+
1
𝑅,
+
1
𝑅.
+ 𝑗𝐶(𝜔
𝐺 𝑗𝜔 =
𝐴
1 + 2𝑗𝑚
𝜔
𝜔,
+ 𝑗
𝜔
𝜔,
? 𝐴 = −1 𝜔, =
1
𝑅 𝐶9𝐶?
𝑚 =
3
2
𝐶?
𝐶9
% Soit sous forme canonique dans le cas où R=R1=R2=R3:

41. FILTRE DU SECOND ORDRE : STRUCTURE DE RAUCH
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
41
% Par application de la structure de RAUCH les
admittances sont:
FILTRE Passe-Haut
𝑌( = 𝑗𝐶(𝜔; 𝑌, =
(
1'
; 𝑌. = 𝑗𝐶,𝜔; 𝑌/ = 𝑗𝐶.𝜔; 𝑌0 =
(
1(
% La fonction de transfert est alors:
𝐺 𝑗𝜔 = −
𝑗 𝐶(𝐶,𝜔
,
𝑗 𝐶,𝐶.𝜔
,
+
1
𝑅,
1
𝑅(
+ 𝑗𝐶(𝜔 + 𝑗𝐶,𝜔 + 𝑗𝐶.𝜔
𝐺 𝑗𝜔 =
𝑗
𝜔
𝜔,
?
1 + 2𝑗𝑚
𝜔
𝜔,
+ 𝑗
𝜔
𝜔,
? 𝐴 = −1 𝜔, =
1
𝐶 𝑅9𝑅?
𝑚 =
3
2
𝑅9
𝑅?
% Soit sous forme canonique dans le cas où C=C1=C2=C3:
ve(t)
-
+
vs(t)
R1
C2
C3 R2
A B
C1

42. FILTRE DU SECOND ORDRE : STRUCTURE DE RAUCH
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
42
% Par application de la structure de RAUCH les
admittances sont:
FILTRE Passe-Bande
ve(t)
-
+
vs(t)
R1
R2
C1
C2 R3
A B
𝑌( =
1
𝑅(
; 𝑌, =
1
𝑅,
; 𝑌. = 𝑗𝐶(𝜔 ; 𝑌/ = 𝑗𝐶,𝜔 ; 𝑌0 =
1
𝑅.
% La fonction de transfert est alors:
𝐺 𝑗𝜔 =
𝑗𝐶,𝜔
𝑅(
𝑅( + 𝑅,
𝑅(𝑅,𝑅.
+ 𝑗𝜔
𝐶( + 𝐶,
𝑅.
− 𝐶(𝐶,𝜔,
𝐺 𝑗𝜔 =
𝐴 2𝑗𝑚
𝜔
𝜔,
1 + 2𝑗𝑚
𝜔
𝜔,
+ 𝑗
𝜔
𝜔,
? 𝐴 = −
𝑅A
2𝑅9
𝜔, =
1
𝐶
𝑅9 + 𝑅?
𝑅9𝑅?𝑅A
𝑚 =
𝑅9𝑅?
𝑅A 𝑅9 + 𝑅?
% Soit sous forme canonique dans le cas où C = C1 = C2:

43. GENERATEUR DE FONCTION
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
v1
-Vsat
+Vsat
t
vs
U-
U+
t
• Le premier AOp est monté en trigger de Schmitt.
La sortie est donc une tension rectangulaire entre
–Vsat et +Vsat.
i= (ve-v1)/(R1+R2)
ve – vA = R1*i = R1*(ve-v1)/(R1+R2)
• Le trigger de Schmitt bascule lors du passage à
zéro de vA, i.e.: ve = U+ = +Vsat . (R1/R2)
ve = U- = -Vsat . (R1/R2)
! Basculement du trigger de Schmitt
+
-
ve(t)
v1(t)
R2
i
i
R1
-
+
vs(t)
C
R
A i’
i’
i’(t)= -v1/R = Cste
• Le condensateur se charge et se décharge à
courant constant:
• Vc(t) à pente positive lorsque V1 = -Vsat
• Vc(t) à pente négative lorsque V1 = +Vsat
! Intégrateur : tension de sortie
Vc(t) = ∫ 𝑖+
𝑑𝑡
• Le second AOp est monté en intégrateur et génère
une tension triangulaire
43

44. AMPLIFICATEUR D’INSTRUMENTATION
AMPLIFICATEUR OPERATIONNEL EN FONCTIONNEMENT LINEAIRE
3
2
1
8
4
U1:A
TL082
5
6
7
8
4
U1:B
TL082
3
2
1
8
4
U2:A
TL082
R1
10k
R2
10k
R3
10k
R4
10k
R5
10k
R6
10k
R7
10k
V1
V2
Vs
Les amplificateurs sont alimentés entre +Vcc et -Vss
• L’amplification peut être réglée par R5
• Le CMRR très élevé. Il dépend des dérives des trois
amplificateurs, l’amplificateur d’instrumentation est
généralement réalisé sur un seul substrat (ex : AD620)
• L’impédance d’entrée est très grande.
Ve
𝑉=C = 𝑉1 − 𝑉2
𝑉𝑒 = 𝑉=C
𝑅4 + 𝑅5 + 𝑅6
𝑅5
𝑉𝑠 = −𝑉𝑒
𝑉𝑠 = − 𝑉1 − 𝑉2
=B;=C;=G
=C
Voir soustracteur
Application numérique: 𝑉𝑠 = −3 𝑉1 − 𝑉2
44