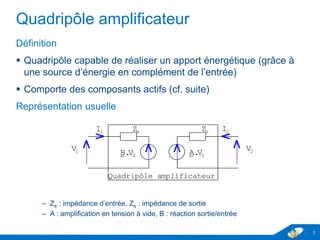
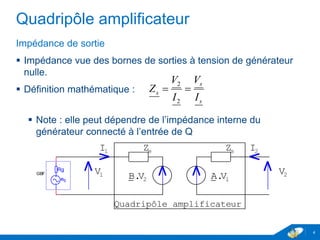
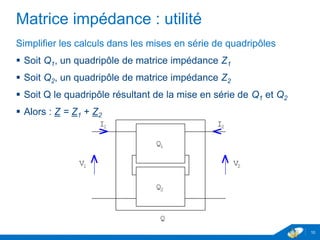
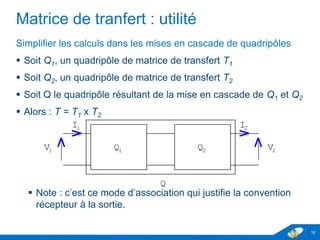
Le document traite des quadripôles en électronique, en se concentrant sur les amplificateurs, leurs impédances d'entrée et de sortie, ainsi que leurs coefficients d'amplification. Il fournit également des méthodes de calcul pour les matrices d'impédance et d'admittance, permettant de simplifier les calculs lors de la mise en série ou en parallèle de quadripôles. Enfin, il aborde les paramètres de transfert et leur utilité pour les associations de quadripôles en cascade.

1. Quadripôles
Enseignement d’électronique de Première Année
IUT de l’Indre
Eric PERONNIN

2. www.geii.eu 2
Quadripôle amplificateur
Définition
 Quadripôle capable de réaliser un apport énergétique (grâce à
une source d’énergie en complément de l’entrée)
 Comporte des composants actifs (cf. suite)
Représentation usuelle
– Ze : impédance d’entrée, Zs : impédance de sortie
– A : amplification en tension à vide, B : réaction sortie/entrée
2
s I1
V A.2 1V
I e 2
B.
Quadripôle amplificateur
21 V
Z Z
V

3. www.geii.eu 3
Quadripôle amplificateur
Impédance d’entrée
 Impédance vue des deux bornes d’entrée.
 Définition mathématique :
 Note : elle peut dépendre de la charge connectée en sortie.
3
e
e
e
I
V
I
V
Z 
1
1

4. www.geii.eu 4
Quadripôle amplificateur
Impédance de sortie
 Impédance vue des bornes de sorties à tension de générateur
nulle.
 Définition mathématique :
 Note : elle peut dépendre de l’impédance interne du
générateur connecté à l’entrée de Q
4
s
s
s
I
V
I
V
Z 
2
2
Z 2
V
I
1
I1 Z
VA.V1 V 2
se
2
Quadripôle amplificateur
B.
Rg
eg
GBF

5. www.geii.eu 5
Quadripôle amplificateur
Amplification en tension à vide
 Transmittance complexe du quadripôle à vide, avec un
générateur de tension parfait à l’entrée.
 Définition mathématique :
5
00
1
2
2 










sI
e
s
I
V
V
V
V
A

6. www.geii.eu 6
Quadripôle amplificateur
Autres paramètres caractéristiques
 Coefficient d’amplification en courant en charge :
 rapport du courant de sortie sur le courant d’entrée.
 Coefficient d’amplification en puissance :
 rapport de la puissance fournie en sortie sur la puissance
fournie à l’entrée (montage en charge).
Autre représentation : paramètres hij
 Note : très souvent h12 = 0.
6
22.
11
12
h1
2 h
-1 V1
I
Quadripôle amplificateur
IV h .21 1
2
2h
I
V

7. www.geii.eu 7
QV
I I
2V
2
1
Quadripôle
1
Quadripôle passif
Définition
 Il se compose uniquement de résistances, capacités et
inductances.
 Par simplicité, on considère que tous les éléments sont
linéaires.
Représentation usuelle :
 V1 et I1 sont les grandeurs du circuit d’entrée.
 V2 et I2 sont les grandeurs du circuit de sortie.
7

8. www.geii.eu 8
Paramètres impédances
Définition
 Système d’équations :
 Sous forme matricielle :
 Z est appelée matrice impédance du quadripôle.
 on retrouve la loi d’Ohm usuelle sous une forme matricielle.
 on montre que Z12=Z21 (et Z11=Z22 si Q est symétrique).
8





2221212
2121111
IZIZV
IZIZV
IZV
I
I
ZZ
ZZ
V
V
























2
1
2221
1211
2
1

9. www.geii.eu 9
Paramètres impédances
Calcul
 L’annulation du courant d’entrée ou du courant de sortie permet
de calculer les Zij.
 Exemple pour Z11 :
 soit l’équation :
 on annule I2, il reste donc :
 d’où :
 Ecriture mathématique des autres paramètres :
9
2121111 IZIZV 
1111 IZV 
01
1
112
1
1
11
2
0





I
I
V
ZencoreouIavec
I
V
Z
02
2
22
01
2
21
02
1
12
121
;;











III
I
V
Z
I
V
Z
I
V
Z

10. www.geii.eu 10
Matrice impédance : utilité
Simplifier les calculs dans les mises en série de quadripôles
 Soit Q1, un quadripôle de matrice impédance Z1
 Soit Q2, un quadripôle de matrice impédance Z2
 Soit Q le quadripôle résultant de la mise en série de Q1 et Q2
 Alors : Z = Z1 + Z2
10
2
2
V1
Q
1 I
V
Q
Q
2
1
I

11. www.geii.eu 11
Paramètres admittances
Définition
 Système d’équations :
 Sous forme matricielle :
 Y est la matrice admittance du quadripôle.
 Notes :
– on retrouve la loi d’Ohm usuelle sous une forme matricielle.
– en dépit de l’absence des barres, les grandeurs sont toutes complexes.
11
VYI
V
V
YY
YY
I
I


















2
1
2221
1211
2
1





2221212
2121111
VYVYI
VYVYI

12. www.geii.eu 12
Paramètres admittances
Calcul
 L’annulation de la tension d’entrée ou de celle de sortie permet
de calculer les Yij.
 Exemple pour Y11 :
 soit l ’équation :
 on annule V2, il reste donc :
 d’où :
 Ecriture mathématique des autres paramètres :
12
2121111 VYVYI 
1111 VYI 
01
1
112
1
1
11
2
0





V
V
I
YencoreouVavec
V
I
Y
02
2
22
01
2
21
02
1
12
121
;;











VVV
V
I
Y
V
I
Y
V
I
Y

13. www.geii.eu 13
2
I
V
Q
V
I
1
1
1 2
Q2
Q
Matrice admittance : utilité
Simplifier les calculs dans les mises en série de quadripôles
 Soit Q1, un quadripôle de matrice admittance Y1.
 Soit Q2, un quadripôle de matrice admittance Y2.
 Soit Q le quadripôle résultant de la mise en parallèle de Q1 et Q2
 Alors : Y = Y1 + Y2
13

14. www.geii.eu 14
Paramètres de transfert
Définition
 Système d’équations :
 Sous forme matricielle :
 T est la matrice de transfert du quadripôle
 Remarque : on prend un convention de signe générateur en
sortie (I2 sortant)
14
QV
I I
2V
2
1
Quadripôle
1





221
221
IDVCI
IBVAV






























2
2
1
1
2
2
1
1
I
V
T
I
V
I
V
DC
BA
I
V

15. www.geii.eu 15
02
1
2
2
1
2
0





I
V
V
AencoreouIavec
V
V
A
Paramètres de transfert
Calcul
 L’annulation de la tension ou du courant de sortie permet de
calculer A, B, C ou D.
 Exemple pour A :
 soit l’équation :
 on annule I2, il reste donc :
 d’où :
 Ecriture mathématique des autres paramètres :
15
221 IBVAV 
21 VAV 
02
1
02
1
02
1
222
;;











VIV
I
I
D
V
I
C
I
V
B

16. www.geii.eu 16
Matrice de tranfert : utilité
Simplifier les calculs dans les mises en cascade de quadripôles
 Soit Q1, un quadripôle de matrice de transfert T1
 Soit Q2, un quadripôle de matrice de transfert T2
 Soit Q le quadripôle résultant de la mise en cascade de Q1 et Q2
 Alors : T = T1 x T2
 Note : c’est ce mode d’association qui justifie la convention
récepteur à la sortie.
16
I
1 2V V
1
1
2
Q2Q
I
Q