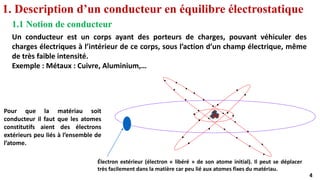
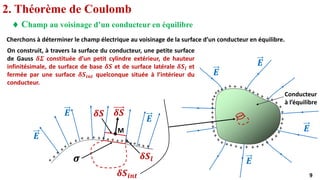
Le document traite des propriétés fondamentales des conducteurs en équilibre électrostatique, en se concentrant sur la manière dont les charges se distribuent à la surface des conducteurs et sur les effets du champ électrique à l'intérieur. Il aborde également le comportement des conducteurs avec des cavités et le phénomène d'influence électrostatique entre conducteurs. Enfin, il présente le théorème des éléments correspondants, qui stipule que les charges sur deux surfaces en interaction sont égales et de signes opposés.

1. 1
1
Electrostatique
Cycle Préparatoire Intégré | 1A
Décembre 2023

2. 2
2
Chapitre 4
Conducteurs en équilibre
électrostatique
|Condensateurs

3. 3
Les matériaux aux propriétés intéressantes pour les applications de l’électricité -
électronique sont de trois classes
✓Les conducteurs
✓Les semi-conducteurs
✓Les isolants
Dans le cadre de ce cours seuls les conducteurs, sous-entendu de l’électricité, nous
intéressent.
1. Description d’un conducteur en équilibre électrostatique
Silicium Mica
Cuivre

4. 4
1. Description d’un conducteur en équilibre électrostatique
1.1 Notion de conducteur
Un conducteur est un corps ayant des porteurs de charges, pouvant véhiculer des
charges électriques à l’intérieur de ce corps, sous l’action d’un champ électrique, même
de très faible intensité.
Exemple : Métaux : Cuivre, Aluminium,…
Pour que la matériau soit
conducteur il faut que les atomes
constitutifs aient des électrons
extérieurs peu liés à l’ensemble de
l’atome.
Électron extérieur (électron « libéré » de son atome initial). Il peut se déplacer
très facilement dans la matière car peu lié aux atomes fixes du matériau.

5. 5
1. Description d’un conducteur en équilibre électrostatique
1.1 Notion de conducteur
Un conducteur est un corps ayant des porteurs de charges, pouvant véhiculer des
charges électriques à l’intérieur de ce corps, sous l’action d’un champ électrique, même
de très faible intensité.
Exemple : Métaux : Cuivre, Aluminium,…
Sous une forme idéale un matériau conducteur va se présenter comme suit
Dans un tel matériau de très nombreux
électrons sont disponibles pour la
conduction.

6. 6
6
1. Description d’un conducteur en équilibre électrostatique
1.2 Conducteur en équilibre électrostatique
On dit qu’un conducteur est en équilibre électrostatique lorsque les charges libres qu’il
contient sont toutes au repos, c.-à-d. aucune force ne les sollicite.
Propriété 1: Le champ électrique à l’intérieur d’un conducteur en équilibre est égal à
zéro : 𝑬𝒊𝒏𝒕 = 𝟎.
On a 𝑭 = 𝟎 ⟺ 𝑬𝒊𝒏𝒕 = 𝟎 (si le champ est non nul, les charges vont se mettre en
mouvement et le conducteur n’est plus en équilibre électrostatique!)
Propriété 2: Si le conducteur est chargé, cette charge ne peut exister qu’à la surface du
conducteur (cette charge constitue une couche mince qu’on assimile à une distribution
surfacique de charge).

7. 7
7
Propriété 2: Si le conducteur est chargé, cette charge ne peut exister qu’à la surface du
conducteur (cette charge constitue une couche mince qu’on assimile à une distribution
surfacique de charge).
On peut démontrer cette propriété de deux façons :
On a 𝑬𝒊𝒏𝒕 = 𝟎
Or div(𝑬𝒊𝒏𝒕) =
𝝆𝒊𝒏𝒕
𝜺𝟎
C.-à-d. 𝝆𝒊𝒏𝒕 = 𝟎
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+ + +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Conducteur à
l’équilibre
𝝆𝒊𝒏𝒕(𝒓) = 𝟎 𝝈(𝒓)
éventuellement ≠ 𝟎
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+ + +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Conducteur à
l’équilibre
Surface de Gauss
interne

+
𝝆𝒊𝒏𝒕 = 𝟎
Considérons une surface 𝜮 quelconque,
fermée, située à l’intérieur du conducteur, et
appliquons le théorème de Gauss :
On a ‫װ‬
𝚺
𝑬𝒊𝒏𝒕 ∙ 𝒅𝑺 =
𝑸𝒊𝒏𝒕
𝜺𝟎
Puisque 𝑬𝒊𝒏𝒕 = 𝟎 𝑸𝒊𝒏𝒕 = 𝟎 = ම 𝝆𝒊𝒏𝒕𝒅𝒗
1
2

8. 8
8
Propriété 3: Le volume d’un conducteur en équilibre électrostatique est équipotentiel. La
surface limitant le conducteur est une surface équipotentielle. Donc le champ 𝑬 en est
perpendiculaire.
Conducteur à
l’équilibre
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+ + +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
A
B
Comme le champ électrique interne est nul, la différence
de potentiel entre deux points A et B du conducteur est
nulle :
𝑽𝑩 − 𝑽𝑨 = − ‫׬‬𝑨
𝑩
𝑬𝒊𝒏𝒕𝒅𝒍 = 𝟎
Le conducteur à l’équilibre est équipotentiel sur tout son
volume de matière. Comme le potentiel est une fonction
continue de l’espace, ce potentiel est aussi celui de sa
surface.
(A l’intérieur du conducteur 𝑬𝒊𝒏𝒕=-𝒈𝒓𝒂𝒅𝑽 = 𝟎, c.à.d. 𝑽 = 𝒄𝒕𝒆)
Si le champ 𝑬 n’est pas orthogonale à la surface du conducteur, la composante tangentielle de ce
champ va provoquer une accélération des charges! D’autres parts, on a 𝒅𝑽 = −𝑬𝒊𝒏𝒕𝒅𝒍. Sur la
surface du conducteur 𝑽 = 𝒄𝒕𝒆 ⟺ 𝒅𝑽 = 𝟎 = −𝑬𝒊𝒏𝒕𝒅𝒍 → 𝑬𝒊𝒏𝒕 ⊥ 𝒅𝒍 c.à.d. le champ est
perpendiculaire à la surface du conducteur.

9. 9
9
 Champ au voisinage d’un conducteur en équilibre
2. Théorème de Coulomb
Conducteur
à l’équilibre
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+ + +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
𝑬
𝑬
𝑬
𝑬
+
+
+
+
+
+
+
+
+
+
+
+
+ + + +
+
+
+
+
+
+
M
𝑬
𝑬
𝑬
𝜹𝑺
𝜹𝑺
𝜹𝑺𝒍
𝜹𝑺𝒊𝒏𝒕
𝝈
Cherchons à déterminer le champ électrique au voisinage de la surface d’un conducteur en équilibre.
On construit, à travers la surface du conducteur, une petite surface
de Gauss 𝜹𝜮 constituée d’un petit cylindre extérieur, de hauteur
infinitésimale, de surface de base 𝜹𝑺 et de surface latérale 𝜹𝑺𝒍 et
fermée par une surface 𝜹𝑺𝒊𝒏𝒕 quelconque située à l’intérieur du
conducteur.

10. 10
10
Conducteur
à l’équilibre
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+ + +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
𝑬
𝑬
𝑬
𝑬
+
+
+
+
+
+
+
+
+
+
+
+
+ + + +
+
+
+
+
+
+
M
𝑬
𝑬
𝑬
𝜹𝑺
𝜹𝑺
𝜹𝑺𝒍
𝜹𝑺𝒊𝒏𝒕
𝝈
Appliquons le théorème de Gauss pour la petite surface fermée 𝜹𝜮. 𝜹𝜮 est l’association des
trois surfaces :
𝜹𝑺, 𝜹𝑺𝒍 𝒆𝒕 𝜹𝑺𝒊𝒏𝒕.
𝜹𝜙(𝑬)/𝜹𝜮 =𝜹𝜙(𝑬)/𝜹𝑺𝒍 + 𝜹𝜙(𝑬)/𝜹𝑺𝒊𝒏𝒕 +𝜹𝜙(𝑬)/𝜹𝑺 =
𝜹𝑸𝒊𝒏𝒕
𝜺𝟎
𝜹𝝓(𝑬)/𝜹𝑺𝒊𝒏𝒕 = 𝟎 car le champ dans le conducteur est nul
𝜹𝝓(𝑬)/𝜹𝑺𝒍 = 𝟎 car le champ à la surface est perpendiculaire à 𝜹𝑺𝒍 (𝑬 ⊥ 𝜹𝑺𝒍 )
𝜹𝝓(𝑬)/𝜹𝑺 = 𝑬(𝑴)𝜹𝑺 car 𝑬(𝑴) ∥ 𝜹𝑺
La charge intérieure de 𝜹𝜮 , celle découpée sur la surface du
conducteur, est donnée par 𝜹𝑸𝒊𝒏𝒕 = 𝝈𝜹𝑺

11. 11
11
Il en résulte l’expression du champ au voisinage de la surface du conducteur à l’équilibre :
𝑬 𝑴 𝜹𝑺 =
𝝈𝜹𝑺
𝜺𝟎
→ 𝑬 𝑴 =
𝝈
𝜺𝟎
D’où
𝑬 𝑴 =
𝝈
𝜺𝟎
𝒏 𝒏 ∶ vecteur unitaire normal à la surface
(dirigé vers l’extérieur du conducteur)
Traduction du théorème de Coulomb
𝑬
+
+
+
+
+
+
+
+
+
+
+
+
+ + + +
+
+
+
+
+
+
M
Conducteur à
l’équilibre
𝝈
𝑬 𝑴 =
𝝈
𝜺𝟎
𝑬𝒗𝒐𝒊𝒔𝒊𝒏𝒂𝒈𝒆 =
𝝈
𝜺𝟎
𝒏
𝑬𝒊𝒏𝒕 = 𝟎
Donc le champ est discontinue à la
traversée d’un conducteur en équilibre.
 Discontinuité de 𝑬

12. 12
12
Il en résulte l’expression du champ au voisinage de la surface du conducteur à l’équilibre :
𝑬 𝑴 𝜹𝑺 =
𝝈𝜹𝑺
𝜺𝟎
→ 𝑬 𝑴 =
𝝈
𝜺𝟎
D’où
𝑬 𝑴 =
𝝈
𝜺𝟎
𝒏 𝒏 ∶ vecteur unitaire normal à la surface
(dirigé vers l’extérieur du conducteur)
Traduction du théorème de Coulomb
𝑬
+
+
+
+
+
+
+
+
+
+
+
+
+ + + +
+
+
+
+
+
+
M
Conducteur à
l’équilibre
𝝈
𝑬 𝑴 =
𝝈
𝜺𝟎
 Discontinuité de 𝑬
𝑬𝒗𝒐𝒊𝒔𝒊𝒏𝒂𝒈𝒆 =
𝝈
𝜺𝟎
𝒏
𝑬𝒊𝒏𝒕 = 𝟎
Ce résultat peut être déduit directement en utilisant simplement la
relation de passage à travers une surface chargée!!

13. 13
13
3. Conséquences : Conducteur à cavité, Effet de pointe
3.1 Conducteur à cavité
On considère un conducteur à cavité, de surface interne 𝑺𝟏.
La cavité ne contient pas de charges.
 A l’intérieur du conducteur à l’équilibre : 𝑽 = 𝒄𝒕𝒆 = 𝑽𝟎 𝒆𝒕 𝑬 = 𝟎
𝑽 = 𝒄𝒕𝒆 = 𝑽𝟎
𝑺𝟏
 La surface 𝑺𝟏 étant équipotentielle, son potentiel ne peut être
que constant, et par continuité est celui du conducteur 𝑽𝟎.
 Il ne peut y avoir de charges sur la surface intérieure de la cavité!
(En appliquant le théorème de Gauss pour une surface fermée quelconque 𝜮 située à l’intérieur du conducteur,
on a ‫װ‬
𝜮
𝑬 ∙ 𝒅𝑺 =
𝑸𝒊𝒏𝒕
𝜺𝟎
= 𝟎 car 𝑬 = 𝟎, d’où 𝑸𝒊𝒏𝒕 = 𝟎)
𝜮
 A l’intérieur de 𝑺𝟏 : 𝑽 = 𝒄𝒕𝒆 = 𝑽𝟎 𝒆𝒕 𝑬 = 𝟎
(Si 𝑽 ≠ 𝒄𝒕𝒆 à l’intérieur de 𝑺𝟏; 𝑽 présente forcément un extremum, or le potentiel ne présente pas d’extremum
en dehors des charges. D’où, 𝑽 = 𝒄𝒕𝒆)

14. 14
14
3. Conséquences : Conducteur à cavité, Effet de pointe
3.1 Conducteur à cavité
𝑽 = 𝒄𝒕𝒆 = 𝑽𝟎
𝑺𝟏
𝑬 = 𝟎
𝝆𝒊𝒏𝒕 = 𝟎
𝑬 = 𝟎
𝑽 = 𝑽𝟎
+
+
+
+
+
+
+ ++
+
+
+
+
+
+
+
+
+
+
+
+ +
+ + +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Résumé
Dans un conducteur plein ou dans un conducteur creux dont la
cavité ne contient pas de charges; lorsque l’équilibre est réalisé :
1) Le champ est nul dans la masse du conducteur et dans la cavité.
2) Le potentiel est constant en tout point du conducteur et de la cavité.
3) Seule la surface extérieure du conducteur peut porter une charge non compensée.
Application : Cage avec grillage pour protéger les montages électriques (électroniques)

15. 15
15
E=0, pas de champ!
Lignes de champ du système « cylindre-disque »
Il faut remarquer que les lignes de champ sont bien perpendiculaires au conducteur et que le champ à
l’intérieur du conducteur cylindrique est nul.

16. 16
16
+ + ++ +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+ + + + ++++++
+
+
+
+
+
+
+
R
Q
O
On considère un conducteur sphérique de rayon R et de charge Q.
𝑽 =
𝑸
𝟒𝝅𝜺𝟎𝑹
𝑸 = 𝝈𝟒𝝅𝑹𝟐
𝑽 =
𝝈𝑹
𝜺𝟎
𝑬 =
𝝈
𝜺𝟎
𝑬 =
𝑽
𝑹
(𝒔𝒊 𝑹 ↘ 𝒂𝒍𝒐𝒓𝒔 𝑬 ↗)
Plus la courbure est importante, plus le
champ est intense.
On a (On peut démontrer ce résultat en utilisant
la relation 𝑬 = −𝒈𝒓𝒂𝒅 𝑽 ou par calcul
direct du potentiel au centre de la sphère)
Or D’où
Le champ au voisinage du conducteur s’exprime par la relation
C.à.d.
3. Conséquences : Conducteur à cavité, Effet de pointe
3.2 Pouvoir des pointes

17. 17
17
On considère maintenant un conducteur présentant des courbures différentes. Puisque le
potentiel est constant alors le champ est plus intense dans les régions à petit rayon de
courbure (pointes) : Pouvoir des pointes.
+++++
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+ + + + + + + + + + + +
+
+
+
+
+
+
+
+ +
+
+
+
+ +
+
+
+
+
3. Conséquences : Conducteur à cavité, Effet de pointe
3.2 Pouvoir des pointes

18. 18
18
4. Théorème des éléments correspondants
4.1 Influence électrostatique
On considère
un conducteur A isolé
neutre
Ce conducteur est placé
dans un champ électrique
uniforme
Quand le conducteur est
placé dans ce champ, les
électrons libres de ce
conducteur se mettent en
mouvement pour annuler
l’effet de ce champ.
Les charges sont réparties de
telle sorte que le champ créé
par les charges est l’opposé du
champ uniforme appliqué.

19. 19
19
La répartition des charges à la surface d’un conducteur se modifie par un champ électrostatique
Le conducteur A prendra une répartition de charge en équilibre telle que le champ
redevienne nul à l’intérieur de A
On dit que le conducteur A s’est chargé par influence.
𝑬𝒆𝒙𝒕

20. 20
20
4. Théorème des éléments correspondants
4.2 Théorème des éléments correspondants
On considère deux conducteurs 𝑪𝟏et 𝑪𝟐 en position d’influence partielle et de potentiel 𝑽𝟏et
𝑽𝟐 𝑽𝟐 < 𝑽𝟏 .
Conducteur 1 à l’équilibre
Conducteur 2 à
l’équilibre
Lignes de champ
Lignes de champ
𝑪𝟏
𝑪𝟐
La situation des lignes de champ dessinée est totalement
arbitraire. C’est une situation d’influence partielle où un
certain nombre de lignes de champ (façon de parler car elle ne
sont pas dénombrables) vont d’un conducteur à l’autre. Une
autre situation d’influence totale sera vue plus loin.

21. 21
21
La charge totale intérieure au tube de flux est celle
portée par les deux surfaces S1 et S2 soit au total
On appelle éléments correspondants les deux surfaces S1 et S2 portant les charges respectives Q1 et Q2 .
+ ++
+
+
++++
+
+
+
+
+
+
+
+
+
+
+
-
-
-
-
-
-
-
---
-
-----
-
---
-
Conducteur 1
Conducteur 2
Tube de flux
Lignes de champ
S2
S1int
S1
S2int
Q1
Q2
Sl
Soit un tube de flux qui intercepte le conducteur 1 sur la
surface S1 et le conducteur 2 sur la surface S2 avec une surface
latérale Sl .
𝑸𝟏 + 𝑸𝟐
On construit une surface de Gauss avec la surface latérale Sl ,
une surface interne S1int au conducteur 1 de forme quelconque
et qui intercepte S1 et une surface S2int construite de la même
manière dans le conducteur 2.
Le théorème de Gauss conduit à la relation suivante pour la charge intérieure au tube de flux
𝑸𝟏 + 𝑸𝟐 = 𝟎
(Le flux du champ sur les surfaces S1int et S2int est nul puisque le champ électrique
est nul dans les conducteurs à l’équilibre. Sur la surface latérale Sl le champ est
tangent, donc le flux y est également nul)

22. 22
22
La charge totale intérieure au tube de flux est celle
portée par les deux surfaces S1 et S2 soit au total
+ ++
+
+
++++
+
+
+
+
+
+
+
+
+
+
+
-
-
-
-
-
-
-
---
-
-----
-
---
-
Conducteur 1
Conducteur 2
Tube de flux
Lignes de champ
S2
S1int
S1
S2int
Q1
Q2
Sl
Soit un tube de flux qui intercepte le conducteur 1 sur la
surface S1 et le conducteur 2 sur la surface S2 avec une surface
latérale Sl .
𝑸𝟏 + 𝑸𝟐
On construit une surface de Gauss avec la surface latérale Sl
une surface interne S1int au conducteur 1 de forme quelconque
et qui intercepte S1 et une surface S2int construite de la même
manière dans le conducteur 2.
(Le flux du champ sur les surfaces S1int et S2int est nul puisque le champ électrique
est nul dans les conducteurs à l’équilibre. Sur la surface latérale Sl le champ est
tangent, donc le flux y est également nul)
Le résultat 𝑸𝟏 = −𝑸𝟐 porte le nom du théorème des éléments correspondants
« Les charges portées par deux éléments correspondants sont égales et de signe contraire »

23. 23
23
4. Théorème des éléments correspondants
4.3 Influence partielle, influence totale
L’influence totale est celle où l’un des conducteurs en influence est entouré
complétement par l’autre. L’influence partielle dans le cas contraire.
-
-
-
-
-
-
-
-
-
-
-
- - - - - - - - -
-
- -
- - -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
𝑺𝟐𝒊𝒏𝒕
𝑺𝟐𝒆𝒙𝒕
𝑸𝟐𝒊𝒏𝒕
𝑸𝟐𝒆𝒙𝒕
+𝒒
Exemple d’influence totale : charge ponctuelle à l’intérieur
d’un conducteur 2 creux non chargé initialement neutre.
La charge +q et le conducteur sont en influence totale.
On peut déterminer la répartition des charges sur les
surfaces 𝑺𝒆𝒙𝒕 et 𝑺𝒊𝒏𝒕 du conducteur 2.
En appliquant le théorème de Gauss pour une surface
fermée quelconque située à l’intérieur du conducteur 2
ou en appliquant directement le théorème des
éléments correspondants, on peut démontrer que
𝑸𝟐𝒊𝒏𝒕 = −𝒒

24. 24
24
4. Théorème des éléments correspondants
4.3 Influence partielle, influence totale
L’influence totale est celle où l’un des conducteurs en influence est entouré
complétement par l’autre. L’influence partielle dans le cas contraire.
-
-
-
-
-
-
-
-
-
-
-
- - - - - - - - -
-
- -
- - -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
𝑺𝟐𝒊𝒏𝒕
𝑺𝟐𝒆𝒙𝒕
𝑸𝟐𝒊𝒏𝒕
𝑸𝟐𝒆𝒙𝒕
+𝒒
Exemple d’influence totale : charge ponctuelle à l’intérieur
d’un conducteur 2 creux non chargé initialement neutre.
La charge +q et le conducteur sont en influence totale.
On peut déterminer la répartition des charges sur les
surfaces 𝑺𝒆𝒙𝒕 et 𝑺𝒊𝒏𝒕 du conducteur 2.
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+ + +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+
+
+
+
Puisque le conducteur 2 est initialement neutre
alors la charge totale du conducteur est nulle
𝑸𝟐𝒊𝒏𝒕 + 𝑸𝟐𝒆𝒙𝒕 = 𝟎
𝑸𝟐𝒆𝒙𝒕 = +𝒒

25. 25
25
On part de la situation ou les deux conducteurs sont en influence totale et on relie (A) à la terre : Les charges sur la surface
externe de (A) sont neutralisées.
(A) (B)
+
-
+
+
+
+
+
+
+
+
•Si on approche un
conducteur (C) de ce
système, il ne subira
aucune action électrique.
Conclusion : un conducteur creux (A) maintenu à un potentiel constant
divise l'espace en deux régions électriquement indépendantes. D'ou le
rôle d'écran électrique (cage de faraday,..)
(A) (B)
(C)
-
-
Application : écran électrique

26. 26
26
 De nombreux appareils électriques utilisent cette propriété pour
protéger des circuits sensibles.
Ecran électrique : Blindage
 Un conducteur protège son intérieur des champs électriques externes.
 Le blindage se produit que le conducteur soit creux ou plein.

27. 27
27
5. Condensateurs
5.1 Introduction
Le condensateur est un ensemble de deux conducteurs en influence totale séparés par
un isolant. Il est capable de stocker des charges électriques, donc d’emmagasiner de
l’énergie. Il est très important en électrocinétique, mais on peut établir ses propriétés en
électrostatique.
5.2 Capacité d’un conducteur isolé dans l’espace
Considérons un conducteur unique supposé seul dans le vide, il porte une charge 𝑸 et
son potentiel est 𝑽.
Le rapport
𝑸
𝑽
est constant, on appelle 𝑪 capacité du conducteur :
𝑪 =
𝑸
𝑽
𝑪
𝑽
= 𝑭 𝑭𝒂𝒓𝒂𝒅

28. 28
28
5. Condensateurs
5.1 Introduction
Le condensateur est un ensemble de deux conducteurs en influence totale séparés par
un isolant. Il est capable de stocker des charges électriques, donc d’emmagasiner de
l’énergie. Il est très important en électrocinétique, mais on peut établir ses propriétés en
électrostatique.
5.2 Capacité d’un conducteur isolé dans l’espace
Exemple : conducteur sphérique de rayon R et de charge Q.
𝑽 =
𝑸
𝟒𝝅𝜺𝟎𝑹
On a
+ + ++ +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+ + + + +++++
+
+
+
+
+
+
+
+
R
Q
O
D’où 𝑪 = 𝟒𝝅𝜺𝟎𝑹

29. 29
29
5. Condensateurs
5.3 Définition d’un condensateur
Deux conducteurs (1) et (2) forment « un
condensateur » lorsqu’ils sont placés en position
d’influence totale. Les conducteurs sont appelés
les armatures : (1) armature interne, (2) armature
externe. Soient 𝑽𝟏 et 𝑽𝟐 les potentiels respectifs
des armatures interne et externe.
On appelle charge du condensateur, la charge 𝑸
de son armature interne.
+
+
+
+
+
+
+ +
+
+
+
+
+
+
+
+
+
+
+
+
+ +
+ + +
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
-
-
-
-
-
-
-
-
-
-
-
- - - - - - - - -
-
- -
- - -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Conducteur (1)
𝑸
-𝑸
𝑽𝟏
𝑽𝟐
On définit la capacité 𝑪 du condensateur par la relation
𝑪 =
𝑸
𝑽𝟏 − 𝑽𝟐

30. 30
30
5. Condensateurs
5.4 Calcul de la capacité dans le cas général
1. On calcule le champ 𝑬 entre les armatures (en utilisant le théorème de
Gauss),
2. On calcule la circulation du champ d’une armature à l’autre,
𝑽𝟏 − 𝑽𝟐 = ‫׬‬𝟏
𝟐
𝑬 ∙ 𝒅𝒍 ,
3. Connaissant la charge 𝑸 = ‫׭‬
𝑺
𝝈𝒅𝑺, on détermine 𝑪 =
𝑸
𝑽𝟏−𝑽𝟐

31. 31
31
a. Cas d’un condensateur plan
e
+Q
-Q
V1
V2
C’est un condensateur dont les armatures sont constituées par deux plaques parallèles séparées par une
distance e très inférieure aux dimensions des plaques. Les plaques sont portées aux potentiels V1 et V2.
Le champ est donc perpendiculaire aux plans et si l’une des plaques porte
une charge +Q, l’autre porte forcément une charge -Q.
La distance entre plaques étant très inférieure aux dimensions des plaques,
nous pouvons considérer le système comme deux plans parallèles infinis.
Le champ est donc nul à l’extérieur des plaques, constant et uniforme à
l’intérieur 𝑬 = 𝝈/𝜺𝟎.
𝑪 =
𝑸
𝑽𝟏 − 𝑽𝟐
=
𝑸
‫׬‬
𝟏
𝟐
𝑬 ∙ 𝒅𝒍
=
𝑸
𝝈
𝜺𝟎
‫׬‬
𝟏
𝟐
𝒅𝒓
=
𝑸
𝑸
𝑺
∙
𝒆
𝜺𝟎
=
𝑺𝜺𝟎
𝒆 𝑪 =
𝑺𝜺𝟎
𝒆
Exemple : 𝑺 = 𝟏 𝒎𝟐, 𝒆 = 𝟎, 𝟓 𝒎𝒎𝟐 ⇒ 𝑪 = 𝟏𝟕, 𝟖 𝒏𝑭
Pour augmenter la valeur de C, il faut remplacer le vide par de la matière (diélectrique), c.à.d. remplacer 𝜺𝟎
par 𝜺𝟎𝜺𝒓!

32. 32
32
Diélectrique
Diélectrique
En réalité entre les armatures d’un condensateur il y a un
isolant (diélectrique). L’expérience montre que l’utilisation de
l’isolant permet d’augmenter la capacité du condensateur :
𝑪 = 𝜺𝒓. 𝑪𝟎
où 𝑪 est la capacité du condensateur avec un isolant entre les
armatures, et 𝑪𝟎 sa capacité lorsqu’il n’ y a rien entre les
armatures « du vide »,
𝑪 =
𝑺𝜺𝟎𝜺𝒓
𝒆
𝜺 = 𝜺𝟎𝜺𝒓 est la permittivité absolue de l’isolant, 𝜺𝟎 est la
permittivité absolue du vide.
Exemples : Valeurs de 𝜺𝒓 pour quelques isolants
Verres : 𝜺𝒓 de 4 à 7, mica : 𝜺𝒓 = 8,
air :𝜺𝒓 = 1,00058
𝜺𝒓 sans unité, est la permittivité relative de l’isolant ou
constante diélectrique, elle ne dépend que de la nature de
l’isolant.

33. 33
33
b. Condensateur cylindrique
Il est constitué de deux conducteurs cylindriques coaxiaux
d’axe (Oz) par exemple.
h
Q
-Q
r
𝑹𝟏
E
d
Surface
de Gauss
𝑹𝟐
Vue en coupe
transversale
Pour calculer la capacité de ce condensateur, il faut
déterminer en premier lieu le champ électrostatique
entre ses armatures.
En appliquant le principe d’invariance et pour des raisons
de symétrie, le champ électrostatique 𝑬 est radial :
𝑬 = 𝑬(𝒓)𝒖𝒓
Considérons la surface de Gauss 𝚺 constituée par un
cylindre d’axe Oz, de rayon 𝒓 et de longueur 𝒉 tel que
𝑹𝟏 < 𝒓 < 𝑹𝟐. Appliquons le théorème de Gauss :
𝑬 𝒓 𝟐𝝅𝒓𝒉 =
𝑸
𝜺𝟎
D’où 𝑬 = 𝑬(𝒓)𝒖𝒓=
𝑸
𝟐𝝅𝜺𝟎𝒓𝒉
𝒖𝒓

34. 34
34
𝑽𝟏 − 𝑽𝟐 = ‫׬‬
𝟏
𝟐
𝑬 ∙ 𝒅𝒍
h
Q
-Q
r
𝑹𝟏
E
d
Surface
de Gauss
𝑹𝟐
Vue en coupe
transversale
𝑽𝟏 − 𝑽𝟐 = ‫׬‬𝟏
𝟐 𝑸
𝟐𝝅𝜺𝟎𝒓𝒉
𝒖𝒓 ∙ 𝒅𝒍
= න
𝟏
𝟐
𝑸
𝟐𝝅𝜺𝟎𝒓𝒉
𝒅𝒓
=
𝑸
𝟐𝝅𝜺𝟎𝒉
න
𝟏
𝟐
𝒅𝒓
𝒓
=
𝑸
𝟐𝝅𝜺𝟎𝒉
𝒍𝒏(
𝑹𝟐
𝑹𝟏
)
𝑪 =
𝟐𝝅𝜺𝟎𝒉
𝒍𝒏(
𝑹𝟐
𝑹𝟏
)
𝑪 =
𝑸
𝑽𝟏 − 𝑽𝟐
Or Soit

35. 35
35
𝐒𝐢 𝑹𝟐 = 𝑹𝟏 + 𝒆 𝒂𝒗𝒆𝒄
𝒆
𝑹𝟏
≪ 𝟏, on a
𝒍𝒏
𝑹𝟐
𝑹𝟏
= 𝒍𝒏(𝟏 +
𝒆
𝑹𝟏
) ≈
𝒆
𝑹𝟏
D’où 𝑪 = 𝜺𝟎
𝟐𝝅𝑹𝟏𝒉
𝒆
On retrouve l’expression du condensateur plan : 𝑪 =
𝑺𝜺𝟎
𝒆

36. 36
36
Généralement, on néglige les effets de bord et on considère que le champ 𝑬
est radial entre les armatures du condensateur cylindrique.

37. 37
37
c. Condensateur sphérique
+Q
-Q
𝑹𝟐
𝑹𝟏
Vue en coupe
transversale
Il est constitué de deux conducteurs sphériques
concentriques de même centre O.
L’armature interne est une sphère pleine de rayon 𝑹𝟏 qui
porte la charge +Q, et l’armature externe est une sphère
creuse de rayon intérieur 𝑹𝟐 qui porte la charge
-Q (les sphères sont en situation d’influence totale).
En appliquant le principe d’invariance et pour des raisons
de symétrie, le champ électrostatique 𝑬 est radial :
𝑬 = 𝑬(𝒓)𝒖𝒓
Appliquons le théorème de Gauss sur une surface sphérique
concentrique de rayon r compris entre 𝑹𝟏 et 𝑹𝟐 :
Le flux sortant d’une telle surface a pour valeur 𝟒𝝅𝒓𝟐𝑬(𝒓) tandis
que la charge intérieure est égale à +𝑸 = 𝟒𝝅𝑹𝟐𝝈𝟏où 𝝈𝟏est la
densité surfacique de charge portée par la sphère intérieure.

38. 38
38
+Q
-Q
𝑹𝟐
𝑹𝟏
Vue en coupe
transversale
C’est-à-dire 𝟒𝝅𝒓𝟐𝑬 𝒓 =
𝑸
𝜺𝟎
𝑬 = 𝑬(𝒓)𝒖𝒓=
𝑸
𝟒𝝅𝜺𝟎𝒓𝟐 𝒖𝒓
D’où
𝑽𝟏 − 𝑽𝟐 = ‫׬‬𝟏
𝟐
𝑬 ∙ 𝒅𝒍
= ‫׬‬𝟏
𝟐 𝑸
𝟒𝝅𝜺𝟎𝒓𝟐 𝒖𝒓 ∙ 𝒅𝒍
= න
𝟏
𝟐
𝑸
𝟒𝝅𝜺𝟎𝒓𝟐
𝒅𝒓
=
𝑸
𝟒𝝅𝜺𝟎
න
𝟏
𝟐
𝒅𝒓
𝒓𝟐
Or

39. 39
39
𝑪 =
𝟒𝝅𝜺𝟎𝑹𝟏𝑹𝟐
𝑹𝟐 − 𝑹𝟏
𝑽𝟏 − 𝑽𝟐 =
𝑸
𝟒𝝅𝜺𝟎
න
𝟏
𝟐
𝒅𝒓
𝒓𝟐
=
𝑸
𝟒𝝅𝜺𝟎
−
𝟏
𝒓 𝑹𝟏
𝑹𝟐
=
𝑸
𝟒𝝅𝜺𝟎
𝟏
𝑹𝟏
−
𝟏
𝑹𝟐
=
𝑸(𝑹𝟐 − 𝑹𝟏)
𝟒𝝅𝜺𝟎𝑹𝟏𝑹𝟐
𝑪 =
𝑸
𝑽𝟏 − 𝑽𝟐
Or Soit
+Q
-Q
𝑹𝟐
𝑹𝟏
Vue en coupe
transversale

40. 40
40
Remarque : ici encore, si l’on se place dans le cas où l’épaisseur diélectrique 𝒆 est très
petite soit 𝑹𝟐 = 𝑹𝟏 + 𝒆 avec 𝒆 ≪ 𝑹𝟏. L’expression de la capacité , limitée au premier
ordre en
𝒆
𝑹𝟏
, devient :
𝑪 =
𝟒𝝅𝜺𝟎𝑹𝟏(𝑹𝟏+𝒆)
𝑹𝟐−𝑹𝟏
= 𝜺𝟎
𝟒𝝅𝜺𝟎𝑹𝟏
𝟐
𝒆
(1+o(
𝒆
𝑹𝟏
))
Cela correspond à l’expression de la capacité surfacique d’un condensateur plan
d’épaisseur 𝒆 :
𝑪 ≈ 𝜺𝟎
𝟒𝝅𝜺𝟎𝑹𝟏
𝟐
𝒆
= 𝜺𝟎
𝑺
𝒆