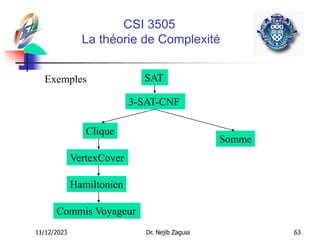
Le document présente un cours sur la conception et l'analyse des algorithmes, abordant des techniques telles que diviser pour régner, la programmation dynamique et les algorithmes voraces. Il illustre également la théorie de la complexité, y compris les notions de difficultés des problèmes, de classe P, NP et NP-complet, ainsi que des exemples pratiques tels que le problème du commis voyageur et la coloration de graphes. Enfin, il discute de l'importance de la classification des problèmes algorithmiques pour identifier des approches efficaces ou des solutions approximatives.








































































![11/12/2023 Dr. Nejib Zaguia 82
CSI 3505
La théorie de Complexité
Un tour pour TSP (moins une arête) représente un arbre recouvrant
donc |M|<|OPT|.
Le tour d’Euler P visite chacune des arêtes de M deux fois, donc
|P|=2|M|
Les raccourcis qu’on fait dans P, n’augmente pas le poids total du tour
[à cause de l’inégalité triangulaire w(a,b) + w(b,c) > w(a,c) ] donc,
|T|<|P|.
Conclusion, |T|<|P|=2|M|<2|OPT|
Tour T obtenu de P Tour Optimal OPT
Tour d’Euler P](https://image.slidesharecdn.com/np-complet-231112124231-c1ab85ec/85/NP-complet-ppt-82-320.jpg)
