Les algorithmes génétiques, inspirés par la biologie, sont utilisés pour résoudre des problèmes d'optimisation combinatoire, notamment le problème du voyageur de commerce. Bien qu'ils ne garantissent pas une solution exacte, ces algorithmes trouvent des solutions proches de l'optimum dans un temps raisonnable. Ce travail présente une adaptation de ces algorithmes au problème du voyageur de commerce, enrichie par une approche d'immigration pour garantir une diversité dans la population et améliorer les résultats.






![7S.BENHMIRA S.MEJDAOUI
Introduction générale
Depuis toujours, les problèmes d’optimisation combinatoire présentent un défi majeur
pour l’être humain. Beaucoup d’applications pratiques touchent aux problèmes combinatoires
notamment la télécommunication, le transport, l’énergie, l’industrie, l’économie et
l’éducation… etc. Dans quel ordre visiter les clients d’une même tournée pour minimiser les
emplacements ? Comment affecter chaque véhicule à un client ? Voici deux exemples qui se
posent fréquemment et qui, malgré leur simplicité apparente, constituent un obstacle pour les
chercheurs et les gestionnaires du terrain les poussant ainsi à trouver une solution. Cela exige
alors un degré de lucidité et d’esprit scientifique afin de trouver de bonnes solutions, et ce,
quelle que soit la complexité du cas proposé. L’un des problèmes d’optimisation combinatoire
le plus célèbre est le problème du voyageur de commerce (TSP) qui peut se décrire comme
suit : Un réseau avec 𝑛 nœuds (ou villes), choisir un nœud comme point de départ et d’arrivée,
une matrice de coût de déplacement (ou distance, ou temps de parcours etc.) 𝐶 = [𝑐𝑖𝑗] d'ordre
𝑛 associée à des paires de nœuds ordonnées (𝑖, 𝑗) est donnée. Le but est de trouver un cycle
hamiltonien au moindre coût. Ce problème parait facile à résoudre à première vue et aussi
simple à représenter, cependant, depuis 1972 ce problème est classé parmi les problèmes NP-
difficiles, c-à-d, il n’existe pas, jusqu’à aujourd’hui, une solution exacte pour un nombre de
paramètres assez grand.
Le TSP attire l’attention de plusieurs des chercheurs dans le monde entier pour le
résoudre en essayant de développer des méthodes appropriées, certaines de ces méthodes sont
exactes, tandis que les autres sont approximatives. Malgré le nombre fini de solutions, la
stratégie de résolution exacte qui consiste à les énumérer toutes, en les évaluant à chaque fois
et en retenant la meilleure, est impraticable car le nombre de solutions agrandit généralement
de manière exponentielle avec la taille du problème. Dans ce sens, il est primordial de mettre
en place une méthode de résolution adéquate qui prend en considération le temps de calcul et
l’efficacité dans l’exploration de l’espace de recherche pour trouver la solution optimale, d’où
les méthodes heuristiques qui ont fait leurs apparition. Ces dernières sont spécifiques au
problème traité, par contre les métaheuristiques sont plus générales et peuvent s’adapter à
n’importe quel problème. Ce sont des algorithmes stochastiques itératifs, qui progressent vers
un optimum par échantillonnage d’une fonction objective. On peut distinguer celles qui
travaillent avec une population de solutions (Algorithme génétiques, essaim de particulaire …)
de celles qui ne manipulent qu’une seule solution à la fois (recuit simulé, recherche locale …).
Dans ce projet nous allons nous concentrer sur celles qui travaillent avec une population de](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-7-320.jpg)


![Chapitre 1 : Le problème du voyageur de commerce
10S.BENHMIRA S.MEJDAOUI
1. Historique
Source d’images : [32]
Le problème du voyageur de commerce (TSP) vient de la traduction anglaise Traveling
Salesman Problem est un problème d’optimisation classique, très connu et utilisé dans le
domaine d’intelligence artificielle et la recherche opérationnelle.
Les premières approches mathématiques envisagées pour le problème du voyageur de
commerce ont été traitées au 19éme siècle par les mathématiciens. En effet, le problème du
voyageur de commerce a été décrit pour la première fois par William Rowan Hamilton et
Thomas Penyngton Kirkman, deux mathématiciens respectivement Irlandais et Britannique. Il
a été posé pour la première fois par Hamilton sous forme d’un jeu qui s’appelle « Icosian
game» en 1857, [1] (Figure-1) C’était un panneau perforé de vingt trous qui exigeait que
chaque sommet soit visible une seule fois, aucun bord n’est à visiter plus d'une fois et le point
final étant le même que le point de départ. Ce type de chemin a finalement été désigné comme
un cycle hamiltonien (Figure-2).
Cycle : chaîne qui revient à son point de départ.
Cycle hamiltonien : cycle simple passant par tous les sommets d'un graphe une et une
seule fois.
Figure 1: Jeu d’Icosien
figure 1
Figure 2: Cycle Hamiltonien
figure 2](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-10-320.jpg)
![Chapitre 1 : Le problème du voyageur de commerce
11S.BENHMIRA S.MEJDAOUI
Le TSP a été étudié pour la première fois dans les années 1930 par un mathématicien et
un économiste Karl Menger. En suite, il a été étudié par les statisticiens: Mahalanobis (1940),
Jessen (1942), Gosh (1948) et Julia Robenson (1949) [2]. Plus tard Hassler Whitney et Merrill
Flood ont mené une enquête approfondie à ce propos à l’université de Princeton.
Durant les années 50, un nombre considérable de solutions optimales a été atteint grâce
à différentes méthodes comme la formulation de George B. Dantzig, Fulkerson et Johnson en
1954 qui a pu résoudre jusqu’à 49 villes. En 1956 Merill M.Flood a publié quelques
heuristiques générant ainsi des bonnes solutions. En 1957, Barachet a mis en œuvre une
méthode graphique pour la résolution du TSP. [2]
Depuis 1954, le souci des chercheurs était d’aller le plus loin possible au niveau du
nombre de villes à considérer dans ce problème. Le tableau suivant illustre les tailles maximales
des instances résolues du TSP :
Année Acteurs Nombre de villes
1954 G.Dantzig, R.Fulkerson et S.Jhonson 49
1971 M. Held et R.M. Karp 64
1975 P.M.Camerini, L.Fratta et F.Maffioli 100
1977 M.Grotschel 120
1980 H.Crowder et M.W.Padberg 318
1987 M.Padberg et G.Rinaldi 532
1987 M. Grotschel et O.Holland 666
1987 M.Padberg et G.Rinaldi 2392
1994 D.Appelgate, R.Bixby. V.Chvatal et W.Cook 7397
1998 D.Appelgate, R.Bixby. V.Chvatal et W.Cook 13509
2001 D.Appelgate, R.Bixby. V.Chvatal et W.Cook 15112
Tableau 1: Taille maximale des instances résolues](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-11-320.jpg)

![Chapitre 1 : Le problème du voyageur de commerce
13S.BENHMIRA S.MEJDAOUI
𝑎𝑑𝑐𝑏, 𝑑𝑐𝑏𝑎, 𝑐𝑏𝑎𝑑, 𝑏𝑎𝑑𝑐 Ont tous la même longueur, seul le point de départ et le sens de
parcours change. On a donc
( 𝑛−1)!
2
chemins candidats à considérer.
Soit un graphe 𝐺 = (𝑉, 𝐴), tel que 𝑉 = { 𝑣1, … , 𝑣 𝑛} l’ensemble des sommets, 𝑛 =
|𝑉| le nombre des sommets du graphe 𝐺, chaque sommet modélisant une ville où 𝑣𝑖 caractérisé
par les coordonnées 𝑥 et 𝑦 et 𝑑 la matrice de distance de taille ( 𝑛 × 𝑛), tel que 𝑑(𝑖, 𝑗)
définit la distance entre les deux sommets 𝑣𝑖 et 𝑣𝑗. 𝐴(𝐺) L’ensemble des arcs, modélise le
coût de déplacement entre deux villes.
L'objectif est de trouver une visite de la longueur totale minimum, dont la longueur est
la somme des coûts de chaque arc dans la tournée.
L'espace de recherche pour le TSP est un ensemble de permutations de 𝑛 villes et la
solution optimale est une permutation qui donne le coût minimum de la tournée.
Le concept de calcule des distances entre les villes 𝑖 𝑒𝑡 (𝑖 + 1) est calculée sous la
règle de la distance euclidienne en utilisant l’équation suivante :
𝑑( 𝑇[ 𝑖 ], 𝑇[ 𝑖 + 1]) = √( ( 𝑥𝑖 − 𝑥𝑖+1)2 + ( 𝑦𝑖 − 𝑦𝑖+1)2 )
Tel que, 𝑇[𝑖] est une permutation sur l’ensemble {1, 2, . . . , 𝑛}
𝑇 = ( 𝑇[1], 𝑇[2] , 𝑇[3], … , 𝑇[𝑛], 𝑇[1] )
Alors, 𝑓 la fonction objective pour calculer le cout de chaque solution du problème donnée
par la formule suivante:
𝑓 = 𝑑( 𝑇[ 𝑛], 𝑇[1] ) + ∑ 𝑑( 𝑇[ 𝑖], 𝑇[ 𝑖 + 1] )
𝑛−1
𝑖=1
D’après (1), (2) 𝑒𝑡 (3) la formule mathématique simple du problème de voyageur de
commerce est donnée par :
𝑀𝑖𝑛 { 𝑓 (𝑇) , 𝑇 = ( 𝑇[1], 𝑇[2], 𝑇[3] … , 𝑇[𝑛], 𝑇[1])}
Il est à noter que, en plus de la règle de calcul euclidienne, il existe plusieurs autres
façons de calculer la distance, à savoir la distance géographique, matrix, pseudo-
euclidienne ... [3] Dans le chapitre 4, on va travailler avec la distance géographique
(2)
(1)
(3)](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-13-320.jpg)
![Chapitre 1 : Le problème du voyageur de commerce
14S.BENHMIRA S.MEJDAOUI
4. Variantes du problème du voyageur de
commerce
Le modèle classique du TSP a été modifié par plusieurs chercheurs pour l’appliquer à
de nombreux problèmes de la vie réelle. Il existe trois variantes de base de TSP à savoir ; TSP
symétrique (sTSP), TSP asymétrique (aTSP) et TSP multiple (mTSP). Ces variantes peuvent
être décrites comme suit :
sTSP : Soit 𝑑(𝑖, 𝑗) la distance Euclidienne entre les villes 𝑖 𝑒𝑡 𝑗. Si 𝑑(𝑖, 𝑗) =
𝑑(𝑗, 𝑖) alors le trajet peut être évalué dans les deux directions pour le même
coût [4]. Le sTSP est donc le même que le TSP consiste à trouver un chemin de
longueur minimale qui visite chaque ville une fois.
aTSP : Si 𝑑(𝑖, 𝑗) ≠ 𝑑(𝑗, 𝑖) pour au moins un sommet, alors le TSP devient un
aTSP.
mTSP : Le modèle fondamental du problème qui consiste à visiter les villes par
un seul voyageur de commerce, peut également être abandonné, un TSP avec
plusieurs voyageurs qui peuvent visiter ces villes s’appelle mTSP [5].
De même, il n’est pas toujours moins cher de prendre le lien direct du nœud 𝑖 au nœud
𝑘, parfois, il peut être moins cher de passer via le nœud j, et donc d’autres variantes qui jeu sur
les contraintes du problème classique de TSP pour l’adapter avec les problèmes réelles de la
vie, on distingue :
Profit Based : TSP avec Profits est une simplification du TSP traditionnel, où il
n’est pas nécessaire de visiter tous les sommets. Chaque sommet est associé à
un bénéfice prédéfini. L'objectif du problème est de trouver un trajet avec un
profit collecté satisfaisant (maximisé) et le coût du chemin (minimisé).
Time Windows based : Le TSP avec fenêtre de temps (TSPTW) nécessite de
trouver une visite à coût minimale en visitant toutes les villes exactement une
fois, où chaque ville doit être visitée dans une fenêtre de temps donnée.
maximal based TSP : Le TSP maximum est équivalent au TSP minimum
traditionnel, alors que le vendeur veut visiter chacune des villes exactement une
fois et revenir à la ville de départ avec la distance maximale possible [6]. Les
techniques utilisées pour le maximum Les TSP semblent utiles pour les
nombreux problèmes combinatoires et géométriques.](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-14-320.jpg)
![Chapitre 1 : Le problème du voyageur de commerce
15S.BENHMIRA S.MEJDAOUI
5. Domaine d’application du problème du voyageur
de commerce
Puisque nous nous intéressons au développement des méthodes algorithmiques pour la
résolution de TSP dans le but de faciliter quelques types de tâches dans la vie réelle et surtout
dans le monde industriels et électroniques, plusieurs applications pratiques [7] peuvent se
modéliser directement avec le TSP ou l’une de ses variantes.
5.1 Forage de cartes de circuits imprimés
Une application directe du TSP est le problème du forage dont la solution joue un rôle
important dans la fabrication économique de cartes de circuits imprimés (PCB).
Pour connecter un conducteur sur une couche avec un conducteur sur une autre couche,
ou pour positionner (dans une étape ultérieure de la production de PCB) les broches des circuits
intégrés, des trous doivent être percés à travers la carte. Les trous peuvent avoir des diamètres
différents. Pour percer consécutivement deux trous de diamètres différents, la tête de la
machine doit se déplacer vers une boîte des outils et changer l'équipement de forage. Cela prend
beaucoup de temps. Ainsi, il est clair au départ qu'il faut choisir un certain diamètre, percer
tous les trous du même diamètre, changer la perceuse, percer les trous du diamètre suivant, etc.
Ainsi, ce problème de forage peut être vu comme une séquence d'instances TSP, une
pour chaque diamètre de trou, où les ‘’villes’’ sont la position initiale et l'ensemble de tous les
trous qui peuvent être percés avec un seul et même perceur. La «distance» entre deux villes est
donnée par le temps qu'il faut pour déplacer la tête de forage d'une position à l'autre. Le but ici
est de minimiser le temps de déplacement de la tête de la machine.
5.2 Routage de véhicule
Supposons que dans une ville 𝑛 boîtes aux lettres doivent être vidées tous les jours dans
une période de temps, disons 1 heure. Le problème est de trouver le nombre minimum de
camions pour le faire et le temps le plus court pour les collectes en utilisant ce nombre de
camions. Comme autre exemple, supposons que 𝑛 clients ont besoin de certaines quantités de
certains produits et qu'un fournisseur doit satisfaire toutes les demandes avec un nombre de
camions fixe. Le problème est de trouver une affectation des clients aux camions et un
calendrier de livraison pour chaque camion afin que la capacité de chaque camion ne soit pas
dépassée et que la distance totale de déplacement soit minimisée. Plusieurs variantes de ces
deux problèmes, où les contraintes de temps et de capacité sont combinées, sont très utilisées
dans de nombreuses applications du monde réel. Ce problème peut être résolu en tant que TSP](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-15-320.jpg)












![Chapitre 3 : les algorithmes génétiques
28S.BENHMIRA S.MEJDAOUI
1. Contexte historique
L'évolution décrit le processus par lequel les différentes espèces et les organismes
vivants ont été changés au cours du temps, impliquant généralement leur adaptation progressive
à un nouvel environnement ou des changements à leur environnement actuel. Elle a été, depuis
longtemps, objet de discussions dans de nombreux domaines, de la science à la religion et
même à la philosophie, car le genre humain désire découvrir et déterminer non seulement leur
propre histoire, mais celle de tous ce qui l’entoure.
« L'origine des espèces » de Charles Darwin [12] reste au cœur de ce concept comme
l'une des premières théories ayant été présentées. La théorie de Darwin décrit le processus de
la sélection naturelle, dans lequel les populations gardent des traits favorables tout en rejetant
les caractéristiques indésirables des générations futures, résultant de la compétition entre ou au
sein des espèces où les individus les plus aptes ont un taux de survie plus élevé, et peuvent
transmettre leurs gènes qui contiennent ces traits avantageux pour la survie.
L'idée de créer des outils basés sur l'évolution qui pourraient être utilisés pour optimiser
les solutions des problèmes d'ingénierie est commencée vers le milieu du 20éme siècle. Le
concept était de faire évoluer une population de solutions candidates en simulant des variations
génétiques et la sélection naturelle. Pendant ce temps, quelques algorithmes inspirés de
l'évolution ont été développés par plusieurs chercheurs.
L’un des chercheurs les plus importants dans le développement et la popularisation des
algorithmes génétiques était John Holland, qui étudiait le processus d'adaptation dans la nature
et comment il pouvait être utilisé dans la programmation, avec ses étudiants et ses collègues de
l'Université du Michigan dans les années 1960 et les années 1970. Holland a publié un livre en
1975 intitulé « Adaptation dans les systèmes naturels et artificiels » [13] qui contenait une
grande partie de son travail présenté de manière détaillée et systématique afin d'établir la
présence et les possibilités des algorithmes génétiques, ainsi que de présenter les nouveaux
concepts de simulation de l'évolution et les processus de sélection naturelle comme un outil
pour résoudre les problèmes grâce à des programmes informatiques adaptatifs utilisant la
sélection, le croisement et les mutations. Son travail s'est avéré être une innovation utilisée
comme une base de presque tous les travaux ultérieurs dans le domaine des algorithmes
génétiques [16].](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-28-320.jpg)
![Chapitre 3 : les algorithmes génétiques
29S.BENHMIRA S.MEJDAOUI
2. aperçu de l’algorithme génétique
Puisque les algorithmes génétiques sont conçus pour simuler un processus biologique,
une grande partie de la terminologie pertinente est empruntée à la biologie. Cependant, les
entités auxquelles cette terminologie fait référence dans les algorithmes génétiques sont
beaucoup plus simples que leurs homologues biologiques [14]. Les composants de base
communs à presque tous les algorithmes génétiques sont :
Une fonction objective (fitness) à optimiser
Une population de chromosomes
Sélection des chromosomes qui se reproduiront
Croisement pour produire la prochaine génération de chromosomes
Mutation sur des chromosomes de nouvelle génération
La fonction fitness est la fonction que l'algorithme tente à optimiser [14]. Le mot
"fitness" est tiré de la théorie de l'évolution. Il est utilisé ici parce que cette fonction nous permet
de tester et quantifier l'adéquation de chaque solution potentielle. La fonction fitness est l'une
des parties les plus importantes de l'algorithme.
Le terme chromosome fait référence à une ou plusieurs valeurs numériques qui
représentent une solution possible au problème que l'algorithme génétique tente de résoudre
[14]. Chaque solution candidate est codée sous la forme d'un tableau de valeurs, le processus
que l'on trouve également dans d'autres algorithmes d'optimisation [15]. Il revient à l’utilisateur
de l'algorithme génétique de concevoir comment traduire l'espace échantillon des solutions
possibles en chromosomes. Une approche consiste à convertir chaque valeur de paramètre en
une chaîne de bits (séquence de 1 et de 0), puis à concaténer les paramètres comme des gènes
de bout en bout dans un ADN pour créer les chromosomes. Historiquement, les chromosomes
étaient généralement codés de cette façon, et il reste une méthode appropriée pour les espaces
de solution discrète. Les ordinateurs modernes permettent aux chromosomes d'inclure des
permutations, des nombres réels et de nombreux autres objets; mais pour l'instant et pour bien
comprendre le fonctionnement de l’algorithme génétique nous allons nous concentrer sur les
chromosomes binaires.](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-29-320.jpg)
![Chapitre 3 : les algorithmes génétiques
30S.BENHMIRA S.MEJDAOUI
Un algorithme génétique commence avec un nombre aléatoire de chromosomes, qui sert
de première génération (population initiale). Ensuite, chaque chromosome de la population est
évalué par la fonction de fitness pour tester son adaptation dans la résolution du problème.
L’opérateur de sélection choisit certains chromosomes pour la reproduction en se basant
sur une probabilité définit par l’utilisateur. Le chromosome le plus adapté est celui qui a plus
de chance d’être sélectionné. Par exemple si 𝑓 une fonction d’adaptation non négative, alors la
probabilité qu’un chromosome 𝐶𝑖 soit sélectionné est donnée par :
𝑃( 𝐶𝑖) =
𝑓( 𝐶𝑖)
∑ 𝑓( 𝐶𝑗)
𝑁 𝑝𝑜𝑝
𝑗=1
Notez que l'opérateur de sélection choisit les chromosomes avec remplacement, donc le
même chromosome peut être choisi plusieurs fois.
L'opérateur de croisement ressemble au croisement biologique et à la recombinaison des
chromosomes dans la cellule. Cet opérateur échange une sous-séquence de deux des
chromosomes choisis pour créer deux descendants. Par exemple, si les chromosomes
parentaux :
[1101|0111001000] et [0101|1101010010]
Sont croisés après le quatrième bit, alors
[0101|0111001000] et [1101|1101010010]
Seront leurs deux fils.
L'opérateur de mutation inverti aléatoirement deux bit d’un individu et nous donne un
nouveau chromosome (remplacer 0 par 1 et vice versa). Dans un premier temps l’opérateur de
mutation semble inutile. En effet, il joue un rôle important même s'il est secondaire à ceux de
la sélection et du croisement, la sélection et le croisement gardent l’information génétique des
chromosomes les mieux adaptés, mais ces chromosomes ne sont plus performants que par
rapport à la génération courante. Cela peut entrainer à une convergence trop rapide de
l’algorithme et la perte d’une gêne potentielle qui peut être utile dans le déroulement de
l’algorithme. En d’autre terme l'algorithme peut rester bloqué à un optimum local avant de
trouver l'optimum global [15]. L'opérateur de mutation aide à protéger contre ce problème en](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-30-320.jpg)
![Chapitre 3 : les algorithmes génétiques
31S.BENHMIRA S.MEJDAOUI
assurant la diversité dans la population, mais il peut aussi faire converger l'algorithme plus
lentement.
Maintenant la seconde génération est évaluée avec la fonction fitness, et ce cycle va se
répéter. Il est recommandé de sauvegarder le chromosome le mieux adapté (qui a une fitness
optimal) pour chaque génération.
L’algorithme est itéré jusqu’à ce que la valeur fitness du chromosome le mieux adapté se
stabilise et ne change pas pendant de nombreuse générations. Cela signifie que l’algorithme est
convergé vers une solution(s).
La performance d'un algorithme génétique dépend fortement de la méthode utilisée pour
coder les solutions candidates dans les chromosomes et de ce que la fonction de fitness mesure
réellement [16]. D'autres détails importants sont la probabilité de croisement, la probabilité de
mutation, la taille de la population et le nombre d'itérations. Ces valeurs peuvent être ajustées
après avoir évalué les performances de l'algorithme sur quelques essais.
Les algorithmes génétiques sont utilisés dans diverses applications. Quelques exemples
importants sont la programmation et l'apprentissage automatique. Ils sont également bien
adaptés à la modélisation des phénomènes en économie, écologie, système immunitaire
humain, génétique des populations et systèmes sociaux.
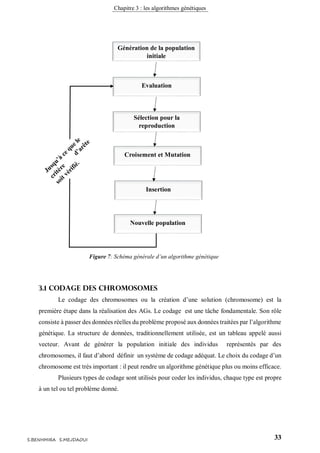
Bref, on peut générer un processus à suivre lors de l’utilisation de l’AG pour la résolution
de n’importe quel problème d’optimisation :
1. Initialiser la population initiale 𝑃( 𝑡)
2. Evaluer 𝑃( 𝑡)
3. TantQue (Critère d’arrêt non atteint) Faire
4. 𝑃( 𝑡 + 1) ← Sélection des parents dans 𝑃( 𝑡)
5. 𝑃( 𝑡 + 1) ← Appliquer Croissement et Mutation sur 𝑃( 𝑡 + 1)
6. 𝑃( 𝑡 + 1) ← Remplacer P(t) par 𝑃( 𝑡 + 1)
7. Evaluer 𝑃( 𝑡)
8. FinTantQue
Algorithme 4 : Algorithme Génétique
figure 10](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-31-320.jpg)


![Chapitre 3 : les algorithmes génétiques
35S.BENHMIRA S.MEJDAOUI
3.2 Création de la population initiale
Plusieurs mécanismes de génération de la population initiale sont utilisés dans la
littérature. Le choix de l’initialisation se fera en fonction des connaissances que l’utilisateur a
sur le problème. S’il n’a pas d’informations particulières, alors une initialisation aléatoire, la
plus uniforme possible afin de favoriser une exploration de l’espace de recherche maximum,
sera la plus adaptée. Par ailleurs, cette étape présente un problème principal qui est celui de
choix de la taille de la population. En effet une taille de population trop grande augmente le
temps de calcul et nécessite un espace mémoire considérable, alors qu’une taille de population
trop petite conduit à l’obtention d’un optimum local [8].
3.3 Evaluation des individus
Afin d'effectuer une sélection naturelle, chaque individu est évalué en fonction de sa
valeur de performance, déterminée par une fonction d'évaluation ou fonction fitness. Cette
valeur mesure la qualité des solutions et permet de les comparer. Le choix des meilleurs
individus se fait grâce au résultat fourni par la fonction d’adaptation. Le choix de la fonction
de fitness retenue est important et dépend du problème à résoudre et de l’espace de recherche
qui en découle. Cette fonction, propre au problème, est souvent simple à formuler lorsqu’il y a
peu de paramètres. Au contraire, lorsqu’il y a beaucoup de paramètres ou lorsqu’ils sont liés
entre eux, elle est plus difficile à définir, et donc c'est le rôle de l'utilisateur de penser à la façon
dont cette fonction est configurée pour répondre au besoin de problème.
3.4 Les opérateurs génétiques
Une fois que la population initiale est créée et nous avons finis d’évaluer ses individus,
nous allons appliquer les opérateurs génétiques pour générer de nouveaux individus ‘fils’ qui
seront la nouvelle génération de notre population, et nous espérons que certains entre eux seront
les meilleures solutions à notre problème. La sélection, le croisement et la mutation sont les
trois opérateurs les plus importants et les plus communs dans un AG.
Premièrement nous commençons par sélectionner les individus qui vont se reproduire
(Croisement) puis mutés (Mutation) pour donner cette nouvelle génération.
3.4.1 Opérateur de sélection
Comme son nom l'indique, la sélection nous permet de garder les individus relativement
performants afin qu’ils se reproduisent, en se basant sur l’évaluation précédemment établie qui
a identifié les meilleurs individus dans la population. Alors, le principe est clair ; sélectionner
une sous-population à partir de la population parente, éliminer les individus les moins](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-35-320.jpg)
![Chapitre 3 : les algorithmes génétiques
36S.BENHMIRA S.MEJDAOUI
28%
18%33%
6%
15%
P1 P2 P3 P4 P5
performants, et générer à leur place les plus performants, simulant ainsi le schéma de la
sélection naturelle de Darwin.
Plusieurs stratégies de sélection ont été mises en place. Voici quelques-unes de ces
méthodes :
3.4.1.1 Sélection par Roulette
La sélection par Roulette (Roulette Wheel Selection) introduit par Goldberg [1989] est
la plus connue et la plus utilisée. Elle consiste à associer à chaque individu un segment (ou case
de la roue) dont la longueur est proportionnelle à sa performance comme l'illustre la Figure 12.
La roue étant lancée, l'individu sélectionné est celui sur lequel la roue s'est arrêtée. Cette
méthode favorise les meilleurs individus, en effet, si un individu est bien plus performant que
les autres, il sera sélectionné plusieurs fois et donc on peut tomber dans un manque de diversité
du problème, mais avec cette méthode généralement, tous les individus conservent néanmoins
des chances d'être sélectionnés.
Si la population d’individus est de taille égale à N, alors la probabilité de sélection d’un
individu 𝑥𝑖 notée 𝑃(𝑥𝑖) est égale à : 𝑃( 𝑥𝑖) =
𝑓(𝑥 𝑖)
∑ 𝑓(𝑥 𝑖)𝑛
𝑖=1
où 𝑓( 𝑥) est la fonction d’adaptation.
Garder P2
comme parent
Chromosome Fitness
P1 28
P2 18
P3 33
P4 6
P5 15
Figure 12: La sélection par la méthode de Roulette
figure 16](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-36-320.jpg)
![Chapitre 3 : les algorithmes génétiques
37S.BENHMIRA S.MEJDAOUI
3.4.1.2 La sélection par Rang
La sélection par roulette présente des inconvénients lorsque la valeur d’évaluation des
individus varie énormément. En effet, on risquerait d’atteindre une situation de stagnation de
l’évolution. Imaginons le cas où 90% de la roulette est allouée à l’individu qui a la meilleure
évaluation, alors les autres individus auront une probabilité très faible d’être sélectionnés. La
sélection par rang trie d'abord la population par fitness. Ensuite, chaque chromosome se voit
associé un rang en fonction de sa position. Ainsi le plus mauvais chromosome aura le rang 1,
le suivant 2, et ainsi de suite jusqu'au meilleur chromosome qui aura le rang N, pour une
population de N chromosomes [17]. La sélection par rang d'un chromosome est la même que
par roulette, mais les proportions sont en relation avec le rang plutôt qu'avec la valeur de
l'évaluation. Le tableau ci-dessous fournit un exemple de sélection par rang. Avec cette
méthode de sélection, tous les chromosomes ont une chance d'être sélectionnés. Cependant,
elle conduit à une convergence plus lente vers la bonne solution. Ceci est dû au fait que les
meilleurs chromosomes ne diffèrent pas énormément des plus mauvais.
Chromosomes 1 2 3 4 5 6 Total
Probabilités
initiales
89% 5% 1% 4% 3% 2% 100%
Rang 6 5 1 4 3 2 21
Probabilités
finales
29% 24% 5% 19% 14% 9% 100%
3.4.1.3 La sélection par Tournois
La sélection par tournoi est l’une des sélections les plus utilisées dans les algorithmes
génétiques, grâce à son efficacité et sa simple implémentation. Le principe consiste à choisir
un sous-ensemble d’individus (K individus) aléatoirement dans la population, l’individu ayant
la meilleure valeur d’adaptation dans ce groupe, sera sélectionné et inclus dans la prochaine
génération pour la reproduction. Ce processus est répété jusqu’ à l’obtention du nombre
d’individus requis. Le nombre de participants à un tournoi (K), appelé la taille de tournoi, est
utilisé pour faire varier la pression de cette sélection. Si ce nombre est grand, alors la pression
sera forte et les faibles individus auront une petite chance d’être choisis. En général, un seul
gagnant est choisi parmi les participants à un tournoi.
Tableau 2: Exemple de sélection par rang pour 6 chromosomes](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-37-320.jpg)
![Chapitre 3 : les algorithmes génétiques
38S.BENHMIRA S.MEJDAOUI
Ce gagnant peut être choisi d’une façon déterministe ou probabiliste [18] [probabilité entre 0.5
et 1]. La méthode de tournoi la plus commune est le tournoi binaire, où on choisit deux
individus aléatoirement (K=2) puis on sélectionne le meilleur.
3.4.1.4 La sélection Elitiste
A la création d’une nouvelle population, il y a de grandes chances que les meilleurs
chromosomes soient perdus après les opérations de croisement et de mutation. Pour éviter cela,
on utilise la méthode d’élitisme. Elle consiste à copier un ou plusieurs des meilleurs
chromosomes dans la nouvelle génération. Ensuite, on génère le reste de la population selon
l’algorithme de reproduction usuel. Cette méthode améliore considérablement les algorithmes
génétiques, car elle permet de ne pas perdre les meilleures solutions.
3.4.2 Opérateur de Croisement
Une fois que l’opérateur de sélection fini de générer la population parente, on applique
sur cette population l’opérateur de recombinaison ou croisement. Ce dernier joue un rôle
primordial dans un AG, il peut accélérer ou décaler le processus de recherche.
Le croisement est l’opérateur principal de l’algorithme génétique, Il a pour objectif
d’enrichir la diversité de la population en manipulant les gènes des chromosomes. D'une
manière générale, le croisement consiste à appliquer des procédures avec une certaine
probabilité Pc (s’appelle le taux de croisement) sur les individus sélectionnés pour donner
naissance à un ou plusieurs (généralement deux) enfants. Ces derniers doivent hériter, par
A
S
Q
H
D
P
B
N
L
Y
23
25
15
12
6
30
47
22
10
29
Fitness Chromosomes
S
D
L
S
Garder le
meilleur
comme parent
Figure 13 : la sélection par Tournoi avec K = 3
figure 17](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-38-320.jpg)
![Chapitre 3 : les algorithmes génétiques
39S.BENHMIRA S.MEJDAOUI
croisement, de certaines caractéristiques des parents. Bien qu'il soit souvent aléatoire, cet
échange d'informations offre aux algorithmes génétiques une part de leur puissance:
quelquefois, de « bons » gènes d'un parent viennent remplacer les « mauvais » gènes d'un autre
et créent des enfants mieux adaptés que les parents [19].
Au début de la recherche, quand les solutions sont plutôt différentes, le croisement a un
rôle d’exploration, car la combinaison des solutions produit des solutions placées aux endroits
non encore visités pendant la recherche. Par contre, à la fin de la recherche, les parents sont
similaires, ce qui produit des enfants similaires, accordant au croisement un rôle plutôt
d’intensification (ou d’exploitation) [18].
Habituellement le croisement peut être classé en deux classes; celui appelé « en un point
» et l’autre appelé « à des points multiples ».
3.4.2.1 Croisement en 1-point
C’est le croisement le plus simple et le plus connu. Il consiste à choisir au hasard un
point de croisement pour chaque couple de chromosomes. Les séquences de bits situées après
ce point sont par la suite inter-changées pour former les fils, (Figure 14).
3.4.2.2 Croisement en N-point
Contrairement au croisement en un point, plusieurs points sont sélectionnés
aléatoirement et l’échange entre les parents s’effectue selon les différentes parties des
séquences cernées par ces points. Dans la Figure 15 deux points de coupure sont choisis au
hasard et le contenu entre ces points est inter-changé pour former les fils.
1 0 0 1 1 1 0 0 1 0 0 1
1 1 0 0 0 1 1 0 0 0 1 0
Figure 14 : Croisement en un point de deux chromosomes
figure 18
Parent 1
Parent 2
1 0 0 1 0 1 1 0 0 0 1 0
1 1 0 0 1 1 0 0 1 0 0 1
Fils 1
Fils 2
1 0 0 1 1 1 0 0 1 0 0 1
1 1 0 0 0 1 1 0 0 0 1 0
1 0 0 0 0 1 1 0 1 0 0 1
1 1 0 1 1 1 0 0 0 0 1 0
Parent 1
Parent 2
Fils 1
Fils 2
Figure 15 : Croisement en 2-point de deux chromosomes
(n=2)
figure 19](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-39-320.jpg)
![Chapitre 3 : les algorithmes génétiques
40S.BENHMIRA S.MEJDAOUI
3.4.2.3 Croisement uniforme
Un autre type de croisement peut être recensé, nommé le croisement uniforme, ce
mécanisme consiste à définir un masque de bits 0,1 dont la longueur est égale au nombre
d’individus parents sur lesquels il sera appliqué [20]. Si le bit du masque égal à «1 » dans la
position « i » alors l’échange entre les parents dans la même position est possible, « 0 » ne
désigne pas d’échange.
3.4.3 Opérateur de Mutation
Une fois que l’opérateur de croisement finit de générer la population des enfants, on
applique sur cette population l’opérateur de mutation afin de l’améliorer encore plus, son but
est de maintenir la diversité de la population des enfants et d'explorer l'espace de recherche en
évitant à l'algorithme de converger trop rapidement vers un optimum local.
Le principe est très simple (dans le cas des chromosomes binaires) ; une mutation est
l’inversion d’un bit aléatoire dans un chromosome. Un bit égale à 1 prendra la valeur 0 et vice
versa, comme il montre la figure 17. Cet opérateur est appliqué avec une probabilité très faible
Pm, nommée taux de mutation. Les petits taux sont recommandés car un grand taux peut
occasionner une destruction de l'information utile contenue dans les solutions et être considéré
probablement comme une recherche aléatoire [18].
Elle assure en outre une recherche aussi bien globale que locale, selon le poids et le
nombre des bits mutés. Plus un individu a été muté, plus la recherche s’éloignera du voisinage
local de ce même individu non muté. De plus, elles garantissent mathématiquement que
l’optimum global peut être atteint [21].
1 0 0 1 1 1 0 0 1 0 1 1
1 1 0 0 0 1 1 0 0 0 1 0
Figure 16: Exemple d’un Croisement uniforme
figure 20
Parent 1
Parent 2
1 1 0 1 1 1 0 0 0 0 0 0
1 0 0 0 0 1 1 0 1 0 1 1
Fils 1
Fils 2
1 1 0 0 0 1 0 1 1 0 0 1Masque
1 1 0 1 0 1 1 1 0 0 1 0 1 1 0 1 0 1 1 0 0 0 1 0Parent Fils
Figure 17 : opérateurs de mutation
figure 21](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-40-320.jpg)




![Chapitre 4 : résolution du problème du voyageur de commerce avec les AG
45S.BENHMIRA S.MEJDAOUI
2. Algorithme génétique appliqué au problème du
voyageur de commerce
Les algorithmes génétiques (AG) décrits dans le chapitre 3 sont souvent utilisés pour
résoudre des problèmes NP-difficiles, comme le problème de voyageur de commerce (TSP).
Dans le contexte de TSP, chaque chromosome est une solution du problème (trajet), la fonction
d’évaluation (fitness) des chromosomes est reliée avec la longueur de ce trajet, qui à son tour
dépend de l’ordre des villes. Puisque le TSP est un problème de minimisation alors la mesure
de trajet la plus élevée correspond à l’individu le plus faible, celle la plus courte sera associée
au meilleur individu.
Le problème dans un AG est comment représenter ou transformer les paramètres du
problème aux chromosomes, cette phase –comme nous le savons- appelée le codage. Dans le
TSP, il y a eu beaucoup de représentations utilisées pour résoudre le problème de TSP en
utilisant les Algorithmes Génétiques [22]. Certains d'entre eux, tels que la représentation
binaire et la représentation matricielle, utilisent des alphabets binaires pour la représentation
du tour. Bien que ces alphabets binaires constituent le mode classique de représentation dans
les AGs, mais les résultats obtenus par les opérateurs de croisement et de mutation ne sont pas
valides. La représentation la plus naturelle s’appelle « la représentation par chemin ».
Dans les parties suivantes de notre projet, nous nous concentrerons exclusivement sur
cette représentation des individus.
2.1 Représentation des chromosomes
La représentation par chemin (path repesentation) est probablement la représentation
la plus naturelle d'un tour. Dans cette représentation, un trajet est représenté par une liste des
entiers ordonnée de 𝑛 ville. Si 𝑖 est le 𝑗-é𝑚𝑒 éléments de la liste, alors la ville 𝑖 est la 𝑗-é𝑚𝑒
ville à visiter.
Par conséquent, le tour 1-3-2-5-6-8-4-7 est simplement représenté par :
L’avantage de la représentation par chemin inclut la simplicité de l'évaluation de la
fonction fitness. On peut calculer la valeur de fitness pour chaque chromosome en additionnant
1 3 2 5 6 8 4 7
Figure 18: codage d’un chemin
figure 22](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-45-320.jpg)

![Chapitre 4 : résolution du problème du voyageur de commerce avec les AG
47S.BENHMIRA S.MEJDAOUI
2.5 Opérateur de croisement pour TSP
Le croisement (ou recombinaison) est le processus par lequel les parents donnent leurs
gènes caractéristiques à leurs fils, formant ainsi la base de la génération suivante. Le rôle
important de cet opérateur est de maintenir la diversité de la population, évitant ainsi la
convergence rapide.
Il est clair que les opérateurs de croisement vus dans le chapitre 3, comme le croisement
en 1-point, sont susceptibles de générer des trajets invalides en utilisant la représentation par
chemin. En effet, appliquer le croisement à la position 3 donne deux solutions invalides.
Comme l’illustre la figure 19.
Les deux fils ne sont pas une permutation de 𝑛 éléments (𝑛 = 8).
Le TSP est un problème de permutation pur. Tous les chromosomes portent exactement les
mêmes valeurs et ne diffèrent que par l'ordre de ces valeurs. En conséquence, des opérateurs
de permutation spécialisés doivent être développés pour ce problème.
2.5.1 Partially Mapped Crossover (PMX)
Exemple tiré de [8].
PMX est un opérateur de croisement à deux points de coupure, introduit par
Goldberg et Lingle en 1985 [23], qui définit un segment de même longueur dans chacun des
parents 𝑃1 𝑒𝑡 𝑃2. Les segments sont entourés avec un rectangle dans la partie (𝑎) de la figure
20. Ces segments sont copiés vers les enfants 𝐹1 𝑒𝑡 𝐹2. 𝐹1 a hérité du segment de 𝑃2 et 𝐹2
de 𝑃1, comme le montre la partie (𝑏) de la figure.
A partir de l’un de ces segments, on établit à chaque gène une liste de
correspondance. Cette liste va servir à placer les gènes redondants et elle est formée de la
manière suivante: pour chaque position du segment on note 𝑥 le gène qui s'y trouve et 𝑦 celui
de l'autre enfant dans la même position. Tant que 𝑦 est retrouvé ailleurs dans le segment de
départ, on note 𝑦′ son correspondant dans l'autre enfant et on remplace 𝑦 par 𝑦′. Par exemple,
le gène correspondant à "1" de 𝐹1 est "6" mais ce gène existe aussi dans 𝐹1 et son
1 3 2 5 6 8 4 7
1 5 6 7 8 2 3 4
P1
P2
1 3 2 7 8 2 3 4
1 5 6 5 6 8 4 7
F1
F2
Figure 19: Application de croisement en 1-point sur deux parents représentés par chemin
figure 24](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-47-320.jpg)
![Chapitre 4 : résolution du problème du voyageur de commerce avec les AG
48S.BENHMIRA S.MEJDAOUI
correspondant est "3". Ainsi dans la liste de correspondance, on note que "1" a pour
correspondant "3". La liste complètement formée se trouve à la marge de la partie (𝑏) du
schéma.
On procède ensuite au placement des gènes hors segment en les copiant des parents
respectifs. Par exemple, copier "l" de 𝑃1 dans 𝐹1 provoque un conflit puisque ce gène existe
déjà. On utilise alors son correspondant dans la liste qui est "3". En procédant de manière
itérative, on arrive à former les enfants 𝐹1 𝑒𝑡 𝐹2 illustrés dans le partie (𝑐) de la figure.
2.5.3 Cycle Crossover (CX)
Exemple tiré de [8].
CX introduit par Oliver et al [24], est un opérateur qui satisfait la condition suivante:
chaque gène d'un enfant provient de l'un des parents à la même position. Les enfants sont donc
formés en copiant un gène d'un parent et en éliminant l'autre à la même position puisqu'il va
appartenir au deuxième enfant. Une fois que les positions occupées sont copiées par
élimination, on a complété un cycle. Les places restantes des deux enfants sont complétées par
les parents opposés.
Dans l’exemple présenté dans la Figure 21 partie (𝑎), la première position de 𝐹1 est
attribuée à "1" provenant de 𝑃1. Le gène de 𝑃2 situé à la même position est "4", il est recherché
dans 𝑃1 et retrouvé à la quatrième position. Le gène "4" est copié dans 𝐹1 et son correspondant
"8" est recherché dans 𝑃1 et retrouvé à la huitième position. "8" est copié dans 𝐹1 à cette même
1 2 3 4 5 6 7 8 9
5 4 6 9 2 1 7 8 3
3 4 5 6
6 9 2 1
3 5 6 9 2 1 7 8 4
2 9 3 4 5 6 7 8 1
Parent 1
Parent 2
(a)
Fils 1
Fils 2
Fils 2
Fils 1
(b)
(c)
𝟏 → 𝟔 → 𝟑
𝟐 → 𝟓
𝟗 → 𝟒
Figure 20: Croisement PMX
figure 25](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-48-320.jpg)
![Chapitre 4 : résolution du problème du voyageur de commerce avec les AG
49S.BENHMIRA S.MEJDAOUI
position et son correspondant "3" est recherché dans 𝑃1 et retrouvé à la troisième position. "3"
est copié dans 𝐹1 et son correspondant "2" est recherché dans 𝑃1 et retrouvé à la deuxième
position. "2" est copié et son correspondant "1" est retrouvé dans 𝑃1 à la première position où
cette position est déjà occupée dans 𝐸1 donc le cycle est terminé. Le cycle de 𝐹1 est "1, 4, 8,
3,2" et de manière analogue, le cycle "4, 1, 2, 3,8" est formé pour 𝐹2.
En dernier lieu, il faut combler les positions vacantes à partir des parents opposés. Par
exemple, les gènes "7 ,6 ,9" de 𝐹1 proviennent de 𝑃2. On obtient ainsi les enfants illustrés
dans la partie (b) de la figure 21.
2.5.4 Order Crossover (OX)
Exemple tiré de [8].
OX est un opérateur avec deux points de coupure introduit par Glodberg [25], qui copie
le segment formé par ces deux points de coupure dans les deux enfants. Par la suite, il recopie,
à partir du deuxième point de coupure ce qui reste des gènes dans l'ordre du parent opposé en
évitant les doublons.
La figure 22 présente un exemple du déroulement du croisement avec l'opérateur OX.
Dans la partie (𝑎), un segment est formé par les points de coupure dans les deux parents et ces
segments sont copiés tels quels dans les enfants 𝐹1 𝑒𝑡 𝐹2 comme le montre la partie (𝑏).
Enfin, on procède à la copie des gènes situés hors du segment copié. Pour cela, on se
place à partir du deuxième point de coupure et on choisit les gènes non redondants provenant
4 1 2 8 7 6 9 3 5
1 2 3 4 5 6 7 8 9Parent 1
Parent 2
1 2 3 4 8
4 1 2 8 3
1 2 3 4 7 6 9 8 5
4 1 2 8 7 6 9 3 5
Fils 1
Fils 2
Fils 2
Fils 1
(a)
(b)
(c)
𝟏 → 𝟒 → 𝟖 → 𝟑 → 𝟐
𝟒 → 𝟏 → 𝟐 → 𝟑 → 𝟖
Figure 21 : Croisement CX
figure 26](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-49-320.jpg)
![Chapitre 4 : résolution du problème du voyageur de commerce avec les AG
50S.BENHMIRA S.MEJDAOUI
du parent opposé. Par exemple, dans la partie (𝑐) de la Figure, on essaie de placer le gène "6"
de 𝑃2 après le deuxième point de coupure dans 𝐹1 mais ce gène existe déjà à l'intérieur du
segment. Il est donc ignoré et on passe au suivant. Le gène "2" ne présente pas de conflit, il est
donc copié et ainsi de suite jusqu'à où on forme les deux enfants 𝐹1 𝑒𝑡 𝐹2 tel qu'elle est illustré
dans la partie (𝑐) de la figure.
2.6 Opérateur de mutation pour TSP
Les deux individus (enfants) résultant de chaque opération de croisement seront
maintenant soumis à l'opérateur de mutation dans l'étape finale pour former la nouvelle
génération. La mutation aide l’algorithme à s’échapper des minima locaux et maintient la
diversité dans la population. Si le croisement est censé exploiter la solution actuelle pour en
trouver d’autres meilleures, la mutation joue sur l'exploration de l'ensemble de l'espace de
recherche.
Contrairement à l'opérateur de mutation classique, qui introduit des petites
perturbations dans le chromosome, les opérateurs de permutation pour le TSP modifient
souvent considérablement le chemin d'origine. Les opérateurs de mutation traditionnels
peuvent générer également des trajets qui ne sont pas convenables. Ainsi, nous allons présenter
ci-dessous quelques opérateurs de mutation pour les problèmes de permutations [26].
1 2 3 4 5 6 7 8 9
5 7 4 9 1 3 6 2 8
4 9 1 3
3 4 5 6
9 1 3 4 5 6 2 8 7
5 6 4 9 1 3 7 8 2
Parent 1
Parent 2
Fils 1
Fils 2
Fils 2
Fils 1
(a)
(b)
(c)
Figure 22: Croisement OX
figure 27](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-50-320.jpg)


![Chapitre 4 : résolution du problème du voyageur de commerce avec les AG
53S.BENHMIRA S.MEJDAOUI
MATLAB comprend de nombreuses fonctions, de calcul ou de traitements de
données, d'affichage, de tracés de courbes, de résolution de systèmes et d'algorithmes de
calculs numériques au sens large du terme.
Toutes ces fonctions sont définies par défaut dans MATLAB dans un langage de
programmation spécifique que l'on appellera MATLAB.
Ce langage comprend de nombreuses fonctions prédéfinies pour le calcul matriciel,
mais pas seulement. De ce fait, les domaines d'application sont extrêmement variés, et l'on
peut citer par exemple :
le calcul numérique dans le corps des réels ou des complexes ;
le calcul intégral ou la dérivation ;
le traitement du signal ;
l'optimisation ;
le traitement d'image ;
l'automatisme.
3.2 Paramètres génétiques de l’expérimentation
Dans cette section, nous allons nous concentrer sur une expérience de calcul qui utilise
l’algorithme génétique adapté pour le TSP, discuté dans ce projet, afin d’obtenir une solution
optimale pour le problème. Les algorithmes sont codés en MATLAB version 2017a sur un PC
Acer ASPIRE 5742G Intel core i5 2.67 GHz et 4GB dans la RAM, système d’exploitation
Windows 7.
Les performances des AGs sont testées sur 4 instances de TSP de solution optimale
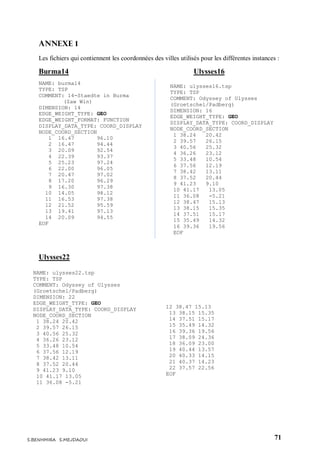
connues provenant de TSPLIB [27] ; burma14, ulysses16, ulysses22, eil51. (Annexe 1)
En premier lieu, nous avons testé le programme avec différentes types d’opérateurs
génétiques de mutation et de croisement implémentés dans ce travail, l’objectif étant de choisir
la meilleure combinaison de ces opérateurs. Pour le croisement, nous avons implémenté celles
d’Order Crossover (OX), Partially Mapped Crossover (PMX) et Cycle Crossover (CX). SWAP
Mutation, RSM et PSM sont testés pour la mutation. L'objectif de l'expérience est d'étudier la](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-53-320.jpg)
![Chapitre 4 : résolution du problème du voyageur de commerce avec les AG
54S.BENHMIRA S.MEJDAOUI
performance des AGs avec ses différents opérateurs génétiques en termes de nombre de
générations et de temps de calcul pour sortir avec une solution satisfaisante pour TSP.
L'une des principales difficultés dans la construction d'une AGs, dans le volet pratique,
réside dans le choix des valeurs appropriées pour des paramètres telles que la taille de la
population, la probabilité de croisement (𝑃𝑐) et la probabilité de mutation (𝑃𝑚). Dans cette
expérience, nous allons commencer avec une 𝑃𝑐 relativement élevée (≥ 0,6), une 𝑃𝑚
relativement faible (0,001 − 0,1) et une population de taille modérée (50 − 80). Les
sélections de valeurs de paramètres dépendent fortement du problème à résoudre. Il est à noter
que plus la taille de la population est grande, plus le temps de calcul est long. Pour chaque
expérience, les algorithmes ont été exécutés plusieurs fois et la distance de déplacement la plus
basse est considérée comme un résultat final. Pour toutes les expériences de cette étude, la
terminaison est effectuée lorsque le nombre de générations atteint le nombre maximal de
générations. Le nombre maximum de générations est défini plus tôt dans le code du
programme. Après ces expériences d’essai, nous avons décidé de travailler avec les paramètres
présentés dans le tableau 4 :
Paramètre génétique Valeur
Nombre de population 50
Probabilité de croisement [0.6-0.7-0.8]
Probabilité de mutation [0.01-0.1]
Taux de sélection 50% et 60%
Type de croisement CX
Type de Mutation PSM
Type de sélection Roulette Whell
Type d’insertion Elitisme
Nombre de générations 1000Tableau 4 : Paramètres génétique utilisés dans l’expérience](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-54-320.jpg)
![Chapitre 4 : résolution du problème du voyageur de commerce avec les AG
55S.BENHMIRA S.MEJDAOUI
3.3 Calcul de distance
Comme nous l’avons déjà vu dans le chapitre 1, le problème du voyageur de commerce
est souvent utilisé avec la distance euclidienne ; il consiste à prendre un nombre de villes dont
on connait les coordonnées, puis à génère la matrice de distance par la méthode euclidienne.
Puisqu’on a utilisé les instances du TSPLIB, alors on doit respecter la manière de calcul
de distance pour chaque instance [3], ou bien le type de distance pour lequel le fichier est
proposé.
Dans notre cas, les instances burma14, ulysses16, ulysses22, utilisent une distance qui
s’appelle « Distance géographique », or, eil51 utilise la distance traditionnelle, elle s’agit de la
distance euclidienne.
3.3.1 Distance Euclidienne
Si l’instance utilisée est de type Euclidienne (EUC_2D) [3], les coordonnées doivent
être spécifiées pour chaque nœud. Soit 𝑥𝑖 et 𝑦𝑖 les coordonnées du nœud 𝑖.
La distance euclidienne 𝑑𝑖𝑗 entre les deux points 𝑖 𝑒𝑡 𝑗 est calculée comme suit :
𝑥 𝑑 = 𝑥𝑖 − 𝑥𝑗
𝑦 𝑑 = 𝑦𝑖 − 𝑦𝑗
𝑑𝑖𝑗 = √ (𝑥 𝑑)2 + (𝑦 𝑑)2
3.3.2 Distance géographique
Si l’instance est de type (GEO) [3], alors les nœuds correspondent à des points sur la
terre, la distance entre deux points égale à leur distance sur la sphère idéalisée avec un
rayon de 6378,388 kilomètres. Les coordonnées du nœud donnent la latitude et la
longitude géographiques du point correspondant sur la terre.
Soit 𝑥𝑖 et 𝑦𝑖 les coordonnées de la ville 𝑖. D'abord, l'entrée est convertie en latitude et
longitude géographiques données en radians.
𝑃𝐼 = 3.141592;
𝑑𝑒𝑔 = 𝑛𝑖𝑛𝑡( 𝑥𝑖 );
𝑚𝑖𝑛 = 𝑥𝑖 − 𝑑𝑒𝑔;
𝑙𝑎𝑡𝑖𝑡𝑢𝑑𝑒[𝑖] = 𝑃𝐼 ∗ (𝑑𝑒𝑔 + 5.0 ∗ 𝑚𝑖𝑛 / 3.0 ) / 180.0;
𝑑𝑒𝑔 = 𝑛𝑖𝑛𝑡( 𝑦𝑖 );
𝑚𝑖𝑛 = 𝑦𝑖 − 𝑑𝑒𝑔;](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-55-320.jpg)
![Chapitre 4 : résolution du problème du voyageur de commerce avec les AG
56S.BENHMIRA S.MEJDAOUI
𝑙𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑒[𝑖] = 𝑃𝐼 ∗ (𝑑𝑒𝑔 + 5.0 ∗ 𝑚𝑖𝑛 / 3.0 ) / 180.0;
La distance 𝑑𝑖𝑗 entre deux villes 𝑖 𝑒𝑡 𝑗 en kilometres est donnée par :
𝑅𝑅𝑅 = 6378.388;
𝑞1 = 𝑐𝑜𝑠( 𝑙𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑒[𝑖] − 𝑙𝑜𝑛𝑔𝑖𝑡𝑢𝑑𝑒[𝑗] );
𝑞2 = 𝑐𝑜𝑠( 𝑙𝑎𝑡𝑖𝑡𝑢𝑑𝑒[𝑖] − 𝑙𝑎𝑡𝑖𝑡𝑢𝑑𝑒[𝑗] );
𝑞3 = 𝑐𝑜𝑠( 𝑙𝑎𝑡𝑖𝑡𝑢𝑑𝑒[𝑖] + 𝑙𝑎𝑡𝑖𝑡𝑢𝑑𝑒[𝑗] );
𝑑𝑖𝑗 = (𝑖𝑛𝑡) ( 𝑅𝑅𝑅 ∗ 𝑎𝑐𝑜𝑠( 0.5 ∗ ((1.0 + 𝑞1) ∗ 𝑞2 − (1.0 − 𝑞1) ∗ 𝑞3) ) + 1.0);
La fonction acos est l’inverse du fonction 𝑐𝑜𝑠𝑖𝑛𝑢𝑠𝑒.
La fonction 𝑛𝑖𝑛𝑡 doit revoie l’entier le plus proche d’un nombre flottant.
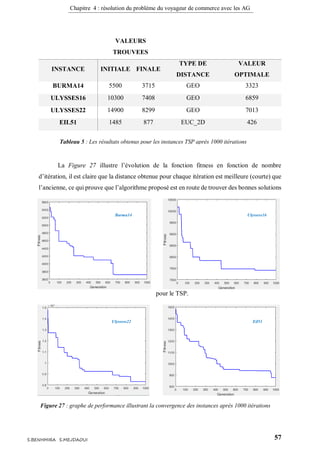
3.4 Résultats de l’expérience
Tableau 5, montre les valeurs numériques obtenues après l’exécution du programme
plusieurs fois, l’algorithme génétique réalisé dans ce travail est capable de trouver des bons
résultats –mais pas optimales- pour le problème du voyageur de commerce dans un temps
raisonnable avec des paramètres génétiques réduits; la taille de la population égale à 50 avec
un nombre d’itération égale à 1000. Si on incrémente le nombre d’itérations, on peut trouver
des résultats encore meilleurs, mais le temps de calcul va s’agrandir.
La première colonne indique les instances TSP utilisées. Les deux colonnes INITIALE
et FINALE exposent respectivement la solution initiale et la solution optimale obtenue après
1000 d'itérations. TYPE DE DISTANCE indique le type de distance qui utilise l’instance. La
dernière colonne correspond aux valeurs optimales d’instances dans le monde.](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-56-320.jpg)


![Chapitre 5 : Amélioration par la stratégie d’immigration
60S.BENHMIRA S.MEJDAOUI
1 – Histoire de l'immigration
L’immigration est un phénomène mondial qui dure depuis longtemps et notamment en
Europe berceau de nombreux flux migratoires. Ce phénomène s’est accentué en Europe depuis
les 2 guerres mondiales. Le plus grand pays, quant à lui, voit sa formation par l’immigration
protestante anglaise. Il s’agit bien sûr des Etats-Unis. Au Brésil aussi et en Amérique du Sud
en général, l’immigration a fondé ces pays. Par exemple le Brésil après l’immigration
portugaise a vu arriver des Italiens, Espagnols puis des Allemands, Japonais, et Syriens depuis
le siècle dernier. C’est un phénomène qui touche tous les pays depuis toujours, un phénomène
historique et de société. L’immigration est un fait de société important puisque la déclaration
des droits de l’homme y fait référence sur certains points. Cependant même si l’immigration a
été voulue elle a été au XXème siècle réglementée et elle devient clandestine, cachée…La
France était le pôle d’immigration le plus attractif. Portugais et Italiens essentiellement mais
aussi des Espagnols venaient s’installer en France [28].
A partir de 1989, l’immigration en Europe a nettement diminué et elle concerne surtout
les pays d’Europe de l’est. Quant à l’immigration animale est un phénomène ubiquitaire sur
Terre. Elle est décrite depuis plusieurs siècles. Aristote, dès l’an 350 avant Jésus-Christ,
souligne la disparition annuelle des oiseaux à la fin de l’été et leur soudaine réapparition au
printemps. En 1757, Linné débute l’étude des mécanismes de la migration des oiseaux [29].
2- Définition
L’immigration définit par un mouvement actif d’un organisme ou d’un groupe
d’organismes, d’un habitat vers un autre, de manière durable ou définitive dans un habitat
étranger. L’immigration, du latin migration, signifiant « changer de séjour », est un phénomène
ubiquitaire, retrouvé chez un grand nombre d’espèces eucaryotes.](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-60-320.jpg)
![Chapitre 5 : Amélioration par la stratégie d’immigration
61S.BENHMIRA S.MEJDAOUI
Une immigration est un déplacement de population d’un lieu à un autre (soit d’une
région à une autre, soit d’un pays à un autre), obligeant donc à changer de lieu de vie/ résidence
dans le cas des personnes ou d’habitat dans le cas des espèces animales, en général pour y
trouver un emploi ou avec l'intention de s'y établir dans la perspective d'une meilleure qualitéde
vie. Ceci-dit, il y deux types de migrations : humaines et les animales.
2.1 Immigration Humaines :
Elle correspond, vue du côté du pays de départ, à l'émigration. Dans le cas des
frontaliers, les migrations peuvent être quotidiennes. Les phénomènes migratoires ont toujours
été présents tout au long de l’histoire de l’humanité. De nombreuses cultures et religions ont
pour référence la migration en quelque sorte [30], et chacun a ses propres raisons de partir.
Aujourd'hui, les flux de migrations sont orientés aussi bien des pays en développement vers les
pays développés que d'un pays développé vers un autre.
Les différentes motivations de l'immigration :
Professionnelle (Ex : mission de longue durée à l'étranger).
Etudes.
Politique (Ex : réfugié politique fuyant des persécutions).
Sécuritaire (Ex : en cas de guerre dans le pays d'origine).
Economique (Ex : recherche d'un meilleur niveau de vie dans les pays riches).
Familiale (Ex : rejoindre le conjoint ou un enfant déjà installé).
Fiscale, dans un pays ayant un niveau d'imposition moins élevé.](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-61-320.jpg)
![Chapitre 5 : Amélioration par la stratégie d’immigration
62S.BENHMIRA S.MEJDAOUI
2.2 Immigration animales :
C’est le déplacement de certains animaux tels que les oiseaux, les poissons et les
mammifères, qui se rendent d’un lieu à un autre. L’immigration implique une attitude active
de la part de l’animal, qui doit être en déplacement pendant de nombreux jours (migrations
saisonnières). Ce peut être pour échapper à un climat trop chaud ou trop froid (températures
extrêmes), pour aller à la rencontre de partenaires pour se reproduire ou encore pour trouver de
la nourriture [30].
La migration permet aussi à la sélection naturelle de faire son travail. Pendant le
voyage, beaucoup seront capturés par des prédateurs, et les animaux faibles ne parviendront
pas souvent à destination. Les plus forts finiront le voyage de migration et s'accoupleront pour
avoir une progéniture plus résistante, et ainsi améliorer la descendance de l'espèce.
Ce ne sont pas seulement les oiseaux qui sont des animaux migrateurs, des insectes, des
mammifères, des poissons.... on remarque simplement plus le vol des oiseaux, comme la
bernache du Canada, qui quitte la région pour l'hiver. Certains papillons quittent le Canada
pour aller jusqu'au Mexique. Même certaines chauves-souris quittent le nord pour aller vers le
sud en hiver.
Exemple des saumons
Les saumons sont d’excellents exemples de poissons migrateurs, vivant en mer et se
reproduisant en eau douce. Ils pondent dans les ruisseaux ou les lacs. La progéniture y reste
jusqu’à trois ans pour certaines espèces, puis migre vers l'océan, où la nourriture y est plus
abondante. Les saumons restent dans l'océan jusqu'à maturation et reviennent ensuite à leur site
de naissance pour se reproduire à leur tour [29].](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-62-320.jpg)

![Chapitre 5 : Amélioration par la stratégie d’immigration
64S.BENHMIRA S.MEJDAOUI
3- Algorithme génétique avec l’approche
d’imigration
La migration mentionnée ci-dessus, qui tourne autour de déplacement d'une population
des espèces d'un habitat vers un autre pour améliorer leur qualité de vie ou la recherche de
nourriture ou d'accouplement ...etc. En route vers l’autre endroit, le groupe fait face à de
nombreuses difficultés, beaucoup seront capturés par des prédateurs, et les individus faibles ne
parviendront pas souvent à destination. Les plus forts finiront le voyage de migration,
s’adapteront avec les membres de l’autre population et s'accoupleront pour avoir une
progéniture hybride plus résistante, et ainsi améliorer la descendance de l'espèce.
Dans notre cas, la stratégie de l’immigration que nous allons introduire eu le même
principe, après l’application des opérateurs principaux de l’algorithme génétique à savoir, la
sélection, le croisement et la mutation, dans la population finale on insère des nouvelles
individus immigrants à la places d’autres en assurant que la taille de la population reste la
même. Cet opérateur de l’immigration qui introduira une diversité de la population et plus de
dynamisme et de l'exploration des différentes solutions probables du problème, afin d'obtenir
une meilleure solution optimale par rapport à celle obtenue par l'algorithme génétique standard.
Selon le choix des individus remplacés et insérés, on peut avoir plusieurs types
d’immigration [31], par exemple les individus sont insérés dans la population créée d’une
manière aléatoire chaque nombre de génération en remplaçant les pires individus par certains
individus choisi au hasard. Cet opérateur appelé « immigration aléatoire ».
Figure 28 : Pincipe d’immigration
aléatoiore
figure 34
Population avant l’immigration Population aprés l’immigration
A
N
L
I
A
M
U
I](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-64-320.jpg)
![Chapitre 5 : Amélioration par la stratégie d’immigration
65S.BENHMIRA S.MEJDAOUI
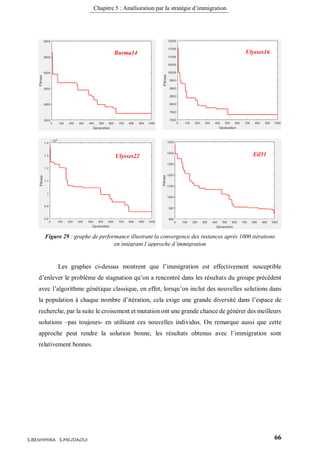
Les résultats présentés dans le figure ci-dessous sont obtenues en appliquant ce type
d’immigration, notée SIG.
En exécutant le programme plusieurs fois sur les même instances et conditions utilisés
dans l’algorithme génétique standard (Voir Tableau 4, chapitre 4). Cette fois ci nous avons
intégrés l’approche d’immigration comme montre l’algorithme ci-dessus.
Le nombre d’immigration utilisé 𝑛 ∈ [1 − 10]. Chaque 𝑛 génération la fonction responsable
de l’immigration est exécutée.
VALEURS
TROUVEES
INSTANCE INITIALE FINALE
TYPE DE
DISTANCE
VALEUR
OPTIMALE
BURMA14 5650 3700 GEO 3323
ULYSSES16 11650 7327 GEO 6859
ULYSSES22 15900 8092 GEO 7013
EIL51 1500 850 EUC_2D 426
𝑖𝑚 = 𝑁𝑜𝑚𝑏𝑟𝑒 𝑑𝑒 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑖𝑜𝑛 𝑝𝑜𝑢𝑟 𝑞𝑢𝑒 𝑙′
𝑖𝑚𝑚𝑖𝑔𝑟𝑎𝑡𝑖𝑜𝑛
𝑒𝑠𝑡 𝑎𝑝𝑝𝑙𝑖𝑞𝑢é𝑒
𝑖 = 1
𝑷𝒐𝒖𝒓 𝑖𝑡𝑒𝑟 = 1 𝒋𝒖𝒔𝒒𝒖’à 𝑛𝑜𝑚𝑏𝑟𝑒_𝑖𝑡𝑒𝑟
𝐴𝑝𝑝𝑙𝑖𝑞𝑢𝑒𝑟 𝑙𝑒𝑠 𝑖𝑛𝑠𝑡𝑟𝑢𝑐𝑡𝑖𝑜𝑛𝑠 𝑑’𝐴𝐺 𝑆𝑡𝑎𝑛𝑑𝑎𝑟𝑑 à 𝑠𝑎𝑣𝑜𝑖𝑟 ∶
𝑆é𝑙𝑒𝑐𝑡𝑖𝑜𝑛, 𝑐𝑟𝑜𝑖𝑠𝑒𝑚𝑒𝑛𝑡 𝑒𝑡 𝑚𝑢𝑡𝑎𝑡𝑖𝑜𝑛
𝑖 = 𝑖 + 1
𝑺𝒊 𝑖 == 𝑖𝑡𝑒𝑟
𝐺é𝑛é𝑟𝑒𝑟 𝑛 𝑖𝑚𝑚𝑖𝑔𝑟𝑎𝑛𝑡𝑠 𝑎𝑙é𝑎𝑡𝑜𝑖𝑟𝑒𝑠
𝐸𝑣𝑎𝑙𝑢𝑒𝑟 𝑐𝑒𝑠 𝑖𝑚𝑚𝑖𝑔𝑟𝑎𝑛𝑡𝑠
𝑅𝑒𝑚𝑝𝑙𝑎𝑐𝑒𝑟 𝑙𝑒𝑠 𝑝𝑖𝑟𝑒𝑠 𝑑𝑎𝑛𝑠 𝑙𝑎 𝑑𝑒𝑟𝑛𝑖è𝑟𝑒 𝑝𝑜𝑝𝑢𝑙𝑎𝑡𝑖𝑜𝑛
𝑭𝒊𝒏𝒔𝒊
𝑭𝒊𝒏𝒑𝒐𝒖𝒓
Algorithme 7: Immigration aléatoire
figure 35
Tableau 6 : Les résultats obtenus pour les instances TSP après 1000 itérations par l’approche
d’immigration](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-65-320.jpg)


![69S.BENHMIRA S.MEJDAOUI
Références
[1] https://interstices.info/jcms/c_37686/le-probleme-du-voyageur-de-commerce .
[2] Mahdi KHEMAKHEM, « Le Problèm du Voyageur de Commerce Multicolore », Mémoire
de DEA AISIH.
[3] Gerhard Reinelt Universitat Heidelberg Institut fur Angewandte Mathematik Im
Neuenheimer Feld 294 D-69120 Heidelberg Gerhard. TSPLIB95.
[4] Rajesh Matai, Surya Prakash Singl and Murari Lal Mittal “Traveling Salesman Problem:
An Overview of Applications, Formulations, and Solution Approaches”
[5] Ms. K. Ilavarasi, “Variants of Travelling Salesman Problem: A Survey”
[6] Alexander Barvinok, Edward Kh. Gimadi, Anatoliy I. Serdyukov ,"The Maximum TSP"
[7] Michael Jünger, Gerhard Reinelt, Giovanni RinaMi, “Chapter 4 The Traveling Salesman
Problem”
[8] Dr. LEMOUARI ALI, Introductions aux Métaheuristiques, université de Jijel
[9] Sanae AROUSSI, “Chapitre 4 : Heuristiques et Métaheuristiques”, Université Blida 1
[10] Arnaud Rioland Alexandre Eudes, Rapport de Projet 3ème année Modélisation et Calcul,
” Optimisation par essaim particulaire pour un problème d’ordonnancement et d’affectation de
ressources Scientifique ” .2007
[11] Sidi Mohamed Douiri, Souad Elbernoussi & Halima Lakhbab. Cours des Méthodes de
Résolution Exactes Heuristiques et Métaheuristiques, Faculté des Sciences de Rabat,
Université Mohammed V
[12] C. Darwin, “On the Origin of Species”, John Murray, London, Albemarle Street, 1859.
[13] J. Holland, “Adaptation in Natural and Artificial Systems”, The MIT Press, Cambridge,
Massachusetts, London, England, fifth printing, 1998
[14] Mitchell, M. (1995).” Genetic Algorithms: An Overview”
[15] Haupt, R. L., & Haupt, S. E. (1998). “Practical Genetic Algorithms.” Edition 2
[16] Mitchell, M. (1996). An Introduction to Genetic Algorithms.
[17] ELMIR Younes, Mémoire, ” Optimisation multi objectif par les algorithmes génétiques et
approche Pareto de paramètres d’un contrôleur PID ”
[18] Mais Haj Rachid, Wahiba Ramdane Cherif, Christelle Bloch, pascal Chatonnay ,
”Différentes opérateurs évolutionnaires de permutation: sélections, croisements et mutations ”
[19] Arnaud Zinflou, Mémoire, ”Système interactif d'aide à la décision basé sur des algorithmes
génétiques pour l'optimisation multi-objectifs ” 2004](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-69-320.jpg)
![70S.BENHMIRA S.MEJDAOUI
[20] Aziza BECHIR, Mémoire, ”RÉSOLUTION DE PROBLÈMES D’OPTIMISATION PAR
LES SYSTÈMES MULTI-AGENTS ET LES APPROCHES ÉVOLUTIONNAIRES ”
[21] Selvaraj Ramkumar, ”Algorithmes Génétiques”, Faculté des sciences-Université libre de
Bruxelles, 26 Avril 2007.
[22] Jean-Yves Potvin, “Genetic algorithms for the traveling salesman problem”
[23] D.E. Goldberg and R. Lingle, Alleles, loci and the traveling salesman problem, in: Proc.
1st Int. Conf. on Genetic Algorithms (1CGA '85), Carnegie-Mellon University, Pittsburg, PA
(1985) pp. 154-159.
[24] I.M. Oliver, D.J. Smith and J.R.C. Holland, A study of permutation crossover operators
on the traveling salesman problem, in: Proc. 2nd Int. Conf. on Genetic Algorithms ( ICGA '87),
Massachusetts Institute of Technology, Cambridge, MA (1987) pp. 224-230.
[25] D. Goldberg, Genetic Algorithm in Search, Optimization, ans Machine Learning. Addison
Wesley, 1989.
[26] Abdoun Otman, Chakir tajani, “Analyzing the Performance of Mutation Operators to
Solve the Travelling Salesman Problem” Article March 2012
[27] http://elib.zib.de/pub/mp-testdata/tsp/tsplib/tsplib.html
[28]http://deste.umons.ac.be/galanet/dossier/fichiers/Fichier%20principal%20associ%E9%20
%E0%20la%20rubrique%203.doc.
[29] THESE de Renard Alix « CONSEQUENCES DES CHANGEMENTS GLOBAUX SUR
LA MIGRATION ANIMALE »
[30] http://lesdefinitions.fr/migration.
[31] C. Tajani , O. Abdoun and J. Abouchabaka, ‘’ Optimization Approach Based on
Immigration Strategies for STSP ’’
[32] http://www.math.uwaterloo.ca/tsp/history/](https://image.slidesharecdn.com/rapportfinal2017-2018-200308185340/85/Solving-Traveling-Salesman-problem-using-genetic-algorithms-implementation-in-MATLAB-70-320.jpg)