traitement-du-signal-avance.pptx

Traitement avancé du signal
Chapitre 1 : Rappels sur les filtres numériques (RIF et RII)
- Transformée en Z
- Structures, fonctions de transfert, stabilité et implémentation des filtres
numériques (RIF et RII)
- Filtre numérique à minimum de phase
- Les méthodes de synthèses des filtres RIF et des filtres RII
- Filtres numériques Multicadences
Chapitre 2: Analyse spectrale paramétrique et filtrage numérique adaptatif
- Méthodes paramétriques
- Modèle AR (Lévinson, Yulewalker, Burg, …..)
- Modèle ARMA
- Algorithme du gradient stochastique LMS
- Algorithme des moindres carrés récursifs RLS

Chapitre 3 : Analyse temps-fréquence et temps-échelle
- Dualité temps-fréquence
- Transformée de Fourier à court terme
- Ondelettes continues, discrètes et ondelettes dyadiques
- Analyse multi-résolution et bases d’ondelettes
- Transformée de Wigner-Ville
- Analyse Temps-Echelle,
Chapitre 4 : Signaux aléatoires et processus stochastiques
- Rappel sur les processus aléatoires
- Stationnarité
- Densité spectrale de puissance
- Notions de processus stochastiques
- Stationnarités au sens large et strict et Ergodicité
- Exemples de processus stochastiques (processus de Poisson, processus gaussien et
processus Markovien)

Références bibliographiques :
1. Mori Yvon, “Signaux aléatoires et processus stochastiques“, Lavoisier, 2014.
2. E. Robine, “Introduction à la théorie de la communication, Tome II: Signaux
aléatoires“, Masson 1970.
3. N. Hermann, “Probabilités de l'ingénieur : variables aléatoires et simulations
Bouleau“, 2002.
4. M. KUNT, “Traitement Numérique des Signaux“, Dunod, Paris, 1981.
5. J. M Brossier, “Signal et Communications Numériques, Collection Traitement
de Signal“, Hermès, Paris, 1997.
6. M. BELLANGER, “Traitement numérique du signal : Théorie et pratique“, 8e
édition, Dunod, 2006.

La transformée de Fourier
La transformée Fourier d’un signal y(t), est définie par :






 dt
e
t
x
f
X
t
x
TF ft
j 
2
)
(
)
(
)]
(
[


















dt
e
t
x
e
dt
e
t
y
f
Y
t
y
TF
t
x
e
t
y
ft
j
t
ft
j
t




2
2
.
).
(
)
(
)
(
)]
(
[
)
(
)
(
La transformée de Fourier d’un signal x(t) sommable , est définie par :

)
(
).
(
).
(
)]
(
[
2
)
2
(
p
X
dt
e
t
x
dt
e
t
x
t
y
TF
p
f
j
pt
t
f
j

















 



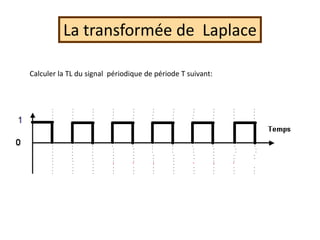
La transformée de Laplace

Définition
• La transformée de Laplace X(p) = TL (x(t)) est la
fonction de la variable complexe p définie par :
• Opérateur de Laplace :
– p : littérature francophone s : littérature anglophone
• Convention d ’écriture :
– fonc. temporelle = minusc. fonc. de L. = majusc.





 dt
e
t
x
p
X pt
).
(
)
(

Principaux théorèmes - linéarité
• Changement d ’échelle :
• Superposition :
par contre :
  )
(
|
|
1
)
.
(
a
p
X
a
t
a
x
TL 
  )
(
)
(
)
(
)
( 2
1
2
1 p
X
p
X
t
x
t
x
TL 


  )
(
)
(
)
(
)
( 2
1
2
1 p
X
p
X
t
x
t
x
TL 



Principaux théorèmes - translations
• Translation (théorème du retard) :
• Translation dans le domaine complexe :
  )
(
)
( p
X
e
t
x
TL p
 


  )
(
)
( a
p
X
t
x
e
TL at



x(t) x(t-)


Principaux théorèmes - équa. diff.
• Dérivation :
• Intégration:
  )
0
(
)
(
)
(
'
x
p
X
p
t
x
TL 

)
(
1
)
(
0
p
X
p
dt
t
x
TL
t









Principaux théorèmes - extrema
• Valeur initiale :
• Valeur finale:
)
(
lim
)
0
( p
X
p
x
p 


)
(
lim
)
(
0
p
X
p
x
p



 
 
0
).
(
0
).
(






a
e
t
u
TL
a
e
t
u
TL
at
at

Calculer la TL du signal périodique de période T suivant:
































































df
e
f
j
X
df
e
e
f
j
X
t
x
df
e
f
j
X
e
t
x
f
j
X
TF
dt
e
e
t
x
dt
e
t
x
f
j
X
p
X
dt
e
t
x
dt
e
t
x
t
y
TF
p
f
j
t
f
j
ft
j
t
ft
j
t
ft
j
t
t
f
j
pt
t
f
j
)
2
(
2
2
1
2
)
2
(
)
2
(
).
2
(
).
.
.
2
.
(
)
(
).
2
(
).
(
))
2
(
(
).
(
).
(
)
2
(
)
(
).
(
).
(
)]
(
[
2
























La transformée de Laplace Inverse











































dp
e
p
X
j
dp
e
p
X
j
t
x
f
j
d
e
f
j
X
j
df
e
f
j
X
df
e
f
j
X
df
e
e
f
j
X
t
x
pt
j
j
pt
t
f
j
t
f
j
t
f
j
ft
j
t
).
(
2
1
).
(
2
1
)
(
)
2
(
).
2
(
2
1
).
2
(
).
2
(
).
2
(
)
(
)
2
(
)
2
(
)
2
(
2























0
)
(
Re
)
(
}
,
.
)
(
{
Re
)
(
0
)
(
Re
)
(
}
,
.
)
(
{
Re
)
(
2
1









t
pour
p
l
tq
p
X
de
poles
p
avec
p
e
p
X
s
t
x
t
pour
p
l
tq
p
X
de
poles
p
avec
p
e
p
X
s
t
x
j
j
j
pt
i
i
i
pt



i
i
i
i
p
p
p
p
Y
p
p
r


 ]
),
(
)
lim[(
i
i
m
i
m
m
i
p
p
p
p
Y
p
p
dp
d
m
r



 

]
),
(
)
[(
lim
)!
1
(
1
1
1
Pole simple
Pole Multiple

4
)
Re(
5
;
4
1
5
2
,
4
)
Re(
;
4
1
5
2
,
5
)
Re(
;
4
1
5
2




















p
p
p
p
p
p
p
p
p
Exemples
Calculer la Transformée de Laplace Inverse des fonctions :

4
)
Re(
5
;
)
4
(
)
5
(
2
,
4
)
Re(
;
)
4
(
)
5
(
2
,
5
)
Re(
;
)
4
(
)
5
(
2
3
3
3

















p
p
p
p
p
p
p
p
p
Exemples

;
3
3
1
2
;
8
6
;
)
10
(
)
1
(
;
2
4
3
,
)
Re(
;
)
(
2
3
2
3
2
2
2
5
2
2
2
















p
p
p
p
p
p
p
p
p
p
p
e
p
p
p
p
a
p
b
a
p
b
p
Exemples

La transformée en Z


 
 
 




















































k
pT
k
k
pkT
e
e
k
pt
pt
e
k
pt
k
e
pt
e
e
e
e
e
z
z
k
x
e
kT
x
dt
T
k
t
e
t
x
dt
e
T
k
t
t
x
dt
e
T
k
t
t
x
dt
e
t
x
t
x
TL
)
(
;
).
(
)
(
)
.
(
.
)
(
)
.
(
).
(
].
)
.
(
).[
(
)
(
)]
(
[



La transformée de Laplace d’un signal échantillonné xe(t) est définie par :

La transformée en z
Définition
Un formalisme adapté au filtrage et à l’analyse en fréquence
des signaux échantillonnés
problèmes liés à la convergence :
importance du domaine de définition






k
k
z
k
x
z
X )
(
)
(
en général une couronne incluant
le cercle de rayon 1
1
Re(z)
Im(z)
k entier : pas d’échantillonnage égal à 1
x(k) signal étudié
z variable complexe

Théorème de Cauchy :






k
U
si
converge
U
serie
la
k
k
k
k
1
)
lim(
:
1
0

Calculer la TZ du signal suivant

ailleurs
k
x
x
x
x
x
x
0
)
(
1
)
4
(
;
4
)
3
(
;
6
)
2
(
;
4
)
1
(
;
1
)
0
(






Exercice 1
Exercice 2
);
(
3
1
2
1
)
(
);
(
3
1
)
(
);
(
)
8
,
0
(
)
(
);
(
)
8
,
0
(
)
(
2
4
3
2
1
k
u
k
x
k
u
k
x
k
u
k
k
x
k
u
k
x
k
k
k
k
k























causal
k
x
k
x
x
x
x
k
y
)
(
)
(
....
)
2
(
)
1
(
)
0
(
)
( 




Exercice 3

La transformée d’une séquence de durée finie
Le retard de k échantillons est associé à z -k




L
t
k
k
z
a
z
X
0
)
(
est un polynôme
La transformée d’un signal composé d’un seul échantillon pour k=0
est une constante )
0
(
)
( x
z
X 
La transformée d’un signal composé d’un seul échantillon pour k=1
est 1
)
1
(
)
( 
 z
x
z
X
Quelques propriétés immédiates de la transformée en z

Transformée d’une convolution discrète












n
n
n
k
x
n
h
n
k
h
n
x
k
y )
(
)
(
)
(
)
(
)
(
Même démonstration que dans le cas de la transformée
de Fourier d’une convolution
(commutativité)
)
(
)
(
)
( z
X
z
H
z
Y 

Transformée d’une convolution discrète






n
n
k
h
n
x
k
y )
(
)
(
)
(
)
(
)
(
)
( z
X
z
H
z
Y 
cf : produit de polynômes




2
0
)
(
)
(
)
(
n
n
k
h
n
x
k
y
les coefficients du produit
s’obtiennent en calculant une
convolution discrète
x
0
x
1
z
1


 x
2
z
2







h
0
h
1
z
1


 h
2
z
2








x
0
h
0

  x
0
h
1
 x
1
h
0


  z
1


 x
0
h
2
 x
1
h
1

 x
2
h
0


  z
2


 x
1
h
2
 x
2
h
1


  z
3


 x
2
h
2
 z
4




10 5 0 5 10 15 20
0
0.6
1.2
.
Exemple
1
)
(
:
0 

 
b
b
k
x
k k
1
)
(
:
0 

 a
a
k
x
k k
x(k)
k
(entier)

10 5 0 5 10 15 20
0
0.6
1.2
.
Exemple
1
)
(
:
0 

 
b
b
k
x
k k
1
)
(
:
0 

 a
a
k
x
k k
1
)
(
0
0


 








k
k
k
k
k
k
z
b
z
a
z
X
convergence si
1
Re(z)
Im(z)
|a| 1/|b|
b
z
a /
1


séries géométriques
1
.
1
1
.
1
1
)
( 1




  z
b
z
a
z
X
(fractions rationnelles)
x(k)
k
(entier)
g
g
g
g
g
k
k









 1
1
1 3
2
0

a et b peuvent être complexes
 
1

g

34
exponentielle
divergente si a>1
1
Re(z)
Im(z)
|a|
1
;
.
1
1
)
( 1


 
z
z
a
z
H
0 50 100
0
0.5
1
a
t
t
a 0.98

0 50 100
0
5
10
a
t
t
a 1.02

0 50 100
0
0.5
1
a
t
t
a 0.5

0 50 100
1
0
1
a
t
t
a 0.95


)
(
:
0 k
a
k
h
k 


0
)
(
:
0 
 k
h
k
oscillations à
½ fréq. d’éch.
très amorti :
a proche de zéro
peu amorti
a proche de 1
a négatif
a > 1
Effet de la valeur de a

2
2
1
0
0
1
.
).
cos(
.
2
1
)
cos(
.
.
)
cos(
)
( 







z
a
z
a
z
a
z
H




0
0
0
pour
)
.
cos(
.
)
( 0




k
k
k
w
a
k
h k

20 0 20 40 60 80 100 120
1
0
1
.
fractions rationnelles : pôles et zéros
1
Re(z)
Im(z)
|a|
convergence si z
a 
racines du dénominateur et du numérateur
1

a
)
(k
h
k

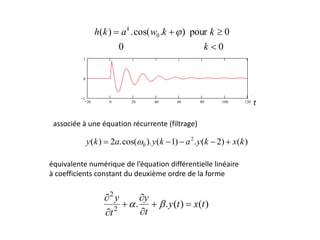
équivalente numérique de l’équation différentielle linéaire
à coefficients constant du deuxième ordre de la forme
)
(
)
(
.
.
2
2
t
x
t
y
t
y
t
y









20 0 20 40 60 80 100 120
1
0
1
.
0
0
0
pour
)
.
cos(
.
)
( 0




k
k
k
w
a
k
h k

associée à une équation récurrente (filtrage)
)
(
)
2
(
.
)
1
(
).
cos(
.
2
)
( 2
0 k
x
k
y
a
k
y
a
k
y 



 
t

37
Argument des pôles et fréquence des oscillations
1
Re(z)
Im(z)
1
Re(z)
Im(z)
Oscillations lentes
(basses fréquences)
Oscillations rapides
(hautes fréquences)
0 10 20 30 40 50 60 70 80 90 100
-2.0
-0.8
0.4
1.6
2.8
4.0
0 10 20 30 40 50 60 70 80 90 100
-3.0
-1.9
-0.8
0.3
1.4
2.5
2
2
1
0 .
).
cos(
.
2
1
1
)
( 




z
a
z
a
z
H

t t

38
Module des pôles et amortissement
pôles près du cercle de rayon 1
pôles proches de l’origine
1
Re(z)
Im(z)
|a|
1
Re(z)
Im(z)
|a|
Très oscillant
Très amorti
0 10 20 30 40 50 60 70 80 90 100
-1.2
-0.7
-0.2
0.3
0.8
1.3
0 10 20 30 40 50 60 70 80 90 100
-0.2
0.1
0.4
0.7
1.0
1.3
2
2
1
0 .
).
cos(
.
2
1
1
)
( 




z
a
z
a
z
H

t
t

39
Module des pôles et stabilité
pôles extérieurs au cercle 1
pôles intérieurs au cercle 1
1 Re(z)
Im(z)
|a|
1
Re(z)
Im(z)
|a|
instable (divergence)
stable (convergence)
0 50 100
1
0
1
a
t
cos 0.5 t

( )

t
a 0.95

0 50 100
20
0
20
a
t
cos 0.5 t

( )

t
a 1.03

2
2
1
0 .
).
cos(
.
2
1
1
)
( 




z
a
z
a
z
H

t t



 



autrement
k
pour
dz
z
j L
k
0
0
1
2
1 1

Inversion de la transformée en z
Pour inverser une transformée en z, on peut s’aider utilement du théorème de
Cauchy qui établit que

2
.
3
)
( 2



z
z
z
z
X

dz
z
z
X
j
k
x
L
k


 1
).
(
2
1
)
(

}
|
|
{
),
( 2
1 R
z
R
z
X 


0
2
1
)
(
1
|
|
)
(
)
,
)
(
(
Re
)
(
k
k
pour
R
a
que
tels
z
z
X
de
poles
a
a
z
z
X
s
k
x
j
k
j
z
X
poles
j
k



 


0
1
1
1
|
|
)
(
)
,
)
(
(
Re
)
(
k
k
pour
R
a
que
tels
z
z
X
de
poles
a
a
z
z
X
s
k
x
i
k
i
i
k


 



 
a
z
a
z
z
z
X
dz
d
q
r q
k
q
q
q



 


)
(
)
(
)!
1
(
1
lim 1
1
1
 
a
z
a
z
z
z
X
r k


 
)
(
)
(
lim 1
1

dans les cas simples : décomposition en fractions rationnelles
du premier degré : le signal x est une somme d’exponentielles
la transformée inverse d’un polynôme est une séquence de durée finie
1
.
1
1
)
( 


z
a
z
X 0
pour
)
( 
 k
a
k
x k
Attention au domaine de convergence !
alors
En traitement du signal ce domaine contient le cercle de rayon 1



C
k
dz
z
z
X
j
k
x 1
)
(
.
2
1
)
(

C contour dans le domaine de convergence : cercle de rayon 1
(expression donnant l’amplitude de l’harmonique d’une série de Fourier)
0
pour
0
)
( 
 k
k
x
(a peut être complexe)

Conversion d’un système analogique
• Méthode la plus « simple »
• Consiste à concevoir un système analogique et à le
convertir en numérique.
• Les deux méthodes les plus utilisés sont :
– L’invariance de la réponse impulsionnelle :
– La transformation :
  e
kT
t
t
h
k
h 

]
[
...
)
(
)
( 
 p
p
H
z
H

 Normalement
 On peut donc dériver H(z) de H(p) par la
transformation
 Cette transformation donne des équations compliquées
Méthode de la transformation
)
ln(
1
)
(
)
(
z
T
p
e
p
H
z
H


)
ln(
1
z
T
p
e
z
e
pTe




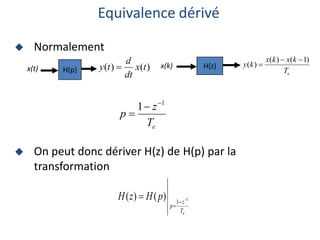
 Normalement
 On peut donc dériver H(z) de H(p) par la
transformation
Equivalence dérivé
e
T
z
p
p
H
z
H 1
1
)
(
)
( 



e
T
z
p
1
1 


x(t) H(p)
x(k) H(z)
)
(
)
( t
x
dt
d
t
y 
e
T
k
x
k
x
k
y
)
1
(
)
(
)
(




e
T
z
p
1
1 


)
Im(
)
Re(
)
Im(
1
)
Re(
1
1
1
)
Im(
)
Re(
z
J
z
z
J
z
T
z
z
T
p
J
p
e
e 






)
Im(
)
Re(
)
Im(
)
Re(
)
Im(
)
Re(
)
Im(
1
)
Re(
1
)
Im(
)
Re(
z
J
z
z
J
z
z
J
z
z
J
z
T
p
J
p
e 






)
(
Im
)
(
Re
)
Im(
)
(
Im
)
Re(
)
(
Re
1
)
Im(
)
Re( 2
2
2
2
z
z
z
J
z
z
z
T
p
J
p
e 





)
(
Im
)
(
Re
)
Im(
1
)
(
Im
)
(
Re
)
(
Im
)
Re(
)
(
Re
1
)
Im(
)
Re( 2
2
2
2
2
2
z
z
z
T
J
z
z
z
z
z
T
p
J
p
e
e 







4
1
)
(
Im
]
2
1
)
(
[Re
0
)
(
Im
4
1
4
1
)
Re(
)
(
Re
0
)
(
Im
)
Re(
)
(
Re
2
2
2
2
2
2











z
z
z
z
z
z
z
z
0
)
(
Im
)
(
Re
)
(
Im
)
Re(
)
(
Re
1
0
)
Re( 2
2
2
2






z
z
z
z
z
T
p
e
x
Im(z)
Re(z)
Im(p)
Re(p)
x
x
x
x

 Normalement
Equivalence intégration
x(t)
H(p)
x(k) H(z)



t
d
x
t
y 
)
(
)
(
?
)
( 
k
y

 Si , alors et jouent le même rôle
dans les domaines P et Z
 On peut donc dériver H(z) de H(p) par la transformation
 
 
 
  )
(
1
1
2
)
(
)
(
2
1
)
(
)
(
2
)
)
1
((
)
(
)
)
1
((
)
(
)
(
1
)
(
)
(
)
(
1
1
1
1
z
Y
z
z
T
z
S
z
Y
T
z
z
S
z
z
S
T
T
k
y
kT
y
T
k
S
kT
S
p
Y
p
p
S
d
y
t
S
e
e
e
e
e
e
e
t





















  

Méthode de la transformation bilinéaire
k-1 k t=kTe
y(t)
y((k-1)Te )
y(kTe )
S((k-1)Te )
p
1
1
1
e
z
1
z
1
2
T




)
kT
(
A
)
t
(
A e

1
1
1
1
2
)
(
)
(






z
z
T
p
e
p
H
z
H
 La transformation bilinéaire utilise l’approximation d’une surface continue par un
ensemble de surfaces trapézoïdales.

1
1
1
1
2





z
z
e
T
p
1
)
Im(
)
Re(
1
)
Im(
)
Re(
2
1
1
1
1
2
)
Im(
)
Re(












z
J
z
z
J
z
T
z
z
e
T
p
J
p
p
e
)
Im(
1
)
Re(
)
Im(
1
)
Re(
2
)
Im(
)
Re(
z
J
z
z
J
z
T
p
J
p
e 





))
Im(
1
)
(Re(
*
))
Im(
1
)
(Re(
))
Im(
1
)
(Re(
*
))
Im(
1
)
(Re(
2
)
Im(
)
Re(
z
J
z
z
J
z
z
J
z
z
J
z
T
p
J
p
e 









)
(
Im
)
1
)
(Re(
))
Im(
*
)
1
)
(Re(
)
Im(
*
)
1
)
(Re(
))
(
Im
1
)
(
(Re
2
)
Im(
)
Re( 2
2
2
2
z
z
z
z
z
z
J
z
z
T
p
J
p
e 










0
)
(
Im
)
1
)
(Re(
))
(
Im
1
)
(
(Re
2
0
)
Re( 2
2
2
2







z
z
z
z
T
p
e
0
))
(
Im
1
)
(
(Re 2
2


 z
z
1
)
(
Im
)
(
Re 2
2

 z
z
x
Re(z)
Im(p)
Re(p)
x
x
x
x
x
x
Im(z)
x

C L
R
x(t)
+
_ y(t)
1
.
.
.
)
(
)
(
2



p
RC
p
LC
p
RC
p
X
p
Y
Lp
1/cp

Analyse des signaux par transformée de
Fourier discrète (T.F.D)

Lien avec la transformée de Fourier
Lien avec la transformée de Laplace
l’intérieur du disque de rayon 1
se transforme dans le demi plan
partie réelle négative




/2
/2
/2
/2
3/4
3/4 /4
/4 /4
/4
fréq.
graduation linéaire en angle
du cercle de rayon un
correspond à une graduation
linéaire de l’axe des fréquences
Re(z)
Im(z)

f
j
p
e
z e
pT

2









k
k
z
k
x
z
X )
(
)
(
max
max
2
,
,
)
)(
(
)
( F
F
f
e
k
x
f
X
k
k
f
J


 






1
,
0
,
)
(
)
(
1
0
2


 



N
n
e
k
x
n
X
N
k
N
nk
J 
TFD

Exercice 1
Calculer la TFD de en fonction de X(n)
)
( 0
k
k
x 














1
2
0
)
(
2
0
1
)
(
N
k
N
pour
k
x
N
k
pour
k
x
Exercice 2
Calculer la TFD de :
1
,
0
,
)
(
1
)
(
1
0
2


 


N
k
e
n
X
N
k
y
N
n
N
nk
J 
Exercice 3
Calculer y(k) en fonction de x(k)

1
,
0
,
)
(
)
(
1
0
2


 



N
n
e
k
x
n
X
N
k
N
nk
J 
TFD
2
/
2
2
/
1
0
.
/
2
;
1
;
1
1
,
0
,
).
(
)
(
N
N
N
N
N
N
N
k
k
n
N
N
j
N
W
W
W
W
or
N
n
W
k
x
n
X
e
W
















 






























































1
3
2
1
0
1
1
1
3
1
2
1
1
3
9
6
3
1
2
4
4
2
1
3
2
1
3
2
1
0
1
1
1
1
1
1
1
1
1
N-
)
)(N-
(N-
N
)
(N-
N
)
(N-
N
N-
N
)
(N-
N
N
N
N
)
(N-
N
N
N
N
N-
N
N
N
N
N- x
:
x
x
x
x
W
..
W
W
W
:
::
:
:
:
:
W
..
W
W
W
W
..
W
W
W
W
..
W
W
W
..
X
:
X
X
X
X
x
X N
W

addition
N
N
tion
Multiplica
N
N
)
1
(
*
*


1
,
0
)
(
)
(
)
1
2
(
)
2
(
)
1
2
(
)
2
(
)
1
2
(
)
2
(
1
,
0
,
)
(
)
(
1
2
0
2
/
1
2
0
2
/
1
2
0
2
1
2
0
2
1
2
0
)
1
2
(
1
2
0
2
1
0
)
(







































N
n
n
X
W
n
X
W
k
x
W
W
k
x
W
k
x
W
W
k
x
W
k
x
W
k
x
N
n
W
k
x
X
n
X
i
n
N
p
N
k
nk
N
n
N
N
k
nk
N
N
k
k
n
N
n
N
N
k
k
n
N
N
k
k
n
N
N
k
k
n
N
N
k
nk
N
N
TFD

2
/
2
/
2
/
)
(
)
(
)
2
/
(
)
2
/
(
)
2
/
(
1
2
/
,
0
)
(
)
(
)
(
N
n
N
N
N
i
n
N
p
i
N
n
N
p
i
n
N
p
TFD
W
TFD
TFD
n
X
W
n
X
N
n
X
W
N
n
X
N
n
X
N
n
n
X
W
n
X
n
X















Filtrage numérique
filtre caractérisé par sa
réponse impulsionnelle
h(k)
Filtrage numérique = convolution discrète*
entrée
(signal
original)
x(k)
sortie
signal filtré
y(k)
y(k) = S h(j) x(k-j)
* filtrage analogique = équation différentielle linéaire
Filtre réel : sa réponse impulsionnelle h(k) est nulle pour les temps négatifs
( nécessité pour la programmation)

Filtrage (numérique) des Signaux
Résultat fondamental pour l’interprétation et
parfois pour l’implémentation
La transformée de Fourier (ou la transformée en z) Y(z)
d’une convolution y(k) de deux fonctions x(t) et h(k)
est le produit des transformées X(z) et H(z) de ces deux
fonctions
y(k) = Sh(j) x(k-j) Y(z)=H(z).X(z)
La transformée de Fourier de x(k)
est X(ei.) : valeur de X(z) pour z= ei.
Fourier / z
Y(ei.)=H(ei.).X(ei.)
 

k
k
z
k
h
z
H ).
(
)
(
transformée en z d’une convolution
~
produit de polynômes

Filtrage numérique
En général on se donne la réponse en fréquence du filtre
(par transformée de Fourier inverse
on obtient la réponse impulsionnelle b(k))




M
i
i
k
x
i
b
k
y
0
)
(
).
(
)
(
filtre à réponse impulsionnelle finie
Convolution = filtre à réponse impulsionnelle finie = filtre non récursif
La fonction de transfert B(z) est un polynôme
B(z)
x(k) y(k)




M
k
k
z
k
b
z
B
0
).
(
)
(
Schéma
Synthèse d’un filtre

synthèse des filtre numériques à réponse impulsionnelle finie

synthèse des filtre numériques
à réponse impulsionnelle finie
Filtre idéal réponse en fréquence (module et éventuellement phase)
« Gabarit » : tolérance
transformée de fourier inverse : réponse impulsionnelle
troncature dans le domaine temporel : modification de la réponse en fréquence
transformée de Fourier : vérification : est ce que le gabarit est respecté
Bande
passante
Bande
de
transition
Fréquence
de coupure
freq.
Bande
atténuée

Propriétés d’un filtre RIF
• Équation d’e/s :






1
0
)
(
)
(
N
i
i i
k
x
b
k
y
X(k) représente les valeurs successives du
signal d’entrée,
bi représente les coefficients de la fonction
de transfert du filtres,
Y(k) représente les valeurs successives du
signal de sortie,
N est le nombre de coefficients du filtre
(l’ordre).

Réponse en fréquence d’un filtre RIF
• La transformée en z de
 La fonction de réponse en fréquence du filtre est
obtenue en remplaçant z par ejTe :
  




1
0
)
(
N
k
k
z
k
h
z
H
    






1
0
)
(
N
k
T
jk
e
z
e
e
T
j e
k
h
H
z
H 








1
0
)
(
)
(
)
(
N
i
i
k
i
b
k
h 
est:

Structure des filtres numériques
• Structure non récursive
x(k)
x(k-1) x(k-M)
b(0) b(1) b(2) b(M-1) b(M)
y(k)
Z-1
Z-1
Z-1
)
(
)
(
)
1
(
)
1
(
)
(
)
0
(
)
( M
k
x
M
b
k
x
b
k
x
b
k
y 




 
• (M ) mémoires (tampon, tableau à M) éléments)
• (M) multiplieurs
• M-1 additionneurs

Propriétés d’un filtre RII
• Équation d’e/s :










1
1
1
0
)
(
)
(
)
(
)
(
)
(
N
i
M
j
i
k
y
i
a
j
k
x
j
b
k
y
X(k) représente les valeurs successives du signal d’entrée,
ai, bj représentent les coefficients de la fonction de
transfert du filtres,
Y(k) représente les valeurs successives du signal de sortie,
N, M représentent les ordres du numérateur et du
dénominateur de H(Z) (N est souvent appelé l’ordre
du filtre).

• Structure récursive
x(k)
x(k-1) x(k-M)
b(0) b(1) b(2) b(M-1) b(M)
Z-1
Z-1
Z-1
-a(N) -a(N-1) -a(N-2) -a(1)
y(k)
Z-1 Z-1 Z-1
)
(
)
(
)
1
(
)
1
(
)
(
)
(
)
1
(
)
1
(
)
(
)
0
(
)
(
N
k
y
N
a
k
y
a
M
k
x
M
b
k
x
b
k
x
b
k
y













• (M+N) mémoires
• (M+N) multiplieurs
• (M+N-1)additionneurs

• Structure cascade
– Décomposition en pôles et zéros




















 2
1
2
1
1
1
*
1
1
1
1
1
*
1
1
1
)
1
)(
1
(
)
1
(
)
1
)(
1
(
)
1
(
)
0
(
)
( P
i
i
i
P
i
i
Q
i
i
i
Q
i
i
z
p
z
p
z
s
z
z
z
z
z
r
b
z
H
Regroupement par paires de pôles et de zéros











N
k k
k
k
k
k
z
a
z
a
z
b
z
b
b
z
H
1
2
2
1
1
2
2
1
1
0
1
)
(
Cellule
2nd ordre
Cellule
2nd ordre
Cellule
2nd ordre

Réponse en fréquence d’un filtre RII
 La transformée z de
 La fonction de réponse en fréquence du filtre est
obtenue en remplaçant z by ejTe :
est :










1
1
1
0
)
(
)
(
)
(
M
j
j
N
i
i j
k
y
a
i
k
x
b
k
y
 









 1
1
1
0
1
M
j
j
j
N
i
i
i
z
a
z
b
z
H
 











 1
1
1
0
1
)
( M
J
T
jJ
J
N
i
T
ji
i
e
z
e
e
e
T
j
e
a
e
b
z
H
H





 Puisque e-j2k = 1, on a :
 La réponse en fréquence est périodique avec
période 2/Te dans le cercle de rayon unité. Si on
normalise Te à 1, on a
Propriétes de la réponse en fréquence
numérique
 


 H
T
k
2
H
e










   


 H
k
2
H 


Comparaison entre RII et RIF
RIF RII
 Stable par défaut
 Demande M>> 1 pour une bonne
performance
 Peut demander un temps de
calcul excessif
 Réponse en phase linéaire
 Ne possède pas d’équivalent
analogique stable
 La stabilité dépend de la position des
pôles de H(z)
 Peut donner une performance
adéquate pour N=1 ou 2
 Peut nuire à la performance
 Réponse en phase non linéaire en
général
 Cumulation d’erreur
  




1
0
)
(
M
k
k
z
k
h
z
H  









 1
1
1
0
1
N
j
j
j
M
i
i
i
z
a
z
b
z
H

Re(z)
t
x(t)
k
y(n)=x(k) pour n=k
signal à temps continu signal échantillonné

X()
transformée de Fourier

X()
périodisation
transformée en z
échantillonnage
X()= Y(ej
)
- 
- 
Im(z)
Y(z)
-

Y(z)
z=ej
enroulement sur le cercle 1
g
f

CTE: conversion du taux d'échantillonnage
systèmes multicadence: taux multiples d'échantillonnage
conversion du taux d'échantillonnage d'un signal discret  2 méthodes
filtrage multicadence.
1- signal discret par C N/A puis filtrage et C A/N  signal analogique au taux désiré
2-CTE en numérique

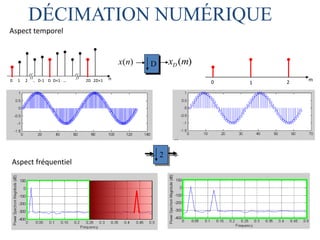
0 1 2 .. D-1 D D+1 … 2D 2D+1 n
( )
x n ( )
D
x m
D
DÉCIMATION NUMÉRIQUE
m
1
0 2
Aspect temporel
Aspect fréquentiel
2

CTE: filtrage linéaire
x(k) échantillonné à Fx=1/Tx et y(m) à Fy=1/Ty
en général: Fy/Fx=I/D rationnel
filtre linéaire temporellement variable de Repense Impulsionnel g(k, m)
CTE: y(m)  valeurs échantillonnées de x(n)
décalage temporel: filtre linéaire à phase linéaire et réponse en amplitude plate
2 taux différents: décalages variables dans le temps requis d'échantillons en échantillons
y(m)
taux Fy
x(k)
taux Fx
filtre linéaire g(k, m)

convertisseur de taux: filtres linéaires de mêmes réponses plate en amplitude avec
retards temporels différents
réduction de taux: décimation ( D) par entier D (sous-échantillonnage par D)
augmentation de taux: interpolation ( I)) par entier I (sur-échantillonnage par I)

Décimation par un facteur D.
x(k): spectre X(jx)) non nul sur 0≤≤ sous-échantillonné par entier D
(x: pulsation normée à Fx)  D
 sortie: version déformée de x(k) avec repliement Fx/2D
 réduction de BP de x(k) à max=/D avant sous-échantillonnage par D
x(k)
taux Fx
h(k) y(m)
taux Fy
décimateur D

x(k) dans filtre LP RI h(k) de réponse en fréquence idéale
filtre linéaire invariant puis sous-échantillonnage 
traitement total de x(k) temporellement variable








 
 w
D
ailleurs
D
w
pour
w
HD élimine
0
/
1
)
(





0
)
(
)
(
)
(
:
i
i
k
x
i
h
k
v
filtre
du
sortie








0
)
(
)
(
)
(
)
(
i
i
mD
x
i
h
mD
v
m
y
D

caractéristiques fréquentielles de y(m) à partir de x(k):


 




 


ailleurs
iD
k
pour
k
v
k
v
Dirac
de
peigne
e
D
k
p
avec
k
p
k
v
k
v
D
i
D
ik
j
0
)
(
)
(
'
)
(
1
)
(
)
(
)
(
)
(
'
1
0
2
-5
-4
-3
-2 -1
-6 -3 3
5
4
3
2
1
0
0
p(k)
v(k)
-6
k
k





















m
D
m
m
m
m
m
z
m
v
z
mD
v
z
m
y
z
Y
mD
v
m
y )
(
)
(
)
(
)
(
)
(
)
(

























 D
D
k
j
D
k
D
D
k
j
D
D z
e
X
z
e
H
D
z
Y
z
X
z
H
z
V
1
2
1
0
1
2
1
)
(
)
(
)
(
)
(


spectre de y(m): évaluation de Y(z) évalué sur z=1 taux de y(m): Fy
0≤x≤/D étiré à 0≤y≤ par sous-échantillonnage
x
y
x
x
x
y
y
y Dw
w
F
f
w
et
D
F
F
avec
F
f
w 





 2
2







 







 

 

 D
k
w
X
D
k
w
H
D
w
Y
spectre
y
D
k
y
D
y

 2
2
1
)
(
1
0

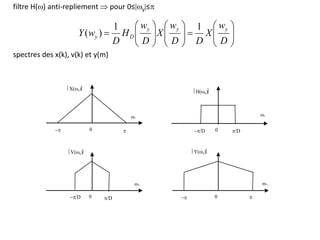
filtre H() anti-repliement  pour 0≤y≤
spectres des x(k), v(k) et y(m)


























D
w
X
D
D
w
X
D
w
H
D
w
Y
y
y
y
D
y
1
1
)
(
x
x
X(x)
H(x)
V(x) Y(y)
x y
0 0
0 0




/D
/D
/D
/D

Interpolation par un facteur I.
augmentation de taux par entier I: (I-1) échantillons nuls placés entre les valeurs successives
de x(k)
Fy=I Fx  y=x/I  X(x) et V(y)
)
(
0
...
2
,
,
0
)
(
)
( x
y F
I
F
taux
ailleurs
I
I
m
pour
I
m
x
m
v 









)
(
)
(
)
(
)
(
)
( I
w
X
w
V
z
X
z
m
x
z
V y
y
I
m
mI



 




x
x
X(x)
V(y)
0 0

 /I
/I 3/I
-3/I

augmentation du taux  spectre V(y) répétition I-périodique avec recouvrement de X(x)
seules fréquences de x(n) dans 0≤y≤/I recherchées 
 > y=/I: réjection par filtre LP idéal (C: facteur d'échelle)
C choisi tel que y(m)=x(m/I) en m=±kI


 


ailleurs
I
w
pour
C
w
H y
y
I
0
/
0
)
(



 


ailleurs
I
w
pour
I
w
CX
w
Y
sortie
de
spectre y
y
y
0
/
0
)
(
)
(
:

I
C
x
I
C
d
X
I
C
y
m
en x
x 



 

)
0
(
)
(
2
1
)
0
(
:
0






CTE par un facteur rationnel I/D.
CTE facteur I/D: cascade (I) - (D)
I puis D: préserve les caractéristiques spectrales désirées de x(n)
2 filtres de RI hu(k) et hd(k) de même taux IFx → filtre LP unique de RI h(k)
y(m)
taux
Fy=(I/D)Fx
x(k)
taux Fx
filtre hi(k) filtre hd(k)
interpolateur
taux I Fx
décimateur
D
I

H(v): inclut filtrage pour interpolation et décimation  caractéristique idéale
w(l)
v(k) y(m)
taux
Fy=(I/D)Fx
x(n)
taux Fx
interpolateur
I
décimateur
D
filtre LP h(l)
taux I Fx=Fv


 


ailleurs
I
D
w
pour
I
w
H v
v
0
)
/
,
/
min(
0
)
(




 




ailleurs
rI
k
pour
I
k
x
k
v
I
de
sortie
temporel
domaine
0
)
/
(
)
(
)
(
:

y(m): sous-échantillonnage de w(k) par un facteur D 
autre forme pour y(m) par changement de variable







r
r
x
rI
mD
h
mD
w
m
y )
(
)
(
)
(
)
(
  
 de
entière
partie
avec
k
I
mD
r 




























k
k
I
mD
x
kI
I
I
mD
mD
h
m
y )
(
)
(
)
(














k
I k
I
mD
x
mD
kI
h
m
y )
(
)
(
)
( )
(












r
r
r
x
rI
k
h
r
v
r
k
h
k
w )
(
)
(
)
(
)
(
)
(

y(m): x(n) filtré par RI g(k, m)=h(kI+(mD)(I))
h(k): RI d'un filtre LP invariant opérant à IFx
g(k, m+kI)= h(nI+(mD)(I))=g(k, m): I-périodique
sortie du filtre linéaire de RI h(k): spectre
spectre de y(m): décimation de v(n) par D 


 






ailleurs
I
D
w
pour
I
w
X
I
I
X
H
V v
v
v
v
v
0
)
/
,
/
min(
0
)
(
)
(
)
(
)
(







0
)
2
(
1
)
(
r
y
y
D
r
w
V
D
w
Y










ailleurs
I
D
w
pour
w
D
I
X
D
I
w
Y v
y
y
0
)
/
,
min(
0
)
(
)
(



Conception du filtre et implémentation d'une CTE.
Structures RIF directes.
réalisation directe: la plus simple mais très peu efficace
filtre LP à phase linéaire et ondulations en BP, atténuation en BA spécifiées





1
0
)
(
)
(
)
(
M
k
k
z
k
h
z
H
FT
et
k
h
RI
de
RIF
filtre

y(m)
x(n)
h(M-1)
h(M-2)
h(1)
h(2)
1

2 
3 
. 
. 
I 
interpolateur
décimateur
 D
z-1
z-1
z-1
h(0)

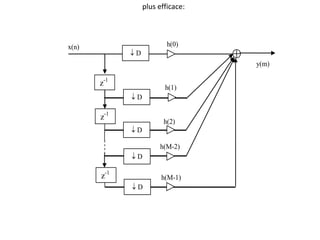
plus efficace:
y(m)
x(n)
h(M-1)
h(M-2)
h(1)
h(2)
z-1
z-1
z-1
h(0)
 D
 D
 D
 D
 D

produits et additions: taux Fx/D
réduction supplémentaire: exploitation des symétries de h(k)
y(m)
x(n)
h(M-1)
h(M-2)
h(1)
h(2)
z-1
z-1
z-1
h(0)
 D
 D
 D
 D
 D
z-1
 D
 D
 D
 D
 D
z-1
z-1
z-1
z-1

principal problème: calculs avec IFx
amélioration:
y(m)
x(n)
h(M-1)
h(M-2)
h(1)
h(2)
h(0)
 I
 I
 I
 I
 I
z-1
z-1
z-1
z-1

Structures de filtres polyphasés.
calculs efficaces: filtre RIF longueur M → filtres de longueur inférieure K=M/I entier
I précédent: seules K sorties parmi M entrées mémorisées multipliées par h(0), h(I), h(2I), ..,
h(M-I)
instant suivant: x(n) ≠0 qui coïncident multipliés par h(1), h(I+1), h(2I+1), .., h(M-I+1) etc. 
filtres plus petits: filtres polyphasés de RI unitaires pk(n)=h(k+nI)
 réseau des I filtres polyphasés en parallèle
sortie de chaque filtre sélectionnée par commutateur de rotation antihoraire en commençant
par m=0

filtres polyphasés: calculs à Fx et CTE par création de I échantillons de sortie
h(k) décomposé en I sous-filtres de RI pk(k): cohérent avec x(k) dans filtre linéaire périodique
temporellement variable de RI g(k,m)=h(nI+(mD)(I))
g(n, m) I-périodique  autre ensemble de coefficients utilisé pour générer les I échantillons de
y(m)
taux Fx
y(m)
taux Fy=I Fx




p0(k)
p1(k)
p2(k)
pI -1(k)
.
.
taux Fy=I Fx
x(k)
taux Fx

caractéristiques des filtres polyphasés: pk(k) à partir de h(k) par décimation de I  H()
plat dans 0/I 
filtres polyphasés à réponse à peu près plate dans 0
filtre polyphasé: I filtres reliés à une ligne à retard
k-ème filtre: décalage avance de (k/I)Tx par rapport à ordre 0
ordre 0 à retard nul: réponse en fréquence d'ordre k pk()=exp[jk/I]
combinaison des deux méthodes  sortie en décalage avant de (k+i/I)Tx par rapport
celle précédente





taux Fx
y(m)
taux Fy=Fx/D
p1(k)
p2(k)
.
.
x(k)
p0(k)
pI -1(k)
RI des filtres polyphasés: pk(k)=h(n+kD)
commutateur: sens antihoraire en débutant par p0(k)
paire équivalente de de commutateurs pour rotation horaire de RI
pk(k)=h(kI-n), n entre 0 et (I-1) (interpolateur)
pk(k)=h(kD-n), n entre 0 et (D-1) (décimateur)

Structures de filtres temporellement variables.
CTE (I/D): filtre linéaire temporellement variable
de RI g(n, m)=h(nI-(mD)(I))
h(n): RI d'un RIF LP de longueur M=KI
 ensemble des g(n, m) I-périodiques de K éléments

calculs dans y(m): traitement des blocs de données de
longueur K par K filtres de coefficients


















1
0
)
(
)
,
(
)
(
N
k
k
I
m
x
I
I
m
m
n
g
m
y


 


ailleurs
I
D
w
pour
I
w
H v
v
0
)
/
,
/
min(
0
)
(


)
,
( I
I
m
m
n
g 







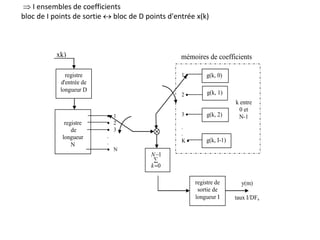
 I ensembles de coefficients
bloc de I points de sortie  bloc de D points d'entrée x(k)
xk) mémoires de coefficients
 1
 2
 3
.
.
 N
y(m)
taux I/DFx
g(k, 1)
g(k, 2)
g(k, 0)
registre
d'entrée de
longueur D
registre
de
longueur
N
1 
2 
3 
.
.
K  g(k, I-1)



1
0
N
k
registre de
sortie de
longueur I
k entre
0 et
N-1

décalage d'une mémoire d'entrée vers 2ième mémoire à un échantillon par période et (mD/I)
incrémentée de 1 par période
chaque sortie y(k): échantillons de 2ième mémoire multipliés par coefficients du filtre g(k, m)
K produits accumulés  y(k)  I sorties pour cette opération répétée avec nouvel ensemble
de D échantillons, etc.

g(K-1, l)
g(2, l)
g(1, l)
x(]mD/I-2)
x(]mD/I-K+1)
x(]mD/I-1)
x(k)
taux Fx
x(]mD/I)
y(m)
taux
(I/D)Fx
g(0, l)
z-1
l entre
0 et
I-1
D/I
z-1
z-1
D/I
D/I
D/I
autre méthode de calcul de la sortie du convertisseur de taux: filtre RIF à coefficients
périodiquement variables

x(k) dans registre à décalage à Fx de longueur L=M/I
échantillonneur couplant les taux entrée Fx et sortie Fy=(I/D)Fx  sortie d'échantillonneur aux
instants mD/I
mD/I entier: entrée d'échantillonneur modifiée  sortie: échantillonnage des nouvelles entrées
K sorties: g(n, m-(m/I)(I)) et produits résultants  y(m)
taux de sortie des échantillonneurs: Fy=(I/D)Fx
CTE de I/D réalisable par filtre polyphasé avec I sous-filtres
y(m) à partir du filtre k d'entrées x(n), x(n-1), .., x(n-K+1) dans ligne à retard: échantillon y(m+1)
issu du sous-filtre im+1 avec décalage de rm+1 nouveaux échantillons dans ligne à retard
avec im+1=(im+D)(I) et rm+1=(im+D)/I

Décimation et interpolation par conversion de fréquence.
équivalence entre SPB x(t) et représentation BF équivalente u(t): modification du taux
d'échantillonnage du signal après échantillonnage du SPB à Fx  conversion en BF puis CTE
sur signal BF
us(k)
uc(k)
filtre LP
filtre LP
oscillateur
cos 2fcn
sin 2fcn
x(k)
BP du
signal

décimation par D: filtre anti repliement devant D + filtre LP  filtre unique approchant
RI idéale







ailleurs
D
w
w
si
w
H
D
D
0
1
)
(

Applications de traitement multicadence du signal.
applications pratiques de traitement multicadence:
- conception de déphaseurs
- interfaçage de systèmes numériques à taux différents
- implémentation de filtres LP à bande étroite
- implémentation de bancs de filtres numériques
- codage sous-bande de signaux de parole
- filtres miroirs en quadrature
- transmultiplexeurs
- sur-échantillonnage dans les CA/N et CN/A

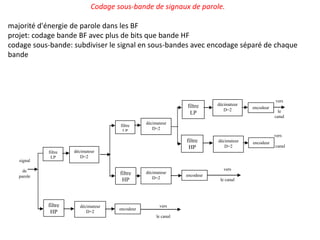
Codage sous-bande de signaux de parole.
majorité d'énergie de parole dans les BF
projet: codage bande BF avec plus de bits que bande HF
codage sous-bande: subdiviser le signal en sous-bandes avec encodage séparé de chaque
bande
vers
le
canal
filtre
LP
filtre
HP
filtre
LP
filtre
LP
encodeur
filtre
HP
signal
de
parole
vers
le canal
vers
le canal
vers
le canal
décimateur
D=2
décimateur
D=2
décimateur
D=2
décimateur
D=2
décimateur
D=2
décimateur
D=2
encodeur
encodeur
filtre
HP
encodeur

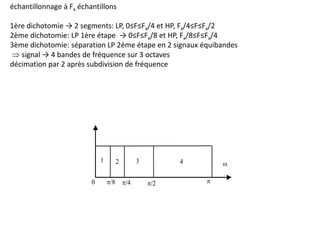
échantillonnage à Fx échantillons
1ère dichotomie → 2 segments: LP, 0≤F≤Fx/4 et HP, Fx/4≤F≤Fx/2
2ème dichotomie: LP 1ère étape → 0≤F≤Fx/8 et HP, Fx/8≤F≤Fx/4
3ème dichotomie: séparation LP 2éme étape en 2 signaux équibandes
 signal → 4 bandes de fréquence sur 3 octaves
décimation par 2 après subdivision de fréquence
/8 /4 /2 
2
1
0
3 4 

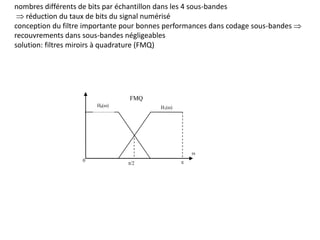
nombres différents de bits par échantillon dans les 4 sous-bandes
 réduction du taux de bits du signal numérisé
conception du filtre importante pour bonnes performances dans codage sous-bandes 
recouvrements dans sous-bandes négligeables
solution: filtres miroirs à quadrature (FMQ)
 
/2

H1()
H0()
FMQ

synthèse d'un signal encodé en sous-bandes: fondamentalement inverse de l'encodage 
signaux dans bandes de fréquences hautes et basses adjacentes interpolés, filtrés puis
combinés
paire de FMQ pour chaque octave du signal
+
-
sortie
décodeur
décodeur
décodeur
décodeur
filtre
filtre
filtre
filtre
 2
 2
 2
 2
 2
 2

autre utilisation de codage sous-bandes: compression de données en traitement d'image
combinaison du codage en sous-bandes avec quantification vectorielle pour chaque
signal en sous-bandes  images codées avec 1/2 bit/pixel contre 8 bits/pixel pour image
non codée
codage sous-bandes efficace pour compression de BP si énergie du signal concentrée
dans région particulière de la bande de fréquence

Transmultiplexeurs.
transmultiplexeurs: conversion de signaux multiplexés par division temporelle (TDM) en
division fréquentielle (FDM)
et vice-versa
TDM-FDM: entrée x(n)  signal multiplexé par division temporelle  L signaux sélectionnés
par commutateur
L signaux modulés par porteuses différentes  signal FDM
FDM-TDM: signal composite séparé par filtrage des L composantes multiplexées puis
division temporelle
téléphonie: transmission BLU avec canaux de largeur de 4 kHz 12 canaux réunis  canal de
base de 48 kHz
FDM avec largeur de bande plus grande: translation en fréquence dans bandes de
fréquence adjacentes de groupes multiples

conversion FDM-TDM: signal analogique FDM dans CA/N
.
.
.
.
signaux
TDM
s1(k)
signal
FDM
démodulateur
BLU
décimateur
C A/N
démodulateur
BLU
décimateur
démodulateur
BLU
décimateur
s2(k)
sN(k)

signal discret démodulé en bande de base par démodulateurs BLU
sortie des démodulateurs: décimateur puis commutateur TDM
FDM à 12 canaux échantillonnés à 96 kHz puis passés dans démodulateur à banc de
filtres
bloc de base du démodulateur FDM: convertisseur de fréquence + filtre LP + décimateur
cos(kk)
 D
 D
x(k)
-sin(kk)
filtre
LP h(k)
filtre
LP h(k)

conversion efficace de fréquence: filtre LP+décimateur implémentés par réseau
polyphasé
base pour FDM-TDM: analyseur à banc de filtres
dans chaque canal: largeur de bande 4 kHz et taux de Nyquist 8 kHz  sortie du filtre
polyphasé divisée par 12
 commutateur TDM à 12x8=96 kHz
conversion TDM-FDM: signal TDM sur 12 canaux démultiplexé en 12 signaux
individuels  signal dans chaque canal interpolé par 12 et fréquence convertie par un
modulateur BLU

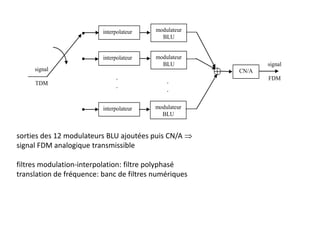
sorties des 12 modulateurs BLU ajoutées puis CN/A 
signal FDM analogique transmissible
filtres modulation-interpolation: filtre polyphasé
translation de fréquence: banc de filtres numériques
signal
TDM



signal
FDM
modulateur
BLU
.
.
.
CN/A
interpolateur
interpolateur
interpolateur
modulateur
BLU
modulateur
BLU
.
.
.

Etendue spectrales des signaux parole
• Etendue spectrale des signaux de parole: 20-12’000 Hz
• L’oreille humaine normale peut capter des signaux
acoustique entre 20 et 20’000 Hz.
• Transmission parole téléphonique: 300-3’400 Hz
(bonne compréhension du langage parlé)
• L’oreille a des caractéristiques perceptives spécifiques
=> psychoacoustique

Exemples d’echantillonage
Largeur de
bande de
transmission Dénomination
Echantillonnage=
nombre
d’echantillons
codées Qualité perçue
Débits en bps
avec 8bits par
ech.
20 - 22'000 Hz hi-fi (CD) 44'100 Hz pas de dégradation 352’000
20 - 12'000 bande “parole” 24’000 hz pas de dégradation 192’000
20 - 8’000 bande large 16'000 Hz idem 128’000
300 - 3'400 bande téléphonique 8'000 Hz dégradation 64’000

Schéma fonctionnel du codage-décodage par quantification scalaire
Convertisseur
A/D
Quantificateur
scalaire Q
Encodage
x(t) x[k] y[k]
c[k]
Décodage
y'[k]
c'[k]

Principe d’une analyse acoustique

Analyse de Fourier à fenêtre glissante

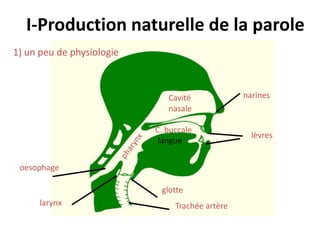
I-Production naturelle de la parole
1) un peu de physiologie
oesophage
Trachée artère
glotte
langue
narines
lèvres
Cavité
nasale
C. buccale
larynx

Le larynx :
- voisé ou non voisé
- fréquence fondamentale (pitch)
glotte
épiglotte
Cordes
vocales
muqueuse

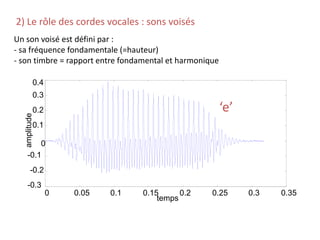
Un son voisé est défini par :
- sa fréquence fondamentale (=hauteur)
- son timbre = rapport entre fondamental et harmonique
2) Le rôle des cordes vocales : sons voisés
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
0.4
temps
amplitude
‘e’

Pharynx
Cavité
buccale
E
souffle
cordes
vocales
Cavité
nasale E
3) Représentation simplifiée :
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
-0.4
-0.2
0
0.2
0.4
0.6
temps
amplitude
b on j ou r

4) Les différents types de sons (phonèmes)
Les voyelles (voisées)
Orales
Nasales
cordes
vocales
Pharynx
Cavité
buccale E
souffle
Cavité
nasale E
cordes
vocales
Pharynx
Cavité
buccale E
souffle
[A, E, I, O, U, OU...]
[IN, UN, AN, ON]

Les consonnes
Liquides
Nasales
cordes
vocales
Pharynx
Cavité
buccale E
souffle
Cavité
nasale E
cordes
vocales
Pharynx
Cavité
buccale E
souffle
[R,L]
[M,N,GN]

Fricatives non voisées
Fricatives voisées
Pharynx
Cavité
buccale E
souffle
cordes
vocales
[F, S, CH]
[V, Z, J] Pharynx
Cavité
buccale E
souffle

0 10 20 30 40 50 60 70 80 90 100
-0.1
-0.05
0
0.05
0.1
t (ms)
[ch]
0 1 2 3 4 5 6 7 8 9 10
-20
-10
0
10
20
30
PSD [ch]
f (kHz)
(dB)

Occlusives non voisées
Occlusives voisées
Pharynx
Cavité
buccale E
souffle
cordes
vocales
[P, T, K]
[B, D, G] Pharynx
Cavité
buccale E
souffle
Cavité
nasale E

0 50 100 150
-1
-0.5
0
0.5
1
t (ms)
[bon]
0 50 100 150
-0.1
-0.05
0
0.05
0.1
t (ms)
[par]
[p]
[on]
[r]
[b]
[a]

Non stationnarité : le spectrogramme
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.4
-0.2
0
0.2
0.4
0.6
t (s)
bonjour
t (s)
f
(MHz)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.5
1
1.5
2

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-0.1
-0.05
0
0.05
0.1
t (s)
sachez parler
t (s)
f
(MHz)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
1
2
3
4

4° Masquage fréquentiel et temporel

Signal aléatoire :
Densité spectrale de puissance
Signal
Transformée de Fourier
Processus stationnaire, ergodique
Plusieurs réalisations,
Energie finie DSP=mean(TSF)

Processus gaussien non corrélé
Signal
Fourier
0
DSP

•source pour les sons non voisés

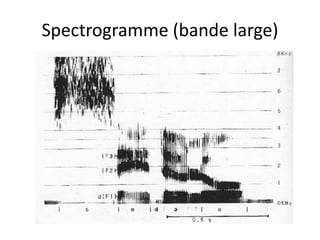
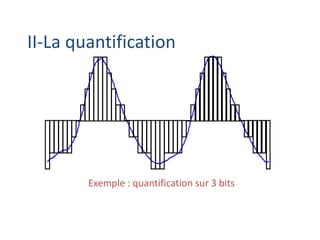
II-La quantification
Exemple : quantification sur 3 bits

•L’erreur de quantification : q(x)=Q(x)-x
- granulation : erreur liée au nombre de valeurs choisies (e
2)
- saturation : erreur liée au dépassement des seuils (d
2).
•signaux aléatoires
le signal de parole est considéré comme un signal aléatoire à
moyenne nulle et variance x
2.
l’erreur de quantification sera donc appelée bruit de
quantification, en général à moyenne nulle (0,e
2).
x(n) y(n)
+ +
q(n) q(n)

[sachez parler]
VS
-0.1 0 0.1
histogramme

•Rapport Signal-Bruit (RSB ou SNR)










 2
2
2
log
10
d
e
x
RSB


 [dB]
•facteur de charge G
G=xs/x
)
log(
20
77
.
4
02
.
6 G



 b
RSB

Analyse de la parole par prédiction linéaire
La méthode LPC est utilisée fréquemment pour l'analyse de la
parole (aussi nommé modélisation auto régressive AR)
• méthode rapide et simple pour estimer les caractéristiques
spectrales de la parole (estimation de l'enveloppe
spectrale)
• Hypothèse: un ech de parole peut être approximée par une
combinaison linéaire des échantillons précédents.
• s(n) = - ( a1s(n-1) +a2s(n-2) +….+ aps(n-p)) + e(n)
• les coeff ai sont supposés être constants durant la fenêtre
d’analyse.

Analyse par prédiction linéaire
Modélisation de la parole sous forme
d’un filtre de prédiction linéaire
Filtre de
prédiction linéaire
e(t) s(t)
)
(
)
(
0
t
e
i
t
s
a
p
i
i 





Analyse par prédiction linéaire
- Calcul de 11 coefficients de corrélation
sur une portion de 25 ms (200 échantillons)
- Application de l ’algorithme de Levinson
pour obtenir les coefficients du filtre récursif
(sous la forme d ’un filtre en treillis)
- Transmission des coefficients et du signal
résiduel (erreur de prédiction) au récepteur
qui en déduit la synthèse du signal
 


199
0
)
(
)
(
t
k k
t
x
t
x
r
10
1
)
10
(
)
1
(
1
1
)
(
1






z
a
z
a
z
A 

7.3 Propriétes de l'analyse LPC
Filtre inverse
optimisé
x[n]
u[n]
Filtre de synthèse
s[n]
erreur de prédiction
Bruit blanc de
variance unité

traitement-du-signal-avance.pptx

Contenu connexe

Tendances

Similaire à traitement-du-signal-avance.pptx

traitement-du-signal-avance.pptx