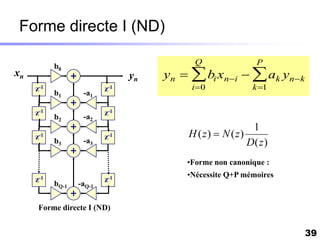
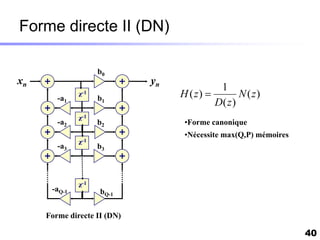
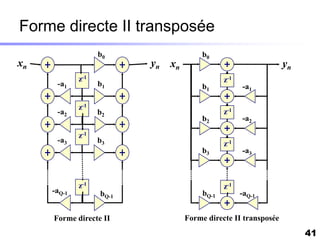
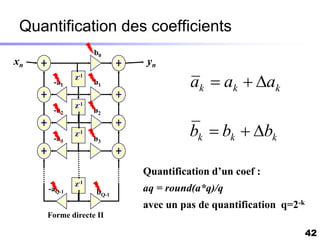
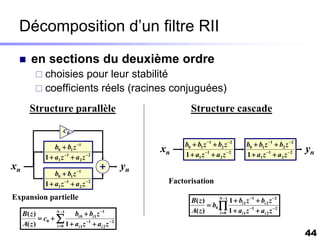
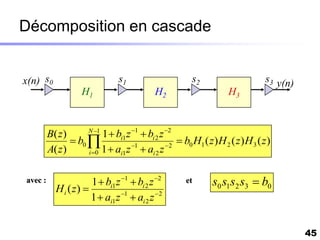
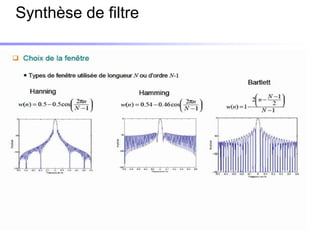
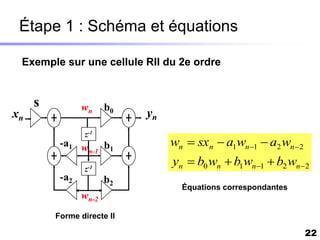
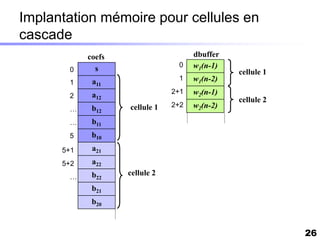
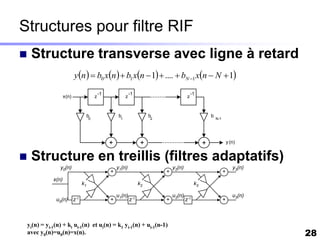
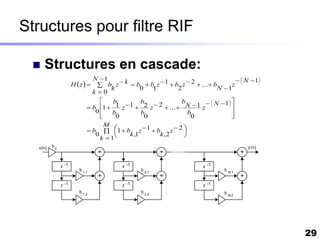
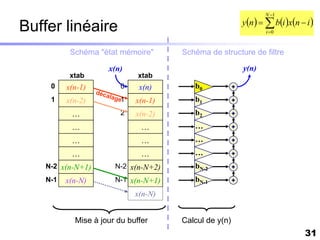
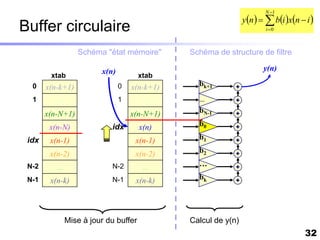
Le document traite du développement d'algorithmes pour des plateformes DSP, incluant la conception, la simulation et l'optimisation de filtres à travers divers langages de programmation et outils. Il aborde également les différentes bibliothèques et structures, ainsi que les méthodes d'implantation spécifiques à chaque type de filtre. Enfin, il met en évidence les caractéristiques des systèmes temps-réel et les étapes d'implémentation nécessaires pour les filtrages RIF et RII.














![Étape 3 : Format Qk et programme C
int coefs[6];
x(n) Q15 int dbuffer[2];
s Q15 int cellule(int x) {
ai Q15 int w;
int y;
bi Q15
/* Calcul */
wk Q15 w=((long)coefs[0]*x
+(long)coefs[1]*dbuffer[0]
–(long)coefs[2]*dbuffer[1]) >> 15;
y=((long)coefs[5]*w
+(long)coefs[4]*dbuffer[1]
Conversion algorithme (calcul sur des réels) +(long)coefs[3]*dbuffer[0]) >> 15;
vers programme (calcul en format Qk)
/* Mise à jour retards */
dbuffer[1]=dbuffer[0];
s*x dbuffer[0]=w;
devient
/* Sortie */
(coefs[0]*x)>>15 return y;
pour un résultat en Q15 }
24](https://image.slidesharecdn.com/chapitre3progdsplf3-120329172023-phpapp01/85/Chapitre3-prog-dsplf3-23-320.jpg)




![Exemple d’implémentation d’un filtre RIF en Q15
short fir_filter (short input)
{
int i;
short output;
int acc=0;
int prod;
R_in[0] = input; /* lire les valeurs des échantillons */
acc = 0; /* initialisation de l’acc à zéro*/
for (i=0; i<128; i++)
{
prod = (h[i]*R_in[i]); /* Q.15 */
acc = acc + prod; /* mise a jour des 32-bit de l’acc */
}
output = (short) (acc>>15); /* mise en forme de l’output (16-bits) */
for (i=127; i>0; i--) /* décalage des échantillons */
R_in[i]=R_in[i-1];
return output;
}](https://image.slidesharecdn.com/chapitre3progdsplf3-120329172023-phpapp01/85/Chapitre3-prog-dsplf3-34-320.jpg)