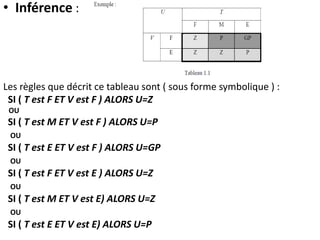
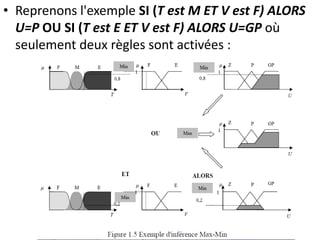
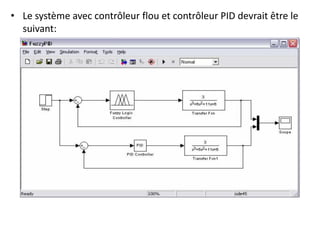
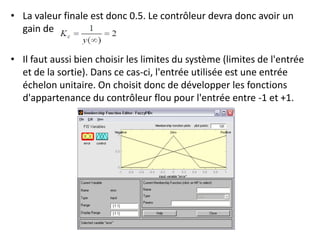
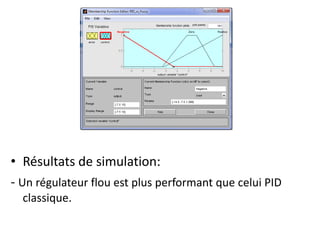
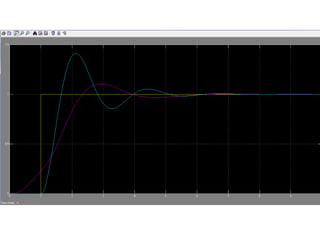
La logique floue, développée par Zadeh, permet de quantifier des notions imprécises comme la température à travers un degré d'appartenance variant entre 0 et 1. L'implication de Mamdani, utilisant une méthode d'inférence max-min, détermine des conclusions basées sur des règles définies par ces degrés d'appartenance. Des simulations montrent que les contrôleurs flous surpassent les contrôleurs PID classiques en termes de performance.

1. Logique floue
implication de Mamdani

2. • La logique floue repose sur la théorie des
ensembles flous développée par Zadeh [ZAD
65].
• A coté d'un formalisme mathématique fort
développé.

3. • Les notions de température moyenne ou de
courant faible sont relativement difficiles à
spécifier de manière précise.
• On peut définir le degré d'appartenance de la
variable température à l'ensemble "faible"
comme le "degré de vérité" de la proposition
"la température est faible".

4. • En logique booléenne, le degré
d'appartenance ( μ ) ne peut prendre que
deux valeurs ( 0 ou 1 ). La température peut
être :
• Elle ne peut pas s’appartenir à deux
ensembles ou plus à la fois.

5. • En logique floue, le degré d'appartenance
devient une fonction qui peut prendre une
valeur réelle comprise entre 0 et 1 inclus.
• Le degré d’appartenance permet de quantifier
le fait que la température puisse être
considérée comme moyenne.
• Dans ce cas, la température peut être
considérée, à la fois, comme faible avec un
degré d'appartenance de 0,2 et comme
moyenne avec un degré d'appartenance de 0,8
( figure 1.2 ).

6. • L'univers de discours est l'ensemble des
valeurs réelles que peut prendre la variable
floue x et μA(x) est le degré d'appartenance de
l'élément x à l'ensemble flou A ( figure 1.3 ).

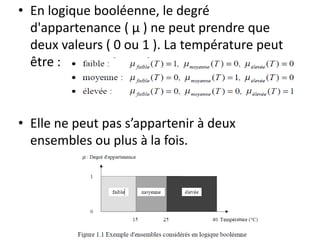
7. • Dans notre exemple, la variable floue est la
température, l'univers de discours est l'ensemble
des réels de l'intervalle [0, 40]. On attribue à
cette variable trois sous-ensembles flous: faible,
moyenne et élevée. Chacun est caractérisé par
sa fonction degré d'appartenance:

8. • On peut définir la fonction degré d'appartenance
μmoyenne sur tout l'univers de discours :

9. • Inférence :
Les règles que décrit ce tableau sont ( sous forme symbolique ) :
SI ( T est F ET V est F ) ALORS U=Z
OU
SI ( T est M ET V est F ) ALORS U=P
OU
SI ( T est E ET V est F ) ALORS U=GP
OU
SI ( T est F ET V est E ) ALORS U=Z
OU
SI ( T est M ET V est E) ALORS U=Z
OU
SI ( T est E ET V est E) ALORS U=P

10. Méthode d'inférence Max-Min
• Cette méthode réalise l'opérateur "ET" par la
fonction "Min", la conclusion "ALORS" de chaque
règle par la fonction "Min" et la liaison entre
toutes les règles (opérateur "OU") par la fonction
Max.
• La dénomination de cette méthode, dite Max-
Min ou "implication de Mamdani", est due à la
façon de réaliser les opérateurs ALORS et OU de
l'inférence.

11. • Reprenons l'exemple SI (T est M ET V est F) ALORS
U=P OU SI (T est E ET V est F) ALORS U=GP où
seulement deux règles sont activées :

12. Exemple d’application:
• Pour mieux illustrer le concept d'un contrôleur flou, on comparera
la performance d'un contrôleur PID classique avec le contrôleur
flou. Le système sous étude est le suivant:
• En utilisant les méthodes classiques, on trouve que le contrôleur
PID idéal a les valeurs suivantes:
• On utilisera la réponse à une entrée échelon du système avec PID
pour comparer la performance.

13. • Le système avec contrôleur flou et contrôleur PID devrait être le
suivant:

14. • Pour le système simple sous étude, on n’utilise que l'erreur
comme variable de contrôle.
• On a donc un système très simple, avec une entrée et une sortie.
Dans plusieurs systèmes flous, on utilise aussi la dérivée de
l'erreur, et on obtient alors un système à deux entrées, une sortie.
• Il faut utiliser un peu de jugement dans le design du contrôleur
flou. Il ne faut pas simplement créer des fonctions
d'appartenance de toute façon. Il faut quand même étudier le
système en détail.
• Une chose importante à remarquer est la valeur finale du système
en boucle ouverte. Ceci déterminera la sortie du contrôleur quand
l'erreur est nulle. Pour le système sous étude, la valeur finale due
à une entrée échelon unitaire est:

15. • La valeur finale est donc 0.5. Le contrôleur devra donc avoir un
gain de
• Il faut aussi bien choisir les limites du système (limites de l'entrée
et de la sortie). Dans ce cas-ci, l'entrée utilisée est une entrée
échelon unitaire. On choisit donc de développer les fonctions
d'appartenance du contrôleur flou pour l'entrée entre -1 et +1.

16. • Résultats de simulation:
- Un régulateur flou est plus performant que celui PID
classique.