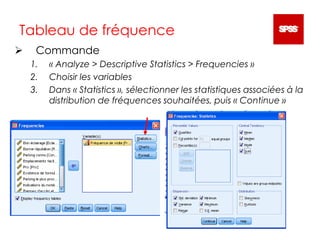
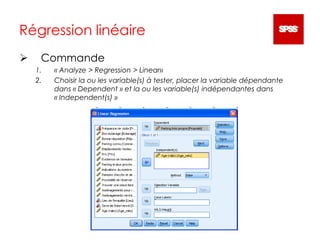
Ce document sert d'introduction à l'utilisation du logiciel PASW Statistics 18 pour l'analyse de données. Il couvre les manipulations de base, différentes analyses statistiques telles que l'analyse descriptive, les tests de moyenne, le chi-carré, l'ANOVA, la régression linéaire et la corrélation. Des instructions détaillées sur l'utilisation des commandes dans le logiciel sont fournies pour réaliser des études sur des variables qualitatives et quantitatives.

1. Initiation au logiciel PASW Statistics 18
Année académique 2011-2012
LSMS2000 : Etudes et modèles de marché
Virginie Bruneau
virginie.bruneau@uclouvain.be A217

2. 1. Où trouver ce logiciel?
a) Salles informatiques 3-4-5
Start > Programs > DOYENS Didactic Softwares > SPSS > PASW
Statistics 18
b) Sur votre ordinateur
demande de licence pour toute la durée de vos études
http://www.uclouvain.be/359151.html
Formulaire d’inscription + 20€ -> permanence SGSI

3. 2. Comment utiliser PASW Statistics 18?
1) Manipulations de base
2) Analyse d’1 variable
1) Tableau de fréquence
2) Analyse descriptive
3) Comparaison des moyennes sur 1 échantillon
3) Analyse de la relation entre 2 variables ou plus
1) Tableau croisé et chi-carré
2) Comparaison des moyennes
3) ANOVA
4) Régression linéaire
5) Corrélation

4. 1. Manipulations de base
a) Ouvrir un fichier SPSS
1. « File > Open > Data »
2. Chercher le fichier SPSS dans le répertoire
3. « open »

5. b) Variable view / data view
1. Data view: observations encodées par l’enquêteur
2. Variable view : « dictionnaire » de la data view
• Name
• Type : numeric ou string
• Label
• Values
• Measure: nominal, ordinal ou scale

6. c) Sauver un fichier SPSS
1. « File > Save as »
2. Choisir un répertoire
3. « Save »

7. Échantillon
unique
Variable
quali
Tableau
de
fréquence

8. 2) Analyse d’une variable
 Utilisation
 Variable qualitative
 Objectif: déterminer le nombre de réponses associées
aux différentes valeurs de la variable
Ex : A quelle fréquence les répondants viennent-ils en visite
dans le centre-ville?
1) Tableau de fréquence

9. Tableau de fréquence
 Commande
1. « Analyze > Descriptive Statistics > Frequencies »

10.  Commande
1. « Analyze > Descriptive Statistics > Frequencies »
2. Choisir les variables
Tableau de fréquence

11.  Commande
1. « Analyze > Descriptive Statistics > Frequencies »
2. Choisir les variables
3. Dans « Statistics », sélectionner les statistiques associées à la
distribution de fréquences souhaitées, puis « Continue »
Tableau de fréquence

12.  Commande
1. « Analyze > Descriptive Statistics > Frequencies »
2. Choisir les variables
3. Dans « Statistics », sélectionner les statistiques associées à la
distribution de fréquences souhaitées, puis « Continue »
4. Dans « Charts », choisir entre bar chart, pie chart et
histogram, puis « Continue »
5. « ok »
Tableau de fréquence

13.  Interprétation
Tableau de fréquence

14. Échantillon
unique
Variable
quali
Variable
quanti
Tableau
de
fréquence
Analyse
descriptive
et Test t

15. Analyse descriptive d’une variable
quantitative
 Faites le tableau des statistiques descriptives
des facteurs influençant le choix du parking
 Utilisation
 Variable(s) quantitative(s)
 Objectif : analyse des statistiques de base

16.  Commande
1. « Analyze > Descriptive Statistics > Descriptives »
Analyse descriptive

17.  Commande
1. « Analyze > Descriptive Statistics > Descriptives »
2. Choisir les variables
Analyse descriptive

18.  Commande
1. « Analyze > Descriptive Statistics > Descriptives »
2. Choisir les variables
3. Dans « Options », sélectionner les statistiques souhaitées,
puis « Continue »
4. « OK »
Analyse descriptive

19.  Interprétation
Analyse descriptive

20.  Est-ce les femmes attachent plus
d’importance au fait de trouver un place
de parking plus rapidement que les
hommes?
Analyse descriptive

21.  Commande
1. « Analyze > Descriptive Statistics > Explore »
Analyse descriptive

22.  Commande
1. « Analyze > Descriptive Statistics > Explore »
2. Choisir les variables à analyser et les placer dans
« Dependent List »
3. Choisir une variable de classement et la placer dans
« Factor List »
4. “ok”
Analyse descriptive

23.  Interprétation
Analyse descriptive

24. One-sample
 Utilisation
 Variable(s) quantitaive(s)
 Échantillon unique
 Objectif: juger une variable par rapport à une norme
connue ou fixée
Ex: L’importance moyenne accordée au prix est-elle égale
ou différente à 3?
Comparaison de moyennes

25. One-sample
 Commande
1. « Analyze > Compare means > One-sample T-test »
Comparaison de moyennes

26. One-sample
 Commande
1. « Analyze > Compare means > One-sample T-test »
2. Choisir la ou les variable(s) à tester, les placer « Test
variable(s) », noter la valeur de test dans « Test Value » et
cliquer sur « OK »
Comparaison de moyennes

27.  Interprétation
P-value < 0.025
Rejet H0 : l’importance moyenne accordée au prix
est différente de 3
Ho : µ = 3
Hi : µ ≠ 3
Comparaison de moyennes
(t-test) bilatéral
Rejet de

28. Test bilatéral
µ=3 3,41
Zone d’acceptationHo : µ = 3
Hi : µ ≠ 3
Test unilatéral
µ=3 3,41
Zone d’acceptation
Ho : µ ≥ 3
Hi : µ < 3
Zone de rejet
Zone de rejet
Ho : µ ≤ 3
Hi : µ > 3
Zone de rejet
p =1- sig(bilatérale)/2
p = sig(bilatérale)/2
µ=3 3,41
Zone d’acceptation
Zone de rejet

29.  Interprétation
P-value = 1- 0/2= 1 > 0.05
NON rejet de H0
Ho : µ ≥ 3
Hi : µ < 3
Comparaison de moyennes
(t-test) unilatéral

31. Échantillon
unique
Deux
échantillons
indépendants
Variable
quali
Variable
quanti
Tableau
de
fréquence
Analyse
descriptive
et Test t
X=quali
Y=quali
Relation de
dépendance
Test du
chi-
carré

32. Tableau croisé et Chi-carré
 Utilisation
 X : variable(s) qualitative(s) et Y : variable(s)
qualitative(s)
 Objectif: déterminer l’existence d’une dépendance
entre 2 variables en évaluant la signification statistique
(test chi-carré)
 Test d’hypothèse :
Ho : les proportions de tous les groupes sont égales (pas de
relation de dépendance)
Hi : il y a (au moins) 1 proportion qui est différente (relation
de dépendance)
Ex: La fréquence de visite est-elle en fonction du sexe?

33.  Commande
1. « Analyze > Descriptive Statistics > Crosstabs »
Tableau croisé et Chi-carré

34.  Commande
1. « Analyze > Descriptive Statistics > Crosstabs »
2. Placer une variable dans « Row » et une variable dans « Column »
Tableau croisé et Chi-carré

35.  Commande
1. « Analyze > Descriptive Statistics > Crosstabs »
2. Placer une variable dans « Row » et une variable dans « Column »
3. Dans « Statistics », sélectionner « Chi-square » et « Correlations », puis
“Continue”
Tableau croisé et Chi-carré

36.  Commande
1. « Analyze > Descriptive Statistics > Crosstabs »
2. Placer une variable dans « Row » et une variable dans « Column »
3. Dans « Statistics », sélectionner « Chi-square » et « Correlations », puis
“Continue”
4. Dans « Cells… », sélectionner « Counts Observed » et « Counts Expected »
ainsi que « Percentages in Row, Column and Total », puis « Continue »
5. « ok »
Tableau croisé et Chi-carré

37.  Interprétation Pourcentage ligne
Pourcentage colonne
Ho : pf = ph
Hi : pf ≠ ph
P-value > 0.05
On ne peut rejeter H0
Pas de relation de dépendance
Tableau croisé et Chi-carré

38. Échantillon
unique
Deux
échantillons
indépendants
Variable
quali
Variable
quanti
Tableau
de
fréquence
Analyse
descriptive
et Test t
X=quali
Y=quali
X=quali
Y=quanti
Relation de
dépendance
Test du
chi-
carré
Test t ou
ANOVA
(si + que 2
échantillons)

39. Comparaison des moyennes (t-test) sur
échantillons indépendants
Independent-samples
 Utilisation
 X : variable non métrique et Y : variable(s) métrique(s)
 2 échantillons indépendants
 Objectif: tester des hypothèses concernant des
paramètres relatifs à 2 populations différentes
Ex: Est-ce les hommes et les femmes accordent la même
importance au prix?

40. Comparaison de moyennes
Independent-samples
 Commande
1. « Analyze > Compare means > Independent-Samples T-test »

41. Comparaison de moyennes
Independent-samples
 Commande
1. « Analyze > Compare means > Independent-Samples T-test »
2. Choisir la ou les variable(s) à tester, les placer dans « Test variable(s) »et
placer la variable de catégorie dans « Grouping Variable »

42. Comparaison de moyennes
Independent-samples
 Commande
1. « Analyze > Compare means > Independent-Samples T-test »
2. Choisir la ou les variable(s) à tester, les placer dans « Test variable(s) »et
placer la variable de catégorie dans « Grouping Variable »
3. Définir des groupes pour cette « Grouping Variable » en cliquant sur
« Define Groups ». Noter 1 pour « Group1 » et 2 pour « Group2 »,
puis »Continue »
4. « ok »

43. Comparaison de moyennes
 Interprétation
P-value < 0.05
Rejet H0 : l’hypothèse d’égalité des variances
n’est pas respectée
P-value < 0.05
Rejet H0 : l’importance moyenne accordée au prix
diffère selon le sexe
Ho : µf = µg
Hi : µf ≠ µg
Ho : σ2
f = σ2
g
Hi : σ2
f ≠ σ2
g

44.  Utilisation
 X : variable qualitative et Y : quantitative
 Objectif: évaluer les écarts des valeurs moyennes d’une
variable dépendante sous l’effet d’une variable
indépendante contrôlée
 Test d’hypothèse:
Ho : la moyenne de tous les groupes est la même
Hi : il y a (au moins) 1 moyenne qui est différente
Ex: Est-ce que l’importance des aménagements pour
retrouver son véhicule rapidement diffère en fonction du
lieu de l’enquête ?
Analyse de la relation
entre 2 variables ou plus
ANOVA

45.  Commande
1. « Analyze > Compare means > One-way ANOVA».
ANOVA

46.  Commande
1. « Analyze > Compare means > One-way ANOVA».
2. Choisir les variables à tester , les placer dans « Dependent list » et placer
la variable de catégorie dans « Factor »
ANOVA

47.  Commande
1. « Analyze > Compare means > One-way ANOVA».
2. Choisir les variables à tester , les placer dans « Dependent list » et placer
la variable de catégorie dans « Factor »
3. Dans « Post Hoc… », sélectionner « Bonferroni », « Scheffe » et « Tukey »,
puis « Continue »
ANOVA

48.  Commande
1. « Analyze > Compare means > One-way ANOVA».
2. Choisir les variables à tester , les placer dans « Dependent list » et placer
la variable de catégorie dans « Factor »
3. Dans « Post Hoc… », sélectionner « Bonferroni », « Scheffe » et « Tukey »,
puis « Continue »
4. Dans « Options… », sélectionner « Descriptive », « Homogeneity of
variance test » et « Welch », puis « Continue ».
5. “ok”
ANOVA

49.  Interprétation
P-value > 0.05
Non rejet de H0 : l’hypothèse
d’homogénéité des variances est respectée
P-value < 0.05
Rejet H0 : l’importance accordée
aux aménagements diffère selon le lieu
de l’enquête
Ho : µLN = µN = µL
Hi : Ǝ au - 1 différence entre µLN µN et µL
Ho : σ2
f = σ2
g
Hi : σ2
f ≠ σ2
g
ANOVA

50.  Interprétation P-value < 0.05
Rejet H0 : les moyennes pour
Namur et Liège sont différentes
ANOVA

51. Échantillon
unique
Deux
échantillons
indépendants
Variable
quali
Variable
quanti
Tableau
de
fréquence
Analyse
descriptive
et Test t
X=quali
Y=quali
X=quanti
Y=quanti
X=quali
Y=quanti
Relation de
dépendance
Test du
chi-
carré
Test t ou
ANOVA
(si + que 2
échantillons)
Régression
linéaire

52. Régression linéaire
 Utilisation
 X : variable(s) quantitative(s) et Y : variable quantitative
 Objectif: analyser la relation de causalité entre une
variable dépendante et une ou plusieurs variables
indépendantes
Ex: Est-ce que l’importance accordée à un parking très
propre peut être expliqué en fonction de l’âge?
3) Analyse de la relation
entre 2 variables ou plus

53. Régression linéaire
 Commande
1. « Analyze > Regression > Linear»

54. Régression linéaire
 Commande
1. « Analyze > Regression > Linear»
2. Choisir la ou les variable(s) à tester, placer la variable dépendante
dans « Dependent » et la ou les variable(s) indépendantes dans
« Independent(s) »

55. Régression linéaire
 Commande
1. « Analyze > Regression > Linear»
2. Choisir la ou les variable(s) à tester, placer la variable dépendante dans
« Dependent » et la ou les variable(s) indépendantes dans « Independent(s) »
3. Dans « Statistics », sélectionner « Model fit », « collinearity diagnostics » « Estimates »
et « Confidence intervals » puis « Continue »
4. « ok »

56. Ho : R2 = 0
Hi : R2 ≠ 0
Régression linéaire
 Interprétation Proportion de la variable totale de Y
expliquée par la variation de X
P-value < 0.05
Rejet H0: Existence d’un
modèle de régression
linéaire
P-value < 0.05
Rejet H0 : β ≠ 0: La contribution
de l’âge est significative
Ho : β = 0
Hi : β ≠ 0
Parking très propre = 2,311 + 0,015 (Age)

57. Échantillon
unique
Deux
échantillons
indépendants
Variable
quali
Variable
quanti
Tableau
de
fréquence
Analyse
descriptive
et Test t
X=quali
Y=quali
X=quanti
Y=quanti
X=quali
Y=quanti
X=quanti
Y=quanti
Relation de
dépendance
Relation
d’association
Test du
chi-
carré
Test t ou
ANOVA
(si + que 2
échantillons)
Régression
linéaire
Corrélation

58. Corrélation
 Utilisation
 Variables quantitatives
 Pas de relation de dépendance entre les 2 variables
 Objectif: analyser le degré d’association linéaire entre 2
variables
Ex: Y a-t-il une corrélation entre le bon éclairage, la bonne
réputation, le parking connu, les emplacements faciles
au niveau des manœuvres et le prix?

59. Corrélation
 Commande
1. « Analyze > Correlate > Bivariate»
2. Choisir la ou les variable(s) à tester
3. « OK »

60. Corrélation
 Interprétation
P-value < 0.05
=> Rejet H0: corrélation significative
P-value > 0.05
=> Non rejet de H0 : corrélation non significative
Ho : ρ = 0
Hi : ρ ≠ 0

61. Échantillon
unique
Deux
échantillons
indépendants
Variable
quali
Variable
quanti
Tableau
de
fréquence
Analyse
descriptive
et Test t
X=quali
Y=quali
X=quanti
Y=quanti
X=quali
Y=quanti
X=quanti
Y=quanti
Relation de
dépendance
Relation
d’association
Test du
chi-
carré
Test t ou
ANOVA
(si + que 2
échantillons)
Régression
linéaire
Corrélation

62. Exercices
1. Quel est le pourcentage de la population qui fréquente les
parkings environ 1 fois par quinzaine?
2. Quelle est l’importance moyenne accordée par la population à la
bonne réputation des parkings?
3. Quelle est l’importance moyenne accordée par les femmes à la
bonne réputation des parkings?
4. L’importance moyenne accordée à la bonne réputation des
parkings diffère-t-elle selon le sexe?
5. La fréquentation des parkings diffère-t-elle selon le sexe?
6. L’importance moyenne accordée au bon éclairage des parkings
est-elle différente de 3?
7. L’importance moyenne accordée à la bonne réputation des
parkings diffère-t-elle selon le lieu de l’enquête?
8. L’importance accordée à la bonne réputation des parkings et au
bon éclairage sont-elles corrélées?
9. L’âge peut-il expliquer la variation de l’importance accordée à la
bonne réputation des parkings?