Codage
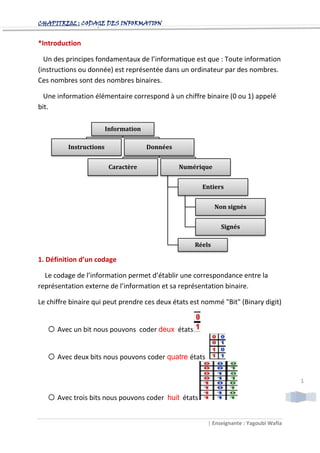
- 1. CHAPITRE02 : CODAGE DES INFORMATION *Introduction Un des principes fondamentaux de l’informatique est que : Toute information (instructions ou donnée) est représentée dans un ordinateur par des nombres. Ces nombres sont des nombres binaires. Une information élémentaire correspond à un chiffre binaire (0 ou 1) appelé bit. Information Instructions Données Caractère Numérique Entiers Non signés Signés Réels 1. Définition d’un codage Le codage de l’information permet d’établir une correspondance entre la représentation externe de l’information et sa représentation binaire. Le chiffre binaire qui peut prendre ces deux états est nommé "Bit" (Binary digit) o Avec un bit nous pouvons coder deux états o Avec deux bits nous pouvons coder quatre états 1 o Avec trois bits nous pouvons coder huit états | Enseignante : Yagoubi Wafia
- 2. CHAPITRE02 : CODAGE DES INFORMATION o A chaque nouveau bit, le nombre de combinaisons possibles est doublé. o Ce nombre est égal à 2 puissances N (N étant le nombre de bits). o Un groupe de bits est appelé un mot, un mot de huit bits est nommé un octet (byte). o Avec un octet, nous pouvons écrire 2 puissance 8 = 256 nombres binaires de 0 à 25 * Description d'un octet 2. Bases de numération 2.1. Système décimal Dix chiffres différents de 0 à 9 pour écrire tous les nombres. Soit un nombre décimal N = 2348. Ce nombre est la somme de 8 unités, 4 dizaines, 3 centaines et 2 milliers. Nous pouvons écrire N = (2 x 103) + (3 x 102) + (4 x 101) + (8 x 100) 10 représente la base et les puissances de 0 à 3 le rang de chaque chiffre 2.2. Système binaire Dans les domaines de l'automatisme, de l'électronique et de l'informatique, nous utilisons la base 2 (0 et 1) Un interrupteur est ouvert ou fermé 2 Une diode est allumée ou éteinte ‰ Une tension est présente ou absente | Enseignante : Yagoubi Wafia
- 3. CHAPITRE02 : CODAGE DES INFORMATION Un champ magnétique est orienté Nord-Sud ou Sud-Nord (disque dur) 2.2.1. Correspondance entre binaire et décimal Conversion d'un nombre binaire en décimal Il suffit donc de faire la somme des poids de chaque bit à 1 .Le nombre ci dessus est égal à 64 + 4 + 1 = 69 2.2.2. Conversion d'un nombre décimal (entier) en binaire Exemple : Conversion d'un nombre décimal en binaire (exemple : N = 172) A. Méthode par soustraction B. Méthode par divisions 3 | Enseignante : Yagoubi Wafia
- 4. CHAPITRE02 : CODAGE DES INFORMATION 2.3. Système hexadécimal Ce système qui emploie seize chiffres est à base 16 ; donc, aux dix chiffres décimaux que nous connaissons, il faut ajouter six lettres : {A, B, C, D, E, F} On attribue à ces caractères alphabétiques les valeurs suivantes, exprimées en nombres décimaux : A = 10 ; B = 11 ; C = 12 ; D = 13 ; E = 14 ; F = 15. Les poids associés aux chiffres hexadécimaux sont des puissances de 16. Exemple : E1A3D = (E x 164) + (1 x 163) + (A x 162) + (3 x 161) + (D x 160) Comme précédemment, on peut également faire un autre genre de lecture, en faisant les calculs avec des nombres décimaux : E x 16 = 14 x 16 = 224 ; 224 + 1 = 225 225 x 16 = 3 600 ; 3 600 + A = 3 600 + 10 = 3 610 3 610 x 16 = 57 760 ; 57 760 + 3 = 57 763 57 763 x 16 = 924 208 ; 924 208 + D = 924 208 + 13 = 924 221 E1A3D en hexadécimal est donc égal à 924 221 en décimal. 4 | Enseignante : Yagoubi Wafia
- 5. CHAPITRE02 : CODAGE DES INFORMATION Les règles sont ici aussi les mêmes que pour le décimal. Exercice Donnez la méthode pour passer de la base décimale a la base hexadécimale (dans les deux sens). Exercice De décimal en hexadécimal Le principe est le même que le schéma du cours, mais en divisant par 16 au lieu de 2. Ainsi 2010 en base 10 s'écrit 7DA en base 16 (Rappelons que A=10 et D=13). D'hexadécimal en décimal 163 162 161 160 A 4 0 F 2. 4. Système octal Dans ce système octal, la représentation des nombres est faite par une succession de groupes de chiffres, choisis dans les huit premiers décimaux (entre 0 et 7). La base est 8 . On pourra donc décomposer un nombre octal, par exemple 3 476, de la façon suivante : 3 476 = (3 x 83) + (4 x 82) + (7 x 81) + (6 x 80) 5 De plus, on peut faire les calculs avec des nombres décimaux et en employant la méthode décrite précédemment pour les nombres décimaux : 3x8= 24 ; 24 + 4 = 28 | Enseignante : Yagoubi Wafia
- 6. CHAPITRE02 : CODAGE DES INFORMATION 28 x 8 = 224 ; 224 + 7 = 231 231 x 8 = 1 848 ; 1 848 + 6 = 1 854 Le nombre octal 3 476 correspond donc au nombre décimal 1 854. 1. 5. - NOTATIONS DES SYSTÈMES NUMÉRIQUES Par exemple, le nombre décimal 318 se représente ainsi : - 100111110 dans le système binaire, - 476 dans le système octal, - 13E dans le système hexadécimal. Pour reconnaître immédiatement le système numérique choisi dans l'écriture d'un nombre, on note en indice et en décimal la base correspondante du système. Exemple : 31810 = 1001111102 = 4768 = 13E16 On utilise aussi en indice la lettre H (hexadécimal) à la place de 16 ; il revient donc au même d'écrire : 13E16 ou 13EH. 2. - CONVERSIONS ENTRE SYSTÈMES NUMÉRIQUES Convertir un nombre écrit dans un système numérique en un autre signifie qu'il faut trouver la disposition correspondante des chiffres propre au nouveau système. On suppose, par exemple, vouloir convertir le nombre décimal 123 dans les trois systèmes (binaire, octal, hexadécimal). La conversion complète de 123 en forme binaire est la suivante : 6 Voici un exemple de vérification pour la deuxième conversion : | Enseignante : Yagoubi Wafia
- 7. CHAPITRE02 : CODAGE DES INFORMATION 1x2= 2 ; 2+1= 3 3x2= 6 ; 6+0= 6 6 x 2 = 12 ; 12 + 1 = 13 13 x 2 = 26 ; 26 + 1 = 27 27 x 2 = 54 ; 54 + 0 = 54 54 x 2 = 108 ; 108 + 1 = 109 109 x 2 = 218 ; 218 + 0 = 218 Le nombre 218 est justement le nombre recherché. Voyons maintenant la conversion, en système octal, du nombre décimal 123 du premier exemple. Le procédé à suivre est toujours le même ; seule la base du nouveau système diffère : Si, par contre, on veut représenter 123 en notation hexadécimale, on divisera successivement le nombre par 16 : 2. 1. - CONVERSIONS ENTRE SYSTÈME BINAIRE ET SYSTÈME OCTAL OU HEXADÉCIMAL ET VICE VERSA Voyons d'abord la conversion dans le système octal. Un nombre binaire peut être converti en octal en appliquant la règle suivante : - en partant de la droite, on divise le nombre binaire par groupes de 3 bits, dits triplets, en ajoutant éventuellement des zéros à gauche pour compléter le triplet de gauche. - on écrit, pour chaque triplet, la valeur en chiffres octaux. 7 - en mettant ces chiffres l'un à côté de l'autre, dans le même ordre, on obtient le nombre octal recherché. Exemple : | Enseignante : Yagoubi Wafia
- 8. CHAPITRE02 : CODAGE DES INFORMATION Transformons en octal le nombre binaire 10 101 001 110 100. La règle de conversion de binaire en octal est un cas particulier qui s'étend à tous les systèmes numériques ayant comme base une puissance de 2. Par exemple, cette règle peut être valable pour le système à base 4 égale à 22, le système octal égal à 23 et le système hexadécimal égal à 24. La règle générale de conversion est la suivante : - en allant de droite à gauche, diviser l'expression binaire en groupes de chiffres, le nombre de ces derniers étant égal à l'exposant de la puissance de 2 caractérisant la base dans laquelle on fait cette conversion. - pour chaque groupe, écrire par ordre la valeur numérique, en utilisant le chiffre approprié du nouveau système. Exemple : Transformons en hexadécimal le nombre binaire de l'exemple précédent. Pour le système hexadécimal, la base étant 16, on divise le nombre binaire en groupes de 4 bits (24 = 16) : Observons maintenant les conversions d'octal et hexadécimal en binaire. Il s'agit là d'opérations inverses, basées sur les mêmes correspondances entre chiffres hexadécimaux et quartets binaires d'une part, puis chiffres octaux et triplets binaires d'autre part (figure 1). 8 | Enseignante : Yagoubi Wafia
- 9. CHAPITRE02 : CODAGE DES INFORMATION Exemples : - Le nombre octal 7336 est converti en binaire de la façon suivante : - Le nombre hexadécimal AA1B est converti en binaire de la façon suivante : 9 2. 2. - NOMBRES FRACTIONNAIRES Pour représenter un nombre fractionnaire, on utilise encore la méthode qui consiste à attribuer à chaque chiffre un poids approprié, en rapport avec la position occupée par ce | Enseignante : Yagoubi Wafia
- 10. CHAPITRE02 : CODAGE DES INFORMATION même chiffre à l'intérieur du nombre écrit. On affecte aux chiffres qui précèdent la virgule les mêmes poids que l'on aurait dans le cas d'un nombre entier ; par contre, on attribue aux chiffres qui suivent la virgule, des poids constitués de puissances aux exposants négatifs, de valeur absolue croissante, en allant vers la droite. Par exemple, le nombre 512,374 doit être défini de la façon suivante : La lecture d'un nombre fractionnaire se fait en deux temps, en utilisant toujours le même procédé. D'abord, on lit la partie entière comme s'il s'agissait d'un nombre entier ; ensuite, on s'occupe de la partie fractionnaire comme pour la précédente mais en ayant toujours à l'esprit qu'elle vient après la virgule. En reprenant le nombre de l'exemple précédent, on en fait la lecture de la façon suivante : On pourrait maintenant étendre ces mêmes observations au système binaire, octal ou hexadécimal et, par conséquent, traiter les conversions des nombres fractionnaires d'un système à l'autre. Un tel travail pourrait être intéressant comme exercice d'arithmétique mais nous nous en tiendrons là sachant qu'un nombre fractionnaire peut être considéré par l'ordinateur comme une union de deux entiers : le premier qui précède la virgule et qui représente une quantité d'unités ; le second qui suit la virgule et qui représente une fraction de ces mêmes unités. Les règles des nombres entiers sont donc suffisantes. 2. 3. - CODE BCD (Binary Coded Decimal) La codification BCD d'un chiffre décimal n'est rien d'autre qu'une substitution de ce chiffre par un groupe de quatre chiffres binaires. Ces derniers sont plus que suffisants pour coder 10 les chiffres décimaux de «0» jusqu'à «9» donc, six des seize codes possibles ne seront pas utilisés dans la représentation BCD (voir le tableau de la figure 2). | Enseignante : Yagoubi Wafia
- 11. CHAPITRE02 : CODAGE DES INFORMATION Prenons comme exemple la conversion du nombre 146 en code BCD, défini selon les correspondances de la figure 2. 11 | Enseignante : Yagoubi Wafia
