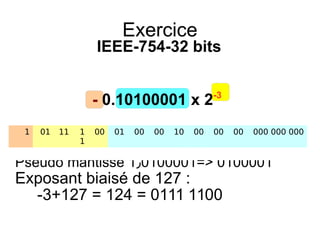
Le document explique la représentation et la conversion des nombres réels en systèmes binaire et décimal, en se concentrant sur les méthodes de conversion des parties entière et fractionnaire. Il aborde également la représentation en virgule fixe et flottante, ainsi que les normes IEEE-754 pour les nombres à virgule flottante. Des exercices sont fournis pour illustrer les conversions et les représentations des nombres en binaire et en décimal.

1. Codage et représetation de
l'information
Taha Zerrouki
MI, semestre 1
• Université de Bouira

2. Programme
• Représentation des nombres réels

3. Les nombres réels
‫الحقيقية‬ ‫الدعداد‬

4. Les nombre réels
•Nombres en virgule fixe
•Nombres en virgule flottantes

5. Un nombre réel
Un nombre réel est constitué de deux partie
15,125
Partie entière, partie décimale

6. Conversion d'un réel en binaire
Partie entière => binaire (division)
Partie fractionnaire en binaire ( multiplication)

7. Conversion d'un réel en binaire
15٫25 => ()2
15 = (1111)2
0٫25 = ( ????)2

8. Partie fractionnaire en binaire
0٫25 * 2 = 0٫5
0٫5 * 2 = 1٫0
0٫0 *2
0٫25 = (0٫01)2

9. Partie fractionnaire en binaire
Exemple 2
0٫625 * 2 = 1٫25
On prend la partie fractionnaire
0٫25 * 2 = 0٫5
0٫5 *2 = 1٫0
0٫0 *2
0٫625 = (0٫101)2

10. Exercice
Convertir en binaire le nombre
17٫325 = ()2

11. Solution
17٫325 = ()2
17 = (10001)2
0٫325 *2 = 0٫65
0٫65 *2 = 1٫3
0٫3 *2 = 0٫6
0٫6
0٫325= (0٫011)2
17٫325 = (10001٫011)2

12. Conversion d'un réel binaire en
décimal
Développement polynomial

13. Binaire en décimal
(101٫01 )2
= ()10
(101٫01 )2
= 1x22
+0x21
+1x20
+0x2-1
+1x2-2
= 4 + 0 +1 + 0 + 0٫25
= 5٫25
22
21
20
2-1
2-2
1 0 1 0 1

14. Exercice
Convertir en binaire le nombre
(10٫101)2
= ()10

15. Binaire en décimal
(10,101 )2
= ()10
(101٫01 )2
= 1x21
+0x20
+1x2-1
+0x2-2
+1x2-3
= 2 + 0 +1/2 + 0 + 1/8
= 2٫125
21
20
2-1
2-2
2-3
1 0 1 0 1

16. Représentation des nombres réels

17. Un nombre réel
Un nombre réel est constitué de deux partie
‫ودعشري‬ ‫صحيح‬ :‫قسمين‬ ‫من‬ ‫مكون‬ ‫الحقيقي‬ ‫العدد‬
15,125
Partie entière, partie décimale

18. Représentation ‫تمثيل‬
10001٫011
• Virgule fixe ‫الثابتة‬ ‫الفاصلة‬
• Virgule flottante ‫المتحركة‬ ‫الفاصلة‬

19. Virgule fixe
10001٫011
1 0 0 0 1 0 1 1 0 0
entière fractionnaire

20. Virgule flottante‫المتحركة‬ ‫الفاصلة‬
Un nombre réel peut être écrit sous la forme
N= ± M * b e
M : mantisse , ‫العشري‬ ‫القسم‬
b : la base , ‫الاساس‬
e : l’exposant ‫الس‬
1.60217657x10-19
-

21. Virgule flottante
N= ± M * b e
M : mantisse normalisé , ‫ودحد‬‫و‬ ‫م‬ ‫العشري‬ ‫القسم‬
-0.160217657x10-20
Remarque :
on dit que la mantisse est normalisée si le premier chiffre
après la virgule est différent de 0 et le premier chiffre avant
la virgule est égale à 0.

22. Virgule flottante en binaire
N = ± M * b e
M : mantisse normalisé , ‫ودحد‬‫و‬ ‫م‬ ‫العشري‬ ‫القسم‬
-101٫00001= - 0.10100001 x 23

23. Exercice
Ecrire les nombres suivant en VF
+101٫100001
-0٫00000011

24. Solution
Ecrire les nombres suivant en VF
+101٫100001 = + 0٫101100001 x 23
-0٫00000011 = - 0٫11 x 2-7

25. Représentation de VF
N = ± M * b e
- 0.10100001 x 23
1bit P bits M bits
Bit de signe exposant La mantisse normalisée

26. Exercice
Représenter le nombre
- 0.10100001 x 23
1bit 5 bits 10 bits

27. Solution
Représenter le nombre
- 0.10100001 x 23
1 0 0 0 0 1 1 1 0 0 0 0 1 0 0 0
1bi
t
5 bits 10 bits

28. Exercice
Représenter le nombre
- 0.10100001 x 2-3
1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0
1bi
t
5 bits 10 bits

29. Solution
Représenter le nombre
- 0.10100001 x 2-3
1 1 1 1 1 0 1 1 0 0 0 0 1 0 0 0
1bi
t
5 bits (CA2) 10 bits

30. Représentation de l'exposant
‫الس‬ ‫تمثيل‬
1- complément à 2 ‫إلى‬ ‫المتمم‬
2- exposant biaisé ‫المزيد‬ ‫الس‬

31. Représentation de l'exposant
Sur p bits de l'exposant on ajout
2p-1
-1
Example : sur 4 bits
Le biais est 24-1
-1 =23
-1 = 7
Exposant 5 = 5+7 =12 = 1100
Exposant -6 = -6+7 =1 = 0001

32. Exercice
Exemple : sur 8 bits
Représenter les exposants biaisés
3, -3

33. Solution
Example : sur 8 bits
Le biais est 28-1
-1 = 27
-1 = 127
3 = 3+127 = 130 = 1000 0010
-3 = -3+127 = 124 = 0111 1100

34. Représentation en VF
+101٫100001 = + 0٫101100001 x 23
-0٫00000011 = - 0٫11 x 2-7

35. La norme IEEE-754
1bit 5 bits 10 bits
1bit 8 bits 23 bits
1bit 11 bits 52 bits
Sur 16 bits
32 bits
64 bits

36. La norme IEEE-754- 16 bits
1bit 5 bits 10 bits
Sur 16 bits
1 bit de signe
5 bits : exposant biaisé de 15
10 bits pour la pseudo-mantisse
Mantisse normalisé 0٫11101
La pseudo mantisse 1٫1101

37. Exercice
Représenter le nombre
- 0.10100001 x 2-3
1bit 5 bits 10 bits

38. Exercice
Représenter le nombre
- 0.10100001 x 2-3
Pseudo mantisse 1٫0100001= 0100001
Exposant biaisé de 15 :
-3+15 = 12 =01100
1 0 1 1 0 0 0 1 0 0 0 0 1 0 0
1bit 5 bits 10 bits

39. Exercice
Exemple : sur 8 bits
Représenter les exposants biaisés
3, -3

40. La norme IEEE-754- 32 bits
1bit 8 bits 23 bits
Sur 16 bits
1 bit de signe
8 bits : exposant biaisé de 127
23 bits pour la pseudo-mantisse
Mantisse normalisé 0٫11101
La pseudo mantisse 1٫1101

41. Exercice
Représenter sous IEEE754-32 bits
- 0.10100001 x 2-3
1bit 8 bits 23 bits

42. Exercice
IEEE-754-32 bits
- 0.10100001 x 2-3
Pseudo mantisse 1٫0100001= 0100001
Exposant biaisé de 127 :
-3+127 = 124 = 0111 1100
1 01 11 1
1
00 01 00 00 10 00 00 00 000000000