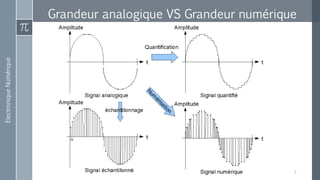
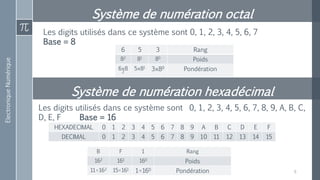
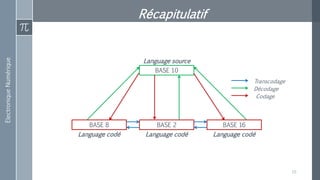
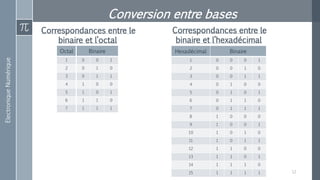
Le document décrit les différences entre les grandeurs analogiques et numériques, ainsi que les principes fondamentaux de l'électronique analogique et numérique. Il présente également divers systèmes de numération, notamment binaire, octal, décimal et hexadécimal, tout en expliquant leur conversion. Enfin, des correspondances entre ces systèmes de numération sont fournies pour faciliter la compréhension des conversions entre bases.

1. Introduction Générale
1

2. ElectroniqueNumérique
Grandeur analogique VS Grandeur numérique
› varie de manière continue › varie de manière discrète
GRANDEUR ANALOGIQUE
• Correspondre à une grandeur
physique (température, pression,
vitesse…) une autre grandeur
(souvent électrique) qui lui est
directement proportionnelle.
GRANDEUR NUMÉRIQUE
• N'est pas strictement proportionnelle
à une autre grandeur
• Exprimée au moyen d’un nombre
indiquant la valeur approximative de
cette grandeur.
2
• Tachymètre analogique: l’aiguille bouge en fonction de
la vitesse.
• Tachymètre numérique : une valeur chiffrée sur des
cristaux liquides.

3. ElectroniqueNumérique
Grandeur analogique VS Grandeur numérique
3

4. ElectroniqueNumérique
Electronique analogique VS électronique numérique
4
L'électronique analogique est la discipline traitant des systèmes
électroniques opérant sur des grandeurs (tension, courant, charge)
à variation continue. On emploie le terme « analogique » car les
grandeurs électriques utilisées sont à proportionnelles au signal à
traiter.
L'électronique numérique est la discipline s'intéressant aux
systèmes électroniques que leur fonctionnement est basé sur des
états électriques précis dont le nombre et la valeur sont fixés à
l'avance pendant la conception de ces systèmes. A chaque état
correspondant en général une valeur numérique.

5. Systèmes et bases de numération
5

6. ElectroniqueNumérique
Définition
Dans un système numérique, la base de numération permet la
représentation de l’information.
Il existe différentes bases de numérations. Les plus connues sont :
• la base binaire (2)
• la base octale (8)
• la base décimale (10)
• la base hexadécimale (16)
6

7. ElectroniqueNumérique
Système de numération décimal
Les digits utilisés dans ce système sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Base = 10
3 2 4 Rang
102 101 100
Poids
3×102 2×101 4×100
Pondération
Le nombre 324 s'écrit de gauche à droite comme étant trois centaines : 3 x 102, auxquelles
s'ajoutent deux dizaines : 2 x 101 et quatre unités : 4 x 100
7

8. ElectroniqueNumérique
Système de numération binaire
Les digits utilisés dans ce système sont 0, 1 et sont appelés bits
Base = 2
1 0 1 1 Rang
23 22 21 20
Poids
1×23 0×22 1×21
1×20 Pondération
1 1 1 0 1 0 1 1
27 26 25 24 23 22 21 20
LSBMSB
LSB= Least Significant bit
Bit le moins significatif
MSB= Most Significant bit
Bit le plus significatif
8

9. ElectroniqueNumérique
Système de numération octal
Les digits utilisés dans ce système sont 0, 1, 2, 3, 4, 5, 6, 7
Base = 8
9
6 5 3 Rang
82 81 80
Poids
6×8
2
5×81
3×80 Pondération
Système de numération hexadécimal
Les digits utilisés dans ce système sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C,
D, E, F Base = 16
B F 1 Rang
162 161 160
Poids
11×162 15×161
1×160 Pondération
HEXADECIMAL 0 1 2 3 4 5 6 7 8 9 A B C D E F
DECIMAL 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

10. ElectroniqueNumérique
Récapitulatif
10
BASE 10
BASE 8 BASE 2 BASE 16
Language source
Language codéLanguage codéLanguage codé
Transcodage
Décodage
Codage

11. ElectroniqueNumérique
Conversion entre bases
11
Conversion d’une base B à la base 10 (codage)
La conversion se réduit à une addition de puissances de la base .
Conversion de la base 10 à une base B (décodage)
La conversion correspond à des divisions entières successives par la base B. Le résultat est
obtenu en prenant les différents restes du dernier vers le premier.
(123)8 = 1×82 + 2×81 + 3×80 = (83)10
(6C5)16 = 6×162 + 12×161 + 5×160 = (1733)10
(10101)2 = 1×24 + 0×23 + 1×22 + 0×21 + 1×20 = (21)10
(25)10 25 ÷ 2 =
12
reste 1
12 ÷ 2 = 6 reste 0
6 ÷ 2 = 3 reste 0
3 ÷ 2 = 1 reste 1
On obtient : (25)10 = (11001)2

12. ElectroniqueNumérique
Conversion entre bases
12
Correspondances entre le
binaire et l’octal
Octal Binaire
1 0 0 1
2 0 1 0
3 0 1 1
4 1 0 0
5 1 0 1
6 1 1 0
7 1 1 1
Hexadécimal Binaire
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1
10 1 0 1 0
11 1 0 1 1
12 1 1 0 0
13 1 1 0 1
14 1 1 1 0
15 1 1 1 1
Correspondances entre le
binaire et l’hexadécimal

13. ElectroniqueNumérique
Conversion entre bases
13
Conversions entre la base 2 et la base 8 (transcodage)
La conversion consiste à faire correspondre, de droite à gauche, chaque chiffre octal par son
équivalent binaire sur 3 bits.
Conversions entre la base 2 et la base 16 (transcodage)
La conversion consiste à faire correspondre, de droite à gauche, chaque chiffre hexadécimal
par son équivalent binaire sur 4 bits.
On obtient : (2A)16 = (0010 10101)2
1 7
001 111
On obtient : (17)8 = (001 111)2
2 A
0010 1010