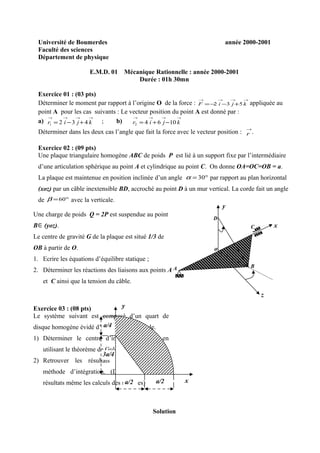
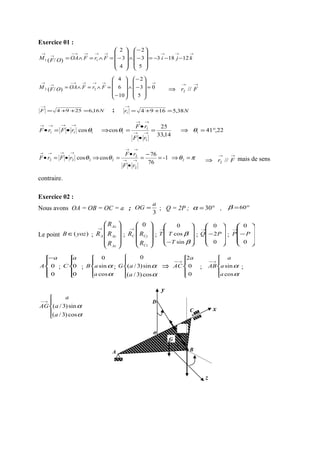
Le document est un exercice de mécanique rationnelle destiné aux étudiants de la faculté des sciences de l'université de Boumerdes pour l'année académique 2000-2001. Il contient des problèmes relatifs à la détermination des moments de force, des équations d'équilibre statique pour des systèmes mécaniques, et le calcul du centre d'inertie à l'aide de théorèmes et d'intégration. Les exercices abordent divers aspects de la mécanique, tels que l'application de forces et les relations géométriques dans des configurations spécifiques.

1. Université de Boumerdes année 2000-2001
Faculté des sciences
Département de physique
E.M.D. 01 Mécanique Rationnelle : année 2000-2001
Durée : 01h 30mn
Exercice 01 : (03 pts)
Déterminer le moment par rapport à l’origine O de la force :
→→→→
+−−= kjiF 532 appliquée au
point A pour les cas suivants : Le vecteur position du point A est donné par :
a)
→→→→
+−= kjir 4321
; b)
→→→→
−+= kjir 10642
Déterminer dans les deux cas l’angle que fait la force avec le vecteur position :
→
r .
Exercice 02 : (09 pts)
Une plaque triangulaire homogène ABC de poids P est lié à un support fixe par l’intermédiaire
d’une articulation sphérique au point A et cylindrique au point C. On donne OA=OC=OB = a.
La plaque est maintenue en position inclinée d’un angle °= 30α par rapport au plan horizontal
(xoz) par un câble inextensible BD, accroché au point D à un mur vertical. La corde fait un angle
de °=60β avec la verticale.
Solution
Une charge de poids Q = 2P est suspendue au point
B∈(yoz).
Le centre de gravité G de la plaque est situé 1/3 de
OB à partir de O.
1. Ecrire les équations d’équilibre statique ;
2. Déterminer les réactions des liaisons aux points A
et C ainsi que la tension du câble.
BA
y
o
C
D
z
x
Exercice 03 : (08 pts)
Le système suivant est composé d’un quart de
disque homogène évidé d’un triangle rectangle.
1) Déterminer le centre d’inertie du solide en
utilisant le théorème de Guldin ;
2) Retrouver les résultats précédents par la
méthode d’intégration. (Démontrer tous les
résultats même les calculs des surfaces)
3a/4
a/4
a/2 x
y
a/2

2. Exercice 01 :
→→→→→→→−
→
→
−−−=










−
−
∧










−=∧=∧= kjiFrFOAOFM 12183
5
3
2
4
3
2
)/( 11
→→→→→−
→
→
=










−
−
∧










−
=∧=∧= 0
5
3
2
10
6
4
)/( 22 FrFOAOFM
→→
⇒ Fr //2
NF 16,62594 =++=
→
; Nr 38,516941 =++=
→
22,41
14,33
25
coscos 1
1
1
1111 °=⇒=
•
•
=⇒•=• →→
→→
→→→→
θθθ
rF
rF
rFrF
πθθθ =⇒=
−
=
•
•
=⇒•=• →→
→→
→→→→
2
2
2
2222 -1
76
76
coscos
rF
rF
rFrF →→
⇒ Fr //2
mais de sens
contraire.
Exercice 02 :
Nous avons OA = OB = OC = a ;
3
a
OG = ; Q = 2P ; °= 30α , °=60β
Le point )(yozB ∈ ;










→
Az
Ay
Ax
A
R
R
R
R ;










→
Cz
CyC
R
RR
0
;










−
→
β
β
sin
cos
0
T
TT ;










−
→
0
2
0
PQ ;










−
→
0
0
PP




−
0
0
a
A ;





0
0
a
C ;





α
α
cos
sin
0
a
aB ;





α
α
cos)3/(
sin)3/(
0
a
aG ⇒





→−
0
0
2a
AC ;





→−
α
α
cos
sin
a
a
a
AB ;





→−
α
α
cos)3/(
sin)3/(
a
a
a
AG
BA
y
o
C
D
z
x
G

3. Le système est en équilibre statique, nous avons alors :
→→
=∑ 0
i
iF ⇔
→→→→→→
=++++ 0PQTRR CA
(1)
→→−
=∑ 0/
i
AiM ⇔
→→→−→→−→→−→→−
=∧+∧+∧+∧ 0PAGQABTABRAC C
(2)
La projection de l’équation (1) sur les axes donne trois équations scalaires :
0=AxR (3)
02cos =−−++ PPTRR CyAy β (4)
0sin =−+ βTRR CzAz (5)
En développant l’équation vectorielle (2), nous obtenons trois autres équations scalaires :










=










−∧










+










−∧










+










−
∧










+










∧










0
0
0
0
0
cos)3/(
sin)3/(
0
2
0
cos
sin
sin
cos
0
cos
sin
0
0
0
2
P
a
a
a
P
a
a
a
T
T
a
a
a
R
R
a
Cz
Cy
α
α
α
α
β
β
α
α
0cos
3
cos2coscossinsin =++−− ααβαβα
aP
aPaTaT (6)
0sin2 =+− βaTaRCz (7)
02cos2 =−−+ aPaPaTaRCy β (8)
Les six équations permettent de trouver toutes les inconnues :
(3) ⇒ 0=AxR (6) ⇒ PT 32,2= ; (7) ⇒ PRCz =
(8) ⇒ PRCy 92,0= ; (5) ⇒ PRAz = ; (4) ⇒ PRAy 92,0=
d’où : PRRRR AzAyAxA 358,1222
=++= ; PRRRR CzCyCxC 358,1222
=++=
Exercice 03 :
1) Centre d’inertie par le théorème de Guldin :
16
3
4
22
aa
Stot −=
π
a
aa
aa
a
S
VV
S
V
x
tot
cônesphèredemi
tot
ytot
G 506,0
16
3
4
.2
4
3
.
2
..
3
1
.
3
4
.
2
1
.2
_
.2 22
2
3
/
=






−






−
===
−
π
π
ππ
ππ
a
aa
aa
a
S
VV
S
V
y
tot
cônesphèredemi
tot
xtot
G 479,0
16
3
4
.2
2
.
4
3
..
3
1
.
3
4
.
2
1
.2
_
.2 22
2
3
/
=






−






−
===
−
π
π
ππ
ππ

4. 1) Centre d’inertie par les intégrales:
a) Soit S1 la surface du quart de disque :
4
.
;
2
0;0;.
22
00
11
a
drdrSardrdrds
a
π
θ
π
θθ
π
==≤≤≤≤= ∫∫
π
θθθ
π
θθ
π
π
3
4
.cos...
.
4
..cos.
.
4
.
1 2
00
2
2
0
21
1
1
1
a
dddrr
a
drdrr
a
xds
S
x
aa
S
G ==== ∫∫∫∫
π
θθθ
π
θθ
π
π
3
4
.sin...
.
4
..sin.
.
4
.
1 2
00
2
2
0
21
1
1
1
a
dddrr
a
drdrr
a
yds
S
y
aa
S
G ==== ∫∫∫∫
a) Soit S2 la surface du triangle :
dydxds .2 = ; la droite limitant le triangle a pour équation :






−= x
a
y
22
3
; où 





−= y
a
x
4
3
3
2
2
2
0
)
2
(
2
3
0
2
0
2
16
3
.
22
3
..
2
adxx
a
dydxdydxS
a
x
aa
S
=





−=== ∫∫∫∫
−
6
.
22
3
.
3
16
.
3
161 2
0
2
)
2
(
2
3
0
2
0
22
2
2
2
a
dxx
a
x
a
dyxdx
a
xds
S
x
a
x
aa
S
G =





−=== ∫∫∫∫
−
4
.
4
3
3
2
.
3
16
.
3
161 4
3
0
2
)
4
3
(
3
2
0
4
3
0
22
2
2
2
a
dyy
a
y
a
dxydy
a
yds
S
y
a
y
aa
S
G =





−=== ∫∫∫∫
−
a
aa
aaaa
SS
xSxS
x GG
G 506,0
16
3
4
6
.
16
.3
3
4
.
4
.
..
22
22
21
2211
=
−
−
=
−
−
=
π
π
π
a
aa
aaaa
SS
ySyS
y GG
G 479,0
16
3
4
4
.
16
.3
3
4
.
4
.
..
22
22
21
2211
=
−
−
=
−
−
=
π
π
π