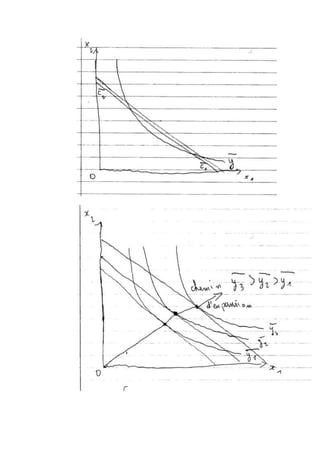
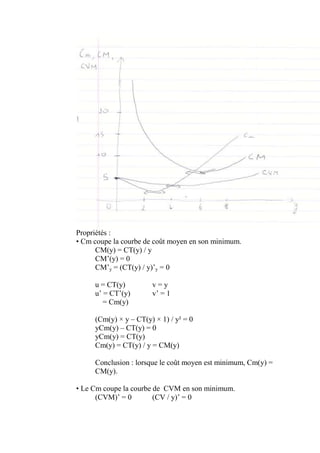
Le document traite de la maximisation du profit par le producteur, en expliquant comment déterminer le profit, les coûts, et les conditionnements par les inputs. Il décrit également les fonctions de coût, les notions de coût moyen et marginal et leur impact sur la maximisation du profit. Finalement, la fonction d'offre du producteur est définie en relation avec le prix de vente et le coût marginal.

1. Chapitre 2 : Le choix optimal du producteur.
Le producteur est rationnel. Un des ses objectifs ça va être de maximiser son
profit. Minimiser ses coûts pour une production donnée.
I : La maximisation du profit.
1) Qu’est-ce que le profit ?
Le profit c’est la différence entre la recette totale de l’entreprise et le coût
total de cette même entreprise.
Hyp : 2 inputs x1 et x2 → p1, p2.
1 output : y → p : prix de vente du produit.
Recette totale :
RT = prix de vente × quantité produite
RT = p × y
Le coût d’une entreprise :
CT = coût d’utilisation de l’input 1 + coût d’utilisation de l’input 2
CT = p1x1 + p2x2
Profit :
Π = py – (p1x1 + p2x2)
Π = py – p1x1 – p2x2
2) Maximisation du profit.
a) Cas où on a un input x1.
Π = py – p1x1

2. Objectif du producteur : atteindre le profit le plus grand possible
compte tenu de sa contrainte technologique qui est donnée par sa
fonction de production.
MAX Π
s.c y = f(x1)
MAX Π : Π = py – p1x1 (1)
s.c y = f(x1) (2)
1→2
Max Π = p . f(x1) – p1x1
Si on veut le maximum d’une fonction : si Π’x1 = 0
dΠ / dx1 = 0 ⇒ df(x1) / dx1 = 0
df(x1) / dx1 = Pm1
Condition : p × Pm1 = p1
p × Pm1 : valeur de la Pm
p : valeur du bien 1
⇔ Pm1 = p1 / p
Approche graphique :
Courbe d’iso profit : une courbe d’iso profit c’est l’ensemble des
combinaisons d’inputs et de production qui permettent d’atteindre
le même profit. Ce sont des droites.
On fixe un niveau de profit .

3. Si on veut atteindre 2 > 1
Est-ce que 1 est le profit maximal ? Non, on peut aussi atteindre
2 .

4. 3 : niveau de profit maximum compte tenu de sa contrainte
technologique.
Au point E, la pente de la courbe d’iso profit est égale à la pente de
la fonction de production.
Pente de la droite d’iso profit : p1 / p
Pm1 : pente de la fonction de production.
Pour atteindre le profit maximum : Pm1 = p1 / p.
Que se passe-t-il si le prix de l’input varie ?
Si le prix augmente, on aura une modification de la pente de la
droite d’iso profit : p1’ / p > p1 / p. La pente augmente.
Si le prix de l’input augmente et si l’entreprise veut conserver le
même profit maximum, alors elle va réduire sa production (y’* <
y*) et sa demande d’inputs (x1’* < x1*).
'
3 3

5. Si p1 augmente on aura 3 effets :
- diminution de la production
- diminution de la quantité de facteurs x1
- diminution de profit maximum
b) Fonction de demande de facteurs avec un seul facteur.
Fonction de demande de facteurs : c’est la quantité optimale
demandée en fonction du prix du facteur lorsque l’entreprise
maximise son profit.
On part de la condition d’optimisation :
Pm1 × p = p1
x1 en fonction de p1 ?
Ex : y =
Pm1 ×p = p1 Pm1 = dy / dx1 = 4 ×1/2 x11/2-1
Pm1 = 2x1-1/2
2 / x11/2 = p1 / p
x11/2 ×p1 = 2p
x11/2 = 2p / p1
x1 = 4p² / p1² ← fonction de demande de facteur

6. C’est la quantité d’inputs qui permet d’atteindre le profit maximum.
y* = f(x1*)
y* =
Π* = py* - p1x1* → ΠMax
c) La maximisation du profit avec 2 variables.
Π = RT – CT
x1 → input 1, p1
x2 → input 2, p2
y = output
p = prix output
Π = p × y – (p1x1 + p2x2)
Objectif : Max Π
Sc : y = f(x1, x2)
Max py – (p1x1 + p2x2) (1)
Sc y = f(x1, x2) (2)
(2) → (1)
Max Π = pf(x1, x2) – (p1x1 + p2x2)
Condition 1er ordre :
dΠ / dx1 = 0
dΠ / dx2 = 0
p × df(x1, x2) / dx1 – p1 = 0
p × df(x1, x2) / dx2 – p2 = 0
p × Pm1 – p1 = 0
p ×Pm2 – p2 = 0
2 conditions :
p × Pm1 = p1
p × Pm2 = p2
Exemple :
y = f(K, L) = K1/2L1/4

7. K : capital → pK
L : travail → pL
Π = p ×y – (pKK + pLL)
Max Π (1)
sc y = K1/2L1/4 (2)
Max Π = p(K1/2L1/4) – (pKK + pLL)
p × PmK = pK
p × PmL = pL
PmK = df(K, L) / dK = (K1/2L1/4)’K = 1/2K1/2-1L1/4
PmK = 1/2K-1/2L1/4
PmL = df(K, L) / dL = (K1/2L1/4)’L = 1/4K1/2L1/4-1
PmL = 1/4K1/2L-3/4
On suppose p = 10.
10 × 1/2K-1/2L1/4 = pK
10 × 1/4K1/2L-3/4 = pL
5K-1/2L1/4 = pK (1)
5/2K1/2L-3/4 = pL (2)
Objectif : trouver les fonctions de demande, de travail et de capital.
(1) × (2) :
25/2 × 1 × L1/4 – ¾ = pK × pL
25/2L-1/2 = pKpL
L-1/2 = 2pKpL / 25
L = (2pKpL / 25)-2 = (25 / 2pKpL)²
L = 625 / 4pK²pL² → fonction de demande de travail
C’est l’ensemble des quantités de travail qui permettent de
maximiser le profit.

8. Pour avoir K, on remplace L dans :
5K-1/2L1/4 = pK
5K-1/2(625 / 4pK²pL²)1/4 = pK
K = 625 / 2pK3pL → fonction de demande de capital
Si on fixe pK = 5 et pL = 5.
L=¼ K=½
On va produire y = 1/21/2 × 1/41/4 = ½
Πmax = 10 × ½ - (1/2 × 5 + ¼ × 5)
RT CT
Πmax = 1,25 um
II : Minimisation du coût total pour un niveau de production donnée.
Problème : le producteur souhaite atteindre un niveau de production y .
Le prix de l’output est donné par le marché : p.
Max Π = p y - CT
La RT est fixée.
A RT fixée, si le producteur veut maximiser son profit, la seule
solution est de minimiser son coût total.
Min CT(x1, x2)
sc f(x1, x2) = y
1) Approche graphique.
a) Droite d’iso-coût.
Définition : c’est l’ensemble des combinaisons d’inputs qui
permettent d’avoir le même coût total. Ce sont des droites qui
s’appellent droites d’iso-coût.
CT = c
c = p1x1 + p2x2
x1 et x2 sont deux inputs.
p2x2 = c - p1x1

9. x2 = c / p2 – (p1 / p2)x1 droites d’iso-coût
Ordonnées à l’origine :
x1 = 0 x 2 = c / p2
x2 = 0 x 1 = c / p1
Pente = -p1 / p2
Min CT
y = f(x1, x2)

11. (x1*, x2*) → Min CT ⇒ Max Π
Propriété :
TMST(x1*, x2*) = pente de la tangente en chaque point de la
p1
fonction de production =
p2
A l’optimum : TMST = p1 / p2
TMST = Pm1 / Pm2 = p1 / p2
Conclusion :
Min CT
sc y = f(x1, x2)
⇔ TMST = p1 / p2
sc y = f(x1, x2)
⇒ On atteint le profit maximum.
b) Sentier d’expansion.
Définition : le sentier d’expansion représente l’ensemble des
paniers d’inputs optimaux qui permettent de minimiser le coût total
lorsque le niveau de production varie, les prix étant constants.

12. Pour avoir le sentier d’expansion :
TMST = p1 / p2 ⇒ x2 = f(x1)
Exemple : x1αx2β = f(x1, x2)
TMST = αx2 / βx1
αx2 / βx1 = p1 / p2 ⇒ αx2 = p1/p2 βx1
x2 = (p1 / p2) • (β / α) x1
c) Exemple.
f(K, L) = K1/2L1/4
pK = 5 pL = 5
Min CT
sc y = f(K, L)

13. TMST = αx2 / βx1 = 1/2L / 1/4K = 4/2 L / K
TSMT = 2L / K
2L / K = pK / pL
2L / K = 1
2L = K
Contrainte : y = f(K, L) = K1/2L1/4
1/2 1/4 1/2 3/4
y = 2L L = 2 L
L3/4 = y / 21/2
L = ( y / 21/2) 4/3
L = y 4/3 / 21/2×4/3 = y 4/3 / 22/3
L = y 4/3 × 2-2/3
K = 21/3 y 4/3
y =½
L = 1/24/32-2/3 = 2-4/32-2/3 = 2-6/3 = 2-2 = 1 / 2² = ¼
K = 1/2
Conclusion :
Max Π
sc y = f(x1, x2)
⇔ Min CT
y = f(x1, x2)
Dans le 1er programme, on cherche le niveau de production à
atteindre alors que dans le 2ème production, on fixe le niveau de
production à atteindre.
Dans les 2 cas, on obtient le profit maximum.
1er programme :
Conditions de maximisation du profit :
p × Pm1 = p1
p × Pm2 = p2

14. 2ème programme :
Min CT
TMST = p1 / p2
Sc y = f(x1, x2)
III : Les fonctions de coût.
1) Fonction de coût total.
Définition : on va chercher la fonction de coût total, notée CT(y), qui,
pour un ensemble de prix d’inputs donnés et pour tout niveau d’output,
fait correspondre le coût minimum pour atteindre le niveau d’output y.
y → CT(y) représente le coût minimum pour atteindre y.
Min CT
Sc y = f(x1, x2)
Fonctions de demande de bien 1 et de bien 2 en fonction de y.
A partir de CT(x1, x2) :
CT = p1x1 + p2x2
CT(y) = p1x1(y) + p2x2(y)
Exemple : f(K, L) = K1/2L1/4
L = 24/3y-2/3
K = 21/3y4/3
pK = pL = 5
CT = 5 × 21/3y4/3 + 5 × 2-2/3y4/3
CT = y4/3 (5 × 21/3 + 5 × 2-2/3)
CT = 9,48y4/3
Propriétés :
• Si on a des rendements d’échelle constants, alors la fonction coût total
sera linéaire.

15. • Si la fonction coût total est concave alors les rendements d’échelle sont
croissants.
• Si la fonction coût total est convexe alors les rendements d’échelle sont
décroissants.
Coûts variables : CV(y), c’est l’ensemble des coûts qui dépendent du
niveau de production.
Coûts fixes : CF qui eux sont indépendants du niveau de production.
CT(t) = CV(y) + CF
2) Fonction coût moyen et coût marginal.
a) Coûts moyens.
CM(y) = CT(y) / y ⇒ coût en moyenne d’une unité produite.
CT(y) = CF + CV(y)
CM(y) = CF + CV(y) / y = CF / y + CV(y) / y
CV(y) / y = CVM(y)
CF / y = CFM
CM(y) = CMV(y) + CFM
b) Coût marginal.
Définition : le coût marginal, Cm, c’est le coût engendré par la
production d’une unité en plus d’output. Cm(y).
Cm(y) = ΔCT(y) / Δy → cas discret
Cas continu : on connaît les fonctions de coût.
Cm(y) = dCT(y) / dy
CT = CV(y) + CF ⇒ Cm(y) = CT’(y)
= (CV(y) + CF)’y
= CV’(y)
Cm(y) = CV’(y)
Ex : CT(y) = 1/6y3 – 3/2y² + 5y + 10
Cm(y) = 1/2y² - 3y + 5

16. Propriétés :
• Cm coupe la courbe de coût moyen en son minimum.
CM(y) = CT(y) / y
CM’(y) = 0
CM’y = (CT(y) / y)’y = 0
u = CT(y) v=y
u’ = CT’(y) v’ = 1
= Cm(y)
(Cm(y) × y – CT(y) × 1) / y² = 0
yCm(y) – CT(y) = 0
yCm(y) = CT(y)
Cm(y) = CT(y) / y = CM(y)
Conclusion : lorsque le coût moyen est minimum, Cm(y) =
CM(y).
• Le Cm coupe la courbe de CVM en son minimum.
(CVM)’ = 0 (CV / y)’ = 0

17. (CV’(y) – CVy’) / y² = 0
CV’(y) – CV = 0
Cm × y = CV
Cm = CV / y = CVM
• CM et économie d’échelle :
Lorsque la production augmente, le coût unitaire diminue :
économies d’échelle.
Lorsque la production augmente, le coût unitaire augmente :
déséconomies d’échelle.
• Rendements d’échelle et Cm :
On peut montrer que lorsque le rendement d’échelle est constant, le
coût marginal est également constant.
Lorsque le rendement d’échelle est croissant, le coût marginal est
décroissant.
Lorsque le rendement d’échelle est décroissant, le coût marginal est
croissant.

18. 3) Coût marginal et maximisation du profit.
Objectif du producteur : MAX Π.
Π = RT – CT(y)
Π = py – CT(y)
Max Π = py – CT(y)
Π’y = 0
(py – CT(y))’y = 0
p – CT’(y) = 0
p – Cm(y) = 0
Le profit sera maximum lorsque p = Cm(y).
• Si le prix (ce que rapporte une unité de bien) est inférieur au coût
marginal (coût d’une unité supplémentaire produite)
⇒ il faut produire jusqu’à ce que p = Cm

19. p* → Q* → Max Π
IV : La fonction d’offre du producteur.
Définition : la fonction d’offre va exprimer les quantités offertes par l’entreprise
par rapport au prix lorsque l’entreprise maximise son profit.
Y = S(p)
1) Détermination de la fonction d’offre.
Pour avoir la fonction d’offre du producteur :
Max Π ⇒p = Cm(y)
⇒y = S(p) = Cm-1(y)
Cm-1(y) : fonction inverse de Cm
Ex : CT = 1/4y² + 2
Cm = (1/4y² + 2)’y ⇒ Cm = 1/2y
Max Π : Cm = p
1/2y = p ⇒ la fonction d’offre est y = S(p).
1/2y = p ⇒ y = 2p

20. La fonction d’offre est une droite qui passe par 0 et qui est croissante.
La fonction d’offre est une fonction croissante des prix.
2) Seuil de rentabilité.
Définition : le seuil de rentabilité correspond au prix en dessous duquel le
profit de l’entreprise devient négatif ou le prix pour lequel le profit de
l’entreprise est nul.
On veut le prix de l’output tel que Π = 0.
RT – CT = 0
py – CT(y) = 0
py = CT(y)
p = CM(y)
SR est atteint lorsque le prix de l’output devient égal au coût moyen de
l’entreprise.
Si pour p = CM(y) ⇒ MAX Π ⇒ p = Cm
SR : Cm = CM(y) pour le minimum de CM.
Le SR c’est le prix qui égalise le Cm et le CM ou encore c’est le
minimum du coût moyen.

21. Pour que l’entreprise fasse du profit, il est nécessaire que le prix proposé
par le marché soit supérieur au seuil de rentabilité.
3) Seuil de fermeture.
Définition : c’est le prix en dessous duquel l’entreprise décide d’arrêter la
production.
Π = RT – CT = RT(y) – (CV(y) + CF)
= RT(y) – CV(y) – CF
= 0 – 0 – CF
Π = - CF
Il va produire si Π(y, p) > -CF
py – CV(y) – CF > -CF
py – CV(y) > 0
py > CV(y)
p > CV(y) / y
p > CVM(y)
Le SF est atteint lorsque p = CVM(y)
Le profit maximum est atteint pour p = Cm.
SF est donné pour Cm(y) = CVM(y)
L’offre du producteur est définie à partir du seuil de fermeture.
Si p < SF y = S(p) = 0
Si p > SF y = S(p)

22. CM(y) ≥ CVM
CT(y) = CV(y) + CF
CM(y) = CV(y) + CF / y = CVF(y) + CFM ≥ CVM(y)
CVM(y) = CM(y) : si l’entreprise n’a pas de CF
Dans ce cas SF = SR
La fonction d’offre c’est la partie croissante de la courbe de coût marginal
située au-dessus du seuil de fermeture.
V : Exemple.
CT(y) = y3 – 8y² + 30y + 5
CM(y) = CT(y) / y = y² - 8y + 30 + 5/y
y² - 8y + 30 = CVM
5/y = CFM
CVM = y² - 8y + 30

23. SF : min CVM ou Cm = CVM
CVM’y = 0
(y² - 8y + 30)’y = 2y – 8 = 0 ⇔ 2y = 8 ⇔ y = 4 → quantité produite par
l’entreprise qui permet d’atteindre le seuil de fermeture.
p = Cm(y)
p = Cm(4) : SF
= CVM(4)
CVM(4) = 4² - 8 × 4 + 30 = 16 – 32 + 30 = 14 → prix qui correspond au SF.
La fonction d’offre sera définie pour tout p ≥ 14
p = Cm(y)
Cm(y) = Ct’y = (y3 - 8y² + 30y + 5)’y
= 3y² - 16y + 30
p = Cm(y) ⇒ y = S(p) ?
3y² - 16y + 30 = p
3y² - 16y + (30 – p) = 0
Δ = 16² - 4 × 3 × (30 - p) = 16² - 12(30 – p)
y1 = (16 + sqrt(16² - 12(30 – p)) / 6 = (16 + sqrt(256 – 12(30 – p)) / 6
= (16 + sqrt(256 – 360 + 12p)) / 6
= (16 + sqrt(4(3p – 26))) / 6
= (16 + 2sqrt(3p-26)) / 6
y2 = (16 - sqrt(16² - 12(30 – p)) / 6 = (16 - 2sqrt(3p-26)) / 6
y = (16 + sqrt(3p – 26)) / 6 → production la plus grande
Si p < 14 y=0
Si p ≥ 14 y = (8 + sqrt(3p - 26)) / 3