Ce document décrit la modélisation d'un moteur à courant continu dans MATLAB/Simulink, en se basant sur les équations électriques et électromécaniques. Il présente les processus de simulation, l'analyse des entrées et sorties, ainsi que l'implémentation d'un limiteur de vitesse pour éviter les surintensités au démarrage. La conclusion souligne l'utilité de la simulation pour l'entraînement aux moteurs à courant continu et la validation des résultats théoriques.

1. Filière Ingénieur : Ingénierie des systèmes
électriques et systèmes embarqués
DépartementGE-GM
Réalisé par :
-Babaoui Mohamed
-Arrakhiz Yassir
Année Universitaire 2020/2021
Proposé par :
- Mr Semma Elalami
TP :Modélisationdes MCC sous MATLAB/SIMULINK

2. Introduction:
Un moteur à courant continu est système permettant de convertir uneénergie électrique
d’entréeen une énergie mécanique de sortie.
Le but de cette manipulation c’est de pouvoir simuler le fonction d’un moteur a courant continu
dans l’environnement MATLAB Simulink en se basant sur les équations électriques et
électromécanique qui decivent le fonctionnement du MCC.
Aussi c’est une occasion pour découvrir les fonctionnalités qui offre Matlab cote entrainement
des machines électriques en essayant de trouver le meilleur modèle possible qui régit le MCC
Modèle de la machineà courantcontinu
D’un point de vue électrique, le moteur courant continu peut être modélisé comme un système
dont l’entrée est la tension de commande de l’induit u(t) et la sortie la vitesse de rotation de
l’arbre moteur ωm(t). L’induit est modélisé par une résistance en série avec une inductance et
une force contre électromotrice. On donne ci-dessous le modèle de connaissance du moteur
courant continu :
Convertir de l’énergie
électrique en énergie
mécanique de rotation
Energie électrique
(U,V)
Energie mécanique
rotative
(C,Ω)

3. 𝑢( 𝑡) = 𝑅𝑖( 𝑡) + 𝐿
𝑑𝑖(𝑡)
𝑑(𝑡)
+ Ke. ωm(t)
𝐽
𝑑(ωm)
𝑑𝑡
= 𝐶𝑚( 𝑡) − 𝐶𝑅( 𝑡) − 𝑓. 𝜔𝑚(𝑡)
Avec :
u(t)=Tension dumoteur [V]
e(t)=Forcecontreélectromotrice dumoteur [V] i(t)=Intensitédanslemoteur
[A]
Cm(t)=Coupleexercéparlemoteur [N.m]
Cr(t)=Couplerésistantsurl’axemoteur [N.m]
ωm(t)=Vitesseangulairedumoteur [rad/s]
R = Valeur de la résistance [Ω]
L=Valeurdel’inductance [H]
Ke=Coefficientdelaforcecontreélectromotrice [V/(rad/s)] J=Inertieéquivalenteramenée
surl’arbre moteur [kg.m²]
f =0,01=Paramètre de«frottement fluide»total [N.m.s] Kt=Constantedecouple [N.m/A]
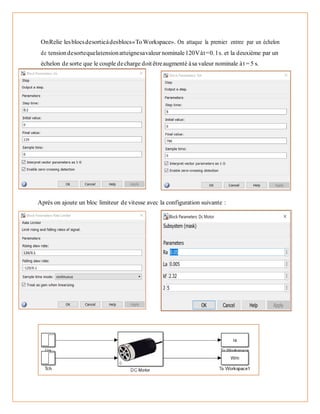
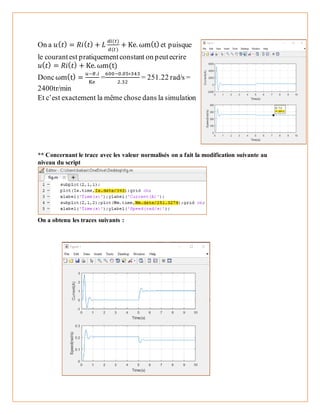
La tension d'induit va et le couple de charge Tch sont les entrées du modèle. Le courant
d'induit ia et la vitesse angulaire du rotor sont les sorties du modèle. Les paramètres du moteur
sont indiqués dans le tableau 1.
Un 600V
In 343A
n 2400tr/min
Tn 796N.m
Ra 0.05
La 0.005H
Kf 2.32Vs
J 100kgm3
D’après la loi des mailles
Equation de la dynamique de l’arbre moteur
e(t) = Ke.ωm(t) Equation de l’électromagnétisme
Cm(t) = Kt .i(t) Equation de l’électromagnétisme

4. D’après les équations ce dessus on arrive à modéliser le moteur à courant continu en reliant les
différents paramètres d’entrées (la tension d’alimentation Ua et le couple moteur Tch et les
éléments qui lui constituer (la résistance et l’inductance des enroulements Ra et La) avec les
coefficient de proportionnalité et le paramètre de LAPLACE (s) pour faciliter la complexité du
calcul temporel :
Après on essayer de rendre tout le modèle sous forme d’une seule entité (Boite noire) avec les
deux entrées et les deux sorties de notre système en sélectionnant tous le modèle et en cliquant
le bouton droit et choisissant l’option create subsystem from selection Ensuite, le subsystem
sera masqué. On ouvre l’éditeur de masque en cliquant avec le bouton droit de la souris sur le
subsystem et en choisissant Masque>Créer un masque. A fin de pouvoir changer les paramètres
du système juste en cliquant sur le subsystem.

5. OnRelie lesblocsdesortieàdesblocs«ToWorkspace». On attaque la premier entree par un échelon
de tensiondesortequelatensionatteignesavaleur nominale120Vàt=0.1s. et la deuxième par un
échelon de sorte que le couple decharge doit êtreaugmenté àsa valeur nominale àt = 5 s.
Après on ajoute un bloc limiteur de vitesse avec la configuration suivante :

6. Pour exécuter et voir le résultat on clique sur simulation> exécuter dans la fenêtre Simulink et
on lance le script suivant qui sert a tracer les deux signaux de sorties Ia(A) et la vitesse
angulaire ω(rad/s)
Voilà les traces :
1) Au démarrage : Ω = 0 ⇒ E = 0 et donc I d =(Un – E)/R
= Un/ R =600/0.05= 12000 A >> In
On a Cm(t) = Kt .i(t) et puisque en régime établi Cm=796
N.m
Donc i=796/232=343A et c’est exactement la même
valeur dans le trace

7. On a 𝑢( 𝑡) = 𝑅𝑖( 𝑡) + 𝐿
𝑑𝑖(𝑡)
𝑑(𝑡)
+ Ke. ωm(t) et puisque
le courantest pratiquementconstant on peutecrire
𝑢( 𝑡) = 𝑅𝑖( 𝑡) + Ke. ωm(t)
Doncωm(t) =
𝑢−𝑅.𝑖
Ke
=
600−0.05∗343
2.32
= 251.22 rad/s =
2400tr/min
Et c’est exactement la même chose dans la simulation
** Concernant le trace avec les valeur normalisés on a fait la modification suivante au
niveau du script
On a obtenu les traces suivants :

8. 2) On limite le taux demontéede la tension à 120 V / 0,1 s à l'aide du bloc
limiteur de vitesse, on lui plaçantentrele gradin detension et le modèle de
moteur. Voiciles résultats:
Interpretation
On remarque que le limiteur de vitesse a pu
régler le problème de surintensité au
démarrage du moteur.
Ce qui va servir a augmenter la durée de vie
du des enroulement rotoriques ainsi que le
cout de la maintenance des balais et du
collecteur justement .
Conclusion:
A la lumière de cette simulation on a pu familiariser avec l’environnement de modélisation
MATLAB/Simulink dans le sens d’entrainement des moteurs à courant continu.
Et aussi on a connu comment à partir des équations différentielles électromécanique élaborer un
système qui sert à interconnecter des entrées avec les paramètres qui définissent le système afin
de trouver des sorties et ensuite les visualiser et interpréter les résultats et les comparer avec les
résultats théoriques.