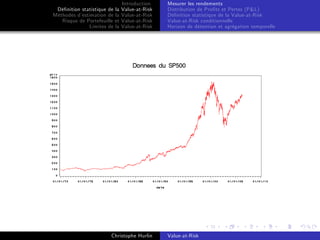
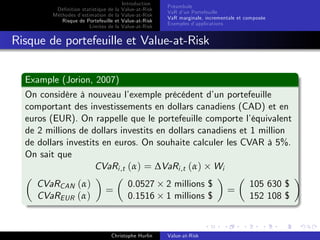
La value-at-risk (VaR) est un outil statistique utilisé pour estimer le risque de perte d'un portefeuille sur une période donnée avec un niveau de confiance déterminé. Popularisée par des institutions financières dans les années 1990, la VaR sert de mesure de référence pour évaluer et gérer les risques sur les marchés financiers. Ses applications se distinguent en reporting, contrôle et management des risques, touchant divers utilisateurs y compris les institutions financières, les régulateurs et les entreprises.

1. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Partie 1. Value-at-Risk
Intoduction à la Value-at-Risk
Christophe Hurlin, Université d’
Orléans, Laboratoire
d’
Economie d’
Orléans (UMR CNRS 6221)
Master Econométrie et Statistique Appliquée (ESA), Université d’
Orléans
Septembre 2008
Christophe Hurlin
Value-at-Risk

2. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Introduction
Introduction
Qu’ ce que la VaR ?
est
Christophe Hurlin
Value-at-Risk

3. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qu’ ce que la VaR ?
est
Un bref aperçu historique :
La notion de Value-at-Risk (VaR) est apparue pour la
première fois dans le secteur de l’
assurance.
A la …n des années 1980, la banque Bankers Trust fut l’
une
des premières institutions à utiliser cette notion sur les
marchés …nanciers aux Etats-Unis.
Christophe Hurlin
Value-at-Risk

4. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qu’ ce que la VaR ?
est
Le terme VaR est apparu pour la première fois dans une
publication grand public en juillet 1993 dans un rapport d’
une
réunion du G-30
Mais c’ principalement la banque JP Morgan qui, dans les
est
années 90, a popularisé ce concept notamment grâce à son
système RiskMetrics (1994).
Christophe Hurlin
Value-at-Risk

5. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qu’ ce que la VaR ?
est
Fact
La Value-at-Risk est devenue, en moins d’
une dizaine d’
années,
une mesure de référence du risque sur les marchés …nanciers,
consacrée notamment par la réglementation prudentielle dé…nie
dans le cadre des accords de Bâle II.
Christophe Hurlin
Value-at-Risk

6. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qu’ ce que la VaR ?
est
De…nition (Value-at-Risk)
De façon générale, la Value-at-Risk correspond au montant des
pertes qui ne devraient pas être dépassées pour un niveau de
con…ance donné sur un horizon temporel donné (Jorion, 2007)
Jorion, P. (2007), Value-at-Risk, Third edition,
McGraw-Hill.
Christophe Hurlin
Value-at-Risk

7. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qu’ ce que la VaR ?
est
La Value-at-Risk correspond à une perte maximale potentielle
qui ne devrait être atteinte qu’
avec une probabilité donnée
sur un horizon temporel donné
Christophe Hurlin
Value-at-Risk

8. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qu’ ce que la VaR ?
est
De…nition (Value-at-Risk)
VaR is an estimate of how much a certain portfolio can lose within
a given time period, for a given con…dence level (Engle et
Manganelli, 2004).
Engle, R. F., and Manganelli, S. (2004), ”CAViaR :
Conditional Autoregressive Value-at-Risk by regression
quantiles”, Journal of Business and Economic Statistics, 22,
pp. 367-381.
Christophe Hurlin
Value-at-Risk

9. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qu’ ce que la VaR ?
est
Example (Value-at-Risk)
Si une banque annonce une VaR quotidienne sur son portefeuille
de 50 millions de dollars pour un niveau de con…ance de 99%, cela
implique qu’ y a seulement une chance sur 100, sous des
il
conditions normales de marché, que la perte associée à la détention
de ce portefeuille sur une journée excède 50 millions de dollars.
Christophe Hurlin
Value-at-Risk

10. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qu’ ce que la VaR ?
est
La simplicité de cette dé…nition constitue l’ des principaux
un
attraits de la Value-at-Risk : il est en e¤et très facile de
communiquer sur la VaR et de ainsi proposer une mesure
homogène et générale (quelle que soit la nature de l’
actif, la
composition du portefeuille etc.) de l’
exposition au risque.
Christophe Hurlin
Value-at-Risk

11. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Introduction
Introduction
Comment utiliser la VaR ?
Christophe Hurlin
Value-at-Risk

12. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Comment utiliser la VaR ?
Comment utiliser la VaR ?
La VaR peut être utilisée de trois façons principales (Jorion, 2007) :
1
de façon passive : reporting d’
information
2
de façon défensive : contrôle des risques
3
de façon active : management des risques
Christophe Hurlin
Value-at-Risk

13. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Comment utiliser la VaR ?
Reporting des risques
La VaR peut être utilisée de façon passive dans le cadre d’
un
reporting régulier sur le risques
Ce fut historiquement la première utilisation de la VaR en vue
de mesurer un risque agrégé (JP Morgan)
La VaR est une mesure du risque simple à interpréter
exprimée en unité monétaire
La VaR est une mesure du risque sur laquelle on peut
communiquer de façon non technique
La VaR permet de synthétiser en une seule mesure une
appréciation sur le risque global
Christophe Hurlin
Value-at-Risk

14. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Comment utiliser la VaR ?
Contrôle des risques
La VaR peut être utilisée de façon défensive dans le cadre d’
un
contrôle des risques
La VaR est utilisée pour déterminer des positions limites qui
seront imposées aux traders (limites individuelles) ou aux
business units (limites collectives)
Le principal avantage de la VaR est qu’ fournit un
elle
dénominateur commun permettant de comparer les
risques engendrés par les activités menées sur di¤érents
marchés, di¤érents produits etc.
Christophe Hurlin
Value-at-Risk

15. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Comment utiliser la VaR ?
Management des risques
La VaR peut être utilisée de façon active dans le cadre d’
un
management des risques
La VaR est utilisée dans l’
allocation du capital entre les
tradeurs, les business lines, les produits et ou les institution.
La VaR est généralement retenue pour le calcul des
rendements ajustés du risque ou Risk-adjusted
performance measures (RAPM)
Optimisation de portefeuille avec des critères de type
moyenne-VaR.
Christophe Hurlin
Value-at-Risk

16. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Introduction
Introduction
Qui utilise la VaR ?
Christophe Hurlin
Value-at-Risk

17. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qui utilise la VaR ?
Qui utilise la VaR ?
En raison de ces très nombreuses utilisations possibles, les
utilisateurs de la VaR sont très di¤érents :
1
Institutions …nancières
2
Régulateurs
3
Entreprises non …nancières
4
Asset Managers
Christophe Hurlin
Value-at-Risk

18. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qui utilise la VaR ?
Les institutions …nancières
Les institutions …nancières ont été à l’
avant garde de la di¤usion
et l’
utilisation de la VaR dans le cadre de la mise en place de
systèmes centralisés de management / surveillance des risques
nécessité liée à l’
évolution de la réglementation
nécessité liée à la complexité croissante des instruments
…nanciers et à la diversi…cation croissante des risques
…nanciers
nécessité liée à la connaissance de grands désastres
…nanciers (Barings, Daiwa..)
Christophe Hurlin
Value-at-Risk

19. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qui utilise la VaR ?
Les régulateurs
Les réglementations prudentielles visent de façon générale à
imposer aux institutions …nancières de garantir un niveau minimum
de capitaux disponibles au regard des risque …nanciers. Par
conséquent se pose le problème de l’
évaluation de ces risques :
Comment évaluer ces risques …nanciers sur des
multi-activités, des actifs très di¤érents, des produits
complexes ?
Qui doit évaluer ces risques ? les autorités de régulation ou
les institutions …nancières elles-mêmes ?
Dans ce dernier cas comment garantir la validité des
évaluations du risque proposées par les institutions
…nancières ?
Christophe Hurlin
Value-at-Risk

20. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qui utilise la VaR ?
Les régulateurs
Fact
Dans les années 80-90, on a assisté à une convergence des
réglementations prudentielles (comité de Bâle sur le contrôle
bancaire, US Federal Reserve, US Securities and Exchange
Commission etc) vers l’
adoption de la VaR comme mesure de
référence du risque.
Christophe Hurlin
Value-at-Risk

21. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qui utilise la VaR ?
Les institutions non …nancières
Les institutions non …nancières : l’
usage de la VaR dépasse le
contexte des seules institutions …nancières :
Le management centralisé des risques est utile à toutes les
entreprises exposées aux risques …nanciers.
On peut citer en exemple les multinationales qui doivent
évaluer et se prémunir contre les risques de change, on peut
alors mener des analyses de type CFAR (Cash Flow at Risk)
Christophe Hurlin
Value-at-Risk

22. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Qui utilise la VaR ?
Les asset managers
La gestion d’
actifs et la VaR : utilisation de la VaR pour gérer
les risques …nanciers et développer les stratégies d’
asset
management
"We can now view our total capital at risk on a
portfolio basis, by asset class and by individual manager.
Our main goal was to ... have the means to evaluate our
portfolio risk going forward" Director of Chrysler pension
fund", cité dans Jorion (2007), interview réalisé après
l’
achat d’ system de VaR
un
Christophe Hurlin
Value-at-Risk

23. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Introduction
Introduction
Quels types de risques mesure la VaR ?
Christophe Hurlin
Value-at-Risk

24. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Quels types de risques peut mesurer la VaR ?
La VaR est une mesure homogène permettant de mesurer
di¤érents risques, sur di¤érents marchés, di¤érents actifs (change,
actions, dérivés..)
De…nition (Portée de la VaR )
L’
objectif de la VaR fournit une mesure du risque total de
portefeuille. Par conséquent, la VaR doit tenir compte des e¤ets
de levier et de diversi…cation (corrélation).
Christophe Hurlin
Value-at-Risk

25. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Les risques …nanciers sont généralement classés en grandes
catégories :
1
Risques de marché
2
Risques de liquidité
3
Risques de crédit
4
Risques opérationnels
Christophe Hurlin
Value-at-Risk

26. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
De…nition
Le risque de marché désigne le risque de perte lié à l’
évolution
des niveaux ou des volatilités des prix de marché. Ces risques
peuvent être exprimés sous deux formes :
1
risques absolus, mesurés en unité monétaire
2
risques relatifs exprimés par rapport à un benchmark (notion
de tracking error ou déviation par rapport à un indice)
Christophe Hurlin
Value-at-Risk

27. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque de marché
Fact
La VaR a été conçue comme une mesure de risque de marché et le
risque de marché demeure aujourd’ le principal champ
hui
d’
application de la VaR, même si ce n’ plus de façon exclusive.
est
Christophe Hurlin
Value-at-Risk

28. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque de liquidité
De…nition (risque de liquidité)
La notion de risque de liquidité regroupe deux types de risques :
le risque de liquidité d’
actif (asset liquidity risk) et le risque de
liquidité de …nancement (funding liquidity risk ou cash ‡ow risk).
Christophe Hurlin
Value-at-Risk

29. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque de liquidité
De…nition (asset liquidity risk)
Le risque de liquidité d’
actif (asset-market-product liquidity risk)
survient lorsqu’
une transaction ne peut pas intervenir au prix au
prix prévu du fait de la taille relative de la position au regard du
volume des transactions usuelles (Jorion, 2007).
Christophe Hurlin
Value-at-Risk

30. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque de liquidité
Remarque : la notion de risque de liquidité est à distinguer de la
notion marché liquide / non liquide (exemple : marché de change
verus emerging-market equities) puisque ce risque peut survenir sur
un marché liquide suivant l’
importance de la position.
Christophe Hurlin
Value-at-Risk

31. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque de liquidité
De…nition (cash ‡ow liquidity risk)
Le risque de liquidité de …nancement (cash ‡ow liquidity risk)
fait référence à l’
impossibilté de faire face à ses obligations de
paiement, impliquant des liquidations de position et donc la
transformation de pertes "papier" en pertes réalisées (Jorion,
2007).
Christophe Hurlin
Value-at-Risk

32. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque de liquidité
La VaR ne s’
applique pas directement au concept de risque
de liquidité, mais :
Il est possible de construire des transformations de la VaR
intégrant ce type de risque comme la LVAR (Liquidity
adjusted Value-at-Risk)
Proposer des concepts similaires dans le domaine des données
de hautes fréquences portant sur la durée séparant deux
transactions successives comme le TaR (Time-at-Risk,
Gouriéroux, 2004)
Christophe Hurlin
Value-at-Risk

33. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque de crédit
De…nition (risque de crédit)
Le risque de crédit désigne le risque de pertes engendrées par une
situation dans laquelle les contreparties sont incapables ou ne
désirent pas remplir leurs obligations contractuelles.
Christophe Hurlin
Value-at-Risk

34. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque de crédit
Le risque de crédit peut être exprimé sous forme d’
exposition
(exposure) c’ à dire de montant soumis au risque ou de taux
est
de recouvrement (recovery rate) qui désigne la proportion
remboursée par l’
emprunteur.
Christophe Hurlin
Value-at-Risk

35. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque de crédit
Dans le cas du risque de crédit, les facteurs de risques sont
nombreux : statut du défaut (partiel ou total), exposition au
défaut, et les pertes étant donnée le défaut sont di¢ ciles à
calculer.
Ce qui explique que la VaR est rarement utilisée en tant
que telle dans le domaine de crédit
On préferre généralement des notions plus spéci…ques comme
l’
expected credit losses (ECT) ou la Worse Credit
Exposure (WCE)
Christophe Hurlin
Value-at-Risk

36. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque opérationnel
De…nition (risque opérationnel)
Le risque opérationnel est le risque qui résulte de processus
internes inapropriés, ou de systèmes défecteux ou d’
événements
externes (Jorion, 2007).
Christophe Hurlin
Value-at-Risk

37. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque opérationnel
Les risques opérationnels couvrent notamment :
1
le risque de modèle (model risk)
2
risque de personne ou de personnel (people risk)
3
risque légal (legal risk)
Christophe Hurlin
Value-at-Risk

38. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Qu’ ce que la VaR ?
est
Comment utiliser la VaR ?
Qui utilise la VaR ?
Quels types de risques mesure la VaR ?
Mesurer quels types de risques ?
Risque opérationnel
Etant donnée l’
importance des risques opérationnels et
certains exemples de désastres …nanciers, il existe aujourd’
hui
une volonté de quanti…er ces risques
Dans ce contexte, des calculs de VaR peuvent
théoriquement être appliqués aux risques opérationnels
Toutefois, la collecte de données de référence permettant
d’
établir la P&L associée à ces risques pose généralement de
très gros problèmes et limite par conséquent la portée de
l’
application de la VaR à ce contexte.
Christophe Hurlin
Value-at-Risk

39. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition statistique de la Value-at-Risk
Préambule
Christophe Hurlin
Value-at-Risk

40. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
De…nition (Value-at-Risk)
La Value-at-Risk (VaR) dé…nie pour un taux de couverture
de α% correspond au quantile d’
ordre α de la distribution de
pro…ts et pertes (pro…ts and losses, P&L) associée à la
détention d’ actif ou d’ portefeuille d’
un
un
actifs sur une
période donnée.
Christophe Hurlin
Value-at-Risk

41. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Christophe Hurlin
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Value-at-Risk

42. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Ainsi, la dé…nition de la Value-at-Risk est fondée sur trois éléments
1
La distribution des pro…ts et pertes (P&L) du portefeuille
ou de l’
actif
2
Le niveau de con…ance (ou de façon équivalente le taux de
couverture égal à un moins le niveau de con…ance) ; appelé
aussi taux de couverture
3
La période de détention de l’
actif (ou horizon du risque)
qui pose parfois le problème de l’
agrégration temporelle de
la VaR
Christophe Hurlin
Value-at-Risk

43. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Au délà des éléments de cette dé…nition, divers aspects de la VaR
doivent être évoqués à ce niveau :
1
La notion de VaR (ou de P&L) conditionnelle
2
et plus générallement la prévision de VaR
Christophe Hurlin
Value-at-Risk

44. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition statistique de la Value-at-Risk
Mesurer les rendements
Christophe Hurlin
Value-at-Risk

45. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
Quelles sont les données qui servent au calcul de la VaR ?
Comment transformer les données de sorte à les exprimer sous
forme de P&L ?
Christophe Hurlin
Value-at-Risk

46. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
Fact
Les données de P&L à partir desquelles on calcule une
Value-at-Risk peuvent prendre di¤érentes formes, mais elles sont
généralement exprimées sous forme de rendements (Dowd,
2005)
Dowd, K. (2005), Measuring market risk, John Wiley & Sons
Ltd.
Christophe Hurlin
Value-at-Risk

47. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
De…nition (pro…ts et pertes)
On note Pt la valeur d’ actif (ou d’ portefeuille) à la …n de la
un
un
période t. On note Dt l’
ensemble des paiements intermédiaires
obtenus entre les dates t 1 et t. Les pro…ts et pertes (P&L)
associés à la détention de l’
actif (ou du portefeuille) sont alors
dé…nis par :
P/Lt = Pt + Dt Pt 1
Christophe Hurlin
Value-at-Risk

48. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
Remarque 1 si les données sont exprimées sous forme de P&L, les
valeurs positives indiquent des pro…ts et les valeurs
négatives indiquent des pertes.
Remaqrue 2 Il est aussi possible d’
exprimer les données sous forme
de pertes et pro…ts (L&P pour losses and pro…ts)
telles que :
L/Pt = P/Lt
Christophe Hurlin
Value-at-Risk

49. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
Remarque 3 Il conviendrait de tenir compte d’ facteur
un
d’
actualisation dans la comparaison des valorisations
aux dates t et t 1. Si l’ évalue la valeur présente
on
des P&L à la …n de la date t 1, il vient :
present value P/L =
Pt + Dt
(1 + d )
Pt
1
où d désigne le taux d’
escompte psychologique.
Christophe Hurlin
Value-at-Risk

50. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
Remarque 4 Si l’ évalue la valeur future des P&L à la …n de la
on
date t, il vient :
forward value P/L = Pt + Dt
(1 + d ) Pt
1
Remarque 5 Généralement on néglige l’
escompte psychologique
dans le calcul des P&L sur des horizons courts
(quotidiens, hebdomadaires, mensuels, etc.)
Christophe Hurlin
Value-at-Risk

51. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
Les P&L sont généralement exprimées sous forme de rendements :
1
Rendements arithmétiques
2
Rendements géométriques
Christophe Hurlin
Value-at-Risk

52. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
De…nition (rendements arithmétiques)
Les rendements arithmétiques associés aux pro…ts et pertes
(P&L), notés rt , sont dé…nis comme :
rt =
Pt + Dt
Pt
Pt
1
1
=
Pt + Dt
Pt 1
1
Cette dé…nition des rendements suppose que les paiements
intérmédiaires Dt ne sont pas ré-investit (problème sur longue
période).
Christophe Hurlin
Value-at-Risk

53. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
De…nition (rendements géométriques)
Les rendements géométriques associés aux pro…ts et pertes
(P&L), notés Rt , sont dé…nis comme suit :
Rt = ln
Christophe Hurlin
Pt + Dt
Pt 1
Value-at-Risk

54. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
On peut passer de l’
une à l’
autre dé…nition par les formules
d’
approximation suivantes :
Rt = ln (1 + rt )
ce qui implique que si les rendements sont "petits" alors :
rt ' Rt
Christophe Hurlin
Value-at-Risk

55. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
Example (rendements géométrique et arithmétique )
Supposons qu’ une certaine date t les rendements arithmétiques
à
rt par unité de temps soient égaux à 5%. Les rendements
géométriques correspondants sont alors égaux à :
Rt = ln (1 + 0.05) = 0.0488
Inversement, si les rendements géométriques sont égaux à 5%, les
rendements arithmétiques sont alors égaux à
rt = exp(Rt )
1 = exp(0.05)
Christophe Hurlin
Value-at-Risk
1 = 0.0513

56. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Pro…ts et Pertes (P&L)
Les rendements géométriques supposent implicitement que les
paiements intermédiaires Dt sont ré-investis de façon continue.
Les rendements géométriques garantissent que le prix d’
actifs
ne devient jamais négatif (contrairement au rendement
arithmétique), y compris en cas de pertes massives
Généralement, on préfére utiliser les rendements
géométriques en lieu et place des rendements arithmétiques
Christophe Hurlin
Value-at-Risk

57. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Example (Rendements géométriques)
Considérons à titre d’
exemple l’
indice Standard & Poor observé en
clôture sur la période du 03/07/1989 au 24/11/2003 ainsi que le
rendement géométrique quotidien associé
Christophe Hurlin
Value-at-Risk

58. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Christophe Hurlin
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Value-at-Risk

59. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Christophe Hurlin
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Value-at-Risk

60. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Distribution de Pro…ts et Pertes (P&L)
Christophe Hurlin
Value-at-Risk

61. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Distribution de Pro…ts et Pertes (P&L)
De…nition (distribution de pro…ts et pertes)
La distribution de pro…ts et de pertes (P&L pour pro…t and
losses) correspond à la fonction de densité des pertes et pro…ts,
supposées aléatoires, associées à la détention de l’
actif ou du
portefeuille sur un horizon donné.
Christophe Hurlin
Value-at-Risk

62. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Distribution de Pro…ts et Pertes (P&L)
On considère les rendements géométriques, notés Rt ,
associés à la détention d’ actif sur un horizon donné
un
(exemple quotidien)
Ces rendements sont exprimés sous une forme P&L : un
rendement positif indique un gain, un rendement négatif une
perte
On suppose que ces rendements sont aléatoires : Rt est une
variable aléatoire réelle (v.a.r)
Christophe Hurlin
Value-at-Risk

63. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Distribution de Pro…ts et Pertes (P&L)
Comme toute v.a.r., le rendement à la date t, Rt , est caractérisé
par une fonction de densité, notée
fR t ( r )
8r 2 R
De…nition (P&L distribution)
C’ précisèment cette fonction de densité que l’ quali…e de
est
on
distribution de pro…ts et pertes (P&L distribution).
Christophe Hurlin
Value-at-Risk

64. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Distribution de Pro…ts et Pertes (P&L)
Remarque 1 : l’
idéal pour caractériser le risque serait de connaître
l’
ensemble de la densité de P&L, toutefois on se limite
généralement à une caractérisation du risque au travers de la
connaissance de certains moments (variance, skeweness, kurtosis)
ou de certains fractiles (VaR).
Christophe Hurlin
Value-at-Risk

65. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Distribution de Pro…ts et Pertes (P&L)
Remarque 2 : si la distribution de P&L est connue, on en déduit
immédiatement la VaR, puisque la VaR n’ rien d’
est
autre qu’
un
fractile de cette fonction de distribution
Christophe Hurlin
Value-at-Risk

66. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Dé…nition statistique de la Value-at-Risk
Dé…nition statistique de la Value-at-Risk
Christophe Hurlin
Value-at-Risk

67. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
De…nition (dé…nition statistique de la VaR)
Pour un taux de couverture (coverage rate) de α%, la
Value-at-Risk, notée VaRt (α) , correspond à l’
opposé du
fractile d’
ordre α de la distribution de pro…ts et pertes
(P&L).
VaRt (α) = FR t 1 (α)
où FR t (.) désigne la fonction de répartition associée à la
fonction de densité fR t (r ) .
Christophe Hurlin
Value-at-Risk

68. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Remarque : la VaR est généralement négative (perte) dans
une représentation P&L. Dès, lors par souci de simpli…cation, dans
la plupart des ouvrages on dé…nit la VaR en valeur positive en
considérant l’
opposé du fractile
VaRt (α) =
Christophe Hurlin
FR t 1 ( α )
Value-at-Risk

69. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Remarque : par dé…nition, on a :
Z
VaR t (α)
∞
Christophe Hurlin
fR t (r ) dr = α
Value-at-Risk

70. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
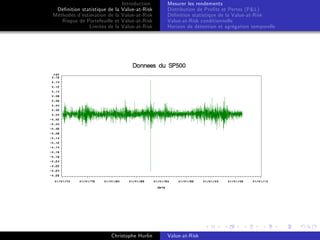
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
De…nition (taux de couverture)
Quelle que soit la dé…nition retenue (positive ou négative) de la
VaR, la probabilité d’
observer une perte supérieure à la VaR sur
l’
horizon de détention …xé est égale par dé…nition au taux de
couverture (coverage rate) :
Pr [Rt <
VaRt (α)] = α si VaRt (α) =
FR t 1 ( α )
Pr [Rt < VaRt (α)] = α si VaRt (α) = FR t 1 (α)
Christophe Hurlin
Value-at-Risk

71. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Remarque : Dans certains ouvrages (Jorion, Dowd..) ou certains
articles, on exprime la VaR en fonction du niveau de con…ance :
VaR (1
α) =
FR t 1 ( α )
On évoque par exemple une VaR à 99% pour un taux de
couverture de 1%, une VaR à 95% de niveau de con…ance etc.
Christophe Hurlin
Value-at-Risk

72. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
De…nition (convention de notation)
Dans le cadre de ce cours, on adoptera pour convention de
dé…nir la VaR de façon positive et en fonction du taux de
couverture et non du niveau de con…ance :
VaRt (α) =
Pr [Rt <
Christophe Hurlin
FR t 1 ( α )
VaRt (α)] = α
Value-at-Risk

73. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Le principe des méthodes paramétriques de calcul de la VaR
(cf. section 5) :
1
Postuler une distribution paramétrique de P&L (normale,
Student, GED etc..)
2
Donner une valeur aux paramètres de cette distribution
(estimation ou étalonnage)
3
Calculer le fractile correspondant
Christophe Hurlin
Value-at-Risk

74. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Hypothèse H1 : On suppose que la distribution des P&L à la date
t est une distribution normale d’
espérance µ et de variance σ2
Rt
Christophe Hurlin
N µ, σ2
Value-at-Risk

75. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Par dé…nition de la VaR on sait que :
Pr [Rt <
VaRt (α)] = α
Par conséquent :
Pr
Rt
µ
σ
VaRt (α)
σ
<
µ
=α
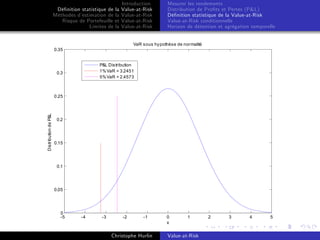
où sous l’
hypothèse H1 la variable centrée réduite (Rt
une loi normale standard N (0, 1)
Rt
µ
σ
Christophe Hurlin
N (0, 1)
Value-at-Risk
µ) /σ suit

76. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Si l’ note Φ (.) la fonction de répartition de la loi N (0, 1), il
on
vient :
VaRt (α) µ
Φ
=α
σ
Ou encore :
VaRt (α)
σ
µ
=Φ
1
(α)
1
(α)
On en déduit l’
expression de la VaR :
VaRt (α) =
Christophe Hurlin
µ
σΦ
Value-at-Risk

77. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
De…nition (VaR sous hypothèse de normalité)
Sous l’
hypothèse de normalité de la distribution de P&L, la VaR
associée à un taux de couverture de α% est égale à :
VaRt (α) =
µ
σΦ
1
(α)
où µ désigne l’
éspérance et σ2 la variance de la distribution de
P&L.
Christophe Hurlin
Value-at-Risk

78. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Example (VaR sous normalité)
On suppose que le rendement géométrique quotidien d’ actif
un
observé à la date t, noté Rt , suit une loi normale d’
espérance égale
à 0.01% et d’
écart-type égale à 1.5. On en déduit immédiatement
les VaR à 1% et 5% :
VaRt (0.01) =
0.01
1.5 Φ
1
(0.01) = 3.2451%
VaRt (0.05) =
0.01
1.5 Φ
1
(0.05) = 2.4573%
Christophe Hurlin
Value-at-Risk

79. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Example (VaR sous normalité, suite)
Si l’ détient cet actif sur une journée, il y a 1% de chance de
on
réaliser une perte au moins égale à 3.2451% du capital investit.
Pour un montant investit de 1M d’ on a :
e
VaR (5%) = 24 573e VaR (1%) = 32 451e
Christophe Hurlin
Value-at-Risk

80. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
VaR sous hy pothèse de normalité
0.35
P&L Distribution
1% VaR = 3.2451
5% VaR = 2.4573
0.3
Distribution de P&L
0.25
0.2
0.15
0.1
0.05
0
-5
-4
-3
-2
-1
Christophe Hurlin
0
x
1
Value-at-Risk
2
3
4
5

81. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Hypothèse H2 : On suppose que la distribution des P&L à la date
t est une distribution de Student à v degrés de liberté
Rt
t (v )
Comment calculer la VaR sous l’
hypothèse H2 ?
Christophe Hurlin
Value-at-Risk

82. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
De…nition (VaR et distribution de Student)
Sous l’
hypothèse de distribution de Student, la VaR associée à un
taux de couverture de α% est égale à :
VaRt (α) = G (α; v )
1
où G (α; v ) désigne la fonction de répartition d’
une loi de Student
à v degrés de liberté.
Christophe Hurlin
Value-at-Risk

83. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Example (VaR sous hypothèse de Student)
On suppose que le rendement géométrique quotidien d’ actif
un
observé à la date t, noté Rt , suit une loi de Student à 5 degrés de
liberté, on en déduit :
VaRt (0.01) = G
VaRt (0.05) = G
Christophe Hurlin
1
(0.01; 5) = 3.3649%
1
(0.05; 5) = 2.015%
Value-at-Risk

84. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Dé…nition de la Value-at-Risk
Example (VaR sous hypothèse de Student, suite)
Si l’ détient cet actif sur une journée, il y a 1% de chance de
on
réaliser une perte au moins égale à 3.3649% du capital investit.
Pour un montant investit de 1M d’ on a :
e
VaR (1%) = 33 649e VaR (5%) = 20 015e
Christophe Hurlin
Value-at-Risk

85. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
VaR sous distribution de Student
0.4
0.35
0.3
Distribution de P&L
0.25
0.2
0.15
P&L Dis tribution de Student t(5)
1% VaR = 3.3649
5% VaR = 2.015
0.1
0.05
0
-5
-4
-3
-2
-1
Christophe Hurlin
0
x
1
Value-at-Risk
2
3
4
5

86. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Christophe Hurlin
Value-at-Risk

87. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Généralement, on caractérise la distribution de P&L de façon
conditionnelle et non de façon marginale.
On dé…nit alors une distribution de pertes et pro…ts
conditionnelle, c’
est-à-dire une fonction de densité
conditionnelle à un ensemble d’
information disponible à la
date t, noté Ωt .
Cette densité conditionnelle est notée :
fR t ( r j Ω t )
Christophe Hurlin
Value-at-Risk

88. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
De…nition (VaR conditionnelle)
Pour un taux de couverture (coverage rate) de α%, la
Value-at-Risk conditionnelle à un ensemble d’
information
Ωt , notée VaRt ( αj Ωt ) , correspond à l’
opposé du fractile d’
ordre
α de la distribution conditionnelle de pro…ts et pertes (P&L) :
VaRt ( αj Ωt ) =
FR t 1 ( α j Ω t )
où FR t ( r j Ωt ) désigne la fonction de répartition associée à la
fonction de densité conditionnelle fR t ( r j Ωt ) .
Christophe Hurlin
Value-at-Risk

89. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Cette densité conditionnelle peut elle aussi être di¤érente
d’
une date à l’
autre, mais généralement on se restreint à des
densités conditionnelles invariantes dans le temps, i.e. telles
que :
fR t ( r j Ω t ) = fR ( r j Ω t ) 8 t
Cela revient à supposer que conditionnellement à un
ensemble d’
information (ou lorsque l’ cherche à
on
prévoir la Value-at-Risk), les rendements sont
identiquement distribués.
Christophe Hurlin
Value-at-Risk

90. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
De…nition (prévision de VaR)
La prévision de la Value-at-Risk pour la date t + 1 et pour
un taux de couverture de α%, obtenue conditionnellement à
l’
ensemble d’
information Ωt disponible à la date t, notée
VaRt +1 ( αj Ωt ) , est dé…nie par :
VaR t +1 jt (α) = VaRt +1 ( αj Ωt ) =
FR 1 ( α j Ω t )
où FR ( r j Ωt ) désigne la fonction de répartition associée à la
fonction de densité conditionnelle fR ( r j Ωt ) .
Christophe Hurlin
Value-at-Risk

91. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Example (prévision de VaR)
Supposons que les P&L à la date t + 1, notées Rt +1 , soient
normalement distribués. On cherche à prévoir la moyenne et la
variance de cette distribution conditionnellement à l’
information
disponible. Supposons que ces estimateurs soient dé…nis par les
moments conditionnels suivants :
b
µ t +1 jt = E ( Rt +1 j Ωt )
bt
σ2 +1 jt = V ( Rt +1 j Ωt )
Christophe Hurlin
Value-at-Risk

92. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Example (prévision de VaR, suite)
La distribution de P&L conditionnelle est alors :
Rt +1 j Ωt
bt
b
N µ t +1 jt , σ 2 +1 jt
On en déduit immédiatement une prévision de la VaR de t + 1
pour un taux de couverture de α% :
VaR t +1 jt (α) =
b
µ t +1 jt
Christophe Hurlin
b
σ t +1 jt Φ
Value-at-Risk
1
(α)

93. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Christophe Hurlin
Value-at-Risk

94. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Le deuxième élément fondamental dans le calcul de la
Value-at-Risk est la période de détention (ou l’
horizon de
risque) de l’
actif ou du portefeuille d’
actifs.
Il n’
existe aucune règle quant au choix de la période de
détention dans le calcul de la Value-at-Risk puisque ce
choix dépend fondamentalement de l’
horizon de reporting ou
de l’
horizon d’
investissement des opérateurs.
Toutefois, les autorités de régulation peuvent spéci…er des
horizons de détention spéci…ques notamment dans le cadre
des procédures de validation de la Value-at-Risk.
Christophe Hurlin
Value-at-Risk

95. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Un problème se lorsque la fréquence d’
observations des
P&L (intra-day, quotidienne, hebdomadaire, mensuelle etc..)
ne correspond pas à l’
horizon de risque
On doit alors transformer une mesure de risque adaptée à un
horizon en une mesure de risque adaptée en autre horizon,
généralement plus long : c’ le problème de l’
est
agrégation
temporelle
Christophe Hurlin
Value-at-Risk

96. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Le problème de l’
agrégation temporelle peut se poser de la
même façon lorsque l’ cherche à prévoir la VaR à un horizon
on
supérieur h à l’
unité. En e¤et pour ce faire deux solutions existent :
1
Soit prévoir directement la VaR en t + h, c’ à dire
est
VaR t +h jt (α) , dans ce cas le problème de l’
agrégation
temporelle ne se pose pas
2
Soit on cherche à établir la prévision de la VaR en t + h,
VaR t +h jt (α) , à partir de prévisions réalisées à un horizon
inférieur, typiquement à un horizon d’
une période, c’ à dire
est
VaR t +1 jt (α) , VaR t +2 jt +1 (α) , .., VaR t +h jt +h 1 (α) .
Christophe Hurlin
Value-at-Risk

97. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Dans le cadre du problème de l’
agrégation temporelle des
mesures de VaR, on doit distinguer deux cas :
1
le cas où l’ suppose que les rendements sont i.i.d.
on
2
le cas où l’ suppose que les rendements ne sont pas i.i.d.
on
Christophe Hurlin
Value-at-Risk

98. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Dans le cas où les rendements sont i.i.d., le problème est
relativement simple.
Supposons que l’ dispose de l’
on
espérance et de la variance de
la P&L exprimés en base annuelle. Soient µy et σ2 ces valeurs.
y
On cherche à déterminer les moments correspondants sur un
horizon di¤érent de l’
année sous l’
hypothèse de rendements
i.i.d. et sous l’
hypothèse que les mêmes positions ont été
maintenues sur l’
année.
Christophe Hurlin
Value-at-Risk

99. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Sous l’
hypothèse i.i.d., on a alors :
E (Rt ) = µy T
V (Rt ) = σ2 T
y
où T désigne l’
horizon du risque mesuré en nombre d’
années.
Exemple : 1/12 pour un horizon mensuel, 1/252 pour un horizon
quotidien si il y a 252 journée de cotation dans une année.
Christophe Hurlin
Value-at-Risk

100. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Example (Jorion, 2007)
Sur une base mensuelle, on suppose que le rendement moyen du
change EUR/$ est -0.15% et la volatilité est 3.28%. Sur une base
annuelle, sous l’
hypothèse i.i.d., le rendement espéré est égal à :
0.15
12 =
1.8% par an
et la volatilité annuelle
3.28
p
12 = 11.4% par an
Christophe Hurlin
Value-at-Risk

101. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Dans le cas où les rendements ne sont pas i.i.d., il convient de
postuler un modèle de dépendance entre les rendements :
Supposons par exemple que les rendements véri…ent
Rt = ρRt
1
+ εt
où εt est i.i.d. 0, σ2 .
ε
Dans ce cas, on montre que :
V
T
∑ Ri
i =1
h
= σ 2 T + 2 (T
R
où σ2 = σ2 1
ε
R
référence
1) ρ + 2 (T
2) ρ2 + .. + 2 (1) ρT
ρ2 désigne la variance sur l’
horizon de
Christophe Hurlin
Value-at-Risk
1

102. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Mesurer les rendements
Distribution de Pro…ts et Pertes (P&L)
Dé…nition statistique de la Value-at-Risk
Value-at-Risk conditionnelle
Horizon de détention et agrégation temporelle
Dé…nition statistique de la Value-at-Risk
Horizon de détention et agrégation temporelle
Example (Jorion, 2007)
Supposons que la volatilité quotidienne soit égale à 1%. Sur deux
semaines (10 jours de cotations), la volatilité est multipliée par
p
10 = 3.16 si l’ suppose l’
on
absence de dépendance des
rendements (ρ = 0). En revanche, si ρ = 0.2, la volatilité
augmente de 3.79. Si ρ = 0.5, il faut mutiplier la volatilité
quotidienne par 5.10 pour obtenir la volatilité en base
bi-hebdomadaire.
Christophe Hurlin
Value-at-Risk

103. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Méthodes d’
estimation de la Value-at-Risk
Préambule
Christophe Hurlin
Value-at-Risk

104. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
On dénombre trois grandes classes de méthodes d’
estimation de la
VaR :
1
Méthodes non-paramétriques (Historical Simulation,
Weighted Historical Simulation, Filtered Historical
Simulation...).
2
Méthodes semi-paramétriques (CAViaR, théorie des
extrêmes).
3
Méthodes paramétriques (ARCH, GARCH univarié, GARCH
multivarié, RiskMetrics).
Christophe Hurlin
Value-at-Risk

105. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Dans cette section, nous limiterons notre analyse aux méthodes
d’
estimation de la VaR de type univariées applicables :
1
aux rendements associés à la détention d’ actif
un
2
aux rendements associés à la détention d’ portefeuille
un
d’
actifs en négligeant les gains liés à la diversi…cation des
risques et les corrélations entre actifs.
Christophe Hurlin
Value-at-Risk

106. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Remarque : on trouve dans certains ouvrage le terme "méthodes
de calcul"’de la VaR. Ce terme est impropre, on doit plutôt utiliser
le terme de "méthodes d’
estimation" de la VaR. La VaR est le
fractile d’
une distribution de P&L, dès lors deux solutions
1
Soit la distribution de P&L est connue, et à ce moment on
calcule le fractile correspondant
2
Mais généralement, la distribution de P&L n’ pas
est
connue ou les paramètres de cette distribution ne sont
pas connues. On doit estimer la densité associée, ou les
paramètres de cette densité, ou son fractile directement. On
parle alors de méthodes d’
estimation de la VaR.
Christophe Hurlin
Value-at-Risk

107. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Méthodes d’
estimation de la Value-at-Risk
Méthodes non paramétriques
Christophe Hurlin
Value-at-Risk

108. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (Méthodes non paramétriques)
Le principe général des méthodes non paramétriques
d’
estimation / prévision de la Value-at-Risk est que l’ impose a
on
priori aucune distribution paramétrique de pertes et pro…ts.
Christophe Hurlin
Value-at-Risk

109. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Les principales méthodes sont les suivantes :
1
Historical Simulation (HS)
2
Bootstrapped Historical Simulation
3
Simulation Historique et Estimation Non Paramétrique de
Densité
4
Weighted Historical Simulation (WHS) ou Hybrid
Method
5
Filtered Historical Simulation (FHS)
Christophe Hurlin
Value-at-Risk

110. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Simulation Historique
Christophe Hurlin
Value-at-Risk

111. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
1
La simulation historique (Historical Simulation, ou HS) est
une méthode très simple qui est sans doute la plus utilisée
actuellement
2
Formellement, la VaR est estimée simplement par le fractile
empirique des rendements passés.
3
Si l’ considère par exemple un niveau de con…ance de 95%
on
et que l’ dispose d’ échantillon de 1000 observations
on
un
historiques de rendements, la VaR est donnée par la valeur du
rendement qui correspond à la 50ème plus forte perte.
Christophe Hurlin
Value-at-Risk

112. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
De…nition
Soit fR1 , R2 , ..RT g la séquence des rendements Rt de l’
actif ou du
portefeuille, observés aux dates t = 1 à T . A cette séquence
correspond un échantillon de T observations fr1 , r2 , .., rT g.
Christophe Hurlin
Value-at-Risk

113. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Problem
Théoriquement, à chaque date, le rendement Rt est une v.a.r qui
admet une certaine distribution, notée fR t (.) , et donc un fractile
d’
ordre α, noté VaRt (α) , qui lui est propre. Or, on ne dispose que
d’une seule réalisation, rt , de cette distribution. A partir de cette
unique réalisation, sans hypothèse supplémentaire, il est
impossible d’
estimer le fractile de la distribution des P&L à la date
t, c’ à dire la VaR.
est
Christophe Hurlin
Value-at-Risk

114. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Dans l’
approche HS, on fait deux hypothèses très fortes :
1
On suppose que la distribution non conditionnelle des
rendements est identique quelle que soit la date t :
fR t ( w ) = fR ( w ) 8 t
par conséquent le fractile de cette distribution non
conditionnelle (la VaR) est aussi identique :
VaRt (α) = VaR (α) 8t
2
On suppose que les rendements R1 , .., RT sont
indépendamment distribués.
Christophe Hurlin
Value-at-Risk

115. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Hypothèse : on suppose que les rendements Rt associés aux P&L,
observés à toute date t, sont identiquement et
indépendamment distribués (i.i.d) avec :
fR t ( w ) = fR ( w ) 8 t
VaRt (α) = VaR (α) 8t
Christophe Hurlin
Value-at-Risk

116. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Solution
Sous l’
hypothèse i.i.d, on dispose alors d’ échantillon de T
un
réalisations fr1 , r2 , .., rT g de T v.a.r. admettant la même
distribution (ou de la même variable aléatoire) et donc la même
VaR. Il est dès lors possible d’
estimer cette VaR.
Christophe Hurlin
Value-at-Risk

117. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (VaR HS)
Sous l’
hypothèse de rendements i.i.d., un estimateur convergent
de la VaR pour un taux de couverture de α% est dé…ni par le
fractile empirique d’
ordre α associés aux T réalisations historiques
des rendements, notées fr1 , r2 , .., rT g.
b
V aR (α) = percentile frj gT 1 , 100α
j=
b
V aR (α)
p
! VaR (α)
T !∞
Christophe Hurlin
Value-at-Risk

118. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Fig.: Source : Jorion (2007)
Christophe Hurlin
Value-at-Risk

119. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Example
On considère les rendements quotidiens dé…nies à partir des cours
à la clotûre du Nikkei entre le 05/01/2004 et le 02/05/2006, soit
un total de 5550 observations. Supposons que l’ classe par ordre
on
croissant les observations r1 , .., r5550 . La VaR HS à 1% est alors
`
égale à la 56eme , soit :
b
V aRt (1%) =
Christophe Hurlin
0, 01507%
Value-at-Risk

120. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Fig.: Rendements Quotidiens Nikkei 05/01/2004 - 02/05/2006
0.06
0.04
0.02
0.00
-0.02
-0.04
1000
2000
Christophe Hurlin
3000
4000
Value-at-Risk
5000

121. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Empiric al CDF of NIKKEI
Quantiles of NIKKEI
1.0
0.06
0.8
0.04
0.6
0.02
0.4
0.00
0.2
-0.02
0.0
-0.02
0.00
0.02
0.04
0.06
Christophe Hurlin
-0.04
0.0
0.2
Value-at-Risk
0.4
0.6
0.8
1.0

122. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Remarque : La VaR HS est l’
estimateur d’
une VaR non
conditionnelle (ou associée à une distribution de P&L non
conditionnelle).
Par conséquent la prévision de VaR selon la méthode HS sera
relativement "invariante" aux modi…cations de
l’
environnement économique.
Les prévisions de VaR selon la méthode HS sont "plates"
ou "pratiquement plates" (dans le cas rolling estimates).
Christophe Hurlin
Value-at-Risk

123. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
C’ le principal défaut de cette méthode (Hendricks, 1996 ;
est
Boudoukh et al. 1998 ; Pritsker, 2006) : il est invraisemblable que
les nombreux facteurs microstructurels et macroéconomiques
concourant à la formation du prix d’ actif demeurent inchangés
un
dans le temps.
Hendricks, D.. (1996), ”Evaluation of Value-at-Risk Models
Using Historical Data ”,Economic Policy Review, Federal
Reserve Bank of New York, April, pp. 39-69.
Pritsker, M. (2006), "The hidden dangers of historical
simulation", Journal of Banking & Finance, Volume 30, Issue
Christophe Hurlin
Value-at-Risk

124. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Problem
Comment construire une prévision de VaR selon la méthode
HS ?
La solution consiste tout simplement à utiliser le fractile empirique
associé aux observations passées R1 , .., R2
VaR T +1 jT (α) = percentile frj gT 1 , 100α
j=
L’
idée est alors que puisque le rendement en T + 1 à la même
distribution que R1 , .., RT , un estimateur de sa VaR peut être
obtenu à partir de l’
estimateur de la VaR des rendements passés.
Christophe Hurlin
Value-at-Risk

125. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Problem
Comment construire une séquence de prévisions de la VaR
selon la méthode HS (backtesting) ?
Comme pour tous les estimateurs, il y a deux solutions :
soit on construit un estimateur glissant (rolling estimate)
de la VaR en t + 1 à partir d’ sous ensemble
un
d’
informations récentes de taille …xe (idée de
conditionnement).
soit on construit une successions d’
estimateurs de la VaR
conditionnellement à toute l’
information disponible, qui
croît au fer et à mesure que le temps passe
Christophe Hurlin
Value-at-Risk

126. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Fig.: Prévision Glissante (Rolling Estimate)
1ère Estimation
Prévision
temps
1
T-N
2ème Estimation
1
T-N+1
Prévision
2
T-N+1
Christophe Hurlin
Value-at-Risk
T-N+2

127. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Fig.: Prévision HS non Glissante
1ère Estimation
Prévision
temps
1
T-N
2ème Estimation
1
T-N+1
Prévision
2
T-N+1
Christophe Hurlin
Value-at-Risk
T-N+2

128. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Fact
Dans la littérature, on utilise généralement des séquences de
prévisions construites à partir d’
une estimation glissante
(rolling estimate) a…n d’
introduire un "minimum de
conditionnement" dans la VaR-HS et de ne pas accorder trop de
poids aux réalisations des rendements les plus anciennes.
Christophe Hurlin
Value-at-Risk

129. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (Prévisions VaR-HS)
Les prévisions glissantes de VaR pour un taux de couverture de α%
obtenues par la méthode de simulation historiques correspondent
au fractile empirique d’
ordre α de la chronique des rentabilités
passées observées sur une fenêtre de taille Te :
VaR t jt
1 (α)
= percentile frj gt=t1
j
Christophe Hurlin
Value-at-Risk
T e , 100α

130. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Plus la taille de la fenêtre Te est petite, plus les prévisions de
VaR seront volatiles
Plus la taille de la fenêtre Te est grande, plus la VaR prévue
convergera vers la VaR non conditionnelle et sera par
conséquent quasi "constante" dans le temps.
Christophe Hurlin
Value-at-Risk

131. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Example (Candelon et al. 2008)
Les auteurs considèrent les rendements quotidiens du Nasdaq et
appliquent trois méthodes de prévisions de la VaR à 5% dont la
méthode HS. Ils considèrent une estimation glissante (rolling
estimation) sur une fenêtre de 250 observations. Sur le graphique
suivant est reportée une séquence de 250 prévisions obtenues pour
la période du 22 Juin 2005 au 20 Juin 2006 ainsi que les
rendements observés ex-post.
Candelon, B, Colletaz, G, Hurlin C. et Tokpavi. (2008),
”Backtesting Value-at-Risk : A GMM duration-based test”,
Working Paper.
Christophe Hurlin
Value-at-Risk

132. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Fig.: Historical Returns and 5% VaR Forecasts. Nasdaq (June 2005June 2006)
Na s d a d
0.03
Re tu rn s
Hi s toric al Sim ulation 5% VaR
0.02
0.01
0
-0.01
-0.02
-0.03
0
50
100
Christophe Hurlin
150
200
Value-at-Risk
250

133. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Example (Christo¤ersen et Pelletier, 2004)
Les auteurs proposent un test de backtesting. A…n d’
étudier les
propriétés de ce test, ils proposent des simulations de Monte Carlo
dans lesquelles ils simulent des rendements selon un processus
GARCH sous Student, puis appliquent la méthodologie HS pour
prévoir les VaR sur ces rendements simulés.
Christoffersen, P. F. and D. Pelletier (2004),
"Backtesting Value-at-Risk : A duration-based approach",
Journal of Financial Econometrics, 2, 1, pp. 84-108.
Christophe Hurlin
Value-at-Risk

134. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Fig.: Source : Christo¤ersen and Pelletier (2004)
Christophe Hurlin
Value-at-Risk

135. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Bootstrapped Historical Simulation (BHS)
Christophe Hurlin
Value-at-Risk

136. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Une amélioration simple de la méthode HS consiste à
estimer la VaR à partir de données simulées par Bootstrap.
Le Bootstrap consiste à ré-échantillonner les données
historiques de rendements avec remise.
Christophe Hurlin
Value-at-Risk

137. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Plus précisément, la procédure consiste à créer un grand
nombre d’
échantillons de rendements simulés, où chaque
observation est obtenue par tirage au hasard à partir de
l’
échantillon original.
Chaque nouvel échantillon constitué de la sorte permet
d’
obtenir une estimation de la VaR par la méthode HS
standard, et l’ dé…nit au …nal une estimation en faisant la
on
moyenne de ces estimations basées sur les ré-échantillonnages.
Christophe Hurlin
Value-at-Risk

138. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (Bootstrapped Historical Simulation)
n oT
Soit ejs
r
une séquence de rendements tirés au hasard avec
j =1
remise dans l’
échantillon de rendements historiques, et soit
e
V aR s (α) la VaR-HS associée à cet échantillon de rendements
bootstrappés. L’
estimateur BHS (Bootstrapped Historical
Simulation) de la VaR correspond à la moyenne empirique des
VaR-HS obtenues à partir de S échantillons de rendements
boostrappés :
1 S e
b
V aR (α) = ∑ V aR s (α)
S s =1
e
r j=
V aR s (α) = percentile fejs gT 1 , 100α
Christophe Hurlin
Value-at-Risk
s = 1, .., S

139. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Remarque 1 : Le fait de construire la moyenne d’ grand nombre
un
de VaR-HS obtenues sur des échantillons de rendements
boostrapés fait que l’ limite l’
on
in‡uence des pertes extrêmes,
notamment lorsque l’ utilise cette méthode pour la prévision. On
on
obtient ainsi des prévisions plus volatiles.
Christophe Hurlin
Value-at-Risk

140. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Remarque 2 : pour construire une prévision glissante par la
méthode BHS, il su¢ t de ré-échantilloner (pour chaque prévision)
non plus T valeurs, mais uniquement Te valeurs, où Te désigne la
taille de la fenêtre.
Christophe Hurlin
Value-at-Risk

141. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Example (Boostrapped Historical Simulation)
A partir des codes développés par Dowd (2005), Dutta et
Bhattacharya (2006) évaluent les peformances des prévisions de
VaR par la méthode BHS sur un indice de valeurs indiennes. Ils
reportent notamment l’
histogramme des réalisations des VAR-HS
obtenues sur les 10 000 échantillons bootstrappés. Dans leur
application, la VaR(5%) HS était égale à 49.935 tandis que la VaR
BHS est égale à 51.23
Debashis Dutta and Basabi Bhattacharya (2006), "A
Bootstrapped Historical Simulation Value at Risk Approach to
S & P CNX Nifty", Working paper, Jadavpur University
Christophe Hurlin
Value-at-Risk

142. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Christophe Hurlin
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Value-at-Risk

143. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Simulation Historique et Estimation Non
Paramétrique de Densité
Christophe Hurlin
Value-at-Risk

144. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Une autre amélioration possible de la HS est d’
utiliser une
estimation non paramétrique de la distribution conditionnelle
de pertes et pro…ts.
On sait en e¤et que l’
histogramme associé aux réalisations
historiques des rendements n’ pas un bon estimateur
est
d’
une fonction de densité. Des estimateurs obtenus par
lissage, comme les estimateurs à noyau, présentent
généralement de meilleures propriétés (voir Yatchew, 2003
pour plus de détails).
Yatchew A. (2003), SemiParametric Regression or the
Applied Econometrician, Cambridge University Press.
Christophe Hurlin
Value-at-Risk

145. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (méthode HS étendue)
Dans cette perspective, la méthode HS étendue consiste à
estimer par une méthode de noyau la densité conditionnelle
de pertes et pro…ts, puis de calculer à partir de cette densité
estimée le fractile correspondant à la Value-at-Risk (Butler et
Schachter, 1998).
Butler J.S. and Schachter B. (1998), "Estimating VaR
with a precision measure by combining Kernel estimation with
Historical Simulation, Working Paper, Vanderbilt University,
Christophe Hurlin
Value-at-Risk

146. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Avantage : Cette méthode permet notamment d’
estimer la
Value-at-Risk pour n’
importe quel niveau de con…ance (et ainsi
d’
éviter les problèmes dus aux contraintes imposées sur la taille des
échantillons). Exemple : calculer une VaR à 1% à partir d’
un
échantillon de 50 points.
Christophe Hurlin
Value-at-Risk

147. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Limite : toutefois, il est connu que les estimateurs kernel
présentent des e¤ets de bords, et que la précision de ces
estimateurs est parfoirs très faibles sur les "bords" de l’
échantillon,
précisèment là où l’ cherche à estimer la VaR
on
Christophe Hurlin
Value-at-Risk

148. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Mise en oeuvre : Estimateurs Kernel
voir le cours d’
économétrie semi et non paramétrique
Christophe Hurlin
Value-at-Risk

149. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (VaR et estimation Kernel)
Un estimateur de la VaR pour un taux de couverture de α% peut
ête obtenu à partir de l’
estimateur à noyau (kernel estimate) de la
fonction de densité des P&L comme suit :
α=
Z V aR t (α)
b
∞
b t (r ) dr
fR
T
b t (r0 ) = 1 ∑ K
fR
T λ t =1
rt
r0
λ
où K (.) désigne une fonction kernel, λ un paramètre de lissage
(bandwidth parameter) et T la taille de l’
échantillon utilisé pour
l’
estimation.
Christophe Hurlin
Value-at-Risk

150. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Example (Rendements quotidiens sur Nikkei)
On considère les rendements quotidiens dé…nies à partir des cours
à la clotûre du Nikkei entre le 05/01/2004 et le 02/05/2006, soit
un total de 5 550 observations. La VaR HS à 1% est égale à
0, 01507%. Dans le cas d’
une estimation kernel de la densité de
P&L on trouve (kernel gaussien), la valeur suivante :
Christophe Hurlin
Value-at-Risk

151. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Fig.: Estimateur Kernel (Gaussien) de la distribution de P&L sur les
rendements quotidiens du Nikkei
Kernel Density (Epanechnikov, h = 0.0015)
100
80
60
40
20
0
-0.02
0.00
Christophe Hurlin
0.02
Value-at-Risk
0.04

152. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Weighted Historical Simulation (WHS)
Christophe Hurlin
Value-at-Risk

153. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
La caractéristique essentielle de la méthode HS traditionnelle
est que l’ accorde le même poids aux observations
on
historiques, quelles soient relativement récentes ou au
contraire très anciennes.
Concrètement, si l’ considère une estimation HS de la Var à
on
5% à partir d’
une fenêtre glissante de 1000 observations, cela
revient à prendre le 50ème rendement le plus faible parmi les
1000 observations les plus récentes.
Christophe Hurlin
Value-at-Risk

154. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Dans cette estimation HS toutes les observations historiques
de rendement datées de moins de 1000 périodes interviennent
avec le même poids.
Une approche alternative consiste à attribuer aux
observations de rendements des poids en fonction soit de
leur ancienneté, soit de la volatilité observée des marchés, ou
de tout autre facteur.
Christophe Hurlin
Value-at-Risk

155. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Cette approche, quali…ée par le terme générique de WHS
(Weighted Historical Simulation) recouvre notamment :
1
La méthode Aged-weighted HS où les poids dépendent de
l’
ancienneté des observations (Boudoukh, Richardson et
Whitelaw, 1998).
2
La méthode Volatility-weighted HS où les poids dépendent
de la volatilité. L’
idée de base (Hullet et White, 1998) est de
prendre en compte les changement récents de volatilité.
3
La méthode Correlation-weighted HS où l’ ajuste les
on
rendements passés de façon à ce qu’ re‡ètent les
ils
changements entre les corrélations passées et futures.
Christophe Hurlin
Value-at-Risk

156. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Présentons la méthodologie de type Aged-wheighted HS appelée
aussi Méthode Hybride proposée par Boudoukh, Richardson et
Whitelaw (1998)
Boudoukh J, M Richardson et R Whitelaw, (1998),
“The Best of Both Worlds”, Risk, 11, p. 64-67.
Christophe Hurlin
Value-at-Risk

157. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Avantages :
Comme le souligne Pritsker (2001), on peut s’
accommoder du
non respect de l’
hypothèse de distributions i.i.d, en supposant
que les observations les plus récentes de l’
ensemble Ωt 1 sont
conditionnellement les plus importantes pour une éventuelle
prévision.
L’
approche demeure non paramétrique, l’
avantage ici est que
l’ exploite une information supplémentaire, à savoir le
on
caractère plus informatif des rentabilités les plus proches de
l’
horizon de prévision.
Christophe Hurlin
Value-at-Risk

158. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (VaR Hybride)
Techniquement, le calcul de la VaR Hybride se fait en trois étapes :
(i ) à chacune des Te rentabilités les plus récentes rt 1 ,
rt 2 , ..., rt Te constituant l’
ensemble Ωt 1 est associée une
pondération décroissante avec le temps de la forme
1 λ
, 11 λλ λ, ..., 11 λλ λTe 1 où λ < 1, puis (ii ) les
Te
Te
1 λTe
rentabilités (et les poids associés) sont ensuite ordonnées de
manière croissante et (iii ) en…n les poids ordonnés suivant les
niveaux de rentabilité croissants sont sommés jusqu’ hauteur de
à
α%. La VaR est alors égale à la rentabilité correspondant au
dernier poids utilisé dans la sommation.
Christophe Hurlin
Value-at-Risk

159. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Example (VaR Hybride)
Dans Hurlin et Tokpavi (2008), nous évaluons les procédures de
backtesting en appliquant les tests usuels sur des prévisions de VaR
issues de sept méthodes di¤érentes parmi lesquelles …gurent la
méthode hybride. Les résultats obtenus sur un échantillon de 250
observations des rendements quotidiens associés aux cours à la
clotûre du Nasdaq sont reproduits sur la …gure suivante. Dans
cette application, les auteurs considèrent des valeurs de λ et Te
respectivement …xées à 0.98 et 250
Hurlin C. et Tokpavi S. (2008), ”Une Evaluation des
Procédures de Backtesting : Tout va pour le Mieux dans le
Meilleur des Mondes", Finance, vol 29(1), pp.53-80,
Christophe Hurlin
Value-at-Risk

160. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Fig.: Prévisions out-of-sample de VaR à 5%, Indice Nasdaq, T = 250
0.04
Méthode Delta Normale
RiskMetrics
GARCH Student
Simulation Historique
Méthode Hybride
CAViaR
Rendements Ex-post
0.03
0.02
0.01
0
-0.01
-0.02
-0.03
-0.04
-0.05
0
50
100
Christophe Hurlin
150
Value-at-Risk
200
250

161. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Méthodes d’
estimation de la Value-at-Risk
Méthodes paramétriques
Christophe Hurlin
Value-at-Risk

162. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Nous ne présenterons ici brièvement (pour plus de détails cf. partie
2) les méthodes paramétriques suivantes :
1
La méthode de Monte Carlo
2
Le modèle RiskMetric
3
Les modèles ARCH-GARCH
Christophe Hurlin
Value-at-Risk

163. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Méthode de Monte Carlo
Christophe Hurlin
Value-at-Risk

164. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (Monte Carlo)
La méthode de Monte Carlo consiste à simuler un grand nombre de
fois les comportements futurs possibles des facteurs de risque selon
un certain nombre d’
hypothèses, et d’ déduire une distribution
en
des pertes et pro…ts à partir de laquelle on estime …nalement un
fractile (HS).
Christophe Hurlin
Value-at-Risk

165. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Si cette approche peut s’
appliquer, en théorie, quelles que
soient les lois de probabilité suivies par les facteurs de risque,
elle est couramment utilisée en pratique, pour des raisons
techniques, en supposant que les variations relatives des
paramètres de marché suivent des lois normales.
Cette méthode convient également à tous les types
d’
instruments, y compris optionnels, et permet de tester de
nombreux scénarios et d’ inclure explicitement des queues de
y
distribution épaisses (événements extrêmes pris en compte
dans une certaine mesure).
Christophe Hurlin
Value-at-Risk

166. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
RiskMetrics
Christophe Hurlin
Value-at-Risk

167. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
RiskMetrics fut developpé par la banque JP Morgan au début
des années 90 et a permis de populariser le concept de VaR
Ce modèle repose sur des hypothèses théoriques assez
contraignantes
Dans ce modèle, les principales hypothèses simpli…catrices
consistent à supposer, d’
une part, que les lois de probabilité
qui régissent les distributions des variations des prix de
marché sont normales et, d’
autre part, que les instruments
présentent un pro…l de risque linéaire.
Christophe Hurlin
Value-at-Risk

168. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (RiskMetrics)
Dans le cas d’
une approche univariée, la VaR issue de RiskMetrics
dé…nie pour un taux de couverture de α% peut s’
écrire sous la
forme :
p
VaRt (α) = Φ (α) ht µ
où µ désigne l’
espérance des rendements et ht la variance
conditionnelle, telle que :
ht = λht
1
+ (1
λ) rt2
1
où λ désigne un paramètre de decalage (decay parameter)
générallement …xé à 0.97.
Christophe Hurlin
Value-at-Risk

169. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Remarque :
Dans le modèle RiskMetrics, la variance conditionnelle est
supposée suivre un processus de type EWMA (Exponentiel
Weighted Moving Average) : la prévision pour la date t est
une combinaison linéaire de l’
innovation passée et de la valeur
passée de la variance
Ce processus est un cas particulier des modèles GARCH,
et plus spéci…quement des modèles IGARCH (cf. partie 2
du cours)
Christophe Hurlin
Value-at-Risk

170. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Avantages : Sous ces hypothèses, la matrice de
variances/covariances peut être appliquée assez directement aux
positions détenues pour calculer la VaR. Les calculs utilisés dans la
méthode RiskMetrics sont rapides et simples, et requièrent
uniquement la connaissance de la matrice des
variances/covariances des rendements du portefeuille.
Christophe Hurlin
Value-at-Risk

171. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Limite : cette méthode s’
avère être inadaptée aux portefeuilles non
linéaires (instruments optionnels) et théoriquement peu adaptée
aux queues de distribution épaisses et aux distributions non
normales des rendements. Par ailleurs, la …xation du decay
parameter peut poser problème sur certains échantillons
(contrairement aux paramètres des modèles GARCH qui sont
estimés par MV)
Christophe Hurlin
Value-at-Risk

172. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Modèles GARCH
Christophe Hurlin
Value-at-Risk

173. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (GARCH univariés)
Les modèles GARCH permettent de modéliser et de prévoir la
variance conditionnelle de la distribution de pertes et pro…ts, ce qui
permet dans un second temps de déduire une modélisation ou une
prévision de la Value-at-Risk sous un certain nombre d’
hypothèses
concernant la distribution conditionnelle des rendements
Christophe Hurlin
Value-at-Risk

174. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Quel est le lien entre la prévision de variance conditionnelle
et la prévision de VaR ?
Engle R.F. (2001), ”The Use of ARCH/GARCH Models in
Applied Econometrics”, Journal of Economic Perspectives,
15(4), 157-168.
Christophe Hurlin
Value-at-Risk

175. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (VaR sous hypothèse de normalité)
Sous l’
hypothèse de normalité de la distribution conditionnelle des
P&L, la prévision de VaR associée à un taux de couverture de α%
est dé…nie par :
p
ht +1 Φ 1 (α)
VaR t +1 jt (α) = µ
où ht +1 désigne la variance conditionnelle des rendements.
Christophe Hurlin
Value-at-Risk

176. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Theorem
Pour toute distribution elliptique, la prévision de VaR est une
transformée linéaire de la prévision de variance (volatilité).
Prévoir la variance permet de prévoir la VaR.
Christophe Hurlin
Value-at-Risk

177. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (Famille de distributions elliptiques)
Une distribution appartient à la famille des distributions
elliptiques si le logarithme de sa densité peut s’
écrire sous la
forme :
x µ 2
=c
σ
où c désigne une constante, µ est un paramètre de location
(location parameter) et σ un terme d’
échelle (scale parameter)
Exemples : distribution normale, distribution de Student, normal
inverse gaussienne (NIG)
Christophe Hurlin
Value-at-Risk

178. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Méthodes d’
estimation de la Value-at-Risk
Méthodes semi paramétriques
Christophe Hurlin
Value-at-Risk

179. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Situées à mi-chemin entre les approches purement paramétriques
et non paramétriques …gurent notamment :
1
La théorie des valeurs extrêmes (EVT)
2
Les régressions quantiles et plus particulierement le modèle
CAViaR
Christophe Hurlin
Value-at-Risk

180. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Théorie des Valeurs Extrêmes
Christophe Hurlin
Value-at-Risk

181. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Parmi les méthodes semi-paramétriques …gurent tout d’
abord
l’
ensemble des méthodes et approches qui relèvent de la
théorie des extrêmes (EVT) qui di¤ère de la théorie statistique
habituelle fondée pour l’
essentiel sur des raisonnements de
type “tendance centrale”.
Les extrêmes sont en e¤et gouvernés par des théorèmes
spéci…ques qui permettent d’
établir sous di¤érentes
hypothèses la distribution suivie par ces extrêmes.
Christophe Hurlin
Value-at-Risk

182. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Il existe deux principales branches de la théorie des valeurs
extrêmes :
1
La théorie des valeurs extrêmes généralisée permet de
modéliser le maximum ou le minimum d’ très grand
un
échantillon
2
La loi de Pareto généralisée (ou approche POT “peaks-over-threshold”) qui permet l’
étude de la distribution
des pertes excessives au dessus d’ seuil (élevé).
un
Christophe Hurlin
Value-at-Risk

183. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Regressions quantiles et CAViaR
Christophe Hurlin
Value-at-Risk

184. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Une seconde grande catégorie de méthodes
semi-paramétriques utilisées actuellement pour le calcul et la
prévision de la Value-at-Risk relève plus généralement de
l’
approche de la régression quantile.
L’
idée est la suivante : plutôt que de modéliser une
distribution et d’ déduire un quantile (la
en
Value-at-Risk), cette approche consiste à modéliser
directement le quantile lui-même en utilisant des
méthodes de régression quantile.
Christophe Hurlin
Value-at-Risk

185. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Un exemple de ces méthodes est le modèle Conditional
Autoregressive Value at Risk (CAViaR) de Engle et Manganelli
(2004) qui spéci…e la dynamique autorégressive du quantile
conditionnel.
Engle, R. F., et S. Manganelli. (2004), ”CAViaR :
Conditional autoregressive Value-at-Risk by regression
quantiles”, Journal of Business and Economic Statistics 22, p.
367-381.
Christophe Hurlin
Value-at-Risk

186. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
De…nition (CAViaR)
Dans le cas du modèle Conditional Autoregressive Value at
Risk (CAViaR), la modélisation porte directement sur le fractile
latent. Ainsi, la VaR conditionnelle à α% est dé…nie par le modèle
suivant :
VaR t jt
1 (α)
= β0 + β1 VaR t
1 jt 2 ( α )
+l β2 , ..., βp , rt
1 , VaR t 1 jt 2 ( α )
où βi 2 R et où l (.) est une fonction de la rentabilité et de la VaR
de la période précédente.
Christophe Hurlin
Value-at-Risk

187. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Remarque : Engle et Manganelli proposent quatre spéci…cations
pour cette fonction, parmi lesquelles …gure la spéci…cation de type
Asymetric Slope :
l β2 , β3 , rt
1 , VaR t 1 jt 2 ( α )
= β2 max (rt
Christophe Hurlin
Value-at-Risk
1 , 0)
β3 min (rt
1 , 0)

188. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Les techniques de régression quantile non linéaire permettent
d’
estimer la valeur des paramètres βi et ensuite celle de la VaR de
la période courante. Le modèle à estimer est alors le suivant :
rt = VaR t jt
1 ( α ) + εt
Quantα ( εt j Ωt ) = 0
La minimisation d’
une fonction quantile objectif introduite par
Koenker et Basset (1978) permet alors d’
obtenir des estimateurs
des paramètres βi asymptotiquement convergents.
Christophe Hurlin
Value-at-Risk

189. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Fig.: Source : Engle et Manganelli (2004)
Christophe Hurlin
Value-at-Risk

190. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Méthodes d’
estimation de la Value-at-Risk
Example (Candelon et al. 2008)
Les auteurs considèrent les rendements quotidiens du Nasdaq et
appliquent trois méthodes de prévision de la VaR à 5% dont la
méthode HS. Ils considèrent une estimation glissante (rolling
estimation) sur une fenêtre de 250 observations. Sur le graphique
suivant est reportée une séquence de 250 prévisions obtenues pour
la période du 22 Juin 2005 au 20 Juin 2006 ainsi que les
rendements observés ex-post.
Candelon, B, Colletaz, G, Hurlin C. et Tokpavi. (2008),
”Backtesting Value-at-Risk : A GMM duration-based test”,
Working Paper.
Christophe Hurlin
Value-at-Risk

191. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Méthodes non paramétriques
Méthodes paramétriques
Les Méthodes Semi-Paramétriques
Nasdad
0.03
Returns
Historical Simulation 5% VaR
CAViaR 5%
0.02
0.01
0
-0.01
-0.02
-0.03
0
50
100
Christophe Hurlin
150
Value-at-Risk
200
250

192. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Risque de portefeuille et Value-at-Risk
Préambule
Christophe Hurlin
Value-at-Risk

193. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Jusqu’ présent, nous avons considéré la VaR associée aux
à
P&L d’ seul actif (change, action, obligation, indice, etc..)
un
Comment calculer la VaR d’ portefeuille composé de
un
plusieurs actifs ?
Christophe Hurlin
Value-at-Risk

194. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Deux solutions :
1
Considérer le rendement global du portefeuille comme celui
d’ actif particulier et calculer la VaR directement sur ce
un
rendement agrégé.
Avantage : simplicité. Inconvénient : en négligeant les
covariances entre les rendements des actifs, on néglige toute
diversi…cation potentielle des risques.
2. Prendre en compte explicitement les corrélations entre les
actifs du portefeuille pour le calcul de la VaR : approche
multivariée de la VaR.
Christophe Hurlin
Value-at-Risk

195. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Remarque : si l’ sait que théoriquement l’
on
approche multivariée
de la VaR est celle qui doit être privilégiée, di¤érentes observations
empiriques montrent que les VaR calculées de façon univariée sur
le rendement agrégé ou de façon multivariée en tenant compte des
corrélations entre actifs peuvent être relativement proches.
Berkowitz, J., et J. O brien. (2002), ”How Accurate are
the Value-at-Risk Models at Commercial Banks”, Journal of
Finance 57, p. 1093-1111.
Christophe Hurlin
Value-at-Risk

196. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Nous allons ici présenter uniquement l’
approche multivariée de
la VaR, dans laquelle la VaR est construite comme une
combinaison des risques associés aux di¤érents actifs du
portefeuille.
Nous reprenons ici la présentation de Jorion (2007)
Si les positions du portefeuille sont maintenues sur
l’
horizon du risque, le rendement du portefeuille est une
combinaison linéaire des rendements des actifs qui le
composent, dans laquelle les poids sont dé…nies par montant
relatifs investits en début de période.
Christophe Hurlin
Value-at-Risk

197. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (rendement d’ portefeuille)
un
Le rendement Rp,t d’ portefeuille de N actifs est dé…ni par :
un
N
Rp,t =
∑ wi Ri ,t
i =1
où Ri ,t désigne le rendement de l’
actif i et wi le poids associé à cet
actif, avec par convention
wi =
Wi
W
N
∑ wi = 1
i =1
où Wi désigne le montant investit dans le titre i en début de
période et W la valeur totale du portefeuille.
Christophe Hurlin
Value-at-Risk

198. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Remarque 1 : Le rendement du portefeuille peut s’
écrire sous
forme vectorielle :
Rp,t = w 0 R
w = (w1 w2 ...wN )0
(N ,1 )
R = (R1 R2 ...RN )
(1,N )
Christophe Hurlin
Value-at-Risk

199. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Les poids wi peuvent être positifs ou négatifs.
On exclut en revanche le cas où la valeur totale du portefeuille
serait nulle, i.e. W = 0, puisque dans ce cas, les poids
wi = Wi /W ne serait pas dé…nis.
Christophe Hurlin
Value-at-Risk

200. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Remarque 2 : Les moments associés aux rendements du
portefeuille sont :
E (Rp,t ) = w 0 E (R ) = µp
V (Rp,t ) = w
0
Σ
w = σ2
p
(1,N ) (N ,N ) (N ,1 )
où Σ désigne la matrice de variance covariance des rendements de
N actifs :
0
1
var (R1 )
cov (R1 , R2 )
cov (R1 , RN )
B
C
var (R2 )
C
Σ=B
@
A
..
cov (RN , R1 )
var (RN )
Christophe Hurlin
Value-at-Risk

201. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
ou encore
0
B
Σ=B
@
σ2
1
σ12
σ2
2
σ1N
..
σ1N
σN
On retrouve ainsi l’
expression :
σ2 =
p
N
N
N
1
C
C
A
∑ wi2 σ2 + 2 ∑ ∑ wi wj σij
i
i =1
Christophe Hurlin
i =1 j <i
Value-at-Risk

202. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Remarque 3 : La variance du rendement du portefeuille peut aussi
être exprimée en unités monétaires sous la forme :
σ2 W 2 = x
p
0
Σ
x
(1,N ) (N ,N ) (N ,1 )
où x désigne le vecteur des montants (en unités monétaires)
investits dans les actifs i = 1, .., N
x = (W1 W2 ... WN )0
Christophe Hurlin
Value-at-Risk

203. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Risque de portefeuille et Value-at-Risk
VaR d’ portefeuille
un
Christophe Hurlin
Value-at-Risk

204. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
A partir d’ portefeuille, certains reporting proposent deux types
un
de VaR :
1
La VaR diversi…ée (diversi…ed VaR) qui tient compte dela
diversi…cation des risques via la structure de covariance des
rendements des titres
2
La VaR non diversi…ée (undiversi…ed VaR) qui néglige toute
diversi…cation des risques dans le portefeuille.
Christophe Hurlin
Value-at-Risk

205. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Hypothèse : Pour commencer on se place dans le cas simple d’
une
distribution normale de P&L pour tous les actifs i = 1, .., N
d’
espérance de rendement nul. Par conséquent, le rendement du
portefeuille Rp,t est lui aussi normal.
Christophe Hurlin
Value-at-Risk

206. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (VaR Diversi…ée)
La Value-at-Risk diversi…ée (ou Value-at-Risk) du portefeuille
tient compte des béné…ces de la diversi…cation des risques au sein
du portefeuille. Pour un taux de couverture de α% et sous
l’
hypothèse de normalité, cette VaR, notée VaRp,t (α) , est dé…nie
par :
p
VaRp,t (α) = Φ 1 (α) σp W = Φ 1 (α) x 0 Σx
Christophe Hurlin
Value-at-Risk

207. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Remarque : on peut aussi proposer une mesure de risque pour
chaque actif (ou VaR individuelle) entrant dans la composition
du portefeuille comme :
VaRi ,t (α) =
Φ
1
( α ) σ i j Wi j =
Φ
1
( α ) σ i j wi j W
la valeur absolue s’
explique par la possibilité d’
avoir des poids
négatifs.
Christophe Hurlin
Value-at-Risk

208. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (VaR non diversi…ée)
La Value-at-Risk non diversi…ée du portefeuille correspond à la
somme des VaR individuelles ou à la VaR d’ portefeuille dans
un
lequel il n’ a pas de position courte et où tous les rendements
y
entre tous les actifs sont parfaitement et positivement corrélés :
N
VaRu,t (α) =
∑ VaRi ,t (α)
i =1
L’
écart entre VaRu,t (α) et VaRp,t (α) donne une mesure de la
réduction du risque de portefeuille liée à la diversi…cation.
Christophe Hurlin
Value-at-Risk

209. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007)
On considère un portefeuille comportant des investissements en
dollars canadiens (CAD) et en euros (EUR). On suppose que les
deux monnaies ne sont pas corrélées et ont une volatilité
respectivement égale à 5% et 12%. Le portefeuille comporte
l’
équivalent de 2 millions de dollars investits en dollars canadiens et
1 million de dollars investits en euros. On cherche à calcule la VaR
à 5% sur ce portefeuille.
Christophe Hurlin
Value-at-Risk

210. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007, suite)
La variance des rendements du portefeuille exprimée en millions de
dollars vaut :
σ2 W 2 = x
p
0
Σ
x =
(1,2 ) (2,2 ) (2,1 )
0.052
0
0
0.122
2 1
σ2 W 2 = 0.0244
p
2
1
106 $
On en déduit la VaR diversi…ée :
VaRp,t (0.05) =
Φ
1
(0.05)
Christophe Hurlin
p
0.0244
Value-at-Risk
106 = 256, 934 $

211. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007, suite)
La VaR non diversi…ée est alors égale à la somme des VaR des
deux actifs :
p
VaRCAN ,t (0.05) = Φ 1 (0.05)
0.05 2 106 = 165, 00 $
p
VaREUR ,t (0.05) = Φ 1 (0.05)
0.12 1 106 = 198, 00 $
La VaR non diversi…ée est alors égale à :
VaRu,t (0.05) = VaRCAN ,t (0.05) + VaREUR ,t (0.05) = 363, 000 $
Christophe Hurlin
Value-at-Risk

212. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007, suite)
On véri…e que dans ce cas la VaR non diversi…ée est supérieure à la
VaR diversi…ée indiquant que la diversi…cation des facteurs de
risques réduit le risque global. Attention : la VaR n’
étant pas une
mesure de risque cohérente, ce résultat ne sera pas toujours valable
sauf dans le cas particulier de distributions de P&L elliptiques. La
loi normale appartient à cette famille de distributions (cf. section
sur les limites de la VaR)
Christophe Hurlin
Value-at-Risk

213. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Risque de portefeuille et Value-at-Risk
VaR marginale, incrementale et composée
Christophe Hurlin
Value-at-Risk

214. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Dans une perspective de management des risques, on peut
être amené à se poser la question : quelle position doit être
modi…ée a…n de réduire ma VaR ?
Pour cela, on utilise di¤érents concepts :
1
La VaR marginale
2
La VaR incrementale
3
La VaR composée
Christophe Hurlin
Value-at-Risk

215. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (VaR marginale)
La Value-at-Risk marginale, notée ∆VaRi (α), correspond à
l’
e¤et marginal d’
une augmentation d’
une unité monétaire
d’
exposition sur un actif particulier d’ portefeuille sur la VaR du
un
portefeuille.
∂VaRp,t (α)
∆VaRi (α) =
∂Wi
`
où Wi désigne le montant investit dans le i eme actif du portefeuille
et VaRp,t (α) désigne la VaR (diversi…ée) du portefeuille.
Christophe Hurlin
Value-at-Risk

216. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Hypothèse : On suppose que tous les actifs i = 1, .., N du
portefeuille admettent une distribution de P&L de type normale.
Par conséquent, le rendement du portefeuille Rp,t est lui aussi
normal.
Christophe Hurlin
Value-at-Risk

217. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Sous l’
hypothèse de normalité, nous avons vu que la VaR du
portefeuille est :
p
VaRp,t (α) = Φ 1 (α) σp W = Φ 1 (α) x 0 Σx
où x désigne le vecteur des montants (en unités monétaires)
investits dans les actifs i = 1, .., N
x = (W1 W2 ... WN )0
Christophe Hurlin
Value-at-Risk

218. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
`
Dès lors, la VaR marginale associée au i eme actif est :
∆VaRi (α) =
=
∂VaRp,t (α)
∂VaRp,t (α)
=
∂Wi
∂wi W
∂σp W
Φ 1 (α)
∂wi W
ou encore
∆VaRi (α) =
Christophe Hurlin
Φ
1
(α)
Value-at-Risk
∂σp
∂wi

219. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Réécrivons cette expression : pour cela étudions la dérivée
∂σp /∂wi . On sait que :
σ2 =
p
N
N
N
∑ wi2 σ2 + 2 ∑ ∑ wi wj σij
i
i =1 j <i
i =1
Dès lors :
∂σ2
p
∂wi
= 2wi σ2 + 2
i
N
∑
wj σij
j =1,j 6=i
N
= 2 wi cov (Ri , Ri ) + 2
∑
j =1,j 6=i
Christophe Hurlin
Value-at-Risk
wj cov (Ri , Rj )

220. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Une autre façon d’
écrire cette expression est :
∂σ2
p
= 2 cov (Ri , Rp )
∂wi
puisque par dé…nition Rp,t = ∑N 1 wi Ri ,t . Par ailleurs
i=
∂σ2
∂σp
∂σp
cov (Ri , Rp )
p
=2
σp =)
=
∂wi
∂wi
∂wi
σp
Christophe Hurlin
Value-at-Risk

221. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (VaR Marginale sous hypothèse de normalité)
Sous l’
hypothèse de normalité des P&L, la VaR marginale associée
`
au i eme actif du portefeuille véri…e :
∆VaRi (α) =
Φ
1
(α)
cov (Ri , Rp )
σp
où σp et Rp désignent respectivement la volatilité et le rendement
du portefeuille et Φ (.) la fonction de répartition de la loi normale
centrée réduite.
Christophe Hurlin
Value-at-Risk

222. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (Vecteur de VaR marginales)
On peut construire un vecteur ∆VaR (α) de VaR marginale
associée au N actif de la façon suivante
∆VaR (α) =
(N ,1 )
Φ
1
(α)
σp
Σ
x
(N ,N ) (N ,1 )
∆VaR (α) = (∆VaR1 (α) ∆VaR2 (α) ... ∆VaRN (α))0
Christophe Hurlin
Value-at-Risk

223. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Remarque : sous hypothèse de normalité, la VaR marginale
correspond à un facteur au beta associé à l’
actif i, :
βi =
cov (Ri , Rp )
σ2
p
qui peut être estimé par le coe¢ cient de la régression linéaire
suivante, correspondant au CAPM (Sharpe, 1964) :
Ri ,t = αi + βi Rp,t + εi ,t
Christophe Hurlin
Value-at-Risk

224. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Rappel : Si l’ note β le vecteur des betas des N actifs
on
i = 1, .., N tel que
β = ( β1 β2 ... βN )0
alors
β=
Christophe Hurlin
Σw
w 0 Σw
Value-at-Risk

225. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (VaR Marginale et beta)
Si la distribution des P&L appartient à la famille des distributions
`
elliptiques, la VaR marginale associée au i eme actif du portefeuille
est proportionnelle au beta (CAPM) correspondant :
∆VaRi (α) =
VaRp,t (α)
W
βi
où VaRp,t (α) et W désignent respectivement la VaR et la
valorisation du portefeuille.
Christophe Hurlin
Value-at-Risk

226. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007)
On considère un portefeuille comportant des investissements en
dollars canadiens (CAD) et en euros (EUR). On suppose que les
deux monnaies ne sont pas corrélées et ont une volatilité
respectivement égale à 5% et 12%. Le portefeuille comporte
l’
équivalent de 2 millions de dollars investits en dollars canadiens et
1 million de dollars investits en euros. Calculons les VaR marginales
à 5% sur les deux actifs.
Christophe Hurlin
Value-at-Risk

227. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007, suite)
On sait que :
∆VaR (0.05) =
(2,1 )
Φ
1
(0.05)
Σ x
σp
(2,2 ) (2,1 )
∆VaR (α) = (∆VaRCAN (α) ∆VaREUR (α))0
Dès lors :
∆VaR (0.05) = Σ
(2,2 )
1.6449
x = p
(2,1 )
0.0244
Christophe Hurlin
0.052
0
0
0.122
Value-at-Risk
2
1

228. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007, suite)
On en déduit …nallement les VaR marginales :
∆VaR (0.05) =
∆VaRCAN (α)
∆VaREUR (α)
Christophe Hurlin
Value-at-Risk
=
0.0527 $
0.1516 $

229. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
L’
approche de la VaR marginale est générallement complétée
par un calcul de VaR incrémentale.
La VaR marginale permet de mesurer la variation de la VaR
engendrée par une variation marginale, comme son nom
lindique, des positions sur un actif particulier.
La VaR incrémentale permet de mesurer la variation des
risques et donc de la VaR, engendrée par le passage d’
une
position initiale à une autre position, impliquant des variations
sur un ou plusieurs actifs d’
ampleur variables (problème des
non linéarités dans la variation de la VaR).
Christophe Hurlin
Value-at-Risk

230. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (VaR incrémentale)
La Value-at-Risk incrémentale correspond à la variation de VaR
engendrée par le passage d’
une position p1 à une position p2 sur
l’
ensemble des N actifs du portefeuille.
VaR incrémentale = VaRp2 ,t (α)
où α désigne le taux de couverture.
Christophe Hurlin
Value-at-Risk
VaRp1 ,t (α)

231. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007)
On considère à nouveau l’
exemple précédent d’ portefeuille
un
comportant des investissements en dollars canadiens (CAD) et en
euros (EUR). On souhaite augmenter la position libéllée en dollar
canadien d’ montant équivalent à 10,000 dollars US. On
un
souhaite calculer la VaR incrémentale à 5% associée au passage du
portefeuille initial à ce nouveau portefeuille.
Christophe Hurlin
Value-at-Risk

232. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007)
On peut calculer explicitement la variation de VaR. Rappelons que
la VaR du portefeuille initial est égale à 256 934$. La VaR du
nouveau portefeuille vaut :
p
x 0 Σx 106
VaRp,t (0.05) =
Φ 1 (0.05)
=
2.01 1
0.052
0
0
0.122
VaRp,t (0.05) = 257 461 $
On en déduit la valeur de la VaR incrémentale :
VaR incrémentale = 527.28 $
Christophe Hurlin
Value-at-Risk
2.01
1

233. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
On peut en…n envisager une décomposition du risque a…n
d’
identi…er les gains liés à la diversi…cation. Pour cela on
utilise la notion de VaR composée (component VaR)
L’
idée de base consiste à déterminer ce que serait le risque si
l’ retirait un actif du portefeuille. La variation de risque par
on
rapport à la situation initiale donne une mesure des
gains/pertes en termes de diversi…cation/risque liés à
l’
introduction de cet actif dans le portefeuille
Christophe Hurlin
Value-at-Risk

234. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (VaR composée)
`
La Value-at-Risk composée (component VaR) associée au i eme
actif, pour i = 1, .., N, notée CVARi (α) , est la variation de VaR
engendrée par la suppression de cet actif du portefeuille.
CVaRi ,t (α) = ∆VaRi ,t (α)
Wi = VaRp,t (α)
βi
wi
où VaRp,t (α) et Wi désignent respectivement la VaR et le
montant investit dans l’
actif i, et où βi désigne le beta (CAPM)
eme titre.
`
associé au i
Christophe Hurlin
Value-at-Risk

235. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Remarque : Par construction, la somme des CVaR est égale à la
VaR :
N
VaRp,t (α) =
∑ CVaRi ,t (α)
i =1
Christophe Hurlin
Value-at-Risk

236. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
De…nition (VaR composée)
On exprime parfois la Value-at-Risk composée (component
`
VaR) associée au i eme actif en pourcentage de la VaR totale .
CVaRi ,t (α)
= βi
VaRp,t (α)
Christophe Hurlin
wi
Value-at-Risk

237. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007)
On considère à nouveau l’
exemple précédent d’ portefeuille
un
comportant des investissements en dollars canadiens (CAD) et en
euros (EUR). On rappelle que le portefeuille comporte l’
équivalent
de 2 millions de dollars investits en dollars canadiens et 1 million
de dollars investits en euros. On souhaite calculer les CVAR à 5%.
On sait que
CVaRi ,t (α) = ∆VaRi ,t (α) Wi
CVaRCAN (α)
CVaREUR (α)
=
0.0527
0.1516
Christophe Hurlin
2 millions $
1 millions $
Value-at-Risk
=
105 630 $
152 108 $

238. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Example (Jorion, 2007)
On peut exprimer ces CVAR en % de la VaR. Sachant que la VaR
du portefeuille vaut 256 934$, on trouve approximativement que :ù
CVaRCAN (α) /VaRp,t (α)
CVaREUR (α) /VaRp,t (α)
=
41%
59%
Retirer l’
actif libéllé en euro du portefeuille conduirait à une
diminution de la VaR de 59% ou dit autrement cet actif contribue
à hauteur de 59% du total de la VaR.
Christophe Hurlin
Value-at-Risk

239. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Risque de portefeuille et Value-at-Risk
Exemple d’
application
Christophe Hurlin
Value-at-Risk

240. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
Nous considérerons ici deux exemples d’
application repris de
Jorion (2007) :
1
Un portefeuille actions
2
Exemple de la Barings
Christophe Hurlin
Value-at-Risk

241. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Christophe Hurlin
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Value-at-Risk

242. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Risque de portefeuille et Value-at-Risk
1
Au moment de l’
éclatement du scandale de la Barings, le
trader Leeson avait pris de façon frauduleuse des positions
longues sur des futures sur le Nikkei pour plus de 7.7 milliards
de dollars et des positions courtes sur les bonds du
gouvernement japonais(JBG) pour plus de 16 milliards de
dollars.
2
Si un calcul de VaR avait été mis en place sur ces positions
frauduleuse, auriat-il permis de détecter la provenance du
risque.
3
Jorion (2007) calcule les di¤érentes VaR à partir du bond
zero-coupon à 10 ans du gouvenemen japonais et de l’
indice
Nikkei.
Christophe Hurlin
Value-at-Risk

243. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Christophe Hurlin
Préambule
VaR d’ Portefeuille
un
VaR marginale, incrementale et composée
Exemples d’
applications
Value-at-Risk

244. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Limites de la Value-at-Risk
Préambule
Christophe Hurlin
Value-at-Risk

245. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
La VaR présente de nombreuses avantages :
1
sa simplicité d’
interprétation
2
son caractère généraliste et général, voir holiste
3
la dimension probabiliste de cette mesure de risque
Christophe Hurlin
Value-at-Risk

246. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Mais la VaR présente certains inconvénients :
1
la VaR est sujette au risque de modèle : une erreur de
spéci…cation de la distribution de P&L par exemple
2
la VaR est sujette au risque d’
implémentation liée à la
structure des données requises pour estimer la P&L
distribution ou la vaR directement
3
Mais tous ces risques ne sont pas propres à la VaR
Christophe Hurlin
Value-at-Risk

247. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
En revanche la VaR présente aussi certaines limites qui lui
sont propres :
1
Cette mesure de risque ne donne aucune information sur les
pertes au delà de la VaR
2
Cette mesure peut conduire des agents à prendre de
"mauvaise décision" d’
investissement
3
Cette mesure peut conduire certains agents à prendre
volontairement plus de risque dans un système de
management des risques décentralisé
Christophe Hurlin
Value-at-Risk

248. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Fact
La Value-at-Risk ne donne aucune information sur l’
ampleur des
pertes extrêmes (ou pertes en excès) qui peuvent apparaître au
delà de la VaR. Par conséquent, deux positions peuvent avoir la
même VaR avec des risques extrêmes totalement di¤érents.
Christophe Hurlin
Value-at-Risk

249. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
P&L1
VaR
P&L2
Christophe Hurlin
Value-at-Risk

250. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Example
Soient deux projets, dont les rendements notés respectivement R1
et R2 admettent une distribution discrète et équiprobables sur les
ensembles de valeurs suivantes :
R1 = f 10;
8;
6;
4;
2; 0; 2; 4; 6; 8g
R2 = f 11;
7;
6;
4;
2; 0; 2; 4; 6; 8g
les deux projets ont la même espérance et la même VaR à 10%
VaR1 (0.1) = VaR2 (0.1) =
9
Or le projet 2 peut engendrer des pertes en excès (-11) plus
importante que le projet 1 (-10).
Christophe Hurlin
Value-at-Risk

251. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Cette limite peut avoir des conséquences importantes pour un
investisseur :
Supposons qu’ investisseur décide de …nancer un projet sur
un
la base d’
une analyse moyenne-VaR
Supposons que ce projet peut générer de très forts
rendements, mais aussi des très fortes pertes
Une analyse fondée sur la VaR peut conduire à adopter le
projet, si les plus fortes pertes n’
a¤ectent pas la VaR (parce
que ces pertes excèdent la VaR), et cela quelle que soit les
rendements positif attendus et la taille des pertes potentielles.
Christophe Hurlin
Value-at-Risk

252. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Fact
L’
analyse moyenne-VaR peut conduire à accepter des projets avec
forts rendements positifs, quelles ques soient les possibles pertes
associées, si tant est que la réalisation de ces pertes est su¢ sament
peu probable : une telle con…guration peut conduire les
investisseurs à s’
exposer à des très fortes pertes (quoique
relativement peu probable).
Christophe Hurlin
Value-at-Risk

253. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
De la même façon, l’
usage de la VaR dans un système de
management des risques reposant sur une relation
principal-agent (délégation) peut conduire à des e¤ets non
désirables :
Supposons que la gestion d’
actif est décentralisée et que les
traders ou les assets managers sont soumis à des limites de
risques en termes de VaR
Le trader peut avoir intérêt alors (politique de bonus) a
prendre des positions très risquées (vente d’
options
out-of-the-money par exemple), mais ayant des probabilité de
réalisation faible a…n de ne pas atteindre les limites de risque
établies par les système de contrôle des risques.
Christophe Hurlin
Value-at-Risk

254. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Plus généralement, on peut se poser la question de savoir si la
VaR est une bonne mesure des risques ?
Mais qu’ ce qu’
est
une "bonne" mesure des risques ?
Notion de mesure cohérente des risques
Christophe Hurlin
Value-at-Risk

255. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Limites de la Value-at-Risk
Mesure cohérente des risques
Christophe Hurlin
Value-at-Risk

256. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
La théorie des mesures cohérentes de risque a été développée par
Artzner et al. (1997, 1999).
Artzner, P., Delbaen, F., Eber, J.M., Heath, D., 1997.
Thinking coherently. Risk 10 (11), 68–71.
Artzner, P., Delbaen, F., Eber, J.M., Heath, D., 1999.
Coherent measures of risk. Mathematical Finance 9(3),
203–228.
Christophe Hurlin
Value-at-Risk

257. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
L’
idée de départ d’
Artzner et al. (1997, 1999) est à la fois
simple et profonde : la notion de risque …nancier est dure, voir
impossible à conceptualiser, à moins que l’ ne dispose d’
on
une
idée claire de ce que l’ entend par mesure de risque
on
Parallèle avec la température et le thermomètre : on a tous
une notion plus ou moins intuitive de la chaleur et de la
température, mais il est impossible de la conceptualiser
clairement sans la notion de thermomètre
Artzner et al. (1997, 1999) postulent donc un ensemble
d’
axiomes (axiomes de cohérence) sur ce que doit véri…er
une mesure de risque.
Christophe Hurlin
Value-at-Risk

258. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
De…nition (Mesure de risque cohérente)
Soient X et Y deux distributions de P&L associées à deux
portefeuilles et soit ρ (.) une mesure de risque sur un horizon
donné. la mesure de risque ρ (.) est dite cohérente ssi elle satisfait
les axiomes suivants :
(i ) Monotonicité : Y X =) ρ (Y ) ρ (X )
(ii ) Subadditivité : ρ (X + Y ) ρ (X ) + ρ (Y )
(iii ) Homogénéité positive : ρ (hX ) = hρ (X ) pour h > 0
(ii ) Invariance translationnelle : ρ (X + n) = ρ (X ) n pour
toute valeur n
Christophe Hurlin
Value-at-Risk

259. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Remarque 1 : l’
axiome le plus important est celui de subadditivité.
Il signi…e qu’ portefeuille constitué de sous portefeuilles ne
un
doit pas être plus risqué (au regard d’
une mesure cohérente)
que la somme des risques associés aux sous portefeuilles.
Cet axiome se fonde sur l’
idée que l’
agrégation des risques
individuels, doit conduire à une diversi…cation des risques et
on donc à une diminution du risque globale, ou dans le pire
des cas à un maintien de celui-ci.
C’ cet axiome qui fonde la diversi…cation des risques.
est
Christophe Hurlin
Value-at-Risk

260. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Si les risques sont subadditifs, l’
addition des risques individuels
donne une sorte d’
enveloppe supérieure des risques ou une
sorte d’
estimation conservatrice des risques. Cela facilite la
supervision des risques dans des structures décentralisées.
Mais si ce n’ pas le cas, l’
est
utilisation du risque agrégré
comme indicateur de risque global peut conduire à largement
sous évaluer ce risque global.
Christophe Hurlin
Value-at-Risk

261. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
La Value-at-Risk est elle une mesure cohérente du risque ?
Christophe Hurlin
Value-at-Risk

262. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Theorem
La Value-at-Risk n’ pas une mesure cohérente du risque et en
est
particulier la Value-at-Risk ne véri…e pas l’
axiome de subadditivité
Christophe Hurlin
Value-at-Risk

263. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Example (Dowd, 2005)
Considérons deux obligations A et B. La probabilité de défaut sur
chaque obligation est de 4% et on anticipe une perte de 100 en cas
de défaut, et une perte nulle en cas de non défaut. La VaR a 5%
de chaque titre est donc égale à 0.
VaRA (5%) = VaRB (5%) = VaRA (5%) + VaRB (5%) = 0
Christophe Hurlin
Value-at-Risk

264. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Example (Dowd, 2005, suite)
Supposons que les défauts soient indépendants. Au niveau du
portefeuille total (une obligation A et une obligation B), la P&L
est la suivante :
8
avec une probabilté p1 = 0.962 = 0.9216
< 0
200 avec une probabilté p2 = 0.042 = 0.0016
P/L =
:
100 avec une probabilté p3 = 0.0768
cela implique une VaR égale à :
VaRA +B (5%) = 100 > VaRA (5%) + VaRB (5%) = 0
La VaR n’ pas subadditive
est
Christophe Hurlin
Value-at-Risk

265. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Remarque : on peut rendre la VaR subadditive en imposant des
hypothèses fortes sur la distribution de P&L. Notamment en
supposant que la distribution appartient à la famille des
distributions elliptiques.(cf. Artzner et al., 1999)
Christophe Hurlin
Value-at-Risk

266. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Existe-il des mesures de risques (i) cohérentes, (ii)
généralistes, (iii) simple d’
interprétation, (iv) aggrégative ?
Une mesure candidate est l’
expected shortfall
Christophe Hurlin
Value-at-Risk

267. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Limites de la Value-at-Risk
Expected shortfall (ES)
Christophe Hurlin
Value-at-Risk

268. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
De…nition (Expected Shortfall)
L’
Expected Shortfall (ES) associée à un taux de couverture de
α% correspond à la moyenne des α% pires pertes attendues telle
que :
Z
1 α
ESt (α) =
F 1 (p ) dp
α 0 Rt
où FR t (.) désigne la fonction de répartition associée à la fonction
de densité fR t (r ) . Par convention, on exprime l’ sous forme
ES
positive comme la VaR, alors qu’ s’
il agit d’
une perte moyenne.
Christophe Hurlin
Value-at-Risk

269. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Remarque 1 : l’
Expected Shortfall nous donne une information sur
la moyenne des pertes dans les pires états de la nature, c’ à dire
est
dans les α% situations où les pertes excèdent la VaR(α) .
Remarque 2 : l’
Expected Shortfall est aussi appellée parfois
Conditionnal Loss ou Expected Tail Loss (ETL)
Christophe Hurlin
Value-at-Risk

270. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Remarque 3 : Pour une distribution discrète, on a :
ES (α) =
1 α eme
∑ p ` plus forte perte
α p =0
Christophe Hurlin
`
Pr p eme plus forte perte
Value-at-Risk

271. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Lemma
L’
Expected Shortfall (ES) est une mesure cohérente de risque et
véri…e en particulier l’
axiome de sub-additivité
Christophe Hurlin
Value-at-Risk

272. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Considérons deux distributions discrètes de P&L, notées A et B,
avec N quantiles équi-probables. Alors :
ESA (α) + ESB (α) = moyenne des Nα plus fortes pertes sur A +
moyenne des Nα plus fortes pertes sur B
Donc par conséquent :
ESA (α) + ESB (α)
moyenne des Nα plus fortes pertes sur A +B
= ESA +B (α)
Christophe Hurlin
Value-at-Risk

273. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Comment calculer l’ ?
ES
1
Pour certaines distributions de P&L (distribution normale
notamment) il existe des formules analytiques permettant de
calculer l’
ES.
2
Dans les autres cas, on utilise des approximations numériques.
Christophe Hurlin
Value-at-Risk

274. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
De…nition (ES dans le cas d’
une distribution normale)
Dans le cas d’
une distribution de P&L normale centrée réduite
N µ, σ2 , l’
Expected Shortfall associée à un taux de couverture
de α% vaut :
!
Ft 1 ( α ) 2
σ
p
ESt (α) = exp
2
α 2π
Christophe Hurlin
Value-at-Risk

275. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Corollary
Dans le cas d’
une loi N (0, 1) , cette expression est équivalente à
l’
expression suivante
ESt (α) =
φ
Φ 1 (α)
0.05
où φ et Φ désignent respectivement la densité et la répartition de
la loi normale standard.
Christophe Hurlin
Value-at-Risk

276. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Example
Voici quelques valeurs d’ sous l’
ES
hypothèse de normalité des P&L
ESt (0.05) = 2.0627 VaRt (0.05) = 1.6449
ESt (0.01) = 2.6652
Christophe Hurlin
VaRt (0.01) = 2.3263
Value-at-Risk

277. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
VaR et ES sous distribution Normale
0.4
0.35
0.3
Distribution de P&L
0.25
0.2
0.15
P&L Distribution Normale
1% VaR = 2.3263
1% ES = 2.6652
0.1
0.05
0
-5
-4
-3
-2
-1
Christophe Hurlin
0
x
1
Value-at-Risk
2
3
4
5

278. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
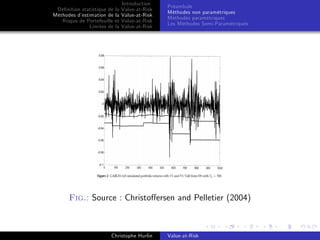
Préambule
Mesure cohérente de risque
Expected shortfall
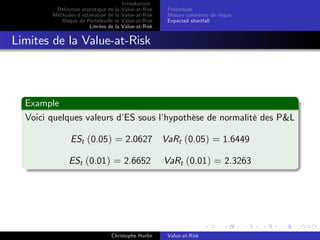
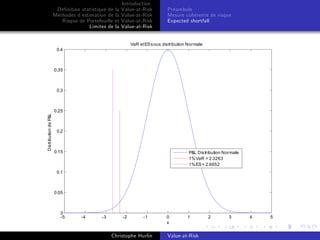
Limites de la Value-at-Risk
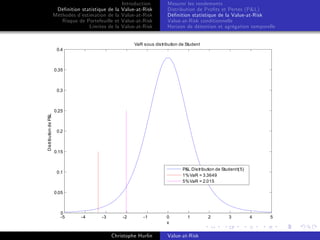
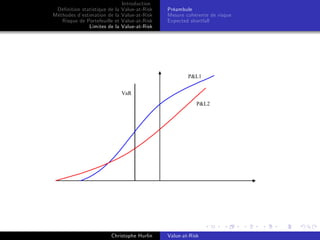
Fact
Dans le cas général, il n’
existe pas de formule analytique pour l’
ES
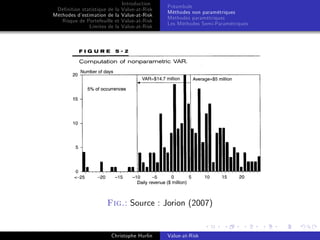
et on utilise des approximations numériques. Une méthode de
calcul possible est alors celle de la moyenne des VaR (average
VaR) : on calcule N VaR associées à N taux de couverture
équi-réaprtis sur le segment ]0, α] et l’ calcule la moyenne de ces
on
VaR. Lorsque N tend vers l’
in…ni, la moyenne empirique des VaR
converge vers l’
ES.
Christophe Hurlin
Value-at-Risk

279. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
Limites de la Value-at-Risk
Example
Reprenons l’
exemple d’
une distribution P&L normale N (0, 1) . On
cherche à calculer l’ pour un taux de couverture α = 5%. Pour
ES
cela on considère 10 VaR dé…nies pour des taux de couverture
équi-répartis entre 0.001 et 0.05. La moyenne empirique des 10
VaR est alors égale à 2.0728 alors que la vraie valeur de l’ est
ES
2.0627
β
VaR( β)
β
VaR( β)
0.001
3.0902
0.0288
1.8991
0.0066
2.4807
0.0343
1.8206
Christophe Hurlin
0.0121
2.2536
0.0399
1.7520
Value-at-Risk
0.0177
2.1045
0.0454
1.6907
0.0232
1.991
0.05
1.644

280. Dé…nition statistique de la
Méthodes d’
estimation de la
Risque de Portefeuille et
Limites de la
Introduction
Value-at-Risk
Value-at-Risk
Value-at-Risk
Value-at-Risk
Préambule
Mesure cohérente de risque
Expected shortfall
FIN PARTIE 1.
Christophe Hurlin
Value-at-Risk