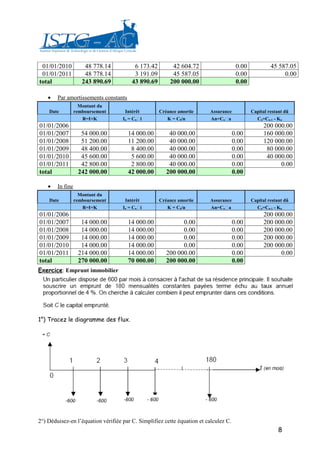
Le document traite des annuités, qui sont des versements effectués à intervalles réguliers, et leur utilisation dans le calcul de la valeur acquise et actuelle d'un capital. Il propose des applications pratiques pour déterminer les montants des placements et des emprunts à un taux d'intérêt donné. Des tableaux d'amortissement et des exercices sont fournis pour illustrer les concepts de remboursement d'emprunt par annuités constantes et autres méthodes similaires.

1. Mathématiques Appliquées
Pr. Alain Ndedi
Email: ndedi.alain@gmail.com
Année 2012/2013
BTS
ANNUITES
Qu’est-ce que sont les annuités ?
Les annuités sont des versements effectués à intervalles de temps égaux appelés périodes. Ces
annuités, placées à intérêts composés, servent à constituer un capital (valeur acquise par ces
versements) ou à rembourser un emprunt (valeur actuelle des versements).
I. Calcul de la valeur acquise par une suite d’annuités constantes.
Considérons un placement de 500 tous les ans pendant 6 ans. Le taux annuel de ce placement est de
5%. On a le schéma suivant :
Capital versé 500 500 500 500 500 500
1ère année 2ème 3ème 4ème 5ème 6ème Temps
Calculer la valeur acquise par le premier versement :
Calculer la valeur acquise par le second versement :
Calculer la valeur acquise par les quatre derniers versements :
Les valeurs acquises successives sont les 6 premiers termes d’une ………………………
……………………………………… de premier terme ………………………… et de raison
…………………… .
A l’aide de votre formulaire, donner la formule qui permet de calculer la somme des n premiers termes
de la suite définie ci-dessus :
Sn =
Appliquons cette formule au cas de notre exercice pour calculer la valeur acquise (donc la somme des
annuités) de notre placement : On la note Vn
Généralisons cet exercice au cas d’un placement par annuités constantes a au taux annuel t
pendant n périodes.
La valeur acquise par ce placement est donnée par la formule :
Vaq = a x ( 1 + i ) − 1
n
i
Application :
 Calculer la valeur acquise par un placement constant chaque année de 1200 (soit 100 par
mois) pendant 8 ans au taux annuel de 5,75%.
 Boujas place 50 par mois au taux annuel de 4,25% pendant 10 ans. Calculer la valeur acquise
par ce placement au terme de ces 10 ans.
1

2.  M. Boujas désire obtenir un capital de 20 000 dans 7 ans afin d’effectuer des travaux dans son
domicile. Son placement sera fait au taux annuel de 4,5%. Quel doit être son placement
annuel?
 M. Beas a effectué un versement de 240 au taux annuel de 3,5% et a obtenu la valeur acquise
de 3 504, 47.
Quelle a été la durée de ce placement ?
II. Calcul de la valeur actuelle d’une suite d’annuités constantes.
Nous choisissons de rembourser un capital par annuités constantes de 4943,30€ pendant 5 ans sachant
que le taux d’emprunt est de 7,5%.
Pour connaître le capital emprunté, il faut actualiser, à intérêts composés, chaque annuité. Il y a
équivalence entre la somme des annuités actualisés et le capital emprunté.
On a le schéma suivant :
Versements
Capital
Emprunté 4943,30 4943,30 4943,30 4943,30 4943,30
1ère année 2ème 3ème 4ème 5ème Temps
Calculer la valeur actuelle du 1er versement :
Calculer la valeur actuelle de 2ème versement :
Calculer de la même façon les valeurs actuelles des trois derniers versements :
La somme de ces valeurs actuelles est égale au capital emprunté. En déduire le capital emprunté
Généralisation :
Le remboursement d’un capital s’effectue par une suite de n annuités constantes de valeur a au taux
périodique t.
Le premier remboursement a lieu 1 période après l’emprunt.
 Exprimer les valeurs actuelles des deux premiers versements en fonction de a et de t:
 Exprimer la valeur actuelle du nième versement :
 En déduire la somme V0 des valeurs actuelles des n versements :
 Dans l’expression ci-dessus, mettre ax(1+t)-n en facteur :
 A l’intérieur de la grande parenthèse, on reconnaît la somme des n premiers termes d’une
suite …………………………… de premier terme ……… et de raison …………
La valeur actuelle d’une suite de n annuités de valeur a, une période avant le premier
remboursement est donnée par :
V0 = ax 1 − ( 1 − i )
−n
i
Application :
 Calculer le capital emprunté (à l’euro près) si le remboursement s’effectue en 12 annuités de
5500 au taux de 7,5%.
 M. Boussi s’engage à rembourser une dette de 1 900 en 4 annuités au taux d’intérêt de 8%.
Quelle doit-être le montant d’une traite ?
 M. Z voudrait connaître le nombre de versements semestriels de 1200 qu’il faut pour
rembourser un capital de 18 498 € au taux annuel de 6%.
 Un emprunt de 13 017 est remboursé en 6 annuités de 2 540. Quel est le taux d’emprunt.
2

3. Récapitulons
Annuités constantes de début de période
Vaq=ax ( 1 + i ) − 1
n
x(1+i)
i
Vac=ax 1 − ( 1 − i )
−n
x(1+i)
i
Annuités de fin de période
Vaq=ax ( 1 + i ) − 1
n
i
Vac=ax 1 − ( 1 − i )
−n
i
Emprunts Indivis et anuités
Emprunts Indivis et autre…
Les emprunts indivis sont les emprunts faits auprès d’un seul prêteur On va étudier le cas où
le prêteur met à disposition de l’emprunteur un capital pour une durée fixée à l’avance, et où
l’emprunteur rembourse ce capital selon un rythme convenu et verse des intérêts à échéances
périodiques.
Lors de chaque annuité (remboursement), on fait la part entre
– La somme qui participe au remboursement du capital emprunté ;
– La somme qui participe au remboursement de l’intérêt.
La somme qui participe au remboursement du capital emprunté s’appelle l’amortissement. Si
Ap est l’annuité de la période p, c’est-à-dire le montant payé à la fin de la période p, on a
Ap = Ip +Mp avec :
– L’intérêt crée pendant la période p et remboursé en fin de cette période, noté Ip;
– L’amortissement de la période p, noté Mp.
On se place dans le cadre d’un emprunt d’un capital D0 au taux d’intérêt i par période pendant
n périodes. On fixe les notations suivantes.
– Le capital restant dû en début de période p est noté Dp−1 ;
– Le montant de l’annuité payée en fin de période p est noté Ap ;
– L’intérêt versé en fin de la période p est noté Ip ;
– L’amortissement versé en fin de la période p est noté Mp.
À chaque début de période p, on a une dette Dp−1, c’est la somme qui reste due et crée un
intérêt Ip = Dp−1i pendant la période. À la fin, de la période, on rembourse l’annuité Ap qui
paye l’intérêt Ip et contribue au remboursement de la dette : Ap = Ip+Mp. La dette de début
de période p+1 est alors Dp = Dp−1 −Mp.
On résume la situation par période dans un tableau, appelé tableau d’amortissement.
Période Capital dû en début Intérêt de la Amortissement Annuité de la
de période période de la période période
1 D0 I1 =D0i M1 A1 = I1 +M1
2 D1 = D0 −M1 I2 =D1i M2 A2 = I2 +M2
3 D2 = D1 −M2 I3 = D2i M3 A3 = I3 +M3
. . . . .
. . . . .
P Dp−1 = Dp−2 −Mp−1 Ip = Dp−1i Mp Ap = Ip +Mp
n Dn−1 = Dn−2 −Mn−1 In = Dn−1i Mn An = In +Mn
3

4. Remboursement par annuités constantes :
On calcule l’annuité constante de remboursement à l’aide de la formule du formulaire
(formule d’actualisation) :
V0 = a×
1−1+)
( t
−n
soit a=
V ×t
• V0 : Capital
0
emprunté avec
1−(1+t)
−n
t • t : taux périodique
• n : nombre
Le tableau d’amortissement s’établie en calculant dans l’ordre :
• L’intérêt, comme pour l’amortissement constant, calculé à intérêts simples en
appliquant le taux d’intérêts au capital restant dû en début de période.
• L’amortissement, différence entre l’annuité et l’intérêt pour l’échéance étudiée.
• Le « capitale restant dû », différence entre le capital restant dû de l’échéance
précédente est de l’amortissement de l’échéance étudiée.
Remboursement par amortissements constants :
L’amortissement constant A est le rapport du capital emprunté sur le nombre de périodes de
remboursement
A= V0 avec V0 : Capital emprunté et n : nombre de
n
période.
Le tableau d’amortissement s’établie en calculant :
• L’intérêt de chaque période calculé à intérêts simples en appliquant le taux d’intérêts
au capital restant dû en début de période.
• L’annuité d’une période : somme de l’amortissement et de l’intérêt de la période.
Exercice
Voici un tableau d’amortissement sur 8 mois d’un emprunt contracté par Boujas au taux
annuel de 2,91%.
Échéance Amortissement Intérêts Annuités Capital restant dû
1 - - - 3 000,00
2 371,83 7,28 379,10 2 628,17
3 372,73 6,37 379,10 2 255,44
4 373,63 5,47 379,10 1 881,81
5 374,54 4,56 379,10 1 507,27
6 375,45 3,66 379,10 1 131,82
7 376,36 2,74 379,10 755,46
8 377,27 1,83 379,10 378,19
9 378,19 0,92 379,10 0,00
Total 3 000,00 32,83 3 032,83
1) Quel est le montant emprunté par Boujas ?
2) Quel type de remboursement a choisi Boujas?
3) Comment retrouver la valeur de l’annuité versée ?
4

5. Exercice
Pour acheter sa voiture Boujas a emprunté une certaine somme. La banque lui a envoyé un
tableau d’amortissement mais certains éléments ont disparus sur ce tableau.
Échéance Amortissement Intérêts Mensualités Capital restant dû
1 0 0 0
2 1 563,67 35,98
3
4
5 14,49
6 7,26 0,00
Total 108,26 7 998,26
1) Retrouver le capital emprunté par Boujas.
2) Retrouver le montant des mensualités versées par Boujas.
3) Déterminer à l’aide des 2 premières échéances le taux d’intérêt mensuel de l’emprunt.
(Arrondir à 10-3)
4) Compléter le reste du tableau.
Exercice
Une entreprise emprunte pour 5 ans le capital de 1,5 millions au taux annuel 7,5%, le
remboursement se faisant in fine, c’est-à-dire en une seule fois au terme de la période de prêt,
les autres années l’entreprise se contente de verser les intérêts. a) Dresser le tableau
d’amortissement de cet emprunt. b) Pour préparer le remboursement du capital l’entreprise
place chaque année à 5% et à intérêts composés une certaine somme. Combien doit-elle placer
chaque année ?
Exercice
La onzième ligne d’un tableau d’amortissement d’un emprunt remboursable par annuités
constantes est:
Dette due Intérêt Amortissement
51676,98 5803,22 1941,38
Quel est le taux d’intérêt ? Quelle est la durée de l’emprunt ?
Exercice
Dresser le tableau d’amortissement d’un emprunt de 500 000 au taux de 10% remboursable par
anuités constantes sur 5 ans.
Réponse
Calcul de ‘anuité constante a=500 000x0.1/1-(1.1)-5= 131 898.94
Période Ktal début Intérêts Amorts Anuités Ktal fin
1 500 000 50 000 81898.74 131 898.94 418 101.26
5

6. 2 418 101.26 41 810.13 90 088.61 -//- 328 012.65
3 328 012.65 32 801.27 99 097.47 -//- 228 915.18
4 228 915.18 22 891.52 109 007.22 -//- 119 907.96
5 119 907.96 -//- 0
Exercice
Une entreprise emprunte un capital remboursable par annuités constantes aux taux d’intérêts annuels
suivants : 5% pendant les cinq premières années, 6% pendant les six années suivantes et 7% pendant
les sept dernières années. Elle rembourse chaque année 50 000.
a) Calculer le montant de l’emprunt. b) Quel est le coût de l’emprunt ? c) À la date anniversaire de la
dixième année de l’emprunt et après paiement de la dixième annuité, l’entreprise décide de rembourser
le solde de l’emprunt. Quel est le montant du remboursement anticipé ? Quel est alors le coût de
l’emprunt ?
Exercice
On emprunte 200000 au taux annuel 12%. Le remboursement se fait en 6 mensualités égales.
Dresser le tableau d’amortissement de ce prêt pour des taux mensuels équivalents.
3) On considère un remboursement d’un emprunt en n versements de fin de période, de
montant a et au taux par période i. Montrer que a) les amortissements forment une suite
géométrique de raison 1 + i et de premier terme a(1 + i)−n ; b) le capital restant dû après le pe
versement est a.1 − (1 + i)p−n / i
Exercice
Mr Missi place dans une banque à intérêt composé le 5 janvier de chaque année une somme
de 300 000. Le premier versement est fait le 5 janvier 2001 et le dernier versement le 5 janvier
2010. Le taux de capitalisation est de 9%. Le capital constitué est resté en banque jusqu’au 5
janvier 2012 et a continué à produire les intérêts à 9%.
Quelle est la somme qu’il disposera le 5/1/2010. Et celle du 5/1/2012.
Réponse
300 000. (1.09)9 -1 / 0.09 et 300 000. (1.09)9 -1. (1.09)2 /0.09
Exercice
Vous disposez de 1.000.000 le 10 mars 2012 que vous placez dans une banque à charge pour
qu’elle vous verse tous les ans une somme constante 70.000. le premier versement de la
banque intervient le 30 mars 2013 au taux d’intérêt de 10%.
Quelle sera la date du dernier versement.
Réponse
1.000.000 = 70 000.1-(1.1)-n /0.1…..après on tire n=…
Exercice (emprunt à taux d’intérêt progressif)
Mr X contracte un emprunt dans le but de financer ses investissements. Taux d’emprunt est
6% pendant 3 ans et 8% pendant 2 ans. Le montant de l’emprunt 800 000 et la durée de
remboursement est de 5 ans.
Etablir le tableau d’amortissement.
Réponse
Calcul de l’annuité constante a…800 000=a.1-(1.06)-3 /0.06 →a=191 833.85
Dette début Intérêts Amorts Anuités Dette fin
800 000 48 000 143 833.85 191 833.85 656 166.15
656 166.15 39 369.97 152 463.88 191 833.85 503 702.27
6

7. 503 702.27 30 222.14 161 611.71 191 833.85 342 090.56
342 090.56 27 367.24 164 466.61 -//- 177 623.95
177 623.95 14 208.90 177 623.95 -//- 0
Exercices et correction -Emprunts Indivis
Exercice 1 : Emprunt
Monsieur Boujas gagne 18 000 par mois et n’anticipe pas de modification de ses revenus dans
l’avenir. Il veut effectuer un emprunt immobilier sur 15 ans.
Sachant que le banquier accepte un ratio mensualité/revenu de 30% et qu’il lui propose un
financement à 7%, quel est le montant peut-il emprunter ?
Solution :
Il faut calculer la capacité de remboursement du client : R = 18 000 × 0.3 = 5 400.
Puis calculons le montant du prêt possible.
0 1 2 15 12=180
180 flux de 5 400
C0 ?
C0 = 5 400 × . ≈ 600 782,17
• Utilisation de la calculatrice
• CLEAR ALL
• 12 P/YR
• 15 x P/YR
• 7 I/YR
• 5 400 PMT
• PV
Résultat ► - 600 782.1711
Exercice 2 : Tableaux d’amortissement
On considère un emprunt indivis de montant 200 000 le 01.01.2006, remboursable en 5 ans au taux
d’intérêt de 7% (assurance comprise). 1er remboursement le 01.01.2007 (remboursements par annuités)
Présenter le tableau d’amortissement correspondant à chacune des trois modalités possibles de
remboursement, les annuités étant perçus tous les 1er janvier. Calculer la somme des intérêts versés.
Solution :
• Par annuités constantes :
Soit : R = 200 000 × ≈ 48 778.14
Montant du
Date remboursement Intérêt Créance amortie Assurance Capital restant dû
R In = Cni Kn = R-In-An An=Cna Cn=Cn-1 - Kn
01/01/2006 200 000.00
01/01/2007 48 778.14 14 000.00 34 778.14 0.00 165 221.86
01/01/2008 48 778.14 11 565.53 37 212.61 0.00 128 009.25
01/01/2009 48 778.14 8 960.65 39 817.49 0.00 88 191.76
7

8. 01/01/2010 48 778.14 6 173.42 42 604.72 0.00 45 587.05
01/01/2011 48 778.14 3 191.09 45 587.05 0.00 0.00
total 243 890.69 43 890.69 200 000.00 0.00
• Par amortissements constants
Montant du
Date remboursement Intérêt Créance amortie Assurance Capital restant dû
R=I+K In = Cni K = C0/n An=Cna Cn=Cn-1 - Kn
01/01/2006 200 000.00
01/01/2007 54 000.00 14 000.00 40 000.00 0.00 160 000.00
01/01/2008 51 200.00 11 200.00 40 000.00 0.00 120 000.00
01/01/2009 48 400.00 8 400.00 40 000.00 0.00 80 000.00
01/01/2010 45 600.00 5 600.00 40 000.00 0.00 40 000.00
01/01/2011 42 800.00 2 800.00 40 000.00 0.00 0.00
total 242 000.00 42 000.00 200 000.00 0.00
• In fine
Montant du
Date remboursement Intérêt Créance amortie Assurance Capital restant dû
R=I+K In = Cni K = C0/n An=Cna Cn=Cn-1 - Kn
01/01/2006 200 000.00
01/01/2007 14 000.00 14 000.00 0.00 0.00 200 000.00
01/01/2008 14 000.00 14 000.00 0.00 0.00 200 000.00
01/01/2009 14 000.00 14 000.00 0.00 0.00 200 000.00
01/01/2010 14 000.00 14 000.00 0.00 0.00 200 000.00
01/01/2011 214 000.00 14 000.00 200 000.00 0.00 0.00
total 270 000.00 70 000.00 200 000.00 0.00
Exercice: Emprunt immobilier
1°) Tracez le diagramme des flux.
2°) Déduisez-en l’équation vérifiée par C. Simplifiez cette équation et calculez C.
8

9. Exercice: Emprunt à annuités constantes
1°) Soit a le montant de l’annuité. Calculez a en détaillant votre calcul.
2°) Dressez le tableau d’amortissement de l’emprunt puis remplissez-le.
Emprunt obligataires
9

10. I – Définition : Les Obligations : un placement presque sûr
1. Qu'est ce que c'est ?
Les obligations font partie des valeurs mobilières. Il s'agit de titres de créance émis par une société, un
établissement public, une collectivité locale ou l'Etat en contrepartie d'un prêt.
L'obligataire détient une reconnaissance de dette que l'émetteur s'engage à rembourser à une échéance
convenue et à servir au porteur un intérêt annuel indépendant de l'évolution de ses résultats et même
en l'absence de bénéfice.
Le contrat d'émission doit indiquer :
• le prix d'émission,
• la date de jouissance (départ du calcul des intérêts),
• la date de règlement, la durée de l'emprunt,
• le coupon (intérêt annuel),
• le taux de rendement actuariel brut (rendement effectivement perçu pendant la durée de
l'emprunt),
• la date de remboursement, le remboursement éventuel par amortissement.
2. Avantages et Inconvénients
L'avantage du placement en obligation est la sécurité du placement : en effet, le rendement est garanti
et la mise de fonds est assurée d'être récupérée à l'échéance.
Cependant, il existe certains risques : ainsi, si l'émetteur est en faillite, il ne pourra pas ni payer les
intérêts ni rembourser l'obligation. C'est ce qu'on appelle le risque de signature. Mais ce risque peut
être évité en choisissant des obligations sûres comme les obligations d'Etat ou de sociétés renommées.
Le revers de la médaille est la faiblesse des taux alors offerts.
Aussi, il y a le risque de taux : lorsque les taux d'intérêt augmentent, le cours des obligations anciennes
baisse puisque les obligations nouvellement émises sont plus attractives. Inversement, lorsque les taux
d'intérêt diminuent, le cours des obligations anciennes augmente car leurs rendements sont supérieurs
à ceux des nouvelles obligations.
Enfin, il y a le risque de perte en capital lorsqu'à la fois les taux d'intérêts augmentent et le titulaire
d'obligations décide de les céder : en effet, ces obligations ne prendront pas toujours preneurs. Mais
dans le cas où les taux d'intérêts baissent, le titulaire d'obligations peut s'attendre à réaliser des plus-
values s'il vend les obligations avant leurs échéances.
• Avantages
o Rendement garanti
o Mise de fonds assurée d'être récupérée à l'échéance
o En cas de diminution des taux d'intérêts, possibilité de réaliser des gains en cas de
vente des obligations avant leurs échéances
• Inconvénients
o Risque de signature
o Risque de taux
o Risque de perte de capital si les obligations ne sont pas conservées jusqu'à l'échéance
3. La gestion des obligations
Le titulaire d'obligation reçoit chaque année un intérêt qu'on appelle le coupon. Ce coupon est versé
généralement en une seule fois mais il peut y avoir des versements trimestriels.
Si l'obligation est à taux fixe, le coupon sera chaque année du même montant. Mais le coupon annuel
peut varier d'une année à l'autre lorsque en cas d'obligations à taux variable ou à taux révisable.
L'achat des obligations lors de leur émission se fait sur le marché primaire (C'est le marché d'émission
des titres (introductions en bourse)) et le règlement des titres est réalisé trois semaines après l'annonce
de l'emprunt. Aussi, l'acquisition des obligations plus anciennes s'effectue sur le marché secondaire
10

11. (C'est le marché ou se négocient et s'échangent les titres en bourse) où s'échangent les obligations
cotées en Bourse : c'est en particulier sur ce marché que les obligations sont revendues avant leurs
échéances.
4. Quelques obligations particulières
• Les obligations assimilables au Trésor (OAT) : ce sont des titres de créance qui
représentent une part d'un emprunt à long terme émis par l'Etat. L'Etat s'engage
alors à rembourser à l'obligataire en une seule fois cette part d'emprunt à une
échéance de sept à trente ans et dont la rémunération est un intérêt annuel. Les
OAT sont cotées en Bourse pendant toute la durée de leur vie, ce qui permet
d'ailleurs à leur porteur de s'en défaire facilement.
La valeur nominale est celle qui sera remboursée à échéance et sur laquelle sont
calculés les intérêts. Le prix d'émission est le prix d'achat de l'obligation, il peut
être différent de la valeur nominale. Depuis octobre 1994, les OAT à dix ans à un
prix fixe peuvent être achetées chaque mois chez un intermédiaire financier du
premier jeudi au vingt quatre du mois. Le prix inclut une commission d'achat de 2
% de la valeur nominale.
• Les obligations convertibles en actions (OCA) : ce sont des obligations ayant la
possibilité d'être converties en actions à tout moment ou plusieurs époques
déterminées à l'avance par l'émetteur. Cependant, ces obligations sont émises à un
taux inférieur aux obligations classiques (on ne peut pas avoir le beurre et l'argent
du beurre !). Cela permet néanmoins au porteur de ce type d'obligation de
bénéficier d'une gestion flexible et attractive : en effet, lorsque le cours de l'action
augmente et devient supérieur à la valeur de remboursement de l'obligation, le
porteur convertira son obligation en action afin de profiter d'un meilleur
rendement.
• Les obligations à coupon zéro : ce sont des obligations émises à un prix bas et
remboursées à un prix élevé, ce qui permet au porteur de ce type d'obligation de
réaliser une plus-value intéressante. En revanche, ces obligations ne rapportent
aucun intérêt.
5. Bilan
Avantages
Pour l’émetteur • Taux d’intérêt versé inférieur à celui des obligations classiques.
• Facilité de placement en cas de conjoncture difficile. Clientèle potentielle large
(amateurs d’actions et amateurs d’obligations).
• En cas de conversion, la dette ne sera pas remboursée.
• Augmentation de capital potentielle réalisée avec une prime d’émission plus
importante qu’en cas d’augmentation de capital immédiate : les OCA
(Obligations Convertibles en Actions) ont un prix de conversion supérieur au
cours initial de l’action.
• Produit anti-OPA, les OCA sont des actions potentielles
Pour le • Rendement garanti.
souscripteur • Si le cours de l’action dépasse le cours de l’obligation, celle-ci peut être
convertie en action si la valeur de conversion est supérieure au cours de
l’obligation.
• Le cours de l’obligation convertible en action augmente quand le cours de
l’action augmente et ne descend pas en dessous d’un certain niveau lorsque
l’action baisse, puisque c’est un titre qui sert un taux d’intérêt fixe.
11

12. 6. Exemple
Cours du jour
Taux Coupon Date du
Cours (en % de la
Code ISN Valeur actuariel couru (en % prochain
précédent valeur
brut du nominal) coupon
nominale)
CREDIT AGRICOLE SA (EX CNCA)
FR0000186
4,90% - 03/2011 CB 98,71 98,76 4,46 2,2311 15/03/06
223
FR0000186
5,60% - 12/2011 CA 107,09 107.9 107.18 4.54
694
4 groupes de cotation :
• CA = titres cotés en continu et ayant un large marché,
• CB = idem avec marché moins important
• FA = 2 cotations par jours
• FB = 1 cotation par jour
II – La cotation
• le nominal
Comme les actions, une obligation a un nominal. C'est sur ce montant que sera calculé les coupons
qui vous seront versés par la société. Le nominal des obligations est souvent fonction du type
d'obligations. Mais dans certains cas, l'AMF (BEAC) peut imposer à l'émetteur d'augmenter la part
de son nominal afin de limiter la souscription à des investisseurs plus avertis.
• le taux d'intérêt nominal
Il s'agit du taux d'intérêt permettant le calcul des coupons. Ainsi avec un nominal de 500 et un taux
d'intérêt nominal de 6%, vous percevrez chaque année 500 × 6% = 30.
• le prix d'émission
Afin d'attirer de nombreux investisseurs, il n'est pas rare que le prix d'émission de l'obligation soit
inférieur à la valeur nominale. Il en est de même pour le marché actions lors de l'introduction en
bourse. Il est possible également, dans des cas plus rares, que le prix d'émission soit supérieur au
montant du nominal. Dans la pratique, l'entreprise remboursera à l'échéance de l'obligation un
montant supérieur à celui emprunté.
• le prix de remboursement
A l'échéance de l'obligation, le montant de cette dernière vous aura été totalement remboursé. Ce
remboursement peut être supérieur au montant du nominal, et ce afin d'accroître l'intérêt pour les
investisseurs. La différence entre le prix de remboursement et le nominal est appelé prime de
remboursement.
• la cotation des obligations
Comme tout instrument financier, une obligation peut être négociée, échangée en toute simplicité.
De fait, le cours d'une obligation évolue en fonction des taux d'intérêts et d'autres éléments
spécifiques à une obligation. Mais il est important de savoir qu'une obligation est cotée en
pourcentage de son nominal et non en unités monétaires.
• Le coupon couru
C’est la fraction du coupon correspondant à la durée écoulée depuis le paiement du dernier coupon
d’intérêts. Il inclut (depuis 1995) le délai s’écoulant entre la date de négociation et la date de
règlement – livraison, soit 3 jours ouvrés. C'est-à-dire un intervalle de temps incluant 3 jours
ouvré. Par exemple si c’est un mardi, on compte 3 jours, si c’est un jeudi, on compte 5 jours.
Attention : Le coupon couru (en %) est exprimé avec 3 décimales.
12

13. ► Exemple 1
Soit une obligation de nominal 2 000, au taux de 6,40%, émise le 25.10.N, remboursable le
25.10.N+5. Quel était le coupon couru à la date du mardi 12.12.N+3 (date de négociation) ?
Solution :
Nombre de jours du 25.10.N+3 au 12.12.N+3 : (31-25)+30+12 = 48 jours
Le 15.12.N+3 étant un mardi, la durée sur laquelle on doit calculer le coupon couru est : 48 + 3 = 51
jours
▪ Coupon couru (en valeur) : ≈ 17,885
▪ Coupon couru (en % du nominal) : = 0,8942 ou ≈ 0,008942 = 0,8952 %
• La valeur d’une obligation à une date donnée
Valeur de l’obligation = Valeur cotée + Valeur du coupon couru
► Exemple 2
Soit une obligation de nominal 2 000, cote du jour 122,60, coupon couru (en %) : 6,396
Solution :
Valeur totale = …… × 2000 = 2579,92
III– Taux actuariel brut (ou taux de rendement actuariel brut)
Il s'agit du taux d'intérêt réellement perçu par l'investisseur. Ce taux se calcule à partir de la valeur
d'acquisition de l'obligation et en fonction des différents coupons.
• Définition :
A une date donnée, le taux actuariel brut d’un emprunt est le taux pour lequel il y a équivalence entre
la valeur des obligations à cette date et l’ensemble des annuités qui restent à recevoir.
Le taux actuariel d’une obligation est le taux de rendement réel de cette obligation si elle est conservée
jusqu’à son remboursement.
• Exemple résolu :
25 25
0 1 2 3
25 +
-495
Supposons que vous investissiez à l'émission dans une obligation de nominal 500 à un prix d'émission
de 495 avec un taux nominal de 5% pendant 3 ans. Vous percevrez donc des coupons de 25€ pendant
3 ans. Le taux actuariel se calcule ainsi :
495 = 25 × (1+t) + 25 × (1+t) + 525 × (1+t)
On peut aussi écrire que t est la solution de l’équation : 495 = 25 × (1+t) – 1 × ….. + 500×(1+t)
Soit 495 = 25×…. + 500×(1+t)
(Écrivez 495 = 25 × (1+t) + 25 × (1+t) + 25 × (1+t) +500 × (1+t) )
13

14. Il faut alors utiliser la calculatrice comme lors du calcul du TRI :
Utilisation de la calculatrice financière (HP BII)
• CLEAR ALL
• 1 P/YR
• - 495 CFj
• 25 CFj
• 2 Nj
• 525 CFj
• IRR/YR Résultat ► 5,3698
Remarque : La différence entre le taux d'intérêt actuariel de 5,37% et le taux d'intérêt nominal de 5%
s'explique par le montant de la prime d'émission qui est positive (5€).
► Exemple 3
Soit un emprunt de 2 00 obligations émis le 1.7.N, de nominal 1 000 euros, prix de remboursement :
1 010 euros ; taux nominal de 5% ; remboursement : in fine, dans 5 ans.
Calculer le taux actuariel brut à l’émission t.
Solution : On peut raisonner sur 1 obligation
t solution de : 1000 = 50 × …….+ 1010×(1+t) – 5 , on trouve
IV– Valeur théorique d’une obligation à une date donnée
Le taux actuariel brut d’une obligation à une date donnée est le taux de rendement exigé par les
investisseurs à cette date pour ce type d’obligations (c’est-à-dire, compte tenu de la durée de
remboursement, de la nature de l’émetteur…). Connaissant le taux actuariel brut, ou taux de marché, il
est possible de retrouver le prix d’achat qu’un investisseur est prêt à payer pour acquérir l’obligation.
► Exemple 4
Dans l’exemple 3, calculer la valeur de l’obligation au 5.3.N+3, sachant que le taux pratiqué sur le
marché est de 6,5 % pour ce type d’obligation. Retrouver alors la valeur cotée (ou valeur nue, ou
valeur au pied du coupon).
Pour 1 obligation
50 50 50 50 50+101
1.7.N 1.7.N+1 1.7.N+2 1.7.N+3 1.7.N+4 1.7.N+5
118 jours
5.3.N+3
-1 000
Solution : On peut raisonner sur 1 obligation
Calcul du nombre de jours du 5.3.N+3 au 1.7.N+3 : (31-5)+30+31+30+1 = 118 jours
5.4.N+ Valeur = 50×(1,065) – 118/365 + 50×(1,065) – (118+365)/365 + 1060×(1,065) – (118 + 2×365)/365
La valeur trouvée est la valeur à payer pour acquérir l’obligation le 5.3.N+3.
On peut aussi retrouver la valeur cotée en déduisant les intérêts courus de ce montant.
14

15. Intérêts courus : 50× ……. ≈ 33,42
Valeur cotée théorique (ou valeur nue ou valeur au pied du coupon) = 1 010,72 – 33,42 ≈
V– Lien entre la valeur théorique d’une obligation et le taux d’intérêt
La valeur totale d’une obligation et la valeur cotée varient de façon inverse à la variation du taux
d’intérêt.
(Quand l’un augmente, l’autre diminue)
► Exemple 5 : Avec les données de l’exemple 4
Taux
d’intérêt
pratiqué Valeur de l’obligation au 5.4.N+3
sur le
marché
1010.72
t = 6,5% 50×(1,065) – 118/365 + 50×(1,065) – (118+365)/365 + 1060×(1,065) – (118 + 2×365)/365
euros
1 031.74
t = 5.5% 50×(1,055) – 118/365 + 50×(1,055) – (118+365)/365 + 1060×(1,065) – (118 + 2×365)/365
euros
990.34
t = 7.5 % 50×(1,075) – 118/365 + 50×(1,075) – (118+365)/365 + 1060×(1,075) – (118 + 2×365)/365
euros
VI– Sensibilité et duration
2. Définition de la sensibilité :
La sensibilité d’une obligation est la variation de la valeur de cette obligation provoquée par la
variation de un point du taux d’intérêt. Cette variation est exprimée en pourcentage.
La sensibilité permet ainsi de connaître la valeur future d'une obligation en utilisant différents
scénarios de taux d'intérêts. Elle mesure la durée de vie moyenne des obligations non encore
remboursées.
► Exemple 6
Calculer la sensibilité de l’obligation de l’exemple 3 en vous plaçant à la date d’émission. Il y a une
ambiguïté, laquelle ?
Solution :
La valeur d’une obligation à l’émission au taux de t % est : V(t) = 50 × ……. + 1010×(1+t) – 5
Donc :
t 5% 6% 4%
V(t) ≈ 1007.8353 ≈ 965.3489 ≈ 1052.7375
Si le taux passe de ti = 5% à tf = 6%, la variation est : ……… ≈ - 4.216 %
Si le taux passe de ti = 5% à tf = 4%, la variation est : ………… ≈ + 4.455 %
On retient généralement la sensibilité liée à une augmentation de 1 point du taux soit une baisse de
4.22%
Cela signifie que le cours de l’obligation diminue de 4.22 % quand le taux d’intérêt du marché
augmente d’un point.
Utilisation de la calculatrice
• CLEAR ALL
• 1 P/YR
15

16. • 5 I/YR
• 0 CFj (flux de 0 le 01.01.N)
• 50 CFj
• 4 Nj (2 flux identiques)
• 1060 CFj
• NPV
Résultat ► 1007.8353 (c’est V((5%))
Puis inutile de tout recalculer,
changez juste le taux
• 6 I/YR
• NPV
Résultat ► 965.3489 (C’est V(%))
3. Définition de la duration :
La duration d’une obligation est la moyenne pondérée des dates d’échéances des diverses annuités
par les flux monétaires (coupons et/ou remboursements) versés aux échéances, ces flux étant actualisés
au taux du marché.
► Exemple 7
En reprenant l’exemple 3/4, calculer la duration de l’emprunt.
Echéances 1 2 3 4 5
Flux
(coupon et/ou 50 (1 +….) – 1 50 (1 +……) – 2 50 (1 +……) – 3 50 (1 +…..) – 4 1060 (1 +….) – 5
remboursement)
4. Relation entre sensibilité et duration :
► Exemple 8
Vérifier la formule avec les exemples 6 et 7.
Solution :
On avait S = - 4.22 et D = 4.53 or - 4.34 ≈ - 4.22
Remarque : La sensibilité est directement proportionnelle à la duration.
16