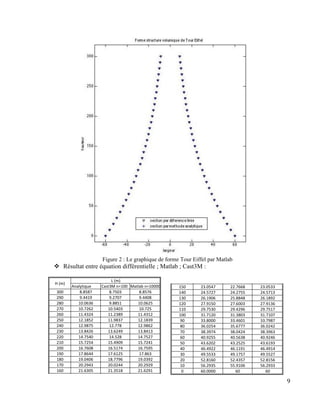
Ce document présente un projet du Master en Génie Civil à l'Institut National des Sciences Appliquées de Rennes, consacré à l'étude numérique et à l'optimisation d'une structure inspirée de la tour Eiffel à l'aide de logiciels tels que Abaqus et Cast3M. L'objectif principal est de modéliser une structure équivalente et d'optimiser les sections et les coordonnées pour minimiser les contraintes. Les résultats seront présentés dans un rapport de 20 pages, à rendre avant le 20 janvier 2013.



![3
∫
𝑑𝐴
𝐴
= ∫ −
𝛾𝑎
𝜎 𝑛
𝑑𝑧
𝑙𝑛A = −
𝛾𝑎
𝜎 𝑛
. 𝑧 + 𝐶
𝐴(𝑧) = 𝐶. exp(−
𝛾𝑎
𝜎 𝑛
. 𝑧)
On sait que au niveau de z=0, A(z=0)=L2
et L=120 m
𝐴(𝑧 = 0) = 𝐶. exp (−
𝛾𝑎
𝜎 𝑛
. 0) = 𝐿2
𝐶 = 𝐿2
Enfin, on a
𝐴(𝑧) = 𝐿2
. 𝑒𝑥𝑝 (−
𝛾𝑎
𝜎 𝑛
. 𝑧)
𝐿(𝑧) = √A = ±𝐿. 𝑒𝑥𝑝 (−
𝛾𝑎
2𝜎 𝑛
. 𝑧)
b. Analyse des fonction et optimiser
La condition nécessaire et suffisante pour avoir une structure d’égale résistance :
𝑑𝜎𝑧
𝑑𝑧
= 0
∭ (
𝑑𝜎𝑧
𝑑𝑧
)
2
𝑑𝑉𝑜𝑙 = ∫ (
𝑑𝜎𝑧
𝑑𝑧
)
2
𝐴(𝑧)𝑑𝑧
𝐻
0
Déterminer contrainte est constante
𝜎𝑧 =
𝑃(𝑧)
𝐴(𝑧)
=
𝜎 𝑛. 𝐴(𝐻) + ∫ 𝛾𝑎. 𝐴(𝑧)𝑑𝑧
𝐻
𝑧
𝐴(𝑧)
𝜎𝑧 =
𝜎 𝑛. 𝐿2
. 𝑒𝑥𝑝 (−
𝛾𝑎
𝜎 𝑛
. 𝐻) + ∫ 𝛾𝑎. 𝐿2
. 𝑒𝑥𝑝 (−
𝛾𝑎
𝜎 𝑛
. 𝑧) 𝑑𝑧
𝐻
𝑧
𝐿2. 𝑒𝑥𝑝 (−
𝛾𝑎
𝜎 𝑛
. 𝑧)
𝜎𝑧 = 𝜎 𝑛. 𝑒𝑥𝑝 [
𝛾𝑎
𝜎 𝑛
(𝑧 − 𝐻)] + 𝛾𝑎. 𝑒𝑥𝑝 (
𝛾𝑎
𝜎 𝑛
. 𝑧) . [−
𝜎 𝑛
𝛾𝑎
. exp(−
𝛾𝑎
𝜎 𝑛
. 𝑧)]
𝐻
𝑧
𝜎𝑧 = 𝜎 𝑛. 𝑒𝑥𝑝 [
𝛾𝑎
𝜎 𝑛
(𝑧 − 𝐻)] − 𝜎 𝑛. 𝑒𝑥𝑝 (
𝛾𝑎
𝜎 𝑛
. 𝑧) . [exp (−
𝛾𝑎
𝜎 𝑛
Z) − 𝑒𝑥𝑝 (−
𝛾𝑎
𝜎 𝑛
𝑍)]
𝜎𝑧 = 𝜎 𝑛. 𝑒𝑥𝑝 [
𝛾𝑎
𝜎 𝑛
(𝑧 − 𝐻)] − 𝜎 𝑛. 𝑒𝑥𝑝 [
𝛾𝑎
𝜎 𝑛
. (𝑧 − 𝐻)] + 𝜎 𝑛
𝜎𝑧 = 𝜎 𝑛 = 𝑐𝑡𝑒
𝑑𝑜𝑛𝑐
𝑑𝜎𝑧
𝑑𝑧
= 0
La contrainte n’a pas changer à cause de ‘z’.
Le minimum global d’une fonction
∭ (
𝑑𝜎𝑧
𝑑𝑧
)
2
𝑑𝑉𝑜𝑙 = ∫ (
𝑑𝜎𝑧
𝑑𝑧
)
2
𝐴(𝑧)𝑑𝑧
𝐻
0](https://image.slidesharecdn.com/a5dab66a-689b-47a7-a84a-b070dc485213-170119150908/85/Projet-Methode-numerique_-MENG-Try-4-320.jpg)
![4
𝜎𝑧 =
𝑃(𝑧)
𝐴(𝑧)
=≫(
𝑑𝜎𝑧
𝑑𝑧
)
2
= (
𝑃′
𝐴 − 𝐴′𝑃
𝐴2
)
2
Φ(𝐴) = ∫ (
𝑑𝜎𝑧
𝑑𝑧
)
2
𝐴(𝑧)𝑑𝑧
𝐻
0
= ∫ [𝛾𝑎
2
+ 2𝛾𝑎.
𝐴′
𝐴
. 𝜎 𝑛 + (
𝐴′
𝐴
𝜎 𝑛)
2
]
𝐻
0
. 𝐴𝑑𝑧
Fonction optimiser :
Min Φ(𝑉) = ∫ 𝐹(𝑥, 𝑉, 𝑉′)𝑑𝑥𝐷
Dans notre cas
𝐹(𝑍, 𝐴, 𝐴′) = 𝛾𝑎
2
𝐴 + 2𝛾𝑎. 𝐴′. 𝜎 𝑛 +
(𝐴′
)2
𝐴
𝜎 𝑛
2
Avec :
𝐹𝐴 =
𝑑𝐹(𝐴, 𝐴′
)
𝑑𝐴
= 𝛾𝑎
2
− (
𝐴′
𝐴
𝜎 𝑛)
2
𝐹𝐴′ =
𝑑𝐹(𝐴, 𝐴′
)
𝑑𝐴′
= 2𝛾𝑎 𝜎 𝑛 + (
2𝐴′
𝐴
𝜎 𝑛
2
)
Mimisation de fonction Φ(𝐴)
𝐹𝐴 −
𝜕
𝜕𝑧
𝐹 𝐴′ = 0
𝛾𝑎
2
− (
𝐴′
𝐴
)
2
. 𝜎 𝑛
2
− 2𝜎 𝑛
2
.
𝐴"𝐴 − 𝐴′2
𝐴2
= 0(1)
On pose :
𝑦 =
𝐴′
𝐴
=≫ 𝑦′
=
𝐴"𝐴 − 𝐴′2
𝐴2
(1) =≫ 𝛾𝑎
2
− 𝑦2
𝜎 𝑛
2
− 2𝜎 𝑛
2
𝑦′
= 0
(
𝛾𝑎
𝜎 𝑛
)
2
− 𝑦2
− 2𝑦′
= 0
pour résoudre l’équation différentiel, on pose b = γa / σn ;
2.
𝑑𝑦
𝑏2 − 𝑦2
= 𝑑𝑧
2
(𝑏 − 𝑦)(𝑏 + 𝑦)
𝑑𝑦 = 𝑑𝑧
1
𝑏
(
1
𝑏 − 𝑦
+
1
𝑏 + 𝑦
) 𝑑𝑦 = 𝑑𝑧
1
𝑏
. ln (
𝑏 + 𝑦
𝑏 − 𝑦
) = 𝑧 + 𝑐1
𝑦 =
𝑏[exp(𝑏𝑧 + 𝑐1) − 1]
1 + exp( 𝑏𝑧 + 𝑐1)
𝐴′
𝐴
=
𝑏[𝑐1exp(𝑏𝑧) − 1]
1 + 𝑐1exp( 𝑏𝑧)
𝑑𝐴
𝐴
=
𝑏[𝑐1exp(𝑏𝑧) − 1]
1 + 𝑐1exp( 𝑏𝑧)
𝑑𝑧](https://image.slidesharecdn.com/a5dab66a-689b-47a7-a84a-b070dc485213-170119150908/85/Projet-Methode-numerique_-MENG-Try-5-320.jpg)
![5
𝑑A
𝐴
= 𝑏 [
𝑐1exp(𝑏𝑧)
1 + 𝑐1exp( 𝑏𝑧)
−
1
1 + 𝑐1exp( 𝑏𝑧)
] 𝑑𝑧
𝑙𝑛𝐴 = 𝑏 [
1
𝑏
∫
𝑏 𝑐1exp(𝑏𝑧)
1 + 𝑐1exp( 𝑏𝑧)
𝑑𝑧 − ∫
𝑑𝑧
1 + 𝑐1exp( 𝑏𝑧)
]
𝑙𝑛𝐴 = [ln(1 + 𝑐1exp(𝑏𝑧)) − 𝑏 ∫
𝑑𝑧
1 + 𝑐1exp( 𝑏𝑧)
]
On pose : u = exp(bz)
du = b.exp(bz)dz = b.u.dz
𝑙𝑛𝐴 = [ln(1 + 𝑐1 𝑢) − 𝑏 ∫
𝑑𝑢
𝑏. 𝑢(1 + 𝑐1u)
]
𝑙𝑛𝐴 = [ln(1 + 𝑐1 𝑢) − ∫ (
1
𝑢
−
𝑐1
1 + 𝑐1 𝑢
) 𝑑𝑢]
𝑙𝑛𝐴 = [ln(1 + 𝑐1 𝑢) − (ln(𝑢) − ln(1 + 𝑐1 𝑢)) + ln( 𝑐2)]
𝑙𝑛𝐴 = 𝑙𝑛 (
(1 + 𝑐1 𝑢)2
𝑢
. 𝑐2)
𝐴 = 𝑐2.
[1 + 𝑐1 exp(𝑏𝑧)]2
exp(𝑏𝑧)
Condition aux limites : A(z=0) = L2
A(z=∞) = 0
lim
𝑧→∞
𝑐2.
[1 + 𝑐1 exp(𝑏𝑧)]2
exp(𝑏𝑧)
= 0
𝑐1 = lim
𝑧→∞
−
1
exp(𝑏𝑧)
= 0
𝐴(𝑧 = 0) = 𝐿2
= 𝑐2.
1
exp(𝑏. 0)
=≫ 𝑐2 = 𝐿2
donc :
𝐴(𝑧) = 𝐿2
. exp(−
𝛾𝑎
𝜎 𝑛
𝑧)
𝐿(𝑧) = ±𝐿. exp(−
𝛾𝑎
2𝜎 𝑛
𝑧)
c. Principe d’optimisation topologique
À partir de la forme initiale, section A constante et hauteur H :
𝑁(𝑧) = 𝐴. 𝛾𝑎(𝐻 − 𝑍)
le diagramme normal a nous montre que au niveau
de H, l’effort normal N=0, c’est à dire on peut
réduire la section A selon l’axe Z.
N(z)](https://image.slidesharecdn.com/a5dab66a-689b-47a7-a84a-b070dc485213-170119150908/85/Projet-Methode-numerique_-MENG-Try-6-320.jpg)
![6
On va changer la forme de la structure à la section variable selon l’axe z :
Section initiale à z=0, A= L2
𝑁 =
1
3
𝛾𝑎(𝐻𝐿2
+ 𝑍𝐿2
+ 𝑍𝐿√𝐴(𝑧) + 𝑍. 𝐴(𝑧))
il faut que la contrainte résistance égale à contrainte action pour
toute niveau:
𝜎 𝑛 =
𝑁
𝐴
= 𝑐𝑡𝑒
𝜎 𝑛 =
𝛾𝑎
3. 𝐴(𝑧)
(𝐻𝐿2
+ 𝑍𝐿2
+ 𝑍𝐿√𝐴(𝑧) + 𝑍. 𝐴(𝑧))
(
3𝜎 𝑛
𝛾𝑎
− 𝑍) 𝐴(𝑧) = (𝐻𝐿2
+ 𝑍𝐿2
+ 𝑍𝐿√𝐴(𝑧))
[(
3𝜎 𝑛
𝛾𝑎
− 𝑍) 𝐴(𝑧) − 𝐻𝐿2
− 𝑍𝐿2
]
2
= (𝑍𝐿√𝐴(𝑧))
2
(
3𝜎 𝑛
𝛾𝑎
− 𝑧)
2
𝐴2(𝑧) + (𝐻 + 𝑍)2
𝐿4
− 2𝐿2(𝐻 + 𝑍) (
3𝜎 𝑛
𝛾𝑎
− 𝑍) 𝐴(𝑧) = (𝐿𝑍)2
𝐴(𝑧)
(
3𝜎 𝑛
𝛾𝑎
− 𝑧)
2
𝐴2(𝑧) − 𝐴(𝑧) [2𝐿2(𝐻 + 𝑍) (
3𝜎 𝑛
𝛾𝑎
− 𝑍) + 𝑍2
𝐿2
] + 𝐿4(𝐻 + 𝑍)2
= 0
𝑎𝐴2(𝑧) − 𝑏𝐴(𝑧) + 𝑐 = 0
Avec :
𝑎 = (
3𝜎 𝑛
𝛾𝑎
− 𝑧)
2
; 𝑏 = − [2𝐿2(𝐻 + 𝑍) (
3𝜎 𝑛
𝛾𝑎
− 𝑍) + 𝑍2
𝐿2
] ; 𝑐 = 𝐿4(𝐻 + 𝑍)2
Après résoudre cette équation, on obtenu :
𝐴(𝑧) =
[2𝐿2(𝐻 + 𝑍) (
3𝜎 𝑛
𝛾𝑎
− 𝑍) + 𝑍2
𝐿2
] + 𝐿2
𝑍√𝑍2 + 4(𝐻 + 𝑍) (
3𝜎 𝑛
𝛾𝑎
− 𝑍)
2 (
3𝜎 𝑛
𝛾𝑎
− 𝑍)
2
travail numérique, Z=0 ; σn = 6Mpa ; γa = 7.8E3x9.81 ; H=300 ; L=120 :
𝐴(𝑧 = 0) =
1202
× 300
3 × 6𝐸6
7.8𝐸3 ∗ 9.81
= 18364.32𝑚2](https://image.slidesharecdn.com/a5dab66a-689b-47a7-a84a-b070dc485213-170119150908/85/Projet-Methode-numerique_-MENG-Try-7-320.jpg)
![7
d. Vérifier les coordonnées géométriques des nœuds
A partir de l’équation L(z) qu’on a déjà montrer dans le partie précédent, on va commence
de vérifier les coordonnées :
A[ L(z=0)/2 ; 0] = A(-60 ; 0)
D[ L(z=0)/2 ; 0] = D(60 ; 0)
B[ L(z=0)/6 ; 0] = B(-20 ; 0)
C[ L(z=0)/6 ; 0] = C(20 ; 0)
𝐿(𝑧 = 0)
2
= ±
120. exp(−
𝛾𝑎
2𝜎 𝑛
. 0)
2
= ±60
E[ L(z=100)/2 ; 100] = E(31.71 ; 100)
F[ 0 ; 100]
G[ L(z=100)/2 ; 100] = G(31.71 ; 100)
𝐿(𝑧 = 100)
2
= ±
120. exp(−
7.8𝐸3𝑥9.81
2𝑥6𝐸6
. 100)
2
= ±31.71
H[ 0 ; 150]
I[ L(z=200)/2 ; 200] = I(-16.76 ; 200)
J[ L(z=200)/2 ; 200] = J(16.76 ; 200)
K[ L(z=300)/2 ; 300] = K(-8.86 ; 300)
L[ L(z=300)/2 ; 300] = L(8.86 ; 300)
Donc, touts les coordonnés sont vérifié.
e. Algorithme numérique
Technique des différences finies :
𝑑𝑓(𝑧)
𝑑𝑧
=
𝑓(𝑧 + ℎ) − 𝑓(𝑧)
ℎ
On a :
𝐴(𝑧) = 𝐿2
. exp(−
𝛾𝑎
𝜎 𝑛
𝑧)
𝑑𝐴(𝑧)
𝑑𝑧
= −
𝛾𝑎
𝜎 𝑛
. 𝐿2
exp(−
𝛾𝑎
𝜎 𝑛
𝑧)
𝑑𝐴(𝑧)
𝑑𝑧
= −
𝛾𝑎
𝜎 𝑛
. 𝐴(1)
𝑑𝐴(𝑧)
𝑑𝑧
=
𝐴(𝑧 + ℎ) − 𝐴(𝑧)
ℎ
(2)
Par équation (1) et (2), on a :
𝐴(𝑧 + ℎ) − 𝐴(𝑧)
ℎ
= −
𝛾𝑎
𝜎 𝑛
. 𝐴
𝐴(𝑧 + ℎ) = (1 −
𝛾𝑎
𝜎 𝑛
. ℎ) . 𝐴(𝑧)
donc, la précision de résultat est grâce à l’hauteur de chaque tranche, si on divise plusieurs
tranche, c’est à dire on obtient plus petit de ‘h’. La technique des différences finies va vérifier
quand h tend vers à 0.](https://image.slidesharecdn.com/a5dab66a-689b-47a7-a84a-b070dc485213-170119150908/85/Projet-Methode-numerique_-MENG-Try-8-320.jpg)