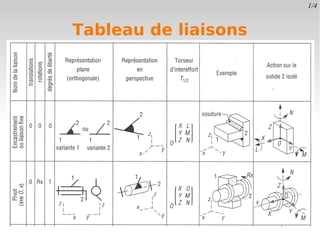
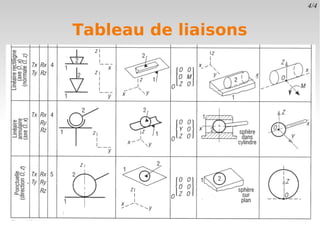
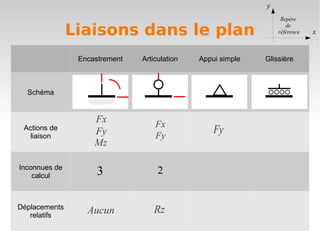
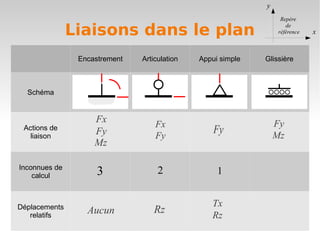
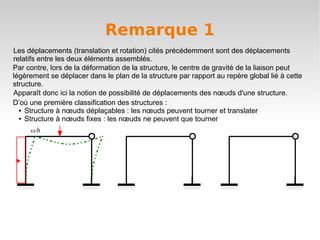
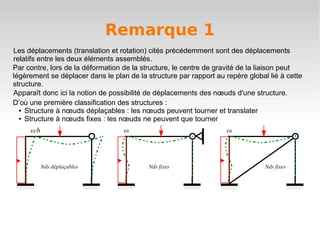
Le document définit le degré de liberté d'un solide par rapport à un solide de référence, en précisant les composantes de mouvement en translation et en rotation dans l'espace et le plan. Il explique également la notion de liaison, qui supprime un ou plusieurs degrés de liberté, et introduit la classification des structures selon la possibilité de déplacements de leurs nœuds. Enfin, il aborde des actions de liaison spécifiques et les conséquences sur les déplacements relatifs lors de la déformation des structures.

1. Liaisons & libertés
E. Bugnet

2. Pour une meilleur lisibilité,
passez en plein écran !
E. Bugnet

3. Définitions

4. Définitions
Degré de liberté :

5. Définitions
Degré de liberté :
On appelle degré de liberté d'un solide II par rapport à un solide I de référence, le nombre
de composantes de déplacement indépendantes et non nulles.

6. Définitions
Degré de liberté :
On appelle degré de liberté d'un solide II par rapport à un solide I de référence, le nombre
de composantes de déplacement indépendantes et non nulles.
Dans l'espace :
● 3 composantes de translation : Tx, Ty, Tz
● 3 composantes de rotation : Rx, Ry, Rz

7. Définitions
Degré de liberté :
On appelle degré de liberté d'un solide II par rapport à un solide I de référence, le nombre
de composantes de déplacement indépendantes et non nulles.
Dans l'espace : Dans le plan :
● 3 composantes de translation : Tx, Ty, Tz ● 2 composantes de translation : Tx, Ty
● 3 composantes de rotation : Rx, Ry, Rz ● 1 composante de rotation : Rz

8. Définitions
Degré de liberté :
On appelle degré de liberté d'un solide II par rapport à un solide I de référence, le nombre
de composantes de déplacement indépendantes et non nulles.
Dans l'espace : Dans le plan :
● 3 composantes de translation : Tx, Ty, Tz ● 2 composantes de translation : Tx, Ty
● 3 composantes de rotation : Rx, Ry, Rz ● 1 composante de rotation : Rz
Degré de liaison :

9. Définitions
Degré de liberté :
On appelle degré de liberté d'un solide II par rapport à un solide I de référence, le nombre
de composantes de déplacement indépendantes et non nulles.
Dans l'espace : Dans le plan :
● 3 composantes de translation : Tx, Ty, Tz ● 2 composantes de translation : Tx, Ty
● 3 composantes de rotation : Rx, Ry, Rz ● 1 composante de rotation : Rz
Degré de liaison :
Une liaison est la suppression d'un degré de liberté.
On appelle degré de liaison le nombre de degrés de liberté supprimés.

10. Définitions
Degré de liberté :
On appelle degré de liberté d'un solide II par rapport à un solide I de référence, le nombre
de composantes de déplacement indépendantes et non nulles.
Dans l'espace : Dans le plan :
● 3 composantes de translation : Tx, Ty, Tz ● 2 composantes de translation : Tx, Ty
● 3 composantes de rotation : Rx, Ry, Rz ● 1 composante de rotation : Rz
Degré de liaison :
Une liaison est la suppression d'un degré de liberté.
On appelle degré de liaison le nombre de degrés de liberté supprimés.
d liaison =6−∑ d liberté
° °
Dans l'espace :

11. Définitions
Degré de liberté :
On appelle degré de liberté d'un solide II par rapport à un solide I de référence, le nombre
de composantes de déplacement indépendantes et non nulles.
Dans l'espace : Dans le plan :
● 3 composantes de translation : Tx, Ty, Tz ● 2 composantes de translation : Tx, Ty
● 3 composantes de rotation : Rx, Ry, Rz ● 1 composante de rotation : Rz
Degré de liaison :
Une liaison est la suppression d'un degré de liberté.
On appelle degré de liaison le nombre de degrés de liberté supprimés.
=3−∑ d
° °
=6−∑ d
° °
Dans l'espace : d liaison liberté Dans le plan : d liaison liberté

12. Définitions
Degré de liberté :
On appelle degré de liberté d'un solide II par rapport à un solide I de référence, le nombre
de composantes de déplacement indépendantes et non nulles.
Dans l'espace : Dans le plan :
● 3 composantes de translation : Tx, Ty, Tz ● 2 composantes de translation : Tx, Ty
● 3 composantes de rotation : Rx, Ry, Rz ● 1 composante de rotation : Rz
Degré de liaison :
Une liaison est la suppression d'un degré de liberté.
On appelle degré de liaison le nombre de degrés de liberté supprimés.
=3−∑ d
° °
=6−∑ d
° °
Dans l'espace : d liaison liberté Dans le plan : d liaison liberté
● Une force supprime une composante de translation
● Un moment supprime une composante de rotation

13. 1/4
Tableau de liaisons

14. 2/4
Tableau de liaisons

15. 3/4
Tableau de liaisons

16. 4/4
Tableau de liaisons

17. Liaisons dans le plan
Encastrement Articulation Appui simple Glissière
Schéma
Actions de
liaison
Inconnues de
calcul
Déplacements
relatifs

18. Liaisons dans le plan
Encastrement Articulation Appui simple Glissière
Schéma
Actions de
liaison
Inconnues de
calcul
Déplacements
relatifs

19. Liaisons dans le plan
Encastrement Articulation Appui simple Glissière
Schéma
Actions de
liaison
Inconnues de
calcul
Déplacements
relatifs

20. Liaisons dans le plan
Encastrement Articulation Appui simple Glissière
Schéma
Actions de
liaison
Inconnues de
calcul
Déplacements
relatifs

21. Liaisons dans le plan
Encastrement Articulation Appui simple Glissière
Schéma
Actions de
liaison
Inconnues de
calcul
Déplacements
relatifs

22. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Actions de
liaison
Inconnues de
calcul
Déplacements
relatifs

23. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx
Actions de
liaison
Fy
Mz
Inconnues de
calcul
Déplacements
relatifs

24. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx
Actions de
liaison
Fy
Mz
Inconnues de
calcul
Déplacements
relatifs

25. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx
Actions de
liaison
Fy
Mz
Inconnues de
calcul 3
Déplacements
relatifs

26. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx
Actions de
liaison
Fy
Mz
Inconnues de
calcul 3
Déplacements
relatifs
Aucun

27. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx
Actions de
liaison
Fy Fy
Mz
Inconnues de
calcul 3
Déplacements
relatifs
Aucun

28. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx
Actions de
liaison
Fy Fy
Mz
Inconnues de
calcul 3
Déplacements
relatifs
Aucun

29. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx
Actions de
liaison
Fy Fy
Mz
Inconnues de
calcul 3 2
Déplacements
relatifs
Aucun

30. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx
Actions de
liaison
Fy Fy
Mz
Inconnues de
calcul 3 2
Déplacements Rz
relatifs
Aucun

31. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx
Actions de
liaison
Fy Fy
Fy
Mz
Inconnues de
calcul 3 2
Déplacements Rz
relatifs
Aucun

32. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx
Actions de
liaison
Fy Fy
Fy
Mz
Inconnues de
calcul 3 2
Déplacements Rz
relatifs
Aucun

33. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx
Actions de
liaison
Fy Fy
Fy
Mz
Inconnues de
calcul 3 2 1
Déplacements Rz
relatifs
Aucun

34. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx
Actions de
liaison
Fy Fy
Fy
Mz
Inconnues de
calcul 3 2 1
Déplacements Tx
relatifs
Aucun Rz Rz

35. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx Fy
Actions de
liaison
Fy Fy
Fy Mz
Mz
Inconnues de
calcul 3 2 1
Déplacements Tx
relatifs
Aucun Rz Rz

36. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx Fy
Actions de
liaison
Fy Fy
Fy Mz
Mz
Inconnues de
calcul 3 2 1
Déplacements Tx
relatifs
Aucun Rz Rz

37. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx Fy
Actions de
liaison
Fy Fy
Fy Mz
Mz
Inconnues de
calcul 3 2 1 2
Déplacements Tx
relatifs
Aucun Rz Rz

38. y
Repère
Liaisons dans le plan de
référence x
Encastrement Articulation Appui simple Glissière
Schéma
Fx Fx Fy
Actions de
liaison
Fy Fy
Fy Mz
Mz
Inconnues de
calcul 3 2 1 2
Déplacements Tx
Aucun Rz Tx
relatifs Rz

39. Remarque 1

40. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.

41. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.

42. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.

43. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner

44. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner

45. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner

46. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ

47. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ
Nds déplaçables

48. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ
Nds déplaçables

49. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ
Nds déplaçables

50. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ ω
Nds déplaçables

51. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ ω
Nds déplaçables Nds fixes

52. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ ω
Nds déplaçables Nds fixes

53. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ ω
Nds déplaçables Nds fixes

54. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ ω ω
Nds déplaçables Nds fixes

55. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ ω ω
Nds déplaçables Nds fixes Nds fixes

56. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ ω ω
Nds déplaçables Nds fixes Nds fixes
Cette notion est fondamentale pour l'analyse du comportement des structures.

57. Remarque 1
Les déplacements (translation et rotation) cités précédemment sont des déplacements
relatifs entre les deux éléments assemblés.
Par contre, lors de la déformation de la structure, le centre de gravité de la liaison peut
légèrement se déplacer dans le plan de la structure par rapport au repère global lié à cette
structure.
Apparaît donc ici la notion de possibilité de déplacements des nœuds d'une structure.
D’où une première classification des structures :
● Structure à nœuds déplaçables : les nœuds peuvent tourner et translater
● Structure à nœuds fixes : les nœuds ne peuvent que tourner
ωδ ω ω
Nds déplaçables Nds fixes Nds fixes
Cette notion est fondamentale pour l'analyse du comportement des structures.
Elle a une influence sur les phénomènes d'instabilité des éléments, sur l'évolution, sur la
conception, sur le dimensionnement…
Exemple : détermination des longueurs de flambement des barres comprimées…

58. Remarque 2

59. Remarque 2
De la remarque précédente découle la notion d'encastrement parfait et d'encastrement
mutuel.

60. Remarque 2
De la remarque précédente découle la notion d'encastrement parfait et d'encastrement
mutuel.
Encastrement parfait : par exemple pied de poteau

61. Remarque 2
De la remarque précédente découle la notion d'encastrement parfait et d'encastrement
mutuel.
Encastrement parfait : par exemple pied de poteau

62. Remarque 2
De la remarque précédente découle la notion d'encastrement parfait et d'encastrement
mutuel.
Encastrement parfait : par exemple pied de poteau
Aucun déplacement relatif entre
les deux éléments, ni par rapport
au repère global.

63. Remarque 2
De la remarque précédente découle la notion d'encastrement parfait et d'encastrement
mutuel.
Encastrement parfait : par exemple pied de poteau
Aucun déplacement relatif entre
les deux éléments, ni par rapport
au repère global.
Encastrement relatif : par exemple jarret de portique

64. Remarque 2
De la remarque précédente découle la notion d'encastrement parfait et d'encastrement
mutuel.
Encastrement parfait : par exemple pied de poteau
Aucun déplacement relatif entre
les deux éléments, ni par rapport
au repère global.
Encastrement relatif : par exemple jarret de portique
A

65. Remarque 2
De la remarque précédente découle la notion d'encastrement parfait et d'encastrement
mutuel.
Encastrement parfait : par exemple pied de poteau
Aucun déplacement relatif entre
les deux éléments, ni par rapport
au repère global.
Encastrement relatif : par exemple jarret de portique
F A

66. Remarque 2
De la remarque précédente découle la notion d'encastrement parfait et d'encastrement
mutuel.
Encastrement parfait : par exemple pied de poteau
Aucun déplacement relatif entre
les deux éléments, ni par rapport
au repère global.
Encastrement relatif : par exemple jarret de portique
F A A
Déplacement des nœuds par
rapport au repère global.
Sous l'effet d'une force, le point A a subit une translation et une rotation.

67. Remarque 3

68. Remarque 3
Le règlement Eurocodes 3 introduit la notion d'assemblages semi-rigides.
Ces assemblages ont un comportement intermédiaire entre l'articulation parfaite et
l'encastrement.

69. Remarque 3
Le règlement Eurocodes 3 introduit la notion d'assemblages semi-rigides.
Ces assemblages ont un comportement intermédiaire entre l'articulation parfaite et
l'encastrement.
En effet, certains assemblages courants utilisés en charpente et autrefois considérés
comme des articulations, possèdent une certaine rigidité et peuvent de ce fait transmettre
un moment, et modifient donc la distribution des efforts dans les éléments de la structure.

70. Remarque 3
Le règlement Eurocodes 3 introduit la notion d'assemblages semi-rigides.
Ces assemblages ont un comportement intermédiaire entre l'articulation parfaite et
l'encastrement.
En effet, certains assemblages courants utilisés en charpente et autrefois considérés
comme des articulations, possèdent une certaine rigidité et peuvent de ce fait transmettre
un moment, et modifient donc la distribution des efforts dans les éléments de la structure.
Inversement, certains assemblages ne sont pas suffisamment rigides pour être
valablement considérés comme des encastrements.

71. Remarque 3
Le règlement Eurocodes 3 introduit la notion d'assemblages semi-rigides.
Ces assemblages ont un comportement intermédiaire entre l'articulation parfaite et
l'encastrement.
En effet, certains assemblages courants utilisés en charpente et autrefois considérés
comme des articulations, possèdent une certaine rigidité et peuvent de ce fait transmettre
un moment, et modifient donc la distribution des efforts dans les éléments de la structure.
Inversement, certains assemblages ne sont pas suffisamment rigides pour être
valablement considérés comme des encastrements.
Cette notion de comportement est caractérisée par le diagramme de comportement
moment / rotation.

72. Remarque 3
Le règlement Eurocodes 3 introduit la notion d'assemblages semi-rigides.
Ces assemblages ont un comportement intermédiaire entre l'articulation parfaite et
l'encastrement.
En effet, certains assemblages courants utilisés en charpente et autrefois considérés
comme des articulations, possèdent une certaine rigidité et peuvent de ce fait transmettre
un moment, et modifient donc la distribution des efforts dans les éléments de la structure.
Inversement, certains assemblages ne sont pas suffisamment rigides pour être
valablement considérés comme des encastrements.
Cette notion de comportement est caractérisée par le diagramme de comportement
moment / rotation.
L'encastrement parfait sans
aucune rotation n'existe pas.
Il existe toujours une
déformation dépendant de la
rigidité de l'assemblage.

73. Remarque 3
Le règlement Eurocodes 3 introduit la notion d'assemblages semi-rigides.
Ces assemblages ont un comportement intermédiaire entre l'articulation parfaite et
l'encastrement.
En effet, certains assemblages courants utilisés en charpente et autrefois considérés
comme des articulations, possèdent une certaine rigidité et peuvent de ce fait transmettre
un moment, et modifient donc la distribution des efforts dans les éléments de la structure.
Inversement, certains assemblages ne sont pas suffisamment rigides pour être
valablement considérés comme des encastrements.
Cette notion de comportement est caractérisée par le diagramme de comportement
moment / rotation.
L'encastrement parfait sans
aucune rotation n'existe pas.
Il existe toujours une
déformation dépendant de la
rigidité de l'assemblage.
L'articulation parfaite sans
aucune résistance n'existe pas.
Il existe toujours une résistance
dépendant de la rigidité de
l'assemblage.

74. The end !
E. Bugnet