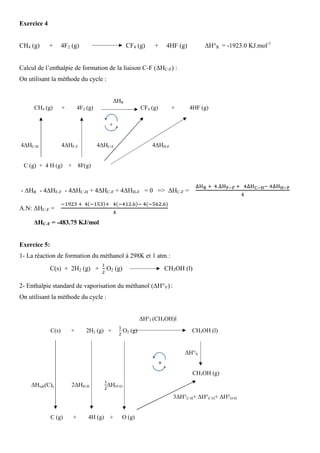
Le document présente des exercices de thermochimie, comprenant des calculs de constantes de gaz parfaits et d'enthalpies de réaction. Les méthodes de Hess et de la combinaison linéaire sont utilisées pour déterminer les enthalpies de diverses réactions, tout en abordant des sujets tels que la chaleur de vaporisation et les réactions de combustion. Enfin, des résultats spécifiques sont obtenus pour des substances telles que le méthanol et l'urée, avec des valeurs d'enthalpies de formation et des capacités calorifiques calculées.

1. La solution de la série d’exercices de thermochimie
Exercice 1
Calcul de la constante des gaz parfaits R en L.atm.mol-1
.K-1
, J. mol-1
.K-1
et Cal. mol-1
.K-1
sachant que n =
1 mole, V= 22.4 l, P= 1 atm, T= 0°C :
• R= ? atm.K-1
.mol-1
L’équation des gaz parfaits est donnée par : P.V = n.R.T
R=
୔.୚
୬.୘
A.N : R =
ଵ . ଶଶ.ସ
ଵ .ଶ଻ଷ
= 0.08205 atm.K-1
.mol-1
• R= ? J.K-1
.mol-1
Pour avoir R en joule il faut que V soit en m3
et P en Pa (Pascal)
R=
୔୚
୬୘
A.N : R =
ଵ଴ଵଷଶହ . ଶଶ.ସ . ଵ଴షయ
ଵ .ଶ଻ଷ
= 8.32 J.K-1
.mol-1
• R= ? Cal.K-1
.mol-1
1 Cal = 4.185 J R =
଼.ଷଶ
ସ.ଵ଼ହ
= 2 Cal.K-1
.mol-1
Exercice 2
La réaction de l’hydrolyse du saccharose :
saccharose + H2O (liq) glucose + fructose
Les enthalpies de formation des réactifs et produits ont été données dans le tableau.
On applique la loi de Hess pour calculer l’enthalpie de la réaction (∆H°R):
∆H°R =(∆H°f (g) +∆H°f (f) ) – (∆H°f (s) + ∆H°f (H2O)liq)
A.N : ∆H°R = (-1258 – 1268.8) – (-2236.9 – 285.8)
∆H°R = - 4.2 KJ
Exercice 3
Soit la réaction suivante à pression constante (1 atm) et à 298 K :
NH3 (g) +
ହ
ସ
O2 (g) NO (g) +
ଷ
ଶ
H2O (g) (1)
Réaction chimique réalisée sous pression constante : ∆H°R = QR
a- Calcul de ∆H°R par la méthode du cycle : Il est possible de construire un cycle de Hess mettant en
jeu la réaction (1) et les autres réactions données dans l’exercice :

2. ∆H°R
NH3 (g) +
ହ
ସ
O2 (g) NO (g) +
ଷ
ଶ
H2O (g)
-∆H°2 + -∆H°4 -
ଷ
ଶ
∆H°1
ଷ
ଶ
H2O (l)
ଷ
ଶ
∆H°3
ଵ
ଶ
N2 (g) +
ଷ
ଶ
H2 (g)+
ହ
ସ
O2 (g)
- ∆H°2 - ∆H°4 +
ଷ
ଶ
∆H°3 -
ଷ
ଶ
∆H°1 - ∆H°R = 0 => ∆H°R = - ∆H°2 - ∆H°4 +
ଷ
ଶ
∆H°3 -
ଷ
ଶ
∆H°1
A.N : ∆H°R = -54.1 KJ
b- ∆H°R par la méthode de la combinaison linéaire :
-∆H°2
NH3(g)
ଵ
ଶ
N2 (g) +
ଷ
ଶ
H2 (g)
+ -∆H°4
ଵ
ଶ
N2 (g) +
ଵ
ଶ
O2 (g) NO (g)
+ -
ଷ
ଶ
∆H°1
ଷ
ଶ
H2O (l)
ଷ
ଶ
H2O (g)
+
ଷ
ଶ
∆H°3
ଷ
ଶ
H2 (g) +
ଷ
ସ
O2 (g)
ଷ
ଶ
H2O (l)
= ∆H°R
NH3 (g) +
ହ
ସ
O2 (g) NO (g) +
ଷ
ଶ
H2O (g)
∆H°R = - ∆H°2 - ∆H°4 -
ଷ
ଶ
∆H°1 +
ଷ
ଶ
∆H°3
A.N: ∆H°R = -(-11) - (-21.6) -
ଷ
ଶ
(-10.5) +
ଷ
ଶ
(-68.3)
∆H°R = -54.1 KJ

3. Exercice 4
CH4 (g) + 4F2 (g) CF4 (g) + 4HF (g) ∆H°R = -1923.0 KJ.mol-1
Calcul de l’enthalpie de formation de la liaison C-F (∆HC-F) :
On utilisant la méthode du cycle :
∆HR
CH4 (g) + 4F2 (g) CF4 (g) + 4HF (g)
+
4∆HC-H 4∆HF-F 4∆HC-F 4∆HH-F
C (g) + 4 H (g) + 8F(g)
- ∆HR - 4∆HF-F - 4∆HC-H + 4∆HC-F + 4∆HH-F = 0 => ∆HC-F =
୼ୌ౎ ା ସ ୼ୌూషూ ା ସ୼ୌిషౄି ସ୼ୌౄషూ
ସ
A.N: ∆HC-F =
ିଵଽଶଷ ା ସሺିଵହଷሻା ସሺିସଵଶ.଺ሻି ସሺିହ଺ଶ.଺ሻ
ସ
∆HC-F = -483.75 KJ/mol
Exercice 5:
1- La réaction de formation du méthanol à 298K et 1 atm :
C(s) + 2H2 (g) +
ଵ
ଶ
O2 (g) CH3OH (l)
2- Enthalpie standard de vaporisation du méthanol (∆H°V) :
On utilisant la méthode du cycle :
∆H°f (CH3OH)l
C(s) + 2H2 (g) +
ଵ
ଶ
O2 (g) CH3OH (l)
∆H°V
+
CH3OH (g)
∆Hsub(C)s 2∆HH-H
ଵ
ଶ
∆HO=O
3∆H°C-H+ ∆H°C-O+ ∆H°O-H
C (g) + 4H (g) + O (g)
E
E

4. - ∆H°f (CH3OH)l +∆Hsub(C)s + 2∆HH-H +
ଵ
ଶ
∆HO=O + 3∆H°C-H + ∆H°C-O + ∆H°O-H - ∆H°V= 0
∆H°V = - ∆H°f (CH3OH)l + ∆Hsub(C)s + 2∆HH-H +
ଵ
ଶ
∆HO=O + 3∆H°C-H + ∆H°C-O + ∆H°O-H
A.N: ∆H°V = -(-239) + 718 +2(-436) +
ଵ
ଶ
(-498) + 3(-414) + (-456)
∆H°V (CH3OH)l = 29 KJ.mol-1
3- La chaleur de la réaction de formation du méthanol à volume constant Qv ( T = 298K , P = 1 atm)
∆H = ∆U + ∆nRT
À volume constant: ∆U = Qv
Qv = ∆H –∆n.R.T avec ∆n = -2.5 (la différence des coefficients stœchiométriques des gaz)
A.N : Qv = -239 – (-2,5 x 8.32 x10-3
x 298)
Qv = -232,8 KJ
4- La capacité calorifique (Cp) de CH3OH (l) :
• Tout d’abord on va calculer ∆Cp de la réaction de formation de CH3OH (l) :
Par application de la loi de Kirchhoff :
∆H2 = ∆H1 + ∆Cp.∆T avec ∆H1 à T1 et ∆H2 à T2
∆Cp =
∆ୌమି∆ୌభ
∆୘
A.N : ∆Cp =
ିଶଷ଼ିሺିଶଷଽሻ
ଷଶ଼ିଶଽ଼
∆Cp = 0.033 KJ.mol-1
.K-1
• On peut maintenant calculer (Cp) de CH3OH (l) par application de la loi de Hess :
∆Cp
C(s) + 2H2 (g) +
ଵ
ଶ
O2 (g) CH3OH (l)
∆Cp = Cp (CH3OH)l - (Cp (C)s + 2Cp(H2)g +
ଵ
ଶ
Cp (O2)g) =˃
Cp (CH3OH)l = ∆Cp + Cp (C)s + 2Cp (H2)g +
ଵ
ଶ
Cp (O2)g
A.N: Cp (CH3OH)l = 0.033 x 10-3
+ 8.56 + 2(20.59) +
ଵ
ଶ
(20.93)
Cp (CH3OH)l = 93.535 J/K.mol

5. Exercice 6
1- La réaction de combustion de l’éthanol liquide à 298 K:
CH3 - C - H (l) +
ହ
ସ
O2(g) 2CO2 (g) + 2H2O (l) ∆H°c = -1165 KJ
O
2- Calcul de ∆H°f (CH3CHO)g et ∆H°f (CH2 CH2)g
O
Par application de la loi de Hess :
∆H°c (CH3CHO)l = 2∆H°f (CO2)g + 2∆H°f (H2O)l - ∆H°f (CH3CHO)l =˃
∆H°f (CH3CHO)l = 2∆H°f (CO2)g + 2∆H°f (H2O)l - ∆H°c (CH3CHO)l
A.N: ∆H°f (CH3CHO)l = 2 (-393 +(-285.5)) + 1165
∆H°f (CH3CHO)l = -192 KJ.mol-1
∆H°V (CH3CHO)l = ∆H°f (CH3CHO)l - ∆H°f (CH3CHO)g =˃
∆H°f (CH3CHO)g = ∆H°f (CH3CHO)l - ∆H°V (CH3CHO)l
A.N: ∆H°f (CH3CHO)g = 30.4 – 192
∆H°f (CH3CHO)g = -161.6 KJ.mol-1
∆H°V ( CH2 CH2 )l = ∆H°f ( CH2 CH2)l - ∆H°f (CH2 CH2)g
O O O
∆H°f (CH2 CH2)g = ∆H°V ( CH2 CH2 )l + ∆H°f (CH2 CH2)l
O O O
A.N: ∆H°f (CH2 CH2)g = 28.5 – 94
O
∆H°f (CH2 CH2)g = -65.5 KJ.mol-1
O
1
3- CH2 CH2 (g) CH3 - C - H (g)
O 2 O
∆S°R = S°f (CH3 - C – H) g - S°f (CH2 CH2 )g
O O
A.N: ∆S°R = -108.3 – (-130.8) = 22.5 J/K
∆S°R = 22.5 J.K-1
∆H°R = ∆H°f (CH3 - C – H) g - ∆H°f (CH2 CH2 )g
O O

6. A.N: ∆H°R = -161.6 – (-65.5) = -96.1 KJ
∆H°R = -96.1 KJ
∆G°R = ∆H°R - T∆S°R
A.N: ∆G°R = -96.1 – 198(22.5 x 10-3
) = -102.805 KJ
∆G°R = -102.805 KJ
Conclusion:
∆G°R ˂ 0 alors la réaction est spontanée dans le sens 1
Exercice 7
La réaction de combustion de l’urée solide à 298 K
NH2
O=C (s) +
ଷ
ଶ
O2 (g) CO2 (g) + N2 (g) + 2H2O (l)
NH2
1- Calcul de ∆H°f CO(NH2)2 (s) :
La réaction de combustion de C(s)
C(s) + O2 CO2(g) alors ∆H°c (C)s = ∆H°f (CO2)g = 395 KJ.mol-1
La reaction de combustion de H2 (g):
H2(g) +
ଵ
ଶ
O2 H2O (l) alors ∆H°c (H2)g= ∆H°f (H2O)l = 286 KJ.mol-1
Par application de la loi de Hess sur la réaction de combustion de l’urée solide:
∆H°c (CO(NH2)2 (s)) = ∆H°f (CO2)g + 2∆H°f (H2O)l - ∆H°f (CO(NH2)2 (s))
∆H°f (CO(NH2)2 (s)) = ∆H°f (CO2)g + 2∆H°f (H2O)l - ∆H°c (CO(NH2)2 (s))
A.N: ∆H°f (CO(NH2)2 (s)) = (395)+2(-286) +636
∆H°f (CO(NH2)2 (s)) = -333 KJ.mol-1
2- Calcul de S°f (CO(NH2)2 (s)) sachant que ∆G°c (CO(NH2)2 (s)) = -677 KJ
∆G°c = ∆H°c - T∆S°c ∆S°c =
୼ୌ° ౙି ୼ୋ° ౙ
୘
A.N: ∆S°c =
ି଺ଷସିሺି଺଻଻ሻ
ଶଽ଼
= 0.14429 KJ = 144.29 J

7. ∆S°c = ( S°f (CO2) + S°f (N2) + 2S°f (H2O)l) - (S°f (CO(NH2)2 (s)) +
ଷ
ଶ
S°f (O2)g)
S°f (CO(NH2)2 (s)) = S°f (CO2) + S°f (N2) + 2S°f (H2O)l -
ଷ
ଶ
S°f (O2)g - ∆S°c
A.N: S°f (CO(NH2)2 (s)) = 213 + 191 + 2(70) -
ଷ
ଶ
(205) – 144.29
S°f (CO(NH2)2 (s)) = 92.21 J.K-1
.mol-1
3- Calcul de ∆H° sub (CO(NH2)2 (s)):
Par application de la méthode du cycle:
∆H° f CO(NH2)2 (s)
C(s) +
ଵ
ଶ
O2 (g) + N2(g) + 2H2(g) CO(NH2)2 (s)
∆H°sub
ଵ
ଶ
∆H°(O2) ∆H°(N2) 2∆H° (H2) + ∆H° sub
∆H°CO+2 ∆H°CN+4 ∆H°NH
C(g) + O(g) + 2N(g) + 4H(g) CO(NH2)2 (g)
∆H° f CO(NH2)2 (s) + ∆H° sub CO(NH2)2 (s) - (∆H°CO+2 ∆H°CN+4 ∆H°NH) - ∆H°sub +
ଵ
ଶ
∆H°(O2) + ∆H°(N2)
+ 2∆H° (H2) = 0
∆H° sub CO(NH2)2 (s) = -∆H° f CO(NH2)2 (s) + ∆H°CO + 2 ∆H°CN+4 ∆H°NH + ∆H°sub -
ଵ
ଶ
∆H°(O2) -
∆H°(N2) - 2∆H° (H2)
A.N: ∆H° sub CO(NH2)2 (s) = -(-333) – 744 + 2(-304) + 4(-391) + 718 -
ଵ
ଶ
(-497) –(-946) -2(-435)
∆H° sub CO(NH2)2 (s) = 199.5 KJ.mol-1
4- Calcul de ∆H° f CO(NH2)2 (g) :
∆H° sub CO(NH2)2 (s)
CO(NH2)2 (s) CO(NH2)2 (g)
∆H° sub CO(NH2)2 (s) = ∆H° f CO(NH2)2 (g) - ∆H° f CO(NH2)2 (s)
∆H° f CO(NH2)2 (g) = ∆H° f CO(NH2)2 (s) + ∆H° sub CO(NH2)2 (s)
A.N: ∆H° f CO(NH2)2 (g) = -333 +199.5
∆H° f CO(NH2)2 (g) = -133.5 KJ.mol-1