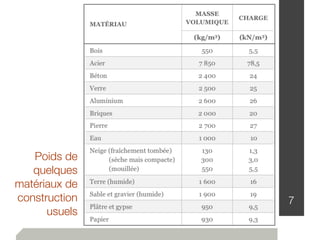
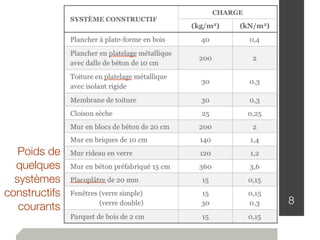
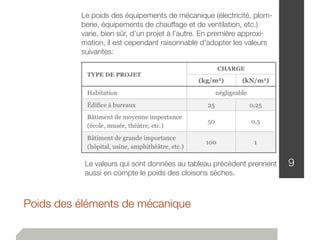
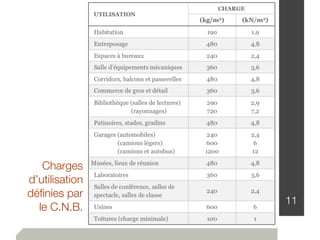
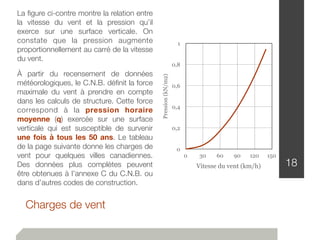
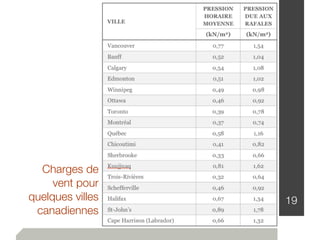
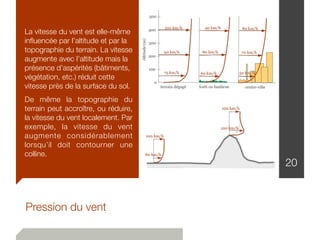
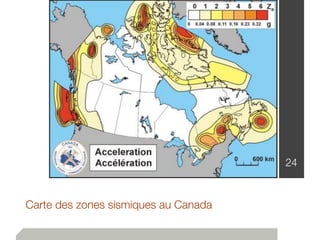
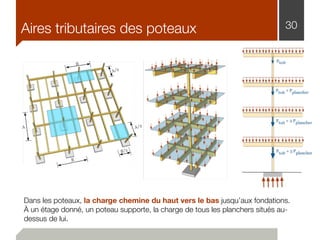
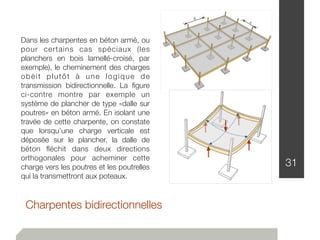
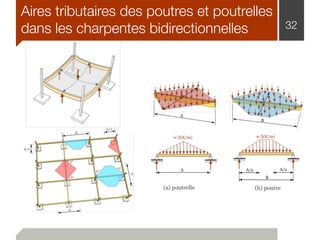
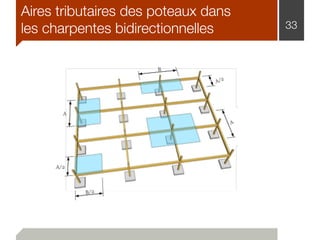
Le document traite de l'estimation des charges dans la conception des structures, en distinguant les charges mortes et vives, ainsi que les charges environnementales comme celles dues à la neige, au vent et aux séismes. Des détails sur les unités de mesure, les méthodes de calcul et les facteurs de sécurité sont également fournis, permettant ainsi aux ingénieurs de construire des bâtiments sûrs et conformes au code national du bâtiment canadien. Les charges sont classées en fonction de leur nature, de leur durée et de leur répartition pour évaluer les impacts sur la structure.

1. Estimation
des charges
ARC-2007
Conception de structures
R. Pleau
École d’architecture, Université Laval

2. 2Classification des charges
Chaque structure est sollicitée par un ensemble de forces que l’on appelle
des charges. La plupart sont des charges de gravité (le poids propre d’un
bâtiment, de son mobilier et de ses occupants, par exemple). D’autres
charges sont liées à l’environnement (la charge de neige, la charge de vent
et la charge sismique notamment).
Par commodité on distingue deux types de charge selon leur durée.
Les charges mortes (aussi appelées charges permanentes) sollicitent la
structure en permanence et sont généralement assez faciles à évaluer.
Les charges vives (aussi appelées surcharges) sont au contraire variables
en intensité et en durée de sorte qu’il est beaucoup plus difficile de les
évaluer avec exactitude.

3. 3Classification des charges
On distingue également les charges concentrées, qui s’appliquent sur un
point précis de la structure et s’expriment en kN, des charges réparties
qui s’appliquent sur une plus grande surface et sont exprimées en kN/m2.
Charge concentrée
Charge répartie

4. 4Unités de mesure
Dans le système impérial, les forces sont exprimées en livres (lbs). Dans le
système international (S.I.) la masse est exprimée en kilogrammes (kg),
l’accélération est exprimée en mètres par secondes au carré (m/s2) et les
forces sont exprimées en Newton (N). Conformément à la deuxième loi de
Newton, la force (F) est le produit de la masse (m) par l’accélération (a) selon
l’expression F = m a. Par définition on a que :
1 N = 1 kg m/s2
Les forces de gravité sont obtenues en multipliant la masse par l’accélération
gravitationnelle (9.81 m/s2). Pour une masse de 1 kg on obtient donc:
Force = 1 kg x 9.81 m/s2 = 9,81 N
Si on arrondi l’accélération gravitationnelle à 10 m/s2 cela signifie qu’une force
de 1 N correspond à une masse d’environ 100 g ce qui est très faible.

5. 5Unités de mesure
Pour plus de commodité, les ingénieurs en
structures préfèrent exprimer les forces en
kiloNewton (1 kN = 1000 N). Une force de 1 kN
correspond approximativement au poids
d’une masse de 100 kg (1 kN = 100 kg x 9.81
m/s2 = 981 N ≈ 1000 N) ce qui est à peu près
égal au poids d’un joueur de football.
Environ 1 tonne (10 kN)
Les poids sont parfois exprimés en
tonnes (1 tonne = 1000 kg =10 kN) ce qui
correspond approximativement au poids
d’une petite voiture compacte.
Environ 1 kN

6. Charges mortes 6
À partir des plans de construction, il est relativement facile de calculer le
poids propre des diverses composantes d’un bâtiment moyennant
quelques approximations. Le poids des équipements mécaniques
(électricité, plomberie, chauffage, ventilation, etc.) fait aussi parti de la
charge morte. Cette charge varie d’un bâtiment à l’autre mais, en première
approximation, le tableau qui est donné à la page 10 fournit des ordres de
grandeur raisonnables.
Le poids de quelques matériaux de construction d’usage courant ainsi
que celui de quelques systèmes constructifs sont donnés aux tableaux
des pages suivantes. Des données plus complètes peuvent être
facilement obtenues dans diverses publications comme, par exemple, le
Handbook of Steel Construction publié par l’Institut canadien de la
construction en acier.
Note importante : Pour les charpentes en acier et en bois, on peut négliger le poids
de la charpente (i.e. l’ensemble des poutrelles, poutres et poteaux)
lors du dimensionnement préliminaire puisque ce poids représente
rarement plus de 5% de la charge totale.

7. 7
Poids de
quelques
matériaux de
construction
usuels

8. 8
Poids de
quelques
systèmes
constructifs
courants

9. Le poids des équipements de mécanique (électricité, plom-
berie, équipements de chauffage et de ventilation, etc.)
varie, bien sûr, d’un projet à l’autre. En première approxi-
mation, il est cependant raisonnable d’adopter les valeurs
suivantes:
9
Poids des éléments de mécanique
Le valeurs qui sont données au tableau précédent prennent
aussi en compte le poids des cloisons sèches.

10. Charges d’utilisation 10
Le Code National du Bâtiment Canada (C.N.B.) impose aux architectes et
ingénieurs de prendre en compte des charges d’utilisation dans la
conception des bâtiments. Le tableau de la page suivante donne quelques
charges d’utilisation courantes. Ces valeurs incluent le poids de occupants
du bâtiment ainsi que celui du mobilier mobile. Des valeurs plus complètes
peuvent être obtenues directement à partir du C.N.B. ou des codes de
construction étrangers.
On notera que ces valeurs sont très conservatrices
et tentent d’évaluer la charge maximale qui pourrait
solliciter une partie du bâtiment durant sa durée de
vie utile. La charge réelle que le bâtiment devra
supporter est habituellement bien inférieure à celle
qui est définie par le C.N.B. En effet, des études
statistiques ont démontré que la charge réelle
d’utilisation excède rarement 40% de la charge
prévue au Code.
Par exemple, la charge d’utilisation dans une salle de classe est égale à 240
kg/m2 ce qui correspond à plus de 3 personnes par m2 sur toute la surface
du plancher.

11. 11
Charges
d’utilisation
définies par
le C.N.B.

12. Charges de neige 12
Le C.N.B. a recensé des données météorologiques pour l’ensemble du
territoire canadien et défini la charge de neige à prendre en compte dans le
calcul des structures.
Cette charge correspond au poids maximal de neige qui est susceptible de
survenir en moyenne une fois à tous les 50 ans.
Le tableau de la page
suivante donne, à titre
d’exemple, la charge de
neige pour quelques villes
canadiennes. Des données
plus complètes peuvent être
obtenues à l’annexe C du
C.N.B. ou dans d’autres
codes de construction.

13. 13
Charges de
neige au sol
pour
quelques
villes
canadiennes

14. Charge de neige
sur une toiture
14
Les images ci-dessus montrent que l’accumulation
de neige sur les toitures peut être considérable et
représenter une charge importante.

15. Accumulations de neige
15
toit supérieur
toit inférieur
direction du vent
La neige transportée par le vent
obéit aux lois de l’aérodynami-
que: elle se dépose peu aux
endroits où l’air est accéléré mais
forme des accumulations
importantes où le vent perd de la
vitesse.
Par exemple, un dénivellé de la
toiture peut entraîner une
accumulation de neige
importante (jusqu’à plus de trois
fois l’épaisseur moyenne de
neige) si la toiture inférieure est
abritée du vent.

16. Accumulations de neige
L’orientation et l’intensité du
vent, la géométrie de
bâtiment et la pente de la
toiture influencent le profil
d’accumulation.
Le C.N.B. prévoit des
dispositions pour tenir
compte de ces facteurs.
16
Influence du vent
Influence de la géométrie du bâtiment
Influence de la pente de la toiture

17. Charges de vent
Les bâtiments constituent des
obstacles qui s’opposent au libre
écoulement du vent. En
contournant les bâtiments, l’air
subit des accélérations et des
décélérations et forme des
tourbillons qui imposent des
charges complexes sur les
bâtiments.
En venant buter sur une surface,
le vent y exerce une pression qui
est proportionnelle à sa vitesse.
À l’inverse l’accélération de l’air
crée un effet de succion au-
dessus de toit ainsi sur les murs
qui sont situés sur la face abritée
du bâtiment. 17

18. Charges de vent
18
La figure ci-contre montre la relation entre
la vitesse du vent et la pression qu’il
exerce sur une surface verticale. On
constate que la pression augmente
proportionnellement au carré de la vitesse
du vent.
À partir du recensement de données
météorologiques, le C.N.B. définit la force
maximale du vent à prendre en compte
dans les calculs de structure. Cette force
correspond à la pression horaire
moyenne (q) exercée sur une surface
verticale qui est susceptible de survenir
une fois à tous les 50 ans. Le tableau
de la page suivante donne les charges de
vent pour quelques villes canadiennes.
Des données plus complètes peuvent
être obtenues à l’annexe C du C.N.B. ou
dans d’autres codes de construction.
0
0,2
0,4
0,6
0,8
1
0 30 60 90 120 150
Pression(kN/m2) Vitesse du vent (km/h)

19. 19
Charges de
vent pour
quelques villes
canadiennes

20. Pression du vent
La vitesse du vent est elle-même
influencée par l’altitude et par la
topographie du terrain. La vitesse
augmente avec l’altitude mais la
présence d’aspérités (bâtiments,
végétation, etc.) réduit cette
vitesse près de la surface du sol.
De même la topographie du
terrain peut accroître, ou réduire,
la vitesse du vent localement. Par
exemple, la vitesse du vent
augmente considérablement
lorsqu’il doit contourner une
colline.
20

21. Calcul des charges de vent 21
La pression due au vent (p) peut être
évaluée à l’aide de la relation suivante:
p = q Ce Cp Cg
où q représente la pression dynamique de
référence, Ce le coefficient d’exposition lié
au profil de vitesse, Cp le coefficient de
pression lié à la façon dont le vent
contourne l’obstacle et Cg un coefficient
prenant en compte l’effet de rafale. En
première approximation on peut prendre
Ce = 1,0 (terrain dégagé) et Cg = 2. La
figure ci-dessous donne la valeur usuelle
de Cp pour deux configurations courantes:
une toiture plate et une toiture à deux
plans inclinés à 45°.

22. Charges horizontales dues au vent 22
Pour chacune des surfaces exposées au
vent, la force exercée par le vent (F) est
donc obtenue en multipliant la pression (p)
par la surface (A)
F = p A
La force horizontale totale qui sera
transmise aux fondations via le système de
contreventement du bâtiment est obtenue
en additionnant les forces de pression (sur
la face du bâtiment exposée au vent) aux
forces de succion (sur sa face abritée).
Pour un bâtiment rectangulaire avec une
toiture plate, la charge horizontale totale
qui s’exerce sur ce bâtiment est égale à:
F = 1,3 q A
direction du vent
vue en élévation d’un bâtiment
0,55 q0,75 q

23. Charges sismiques 23
Les charges sismiques résultent de l’accélération horizontale du sol lors d’un
tremblement de terre. Cette accélération induit des efforts internes importants
dans les charpentes de bâtiment.
Les charges sismiques dépendent de plusieurs facteurs comme le poids du
bâtiment, la nature du sol et la capacité de la charpente à dissiper de l’énergie.
Au Canada, les charges sismiques constituent une préoccupation importante
et font l’objet de nombreuses exigences dans les codes de calcul nationaux.
Le calcul parasismique est un science complexe que nous n’aborderons pas
dans ce cours d’introduction à la conception de structures.

24. Carte des zones sismiques au Canada
24

25. Carte mondiale des zones sismiques
25

26. Wf = 1,25 WD + 1,5 WL
Où: Wf = charge totale
WD = charge morte
WL = charge vive
26Pondération des charges
Par souci de sécurité, et afin de prévoir l’imprévisible (surcharges plus fortes que
prévues, erreurs de calcul, malfaçons et vices de construction, défaillance des
matériaux, cas de charge imprévus, etc.), les charges sont majorées par un
facteur de sécurité.
Les charges mortes sont ainsi majorées de 25% alors que les charges vives sont
majorées de 50% (le facteur de majoration est plus élevée pour les charges vives
car elles sont plus difficiles à évaluer que les charges mortes).

27. Cheminement des charges verticales
dans une charpente unidirectionnelle 27

28. Notion d’aire tributaire 28
Une structure est constituée de plusieurs éléments (pontage, poutrelles,
poutres, poteaux, murs, etc.) assemblés les uns aux autres.
L’aire tributaire est définie comme la surface de plancher (pour les
charges verticales) ou de murs (pour les charges horizontales) qui est
supportée par un élément structural donné.
Pour évaluer la charge maximale qui sollicite un élément structural on
utilisera la notion d’aire tributaire.
L’aire tributaire est relativement facile à évaluer si on comprend bien le
cheminement des charges dans la structure.
Les pages suivantes donnent quelques exemples d’aire tributaire pour des
charpentes unidirectionnelles et bidirectionnelles.

29. Aires tributaires des poutres et poutrelles
dans les charpentes unidirectionnelles 29

30. 30Aires tributaires des poteaux
Dans les poteaux, la charge chemine du haut vers le bas jusqu’aux fondations.
À un étage donné, un poteau supporte, la charge de tous les planchers situés au-
dessus de lui.

31. Charpentes bidirectionnelles
31
Dans les charpentes en béton armé, ou
pour certains cas spéciaux (les
planchers en bois lamellé-croisé, par
exemple), le cheminement des charges
obéit plutôt à une logique de
transmission bidirectionnelle. La figure
ci-contre montre par exemple un
système de plancher de type «dalle sur
poutres» en béton armé. En isolant une
travée de cette charpente, on constate
que lorsqu’une charge verticale est
déposée sur le plancher, la dalle de
béton fléchit dans deux directions
orthogonales pour acheminer cette
charge vers les poutres et les poutrelles
qui la transmettront aux poteaux.

32. Aires tributaires des poutres et poutrelles
dans les charpentes bidirectionnelles 32

33. Aires tributaires des poteaux dans
les charpentes bidirectionnelles 33

34. Facteur de réduction de la
charge d’utilisation 34
Dans les bâtiments multi-étagés il est fréquent qu’un poteau supporte de
grandes surfaces de plancher. Il devient alors peu probable que la charge
maximale d’utilisation prévue par le C.N.B. s’applique sur toute la surface.
Pour éviter de surdimensionner inutilement les poteaux, le C.N.B. permet de
réduire l’aire tributaire associée aux charges d’utilisation en la multipliant par
un facteur de réduction.
Pour les planchers supportant des aires de réunion ou d’entreposage sur une
surface totale (A) de plus de 80 m2, le facteur de réduction est le suivant:
Pour les planchers de plus de 20 m2 supportant des espaces à bureaux, des
salles de classe ou de laboratoires, le facteur de réduction est égal à:
où A représente la surface totale des planchers.

35. Cheminement des
charges horizontales 35
Lorsqu’un bâtiment est exposé au vent, celui-ci
exerce une pression sur les murs de la face exposée
au vent ainsi qu’une succion sur les murs de la face
abritée du vent.
Un diaphragme est un élément structural plat (comme
un plancher, une plaque ou une coque) qui est
considéré comme étant infiniment rigide et
indéformable dans son plan.
Les murs transmettent la force horizontale du vent
aux planchers qui agissent eux-mêmes comme
des diaphragmes pour transmettre la résultante
des forces horizontales aux éléments de
contreventement verticaux qui les acheminent
jusqu’aux fondations.
aire tributaire de mur
associée à un plancher
action diaphragme
des planchers

36. Cheminement des
charges horizontales 36
Le mécanisme d’acheminement des
charges horizontales s’exerce du
haut vers le bas. À partir du toit,
chaque plancher transmet une
charge horizontale au système de
contreventement qui l’achemine à
l’étage inférieur. Ce transfert se
répète d’étage en étage jusqu’à ce
que la résultante des charges
horizontales soit transmise au sol via
les fondations. Chacun des éléments
de contreventement agit alors
comme une poutre verticale en
porte-à-faux sollicité en flexion.
orientation du vent

37. Aire tributaire d’une poutrelle 37

38. Aire tributaire d’une poutre 38

39. Aire tributaire d’une poteau 39