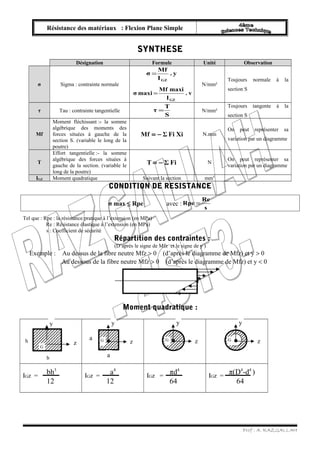
Synthes eflexion 4t
- 1. Résistance des matériaux : Flexion Plane Simple SYNTHESE Désignation Formule Unité Observation σ Sigma : contrainte normale . y σ Mf I GZ = . v σ maxi Mf maxi I GZ = N/mm² Toujours normale à la section S τ Tau : contrainte tangentielle τ = T N/mm² S Toujours tangente à la section S Mf Moment fléchissant :- la somme algébrique des moments des forces situées à gauche de la section S. (variable le long de la poutre) Mf = - Σ Fi Xi N.mm On peut représenter sa variation par un diagramme T Effort tangentielle :- la somme algébrique des forces situées à gauche de la section. (variable le long de la poutre) T = - Σ Fi N On peut représenter sa variation par un diagramme IGZ Moment quadratique Suivant la section mm4 CONDITION DE RESISTANCE Rpe = Re σ max ≤ Rpe avec : s Tel que : Rpe : la résistance pratique à l’extension (en MPa) Re : Résistance élastique à l’extension (en MPa) s : Coefficient de sécurité Répartition des contraintes : (D’après le signe de Mfz et le signe de y ) Exemple : Au dessus de la fibre neutre Mfz > 0 (d’après le diagramme de Mfz) et y > 0 Au dessous de la fibre neutre Mfz > 0 (d’après le diagramme de Mfz) et y < 0 Moment quadratique : bh3 a4 πd4 IGz = IGz = IGz = IGz = π(D4-d4 ) Prof : A. RAZGALLAH y G z y G z y G z a a z y G h b 12 12 64 64
- 2. Résistance des matériaux : Flexion Plane Simple Activité Un arbre de boite à vitesse est assimilé à une poutre cylindrique de diamètre d mini =16mm. Les actions sur les roues dentées engendrent une flexion supposée simple sur cet arbre. Le problème est représenté par le schéma ci- dessous. 1°) Vérifier par calcul que les modules de RA et RD sont convenables pour que la poutre soit en équilibre. On donne RA = 800N et RD = 700N . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . On donne F1 =500N, F2 =1000N A B C D 2°) Ecrire les équations et donner les valeurs des efforts tranchants et des moments fléchissants sur le tableau Zones Expressions Valeurs aux limites de zones [AB[ Ty = . . . . . . . . . . . . . . . . . . . . . . . Mf = . . . . . . . . . . . . . . . . . . . . . . . En A , X= . . . En B , X= . . . Ty = . . . . . . . . . . . . . . . . . . . . Mf = . . . . . . . . . . . . . . . . . . . . Mf = . . . . . . . . . . . . . . . . . . . . ……… . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . En … , X= . . . En … , X= . . . Ty = . . . . . . . . . . . . . . . . . . . . Mf = . . . . . . . . . . . . . . . . . . . . Mf = . . . . . . . . . . . . . . . . . . . . ……… . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . En … , X= . . . En … , X= . . . Ty = . . . . . . . . . . . . . . . . . . . . Mf = . . . . . . . . . . . . . . . . . . . . Mf = . . . . . . . . . . . . . . . . . . . . 3°) Tracer les diagrammes des efforts tranchants et des moments fléchissant. A B D x Echelle : 1mm 50N Prof : A. RAZGALLAH x Y RD RA F1 F2 + 25 29 41 F2 C RD RA F1 Y + X T(N) MF(Nm) X Echelle : 1mm 1mN
- 3. Résistance des matériaux : Flexion Plane Simple 4°) Calculer : a) La contrainte normale smaxi : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . b) La contrainte tangentielle t max : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5°) Représenter la répartition de la contrainte normale dans la section la plus sollicitée de la poutre. Echelle : 1mm 10N/mm2 6°) En utilisant le tableau ci-dessous encercler les matériaux qui vérifier la condition de résistance de la poutre. Sachant que le coefficient de sécurité adopté est s = 5 …………………………………………………………………………………………………………………… …………………………………………………………………………………………………………………… …………………………………………………………………………………………………………………… ………………………… N U A N C E D E M A T É R I A U S 185 E 335 C 22 C 25 Re [MPa] 185 335 255 285 Rp ……. … ….. ……… Prof : A. RAZGALLAH y x