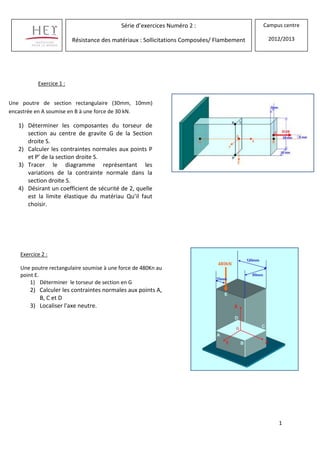
1. 1
Exercice 1 :
Exercice 2 :
Exercice 3 :
Série d’exercices Numéro 2 :
Résistance des matériaux : Sollicitations Composées/ Flambement
Campus centre
2012/2013
Une poutre de section rectangulaire (30mm, 10mm)
encastrée en A soumise en B à une force de 30 kN.
1) Déterminer les composantes du torseur de
section au centre de gravite G de la Section
droite S.
2) Calculer les contraintes normales aux points P
et P’ de la section droite S.
3) Tracer le diagramme représentant les
variations de la contrainte normale dans la
section droite S.
4) Désirant un coefficient de sécurité de 2, quelle
est la limite élastique du matériau Qu’il faut
choisir.
Exercice 2 :
Une poutre rectangulaire soumise à une force de 480Kn au
point E.
1) Déterminer le torseur de section en G
2) Calculer les contraintes normales aux points A,
B, C et D
3) Localiser l'axe neutre.

2. 2
Exercice 3 :
Calculer la charge critique, le rayon de giration et l’élancement d’une section carrée.
Calculer la charge critique, le rayon de giration et l’élancement d’une section circulaire.
Qui résiste mieux au flambement ?
Exercice 4 :
Déterminer la charge et la contrainte critique d’un tube en acier
(E = 200 GPa, Re=240 MPa, L=3 m) supposé articulé à ses deux extrémités.
R= 40 mm
R= 35 mm
F
-F
a
d