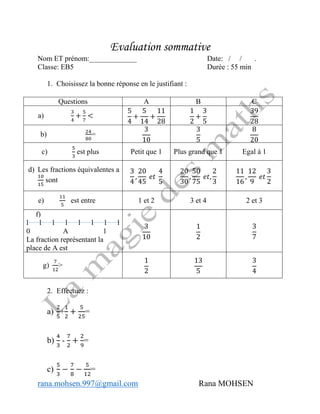
Ce document présente une leçon de mathématiques destinée aux élèves de la classe EB5 sur les fractions, abordant des concepts comme les fractions supérieures à l'unité, la comparaison, l'addition et la soustraction. Il décrit plusieurs activités ayant des durées et des objectifs spécifiques, telles que la représentation des fractions sur une droite numérique et l'identification des fractions équivalentes. Les élèves sont encouragés à travailler en individuel et en groupe pour explorer les notions mathématiques et appliquer des règles générales.