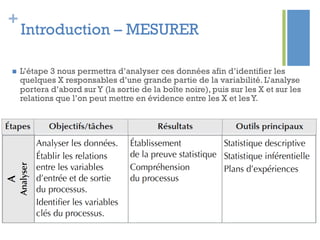
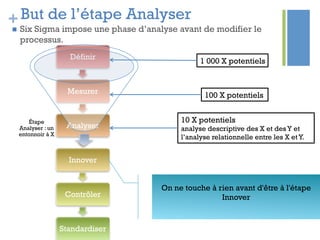
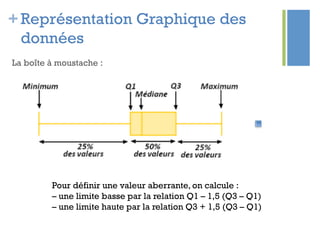
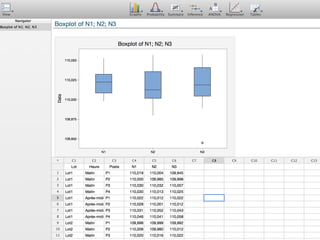
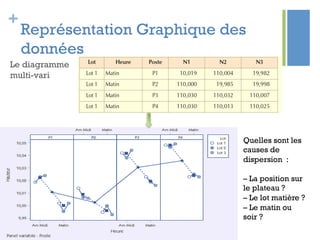
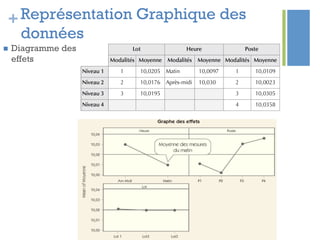
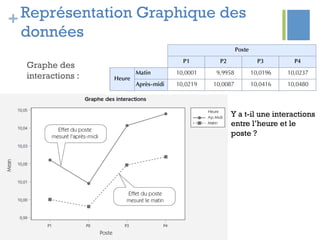
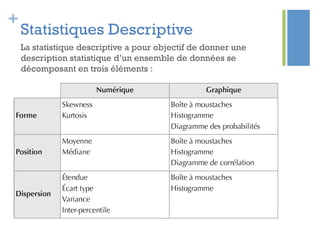
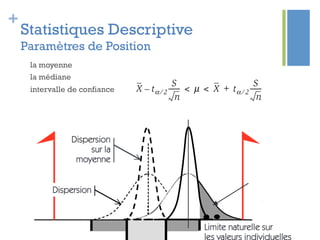
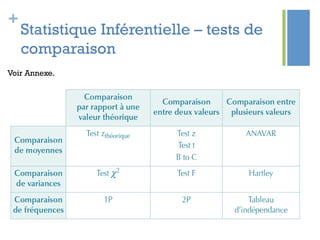
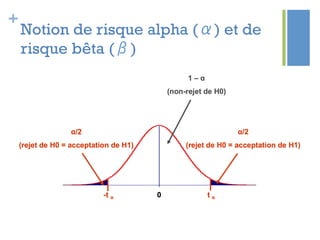
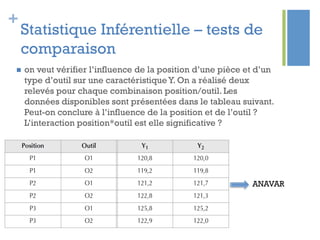
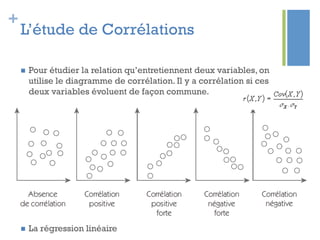
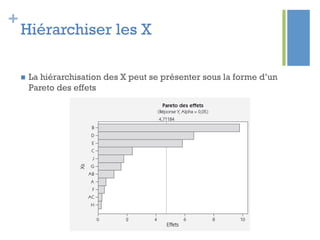
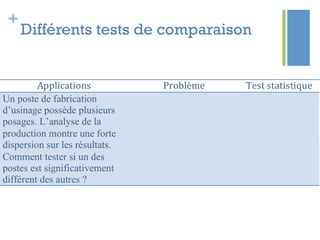
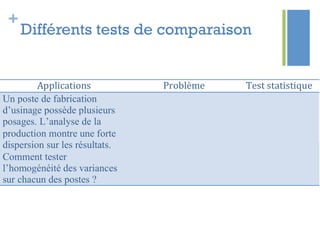
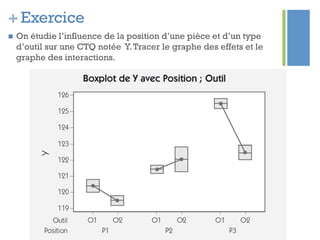
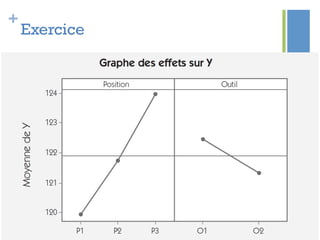
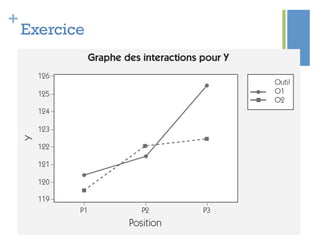
Ce document traite de l'étape d'analyse dans le processus Six Sigma, où l'on examine les variables (x) et les résultats (y) pour identifier les causes de variabilité. Il inclut des méthodes d'analyse descriptive et relationnelle, ainsi que des tests statistiques pour évaluer les interactions et les influences. L'objectif est de prioriser les variables pertinentes afin d'améliorer le processus en question.

1. +

2. +
Introduction – MESURER
n L’étape 3 nous permettra d’analyser ces données afin d’identifier les
quelques X responsables d’une grande partie de la variabilité. L’analyse
portera d’abord surY (la sortie de la boîte noire), puis sur les X et sur les
relations que l’on peut mettre en évidence entre les X et lesY.

3. +But de l’étape Analyser
n Six Sigma impose une phase d’analyse avant de modifier le
processus.
Définir
Mesurer
Analyser
Innover
Contrôler
Standardiser
Étape
Analyser : un
entonnoir à X
1 000 X potentiels
100 X potentiels
10 X potentiels
analyse descriptive des X et desY et
l’analyse relationnelle entre les X etY.
On ne touche à rien avant d'être à l'étape
Innover

4. +
La conduite de l’étape Analyser
== > Comprendre les règles qui régissent le fonctionnement
du processus.
1 • une analyse descriptive : afin de détecter d’éventuelles
anomalies telles que la présence de valeurs aberrantes,
une non-normalité, qui sont sources d’informations;
2 • une analyse relationnelle : afin de comprendre en quoi
les X ont une influence sur la caractéristique Y que l’on
cherche à améliorer.

5. + Analyse du comportement desY et
des X
u une étude du comportement par rapport aux spécifications existantes;
u une analyse statistique : moyenne, écart type, présence de valeurs
aberrantes… ;
u une analyse de normalité et l’analyse des causes en cas de non normalité ;
u une analyse des variations dans le temps des caractéristiques afin de
vérifier si la caractéristique est sous contrôle (utilisation des cartes de
contrôle) ;
u une analyse des chutes de capabilité.
Etape Mesurer
Collecte des
données
tableaux
d’observation
Analyser ces
données :

6. +Analyser les relations entre les X et
lesY
n Quels sont les X qui expliquent la variabilité desY ?
On dissocie en général trois types dans l’origine des variations :
Variations de position
– Position sur une
machine multi-
posages.
– Chip particulier
dans un wafer.
– Empreinte dans un
moule sur une presse
à injecter.
– Variation entre 2
machines, 2
opérateurs, 2
ateliers.
– ...
•Variations cycliques
– Variation d’un lot à
un autre.
– Variation d’une
coulée à une autre.
– Variation parmi un
groupe d’unités
(usure d’outils).
– ...
Variations
temporelles
– Variation d’une
équipe à l’autre,
matin et soir, jours de
la
semaine...

7. +
Représentation Graphique des
données
Diagramme des effets et
diagramme des interactionsBoxplot Le Diagramme multi-vari

8. +Représentation Graphique des
données
La boîte à moustache :
Pour définir une valeur aberrante, on calcule :
– une limite basse par la relation Q1 – 1,5 (Q3 – Q1)
– une limite haute par la relation Q3 + 1,5 (Q3 – Q1)

9. +
n

10. +
Représentation Graphique des
données
Le diagramme
multi-vari
Quelles sont les
causes de
dispersion :
– La position sur
le plateau ?
– Le lot matière ?
– Le matin ou
soir ?

11. +Représentation Graphique des
données
n Diagramme des
effets

12. +Représentation Graphique des
données
Graphe des
interactions :
Y a t-il une interactions
entre l’heure et le
poste ?

13. +
Statistiques Descriptive
La statistique descriptive a pour objectif de donner une
description statistique d’un ensemble de données se
décomposant en trois éléments :

14. +
Statistiques Descriptive
Paramètres de Position
la moyenne
la médiane
intervalle de confiance

15. +
Exemple
Exemple :
n calculer l’intervalle dans lequel on a 95 % de chances
de trouver μ ?
n Moy =7,7037
n S = 0,0077
n n = 50 soit 49 ddl
n tα/2 = 2,0096

16. + Solution

17. +
Statistiques Descriptive
Paramètres d’échelle
n l’étendue ;
n l’écart type ;
n la variance ;
n la position des quartiles.

18. +
Statistiques Descriptive
Paramètres d’échelle
n Il est important lorsque l’on observe une répartition de
savoir si elle suit une répartition normale ou non.
n À cette fin, on peut mettre en oeuvre différents tests, tels
que :
n • test du χ2 ;
n • test d’ANDERSON-DARLING ;
n • test de SHAPIRO-WILK ;
n • test de KOLMORONOV-SMIRNOV…

19. +
Statistique Inférentielle – tests de
comparaison
n Problème de type 1 – Comparaison à une valeur théorique
Mon produit possède actuellement une caractéristique que je
souhaite améliorer. Je fais un essai et les résultats semblent
indiquer une amélioration. Puis-je réellement conclure à une
amélioration ou est-ce simplement dû à l’effet de la
dispersion ?

20. +
Statistique Inférentielle – tests de
comparaison
n Problème de type 2 – Comparaison de deux (ou plusieurs)
Valeurs J’hésite entre le choix de deux types de colle, la colle
numéro 2 testée sur 2 prototypes semble donner de meilleurs
résultats que la colle 1 testée sur 5 prototypes ; la différence
que présentent ces produits est elle suffisante pour conclure ?

21. +
Statistique Inférentielle – tests de
comparaison
Voir Annexe.

22. +
Notion de risque alpha (α) et de
risque bêta (β)
n Risque alpha (α) = c’est le risque de conclure qu’il y a une
différence significative (H1) alors que cela n’est pas vrai.
n Risque bêta (β) = c’est le risque de conclure qu’il n’y a pas de
différence significative (H0) alors que cette différence existe bien.

23. +
Notion de risque alpha (α) et de
risque bêta (β)
n

24. +
Statistique Inférentielle – tests de
comparaison
n on veut vérifier l’influence de la position d’une pièce et d’un
type d’outil sur une caractéristique Y. On a réalisé deux
relevés pour chaque combinaison position/outil. Les
données disponibles sont présentées dans le tableau suivant.
Peut-on conclure à l’influence de la position et de l’outil ?
L’interaction position*outil est elle significative ?
ANAVAR

25. +
L’étude de Corrélations
n Pour étudier la relation qu’entretiennent deux variables, on
utilise le diagramme de corrélation. Il y a corrélation si ces
deux variables évoluent de façon commune.
n La régression linéaire

26. +
Hiérarchiser les X
n Tout ce que nous avons vu comme outils statistiques peuvent
être utilisés pour analyser les relations entre les X et lesY.
n Résultats : mettre en évidence les principales causes de
variation par les analyses statistiques que l’on a réalisées sur
les données récoltées.
n Etape suivante : hiérarchiser les causes afin de connaître
quels sont les X sur lesquels les efforts les plus importants
devront être apportés lors de l’étape Innover/Améliorer
Exemple : Supposons qu’une CTQY dépend de deux variables X1 et
X2 :Y = X1 + X2 ,σX1 = 5 et σX2 = 1.
Qu’apporterait surY une amélioration qui consisterait à diminuer de 1
l’écart type sur un X ?

27. +
Hiérarchiser les X
n La hiérarchisation des X peut se présenter sous la forme d’un
Pareto des effets

28. +
Différents tests de comparaison

29. +
Différents tests de comparaison

30. +
Différents tests de comparaison

31. +
Différents tests de comparaison

32. +
Différents tests de comparaison

33. +
Différents tests de comparaison

34. +
Différents tests de comparaison

35. +
Différents tests de comparaison

36. +Exercice
n On étudie l’influence de la position d’une pièce et d’un type
d’outil sur une CTQ notée Y.Tracer le graphe des effets et le
graphe des interactions.

37. +
Exercice
n

38. +
Exercice
n

39. +
Étape 3 – ANALYSER Résumé
Durant cette étape, on analyse lesY (sorties du processus), les X (variables du processus)
et les relations entre les X et lesY afin d’identifier les quelques X responsables en grande
partie de la variabilité surY.
1. Analyse deY
• Étude de la normalité.
• Étude des variations temporelles.
• Étude de la chute des capabilités.
2. Analyse des X
• Rédiger le diagramme d’Ishikawa afin de déterminer les facteurs X qui peuvent influer
sur les résultats précédents (variation de positions, cycliques, temporelles).
• Faire une observation sur la normalité, les variations temporelles et la chute des
capabilités sur les X.

40. +
Étape 3 – ANALYSER Résumé
3. Analyse des symptômes
• Faire une liste des symptômes (d’après un jugement technique et l’expérience du
groupe).
• Faire des hypothèses sur les causes des variations observées.
4. Analyser les relations entre lesY et les X
• Mettre en évidence graphiquement les relations entre Y et les X (boîte à moustache,
multi-vari, graphe des effets…).
• Réaliser les tests statistiques permettant d’apporter la preuve statistique attendue.
• Donner une explication rationnelle pour les effets observés.

41. +
Étape 3 – ANALYSER Résumé
5. Hiérarchiser les X
• Mettre en évidence le poids des X pertinents avec Anova ou Regression.
• Focalisation sur les X les plus pertinents.
• Prévoir un éventuel plan d’expériences pour formaliser la relation.
6. Gains mesurables et gains non mesurables (réactualisation)
• À nouveau, une analyse des gains et des coûts doit être faite afin
d’évaluer si le gain recherché peut être obtenu.