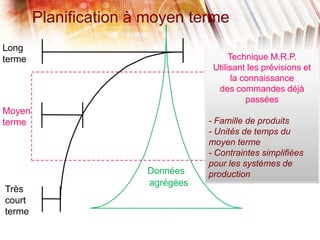
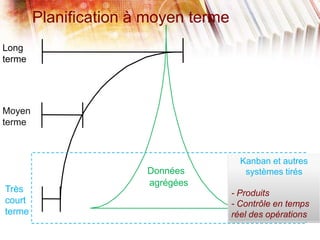
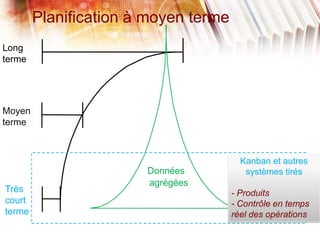
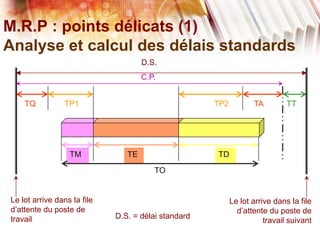
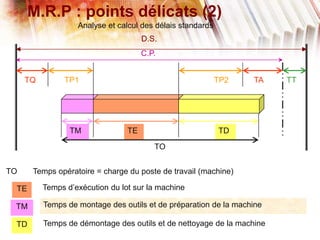
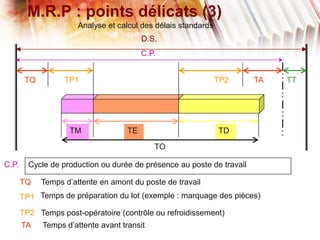
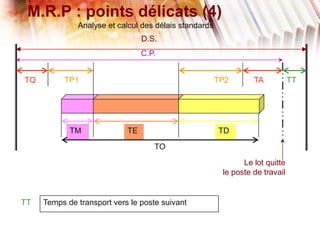
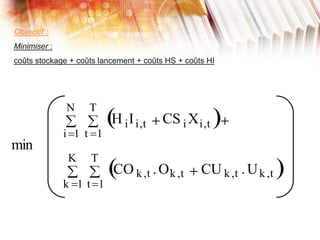Le document traite de la planification de la production MRP II, en abordant la gestion des données agrégées, les délais standards et les difficultés liées à l'optimisation des processus. Il présente également la programmation linéaire comme méthode pour minimiser les coûts et respecter les contraintes relatives aux capacités de production et aux délais. Enfin, des définitions des paramètres, des contraintes et une étude de cas illustrent l'application de ces concepts dans un modèle MRP.

1. III. La planification de la
production MRP2

2. Données
agrégées
Technique M.R.P.
Utilisant les prévisions et
la connaissance
des commandes déjà
passées
- Famille de produits
- Unités de temps du
moyen terme
- Contraintes simplifiées
pour les systèmes de
production
Planification à moyen terme
Long
terme
Très
court
terme
Moyen
terme

3. Données
agrégées
Planification à moyen terme
Long
terme
Très
court
terme
Moyen
terme
Kanban et autres
systèmes tirés
- Produits
- Contrôle en temps
réel des opérations

4. Long
terme
Très
court
terme
Données
agrégées
Moyen
terme
Kanban et autres
systèmes tirés
- Produits
- Contrôle en temps
réel des opérations
Planification à moyen terme

5. M.R.P : points délicats (1)
Analyse et calcul des délais standards
C.P.
TQ TA TTTP1 TP2
TM TE TD
TO
D.S.
D.S. = délai standard
Le lot arrive dans la file
d’attente du poste de
travail
Le lot arrive dans la file
d’attente du poste de
travail suivant

6. M.R.P : points délicats (2)
Analyse et calcul des délais standards
D.S.
C.P.
TQ TA TTTP1 TP2
TM TE TD
TO
TE
TM
TD
TO
Temps d’exécution du lot sur la machine
Temps de montage des outils et de préparation de la machine
Temps de démontage des outils et de nettoyage de la machine
Temps opératoire = charge du poste de travail (machine)

7. M.R.P : points délicats (3)
Analyse et calcul des délais standards
D.S.
C.P.
TQ TA TTTP1 TP2
TM TE TD
TO
Temps de préparation du lot (exemple : marquage des pièces)
Temps post-opératoire (contrôle ou refroidissement)
Temps d’attente en amont du poste de travail
Temps d’attente avant transit
TP1
TP2
TQ
TA
Cycle de production ou durée de présence au poste de travailC.P.

8. M.R.P : points délicats (4)
Analyse et calcul des délais standards
D.S.
C.P.
TQ TA TTTP1 TP2
TM TE TD
TO
Temps de transport vers le poste suivantTT
Le lot quitte
le poste de travail

9. (Rappel) : Qu’est-ce qu’un programme
linéaire ?
• Un programme linéaire (PL) est un problème d’optimisation consistant
à maximiser (ou minimiser) une fonction objectif z linéaire de n
variables de décision xi soumises à un ensemble de contraintes
exprimées sous forme d’´equations ou d’inéquations linéaires.

10. Rappel : formulation mathématique

12. Objectif :
Minimiser : coûts stockage + coûts lancement + coûts HS + coûts HI
Programmation linéaire en variables mixtes
pour tenir compte simultanément
dans un modèle de type MRP
de tailles des lots, de délais et de capacités
Définitions des paramètres
Produits, Stocks , Machines, Coûts, ….
Contraintes
Capacités, nomenclatures, délais, cohérence

13. Programmation linéaire en variables mixtes
pour tenir compte simultanément
dans un modèle de type MRP
de tailles des lots, de délais et de capacités
Définitions des paramètres connus et des inconnues (éventuellement
redondantes) :
N = nombre de types de produits
K = nombre de machines
T = nombre de périodes
Pi,t = quantité du produit i produite
pendant la période t = taille de la série
Yi = rendement de fabrication du produit i
(il peut exister rebuts et déchets)

14. Li = délai minimum imposé de disponibilité
de fabrication en nombre d'unités de temps
du moyen terme ; lié au procédé de fabrication
et non pas aux capacités ou à la charge
(Yi . Pi,t deviennent disponible à t + Li)
Ii,t = niveau de stock du produit i,
en fin de période t
1 si du produit de type i est fabriqué
Xi,t = pendant la période t
0 sinon (pas de lancement)

15. Ok,t = heures supplémentaires sur la machine k
à la période t
Uk,t = heures inemployées sur la machine k
à la période t
Hi = coût unitaire de stockage du produit i sur une période
CSi = coût d'initialisation d'une série de produits i
= coût de lancement
COk,t = coût d'une heure supplémentaire
sur la machine k pendant la période t
CUk,t = coût d'une heure inemployée
sur la machine k pendant la période t

16. ai,j = nombre de produits i nécessaire
pour obtenir une unité de produits j
(facteur de répétition des nomenclatures)
di,t = demande externe du produit i à la période t
Ri,t = besoin brut total du produit i à la période t

17. Si,k = temps nécessaire au réglage de la machine k
pour le produit i
bi,k = temps unitaire de production du produit i sur la machine k
CAPk,t = capacité normale de production, en heures,
de la machine k durant la période t
q = un nombre très grand

18. Hypothèse importante :
Une série de produits i lancée à la période t sur la machine k est entièrement
exécutée par k pendant la période t :
Li ne contient que des temps post-opératoires et/ou des temps de transport.

19. Objectif :
Minimiser :
coûts stockage + coûts lancement + coûts HS + coûts HI
min
i 1
N
t 1
T
H iIi,t CS i Xi,t
k 1
K
t 1
T
CO k,t .Ok,t CU k,t .Uk,t

20. Contraintes :
Respecter les capacités.
Respecter les nomenclatures.

i 1
N
( bi,k .Pi,t
durées
opératoires
 
Si,k .Xi,t
montage /
démontage
 
) Uk,t
HI

Ok,t
HS

CAPk,t k , t

Ri,t
besoin
total de
i à t

di,t
demande
externe

a i,jPj,t
j
demande int erne due aux
produits qui utilisent i
 
i, t

21. Contraintes (suite) :
Respecter les délais dans les mouvements du stock.

Ii,t 1
stock
en t 1

Yi .Pi,t Li
produits
ter min és en t
  
Ri,t
besoin
total en t

Ii,t
stock
en t

i, t
Ii,t 1 Yi .Pi,t Li
Ii,t a i, jPj,t
j
di,t i , t

22. Contraintes (suite) :
Cohérence entre lancement et quantité lancée.
Nature des inconnues
Réels ou entiers
Entiers bivalents
Pi,t qX i,t 0 i, t
Ii,t ,Pi,t ,U k,t ,Ok,t 0
Xi,t 0 ou 1

23. Etude de cas MRP2