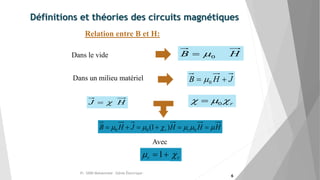
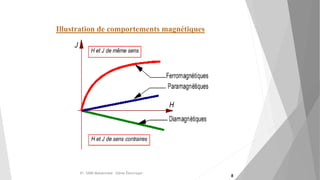
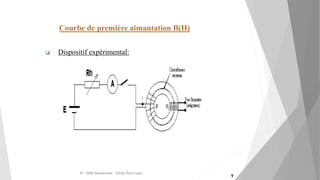
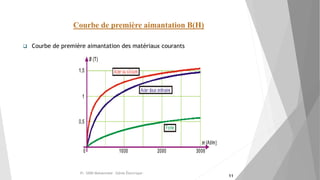
Le document explore les circuits magnétiques et leurs analogies avec les circuits électriques, en présentant des définitions, théories et applications pratiques, comme l'effet des matériaux magnétiques. Il détaille également des concepts clés tels que le théorème d'Ampère, la loi de Faraday, l'hystérésis et la classification des matériaux ferromagnétiques. Les conclusions soulignent que les problèmes de circuits magnétiques peuvent être analysés à l'aide de modèles électriques correspondants.