Le livre de Maurice Pillet, 'Six Sigma : Comment l'appliquer', propose une méthode systématique pour améliorer la performance des processus grâce à l'approche Six Sigma. Il couvre des concepts clés, notamment la réduction de la variabilité et l'intégration dans des systèmes de gestion de la qualité et de management lean. L'ouvrage fournit également des étapes pratiques pour mener des projets Six Sigma, avec des outils et techniques pour assurer la satisfaction des clients.



































































![Les concepts de Six Sigma
Après avoir déterminé la cible, on doit valider les limites de spécifica-tions.
Sur le graphique suivant (figure 2.19), on donne un exemple du
travail que devra réaliser le Black Belt dans cette phase. La tolérance
souhaitée sur Y est l’intervalle [3.5 – 4.1] et on a montré une corréla-tion
entre les X et Y. Graphiquement (mais on apprendra également à
le faire par calcul), on peut facilement déterminer les limites sur X qui
permettent de « garantir » le respect des spécifications sur Y.
Le cas présenté est relativement simple, une seule caractéristique est
corrélée avec Y. Cette phase devra prendre en compte les cas plus com-plexes
où Y dépend de plusieurs caractéristiques X.
Figure 2.19 – Tolérance sur X versus tolérance sur Y
22
4,2
4,1
4,0
3,9
3,8
3,7
3,6
3,5
3,4
3,3
3,2
Y
22,5 23 23,5 24 24,5 25 25,5 26 26,5 27 27,5 28
X
Cette phase a aussi une autre fonction qui est d’assurer la robustesse
des spécifications par rapport aux bruits. Rappelons qu’on appelle
bruit toutes les caractéristiques qui varient indépendamment de la
volonté de l’entreprise. Il peut y avoir des bruits sur le processus de
production (vibrations, variation de température…) ou sur le produit
(conditions d’utilisation, température…).
Pour valider la robustesse, on étudiera à partir des données récoltées
dans les étapes précédentes l’influence des X sur la dispersion de Y
afin de choisir la configuration qui minimise cette dispersion.
© Éditions d’Organisation 53](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-68-320.jpg)


![Six Sigma
Ex
Dans cet exemple, on a calculé les limites naturelles du proces-sus
en se basant sur la moyenne historique [24,64 – 25,86]. Tant
que la moyenne des échantillons prélevés reste dans ces limites,
on ne peut pas conclure à un décentrage, aucune intervention
n’est utile. Lorsqu’un point sort des limites (comme c’est le cas
pour le 25e échantillon), il y a une forte probabilité que le proces-sus
soit décentré et qu’il requière une intervention.
Toutes les caractéristiques critiques susceptibles de dériver en
position ou en dispersion devront faire l’objet d’un tel suivi.
Éliminer les causes d’erreur
Mise en place de Poka Yoke
La meilleure façon de garantir que le processus reste sous contrôle
consiste à introduire des points « zéro défaut » garantissant la qualité
des produits. Plutôt que de chercher à éliminer le défaut par un con-trôle,
il faut rechercher un dispositif qui évite de produire le défaut.
C’est le rôle assigné aux points « zéro défaut », appelés également Poka
Yoke. Il existe plusieurs types de points « zéro défaut » que l’on peut
classer en quatre grandes catégories (figure 2.22).
Figure 2.22 – Les Poka Yoke
Type Fonction Exemples
Par contact Détecter les défauts de
formes et de dimensions
en utilisant le contact
entre les éléments.
Présence d’un détrompeur qui garantit
que l’on a posé la bonne pièce dans
la bonne position.
Forme de la prise de connexion
d’une souris d’ordinateur.
Valeur
constante
Compter ou détecter une
valeur préalablement fixée.
Détection automatique du niveau
de remplissage d’une cartouche
d’encre, redondant avec une pompe
doseuse.
00253
56 © Éditions d’Organisation](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-71-320.jpg)





























































































![Six Sigma
Prise en compte du décentrage Cpm
Figure 4.36 – Indice Cpm
Cible
LSI LSS – μ LSS
3σ
Dispersion = 6σ
L = K(Y – Cible)2
L = K[σ2 + (μ – Cible)2]
C pm = LSS – LSI
6 σ2 + (μ – Cible)2
Une autre façon de tenir compte du décentrage consiste à considérer la
perte financière qui en découle. Taguchi a démontré que cette perte
financière est à proportion de l’écart entre la valeur et la cible élevée
au carré :
L = K(Y – Cible)2
La valeur K est une constante. La perte moyenne pour une production
de moyenne μ et d’écart type σ se calcule par la relation :
L = K[σ2+(μ – Cible)2]
L’indice Cpm est calculé de façon à être proportionnel à cette perte. Il
est défini par la relation :
Cpm LSS – LSI
= --------------------------------------------------
6 σ2 + (μ – Cible )2
Le Cpm est un indicateur qui se dégrade à proportion du coût de non-qualité.
Relations entre Cp, Cpk, Cpm et z
Compte tenu des relations que nous venons de définir, nous avons :
Cp ≥ Cpk ; les deux indicateurs sont égaux lorsque le procédé est
centré.
150 © Éditions d’Organisation](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-165-320.jpg)

























![Six Sigma
La figure suivante (figure 5.13) donne un exemple de résumé graphi-que
de statistique descriptive, fourni par Minitab®. L’estimation des
paramètres d’échelle et de position est donnée par une estimation et
par un intervalle de confiance. Dans ce cas, l’estimation de la moyenne
est de 7,7037, et l’intervalle de confiance ayant 95 % de chance
d’inclure μ est de [7,7015 – 7,7059].
Figure 5.13 – Statistiques descriptives avec Minitab
Statistiques descriptives du Diam 7,7
7,68 7,69 7,70 7,71 7,72
7,69 7,70 7,71 7,72 7,73
95 % Confidence intervals
7,68
*
7,701
7,702 7,703 7,704 7,705 7,706
Mean
Median
3.1 Paramètres de position
Anderson-Darling Normality Test
A-Squared 0,24
P-Value 0,316
Mean 7,7037
St Dev 0,0077
Variance 0,0001
Skew ness –0,117743
Kurtosis 0,823668
N 50
Minimum 7,6820
1st Quartile 7,6990
Median 7,7030
3rd Quartile 7,7093
Maximum 7,7240
95 % Confidence Interval for Mean
7,7015 7,7059
95 % Confidence Interval for Median
7,7020 7,7060
95 % Confidence Interval for St Dev
0,0064 0,0096
Comme son nom l’indique, un paramètre de position donne une indi-cation
sur la position de la distribution par rapport à la grandeur mesu-rée.
Voici les principaux indicateurs :
• la moyenne
X
Xi
nΣ
i = 1
= -----------------------
n
176 © Éditions d’Organisation](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-191-320.jpg)




![Étape 3 – Analyser
Si on pose comme notation :
• Si : σn-1 de l’échantillon i (estimation de l’écart type σ calculé sur
n valeurs)
• σ : écart type de la population totale
2
-σ---2- = ×
R (n – 1)
Si
on peut montrer que le rapport : est distribué selon
une loi du χ2.
Les valeurs de χ2 pour une probabilité p donnée se trouvent en fonc-tion
du nombre de degrés de liberté ν = (n–1) dans la table de χ2.
χ(α ⁄ 2)
2 (n – 1 )
Si
2
× ----- χ(σ2 1 – α ⁄ 2)
2
On peut écrire : qui permet de donner
l’intervalle de confiance sur l’écart type :
Ex
Exemple
S
χ(α ⁄ 2)
2
(---n-----–----1-----) σ S
χ(2
1 – α ⁄ 2)
---(--n-----–-----1---)---
Dans le cas de la figure 5.13, on avait :
S = 0,0077
χ0,025
2 χ0,975
2
n = 50 soit = 31,55 et = 70,22 pour 49 degrés de
liberté
ce qui permet de calculer l’intervalle :
soit [0,0062 – 0,0092]
0,0077
31,55
49
-------------
------------- σ 0,077
70,22
49
© Éditions d’Organisation 181](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-196-320.jpg)





















































![Étape 3 – Analyser
Il s’agit de trouver les coefficients α0 et α1 qui minimisent les écarts
ei2 entre la droite et les points. Lorsque ces écarts sont minimaux, on
obtient la droite qui passe « au mieux » des points. On appelle cette
méthode la minimisation des moindres carrés de Gauss.
Solution
La somme des écarts ei
Minimiser e.te consiste à trouver les valeurs de α0 et α1 qui
anulent la dérivée de e.te par rapport à a
e.te = [Y – Xa]t[Y – Xa] = YtY – 2atXtY + atXtXa
∂et ⋅ e
∂a --------------
Pour annuler cette dérivée, on a alors : â = (XtX)-1.XtY
Application
2 s’écrit e.te avec te matrice transposée de e.
= –2XtY + 2XtXa
Tous les logiciels statistiques calculent facilement les coefficients α0 et
α1 ; il est possible également d’utiliser un tableur pour retrouver ces
valeurs. Appliquons la relation â = (XtX)-1.XtY sur les données de
l’exemple à partir d’un tableur Excel.
1 108
… …
1 117
Matrices et
X
= Y
=
9 1002
1002 111974
XtX = ; (XtX)-1 =
174
…
204
29,76 –0,266
–0,266 0,0024
31,719
1,3947
â = (XtX)-1.XtY = qui détermine les coefficients de la droite
de régression.
© Éditions d’Organisation 235](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-250-320.jpg)

![Étape 3 – Analyser
Démonstration
â = (XtX)-1.XtY donc V(â) = V[(XtX)-1.XtY]
X est la matrice des essais, c’est une constante on peut donc
écrire :
V(â) = (XtX)-1.Xt.V(Y).X(XtX)-1
Dans l’hypothèse nulle, V(Y) = V(ei) est la variance des résultats
des essais, que l’on suppose homogène dans tout le domaine
d’étude.
On peut écrire V(Y) = σr
2I
2 Variance résiduelle)
(I matrice identité et σr
2(XtX)-1XtIX(XtX)-1 = σr
V(â) = σr
Application sur notre exemple
2(XtX)-1
Figure 5.59 – Calcul des ei
X 108 102 112 118 118 119 100 108 117
Y 174 173 185 197 191 197 174 188 204
α0 + α1X 182,4 174,0 187,9 196,3 196,3 197,7 171,2 182,4 194,9
ei = Y – (α0 + α1X) –8,4 –1,0 –2,9 0,7 –5,3 –0,7 2,8 5,6 9,1
On calcule V(ei) =
σr
2
ei
Σ 2
ddl
= ------------ = 32,98
avec ici le nombre de degrés de liberté = 9 (données) – 2 (coefficients)
= 7 soit σr = 5,74
Connaissant σr on détermine facilement V(â) = σr
2(XtX)-1
29,76 –0,266
–0,266 0,0024
2(XtX)-1 = 32,98 =
σr
981,66 –8,78
–8,78 0,079
© Éditions d’Organisation 237](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-252-320.jpg)








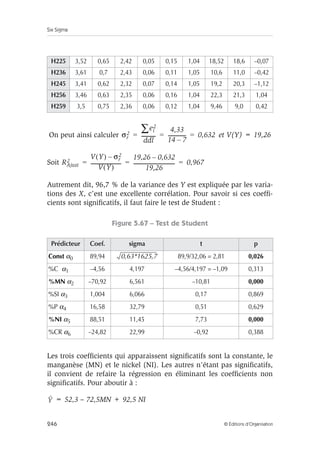




















![Étape 4 – Innover/améliorer
Définition d’une interaction
Il y a interaction lorsque l’effet d’un facteur dépend de l’état d’un autre
facteur.
Sur le schéma de la figure 6.4, on va voir que, lorsque la pression
passe de 500 à 300, la réponse Y monte légèrement. Mais en fait,
comme il y a une interaction, lorsque la température est à 60, la pres-sion
n’a pas d’effet, alors que lorsque la température est à 40 le pas-sage
d’une pression de 500 à 300 modifie de façon importante la
réponse.
Avec les quatre essais que propose la solution traditionnelle, il n’est
pas possible de voir cette interaction, alors qu’elle apparaît de façon
claire avec les quatre essais de la solution « plans d’expériences ».
Précision sur les résultats
Si l’on veut calculer l’effet de la température dans le cas de la stratégie
traditionnelle, il suffit de comparer le résultat de l’essai 2 au résultat de
l’essai 1.
On calcule ET = Y2 – Y1
Dans la stratégie plans d’expériences, on doit faire la moyenne des
deux écarts constatés entre Y5 /Y6 et Y7 /Y8
On calcule
ET
1
2
= --[(Y6 – Y5) + (Y8 – Y7)]
Comme il y a de la dispersion sur Y lorsque l’on fait des essais, cette
dispersion se retrouvera forcément dans la précision de calcul des
effets des facteurs. Si on suppose que la dispersion est uniforme dans
le domaine d’étude, on a alors
Variance(Y1) = […] = Variance(Y8) = Variance(Y).
Calculons la variance sur l’effet de la température dans les deux situa-tions
(rappelons que la variance a la propriété d’additivité – voir
chapitre 5).
Situation traditionnelle
V(ER) = V(Y2 – Y1) = V(Y2) + V(Y1) = 2V(Y)
© Éditions d’Organisation 267](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-282-320.jpg)
![Six Sigma
Situation « plan d’expériences »
ET V 1
--[(Y6 – Y5) + (Y8 – Y7)]
2
=
= 1
--[V(Y6) + V(Y5) + V(Y8) + V(Y7)] = V(Y)
4
On le constate, la variance sur l’effet (et donc la précision de la modé-lisation)
sera deux fois plus faible dans la situation « plans d’expérien-ces
» que dans la situation traditionnelle.
Ces deux avantages en matière d’étude des interactions et de précision
des résultats font qu’on privilégie toujours la démarche « plans d’expé-riences
» par rapport à la démarche « un facteur à la fois » lorsqu’une
expérimentation concerne plusieurs facteurs.
4. Les plans d’expériences à 2 niveaux
Les plans d’expériences à 2 niveaux sont sans aucun doute les plans le
plus utilisés compte tenu de leur pertinence en termes de résultats au
vu du nombre d’essais réalisés.
4.1 Deux facteurs à 2 niveaux – plan complet
Considérons le problème de l’optimisation de la rugosité sur un proces-sus
de fabrication. Le Black Belt a identifié deux facteurs susceptibles
d’améliorer le résultat (la vitesse de coupe et l’avance par tour). L’ana-lyse
technique le conduit à mener une expérience avec 2 niveaux par
facteurs.
268 © Éditions d’Organisation](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-283-320.jpg)













![Six Sigma
Figure 6.21 – Deux stratégies de plans fractionnaires
C
Y4
Y1 Y3
Y2
B
C
Y7
Y6
Y5
Y8
B
A
Un facteur à la fois Stratégie plan d’expériences
A
N° A B C N° A B C
1 1 1 1 5 1 1 1
2 2 2 2 6 1 2 2
3 1 2 1 7 2 1 2
4 1 1 2 8 2 2 1
Dans la première stratégie, on réalise un essai de référence (1) et on
modifie à chaque essai un facteur par rapport à cette référence.
• l’effet du facteur A est calculé par EA = Y2 – Y1
• la variance sur l’effet de A est calculée par
V(EA) = V(Y2) + V(Y1) = 2V(Y)
Dans la seconde stratégie lorsqu’un facteur est placé à un niveau, tous
les autres facteurs sont placés autant de fois au niveau 1 qu’au niveau
2. On dit qu’on a un plan orthogonal. Cette configuration correspond
aux 3 colonnes de la table L4 de Taguchi.
On peut calculer :
• l’effet de A par EA = 1/2[(Y7 + Y8) – (Y6 + Y5)]
• la variance sur l’effet de A
V(EA)=1/4[V(Y7)+V(Y8)+V(Y6)+V(Y5)]=V(Y)
Dans ce cas, la variance sur l’effet de A est deux fois plus faible dans la
stratégie « plan d’expériences » que dans la stratégie « un facteur à la
fois ».
282 © Éditions d’Organisation](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-297-320.jpg)












































































![Six Sigma
Dans la carte EWMA, pour chaque point, on va tenir compte de l’histo-rique
des valeurs mesurées. Pour chaque échantillon, on calcule une
moyenne pondérée par un coefficient λ, telle que :
Mi = λxi + (1 – λ)Mi–1
C’est cette valeur Mi qui apparaît sur la carte EWMA
avec :
• λ ≤ 1 une constante (on prend souvent λ = 0,2)
• M0, valeur initiale = cible
No 1 2 3 4 5 6
Y 0,77 –1,13 1,02 –0,14 2,13 …
M 0,1543 –0,102 0,1226 0,0695 0,4822 …
Par exemple (M0 = 0 ; λ = 0,2) :
• pour le point 1 : M1 = 0,2 × 0,77 + 0,8 × 0 = 0,1543
• pour le point 2 : M2 = 0,2 × (–1,13) + 0,8 × 0,1543 = –0,102
• …
On détectera la présence d’une cause spéciale lorsque Mi franchira une
limite supérieure ou inférieure de contrôle.
Calcul des limites d’une carte EWMA
Les limites sont calculées à ± 3 écarts types de la valeur Mi. On mon-tre
que les limites se calculent par les relations :
avec :
LSCMi
Cible 3σ λ 1– (1 – λ )[ 2i]
= + --------------------------------------
LICMi
Cible–3σ λ[1– (1 – λ )2i]
= --------------------------------------
• i : le numéro de l’échantillon
• σ : l’écart type de la population
n(2 – λ)
n(2 – λ)
358 © Éditions d’Organisation](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-374-320.jpg)
![Étape 5 – Contrôler
• n : la taille de l’échantillon
• λ : le coefficient de pondération
• Cible : la valeur sur laquelle on veut centrer la carte
Les limites dépendent donc du numéro de l’échantillon, mais elles con-vergent
très vite vers une droite comme le montre le graphique de la
figure 7.26. Lorsque i augmente, le terme [1 – (1 – λ)2i] tend vers 1, les
limites deviennent donc :
LSCMi
Cible 3σ λ
= + --------------------
n(2 – λ)
LICMi
Cible–3σ λ
= --------------------
n(2 – λ)
Ces limites sont deux droites qui dépendent du coefficient λ, de la
taille des échantillons n et bien sûr de l’écart type σ.
Ex
Exemple de calcul de limites de contrôle
Dans le cas de l’exemple de la figure 7.26, il s’agit de valeurs
individuelles ; la taille de l’échantillon est donc n = 1. On prend
λ = 0,2 et Cible = 0.
On estime l’écart type à partir de la loi des étendues réduites :
σ R
= -------------
= ------------- = 0,98
1,128
1,11
1,128
LSCMi
Cible 3σ λ
+ -------------------- 0 3 × 0,98 0,2
= = + --------------------- = 0,98
n(2 – λ)
(2 – 0,2)
LICMi
Cible–3σ λ
-------------------- 0–3 × 0,98 0,2
= = --------------------- = –0,98
n(2 – λ)
(2 – 0,2)
© Éditions d’Organisation 359](https://image.slidesharecdn.com/gestionqualit6sigma-141122031404-conversion-gate02/85/Gestion-qualite-6-sigma-375-320.jpg)






























































































































